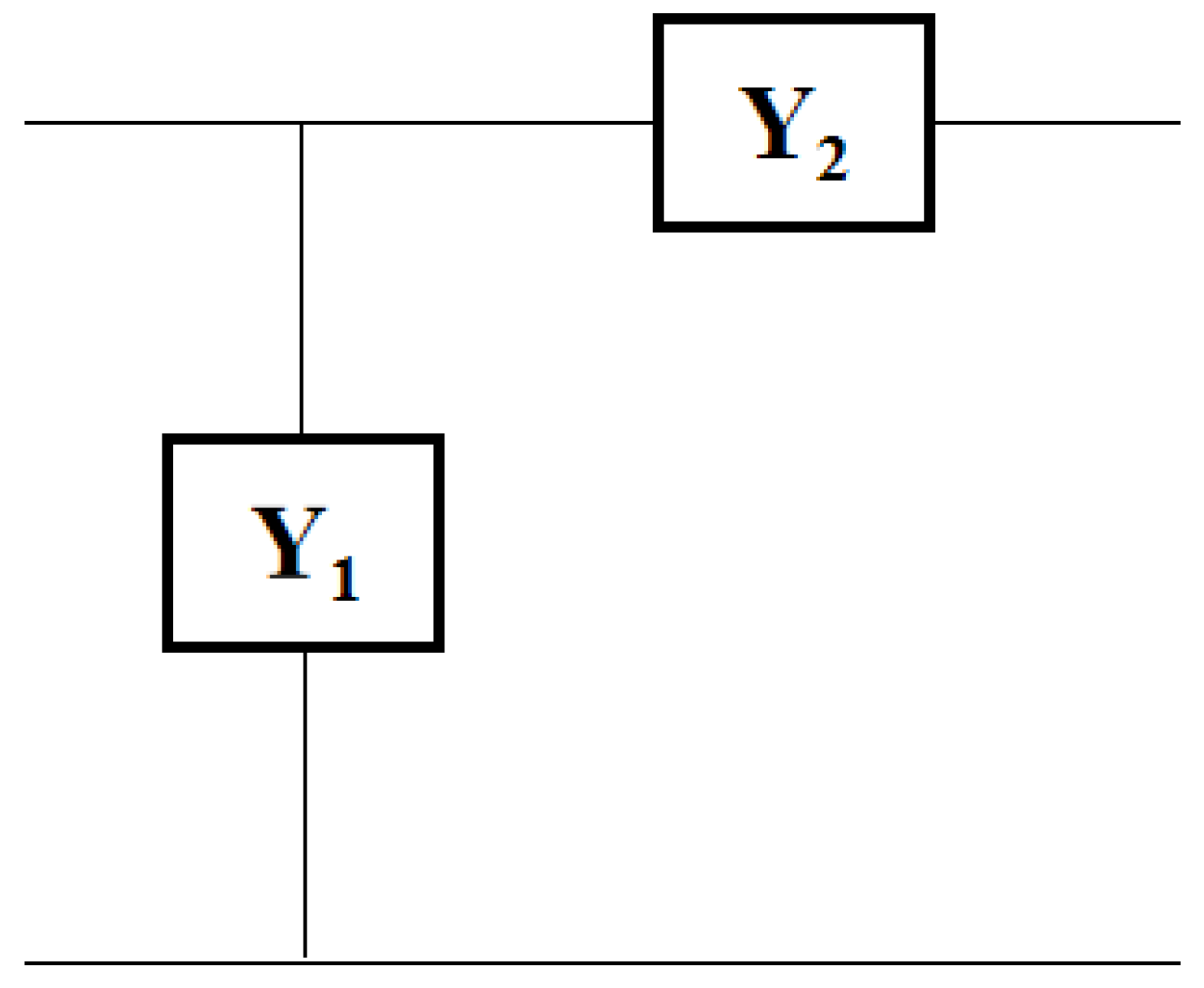
Figure 1.
Negative group delay circuit structure diagram.
Figure 1.
Negative group delay circuit structure diagram.
Figure 2.
Equivalent [ABCD] matrix model.
Figure 2.
Equivalent [ABCD] matrix model.
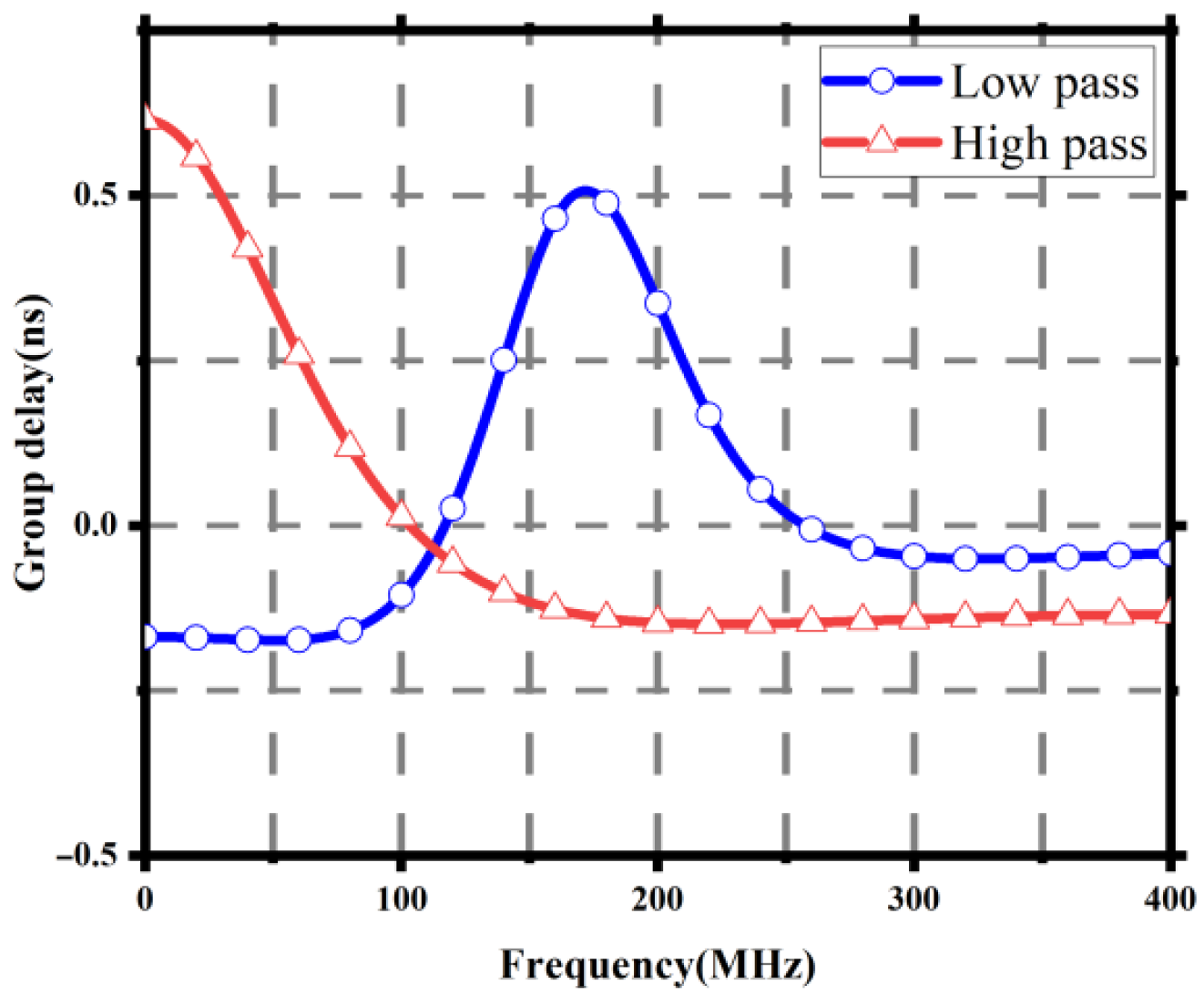
Figure 3.
The group delay result generated by the circuit shown in
Figure 1.
Figure 3.
The group delay result generated by the circuit shown in
Figure 1.
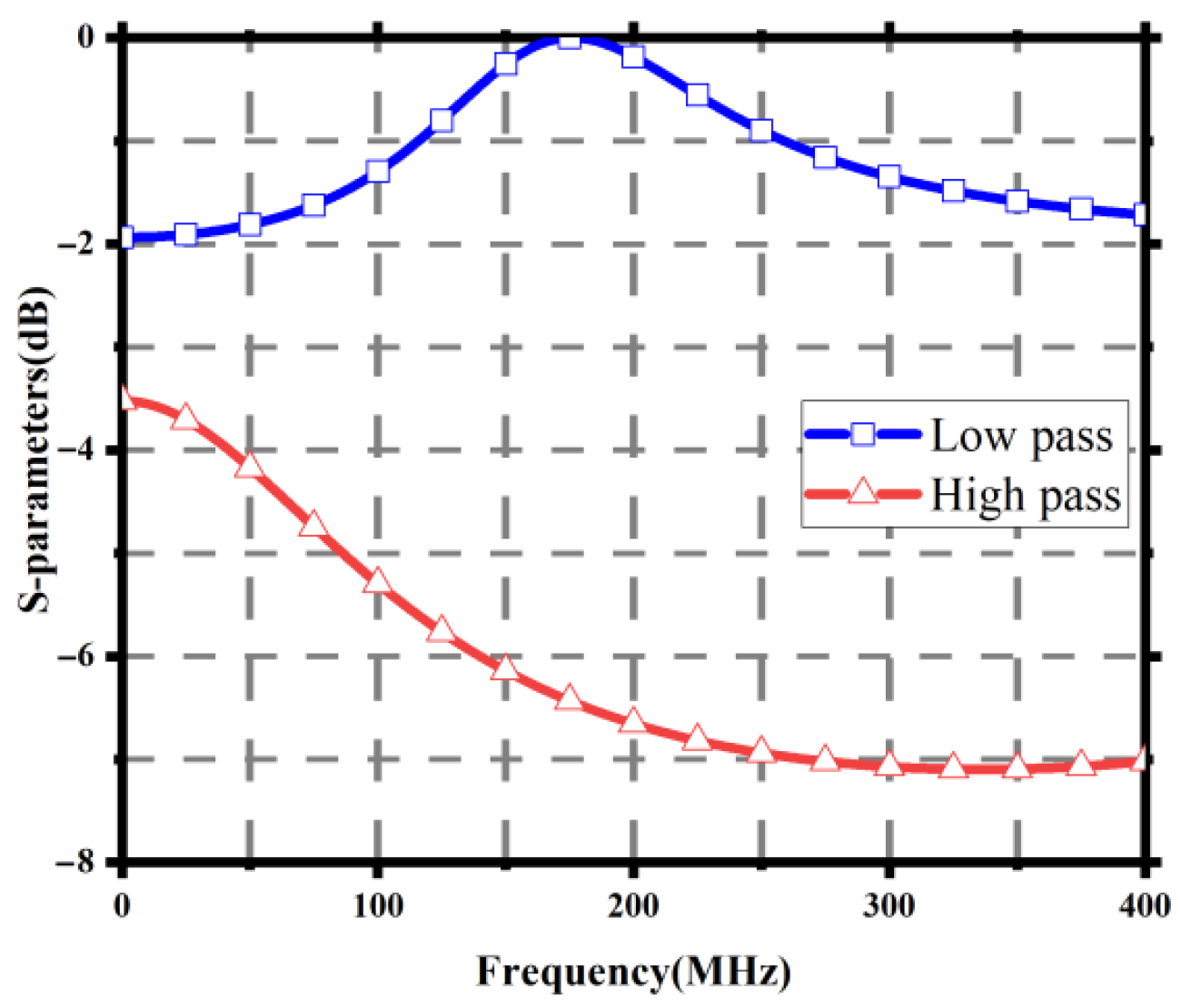
Figure 4.
The
S21 result generated by the circuit shown in
Figure 1.
Figure 4.
The
S21 result generated by the circuit shown in
Figure 1.
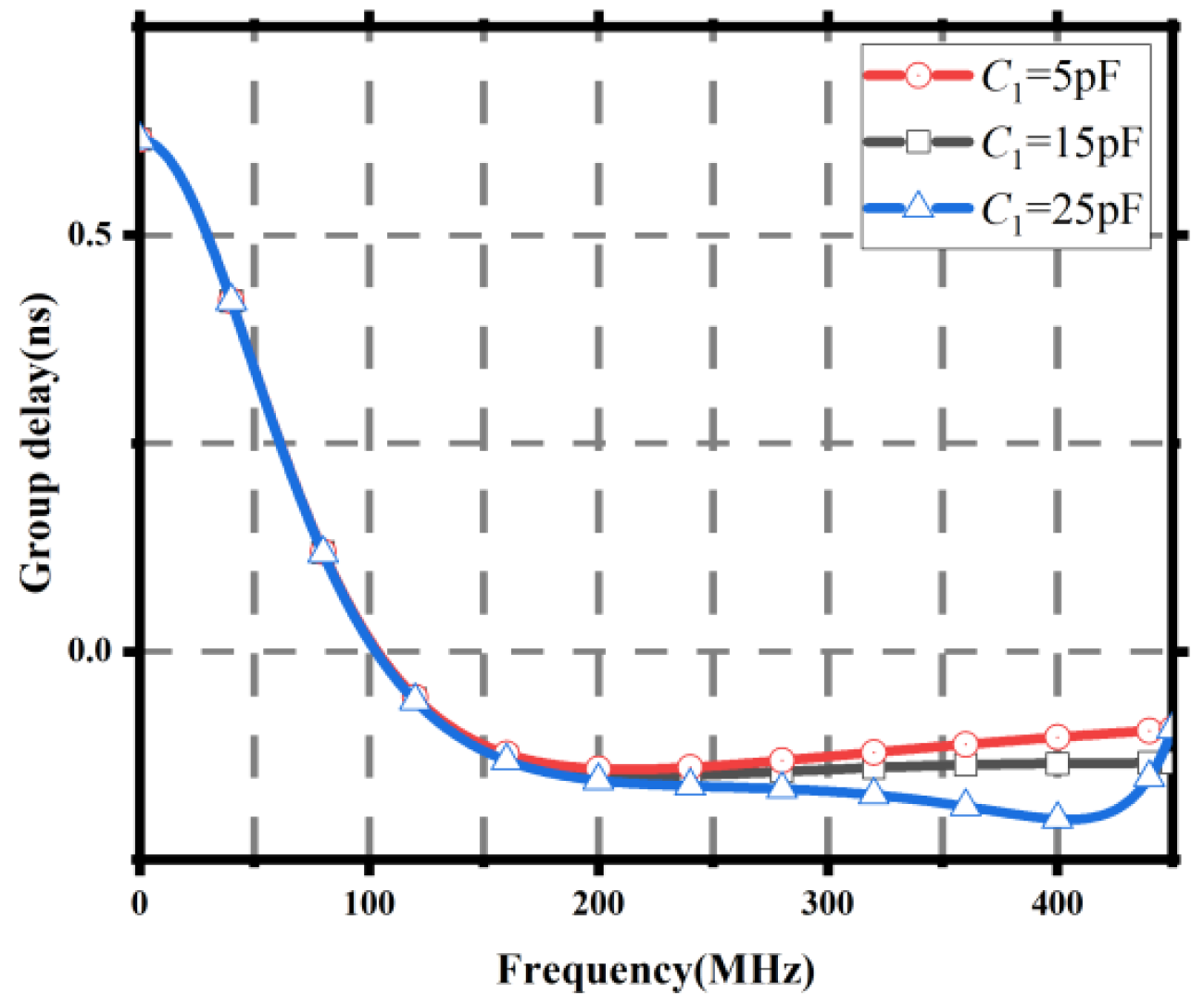
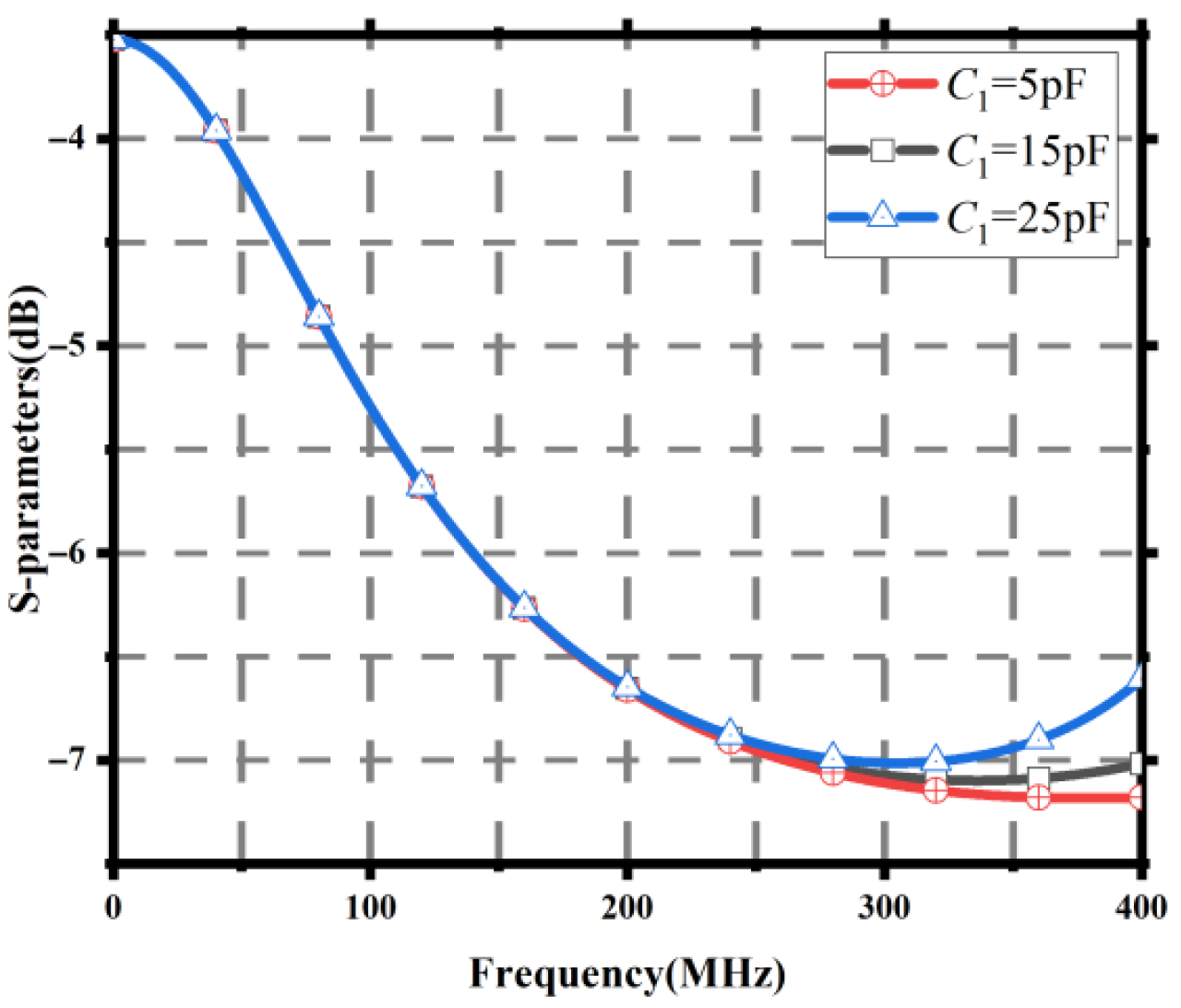
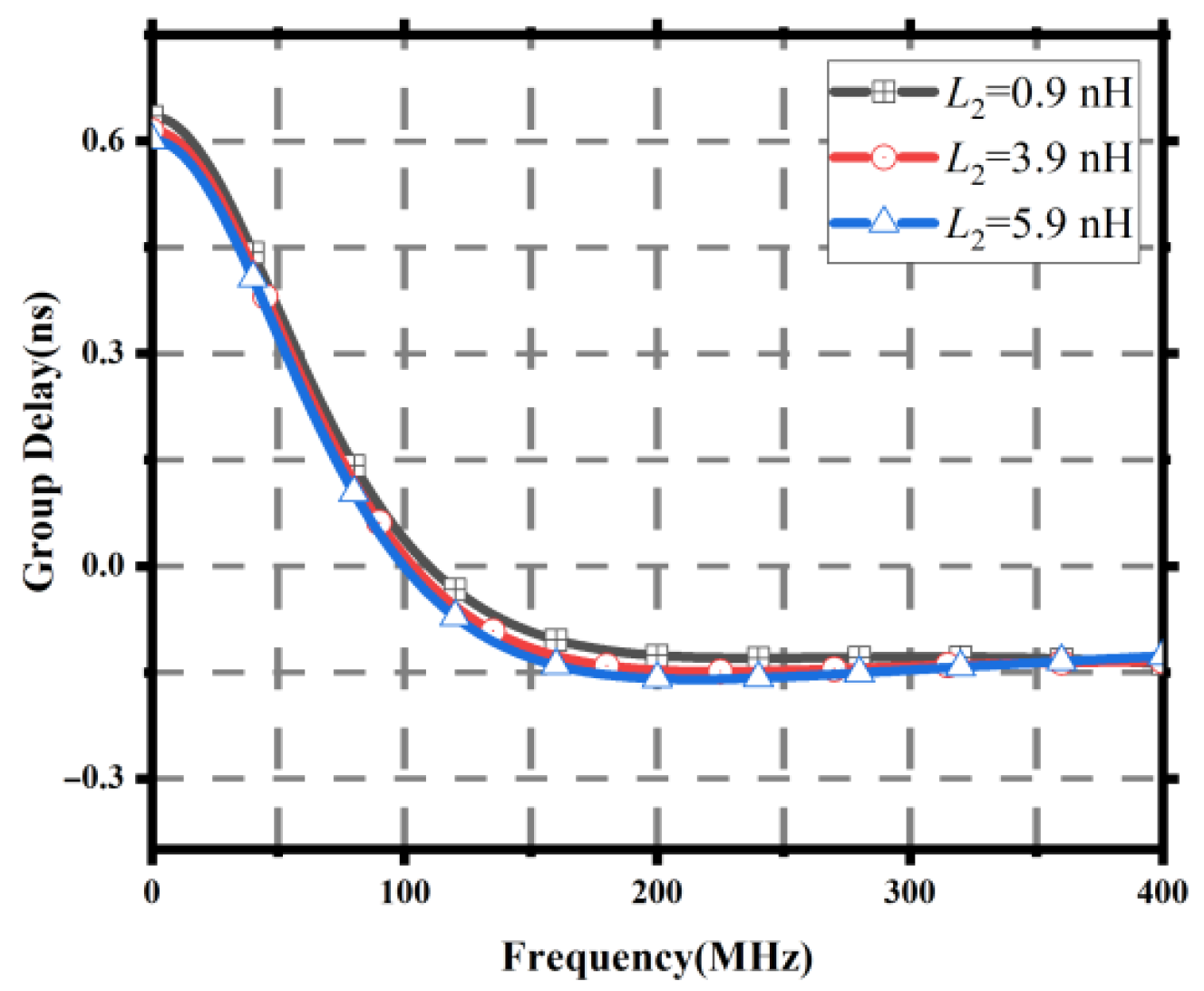
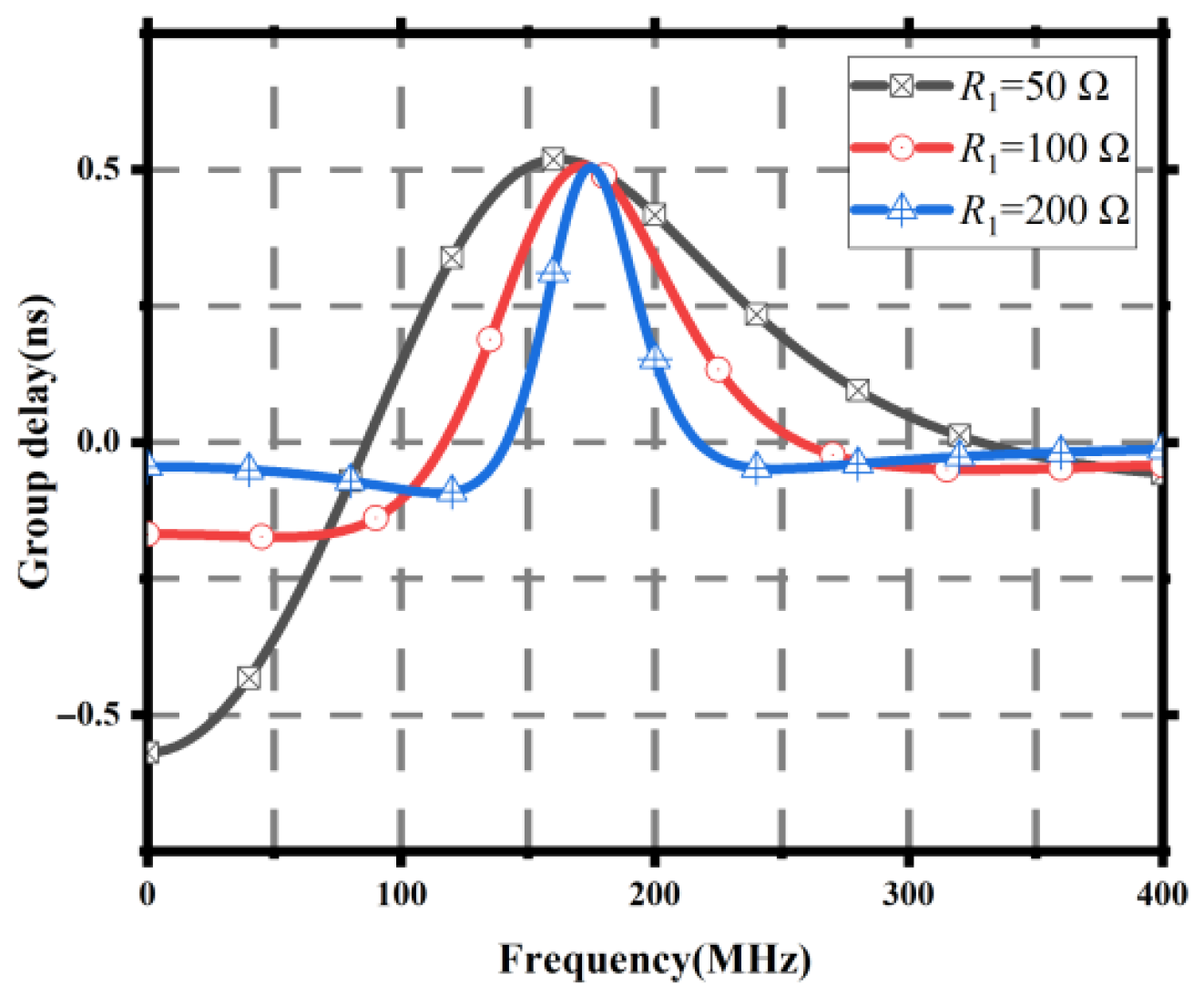
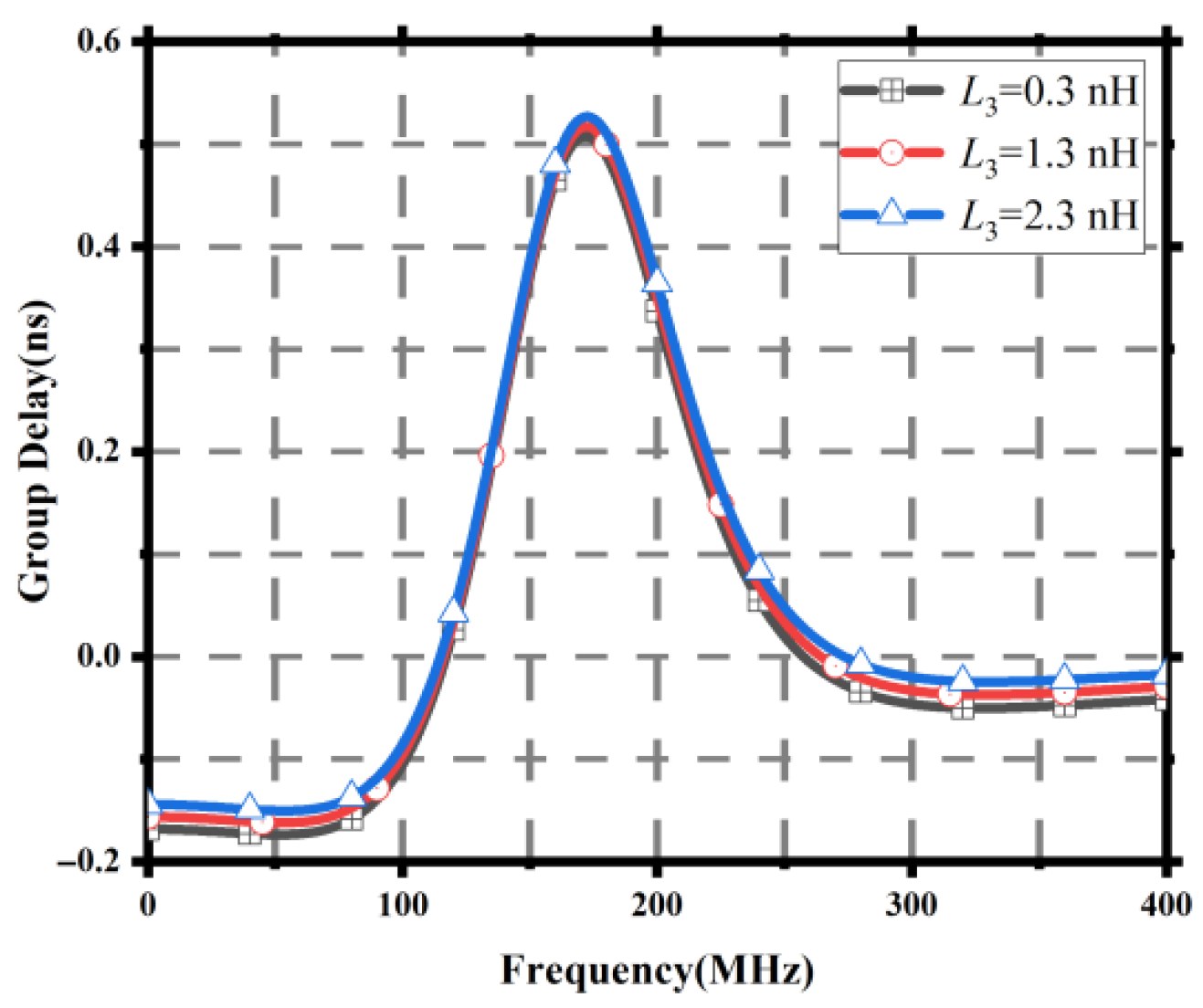
Figure 5.
Group delay results for different 1 values.
Figure 5.
Group delay results for different 1 values.
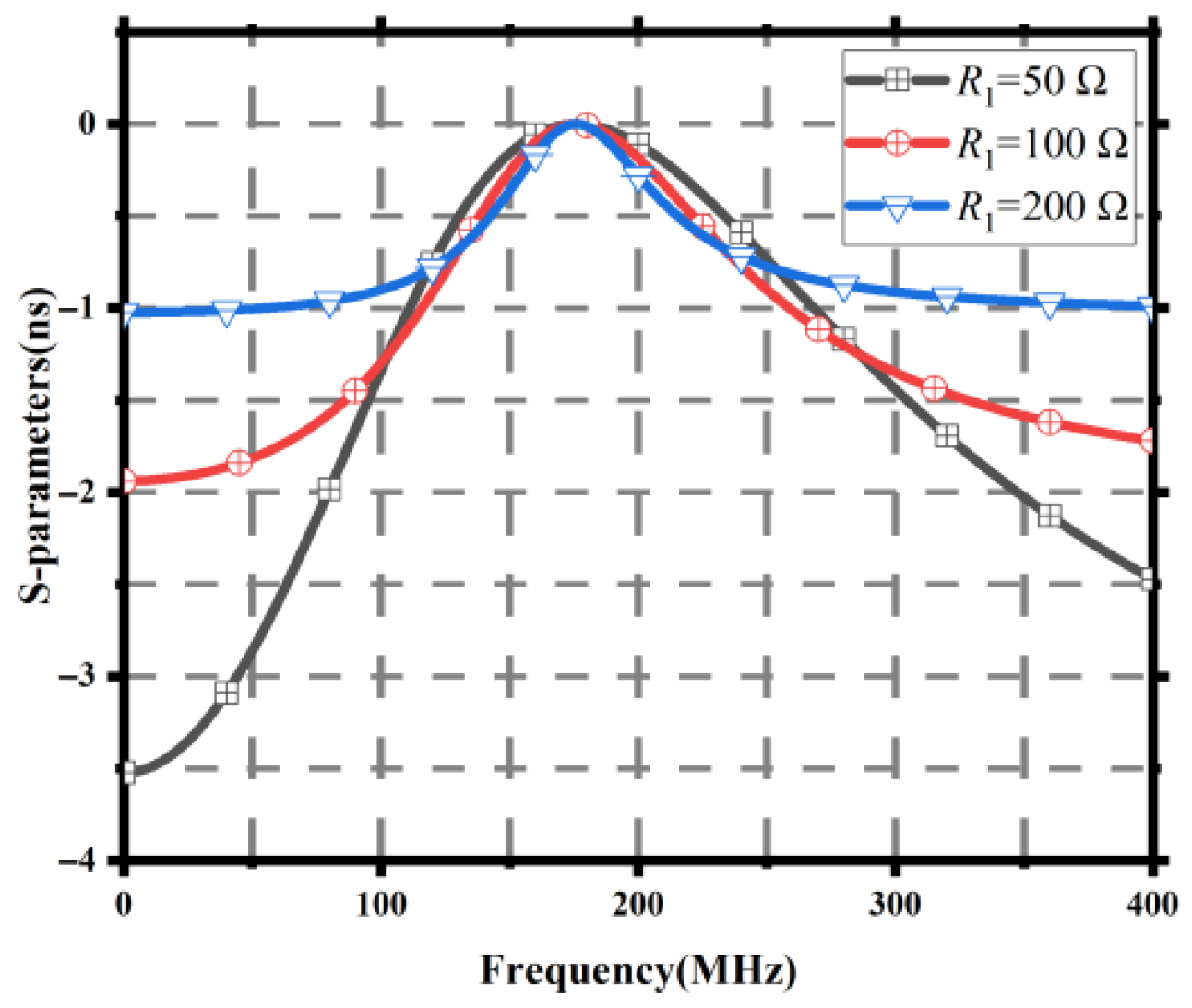
Figure 6.
21 results for different 1 values.
Figure 6.
21 results for different 1 values.
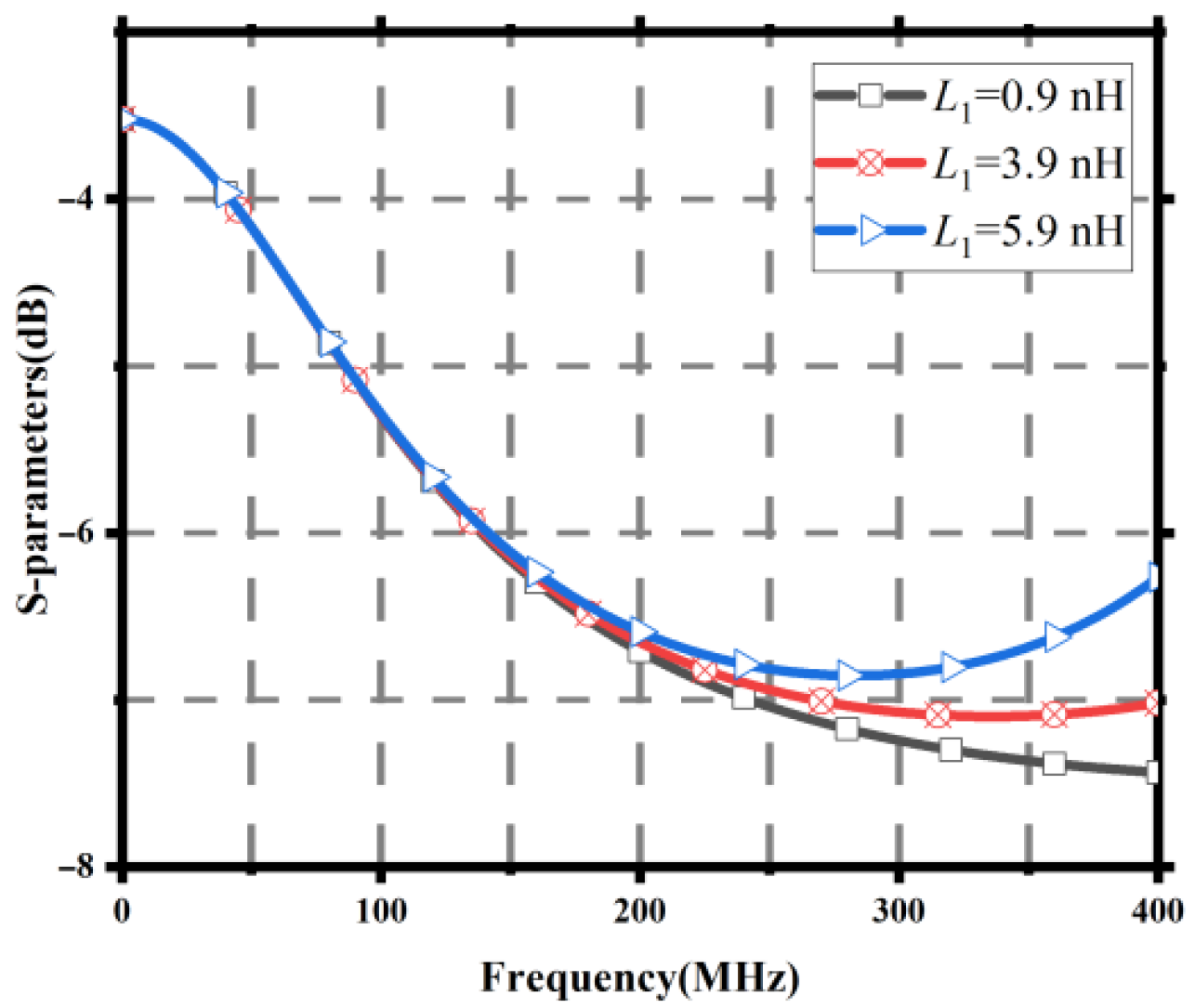
Figure 7.
Group delay results for different 1 values.
Figure 7.
Group delay results for different 1 values.
Figure 8.
21 results for different 1 values.
Figure 8.
21 results for different 1 values.
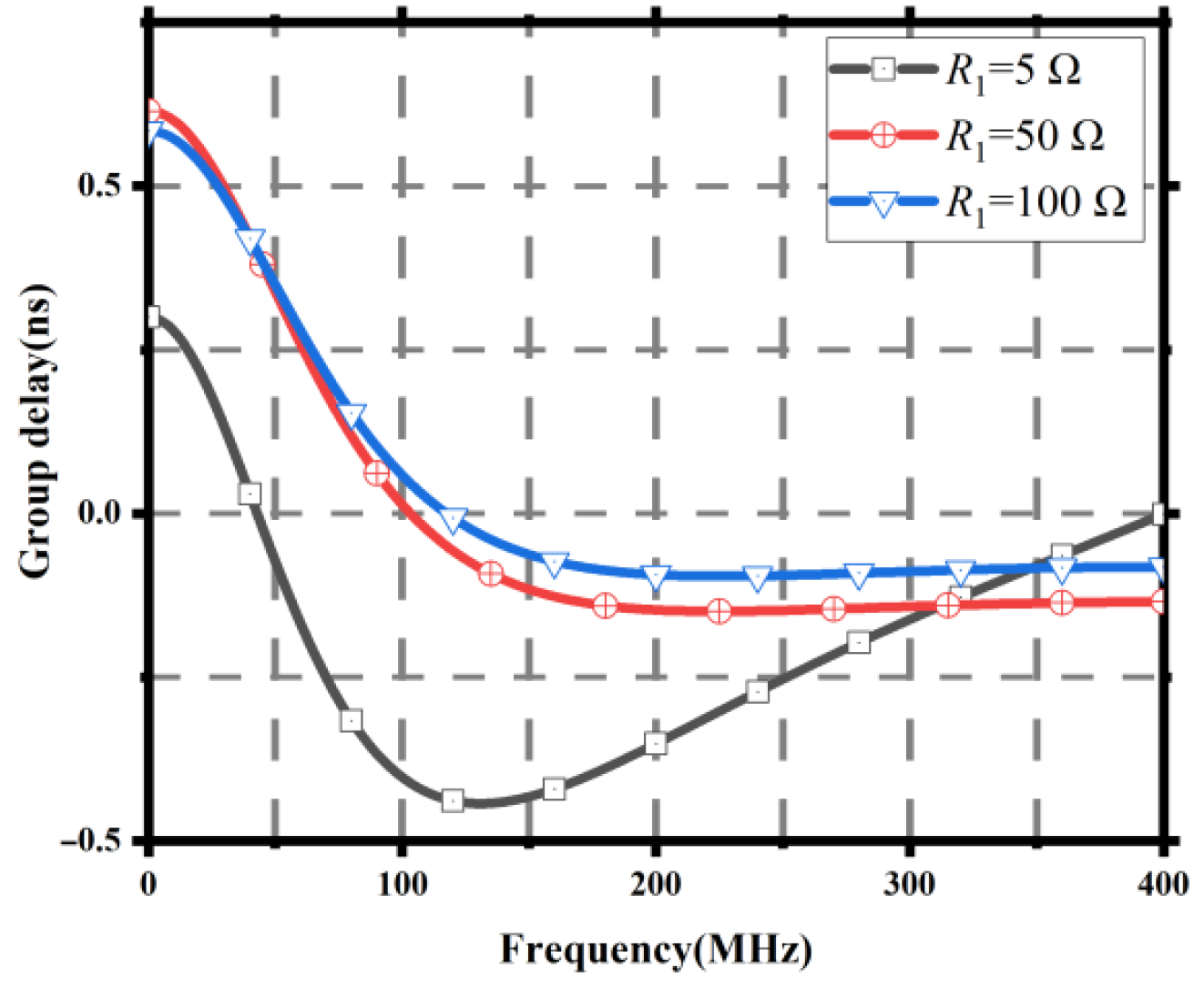
Figure 9.
Group delay results for different 1 values.
Figure 9.
Group delay results for different 1 values.
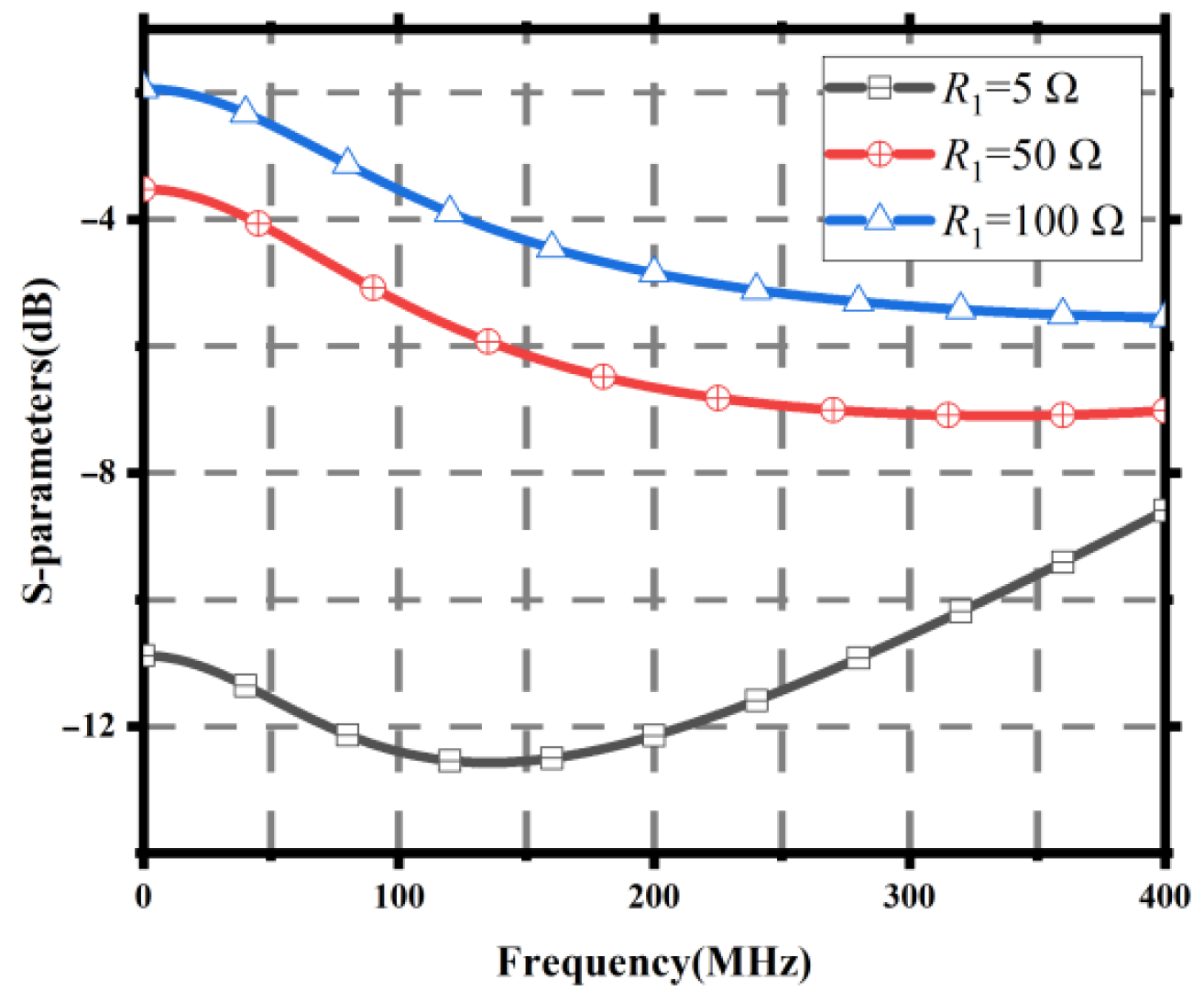
Figure 10.
21 results for different 1 values.
Figure 10.
21 results for different 1 values.
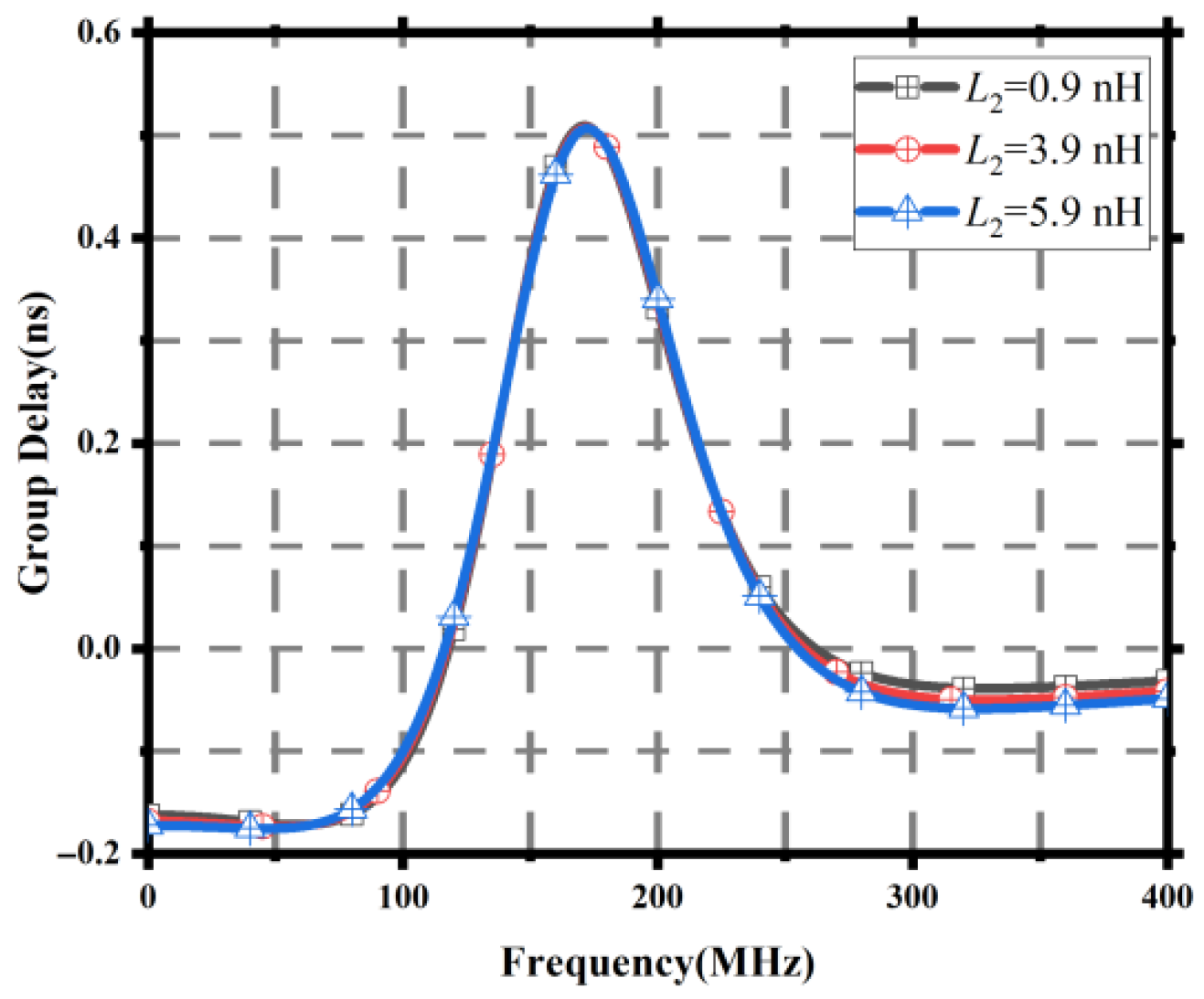
Figure 11.
Group delay results for different 2 values.
Figure 11.
Group delay results for different 2 values.
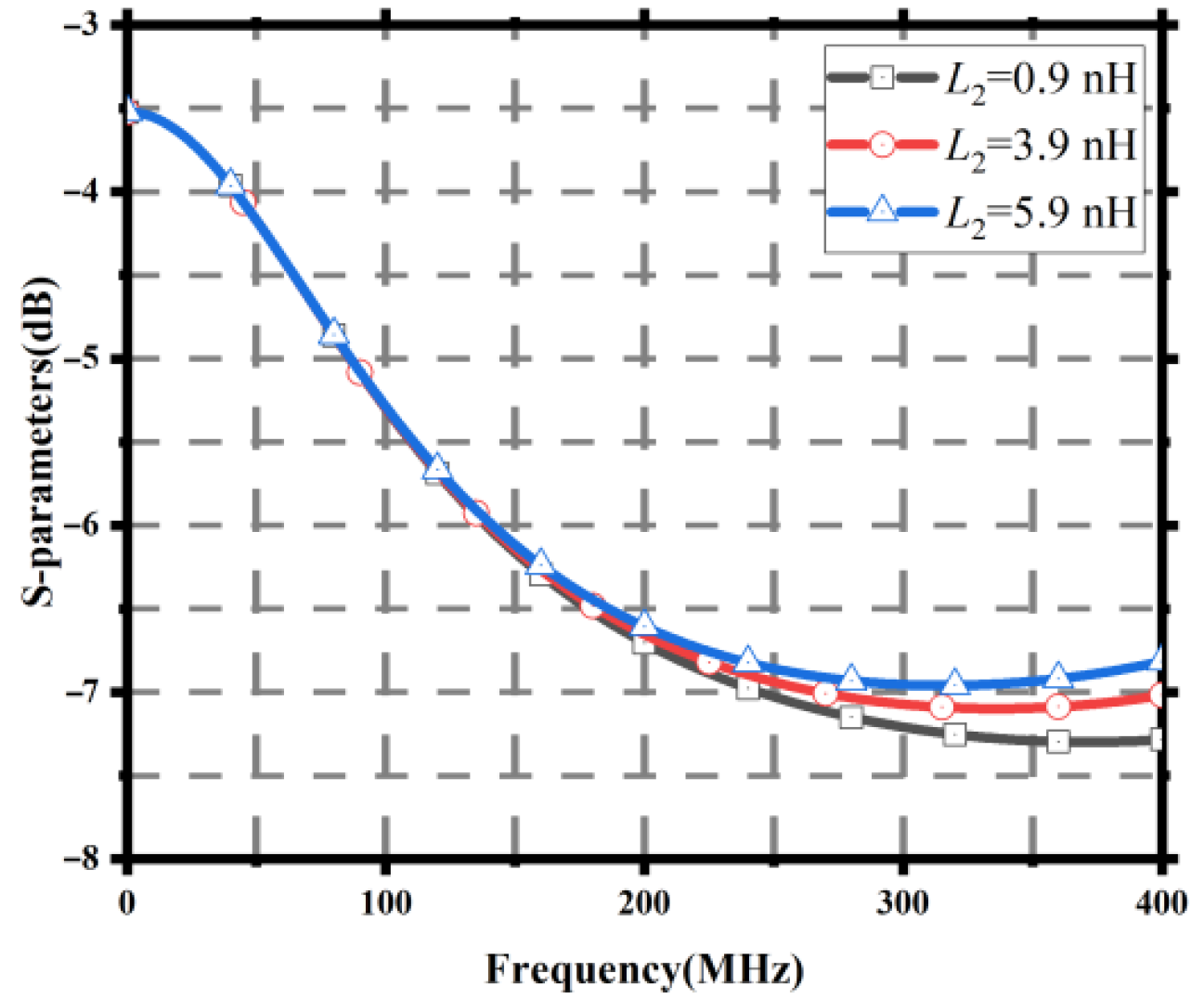
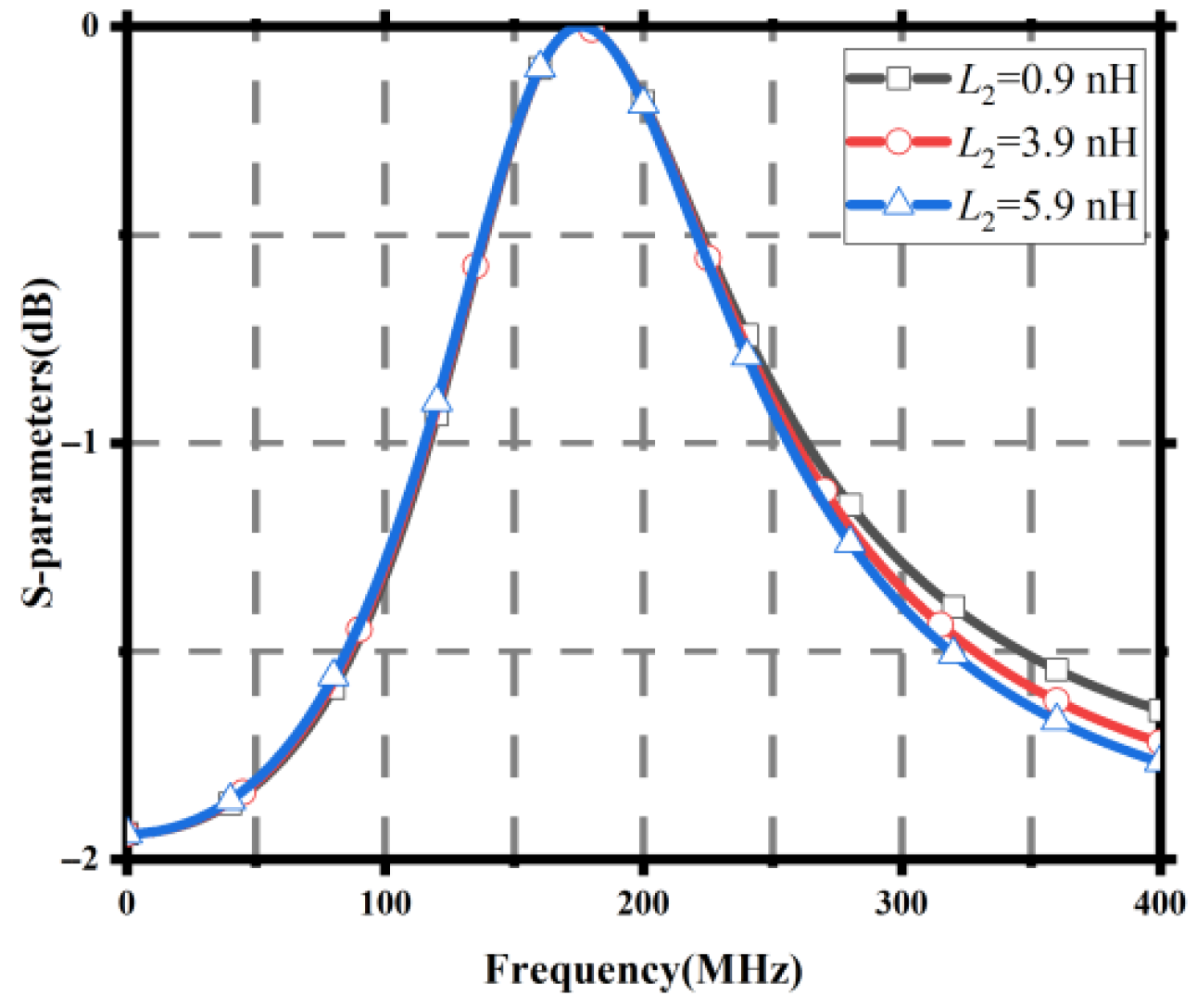
Figure 12.
21 results for different 2 values.
Figure 12.
21 results for different 2 values.
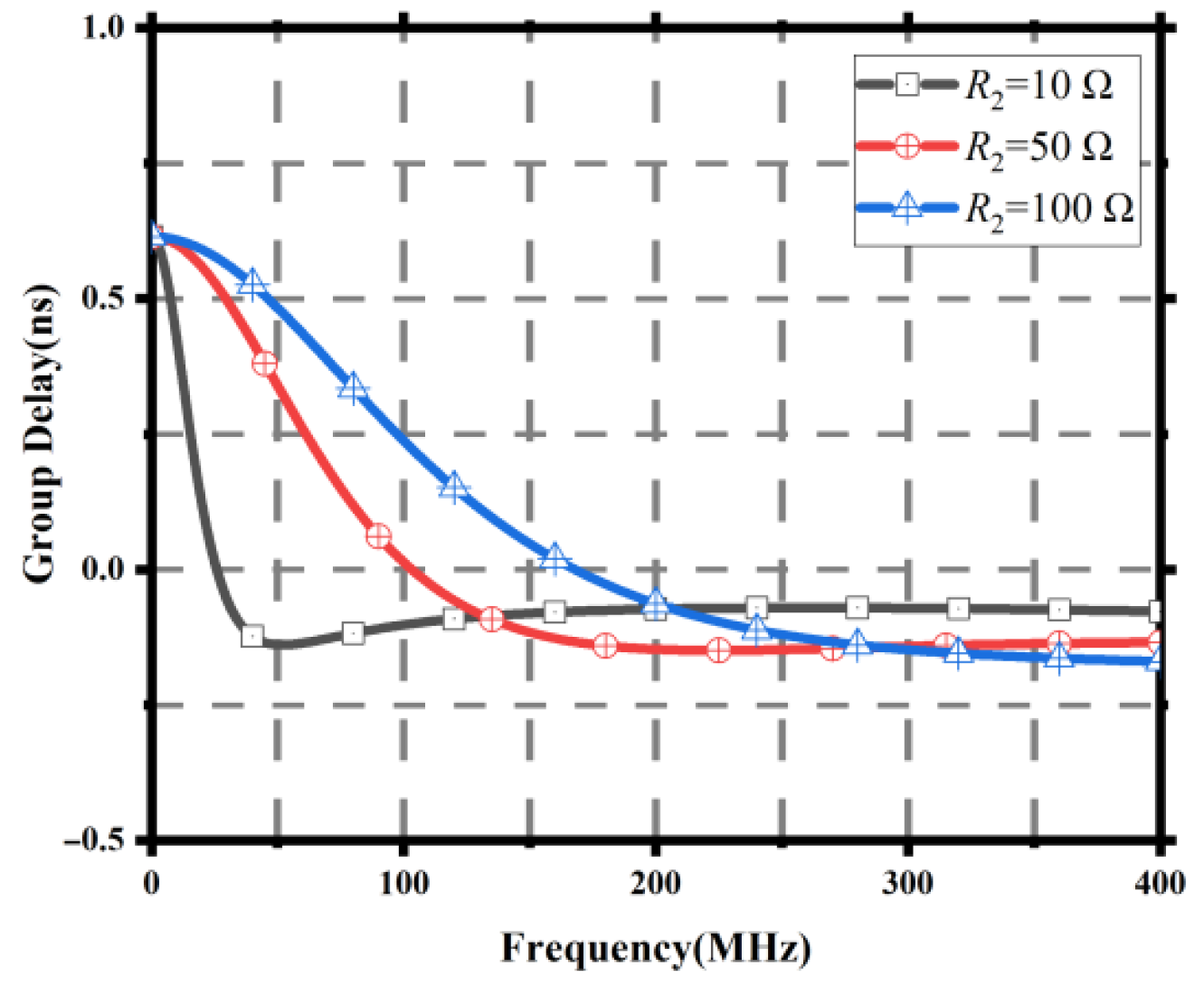
Figure 13.
Group delay results for different 2 values.
Figure 13.
Group delay results for different 2 values.
Figure 14.
21 results for different 2 values.
Figure 14.
21 results for different 2 values.
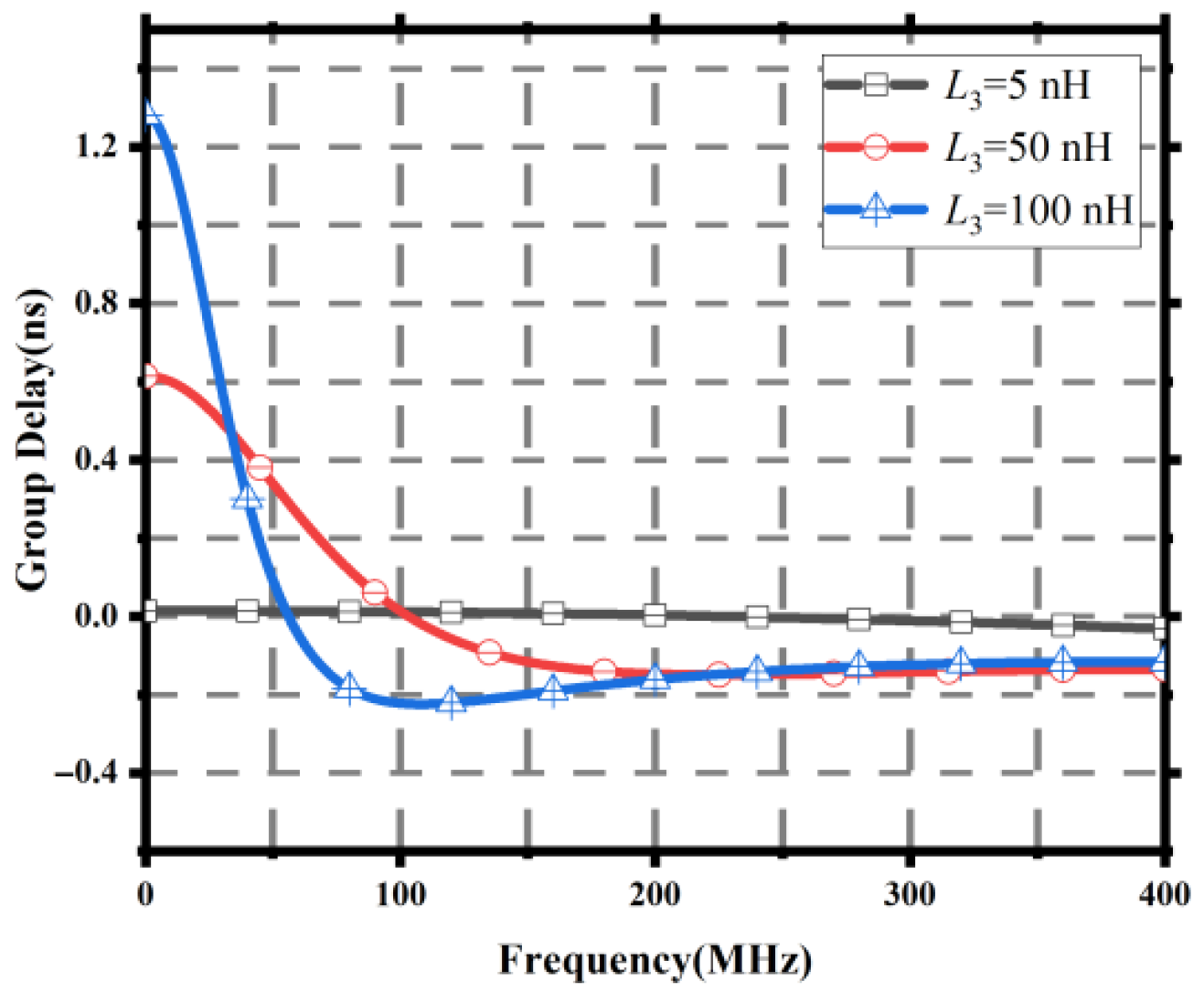
Figure 15.
Group delay results for different 3 values.
Figure 15.
Group delay results for different 3 values.
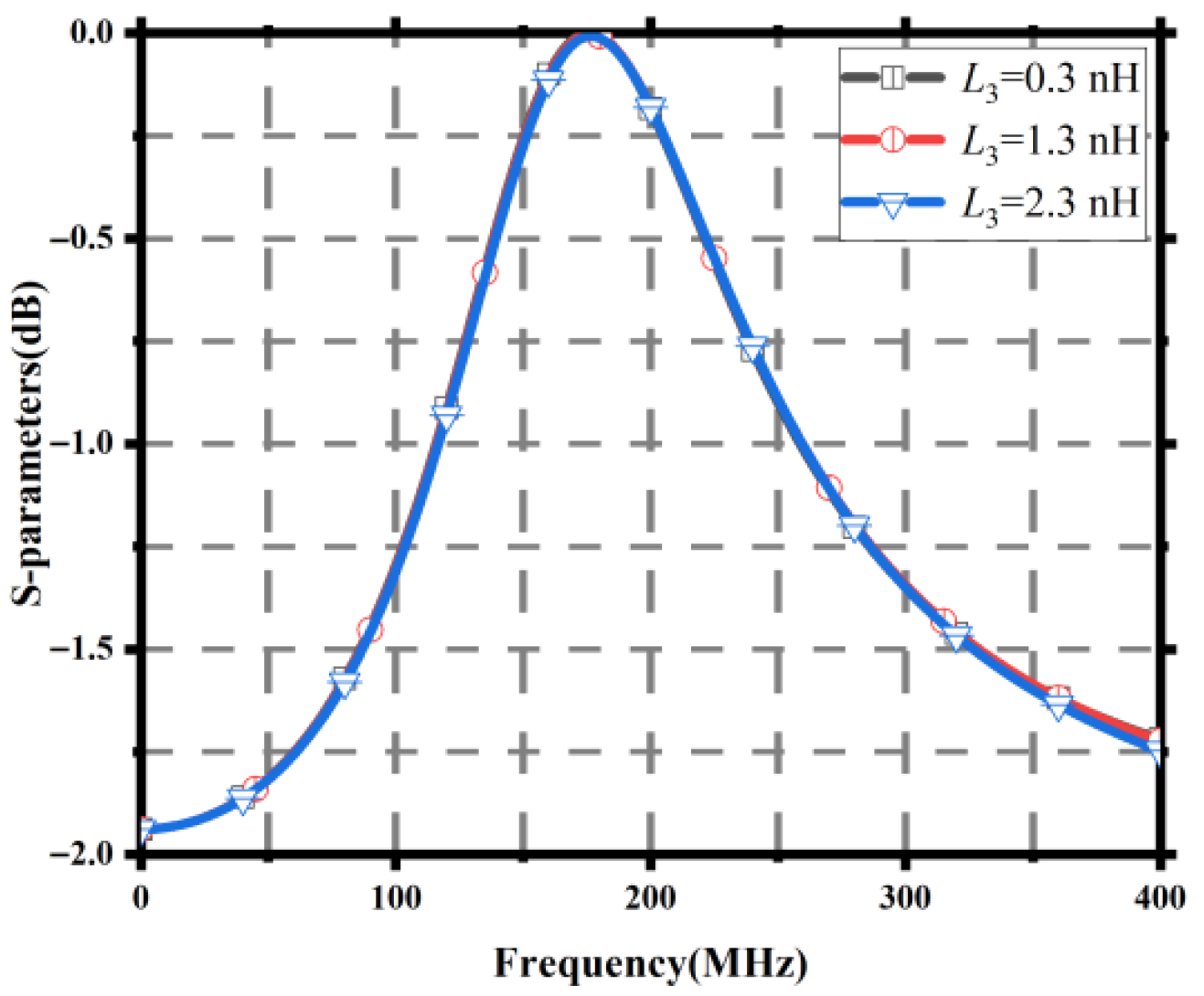
Figure 16.
21 results for different 3 values.
Figure 16.
21 results for different 3 values.
Figure 17.
Group delay results for different 1 values.
Figure 17.
Group delay results for different 1 values.
Figure 18.
21 results for different 1 values.
Figure 18.
21 results for different 1 values.
Figure 19.
Group delay results for different 1 values.
Figure 19.
Group delay results for different 1 values.
Figure 20.
21 results for different 1 values.
Figure 20.
21 results for different 1 values.
Figure 21.
Group delay results for different 1 values.
Figure 21.
Group delay results for different 1 values.
Figure 22.
21 results for different 1 values.
Figure 22.
21 results for different 1 values.
Figure 23.
Group delay results for different 2 values.
Figure 23.
Group delay results for different 2 values.
Figure 24.
21 results for different 2 values.
Figure 24.
21 results for different 2 values.
Figure 25.
Group delay results for different 3 values.
Figure 25.
Group delay results for different 3 values.
Figure 26.
21 results for different 3 values.
Figure 26.
21 results for different 3 values.
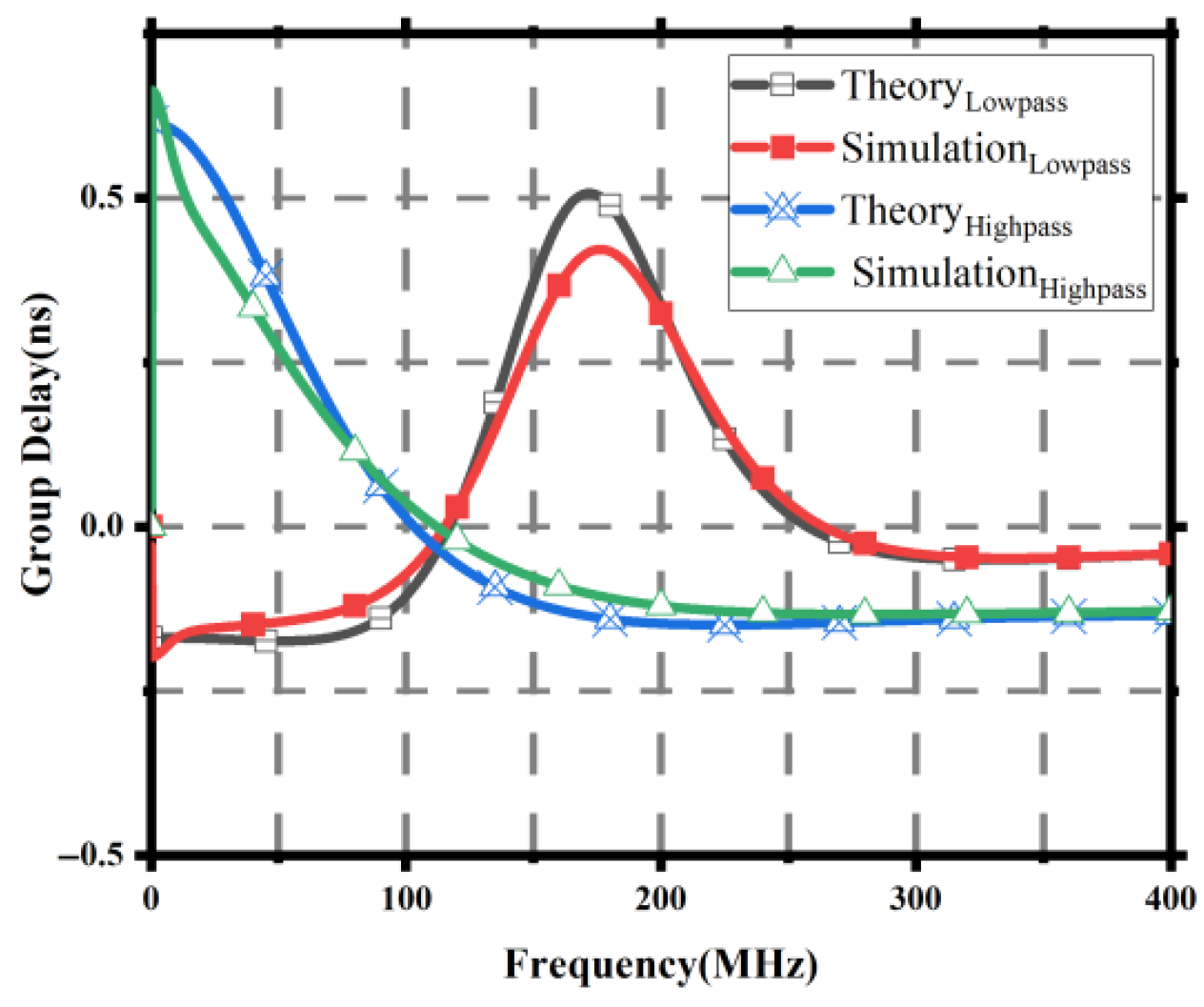
Figure 27.
Theoretical and simulation group delay results.
Figure 27.
Theoretical and simulation group delay results.
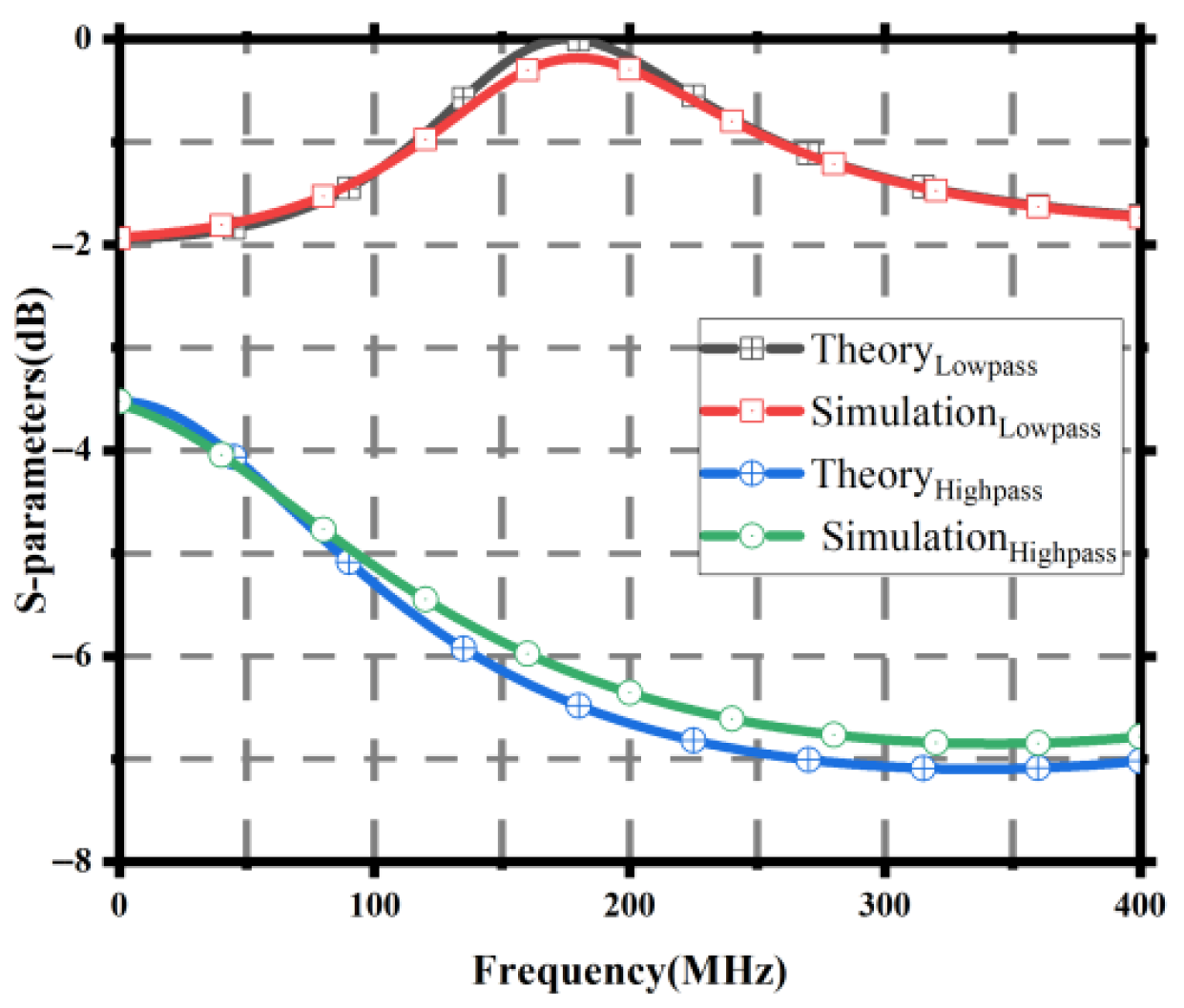
Figure 28.
Theoretical and simulation S21 results.
Figure 28.
Theoretical and simulation S21 results.
Figure 29.
Cluster delay results for 3 with different tolerances.
Figure 29.
Cluster delay results for 3 with different tolerances.
Table 1.
Component values for high-pass flat negative group delay low-loss circuit.
Table 1.
Component values for high-pass flat negative group delay low-loss circuit.
| C1(pF) | L1 (nH) | R1 (Ω) | L2 (nH) | R2 (Ω) | L3 (nH) |
|---|
| 15 | 3.9 | 50 | 3.9 | 50 | 50 |
Table 2.
Circuit results with different 1 values.
Table 2.
Circuit results with different 1 values.
| C1 (pF) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 5 | −0.141 | 102.5 | −7.178 |
| 15 | −0.147 | 302 | −7.098 |
| 25 | −0.154 | 140 | −7.012 |
Table 3.
Circuit results with different 1 values.
Table 3.
Circuit results with different 1 values.
| L1 (nH) | (ns) | FBW (MHz) | IL (dB) |
|---|
| 0.9 | −0.117 | 134.5 | −7.463 |
| 3.9 | −0.147 | 302 | −7.098 |
| 5.9 | −0.172 | 201 | −6.852 |
Table 4.
Circuit results with different 1 values.
Table 4.
Circuit results with different 1 values.
| R1 (Ω) | (ns) | FBW (MHz) | IL (dB) |
|---|
| 10 | −0.443 | 28.5 | −4.59 |
| 50 | −0.147 | 302 | −7.098 |
| 100 | −0.079 | 293 | −12.565 |
Table 5.
Circuit results with different 2 values.
Table 5.
Circuit results with different 2 values.
| L2 (nH) | (ns) | FBW (MHz) | IL (dB) |
|---|
| 0.9 | −0.126 | 225 | −7.729 |
| 3.9 | −0.147 | 302 | −7.098 |
| 5.9 | −0.160 | 127.5 | −6.958 |
Table 6.
Circuit results with different 2 values.
Table 6.
Circuit results with different 2 values.
| R2 (Ω) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 10 | −0.170 | 191.5 | −4.516 |
| 50 | −0.147 | 302 | −7.098 |
| 100 | −0.139 | 25 | −8.734 |
Table 7.
Circuit results with different 3 values.
Table 7.
Circuit results with different 3 values.
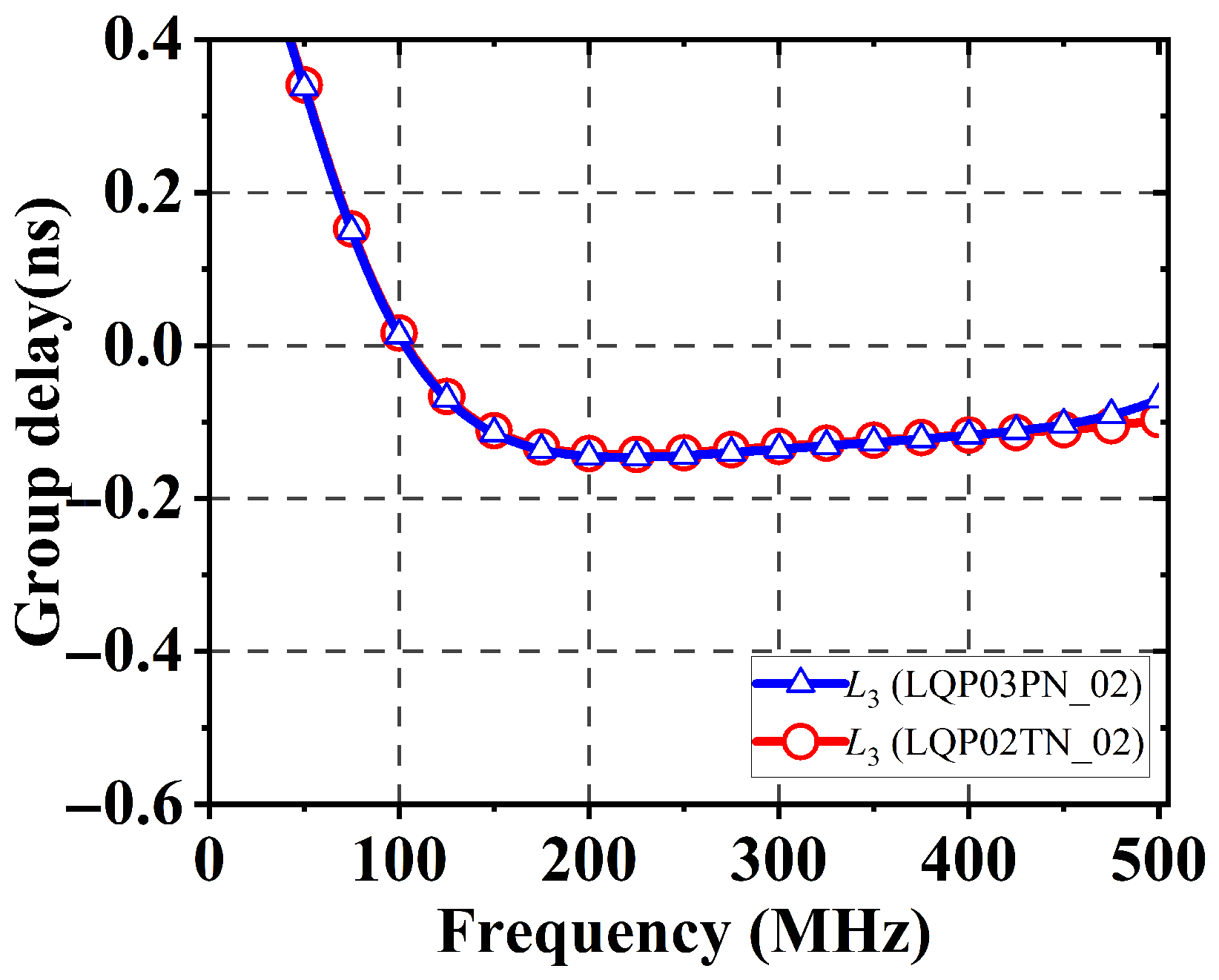
| L3 (nH) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 5 | +0.134 | / | −3.577 |
| 50 | −0.147 | 302 | −7.098 |
| 100 | −0.224 | 35.5 | −7.536 |
Table 8.
Component values for low-pass flat negative group delay low-loss circuit.
Table 8.
Component values for low-pass flat negative group delay low-loss circuit.
| C1 (pF) | L1 (nH) | R1 (Ω) | L2 (nH) | R2 (Ω) | L3 (nH) |
|---|
| 10 | 82 | 100 | 3.9 | 100 | 0.3 |
Table 9.
Circuit results with different 1 values.
Table 9.
Circuit results with different 1 values.
| C1 (pF) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 5 | −0.149 | 61 | −1.938 |
| 10 | −0.168 | 85.5 | −1.938 |
| 15 | −0.199 | 43.5 | −1.938 |
Table 10.
Circuit results with different 1 values.
Table 10.
Circuit results with different 1 values.
| L1 (nH) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 20 | −0.044 | 158.5 | −1.938 |
| 82 | −0.168 | 85.5 | −1.938 |
| 160 | −0.324 | 26 | −1.938 |
Table 11.
Circuit results with different 1 values.
Table 11.
Circuit results with different 1 values.
| R1 (Ω) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 50 | −0.569 | 16 | −3.522 |
| 100 | −0.168 | 85.5 | −1.938 |
| 200 | −0.044 | 71 | −1.023 |
Table 12.
Circuit results with different 2 values.
Table 12.
Circuit results with different 2 values.
| L2 (nH) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 0.9 | −0.162 | 84 | −1.938 |
| 3.9 | −0.168 | 85.5 | −1.938 |
| 5.9 | −0.172 | 86.5 | −1.938 |
Table 13.
Circuit results with different 3 values.
Table 13.
Circuit results with different 3 values.
| L2 (nH) | τ (ns) | FBW (MHz) | IL (dB) |
|---|
| 0.3 | −0.168 | 85.5 | −1.938 |
| 1.3 | −0.156 | 85.5 | −1.938 |
| 2.3 | −0.144 | 85.5 | −1.938 |
Table 14.
High-pass circuit theory and simulation results.
Table 14.
High-pass circuit theory and simulation results.
| | τ (ns) | FBW (MHz) | IL (dB) | GD Ripple |
|---|
| Theory | −0.147 | 302 | −7.098 | 5.53% |
| Simulation | −0.131 | 295.5 | −6.851 | 2.19% |
Table 15.
Low-pass circuit theory and simulation results.
Table 15.
Low-pass circuit theory and simulation results.
| | τ (ns) | FBW (MHz) | IL (dB) | GD Ripple |
|---|
| Theory | −0.168 | 85.5 | −1.938 | 1.67% |
| Simulation | −0.160 | 43.5 | −1.938 | 3.44% |
Table 16.
Comparison with other studies.
Table 16.
Comparison with other studies.
| Ref. | IL (dB) | τ (ns) | NBW (MHz) | Relatively FBW | GD Ripple |
|---|
| [7] | 14 | −0.2 | 310 | 9.3% | 20% |
| [10] | 16.6 | −0.49 | 550 | 14.7% | 8% |
| [18] | 9.75 | −1.11 | - | 6.1% | 11.5% |
| [20] | 40 | | | - | 0% |
This work
(high) | 6.833 | −0.147 | 469 | 169% | 5.53% |
| This work (low) | 1.76 | −0.168 | 120 | 133% | 1.67% |