Design and Hardware Implementation of a Highly Flexible PRNG System for NIST-Validated Pseudorandom Sequences

Abstract

This work presents the design of a system of a highly flexible pseudorandom number generator system (PRNG) incorporating both conventional and neuro-generators. The system integrates four internal generators with different conditions to produce new output sequences with adequate bits distribution and complexity. Two generators function at a frequency of 100 MHz with adjustable frequency settings, while two neuro-generators employ impulse neurons with distinct behaviours at 4 kHz, also modifiable. The proposed system meets 12 statistical randomness standards based on NIST’s (National Institute of Standards and Technology of U. S.) test suite, including the Frequency test, Binary Matrix Rank test, Linear Complexity test, and Random Excursion test, among others. Each resulted in a P-value greater than 0.01, confirming the pseudo-randomness of the generated sequences. The system is implemented on a reconfigurable device FPGA (Field Programmable Gate Array), with a low occupancy percentage, demonstrating its feasibility for various applications.

1. Introduction

Random numbers are widely used in a variety of applications, including statistics, computer programming, video games, numeric analysis, and cryptography, among others [1,2,3]. Random numbers can be obtained from random sequences produced by random number generators (RNGs) [1]. The quality of an RNG is determined by its ability to produce sequences with good statistical properties, minimal predictability, and uniform digit distribution [4,5,6,7].

The development of random number generation methods dates back to the 1940s, with contributions from Von Neumann, Metropolis, Ulam, and Lehmer. They pioneered the Monte Carlo simulation method [8,9,10], which was published by N. Metropolis and Stanislaw M. Ulam in 1949 [9,11]. The method estimates outcomes in unpredictable events across multiple fields, including sales forecasting, integral approximations, sampling experiments, and artificial intelligence [12,13,14,15]. The Monte Carlo method is based on sequences of pseudorandom numbers, where a set of results is predicted in an estimated range of values, building a model with possible results [12,13,14,15]. However, unlike random numbers, pseudorandom numbers are deterministic, meaning their sequences eventually repeat [6,7]. Thus, pseudorandom numbers must meet specific statistical criteria to ensure unpredictability, e.g., the random appearance of the length and uniformly distributed bits [6,7]. Some applications of pseudorandom sequences include cryptography, financial models, communications, artificial intelligence, etc., [6,7,16,17].

Random Number Generators (RNGs) and Pseudorandom Number Generators (PRNGs)

Various types of random number and pseudorandom number generators (RNGs and PRNGs) have been designed. Examples of RNGs are the QRNG (Quantum Random Generator) and the TRNG (True Random Generator) [18,19,20], which use physical variables, such as electronic noise from electronic circuits, biological signals, and quantum processes (e.g., semiconductors) [18,19,20]. 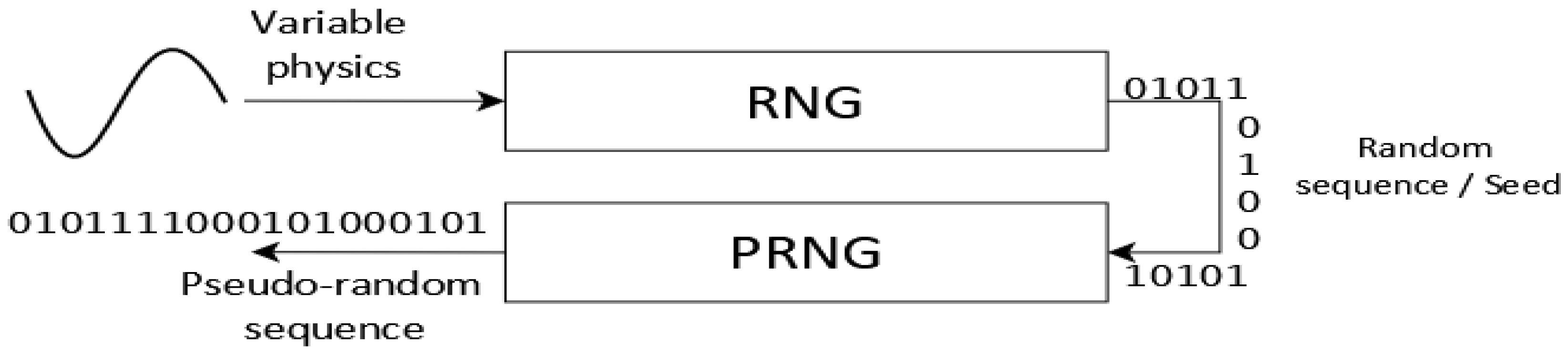The quality of the generators depends on the concordance between their output properties and those of a process of generating uniform and independent data [21]. The goal is to ensure that the random number sequences meet the necessary characteristics for various applications, such as generating initial data or seed data for a PRNG, as shown in Figure 1. From the seed data, the PRNG is initialized to produce a new pseudorandom sequence [4].

PRNGs use deterministic algorithms to generate sequences, ensuring uniformity and independence [22]. A common method is the Linear Congruential Generator (LCG) invented by D. H. Lehmer, defined by the recursive relation in Equation (1), where each number is computed as a function of the previous number. $X_0$ is defined as the seed ($X_0$ $>0$), a is the constant multiplier ($a>0$), $c$ is the active constant (c > 0), and m is the modulus ($m>X_0, m>a y m>c$). According to the recursive relation, $X_{n+1}$ is the remainder when dividing $aXn+c$ by the modulus [22,23,24,25,26,27].

$$X_{n+1}=\left(aXn+c\right)mod m$$

(1)

Another widely used PRNG method is the Linear Feedback Shift Register (LFSR), which employs storage registers that shift bits in response to clock pulses, generating pseudorandom sequences. Each register cell stores a bit that is shifted one position to the right for each clock pulse [28,29,30,31,32,33]. This component is often used in generators for stream encryption due to the flexibility of hardware implementation. Additionally, the register’s statistical properties [28,29,30,31,32,33] allow it to be used for the design of news generators.

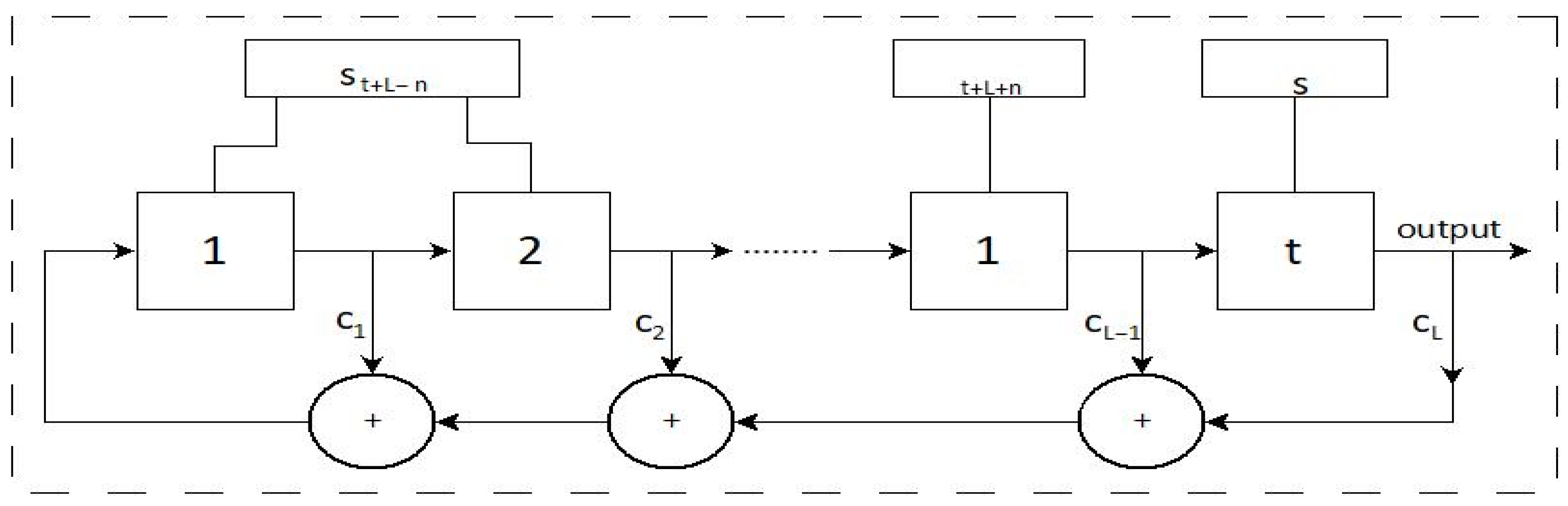
Every time a shift to the right occurs in the LFSR, a cell in the register becomes empty, allowing a new bit to be stored in the vacant position [28,29,30,31,32,33]. Feedback is a linear feedback function, as shown in Equation (2). In an LFSR of length L over $F_q$, the system functions as a finite state automaton that generates a semi-infinite sequence of elements of $F_q$, denoted $s=(s_t{)}_{t\ge 0}=s_0{s}_{1\dots .}$, which satisfies a linear recurrence relation of degree L over $F_q$ [28,29,30,31,32,33]. The coefficients of L $c_1, \dots , c_L$ are elements of $F_q$ and are referred to as feedback coefficients of the LFSR; Figure 2 illustrates an LFSR representing this concept [28].

$$s_{t+L}={\sum }_{i=1}^L{c}_1{s}_{t+L-i}, \forall t\ge 0$$

(2)

Some recent PRNG generator designs include the one proposed in [34], which uses multiple LFSRs to produce 16-bit pseudorandom numbers at 50 kHz and ambient electromagnetic noise to generate the generator seeds [34]. Thus, the efficiency of LFSRs in the design of pseudorandom number generators for different applications is once again confirmed. Another is proposed by [35], which consists of a generator called a multi-PRNG. This generator produces multiple pseudorandom number streams. A multi-PRNG is implemented using a field programmable gate array FPGA, based on a chaotic multi-scroll memristive Hopfield neural network (MHNN) [35]. The objective is to produce multiple spatially dependent PRNG streams from the chaotic multi-scroll system. Each multiple shift produced functions as an independent PRNG [35].

All random and pseudorandom number generators must be validated through statistical tests to determine whether the sequences they produce exhibit randomness or pseudo-randomness. Examples include the Diehard tests and the NIST statistical tests [36,37,38,39], which consist of 15 tests proposed by the National Institute of Standards and Technology to evaluate the RNG or PRNG generator sequences. Some of the tests include the Frequency (Monobit) test [37,40,41], which ensures that the sequence contains approximately equal proportions of zeros and ones with uniform a distribution [37,40], the Frequency within a Block test, which examine the proportion of ones within M-bits bocks [37,40,42], the Runs test, which evaluates the total number of runs (uninterrupted by identical) in the entire sequence [37,40,43], the Binary Matrix Rank test, which checks the linear dependence between fixed length substrings of the original sequence [36,37,40,44], the Maurer’s Universal Statistical test, which measures the number of bits between matching patterns to determine whether the sequence can be compressed without losing information [37,40,45], the Linear Complexity test, which assesses whether the sequence is complex enough to be considered random [37,40,46,47], the Cumulative Sums (Cusums), which analyzes the maximum deviation from zero in a random walk defined by the cumulative sum, where sequence digits are adjusted to −1 and +1 [37,40,48], the Random Excursion test, which determine the number of K visit cycles in a cumulative random walk [37,40,48], and the Random Excursion Variant test, which examines the total number of times a particular state is visited in a sequence [37,40,48]. These statistical tests help validate the quality of RNG and PRNG sequences, ensuring their suitability for cryptographic, simulation, and other applications.

Each test in the suite evaluates pseudo-randomness independently, calculating the P-value, as shown in

Table 1. P-value equations of each test proposed by the NIST.

Test	Equation
Frequency (Monobit)	$P\text{-}value=erfc\left({\displaystyle \frac{S_{obs}}{\sqrt{2}}}\right)$
Frequency within a Block	$P\text{-}value=igmc({\displaystyle \frac{N}{2}}, {\displaystyle \frac{{X^2}_{\left(obs\right)}}{2}})$
Runs	$P\text{-}value=erfc\left({\displaystyle \frac{\left|V_n\left(obs\right)-2n\pi (1-\pi )\right|}{2\sqrt{2n\pi (1-\pi )}}}\right)$
Longest-Run-of-Ones in a Block	$P\text{-}value=igamc({\displaystyle \frac{K}{2}}, {\displaystyle \frac{{X^2}_{\left(obs\right)}}{2}})$
Binary Matrix Rank	$P\text{-}value=igamc\left(1, {\displaystyle \frac{{X^2}_{\left(obs\right)}}{2}}\right)$
Discrete Fourier Transform (Spectral)	$P\text{-}value=erfc\left({\displaystyle \frac{\left|d\right|}{\sqrt{2}}}\right)$
Non-overlapping Template Matching	$P\text{-}value=igamc({\displaystyle \frac{N}{2}}, {\displaystyle \frac{{X^2}_{\left(obs\right)}}{2}})$
Overlapping Template Matching	$P\text{-}value=igamc({\displaystyle \frac{5}{2}}, {\displaystyle \frac{{X^2}_{\left(obs\right)}}{2}})$
Maurer’s Universal Statistical	$P\text{-}value=erfc\left(\left|{\displaystyle \frac{f_n-expectedValue\left(L\right)}{\sqrt{2\sigma )}}}\right|\right)$
Linear Complexity	$P\text{-}value=igamc({\displaystyle \frac{N}{2}}, {\displaystyle \frac{{X^2}_{\left(obs\right)}}{2}})$
Serial	$P\text{-}value1=igamc\left(2^{m-2},\nabla {\psi }_m^2\right)$ $P\text{-}value2=igamc\left(2^{m-3},{\nabla }^2 {\psi }_m^2\right)$
Approximate Entropy	$P\text{-}value=igamc\left(2^{m-1},{\displaystyle \frac{x^2}{2}}\right)$
Cumulative Sums (Cusums)	$\begin{array}{ll}P\text{-}value=1 -& {\displaystyle \sum _{k=({\displaystyle \raisebox{1ex}{$-n$}\!\left/ \!\raisebox{-1ex}{$z$}\right.}+1)/4}^{{\displaystyle \raisebox{1ex}{$(\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$z$}\right.-1)$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}}}\left[\Phi \left({\displaystyle \raisebox{1ex}{$\left(4k+1\right)z$}\!\left/ \!\raisebox{-1ex}{$\sqrt{n}$}\right.}\right)-\Phi \left({\displaystyle \raisebox{1ex}{$\left(4k-1\right)z$}\!\left/ \!\raisebox{-1ex}{$\sqrt{n}$}\right.}\right)\right]+\\ & {\displaystyle \sum _{k=({\displaystyle \raisebox{1ex}{$-n$}\!\left/ \!\raisebox{-1ex}{$z$}\right.}-3)/4}^{{\displaystyle \raisebox{1ex}{$(\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$z$}\right.-1)$}\!\left/ \!\raisebox{-1ex}{$4$}\right.}}}\left[\Phi \left({\displaystyle \raisebox{1ex}{$\left(4k+3\right)z$}\!\left/ \!\raisebox{-1ex}{$\sqrt{n}$}\right.}\right)-\Phi \left({\displaystyle \raisebox{1ex}{$\left(4k+1\right)z$}\!\left/ \!\raisebox{-1ex}{$\sqrt{n}$}\right.}\right)\right]\end{array}$
Random Excursions	$P\text{-}value=igamc({\displaystyle \frac{5}{2}}, {\displaystyle \frac{{X^2}_{\left(obs\right)}}{2}})$
Random Excursions Variant	$P\text{-}value=erfc\left({\displaystyle \frac{\left|\xi \left(x\right)-J\right|}{\sqrt{2J(4\left|x\right|-2}}}\right)$

, where the corresponding equation is observed [37]. A sequence is considered satisfactory only if the P-value is greater than 0.01; otherwise, the sequence is deemed completely non-random or non-pseudorandom [37,40]. The P-value is derived from hypothesis testing, assessing whether the observed result is consistent with the assumption of randomness [37,40]. Each test follows a hypothesis-testing framework. Under the null hypothesis H0, the sequence is random, while under the alternative hypothesis Ha, the sequence is not random [37,40]. Two types of errors can occur during hypothesis tests: type I error, where H0 is rejected (concluding non-randomness) when the sequence is actually random [37,40], or type II error, where H0 is accepted (concluding randomness) when the sequence is actually non-random [37,40]. For a sequence to pass the test, it must be random enough to accept H0; if it is non-random, H0 is rejected in favor of Ha [37,40].

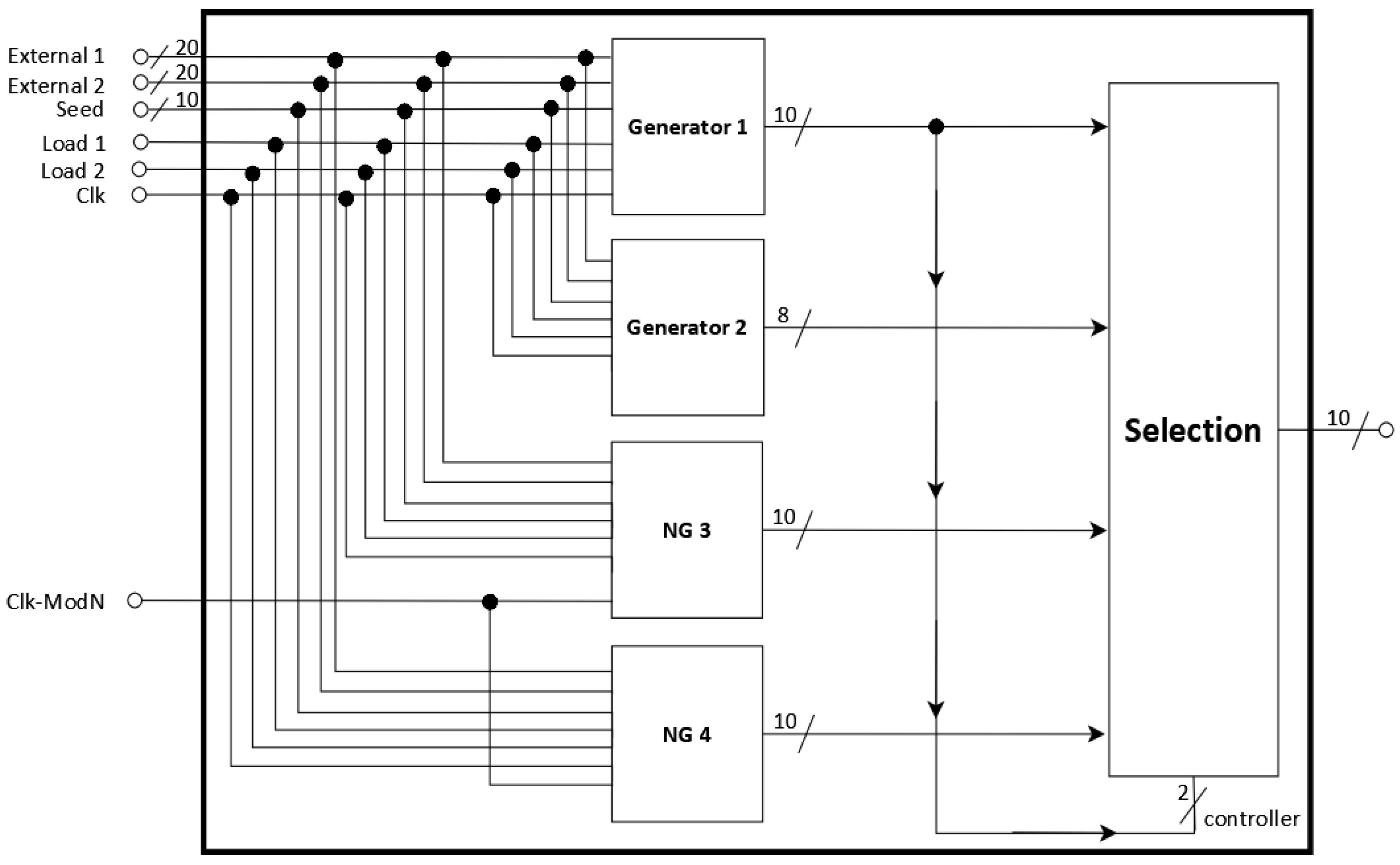
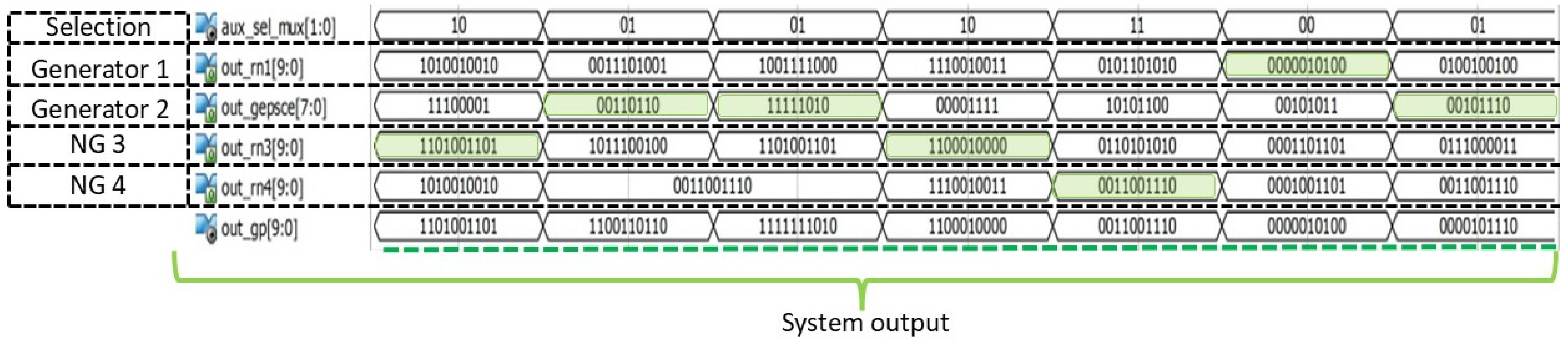
This work presents the design and implementation of a system incorporating PRNG generators and neuro-generators on the Virtex 7 xc7vx485t-ffg1761 reconfigurable FPGA (Field Programmable Gate Array) device [40,49,50,51]. The system features four internal PRNG generators with good statistical properties and a uniform bit distribution, which meet the criteria to pass various NIST tests. The system allows for the generation of new pseudorandom sequences by selecting from all internal generators. In addition, a specific generator can be chosen to produce a previously validated sequence. Some of the tests confirming the pseudo-randomness of the generated sequences include the Frequency (Monobit) test, Frequency within a Block test, Linear Complexity test, and Binary Matrix Rank test, among others. The results demonstrate that the generator system is suitable for various applications, such as biological systems, simulations, testing electronic circuits, etc.

2. Design of a System of PRNG Generators and Neuro-Generators

A system of pseudorandom number generators and neuro-generators was designed, as shown in Figure 3. The proposed system consists of two PRNG generators (Generator 1 and Generator 2) and two neuro-generators (NG 1 and NG 2). Each of these was designed individually with specific conditions to pass different NIST statistical tests with satisfactory pseudo-randomness results [40,49,50,51].

The system’s generators are connected to a selection device that determines which set of bits is passed to the output. It features four input connections for initial data: External 1 and External 2 (each 20 bits) or Seed data (10 bits per generator). These inputs are loaded into the internal LFSRs of each generator only when the Load signals are active. Additionally, the system includes an independent clock signal for the neuro-generator neuronal blocks, allowing their frequency to be adjusted without affecting the entire system. The sequences produced by each generator, along with different selection combinations, were validated by NIST statistical tests to confirm their pseudo-randomness.

Generator 1, shown in Figure 4a [49], is a PRNG with a 10-bit output and two LFSR shift registers. These registers are loaded in parallel with either external data or seed data, depending on the Load signals and the selection of the multiplexer, which is controlled by a controller [49]. Once both LFSRs are loaded, each CLK signal pulse generates a 10-bit output while simultaneously shifting a bit to the right, allowing a feedback bit to enter the register. This feedback is produced by an XOR gate, with one of its inputs negated, connected to bits 16 and 20, a configuration recommended by Xilinx to maximize the number of LFSR output sequences before repetition occurs. The outputs of LFSR1 and LFSR2 are further processed by two logic blocks, referred to as Logic Field 1, Logic Field 2, Xor Field 1, and Xor Field 2. The final output is determined by multiplexer Mux 3, which directs the bit word to the generator output. The Mux 3 Controller selects LFSR1 data when set to 0 and LFSR2 data when set to 1 [49].

On the other hand, Generator 2, shown in Figure 4b [50], consists of a general block with an LFSR connected to a parallel register for seed data input. Similar to Generator 1, each CLK pulse shifts the sequence one bit to the right, allowing the input of the feedback bit while simultaneously producing the LFSR output sequence. In this design, outputs 2, 4, 6, 7, 10, 13, 15, and 17 are connected to an addressing bus, which enables random access to predefined words in the generator and produces the output sequence [50].

The NG 3 and NG 4 neuro-generators, shown in Figure 5 [40,51], follow a similar topology to Generator 1 but incorporate a neuronal module connected to each neuro-generator. These modules generate a non-periodic clock signal that enters the CLK of the LFSR 1, causing the bits to shift and producing an output sequence whenever the CLK of the LFSR 1 receives a pulse from the neuronal module. Meanwhile, the LFSR 2 operates at a periodic frequency of 100 MHz [40,51].

The neuronal modules are designed with hardware impulse neurons (Figure 6) operating at a 4 kHz clock signal, with the option to modify this frequency. Their behavior is based on Izhikevich biological neurons [40,51,52,53]. For neuro-generator NG 3, shown in Figure 5a, the neuronal module exhibits phasic bursts, producing 6 impulses and tonic bursts, generating 16 impulses at the output. These impulses are triggered only when the neuron is stimulated by an input impulse without the need to remain in a high state. On the other hand, the neuronal module of the neuro-generator NG 4, shown in Figure 5b, consists of six impulse neurons with different behaviors: frequency adaptation, tonic impulse, mixed mode, phasic bursts, tonic bursts, and phasic impulse. Each neuron produces a unique number of impulses per series, activated only upon stimulation [40,51,52,53]. In both neuro-generators, the output data from the LFSRs are processed by Channel 1 and Channel 2, which are then passed through a selection module to form the final output sequence. This sequence is subsequently validated by the NIST statistical tests.

3. Simulation and Implementation of the System Generators

The design of the generators and neuro-generators system was implemented using the VHDL hardware description language and developed in ISE 14.6, a software tool from the Xilinx AMD design platform [54]. This software was used to simulate the system and test its operation. Additionally, it generated a txt text file containing the new output sequences, which were subsequently using NIST statistical tests. The system also provided occupation percentages, detailing the resource usage of each generator within the Virtex 7 xc7vx485t-2ffg1761 reconfigurable FPGA device [55].

3.1. Simulation Results

The simulation was performed at a frequency of 100 MHz for the entire system, including the neuronal modules of the neuro-generators. This is despite the fact that the clock frequency of the impulse neurons in hardware is 4 kHz. In Figure 7a, the initial data (external1 and external2) are loaded into each of the LFSRs of the generators when the Load signals are activated (set to 1). The loaded data are visible in the in_lfsr signals, which are color-coded to indicate their respective generators. For Generator 2, represented by the brown d signal, only a single shift register is used, and the external 1 data are loaded into it. A similar process occurs when the seed data are used instead of external data, as shown in Figure 7b. However, in this case, the bits are distributed differently when loaded into the LFSR due to the difference in the bit word length between each one.

With the Load signal disabled, the data are processed by each of the generator stages to produce the system output sequences, as shown in Figure 8. The selector corresponding to the aux_sel_mux signals indicates the output data that form a new sequence. In this case, the corresponding bit word is marked in green, starting with 1101001101 of the neuro-generator NG 3 and ending with 00101110 of the Generator 2. In the latter, the output is eight bits, so in the ten-bit word of the output system, only the first eight bits change from right to left, keeping the last two bits of the previous word. As well as the generator sequences, this one is also validated by NIST statistical tests to demonstrate its pseudo-randomness in specific tests or the entire set.

The design of this system has the flexibility to select the output of a single generator to obtain the sequence already validated by NIST, as shown in Figure 9. Where the sel_mux4 signal in Figure 9a shows only the output of Generator 1 with the combination 00 and in Figure 9b of the neuro-generator NG 4 by having 11 in the selector. Therefore, the system is not limited to just the combination of the generators to produce new sequences, but it also has the option of obtaining the output of a specific generator immediately.

3.2. Occupancy Percentages of the System Generators and Neuro-Generators in the FPGA Virtex 7 xc7vx485T-2FFG1761

The resource occupancy percentages of the FPGA for each of the system generators are shown in

Table 2. Occupancy percentages of the generators and neuro-generators of the generator system in the Virtex 7 xc7vx485T-2FFG1761.

Logic Utilization	Available	Generator 1		Generator 2		NG 3		NG 4
		Used—Utilization
Slices Registers	607,200	60	0.009%	60	0.009%	104	0.01%	156	0.025%
Slice LUTs	303,600	82	0.02%	21	0.006%	247	0.08%	409	0.134%
LUT-FF	429	55	12.82%	20	4.66%	86	20.04%	136	31.70%
IOBs	700	105	15%	35	5%	66	9.42%	110	15.71%
BUFG/BUF GCTRLs	32	2	6.25%	3	9.37%	3	9.37%	3	9.37%
RAM/FIFO	1030	-	-	1	0.097%	-	-	-	-

, where all generators have a low percentage of resources used, including the neuro-generators NG 3 and NG 4, which reach 20.04% and 31.70% of LUT-FF, which is the number of Flip-Flops used by the system as the number of highest resources. These results show that each of the generators can be implemented individually. However, in

Table 3. Generators system occupancy rates in Virtex 7 xc7vx485T-2ffg1761.

Logic Utilization	Available	Used	Utilization
Slices Registers	607,200	343	0.056%
Slice LUTs	303,600	667	0.219%
LUT-FF	734	276	37.602%
IOBs	700	115	16.428%
BUFG/BUF GCTRLs	32	7	21.875%
RAM/FIFO	1030	1	0.097%

, it can be observed that the system has the flexibility to be implemented in the same reconfigurable device as the generators and neuro-generators. This is due to the percentages that the design occupies in each of the resources, where none reaches 50% utilization, with 37.602% in LUT-FF, being the resource with the highest percentage of occupation and the lowest number of registers, with 0.056%. In addition, it has 0.097% of RAM (Read Access Memory), which corresponds to the data storage block of Generator 2, 0.219% of LUTs (LookUp Table) occupancy, 16.428% of IOBs inputs and outputs, and 21.875% of BUFGs (Global Clock Buffer), which are clock inputs and outputs.

4. Results and Discussion

The PRNG generators and neuro-generator of the system were validated by NIST statistical tests to demonstrate that the sequences they produce are pseudorandom for a set or a specific test, as shown in

Table 4. NIST statistical tests passed on the system’s PRNG generators and neuro-generators.

Test	Generator 1	Generator 2	NG 3	NG 4
Frequency (Monobit)	X			X
Frequency within a Block
Runs	X			X
Longest-Run-of-Ones in a Block
Binary Matrix Rank	X
Discrete Fourier Transform (Spectral)
Non-overlapping Template Matching	X
Overlapping Template Matching
Maurer’s Universal Statistical	X
Linear Complexity	X		X	X
Serial
Approximate Entropy	X
Cumulative Sums (Cusums)	X
Random Excursions	X	X
Random Excursions Variant	X	X

. In the case of Generator 1, the sequences produced by this design are considered pseudorandom for a set of ten statistical tests proposed by NIST. These are the Frequency (Monobit) test, Runs test, Binary Matrix Rank test, Non-overlapping Template Matching test, Maurer’s Universal Statistical test, Linear Complexity test, Approximate Entropy test, Cusums test, Random Excursion test, and Random Excursion Variant test. Instead, Generator 2 is designed to meet the number of cycles required for the Random Excursion and the Random Excursion Variant tests, with satisfactory P-value values in some of the states that make up this test. The first neuro-generator NG 3 of the system, the sequence generated with the entire system at 100 MHz and then at 4 kHz, is considered complex enough to be considered pseudorandom. The same occurs for the neuro-generator NG 4, which is also pseudorandom for the Frequency (Monobit) and Runs test.

In the graph of Figure 10, the distribution of the P-value of the validated output of each generator of the system can be observed at a frequency of 100 MHz. Figure 10a shows the pseudo-randomness results, with the external 1 and external 2 data loaded to the LFSRs of the generators. It is observed that the majority of the P-value values are above 0.5, reaching values with a high level of pseudo-randomness, as in the case of Generator 1. The same occurs with the P-value data in Figure 10b, where it is observed that, again, Generator 1 maintains, in some cases, values of P-value = 1.

Otherwise, when loading the seed data to the neuro-generators NG 3 and NG 4, the output sequence maintains its complexity and pseudo-randomness for the NIST Linear Complexity test, as shown in Table 3 and Figure 10. All the values of the P-value can be consulted in [40,49,50,51], which corresponds to the scientific articles where the first results obtained from each generator were presented with frequencies of 100 MHz and 4 kHz, with the aim of respecting the frequency of the neuronal module connected to the neuro-generator and with the initial seed and external data modified [40,49,50,51].

The first validation results of pseudo-randomness of the generators and neuro-generators system were with the entire system at a frequency of 4 kHz, where the external data and then the seed data were loaded. The results observed in

Table 5. NIST statistical testing passed the system at 4 kHz frequency.

Test	Loaded Data	4 kHz
		P-value
Frequency (Monobit)	external	0.810078
Frequency within a Block	external	0.464674
Runs	seed	0.753905
Longest-Run-of-Ones in a Block	seed	0.655972

show satisfactory conclusions for the Binary Matrix Rank test with a P-value = 0.810078 and the Linear Complexity test with a P-value = 0.464674 when loading the external data. These same tests are approved when loading the seed data but with a difference between the P-value values of 0.056173 for the first test and 0.191298 for the Linear Complexity test.

The results were also obtained with the system at a frequency of 100 MHz, including the neuronal module of each neuro-generator NG 3 and NG 4, and with the external data loaded to the LFSRs, where the results were satisfactory for the Binary Matrix Rank test with a P-value = 0.390736 and the Linear Complexity test with a P-value = 0.563232, as observed in Figure 11a. When the seed data were loaded, the results were greater than 0.01 for the same tests but with different levels of pseudo-randomness in P-value, as shown in Figure 11b. This indicates that the system sequences maintain their complexity and pseudo-randomness without being influenced by the working frequency.

Keeping the system at 100 MHz, the combination between two different generators was made to obtain new pseudorandom sequences, which had good statistical properties to pass different NIST tests. These were performed following the combination shown in Figure 12, beginning with the selection of Generator 1 and Generator 2. Continuing with the same generator, but now combined with neuro-generators NG 3 and NG 4, these with Generator 2 and the last combination with themselves.

For each case, the new output sequences of the system were validated by NIST statistical tests. The P-value results were satisfactory for the Binary Matrix Rank test and Linear Complexity test, as seen in

Table 6. P-value results from the NIST statistical tests Binary Matrix Rank and Linear Complexity when selecting two generators to produce different sequences.

Test	Selection
	Generator 1			Generator 2		NG 3
	Generator 2	NG 3	NG 4	NG 3	NG 4	NG 4
Binary Matrix Rank	0.472606	0.855380	0.232187	0.908661	0.078402	0.067799
Linear Complexity	0.668705	0.794940	0.970823	0.198228	0.081943	0.338502

, which shows variation in the P-value value without affecting the pseudo-randomness of the sequence. However, when selecting only the neuro-generators NG 3 and NG 4, the sequence is pseudorandom for all states of the Random Excursions and Random Excursion Variant tests, as shown in

Table 7. P-value results of the Random Excursion and Random Excursion Varian tests when selecting neuro-generators NG 3 and NG 4.

Test	State	P-value
Random Excursion	−4	0.144909
	−3	0.634359
	−2	0.205829
	−1	0.663797
	1	0.654933
	2	0.359742
	3	0.361715
	4	0.462300
Random Excursion Variant
	−9	0.646087
	−8	0.754622
	−7	0.972531
	−6	0.415538
	−5	0.296039
	−4	0.981281
	−3	0.461922
	−2	0.184810
	−1	0.113429
	1	0.641517
	2	0.389698
	3	0.211564
	4	0.296439
	5	0.346447
	6	0.359074
	7	0.339301
	8	0.214167
	9	0.130250

. Therefore, all sequences produced by the system when taking the bits from two generators are complex and pseudorandom.

Considering the P-value results obtained in each situation in which the generators and neuro-generators system were used, it is demonstrated that the sequences with an adequate bit distribution are generated. In addition to being complex enough to pass different statistical tests proposed by NIST, such as the Frequency (Monobit) test, Runs test, Binary Matrix Rank test, Non-overlapping Template Matching test, Maurer’s Universal Statistical test, Linear Complexity test, Approximate Entropy test, Cumulative Sum (Cusums) test, Random Excursion test, Random Excursion Variant test and including the Frequency within a Block test and the Longest-Run-of-Ones in a Block test. These are added to the tests approved by the generator and neuro-generator system, as shown in

Table 8. NIST statistical tests passed by the PRNG generators and neuro-generators of the system.

Test	System
Frequency (Monobit)	X
Frequency within a Block	X
Runs	X
Longest-Run-of-Ones in a Block	X
Binary Matrix Rank	X
Discrete Fourier Transform (Spectral)
Non-overlapping Template Matching	X
Overlapping Template Matching
Maurer’s Universal Statistical	X
Linear Complexity	X
Serial
Approximate Entropy	X
Cumulative Sums (Cusums)	X
Random Excursions	X
Random Excursions Variant	X

, marked with X, with 12 tests approved out of 15 proposed by NIST, even when combining the bits from two different generators, as demonstrated by the results in Table 5 and Table 6, where different levels of pseudo-randomness were observed for the sequence obtained from each combination.

5. Conclusions

The system of generators and neuro-generators can produce sequences with adequate bit distribution and statistical properties at a frequency of 100 MHz and 4 kHz, respectively. As observed in the Section 4, the P-value showed variation only in the levels of pseudo-randomness due to the condition that each internal generator must pass tests independently or in specific sets. For the neuro-generators, the neuronal module operates at 4 kHz, but it can be adjusted to operate at a frequency of 100 MHz without affecting the complexity and bit distribution of the output sequence. The same results are observed with Generators 1 and 2, which were designed to pass a specific set of tests, regardless of whether the working frequency matches that of the neuro-generators or whether the initial data were external or seed data.

It was also demonstrated that the combination of two generators can produce pseudorandom sequences that pass the Binary Matrix Rank test, Linear Complexity test, and all the states of the Random Excursion and Random Excursion Variant tests. Therefore, the system of generators and neuro-generators is capable of generating sufficiently complex sequences, with adequate bit distribution, to pass 80% of the 15 NIST statistical tests proposed. This design offers flexibility, allowing for the selection of a specific generator to obtain a validated output sequence and the ability to adapt to different frequencies without affecting the pseudo-randomness of the sequences. This makes the system suitable for use in a wide range of different applications, including biological systems, mathematical systems simulation, electronic circuit testing, and even as initial data for other generators. In addition, it can be implemented in reconfigurable FPGA devices, such as the Virtex 7 xc7vx485T-2ffg1761.

Each of the system’s generators will be updated, including the generators’ neural modules, to increase the pseudo-randomness levels of each approved test and to analyze the sequences produced to pass other NIST statistical tests.