Analysis and Design of Noise-Shaping SAR ADC with Capacitor Stacking and Buffering

Abstract

The noise-shaping (NS) successive-approximation-register (SAR) is a promising analog-to-digital converter (ADC) architecture which combines the benefits of SAR and Delta-Sigma ($\mathsf{\Delta }\Sigma$) ADCs. Among the various NS-SAR approaches, the recent emerged one with capacitor stacking and buffering exhibits excellent energy efficiency. This paper presents a tutorial for the design of NS-SAR ADC with capacitor stacking and buffering. The fundamental principle of the NS-SAR loop filter is analyzed, an ADC design example is provided, and the circuit implementation details with considerations on the non-idealities and trade-offs are discussed. This paper can be used as a tutorial for designing high-resolution and high-order NS-SAR ADC.

1. Introduction

The noise-shaping (NS) successive-approximation register (SAR) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] is a hybrid analog-to-digital converter (ADC) architecture that tries to combine the benefits of both SAR and $\mathsf{\Delta }\Sigma$ ADCs, aiming to realize high resolution with low cost. It retains the simple structure of SAR ADC, and in the meantime, introduces the noise-shaping filter of $\mathsf{\Delta }\Sigma$ ADC. The key to an NS-SAR ADC is the noise-shaping filter. It is expected to be low-cost, robust and able to provide sharp NTF.

There are several ways to realize a noise-shaping filter. The conventional way is to use a closed-loop amplifier-based integrator [1,2,3]. As shown in Figure 1, with sufficient gain of the amplifier, this type of integrator can realize a sharp NTF. Also, the gain of the integrator is determined by the capacitor ratio, and thus, the integrator is PVT-robust. However, a high-gain amplifier requires multi-stage implementation. It produces large noise and is power-consuming. In addition, the closed-loop amplifier suffers from poor CMOS scaling compatibility. Its performance deteriorates with the reduction in power supply and the transistor’s intrinsic gain.

To avoid the issues of closed-loop amplifiers, researchers propose building passive filters. Passive filters employ charge sharing between capacitors to perform error feedback [5,8,9] or integration [6,7,10,11]. As shown in Figure 2, they use only switches and capacitors and thus are simple, scaling-friendly, and consume no static power. Moreover, their transfer function is set by the capacitor ratios; therefore, they are robust against process, temperature, and voltage (PVT) variations. However, the prior NS-SAR ADCs with passive filters show limited resolution (<13-bit ENOB) because the loop filter suffers from significant signal attenuation and lacks effective gain, leading to mild NTF. Moreover, in the passive NS-SAR ADCs, the multi-input-pair comparators are often used to provide the gain ratios between the analog input and the integration results. However, the multi-input-pair comparators suffer from significant input-referred noise.

To improve the NTF and noise suppression capability, some works place an open-loop amplifier before the passive filters to provide the required gain [8,9,10,11], as shown in Figure 3. The open-loop amplifiers are usually power efficient and can provide effective noise suppression. However, the gain of open-loop amplifiers is sensitive to PVT, which may cause ADC instability. To alleviate this problem, one approach is to use digital calibration to ensure the gain robustness of the open-loop amplifier [8]; the other approach is to sacrifice noise suppression effects to minimize the impact of gain variations [9].

Instead of using open-loop amplifiers, some works propose implementing the passive gain after the passive filter [12,13,14], as shown in Figure 4. For example, the work [13] realizes the 2× passive gain with differential residue sampling, while [14] realizes the 4× passive gain with differential integration and capacitor split-stack. Nevertheless, due to the parasitic capacitance from switches and capacitor plates, the passive gain that can be realized is very limited. The highest capacitor stacking number reported for NS-SAR is only 2, providing a passive gain of roughly 4× [14].

To address the issues of loop filters above, a new class of integrator is proposed in [16]. By using capacitor stacking and buffering (CSB) for integration, this integrator avoids the large signal attenuation of passive charge sharing; thus, it can realize sharp NTF and strong noise suppression. It does not require a closed-loop or open-loop amplifier and thus is power efficient and PVT-robust. The integrator only contains a buffer and capacitors; the hardware complexity is low, and it is easy to extend to high-order noise shaping. Figure 5 compares the NS-SAR ADCs with CSB filter [16,17,18,19] and others. It shows that the NS-SAR ADCs with CSB filters have obvious advantages in energy efficiency over those with other filters.

This paper provides a tutorial on noise-shaping SAR ADCs with capacitor stacking and buffering. The rest of the paper is organized as follows: Section 2 analyzes the fundamental principle of the CSB integrator. Section 3 presents the realization of NS-SAR ADCs with CSB integrators. Section 4 discusses the design considerations and circuit implementation. Section 5 concludes this paper.

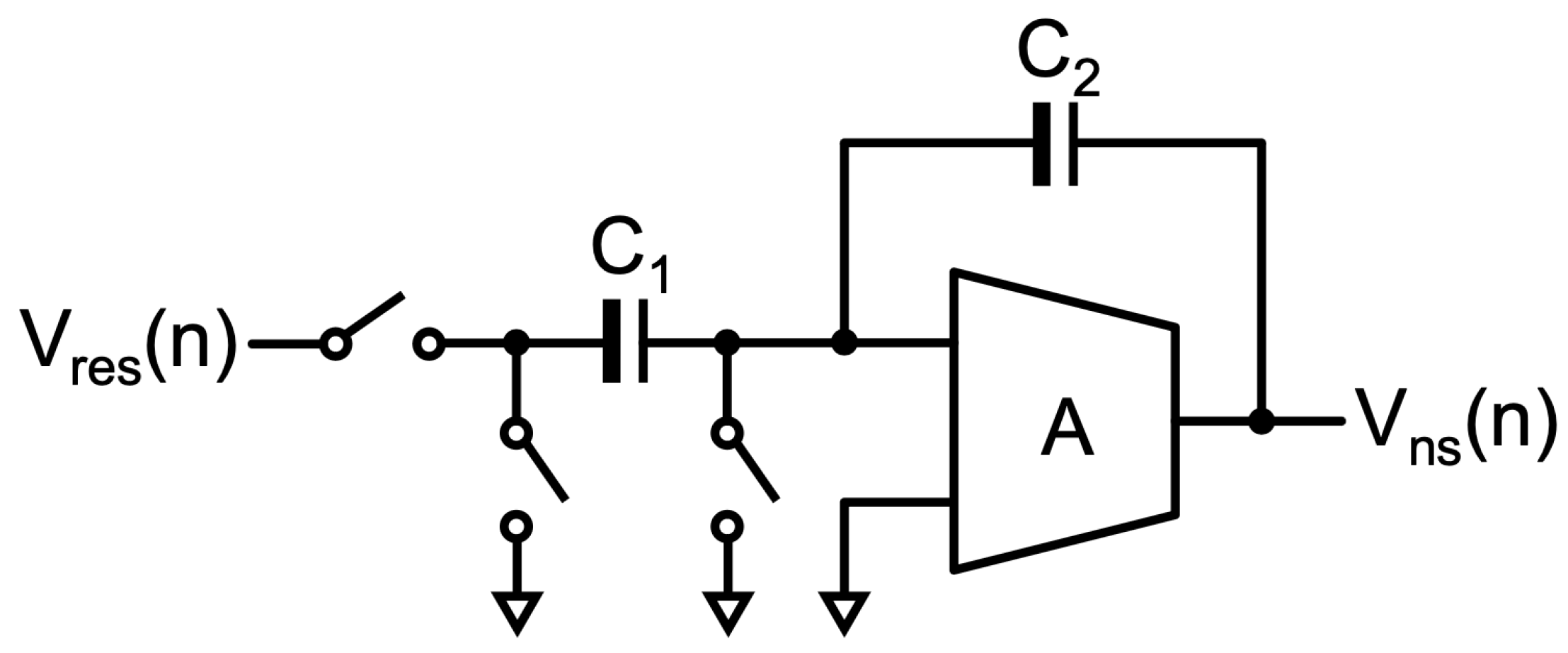
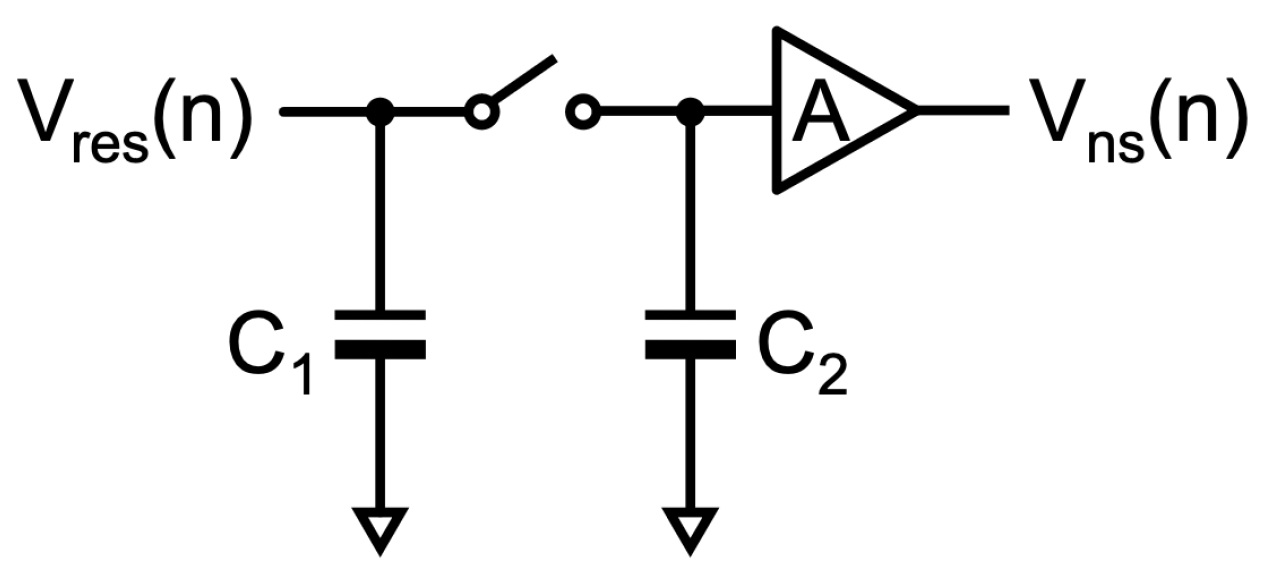
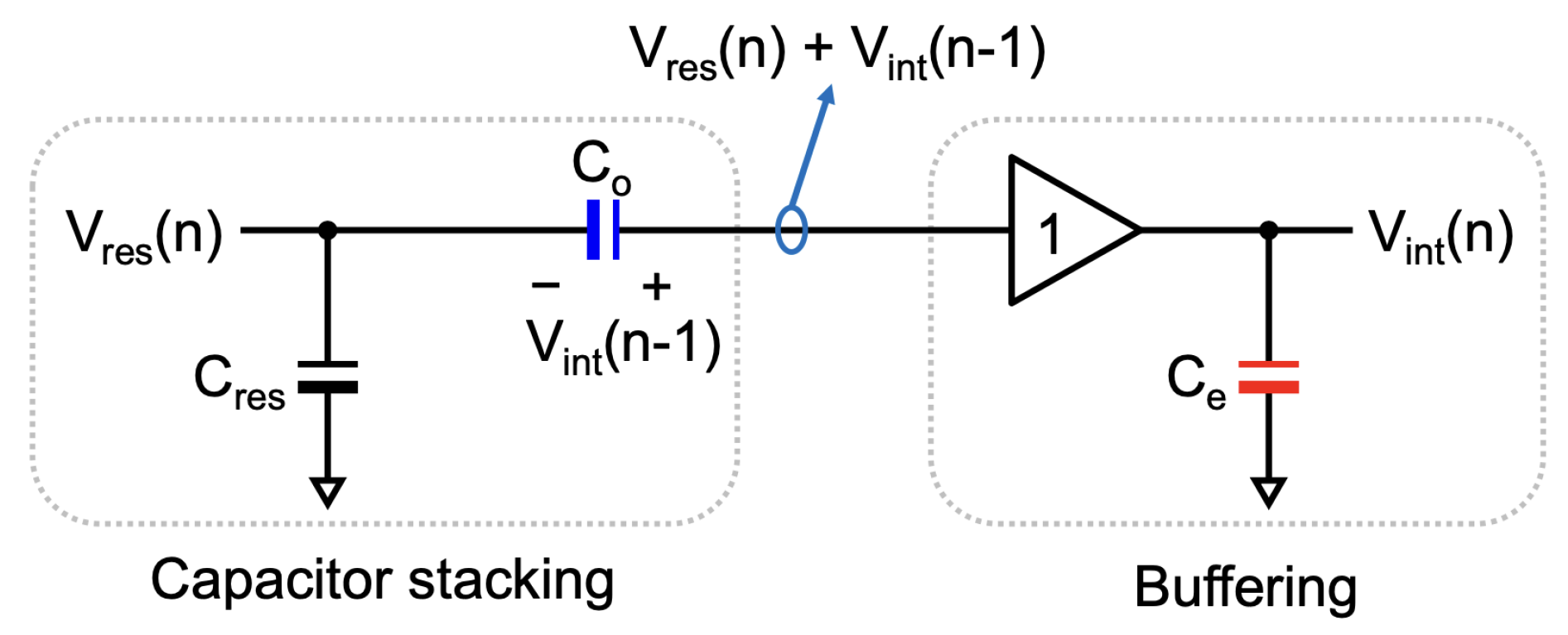
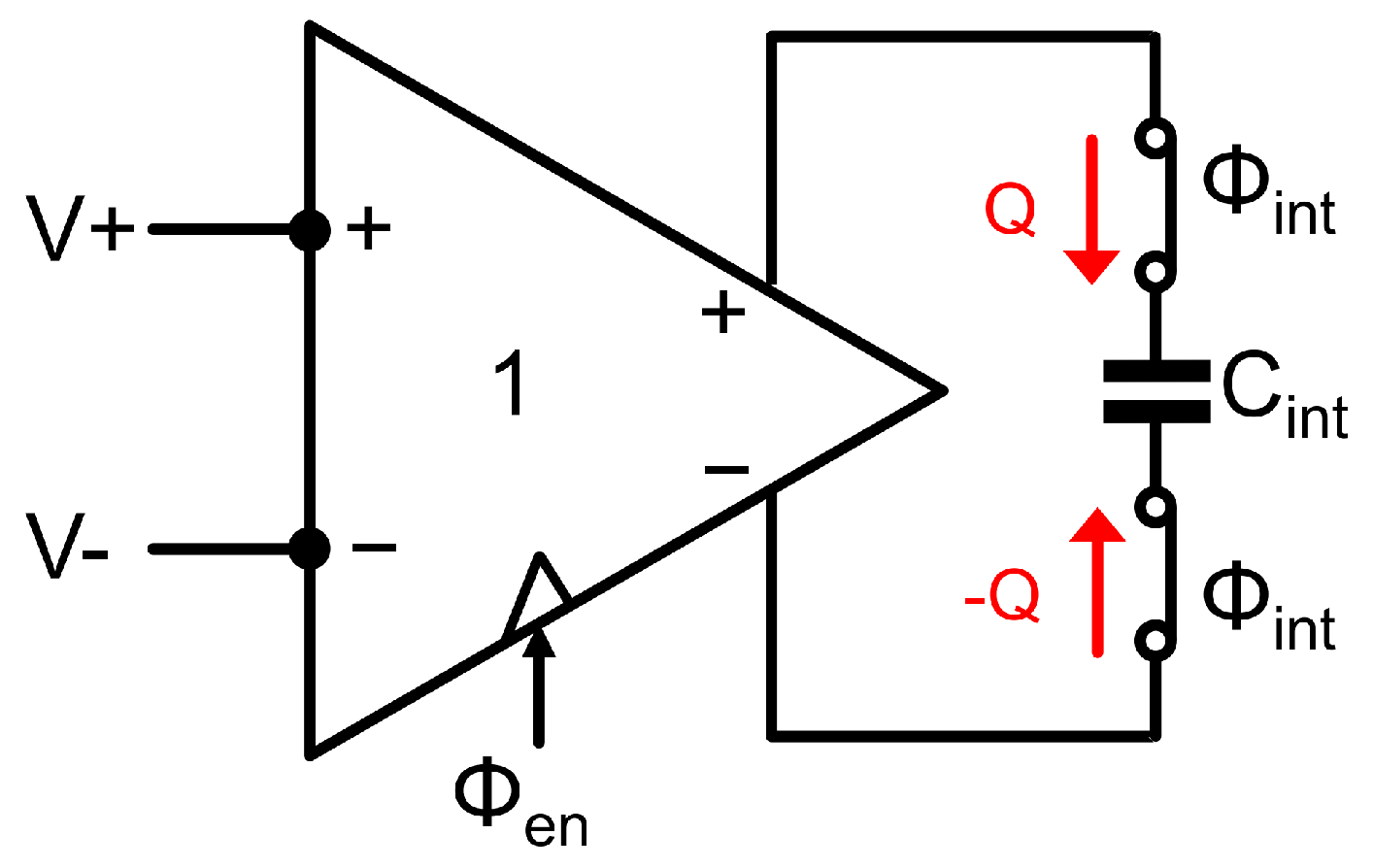
2. Principle of Integrator with Capacitor Stacking and Buffering

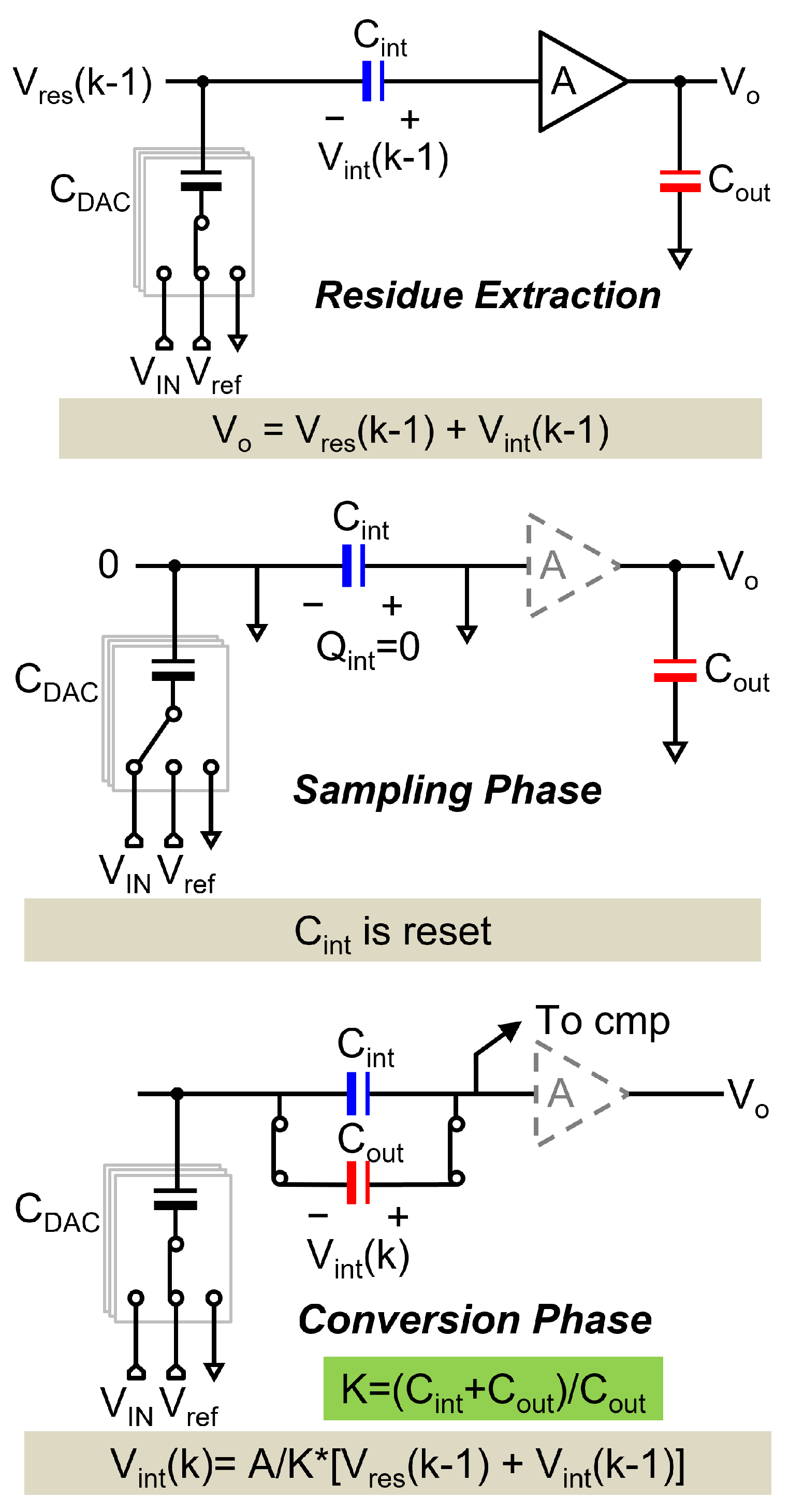
2.1. One-Time Integration

To illustrate the operation principle, the basic model of the integrator with capacitor stacking and buffering is shown in Figure 6. In discrete-time systems, an integration operation is basically an addition. The present integration voltage $V_{int}\left(n\right)$ can be obtained by adding the previous integration voltage $V_{int}(n-1)$ with the present residue voltage $V_{res}\left(n\right)$, as shown in the following

$$\begin{array}{cc}\hfill V_{int}\left(n\right)& =V_{res}\left(n\right)+V_{int}(n-1)\hfill \end{array}$$

(1)

In circuit implementation, the voltage addition can be simply realized by stacking the residue capacitor with the integrator capacitor. Compared to the passive filters using charge sharing, the capacitor stacking does not cause signal attenuation. By capacitor stacking, the voltage at the right side of capacitor $C_o$ is equal to the integration result, $V_{res}\left(n\right)+V_{int}(n-1)$. However, the capacitor stacking result cannot be directly used in the consequent ADC conversions.

To address this issue, another capacitor $C_e$ is used to store the integration result through a unity-gain buffer. A source follower can be used as the buffer, which is simple and PVT-robust. However, this configuration only realizes the one-time integration.

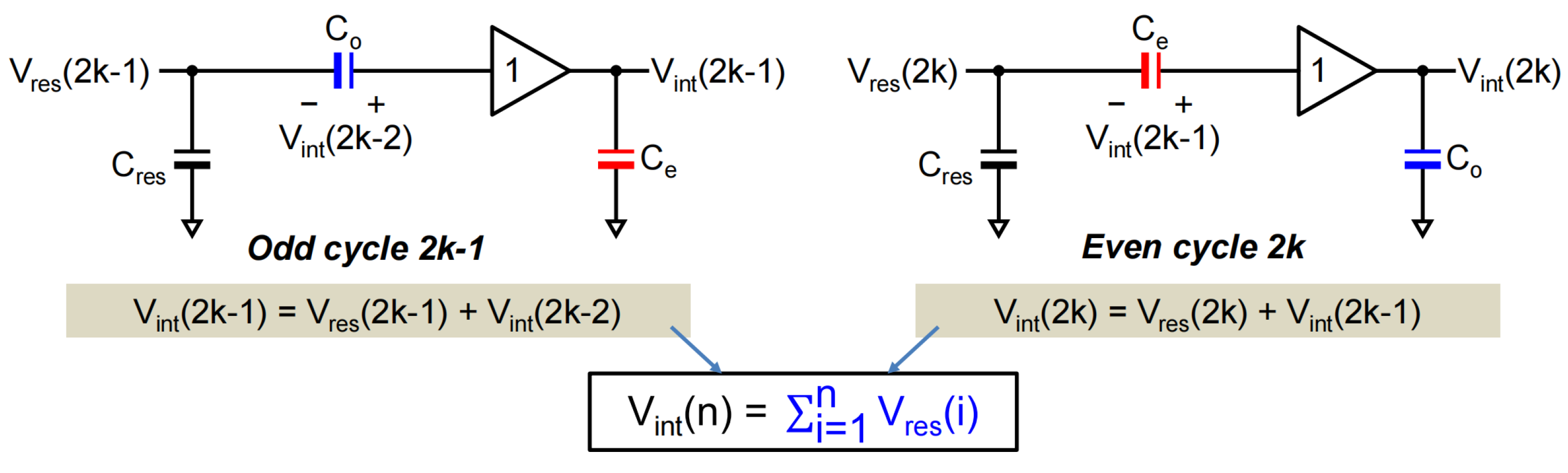
2.2. Continual Integration

As shown in Figure 7, to perform continuable integration, the two integration capacitors $C_o$ and $C_e$ are operated in a ping-pong fashion. For simplicity, the operation principle of the integrator is explained here in a single-ended form. In an odd ADC operation cycle $2k-1$, the integration capacitor $C_o$ is stacked with the residue capacitor $C_{res}$, obtaining the sum of the residue voltage $V_{res}(2k-1)$ and the previous integration voltage $V_{int}(2k-2)$, while $C_e$ is used to store the integration result $V_{int}(2k-1)$. The voltage stored on $C_e$ can be expressed as

$$V_{int}(2k-1)=V_{res}(2k-1)+V_{int}(2k-2)$$

(2)

In the next even operation cycle $2k$, the previous integration capacitor $C_e$ is stacked with the residue capacitor $C_{res}$, while the previous stacked capacitor $C_o$ is used to store the even integration result $V_{int}\left(2k\right)$, which can be expressed as

$$V_{int}\left(2k\right)=V_{res}\left(2k\right)+V_{int}(2k-1)$$

(3)

In this way, a high-quality integrator is realized without the use of a power-hungry closed-loop amplifier or a PVT-sensitive open-loop amplifier, as shown in Equation (4). With the robust unity-gain buffer, this integrator can be used to build an NS-SAR ADC with a sharp and robust NTF.

$$V_{int}\left(n\right)=\sum _{i=1}^n{V}_{res}\left(i\right)$$

(4)

However, as shown in Figure 8, a problem with the single-ended integration is that it is prone to saturation due to the DC component across the integration capacitor, which includes the buffer offset and the common-mode voltage mismatch at both ends of the capacitor. As shown in this figure, if there is a DC offset, $V_{os}$, in the integration path, the offset voltage will accumulate on the integration capacitors. The integration result after n integrations can be expressed as

$$V_{int}\left(n\right)=\sum _{i=1}^n{V}_{res}\left(i\right)+n·V_{os}$$

(5)

Finally, the integrator will be saturated by the offset.

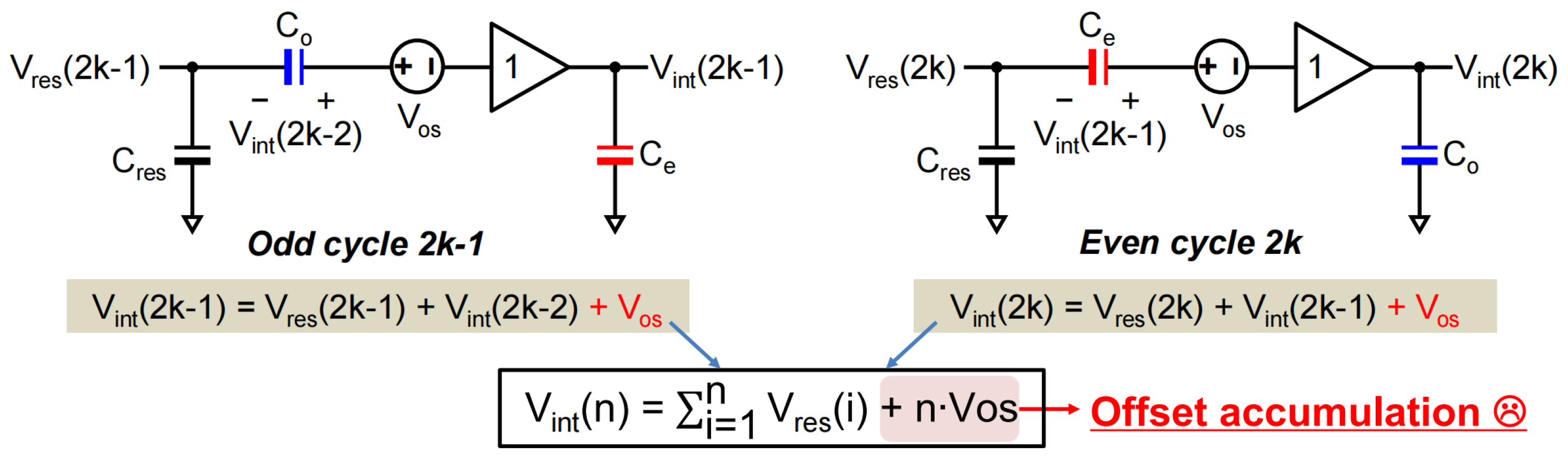
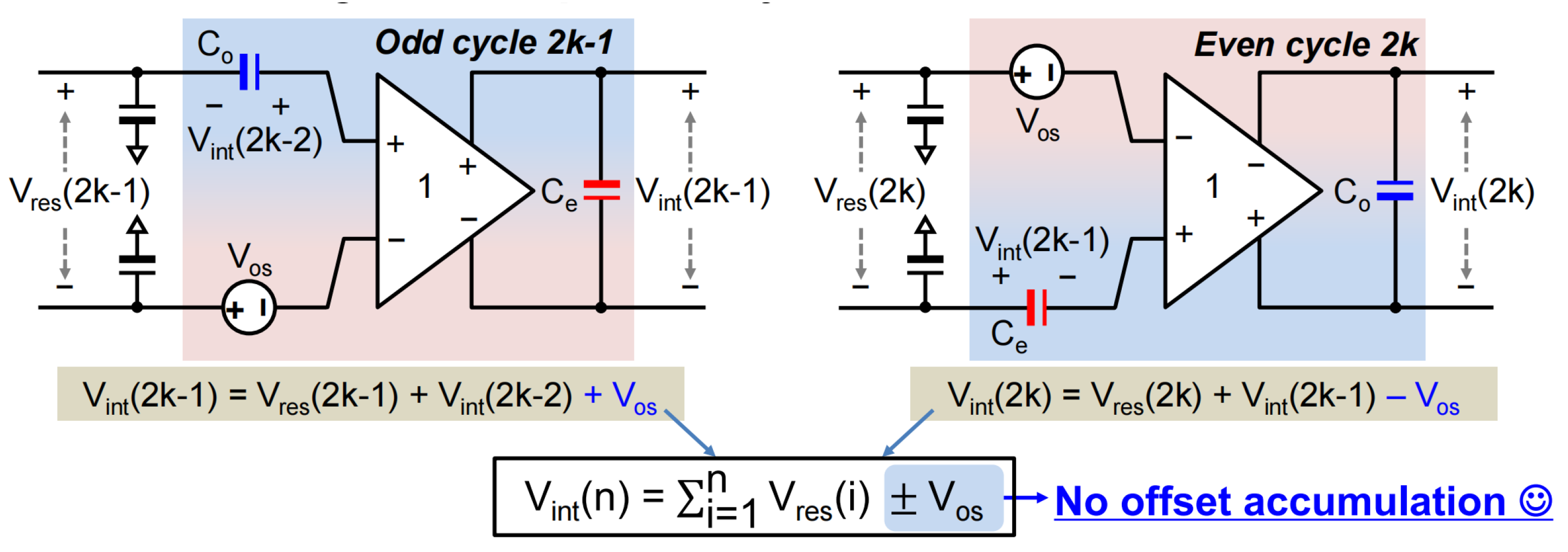
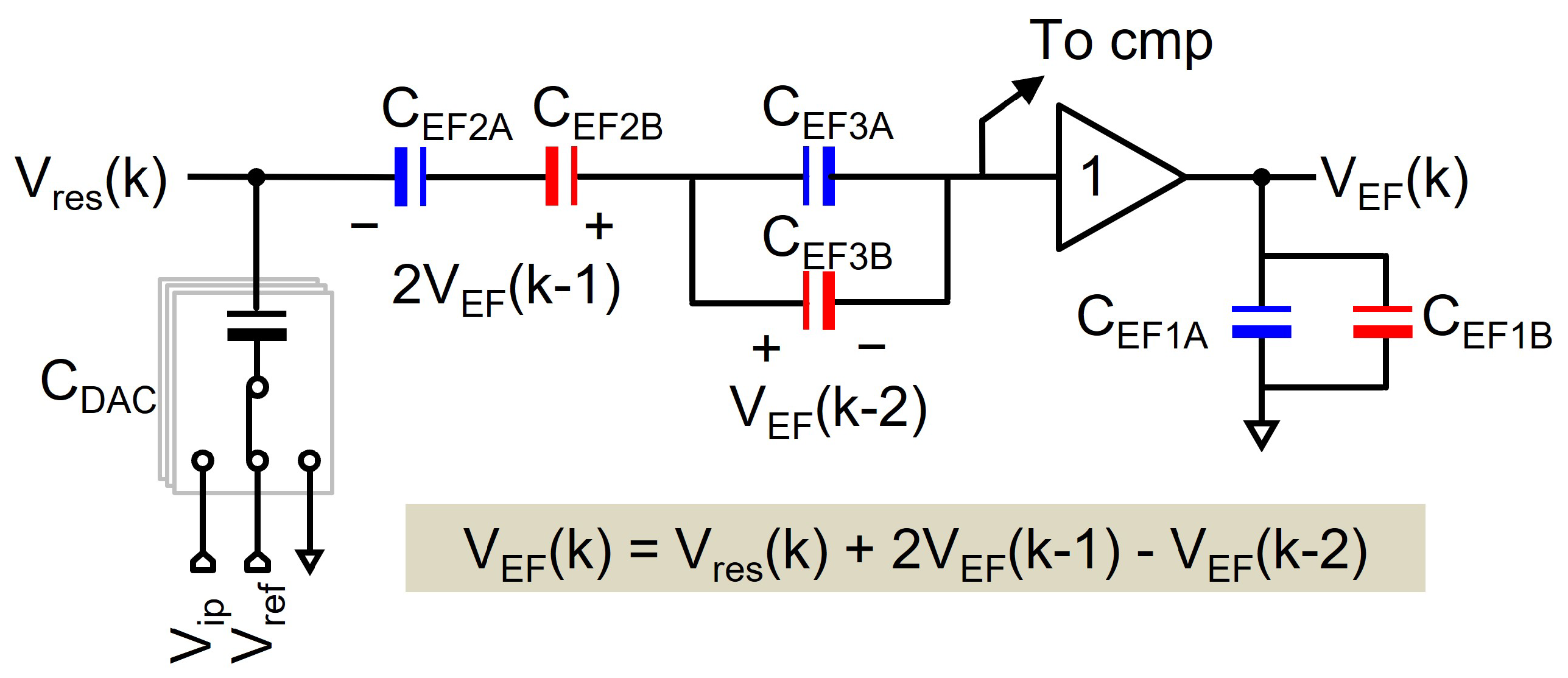
2.3. Differential Integration

This problem can be addressed by performing differential integration and chopping. The differential integration is to place the integration capacitor between the outputs of a differential buffer [14]. By this, most of the DC offset resulting from the mismatch of buffer common-mode voltages is canceled. The remaining offset resulting from the buffer can be solved by chopping.

As shown in Figure 9, in the odd cycle $2k-1$, $C_o$ is stacked with the residue capacitor $C_{res}$ and then connected to the positive terminal of the buffer, so the offset voltage is added to the integration result $V_{int}(2k-1)$

$$V_{int}(2k-1)=V_{int}(2k-2)+V_{res}(2k-1)+V_{os}$$

(6)

In the next even cycle $2k$, using the chopper technique, the polarity of the differential buffer is reversed and the offset voltage is subtracted from the integration result $V_{int}\left(2k\right)$, which can be expressed as

$$V_{int}\left(2k\right)=V_{int}(2k-1)+V_{res}\left(2k\right)-V_{os}$$

(7)

In this way, after n times of integrations, the output voltage of the buffer is

$$V_{int}\left(n\right)=\sum _{i=1}^n{V}_{res}\left(i\right)\pm V_{os}$$

(8)

It can be seen that the offset accumulation issue is addressed. As with the offset, the flicker noise of the buffer is also transferred to high frequencies by chopping.

In addition, for the same $kT/C$ noise budget, the total integration capacitor size can be reduced $4\times$ by using differential integration, comparing with that using single-ended integration [14,15].

It is important to be aware of the polarity of the integration capacitor $C_e$ to ensure correct summation of $V_{int}$ and $V_{res}$.

In general, the CSB integrator avoids the large signal attenuation of passive charge sharing, and thus it can realize a sharp NTF ($\approx 1-z^{-1}$) with strong in-band noise suppression. Meanwhile, this approach requires neither a closed-loop amplifier nor an open-loop amplifier; thus, it is both energy-efficient and PVT-robust. Moreover, this approach only uses buffers and capacitors which have a simple circuit structure and are easy to extend to the high-order noise shaping.

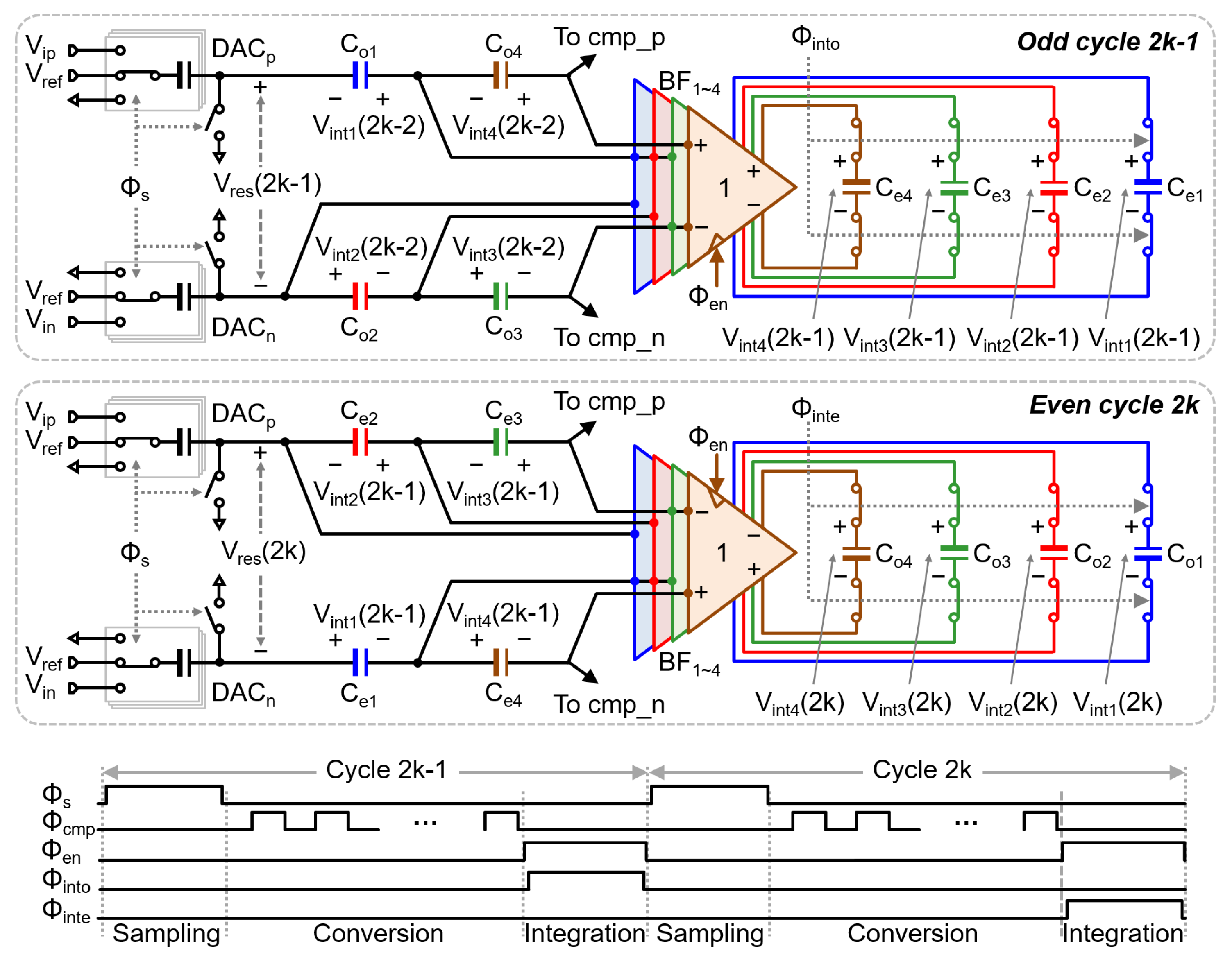
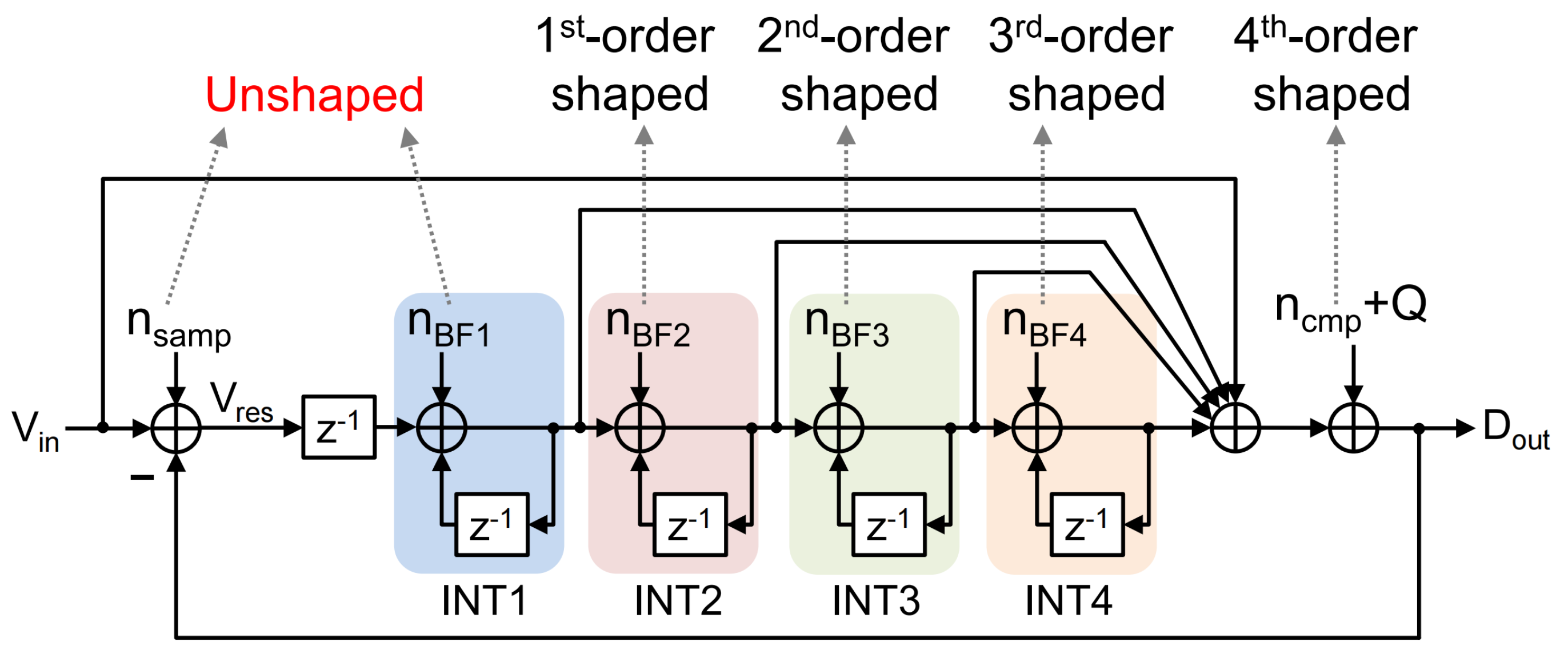
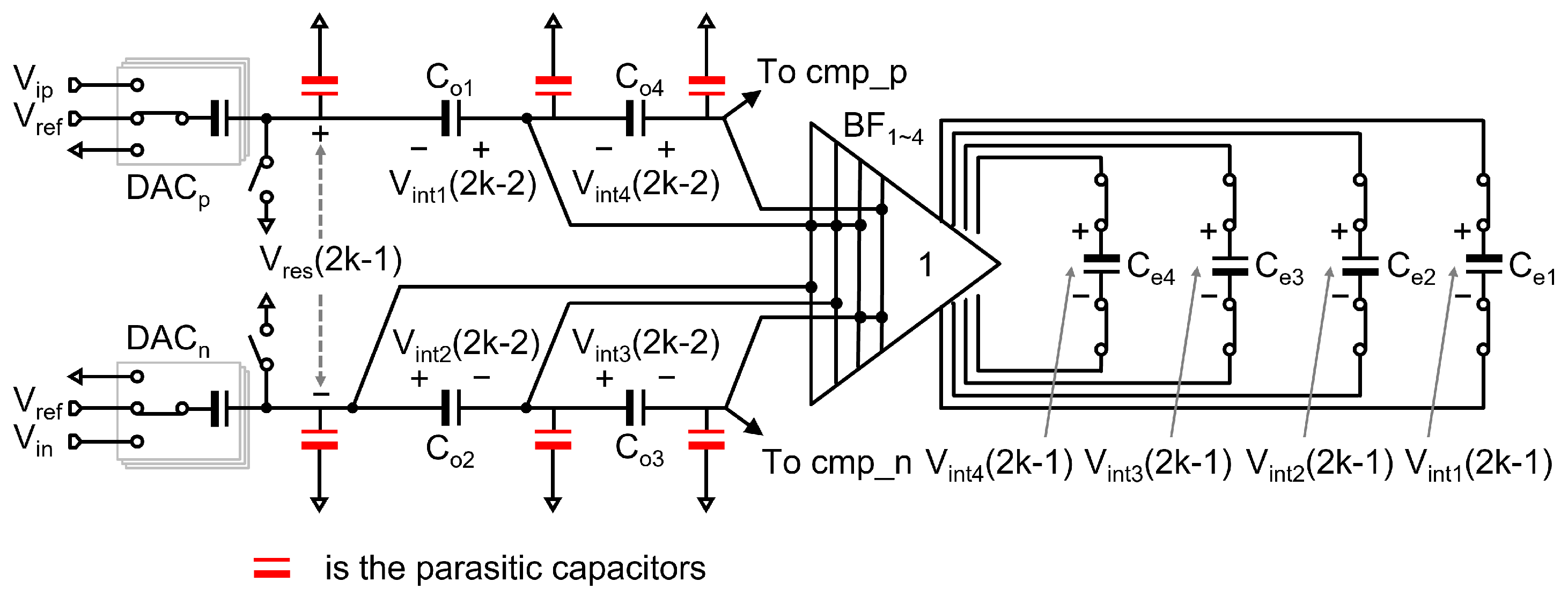
3. Noise-Shaping SAR ADC with CSB Integrator

The CSB integrator is easy to extend to the high order. As shown in Figure 10, four differential buffers and four pairs of integration capacitors ($C_{oi}$-$B{F}_i$-$C_{ei}$, $i=1\sim 4$) form the fourth-order CSB integrator. Incorporating this CSB integrator in an SAR ADC, a fourth-order NS-SAR ADC can be realized, as shown in Figure 10. For simplicity, the comparator and SAR logic are not shown.

The operation of the fourth-order NS-SAR with capacitor stacking and buffering is illustrated in the following.

During the sampling and conversion phases of an odd ADC cycle $2k-1$, the buffers are disabled to save power and the integration capacitors $C_{o1}$ to $C_{o4}$ are stacked over the DACs in the p-side and n-side. Since $C_{o1}$ to $C_{o4}$ hold the previous integration results $V_{int1}\sim V_{int4}(2k-2)$, the stacking operation realizes the addition of the present input signal with the previous integration results and avoids significant signal attenuation. Therefore, a standard one-input-pair comparator connected between the right side of $C_{o3}$ and $C_{o4}$ can be used for SAR conversion.

At the end of SAR conversion, the residue voltage $V_{res}(2k-1)$ is obtained across the top plates of the DACs, and the differential buffers $B{F}_{1\sim 4}$ are enabled. Simultaneously, $B{F}_1$ (connected across $C_{o1}$-$DA{C}_p$-$DA{C}_n$) delivers the first-order integration result $V_{int1}(2k-1)$ to $C_{e1}$:

$$\begin{array}{cc}\hfill V_{int1}(2k-1)& =V_{res}(2k-1)+V_{int1}(2k-2)\hfill \end{array}$$

(9)

$B{F}_2$ (connected across $C_{o1}$-$DA{C}_p$-$DA{C}_n$-$C_{o2}$) delivers the second-order integration result $V_{int2}(2k-1)$ to $C_{e2}$:

$$\begin{array}{cc}\hfill V_{int2}(2k-1)& =V_{res}(2k-1)+V_{int1}(2k-2)+V_{int2}(2k-2)\hfill \\ \hfill & =V_{int1}(2k-1)+V_{int2}(2k-2)\hfill \end{array}$$

(10)

$B{F}_3$ (connected across $C_{o1}$-$DA{C}_p$-$DA{C}_n$-$C_{o2}$-$C_{o3}$) delivers the third-order integration result $V_{int3}(2k-1)$ to $C_{e3}$:

$$\begin{array}{cc}\hfill V_{int3}(2k-1)& =V_{res}(2k-1)+V_{int1}(2k-2)+V_{int2}(2k-2)+V_{int3}(2k-2)\hfill \\ \hfill & =V_{int2}(2k-1)+V_{int3}(2k-2)\hfill \end{array}$$

(11)

$B{F}_4$ (connected across $C_{o4}$-$C_{o1}$-$DA{C}_p$-$DA{C}_n$-$C_{o2}$-$C_{o3}$) delivers the 3rd-order integration result $V_{int4}(2k-1)$ to $C_{e4}$.

$$\begin{array}{cc}\hfill V_{int3}(2k-1)& =V_{res}(2k-1)+V_{int1}(2k-2)+V_{int2}(2k-2)\hfill \\ \hfill & +V_{int3}(2k-2)+V_{int4}(2k-2)\hfill \\ \hfill & =V_{int3}(2k-1)+V_{int4}(2k-2)\hfill \end{array}$$

(12)

After the fourth-order integration, the dynamic buffers are disabled to save power. It must be mentioned that the four integrations can be performed at the same time. This saves the integration time compared to the prior noise-shaping SAR ADCs, which need to perform the integrations one by one.

During the next even cycle 2k, the buffer and integration capacitor network is flipped to perform chopping. Also, the roles of $C_o$ and $C_e$ are swapped, $C_{e1}$ to $C_{e4}$ are stacked over the DACs, and $C_{o1}$ to $C_{o4}$ are used to store the new integration results.

Based on the previous analysis of the operation of NS-SAR ADC, we can draw its signal flow diagram, as shown in Figure 11, considering the noise of the buffers as $n_{BF1\sim 4}$. The final digital output can be expressed as

$$\begin{array}{cc}\hfill D_{out}\left(z\right)\approx & V_{in}\left(z\right)+n_{samp}\left(z\right)+(n_{cmp}\left(z\right)+Q\left(z\right))·{(1-z^{-1})}^4\hfill \\ \hfill & +n_{B{F}_1}\left(z\right)+n_{B{F}_2}\left(z\right)·(1-z^{-1})\hfill \\ \hfill & +n_{B{F}_3}\left(z\right)·{(1-z^{-1})}^2+n_{B{F}_4}\left(z\right)·{(1-z^{-1})}^3\hfill \end{array}$$

(13)

For the buffer $B{F}_1$ used for the first-order integration, its noise $n_{BF1}$ is unshaped, which is the most significant noise of the integrator. For other buffers $B{F}_{2\sim 4}$, their noise is first-order, second-order and third-order shaped, respectively.

4. Design Consideration and Circuit Implementation

4.1. The Parasitic Capacitance from Capacitor Stacking

As discussed above, ideally, the CSB integrator has no signal attenuation issue and therefore can realize a lossless integrator. However, in practice, the signal attenuation issue is unavoidable due to the parasitic capacitance of capacitors, switches, metal wire and buffer input transistors [21], as shown in Figure 12. The parasitic capacitance causes the NTF degradation, the resulting NTF becomes

$$\begin{array}{cc}\hfill NTF\approx & (1-{\alpha }_1{z}^{-1})(1-{\beta }_1{z}^{-1})(1-{\alpha }_2{z}^{-1})(1-{\beta }_2{z}^{-1}),\hfill \\ \hfill & {\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2<1\hfill \end{array}$$

(14)

Note that the parasitic capacitance increases with the number of capacitor stacking, which makes the capacitor stacking number higher than 2 impractical. Owing to differential circuit implementation [16], the fourth-order noise shaping can be realized by only stacking 2 layers of capacitors.

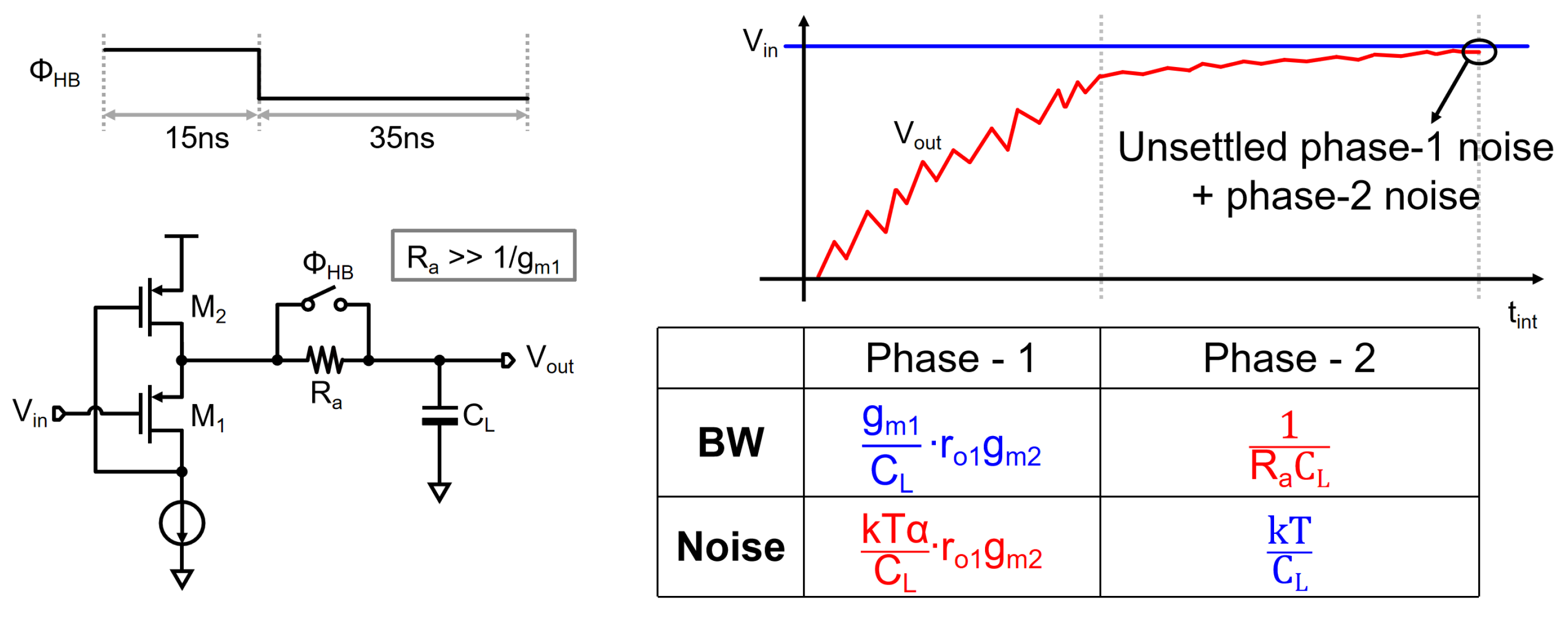
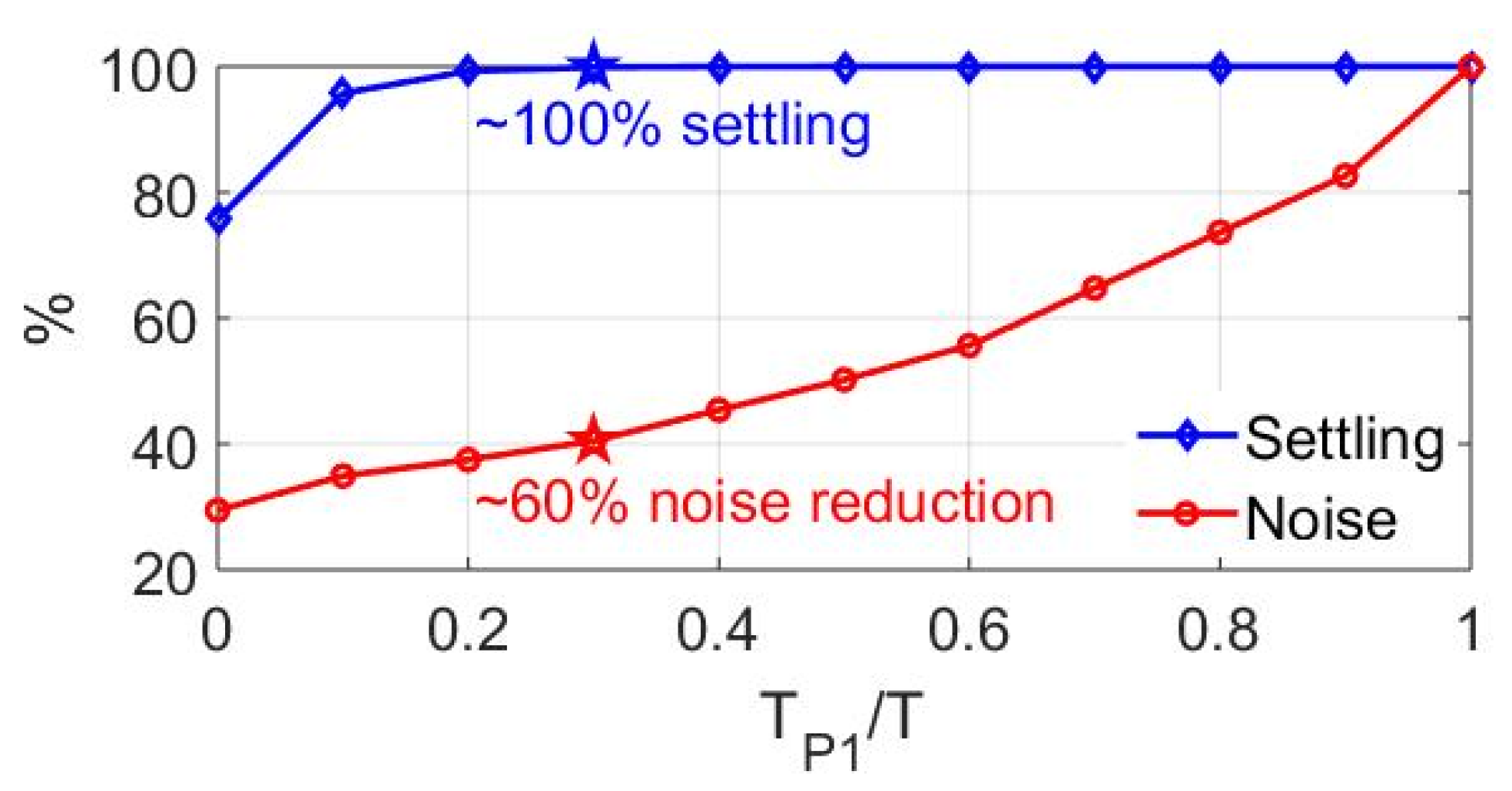
4.2. Non-Idealities from Switches

Due to the ping-pong operation and the fourth-order integration, many switches are used in the signal path, and it is necessary to consider the effect of undesirable switching characteristics on system performance.

First, we need to consider the charge injection of switches. As shown in Figure 13, after the buffer stores the integration voltage $V_{int}=(V_{+}-V_{-})$ in $C_{int}$, we can model the charge from switching off as Q, and the error voltage $V_{ci}$ can be written as $Q/C_{int}$. The integration voltage with charge injection is $V_{int}^{\prime }=V_{int}+V_{ci}=V_{int}+Q/C_{int}$. Moreover, the switches in series with stacked capacitors also introduce integration errors, and then the fourth-order integration voltage can be written as Equation (15), where $V_{ci}\propto N/C_{int}$, N is the number of switches.

$$\begin{array}{cc}\hfill V_{int4}\left(n\right)\approx & V_{int1}(n-1)+V_{int2}(n-1)\hfill \\ \hfill & +V_{int3}(n-1)+V_{int4}(n-1)+V_{ci}\hfill \end{array}$$

(15)

Fortunately, since the integrator only processes the small residue signal, the charge leakage has a constant error. Therefore, as with offset and flicker noise, the charge leakage can also be addressed by chopping.

Another potential issue is the switch leakage, which can also make $V_{int}$ inaccurate. During sampling and conversion, ${\varphi }_{en},{\varphi }_{int}=0$, the charge on $C_{int}$ is partially released by leakage current, resulting in inaccurate integration voltage, as shown in Equation (16).

$$\begin{array}{cc}\hfill V_{int}^{\prime }\approx & V_{int}-{\displaystyle \frac{I_{leak}·(T_{samp}+T_{conv})}{C_{int}}}\hfill \end{array}$$

(16)

To reduce charge leakage, we need to reduce the leakage current or increase the off-resistance of switches. However, this necessitates switches with small $W/L$ and high on-resistance, leading to a long settling time during integration. It can be helpful to use the bootstrapped technique to reduce the switch size while maintaining the low on-resistance of switches.

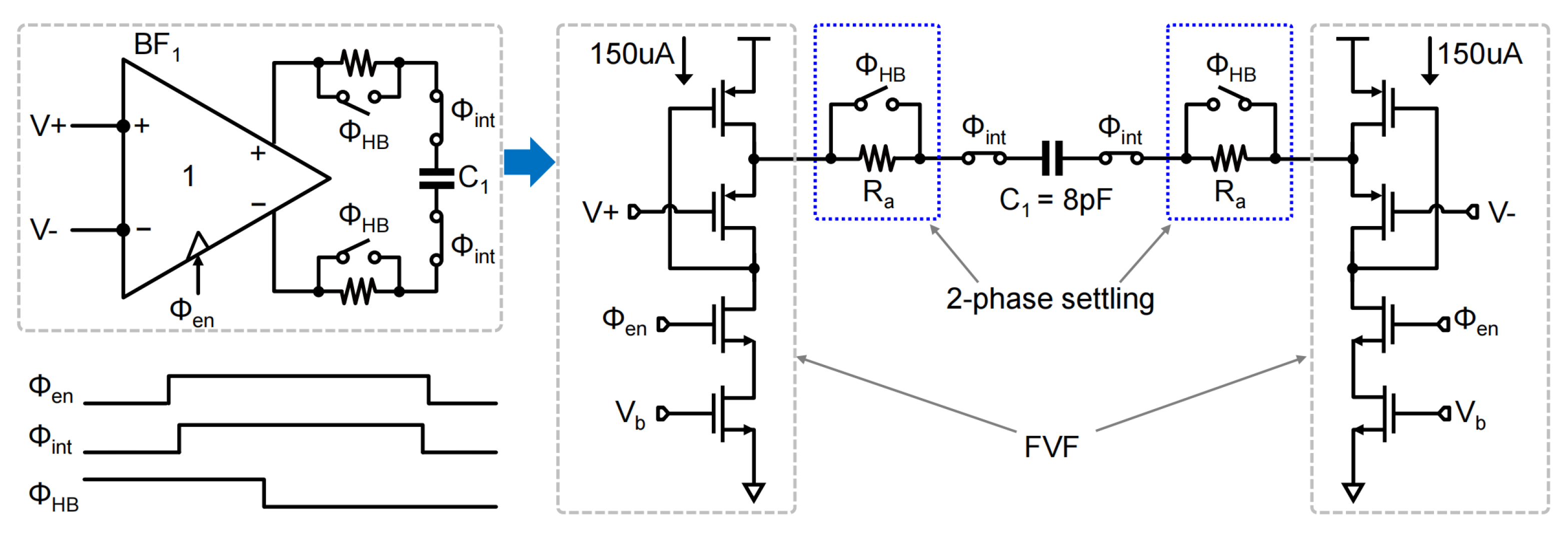
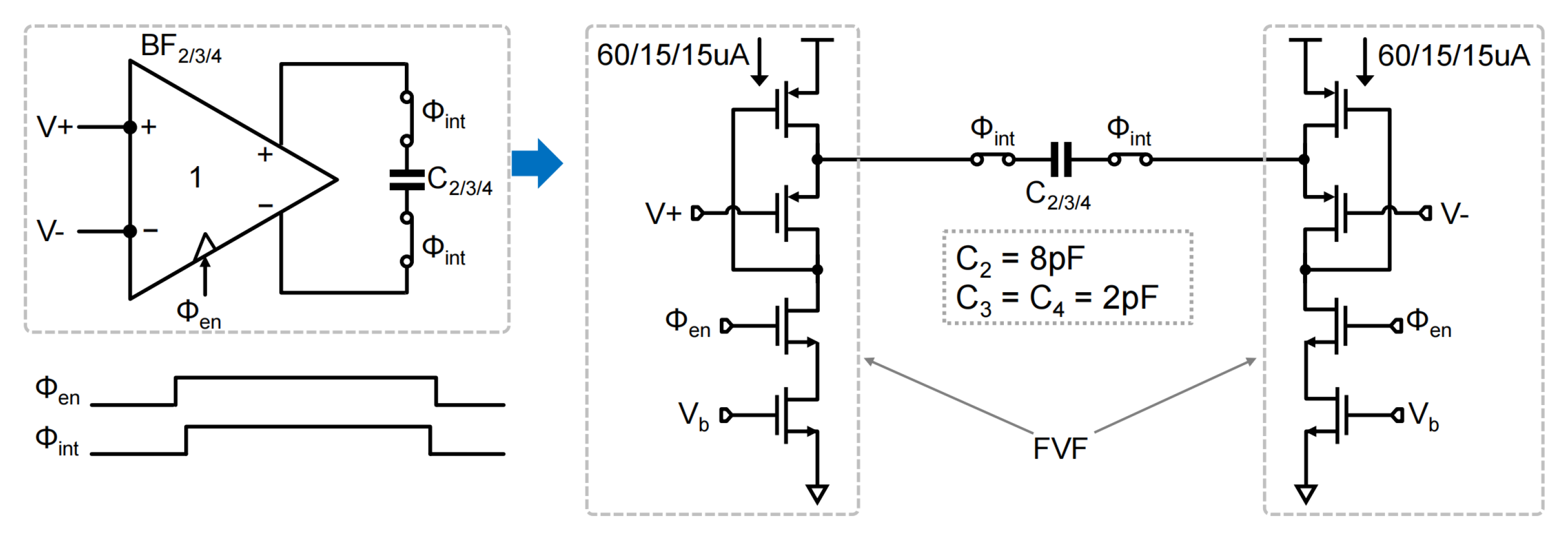
4.3. Integrator Design

In works [16,18], the unity-gain buffers are used to realize the CSB integrator, while there are some other approaches. The works [17,19,22] use open-loop amplifiers instead of buffers to provide extra gain for the integration path, as shown in Figure 14.

After the SAR conversion of $k-1$ cycle, the integration capacitor that holds the integration results $V_{int}(k-1)$ is stacked over the DACs that hold the residue voltage $V_{res}(k-1)$. The amplifier then transfers this new result $V_{res}(k-1)+V_{int}(k-1)$ to a temporary holding capacitor $C_{out}$. During the sampling phase, the capacitor $C_{int}$ is reset and the amplifier is switched off to reduce power. Then, during conversion, $C_{out}$ is merged with $C_{int}$ to deliver the integration results through charge sharing. The new integration results can be obtained as

$$\begin{array}{cc}\hfill V_{int}\left(k\right)& ={\displaystyle \frac{A}{K}}[V_{res}(k-1)+V_{int}(k-1)]\hfill \\ \hfill K& ={\displaystyle \frac{C_{int}}{C_{int}+C_{out}}}\hfill \end{array}$$

(17)

As shown in Equation (17), if one can make the amp gain A equal to the charge sharing ratio K, an integrator with a transfer function of $z^{-1}/\left(1-z^{-1}\right)$ can be realized.

Compared to the unity-gain buffer-based CSB integrator, the merit of the amplifier approach is that it only needs to switch a small capacitor. For the same kT/C noise budget, the buffered capacitor is A times smaller than that in the unity-gain buffer-based CSB integrator. Considering the same settling speed, the reduced capacitor size relaxes the on-resistance of switches and therefore reduces the switch size and parasitic capacitance. The reduced parasitic capacitance further enhances the noise-shaping effect.

In addition, the passive gain can be introduced to reduce the power consumption and hardware complexity for realizing the high-order CSB-based NS filter [18,23]. As shown in Figure 15, in the k-th cycle, the unity-gain buffer extracts and stores the residue error of $V_{EF}\left(k\right)$ on $C_{EF1A}$ and $C_{EF1B}$. Those two capacitors, $C_{EF2A}$ and $C_{EF2B}$, which store the residue error $V_{EF}(k-1)$ in (k − 1)-th cycle are stacked in series to implement a 2× passive gain. Together with the reversely connected EF capacitors $C_{EF3A}$ and $C_{EF3B}$ from the (k − 2)-th cycle, it realizes $2·V_{EF}(k-1)-V_{EF}(k-2)$ for the second-order FIR filter. With capacitor stacking, the passive summation of the NS-SAR input and the FIR filter is naturally realized. Compared to [16], only one buffer is required to realize the second-order NS. However, using more stacked capacitors introduces more parasitics, which leads to NTF degradation.

4.4. Buffer Design

In the integrator with CSB, the buffer serves as the core component. There are several ways to implement a buffer, as shown in Figure 16.

First, we can use an amplifier. However, the gain of the amplifier is sensitive to PVT variations. Second, as mentioned before, we can use a source follower. Considering the actual buffer whose gain is A, Equation (1) can be rewritten as Equation (18):

$$\begin{array}{cc}\hfill V_{int}\left(n\right)& =A\ast (V_{res}\left(n\right)+V_{int}(n-1))\hfill \end{array}$$

(18)

Then, we can obtain the NTF as shown in Equation (19):

$$\begin{array}{cc}\hfill NTF={\displaystyle \frac{V_{int}\left(z\right)}{V_{res}\left(z\right)}}& ={\displaystyle \frac{A}{1-A{z}^{-1}}}\hfill \end{array}$$

(19)

By using a long-channel PMOS as the input transistor, the gain A of the source follower can approach 1. This leads to a sharp and robust NTF for the NS-SAR ADC. However, the bandwidth of a conventional source follower is small, which results in slow settling of the integration results. To improve settling, we can use the flipped voltage follower (FVF). Compared to the conventional source follower, the FVF provides smaller output resistance, larger bandwidth, and faster settling. It extends the bandwidth by approximately $r_{o1}·g_{m2}$ times, but the increased bandwidth comes at the cost of increased noise.

In order to reduce the noise of the FVF buffer, a two-phase settling technique is used in [16]. As shown in Figure 17 and Figure 18, a switch-controlled resistor $R_a$ is added at the FVF output to adjust its bandwidth. During phase 1, $R_a$ is bypassed. This enables fast settling, but the FVF generates large noise. During phase 2, $R_a$ is switched on.

$R_a$ is a large resistor; it limits the bandwidth of the FVF, slowing the settling and lowering the noise. For $R_a$ much larger than $1/g_{m1}$, the noise from $R_a$ will be the dominant noise source of the FVF buffer in phase 2. Therefore, the total noise contribution in phase 2 is about $kT/C_L$, which is much smaller than the noise of phase 1. The final noise at the end of the integration phase has two parts. One is the large noise from phase 1, which settles during phase 2 and becomes small. The other comes directly from phase 2. Although phase 1 generates large noise, this noise settles during phase 2. Therefore, the proposed FVF buffer with two-phase settling combines the benefits of fast settling and low noise.

Considering both settling and noise, there is a trade-off between them. If we set a short phase 1 and long phase 2, the phase 1 noise can settle well during phase 2, leading to low noise at the end of the integration phase. However, because phase 1 is short, the signal settling will not be optimal. Conversely, if we set a long phase 1 and a short phase 2, the signal settling will be better, but the unsettled noise from phase 1 will be large, resulting in large noise at the end of the integration phase.

In order to select an appropriate time ratio of $T_{p1}/T_{int}$ during the total integration time 50 ns from the simulation, as shown in Figure 19, it can be seen that when $T_{p1}/T_{int}=0.3$ (i.e., $T_{p1}=15$ ns and $T_{p2}=35$ ns), the signal can be fully settled for the certain integration time, but the noise is reduced by about $60\%$ compared to the FVF alone. In this way, the buffer with two-phase settling combines the benefits of fast settling and low noise.

For the buffer used in the first-order integration, its noise is unshaped. Therefore, the two-phase settling technique is used to reduce the noise. As shown in Figure 17 and Figure 20, the differential buffer consists of a pair of FVFs and the FVFs are dynamically controlled by ${\varphi }_{en}$ to save power. For other buffers, their noises can be shaped and thus are negligible, so we can just use the conventional FVFs for simplicity. In addition, the bias currents of the FVFs are scaled according to their load capacitors to ensure a similar settling. Moreover, Monte Carlo simulation shows that the gain of the FVF is around 0.95 with $1\%$ $3\delta$ variation. This ensures a robust and sharp NTF.

5. Conclusions

As shown in

Table 1. Performance summary and comparison.

	ISSCC 16 Shu [2]	ISSCC 17 Liu [10]	ISSCC 20 Liu [14]	ISSCC 20 Tang [3]	ISSCC 20 Jie [9]	ISSCC 22 Wang [19]	ISSCC 23 Wang [18]	ISSCC 24 Cheng [17]	ISSCC 21 Liu [16]
Process	55 nm	28 nm	40 nm	40 nm	28 nm	65 nm	28 nm	28 nm	40 nm
NS Technique	Closed-loop OTA	Open-loop DA	CS 1	Closed-loop DA	Open-loop amp.	Cap stack. 2 & DA & CS	Cap stack. & dynamic buffering & Passive gain	Cap stack. & DA & Passive gain	Cap stack. & dynamic buffering
NS Order	1	1	1	2	4	4	2	4	4
Sharp NTF Across PVT	Yes	No	No	Yes	No	Yes	Yes	Yes	Yes
Supply (V)	1.2	1	1.1	1.1	1	1.2/2	2	1	1.1
Area (mm2)	0.072	0.0049	0.061	0.037	0.02	0.075	0.026	0.09	0.094
$F_s$ (MS/s)	1	132	2	10	2	5	2.4	5	5
Power (μW)	15.7	460	67.4	107	120	73.8/133.88 3	160	107.38	340
OSR	500	13.2	25	8	10	5	8	25	10
BW (kHz)	1	5000	40	625	100	500	150	100	250
SNDR (dB)	101	79.7	90.5	83.8	87.6	84.1	92.5	94.3	93.3
DR (dB)	101.7	81.8	94.3	85.5	89	84.9	93.9	94.6	95
$Fo{M}_s$ 4 (dB)	178.9	180.1	178.2	181.5	176.8	182.4/180 3	182.2	184	182

¹ CS = Charge sharing. ² Cap stack = Cap stacking. ³ With Buffer Power Included. ⁴ $Fo{M}_s=\mathrm{SNDR}+10{log}_{10}(\mathrm{BW}/\mathrm{Power})$.

, we listed all NS-SARs using the CSB technique, and compared to other methods, the CSB technique is a more energy-efficient way to realize high-order NS-SAR ADC. It realizes the integration by stacking the residue capacitor with the integration capacitor and storing the stacking result through a unity-gain buffer. A source follower can be used as the buffer, which is simple and PVT-robust. This integrator does not require any amplifier and can realize the sharp NTF with zeros close to the unit circle. It has low hardware complexity and is easy to extend to high order.

Following the work of [16], this paper gives a tutorial on the NS-SAR ADC with capacitor stacking and buffering. The principle of the CSB integrator and the NS-SAR ADC are analyzed from the fundamental first-order single-ended one to the advanced high-order differential one. The non-idealities in the ADC are considered, including the parasitic capacitance and charge leakage. We also present the design of core building circuits and discuss the design trade-offs between the noise, settling and shaping effects. This paper can be helpful for researchers who are interested in high-resolution ADCs.