Equivalence Checking of System-Level and SPICE-Level Models of Linear Circuits †
Abstract
1. Introduction
- A novel equivalence checking methodology for SPICE-level models and behavioral system-level models that go beyond single LTFs.
- Leverage SFGs, canonical representations, and linear graph modeling techniques.
- Extension of applicability to the complete class of complex SISO linear analog circuits.
- Demonstration of equivalence checking on complex filter models, Small-Signal Models (SSM), series connections, and linear analog computers.
2. Related Work
3. Preliminaries
3.1. Signal-Flow Graphs
3.2. Simplification Operations for Signal-Flow Graphs
- Removal of a non-input node
- Parallel edge unification
- Reflexive edge elimination
3.3. SystemC and SystemC AMS
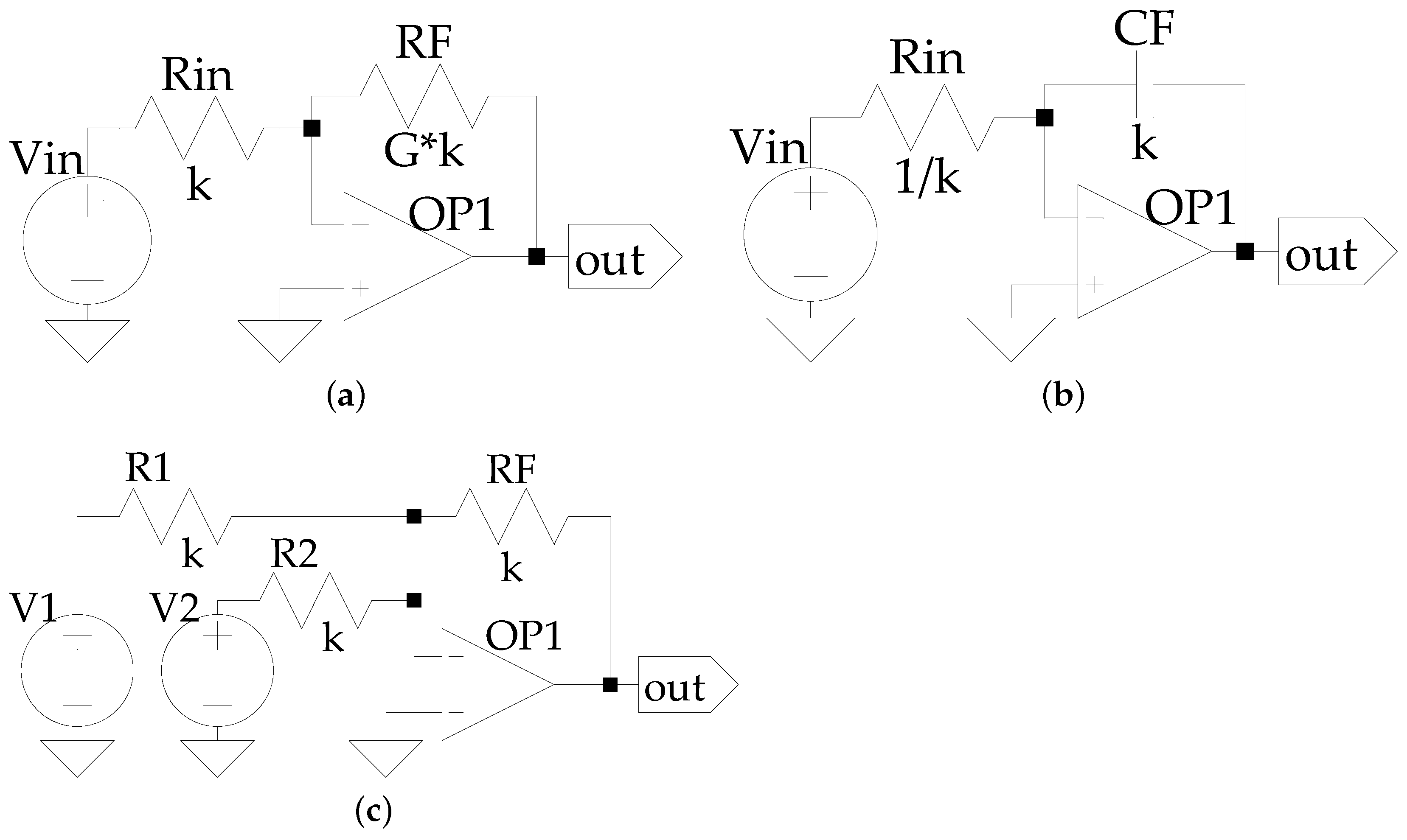
3.4. Motivating Example: Series-Connected HPF and SSM of Common-Source (CS) Amplifier
4. Signal-Flow Driven Equivalence Checking Methodology
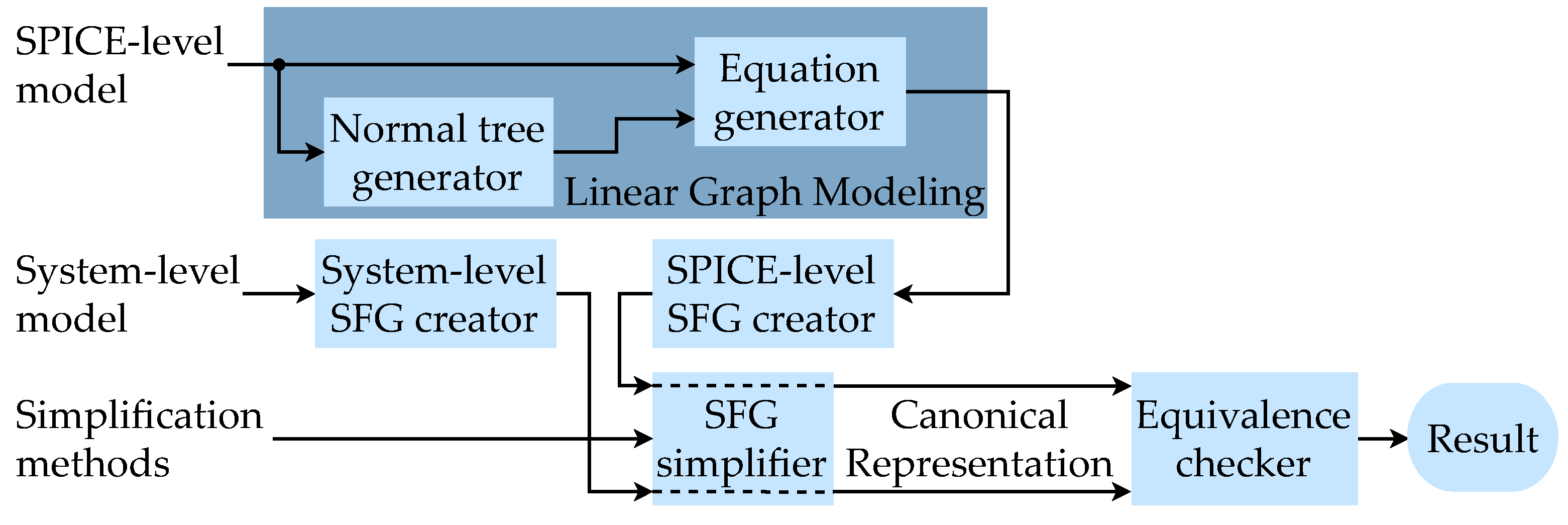
4.1. Methodology Overview
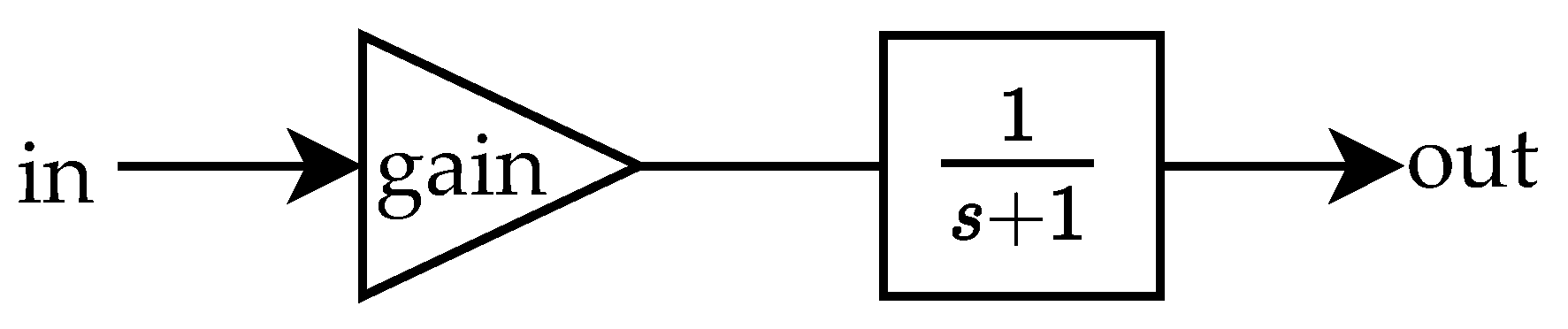
4.2. Creating the Signal-Flow Graph from System-Level Descriptions
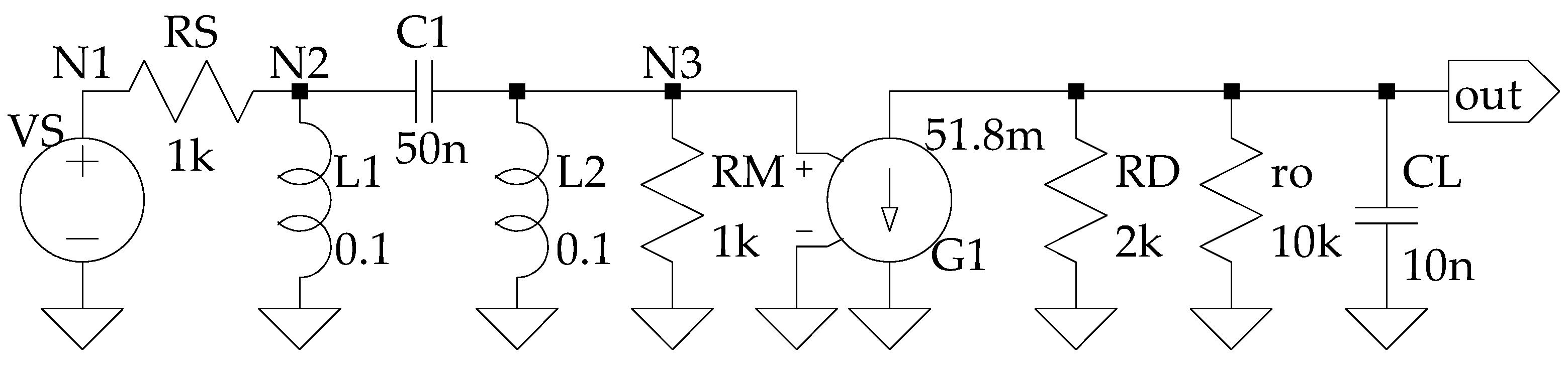
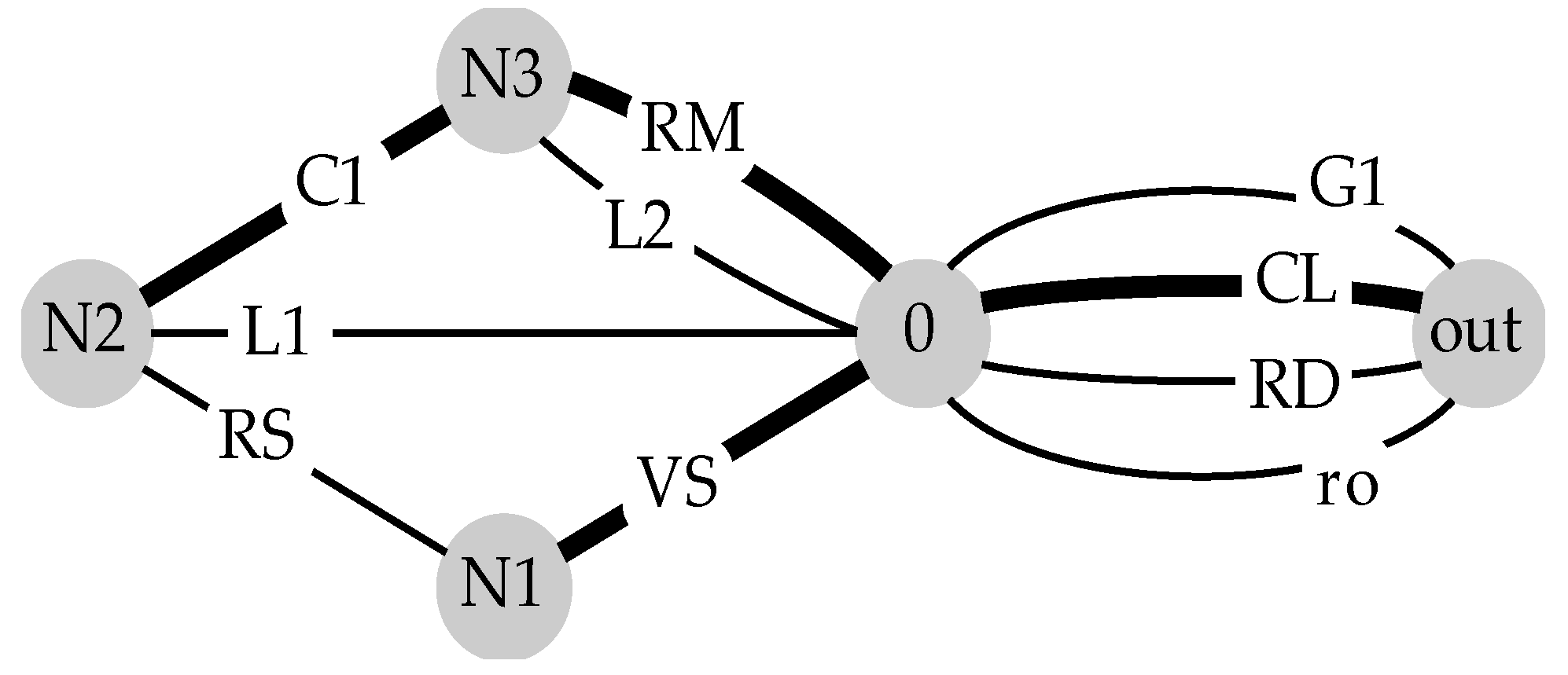
4.3. Creating the Signal-Flow Graph from SPICE-Level Descriptions
- Voltages of components on the normal tree, from elemental equations.
- Currents of components on the normal tree, from continuity equations.
- Voltages of components on the tree links, from compatibility equations.
- Currents of components on the tree links, from elemental equations.
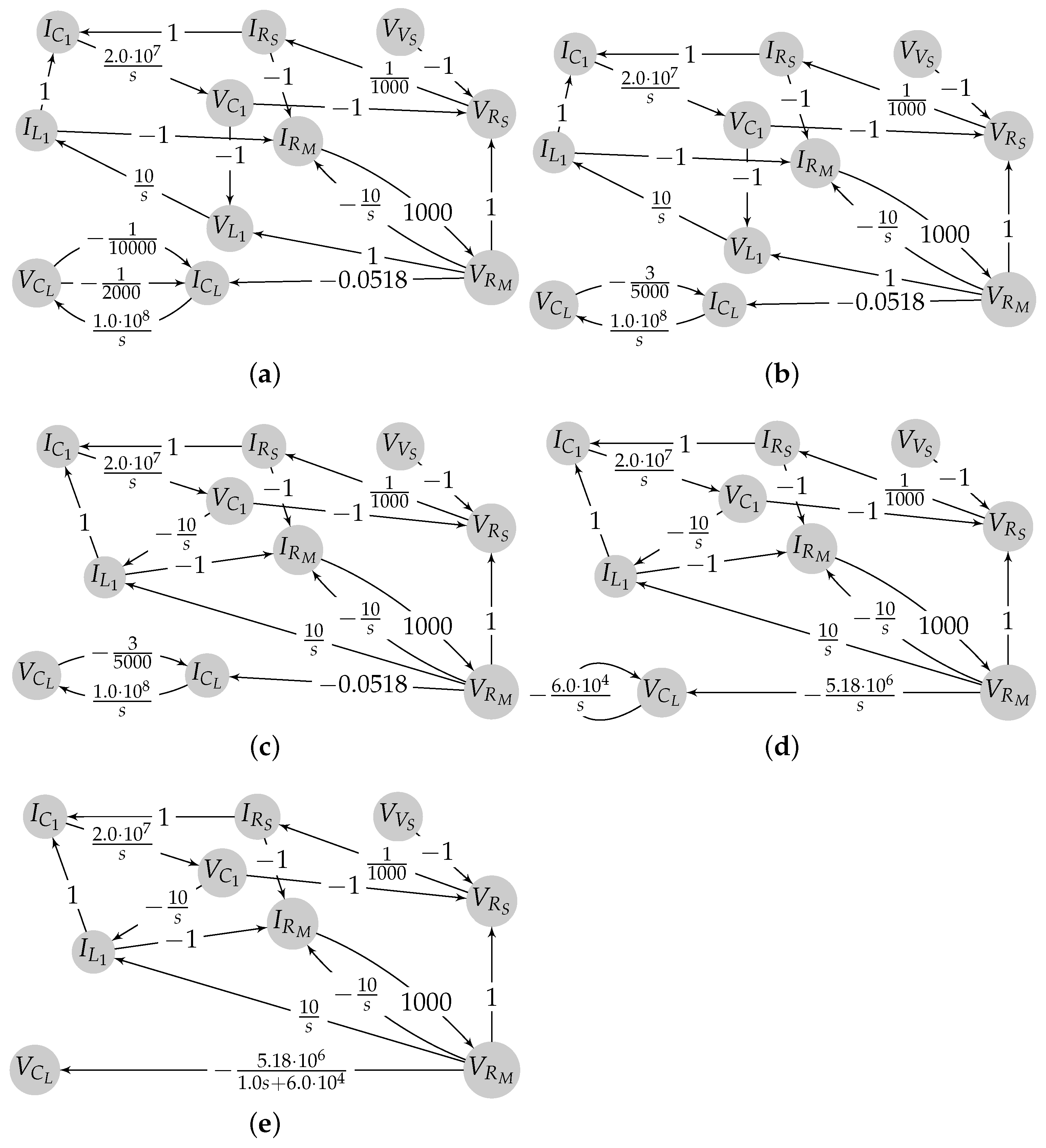
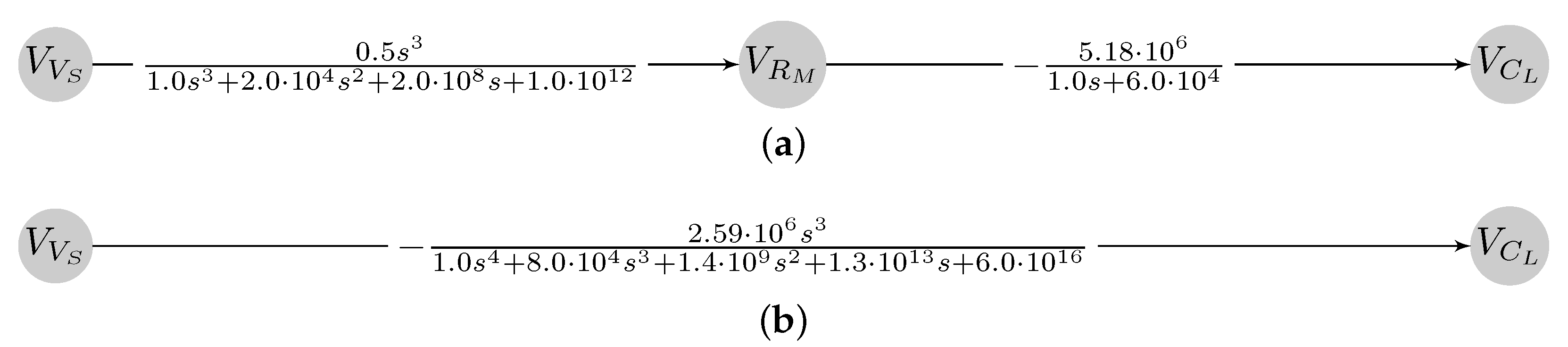
4.4. Reducing the Signal-Flow Graph
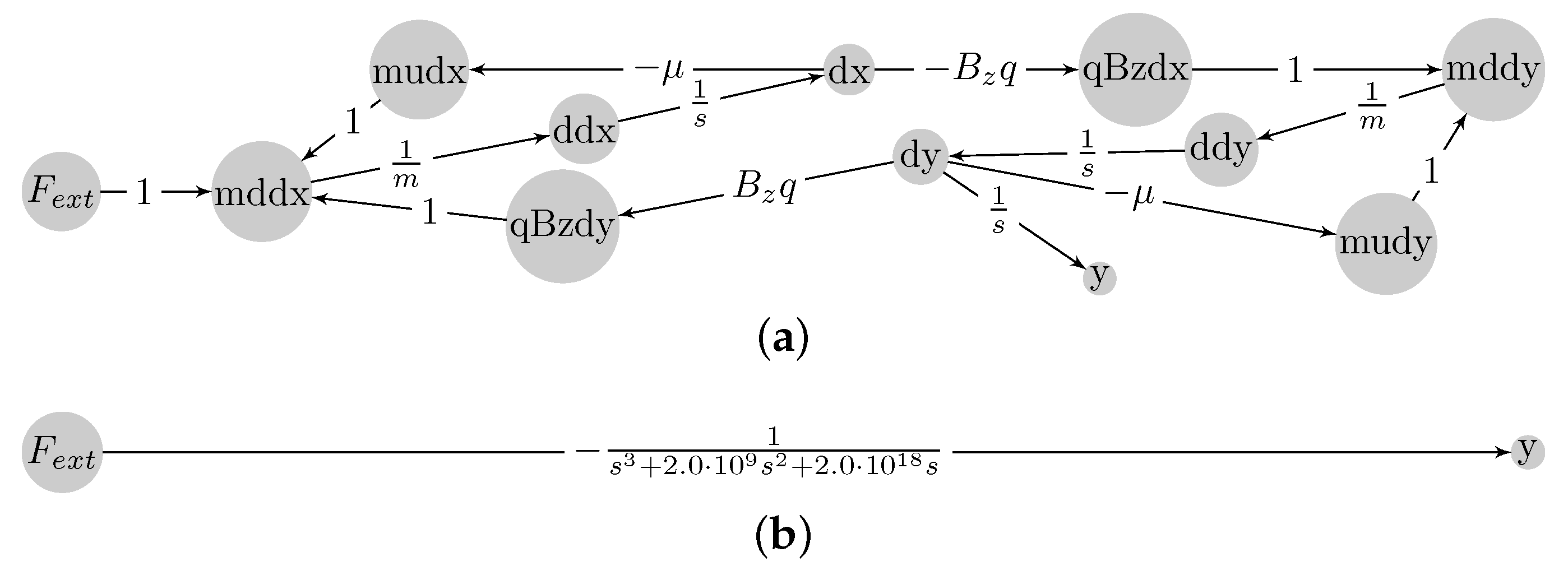
4.5. Illustration
5. Experimental Evaluation
5.1. Experimental Setup
5.2. Equivalence Checking
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SoC | System-on-chip |
| SFG | Signal-flow graph |
| LPF | Low-pass filter |
| HPF | High-pass filter |
| DUV | Design under verification |
| VP | Virtual prototyping |
| ESL | Electronic system level |
| TDF | Timed data flow |
| LSF | Linear signal flow |
| ELN | Electrical linear networks |
| MoC | Model of computation |
| LTF | Laplace transfer function |
| RF | Radio frequency |
| SSM | Small-signal model |
| CS | Common source |
| AMS | Analog/mixed-signal |
References
- Barnasconi, M. SystemC AMS Extensions: Solving the Need for Speed; DAC Knowledge Center: San Francisco, CA, USA, 2010. [Google Scholar]
- Nagel, L.W. SPICE-Simulation Program with Integrated Circuit Emphasis; Electronics Research Laboratory, University of California: Berkeley, CA, USA, 1973. [Google Scholar]
- Grimm, C.; Barnasconi, M.; Vachoux, A.; Einwich, K. An Introduction to Modeling Embedded Analog/Mixed-Signal Systems Using SystemC AMS Extensions; Open SystemC Initiative: Sunnyvale, CA, USA, 2008. [Google Scholar]
- Barnasconi, M.; Grimm, C.; Damm, M.; Einwich, K.; Louërat, M.; Maehne, T.; Pecheux, F.; Vachoux, A. SystemC AMS Extensions User’s Guide; Accellera Systems Initiative: Elk Grove, CA, USA, 2010. [Google Scholar]
- Barnasconi, M.; Einwich, K.; Grimm, C.; Maehne, T.; Vachoux, A. Advancing the SystemC Analog/Mixed-Signal (AMS) Extensions; Open SystemC Initiative: Sunnyvale, CA, USA, 2011. [Google Scholar]
- Pêcheux, F.; Grimm, C.; Maehne, T.; Barnasconi, M.; Einwich, K. SystemC AMS Based Frameworks for Virtual Prototyping of Heterogeneous Systems. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–4. [Google Scholar]
- Drechsler, R. (Ed.) Advanced Formal Verification; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 2004. [Google Scholar]
- Molitor, P.; Mohnke, J. Equivalence Checking of Digital Circuits: Fundamentals, Principles, Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Drechsler, R. Formal System Verification; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Zaki, M.H.; Tahar, S.; Bois, G. Formal Verification of Analog and Mixed Signal Designs: A Survey. Microelectron. J. 2008, 39, 1395–1404. [Google Scholar] [CrossRef]
- Tarraf, A.; Hedrich, L.; Kochdumper, N.; Rechmal-Lesse, M.; Olbrich, M. Equivalence Checking Methods for Analog Circuits Using Continuous Reachable Sets. In Proceedings of the 2020 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Limassol, Cyprus, 6–8 July 2020; pp. 7–12. [Google Scholar] [CrossRef]
- Hedrich, L.; Barke, E. A Formal Approach to Nonlinear Analog Circuit Verification. In Proceedings of the IEEE International Conference on Computer Aided Design (ICCAD), San Jose, CA, USA, 5–9 November 1995; pp. 123–127. [Google Scholar] [CrossRef]
- Hedrich, L.; Hartong, W. Approaches to Formal Verification of Analog Circuits. In Low-Power Design Techniques and CAD Tools for Analog and RF Integrated Circuits; Wambacq, P., Gielen, G., Gerrits, J., van Leuken, R., de Graaf, A., Nouta, R., Eds.; Springer: Boston, MA, USA, 2001; pp. 155–191. [Google Scholar] [CrossRef]
- Hartong, W.; Klausen, R.; Hedrich, L. Formal Verification for Nonlinear Analog Systems: Approaches to Model and Equivalence Checking. In Advanced Formal Verification; Drechsler, R., Ed.; Springer: Boston, MA, USA, 2004; pp. 205–245. [Google Scholar] [CrossRef]
- Steinhorst, S.; Hedrich, L. Advanced Methods for Equivalence Checking of Analog Circuits with Strong Nonlinearities. Form. Methods Syst. Des. 2010, 36, 131–147. [Google Scholar] [CrossRef]
- Singh, A.; Li, P. On Behavioral Model Equivalence Checking for Large Analog/Mixed Signal Systems. In Proceedings of the 2010 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 7–11 November 2010; pp. 55–61. [Google Scholar] [CrossRef]
- Ain, A.; Sanyal, S.; Dasgupta, P. A Framework for Automated Feature Based Mixed-Signal Equivalence Checking. In Proceedings of the VLSI Design and Test; Communications in Computer and Information Science; Kaushik, B.K., Dasgupta, S., Singh, V., Eds.; Springer: Singapore, 2017; pp. 779–791. [Google Scholar] [CrossRef]
- Saglamdemir, M.O.; Dundar, G.; Sen, A. An Analog Behavioral Equivalence Checking Methodology for Simulink Models and Circuit Level Designs. In Proceedings of the 2015 International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Istanbul, Turkey, 7–9 September 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Coskun, K.C.; Hassan, M.; Drechsler, R. Equivalence Checking of System-Level and SPICE-Level Models of Linear Analog Filters. In Proceedings of the Design and Diagnostics of Electronic Circuits and Systems (DDECS), Prague, Czech Republic, 6–8 April 2022. [Google Scholar]
- Mason, S.J. Feedback Theory-Some Properties of Signal Flow Graphs. Proc. IRE 1953, 41, 1144–1156. [Google Scholar] [CrossRef]
- Robichaud, L.P.A. Signal Flow Graphs and Applications; Prentice Hall: Englewood Cliffs, NJ, USA, 1962. [Google Scholar]
- Rasim, F.R.; Sattler, S.M. Analysis of Electronic Circuits with the Signal Flow Graph Method. Circuits Syst. 2017, 8, 261–274. [Google Scholar] [CrossRef][Green Version]
- Analog Devices. LTspice. Available online: https://www.analog.com/en/design-center/design-tools-and-calculators/ltspice-simulator.html (accessed on 23 March 2022).
- Ho, C.W.; Ruehli, A.; Brennan, P. The modified nodal approach to network analysis. IEEE Trans. Circuits Syst. 1975, 22, 504–509. [Google Scholar]
- Rowell, D.; Wormley, D.N. System Dynamics: An Introduction; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Ulmann, B. Analog and Hybrid Computer Programming; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2020. [Google Scholar]

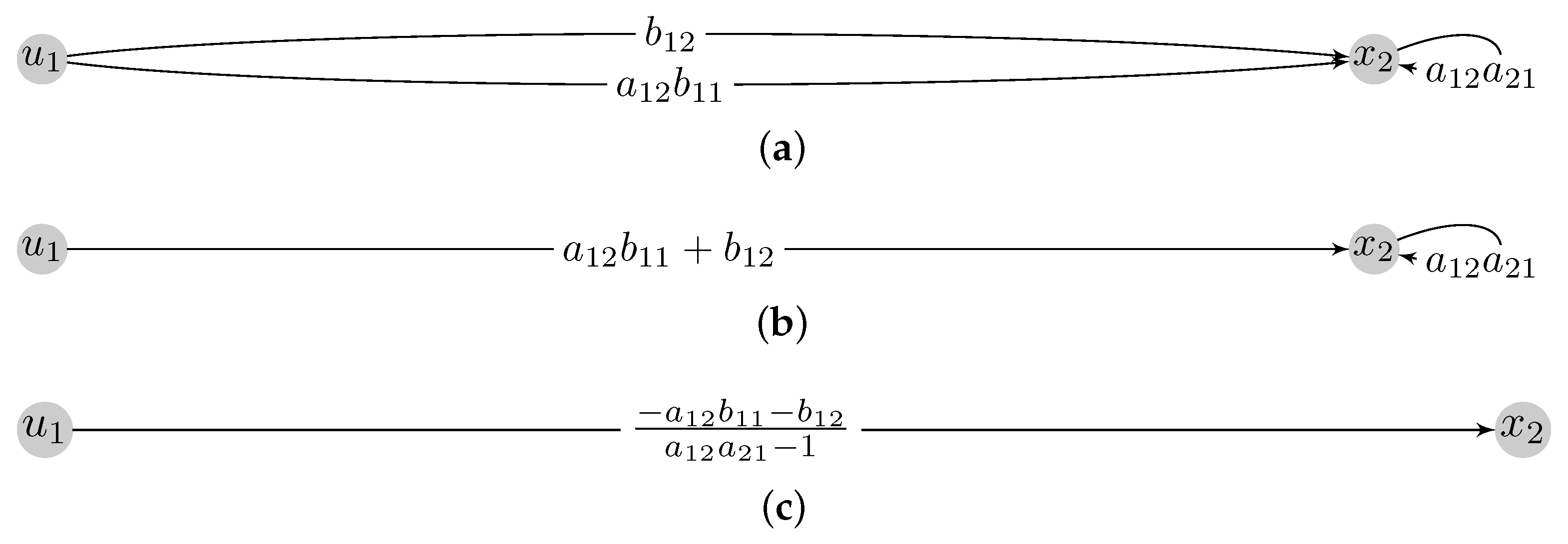












| Source | Approach | Verification Coverage | Applicable Circuits |
|---|---|---|---|
| [12,13,14,15] | State-space-based | Only at finite number of locations in the state-space | All |
| [16,17,18] | Simulation-based | Only for finite number of input signals | All |
| Proposed work | Structural analysis | Complete coverage | Only linear |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coşkun, K.Ç.; Hassan, M.; Drechsler, R. Equivalence Checking of System-Level and SPICE-Level Models of Linear Circuits. Chips 2022, 1, 54-71. https://doi.org/10.3390/chips1010006
Coşkun KÇ, Hassan M, Drechsler R. Equivalence Checking of System-Level and SPICE-Level Models of Linear Circuits. Chips. 2022; 1(1):54-71. https://doi.org/10.3390/chips1010006
Chicago/Turabian StyleCoşkun, Kemal Çağlar, Muhammad Hassan, and Rolf Drechsler. 2022. "Equivalence Checking of System-Level and SPICE-Level Models of Linear Circuits" Chips 1, no. 1: 54-71. https://doi.org/10.3390/chips1010006
APA StyleCoşkun, K. Ç., Hassan, M., & Drechsler, R. (2022). Equivalence Checking of System-Level and SPICE-Level Models of Linear Circuits. Chips, 1(1), 54-71. https://doi.org/10.3390/chips1010006






