Selective Separation of SiO2 and SnO2 Particles in the Submicron Range: Investigating Salt and Surfactant Adsorption Parameter
Abstract
1. Introduction
2. Materials and Methods
2.1. Particle Characterization
2.1.1. Particle Size Distribution
2.1.2. Determination of the Specific Surface Area According to BET SBET
2.1.3. Calculation of the Concentration Needed to Cover the Particles with the Different Ions and SDS
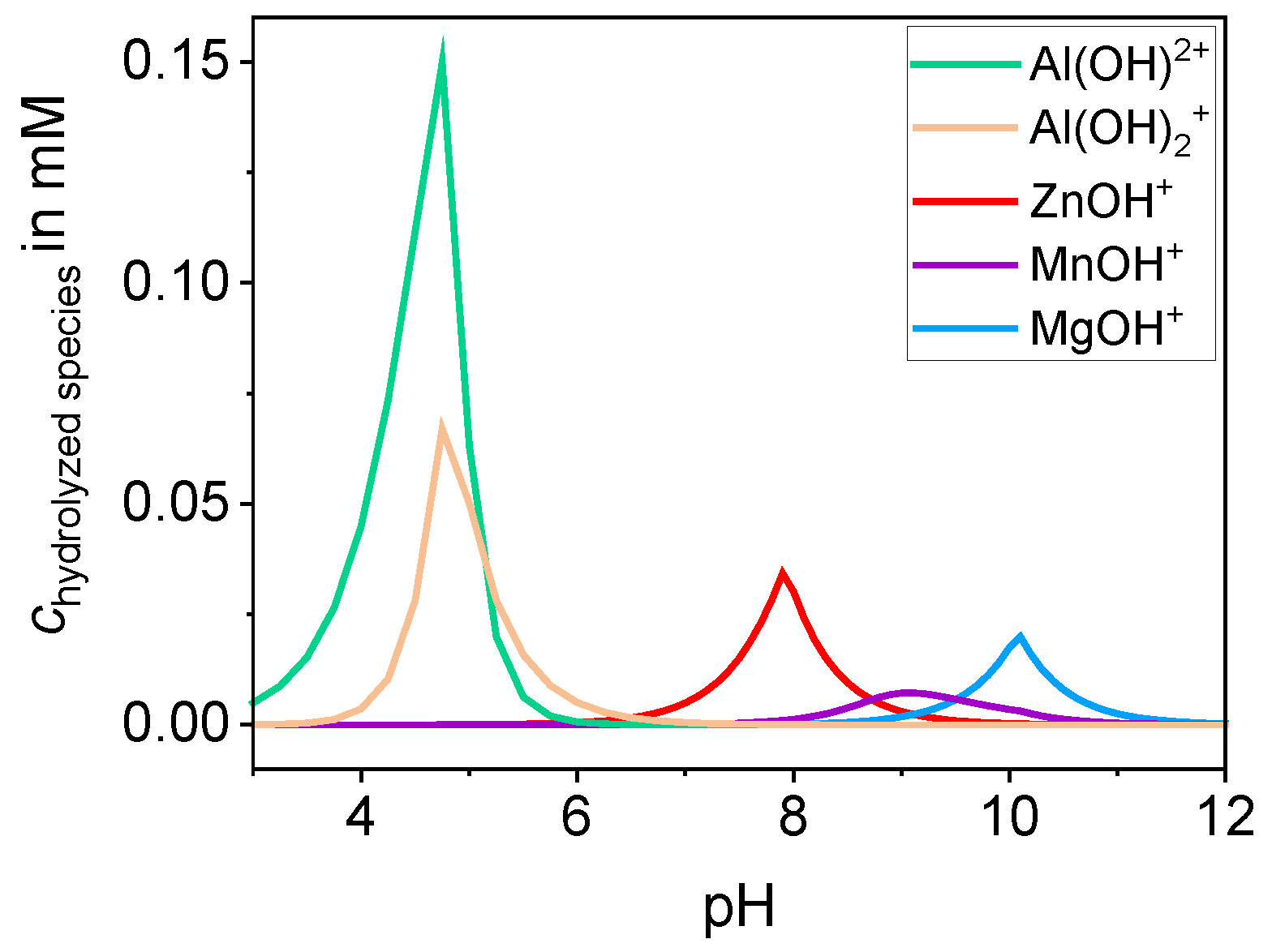
2.2. Formation of the Hydrolyzed Species
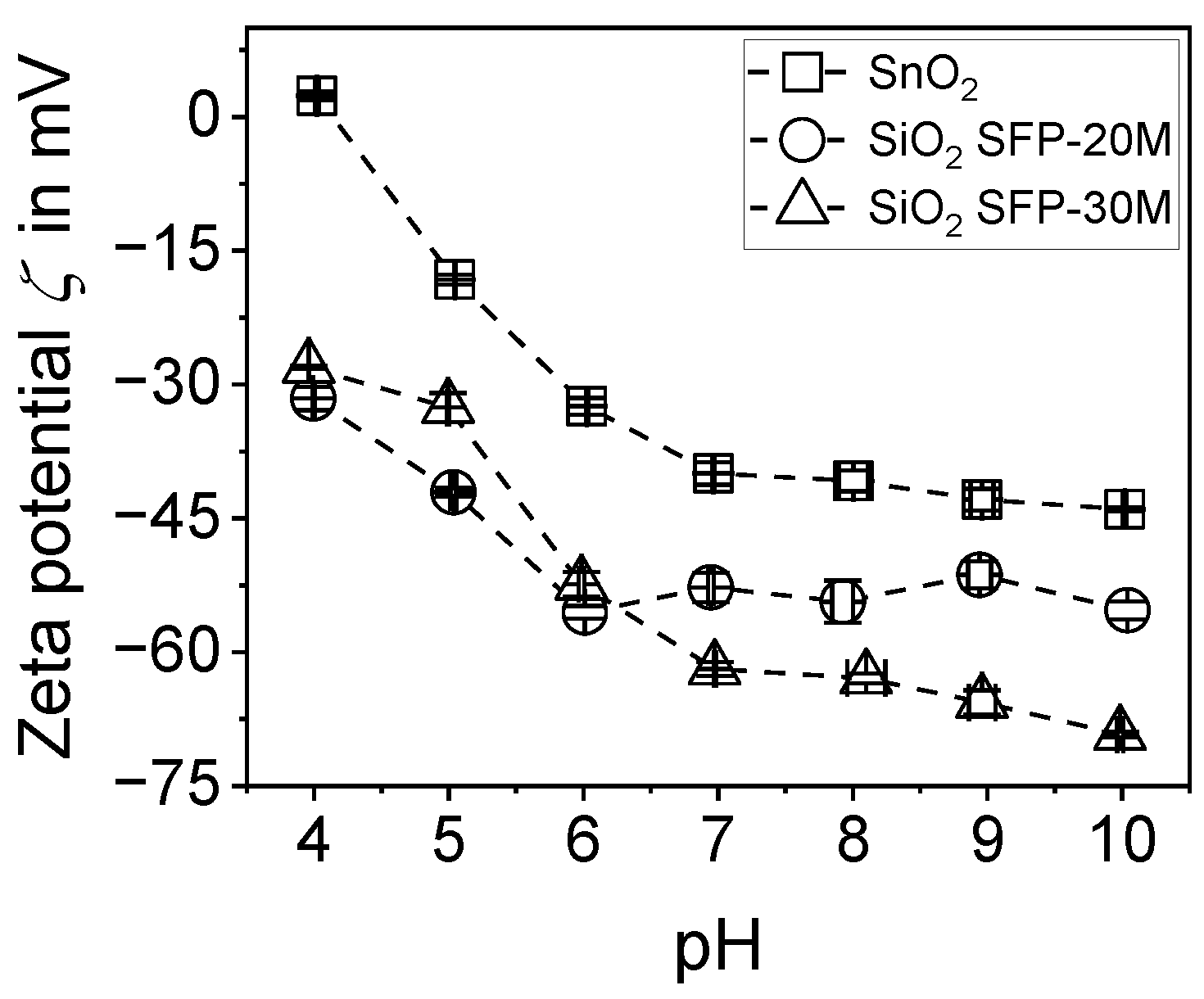
2.3. Determination of the Zeta Potential ζ via Electroacoustic Measurements
2.4. Determination of the Zeta Potential ζ via Electrophoresis Measurements
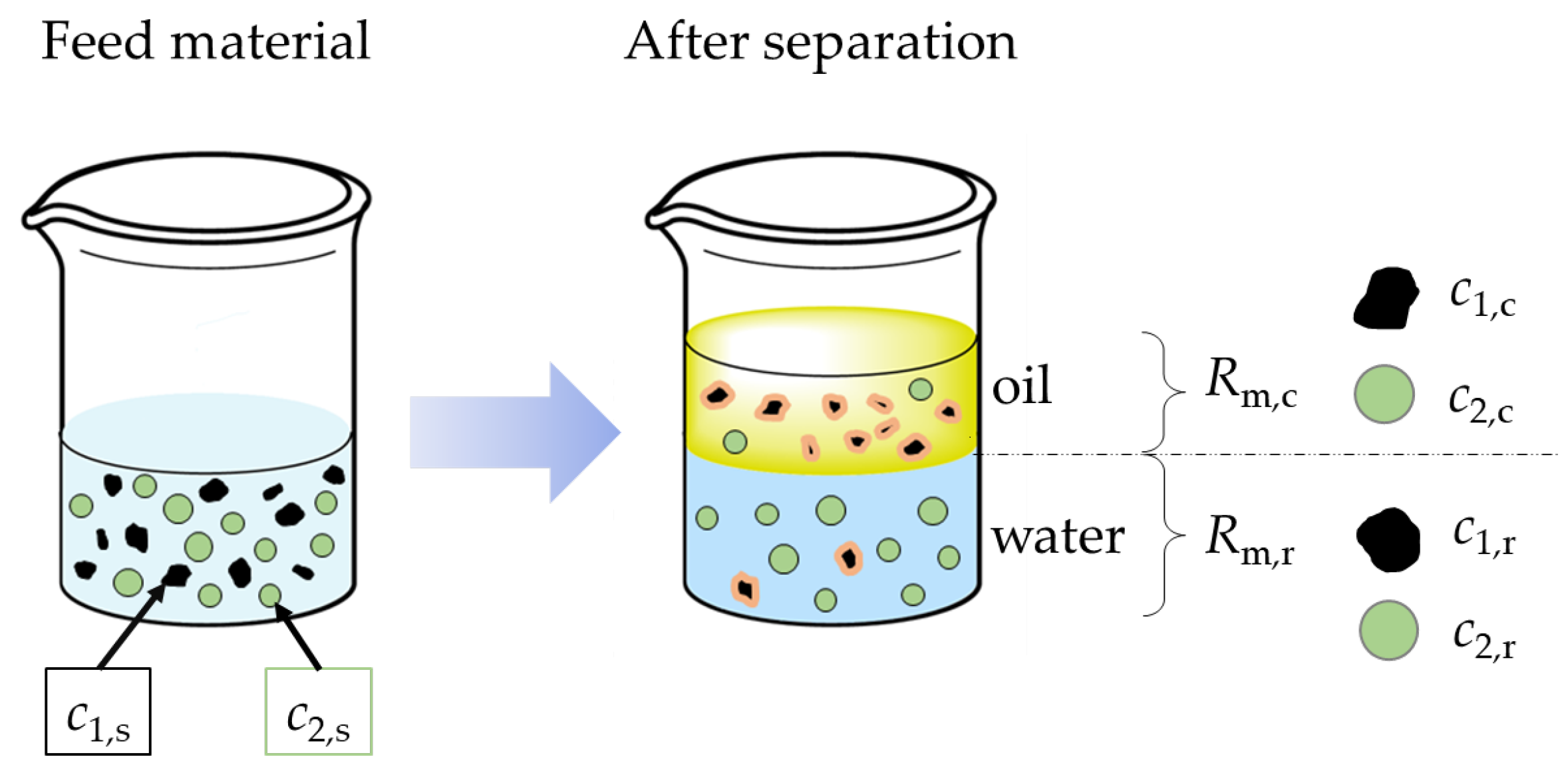
2.5. Liquid–Liquid Extraction and Separation of the Particles
2.6. Determination of the Material Content via XRF Measurements
3. Results
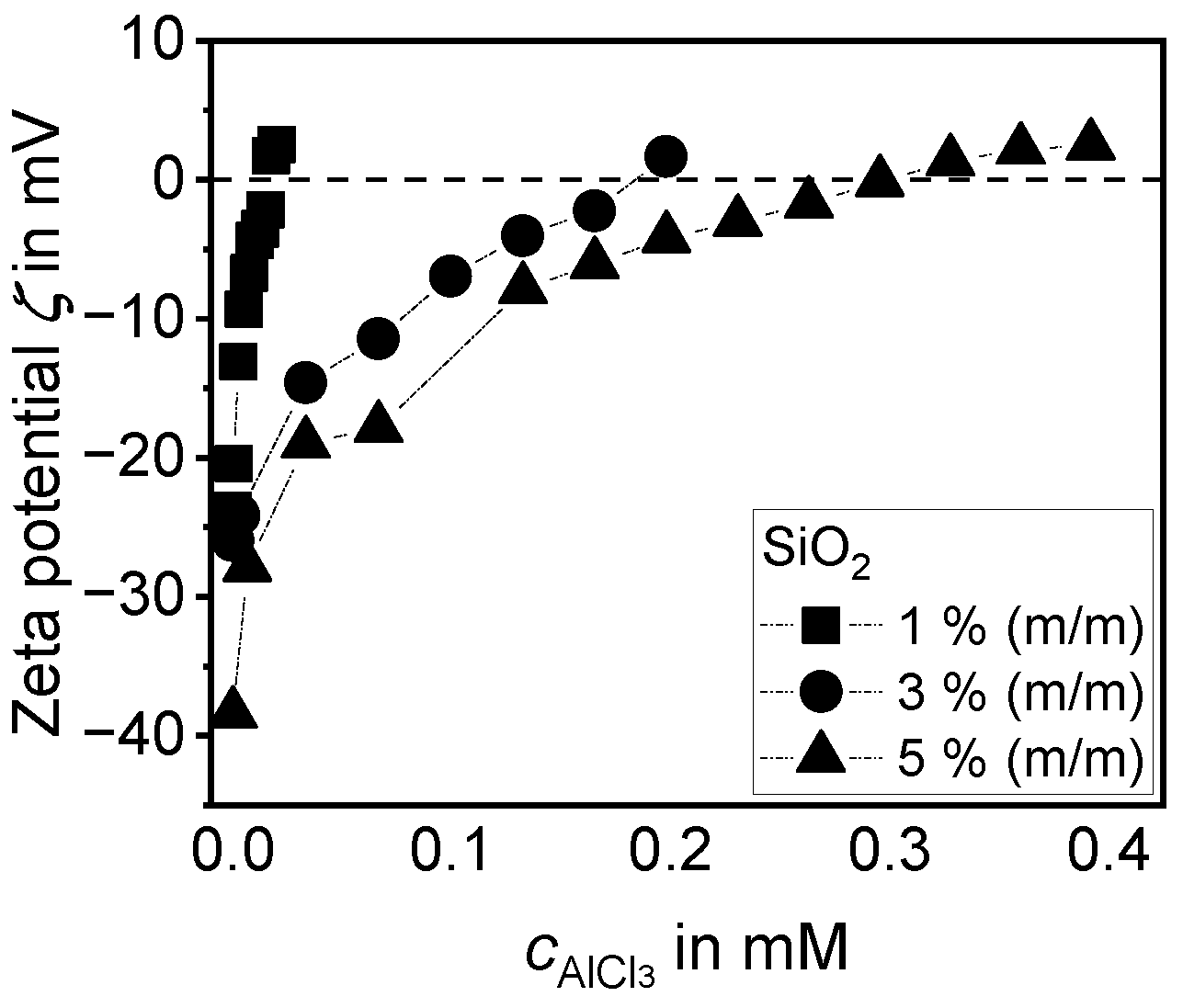
3.1. Investigations for the Charge Reversal of Particles
3.1.1. Investigations with the Aid of Electroacoustics
3.1.2. Investigations with the Aid of Electrophoresis
3.2. Liquid–Liquid Extraction of SiO2 and SnO2
3.3. Separation of SiO2 and SnO2
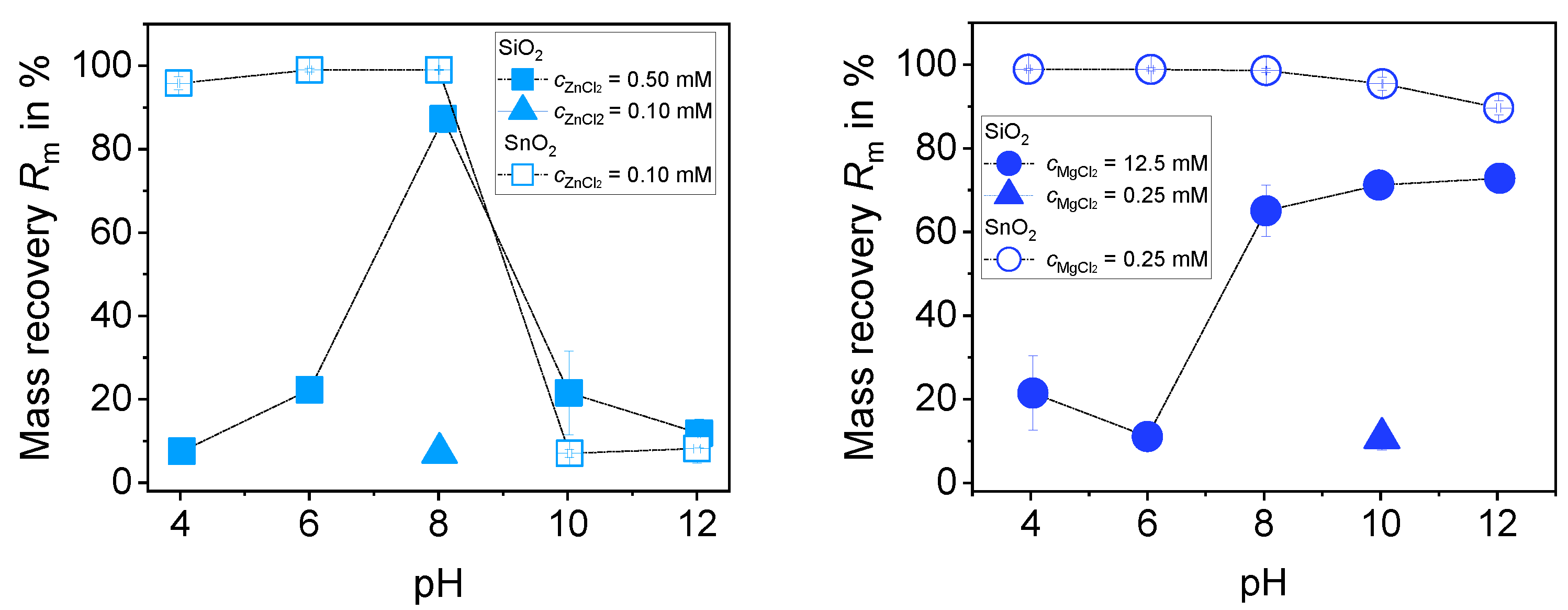
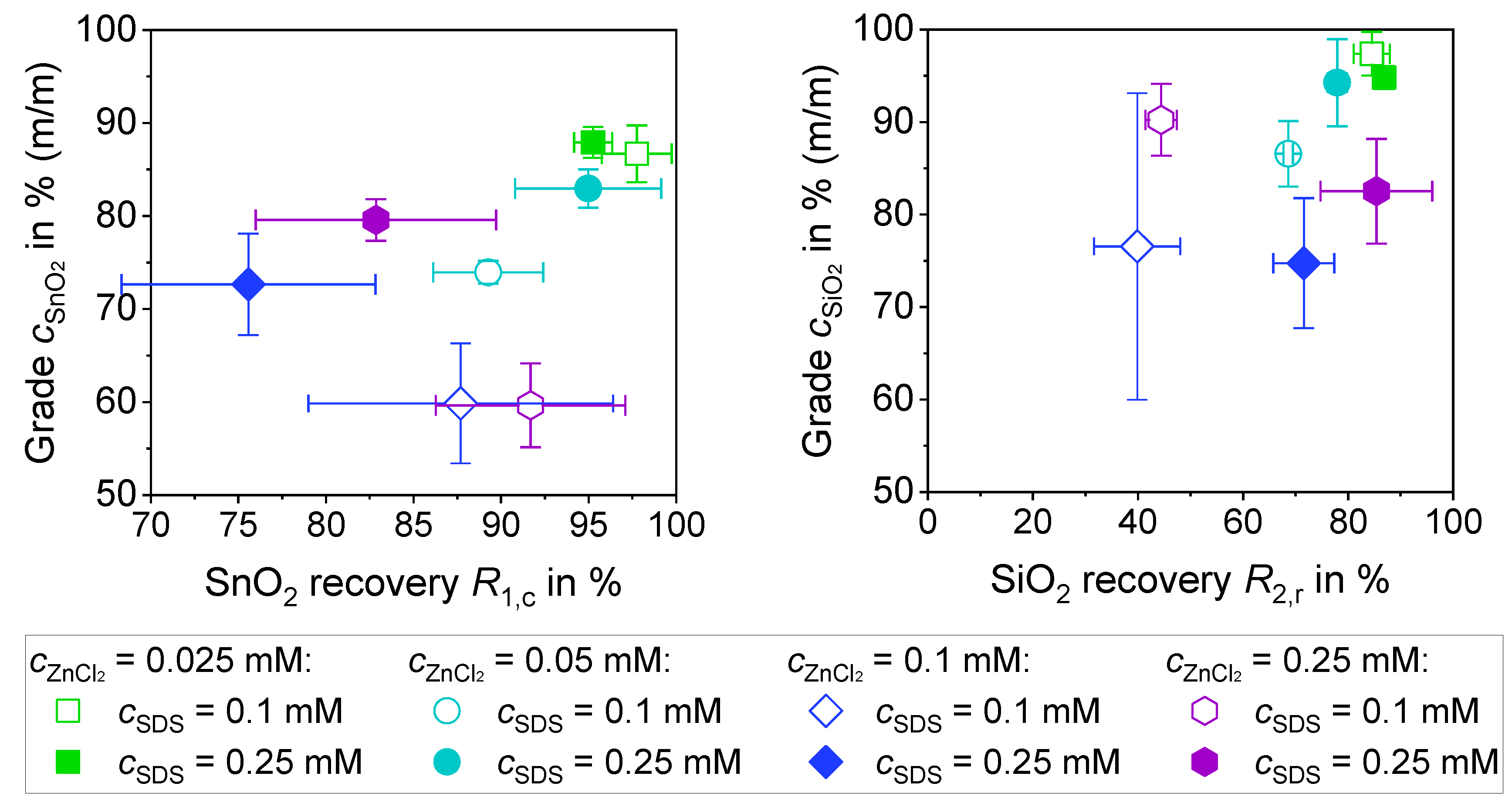
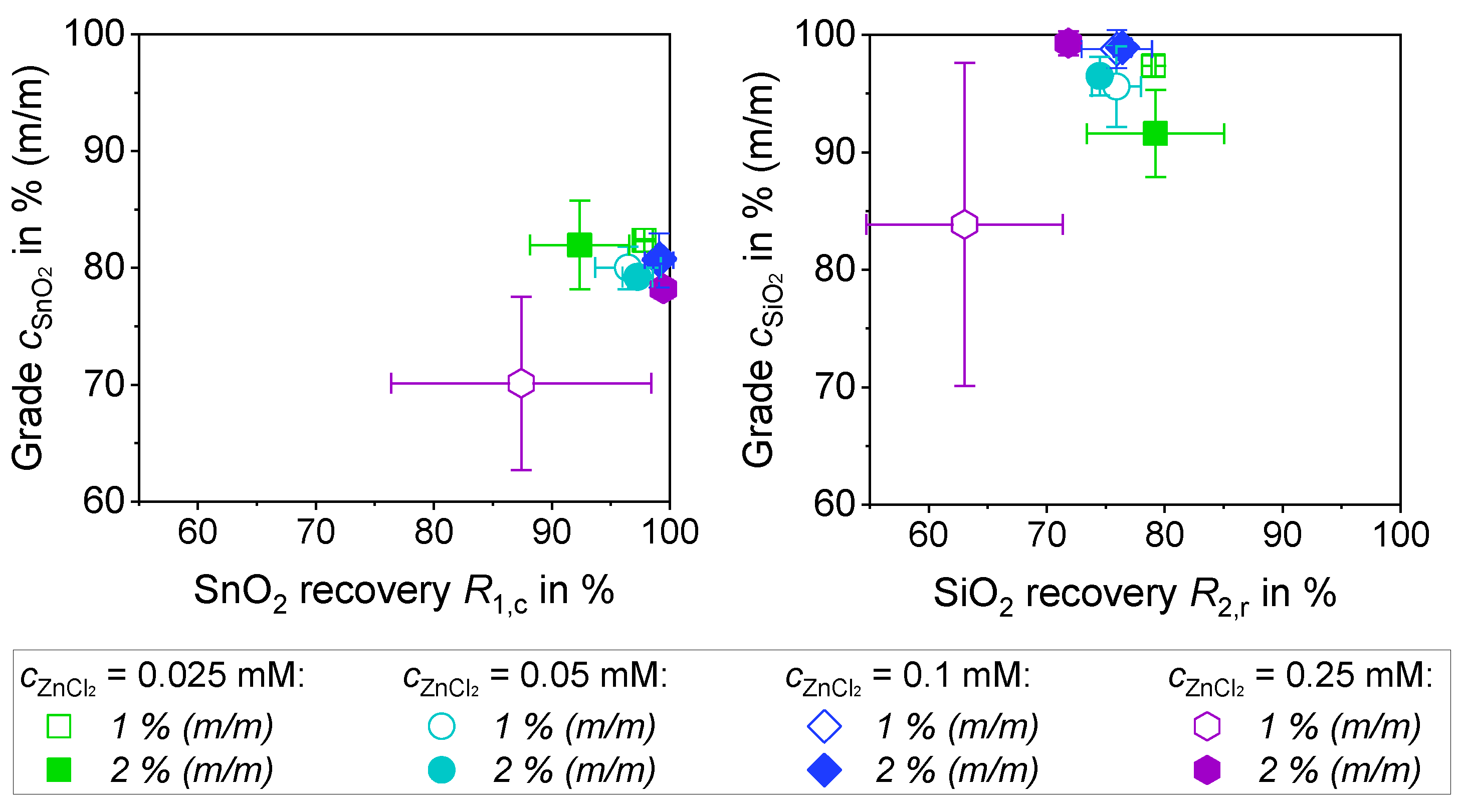
3.3.1. Separation of a 1:1 Mixture of SiO2 and SnO2 with ZnCl2 (0.5% (m/m))
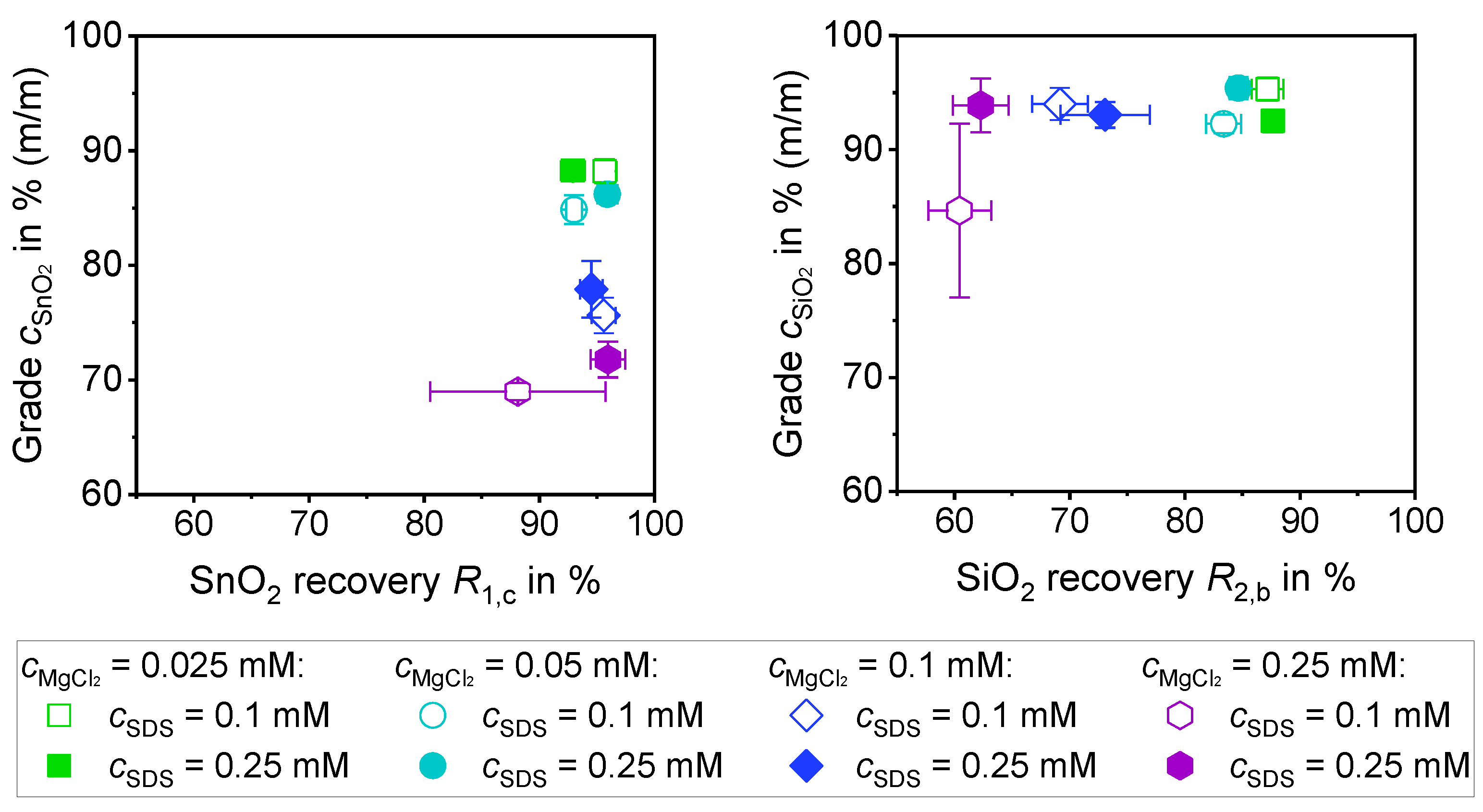
3.3.2. Separation of a 1:1 Mixture of SiO2 and SnO2 with MgCl2 (0.5% (m/m))
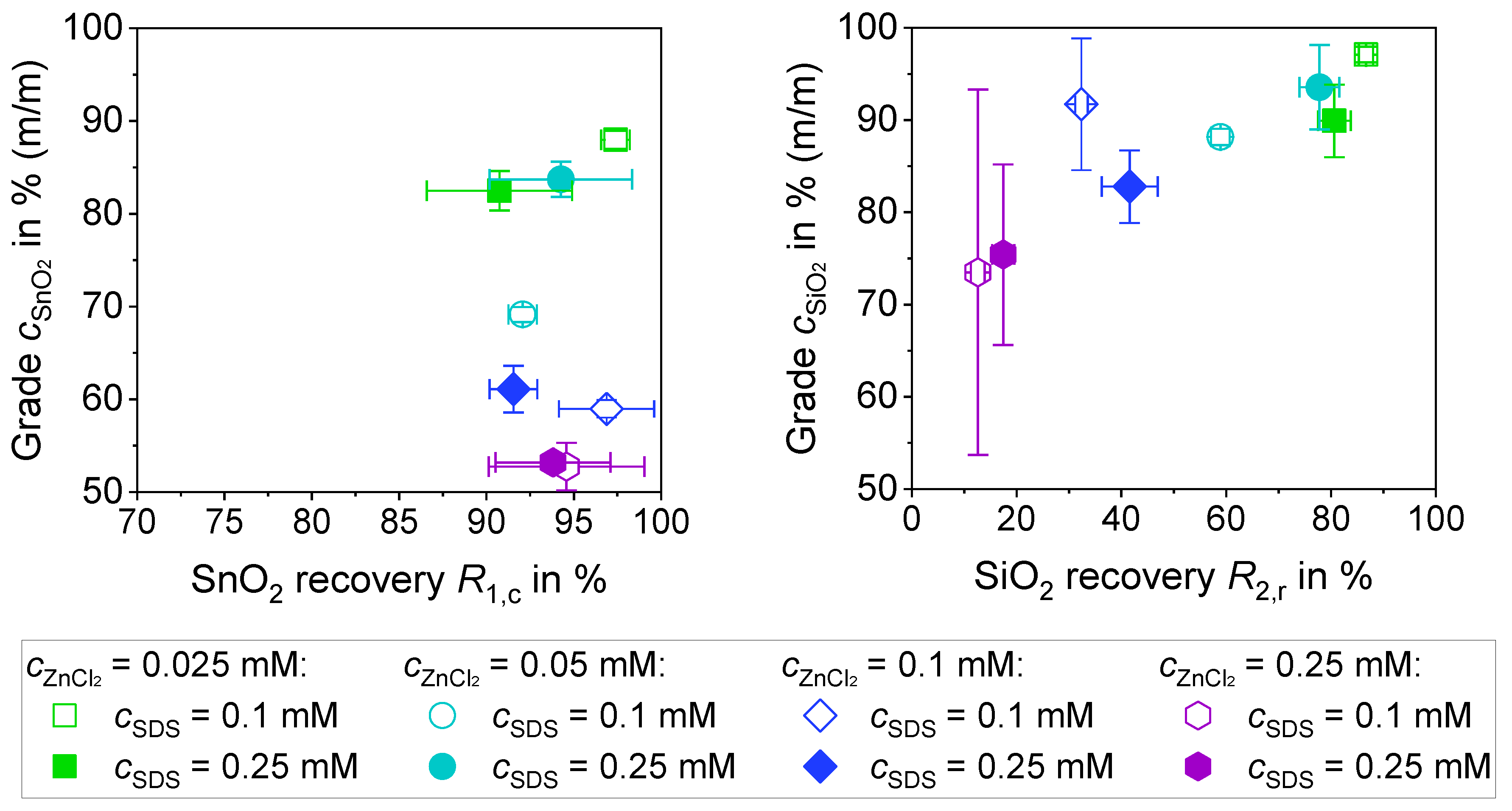
3.3.3. Separation of a 1:1 Mixture of SiO2 and SnO2 with ZnCl2 (1% (m/m) and 2% (m/m))
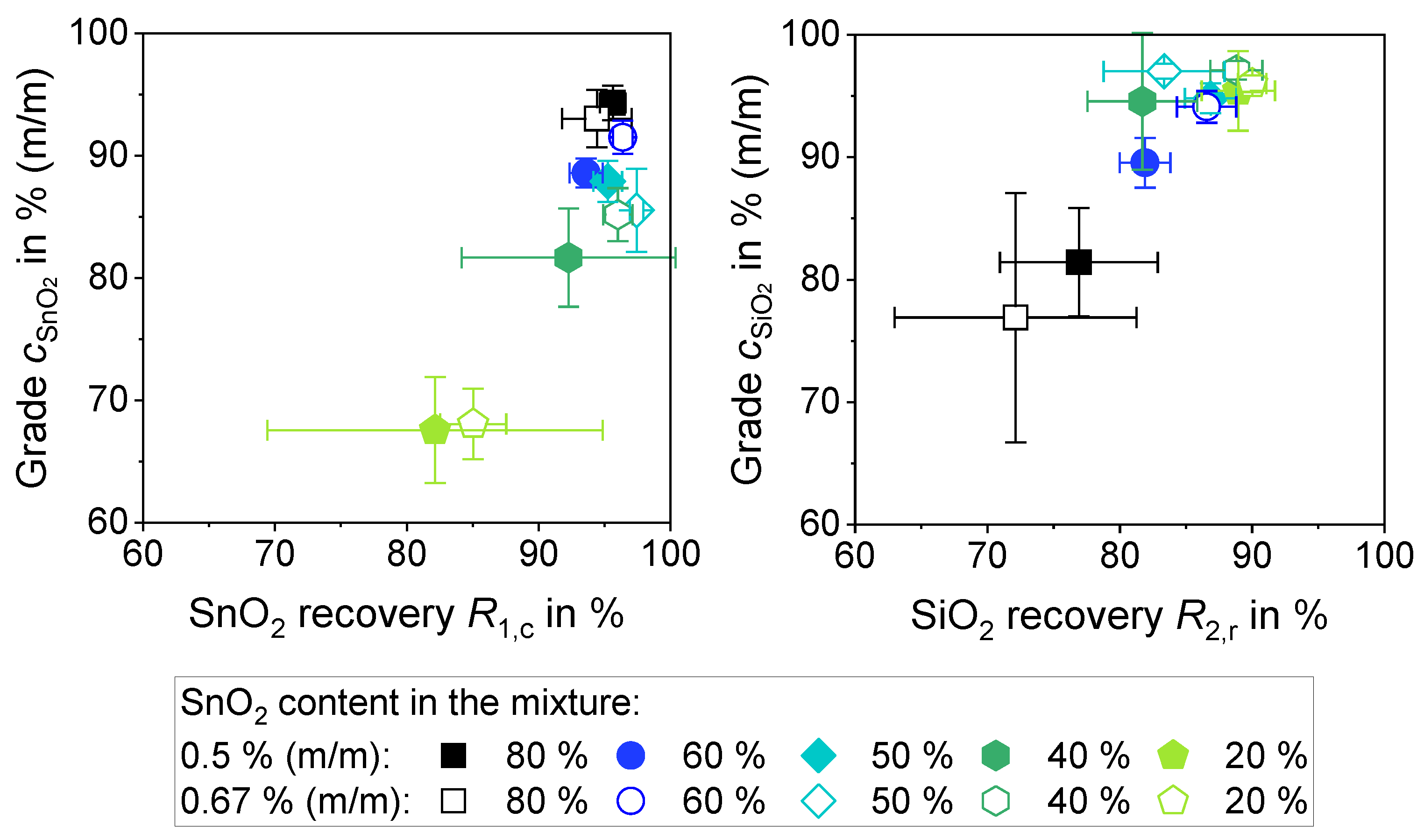
3.3.4. Separation of Varied Mixing Ratios
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nguyen, A.; Schulze, H.J. Colloidal Science of Flotation, 1st ed.; Taylor & Francis Group: London, UK, 2004. [Google Scholar]
- Zhang, L.; Khoso, S.A.; Tian, M.; Sun, W. Cassiterite recovery from a sulfide ore flotation tailing by combined gravity and flotation separations. Physicochem. Probl. Miner. Process. 2021, 57, 206–215. [Google Scholar] [CrossRef]
- De, F.; Gontijo, C.; Fornasiero, D.; Ralston, J. The Limits of Fine and Coarse Particle Flotation. Can. J. Chem. Eng. 2007, 85, 739–747. [Google Scholar]
- Gaudin, A.M.; Malozemoff, P. Recovery by Flotation of Mineral Particles of Colloidal Size. J. Phys. Chem. 1933, 37, 597–607. [Google Scholar] [CrossRef]
- Gaudin, A.M.; Schuhmann, R., Jr.; Schlechten, A.W. Flotation Kinetics. II. The Effect of Size on the Behavior of Galena Particles. J. Phys. Chem. 1942, 46, 902–910. [Google Scholar] [CrossRef]
- Rhein, F.; Zhai, O.; Schmid, E.; Nirschl, H. Multidimensional Separation by Magnetic Seeded Filtration: Experimental Studies. Powders 2023, 2, 37. [Google Scholar] [CrossRef]
- Schubert, H. Aufbereitung Fester Stoffe Band II: Sortierprozesse, 4th ed.; Deutscher Verlag für Grundstoffindustrie: Stuttgart, Germany, 1996. [Google Scholar]
- Englert, A.H.; Rodrigues, R.T.; Rubio, J. Dissolved air flotation (DAF) of fine quartz particles using an amine as collector. Int. J. Miner. Process. 2009, 90, 27–34. [Google Scholar] [CrossRef]
- Crawford, R.; Ralston, J. The influence of particle size and contact angle in mineral flotation. Int. J. Miner. Process. 1988, 23, 1–24. [Google Scholar] [CrossRef]
- Machunsky, S.; Grimm, P.; Schmid, H.-J.; Peuker, U.A. Liquid–liquid phase transfer of magnetite nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2009, 348, 186–190. [Google Scholar] [CrossRef]
- Yao, H.; Momozawa, O.; Hamatani, T.; Kimura, K. Stepwise Size-Selective Extraction of Carboxylate-Modified Gold Nanoparticles from an Aqueous Suspension into Toluene with Tetraoctylammonium Cations. Chem. Mater. 2001, 13, 4692–4697. [Google Scholar] [CrossRef]
- Heilmann, C.; Ditscherlein, L.; Peuker, U.A. Influence of Hydrolyzed Metal Ions and Surfactants on the Phase Transfer of Al2O3, SiO2, and SnO2. Langmuir 2024, 40, 2543–2550. [Google Scholar] [CrossRef]
- Machunsky, S.; Peuker, U.A. Liquid-Liquid Interfacial Transport of Nanoparticles. Phys. Sep. Sci. Eng. 2007, 2007, 034832. [Google Scholar] [CrossRef]
- Erler, J.V.; Machunsky, S.; Franke, S.; Grimm, P.; Schmid, H.-J.; Peuker, U.A. Process Development of a Liquid-Liquid Phase Transfer of Colloidal Particles for Production of High-Quality Organosols. In Colloid Process Engineering; Kind, M., Peukert, W., Rehage, H., Schuchmann, H.P., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 371–398. [Google Scholar]
- Leistner, T.; Embrechts, M.; Leißner, T.; Chehreh Chelgani, S.; Osbahr, I.; Möckel, R.; Peuker, U.A.; Rudolph, M. A study of the reprocessing of fine and ultrafine cassiterite from gravity tailing residues by using various flotation techniques. Miner. Eng. 2016, 96–97, 94–98. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Tong, X.; Wang, X.; Deng, Z.B.; Xie, X.; Xie, F. Beneficiation of Ultrafine Cassiterite from a Tin Tailings by Flotation. Adv. Mater. Res. 2013, 616–618, 643–648. [Google Scholar] [CrossRef]
- Lan, Z.Y.; Zhou, Y.C.; Tong, X. Recovery of Fine Cassiterite from Tin Tailings Slime by Froth Flotation. Adv. Mater. Res. 2013, 634–638, 3478–3483. [Google Scholar] [CrossRef]
- Leistner, T.; Türk, M.; Weber, A.; Weber, C.; Peuker, U.A. Selective Separation Using Fluid-Liquid Interfaces. Mater. Sci. Forum 2019, 959, 113–124. [Google Scholar] [CrossRef]
- Fuerstenau, D.W.; Pradip. Zeta potentials in the flotation of oxide and silicate minerals. Adv. Colloid Interface Sci. 2005, 114–115, 9–26. [Google Scholar] [CrossRef]
- Fuerstenau, D.W.; Colic, M. Self-association and reverse hemimicelle formation at solid-water interfaces in dilute surfactant solutions. Colloids Surf. A Physicochem. Eng. Asp. 1999, 146, 33–47. [Google Scholar] [CrossRef]
- Feng, Q.; Wen, S.; Zhao, W.; Chen, Y. Effect of calcium ions on adsorption of sodium oleate onto cassiterite and quartz surfaces and implications for their flotation separation. Sep. Purif. Technol. 2018, 200, 300–306. [Google Scholar] [CrossRef]
- Weber, C.; Peuker, U.A. On the Role of Hydrolyzable Metal Cations in the Adsorption of Anionic Surfactants on Negatively Charged Surfaces. Front. Mater. 2020, 7, 40. [Google Scholar] [CrossRef]
- Tian, M.; Khoso, S.A.; Wang, L.; Sun, W.; Zhang, C.; Hu, Y. Selective separation behavior and its molecular mechanism of cassiterite from quartz using cupferron as a novel flotation collector with a lower dosage of Pb2+ ions. Appl. Surf. Sci. 2019, 486, 228–238. [Google Scholar] [CrossRef]
- Feng, Q.; Wen, S.; Zhao, W.; Chen, H. Interaction mechanism of magnesium ions with cassiterite and quartz surfaces and its response to flotation separation. Sep. Purif. Technol. 2018, 206, 239–246. [Google Scholar] [CrossRef]
- Kusaka, E.; Nakahiro, Y.; Wakamatsu, T. The role of zeta potentials of oil droplets and quartz particles during collectorless liquid-liquid extraction. Int. J. Miner. Process. 1994, 41, 257–269. [Google Scholar] [CrossRef]
- Kusaka, E.; Kamata, Y.; Fukunaka, Y.; Nakahiro, Y. The role of hydrolyzed metal cations in the liquid-liquid extraction of ultrafine silica with dodecyl sulfate. Miner. Eng. 1997, 10, 155–162. [Google Scholar] [CrossRef]
- Fuerstenau, M.C.; Rice, D.A.; Somasundaran, P.; Fuerstenau, D.W. Metal Ion Hydrolysis and Surface Charge in Beryl Flotation. Trans IMM 1964, 73, 381. [Google Scholar]
- Ruan, Y.; Zhang, Z.; Luo, H.; Xiao, C.; Zhou, F.; Chi, R. Effects of Metal Ions on the Flotation of Apatite, Dolomite and Quartz. Minerals 2018, 8, 141. [Google Scholar] [CrossRef]
- De Vos, W.M.; Lindhoud, S. Overcharging and charge inversion: Finding the correct explanation(s). Adv. Colloid Interface Sci. 2019, 274, 102040. [Google Scholar] [CrossRef]
- Lyklema, J. Overcharging, charge reversal: Chemistry or physics? Colloids Surf. A Physicochem. Eng. Asp. 2006, 291, 3–12. [Google Scholar] [CrossRef]
- Jiménez, M.L.; Delgado, Á.V.; Lyklema, J. Hydrolysis versus Ion Correlation Models in Electrokinetic Charge Inversion: Establishing Application Ranges. Langmuir 2012, 28, 6786–6793. [Google Scholar] [CrossRef]
- Wernersson, E.; Kjellander, R.; Lyklema, J. Charge Inversion and Ion−Ion Correlation Effects at the Mercury/Aqueous MgSO4 Interface: Toward the Solution of a Long-Standing Issue. J. Phys. Chem. C 2010, 114, 1849–1866. [Google Scholar] [CrossRef]
- Matijević, E.; Couch, J.P.; Kerker, M. Detection Of Metal Ion Hydrolysis By Coagulation. IV. Zinc. J. Phys. Chem. 1962, 66, 111–114. [Google Scholar] [CrossRef]
- Delgado, A.V.; González-Caballero, F.; Hunter, R.J.; Koopal, L.K.; Lyklema, J. Measurement and interpretation of electrokinetic phenomena. J. Colloid Interface Sci. 2007, 309, 194–224. [Google Scholar] [CrossRef] [PubMed]
- Binks, B.P.; Rodrigues, J.A. Influence of surfactant structure on the double inversion of emulsions in the presence of nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2009, 345, 195–201. [Google Scholar] [CrossRef]
- Lyklema, H. Fundamentals of Interface and Colloid Science, Solid-liquid interfaces, 1st ed.; Academic Press: London, UK, 1995; Volume 2. [Google Scholar]
- Somasundaran, P.; Healy, T.W.; Fuerstenau, D.W. Surfactant Adsorption at the Solid-Liquid Interface-Dependence of Mechanism on Chain Length. J. Phys. Chem. 1964, 68, 3562–3566. [Google Scholar] [CrossRef]
- Heilmann, C.; Ditscherlein, L.; Asadijozani, M.; Rudolph, M.; Peuker, U.A. Separation of submicron SiO2 and SnO2 particles via liquid-liquid extraction using ZnCl2 and SDS. Sep. Purif. Technol. 2025, 366, 132758. [Google Scholar] [CrossRef]
- Leistner, T.; Müller, M.; Erler, J.V.; Rudolph, M.; Peuker, U.A. Selektive Trennung sehr feiner Partikelsysteme mittels Flüssig/Flüssig-Flotation. Chem. Ing. Tech. 2014, 86, 831–839. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.Academic Press: London, UK, 2011. [Google Scholar]
- Atkins, P.W.; de Paula, J. Kurzlehrbuch Physikalische Chemie, 4th ed.; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Atkins, P.W.; de Paula, J.; Keeler, J. Atkins’ Physical Chemistry, 11th ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Wiberg, N. Lehrbuch der Anorganischen Chemie; De Gruyter: Berlin, Germany, 2008. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 86th ed.; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Müller, B.; ChemEQL—A Software for the Calculation of Chemical Equilibria. 2024, from the Department Surface Waters—Research and Management. Available online: https://www.eawag.ch/en/department/surf/projects/chemeql/ (accessed on 28 May 2025).
- Kosmulski, M. Isoelectric points and points of zero charge of metal (hydr)oxides: 50 years after Parks’ review. Adv. Colloid Interface Sci. 2016, 238, 1–61. [Google Scholar] [CrossRef]
- Peuker, U.A.; Leißner, T. Solid–Solid Separation. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH GmbH: Weinheim, Germany, 2023; pp. 1–20. [Google Scholar]
- Küster, F.W.; Thiel, A. Ruland, Rechentafeln für die Chemische Analytik, 104th ed.; De Gruyter: Berlin, Germany, 1993. [Google Scholar]
- Davies, S.H.R.; Morgan, J.J. Manganese (II) oxidation kinetics on metal oxide surfaces. J. Colloid Interface Sci. 1989, 129, 63–77. [Google Scholar] [CrossRef]
- Kumar, K.Y.; Raj, T.N.V.; Archana, S.; Prasad, S.B.B.; Olivera, S.; Muralidhara, H.B. SnO2 nanoparticles as effective adsorbents for the removal of cadmium and lead from aqueous solution: Adsorption mechanism and kinetic studies. J. Water Process Eng. 2016, 13, 44–52. [Google Scholar] [CrossRef]
- Jańczuk, B.; Bruque, J.M.; González-Martín, M.L.; del Pozo, J.M. The surface free energy of fluorite in presence of sodium dodecyl sulfate. Powder Technol. 1994, 80, 127–131. [Google Scholar] [CrossRef]
- Talens-Alesson, F.I. Behaviour of SDS micelles bound to mixtures of divalent and trivalent cations during ultrafiltration. Colloids Surf. A Physicochem. Eng. Asp. 2007, 299, 169–179. [Google Scholar] [CrossRef]


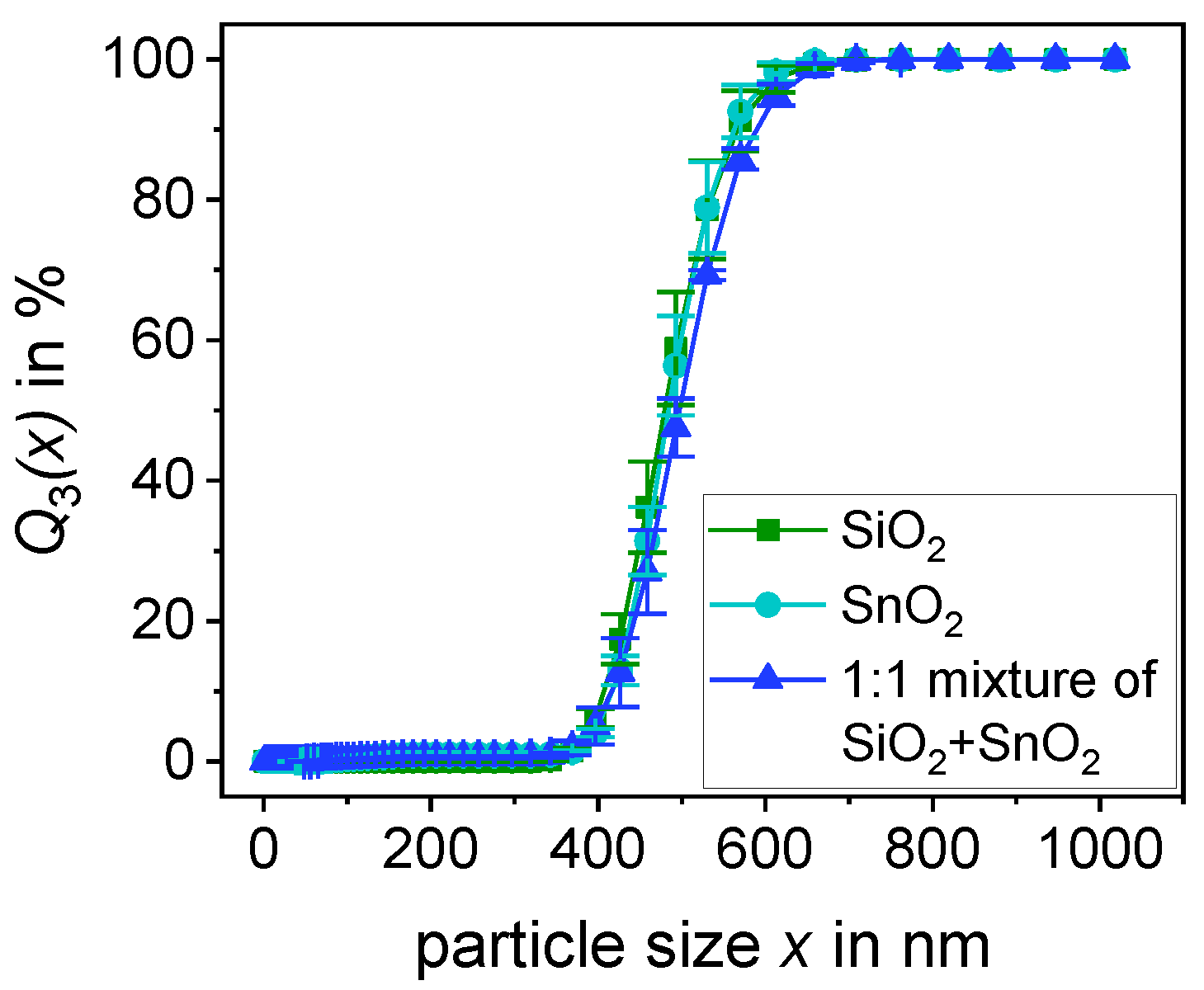




| SiO2 | SnO2 | 1:1 Mixture of SiO2 + SnO2 | |
|---|---|---|---|
| x10 in nm | 407.8 ± 5.2 | 417.6 ± 6.2 | 416.9 ± 14.4 |
| x50 in nm | 480.4 ± 11.0 | 485.1 ± 9.2 | 496.4 ± 5.9 |
| x90 in nm | 565.4 ± 20.5 | 561.8 ± 15.3 | 589.7 ± 7.0 |
| Material | SBET in m2/g |
|---|---|
| SiO2 | 10.05 ± 0.01 |
| SnO2 | 6.70 ± 0.06 |
| 1:1 mixture of SiO2 + SnO2 | 8.27 ± 0.08 |
| Ions | CN | rIon in Å | M in g/mol |
|---|---|---|---|
| Al3+ | 6 [42] | ~0.54 [42,44,45] | 27.0 |
| Mg2+ | 6 [42] | 0.72 [41,42,44] | 24.3 |
| Zn2+ | 6 [45] | 0.74 [44,45] | 65.4 |
| OH- | 2 [45] | 1.32 [44,45] | 17.0 |
| Calculated Quantities Required for the Complete Covering of 1 g Particles for: | |||
|---|---|---|---|
| Ions | Coverage of SiO2 in mg | Coverage of SnO2 in mg | Coverage of 1:1 Mixture of SiO2 + SnO2 in mg |
| Al3+ | 49.2 ± 0.1 | 32.8 ± 0.3 | 40.5 ± 0.4 |
| Mg2+ | 24.9 ± 0.0 | 16.6 ± 0.2 | 20.5 ± 0.2 |
| Zn2+ | 63.5 ± 0.1 | 42.3 ± 0.4 | 52.2 ± 0.5 |
| SDS | 9.6 ± 0.0 | 6.4 ± 0.1 | 7.9 ± 0.1 |
| Species | rIon in Å | Requirement for the Individual Ions in mM for: | ||
|---|---|---|---|---|
| 1% (m/m) | 3% (m/m) | 5% (m/m) | ||
| Al3+ | 0.54 | 0.49 | 1.46 | 2.43 |
| Al(OH)2+ | 1.86 | 0.07 | 0.20 | 0.33 |
| Al(OH)2+ | 3.18 | 0.03 | 0.10 | 0.16 |
| Experiment AlCl3 | 0.11 | 0.18 | 0.30 | |
| Species | rIon in Å | Required Concentration for the Individual Ions in mM for: | |
|---|---|---|---|
| SnO2 5% (m/m) | SiO2 5% (m/m) | ||
| Zn2+ | 0.74 | 16.34 | 24.53 |
| Zn(OH)+ | 2.06 | 2.66 | 3.99 |
| Experiment ZnCl2 | 1.36 | 2.86 | |
| Mg2+ | 0.72 | 9.18 | 13.7 |
| Mg(OH)+ | 2.04 | 1.94 | 2.92 |
| Experiment MgCl2 | 0.79 | 12.98 | |
| Species | Required Concentration for the Individual Ions in mM for: | ||
|---|---|---|---|
| SnO2 | SiO2 | 1:1 Mixture of SiO2 + SnO2 | |
| Zn2+ | 1.55 | 2.33 | 1.92 |
| Zn(OH)+ | 0.25 | 0.38 | 0.31 |
| Mg2+ | 0.87 | 1.31 | 1.08 |
| Mg(OH)+ | 0.18 | 0.28 | 0.23 |
| SDS | 0.11 | 0.17 | 0.14 |
| Species | Required Concentration for the Individual Ions for a 1:1 Mixture of SiO2 + SnO2 in mM for: | |
|---|---|---|
| 1% (m/m) | 2% (m/m) | |
| Zn2+ | 3.83 | 7.67 |
| Zn(OH)+ | 0.62 | 1.25 |
| SDS | 0.27 | 0.55 |
| Species | Required Concentration for the Individual Ions for Different SiO2 + SnO2 Mixtures in mM for: | ||||
|---|---|---|---|---|---|
| 80% SnO2 + 20% SiO2 | 60% SnO2 + 40% SiO2 | 50% SnO2 + 50% SiO2 | 40% SnO2 + 60% SiO2 | 20% SnO2 + 80% SiO2 | |
| Zn2+ | 1.71 | 1.86 | 1.91 | 2.02 | 2.17 |
| Zn(OH)+ | 0.28 | 0.30 | 0.31 | 0.33 | 0.35 |
| SDS | 0.12 | 0.13 | 0.14 | 0.14 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heilmann, C.; Ditscherlein, L.; Rudolph, M.; Peuker, U.A. Selective Separation of SiO2 and SnO2 Particles in the Submicron Range: Investigating Salt and Surfactant Adsorption Parameter. Powders 2025, 4, 19. https://doi.org/10.3390/powders4030019
Heilmann C, Ditscherlein L, Rudolph M, Peuker UA. Selective Separation of SiO2 and SnO2 Particles in the Submicron Range: Investigating Salt and Surfactant Adsorption Parameter. Powders. 2025; 4(3):19. https://doi.org/10.3390/powders4030019
Chicago/Turabian StyleHeilmann, Claudia, Lisa Ditscherlein, Martin Rudolph, and Urs Alexander Peuker. 2025. "Selective Separation of SiO2 and SnO2 Particles in the Submicron Range: Investigating Salt and Surfactant Adsorption Parameter" Powders 4, no. 3: 19. https://doi.org/10.3390/powders4030019
APA StyleHeilmann, C., Ditscherlein, L., Rudolph, M., & Peuker, U. A. (2025). Selective Separation of SiO2 and SnO2 Particles in the Submicron Range: Investigating Salt and Surfactant Adsorption Parameter. Powders, 4(3), 19. https://doi.org/10.3390/powders4030019








