A Review of the Homogenized Lattice Boltzmann Method for Particulate Flow Simulations: From Fundamentals to Applications
Abstract
1. Introduction
1.1. Overview of Particle-Laden Flows Characteristics
- Aerosols occur when the carrier component is a gas and the dispersed component is either a liquid (fog, mist) or a solid (dust, soot).
- Bubble flows occur when the carrier component is a liquid and the dispersed component is a dilute gas.
- Suspensions occur when the carrier component is a liquid and the dispersed component is a solid.
- Emulsions occur when both components are in a liquid state.
- molecularly dispersed dissolved particles having a size of less than 1 nm,
- colloidally dispersed dissolved particles having a size between 1 nm and 1 μm,
- coarsely dispersed dissolved particles having a size greater than 1 μm.
1.2. Overview of Modeling Approaches and Their Limitations
1.3. Overview of Numerical Solution Approaches and Their Limitations
1.4. Aims of the Homogenized Lattice Boltzmann Method
1.5. Structure of This Review Paper
2. Modeling
2.1. Fluid Dynamics
2.2. Particle Dynamics
2.3. Contact
3. Numerical Methods
3.1. Lattice Boltzmann Method
3.2. Homogenized Lattice Boltzmann Method
3.3. Discrete Contacts
4. Applications
| Publication | Spatial Dimensions | Particle Shapes | Particle Number per Simulation | Coupling |
|---|---|---|---|---|
| Krause et al. [55] | 2 | Circles, squares, and triangles | 1–24 | Two- and four-way |
| Trunk et al. [56] | 3 | Spheres and limestone CT scans | 1–15 | Two-way |
| Dapelo et al. [78] | 3 | Spheres | 1 | Two-way |
| Haussmann et al. [67] | 2 | Circles | 1 | Two-way |
| Bretl et al. [79] | 3 | Symmetric regarding the principal planes | 1 | Two-way |
| Trunk et al. [68] | 2 and 3 | Circles and spheres | 1–1865 | Two-way |
| Trunk et al. [6] | 3 | Superellipsoids | 1 | Two-way |
| Hafen et al. [73] | 3 | Cubic disks | 48–240 | Two-way |
| Marquardt et al. [43] | 3 | Spheres | 1 | Four-way |
| Hafen et al. [80] | 3 | Cubic disks | 1 | Two-way |
| Hafen et al. [81] | 3 | Cubic disks | 1–480 | Two-way |
| Hafen et al. [64] | 3 | Cubic disks | 240–720 | Four-way |
| Marquardt et al. [82] | 3 | Spheres | 166–991 | Two-way |
| Marquardt et al. [77] | 3 | Spheres and cubes | 191–1934 | Four-way |
| Marquardt et al. [83] | 3 | Cubes | 394–784 | Four-way |
4.1. Flow Around a Cylinder
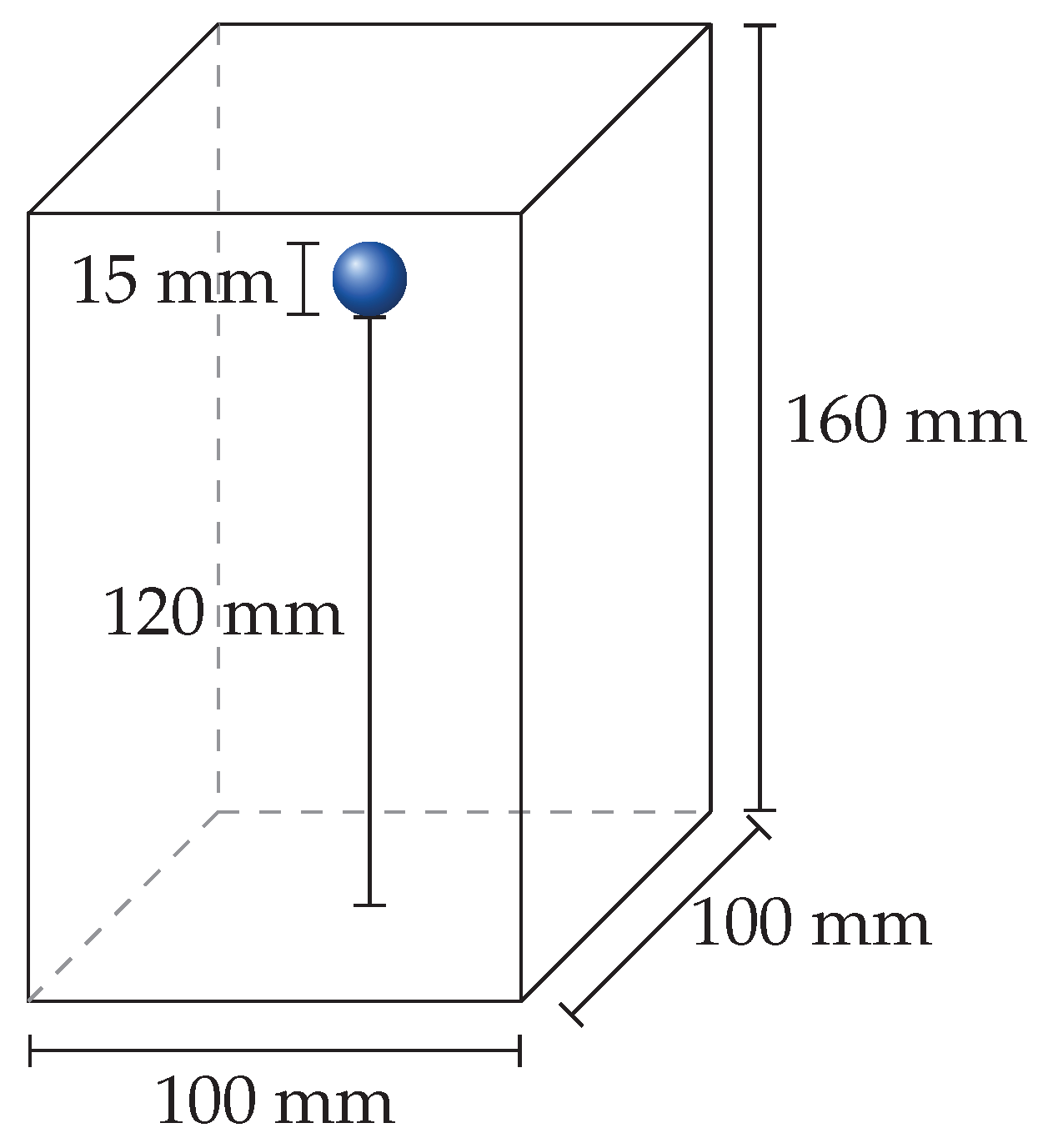
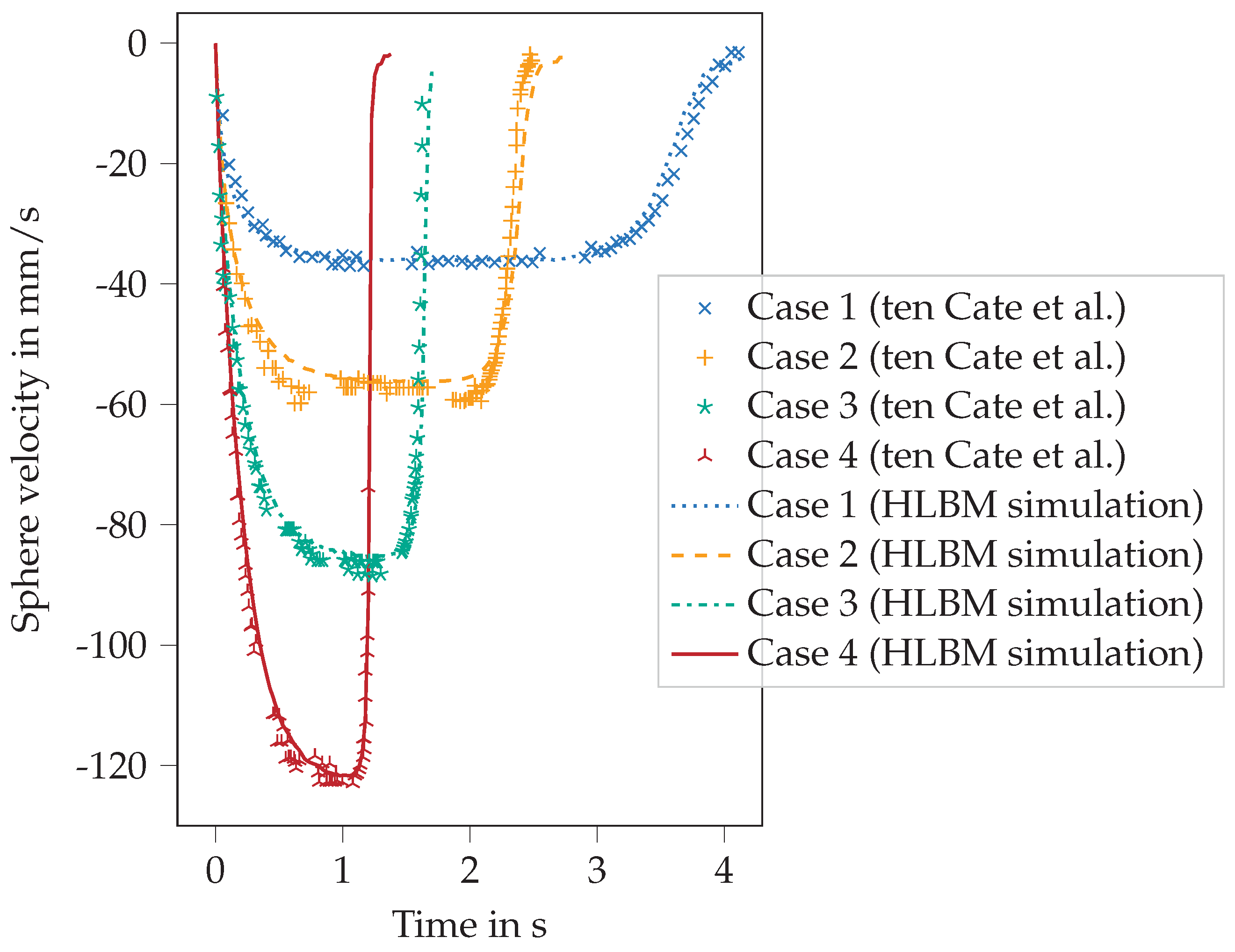
4.2. Settling Sphere
4.3. Shape-Dependent Settling of Single Particles
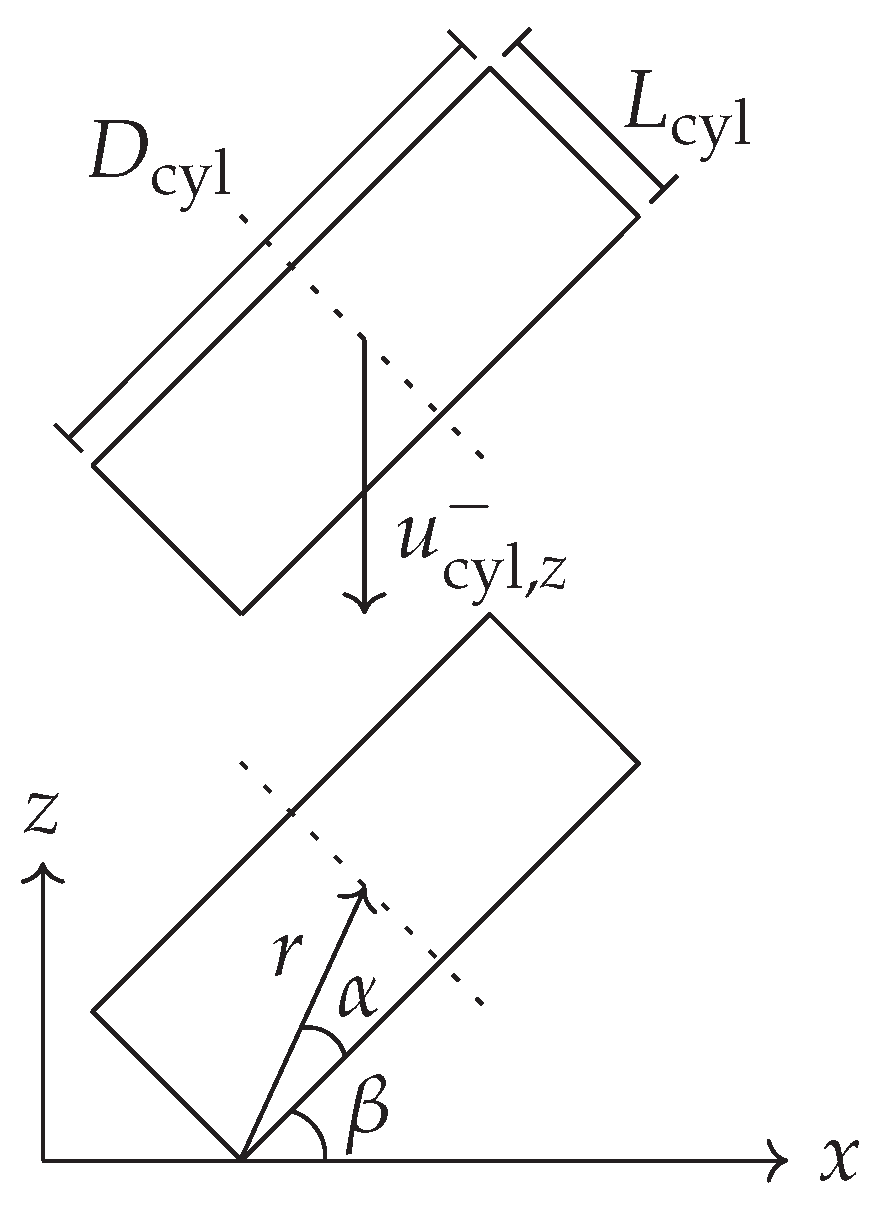
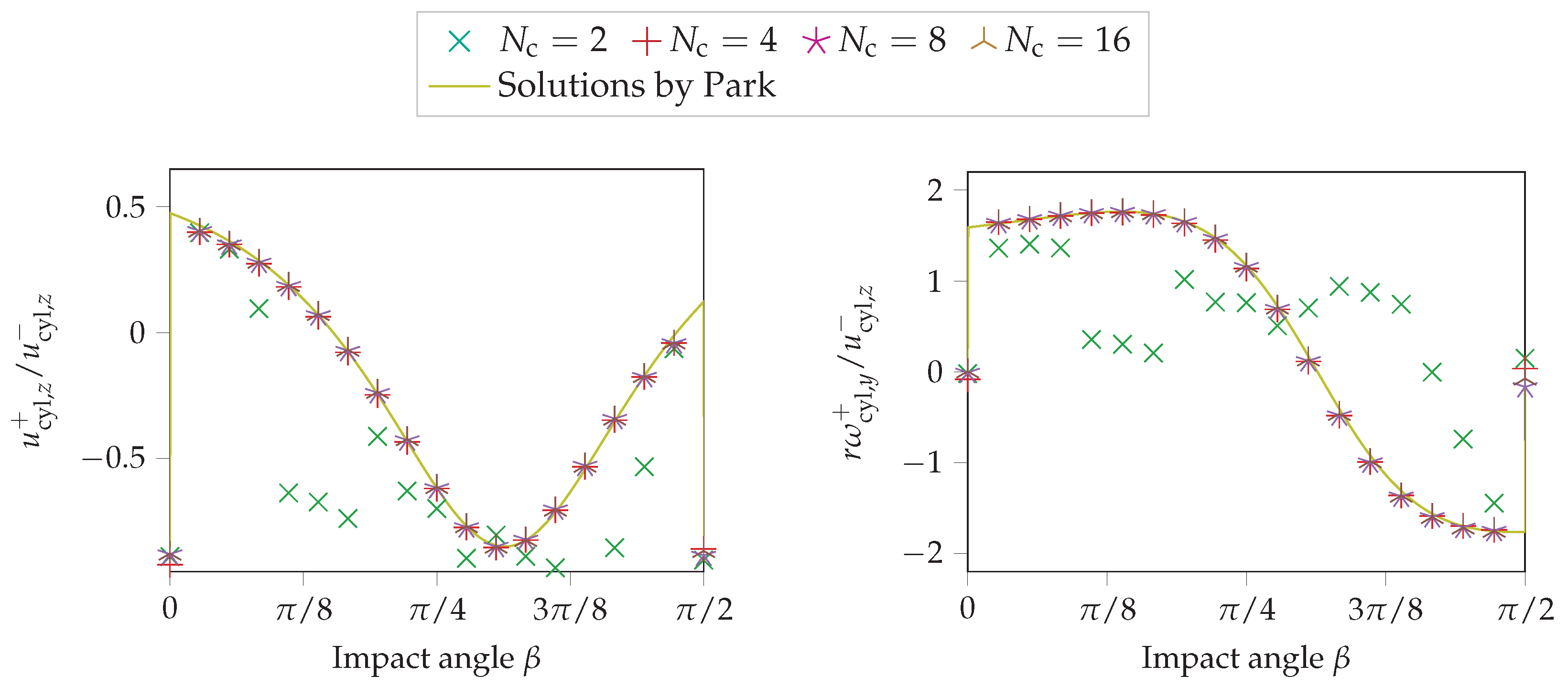
4.4. Cylinder-Wall Impact
4.5. Sphere Rebound
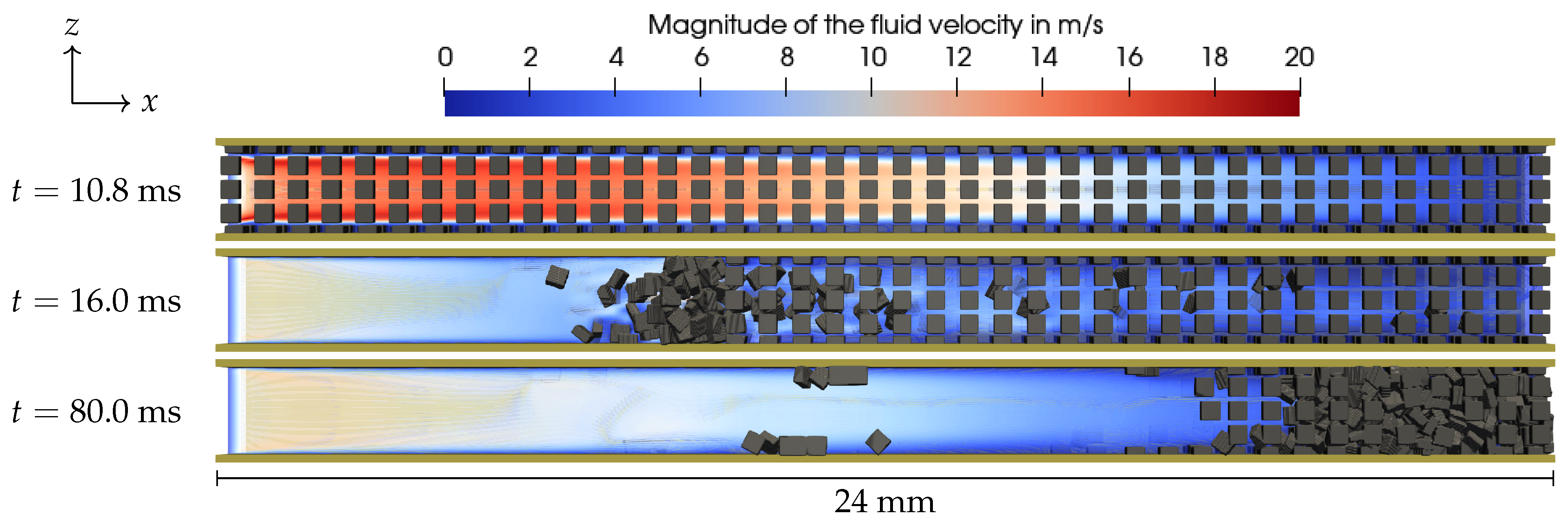
4.6. Wall-Flow Filters
4.7. Hindered Settling
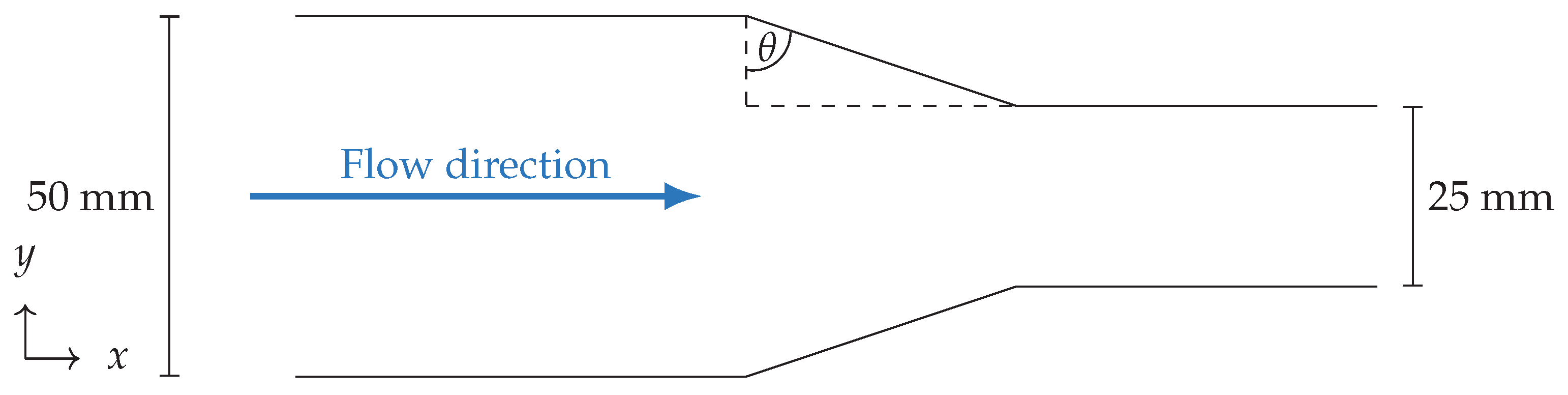
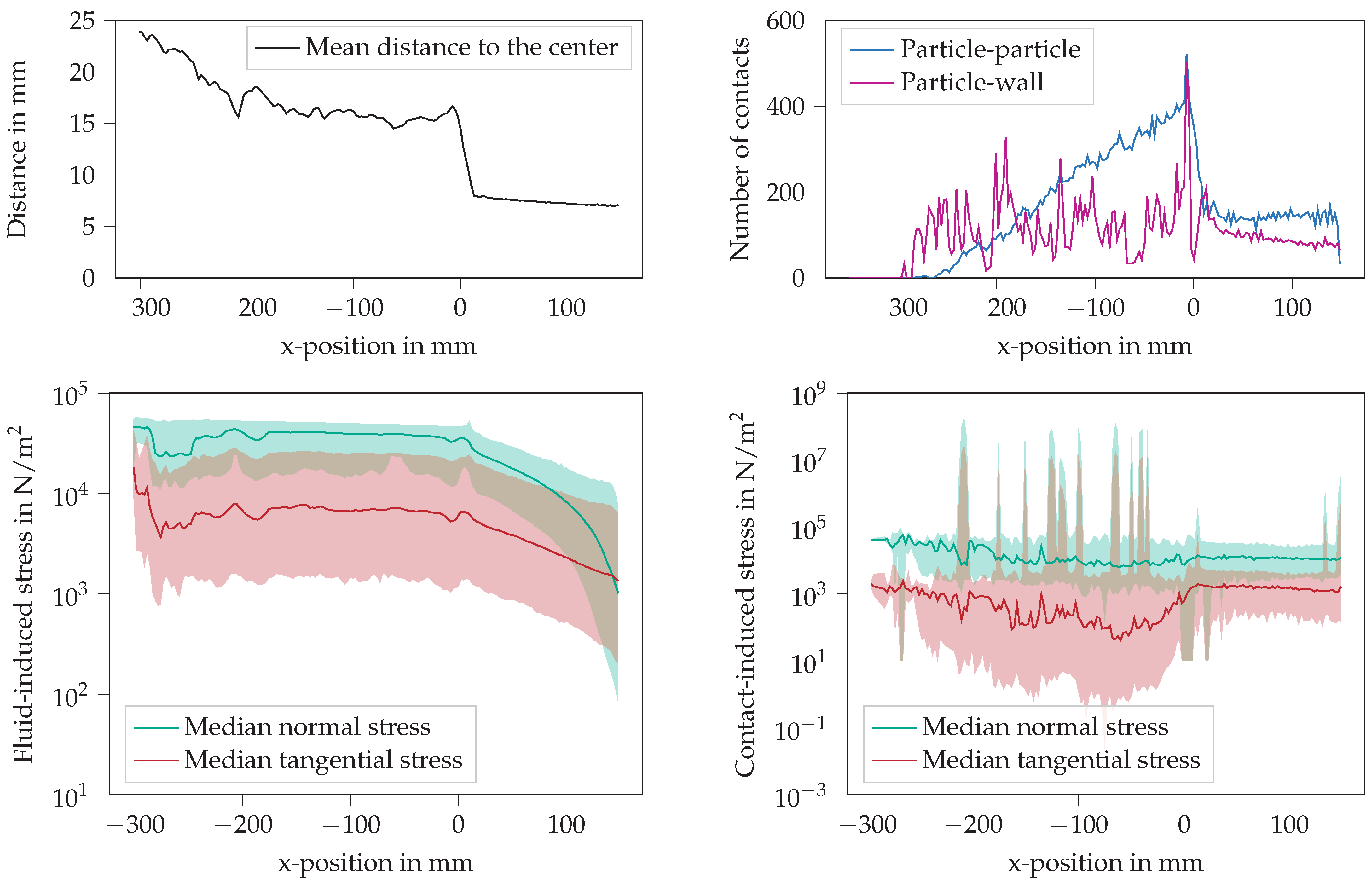
4.8. Transport Through a Cross-Sectional Constriction
5. Discussion
5.1. Strengths and Weaknesses
5.2. Outlook on Future Development
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BGK | Bhatnagar–Gross–Krook |
| DEM | discrete element method |
| DNS | direct numerical simulation |
| EDM | exact difference method |
| EOC | experimental order of convergence |
| GPU | graphics processing unit |
| HLBM | homogenized lattice Boltzmann method |
| IBM | immersed boundary method |
| LBM | lattice Boltzmann method |
| MEA | momentum exchange algorithm |
| VANSE | volume-averaged Navier–Stokes equations |
| Roman Symbols | |
| A | surface area |
| Archimedes number | |
| intermediate half axis | |
| longest half axis | |
| shortest half axis | |
| B | weighting factor |
| drag coefficient | |
| lift coefficient | |
| discrete velocity | |
| c | damping factor |
| lattice speed of sound | |
| D | diameter |
| d | indentation depth |
| temporal change of indentation depth | |
| signed distance | |
| E | Young’s modulus |
| effective Young’s modulus | |
| e | signed coefficient of restitution |
| force | |
| f | particle population |
| post-collision particle population | |
| gravitational acceleration vector | |
| g | standard gravity |
| moment of inertia | |
| permeability tensor | |
| K | eigenvalue of the permeability tensor |
| k | constant parameter for calculation of normal contact force |
| L | length |
| m | mass |
| N | resolution |
| n | expansion index |
| normal | |
| p | pressure |
| Q | collision operator |
| Reynolds number | |
| r | distance from contact point to the cylinder’s center |
| S | source term |
| torque | |
| t | time |
| velocity | |
| reference velocity of a single settling sphere | |
| initial relative velocity of two objects in contact | |
| transition velocity from static to kinetic friction | |
| V | volume |
| w | weight for the equilibrium distribution calculation |
| center of mass | |
| position | |
| x | first coordinate value of the position vector |
| y | second coordinate value of the position vector |
| z | third coordinate value of the position vector |
| Greek Symbols | |
| angle between the cylinder’s face and the line to its center from the contact point | |
| impact angle | |
| particle surface | |
| time step size | |
| grid spacing | |
| porosity | |
| size of the smooth boundary | |
| dynamic viscosity | |
| taper angle | |
| elongation | |
| roundness | |
| Hofmann shape entropy | |
| coefficient of kinetic friction of the objects p and q | |
| coefficient of static friction of the objects p and q | |
| Poisson’s ratio | |
| density | |
| stress tensor | |
| relaxation time | |
| volume fraction | |
| domain | |
| angular velocity | |
| Superscripts | |
| + | refers to values after the contact |
| − | refers to values before the contact |
| local | denotes a local quantity or property |
| Subscripts | |
| 0 | refers to initial values |
| b | refers to positions inside a particle’s boundary |
| c | refers to a particle-particle or particle-wall interaction |
| cyl | refers to a cylinder |
| eq | refers to a volume equivalent sphere |
| f | refers to the fluid |
| h | refers to the hydrodynamic force |
| i | refers to the corresponding discrete velocity |
| n | refers to the normal direction |
| P | refers to a set of particles |
| p | refers to a particle |
| q | refers to an object or particle that is not p |
| s | refers to a sphere |
| t | refers to the tangential direction |
| V | refers to a volume |
| x | refers to the x-direction |
| y | refers to the y-direction |
| z | refers to the z-direction |
| refers to the surface | |
References
- de Vasconcelos, T.F.; Sapoval, B.; Andrade, J.S.; Grotberg, J.B.; Hu, Y.; Filoche, M. Particle capture into the lung made simple? J. Appl. Physiol. 2011, 110, 1664–1673. [Google Scholar] [CrossRef] [PubMed]
- Barths, H.; Hasse, C.; Bikas, G.; Peters, N. Simulation of combustion in direct injection diesel engines using a eulerian particle flamelet model. Proc. Combust. Inst. 2000, 28, 1161–1168. [Google Scholar] [CrossRef]
- Kashiwaya, K.; Noumachi, T.; Hiroyoshi, N.; Ito, M.; Tsunekawa, M. Effect of particle shape on hydrocyclone classification. Powder Technol. 2012, 226, 147–156. [Google Scholar] [CrossRef]
- Schwister, K. (Ed.) Taschenbuch der Verfahrenstechnik, 5th ed.; Fachbuchverlag Leipzig im Carl Hanser Verlag: Munich, Germany, 2017. [Google Scholar]
- Merkus, H.G. Particle Size, Size Distributions and Shape. In Particle Size Measurements: Fundamentals, Practice, Quality; Springer: Dordrecht, The Netherlands, 2009; pp. 13–42. [Google Scholar] [CrossRef]
- Trunk, R.; Bretl, C.; Thäter, G.; Nirschl, H.; Dorn, M.; Krause, M.J. A Study on Shape-Dependent Settling of Single Particles with Equal Volume Using Surface Resolved Simulations. Computation 2021, 9, 40. [Google Scholar] [CrossRef]
- Dal Pont, J.P. (Ed.) Process Engineering and Industrial Management; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Johansson, R.; Evertsson, M. CFD simulation of a centrifugal air classifier used in the aggregate industry. Miner. Eng. 2014, 63, 149–156. [Google Scholar] [CrossRef]
- Meier, J.; Klein, G.M.; Kottke, V. Crossflow filtration as a new method of wet classification of ultrafine particles. Sep. Purif. Technol. 2002, 26, 43–50. [Google Scholar] [CrossRef]
- Saunders, S.R.; Roberts, C.B. Size-selective fractionation of nanoparticles at an application scale using CO2 gas-expanded liquids. Nanotechnology 2009, 20, 475605. [Google Scholar] [CrossRef]
- Saunders, S.R.; Roberts, C.B. Nanoparticle separation and deposition processing using gas expanded liquid technology. Curr. Opin. Chem. Eng. 2012, 1, 91–101. [Google Scholar] [CrossRef]
- Peukert, W.; Wadenpohl, C. Industrial separation of fine particles with difficult dust properties. Powder Technol. 2001, 118, 136–148. [Google Scholar] [CrossRef]
- Williams, A.; Varela, E.; Meehan, E.; Tribe, K. Characterisation of nanoparticulate systems by hydrodynamic chromatography. Int. J. Pharm. 2002, 242, 295–299. [Google Scholar] [CrossRef]
- Liu, J.F.; Yu, S.J.; Yin, Y.G.; Chao, J.B. Methods for separation, identification, characterization and quantification of silver nanoparticles. TrAC Trends Anal. Chem. 2012, 33, 95–106. [Google Scholar] [CrossRef]
- Spelter, L.E.; Meyer, K.; Nirschl, H. Screening of colloids by semicontinuous centrifugation. Chem. Eng. Technol. 2012, 35, 1486–1494. [Google Scholar] [CrossRef]
- van Kemenade, E.; Brouwers, B.; van Benthum, R. Centrifugal separation with emphasis on the rotational particle separator. ChemBioEng Rev. 2014, 1, 262–272. [Google Scholar] [CrossRef]
- Boskovic, L.; Altman, I.S.; Agranovski, I.E.; Braddock, R.D.; Myojo, T.; Choi, M. Influence of particle shape on filtration processes. Aerosol Sci. Technol. 2005, 39, 1184–1190. [Google Scholar] [CrossRef]
- Lecrivain, G.; Rayan, R.; Hurtado, A.; Hampel, U. Using quasi-DNS to investigate the deposition of elongated aerosol particles in a wavy channel flow. Comput. Fluids 2016, 124, 78–85. [Google Scholar] [CrossRef]
- Krause, M.J. Fluid Flow Control and Simulation in Process Engineering: Homogenised Lattice Boltzmann Methods. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2022. [Google Scholar]
- Jones, J.E. On the determination of molecular fields—II. From the equation of state of a gas. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1924, 106, 463–477. [Google Scholar] [CrossRef]
- Verwey, E.J.W. Theory of the stability of lyophobic colloids. J. Phys. Chem. 1947, 51, 631–636. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Yow, H.; Pitt, M.; Salman, A. Drag correlations for particles of regular shape. Adv. Powder Technol. 2005, 16, 363–372. [Google Scholar] [CrossRef]
- Richardson, J.F.; Zaki, W.N. Sedimentation and fluidisation: Part I. Chem. Eng. Res. Des. 1954, 75, S82–S100. [Google Scholar] [CrossRef]
- Blais, B.; Tucny, J.M.; Vidal, D.; Bertrand, F. A conservative lattice Boltzmann model for the volume-averaged Navier–Stokes equations based on a novel collision operator. J. Comput. Phys. 2015, 294, 258–273. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.; Yu, A. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, Z.; Yang, R.; Yu, A. Discrete particle simulation of particulate systems: A review of major applications and findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]
- Guises, R.; Xiang, J.; Latham, J.P.; Munjiza, A. Granular packing: Numerical simulation and the characterisation of the effect of particle shape. Granul. Matter 2009, 11, 281–292. [Google Scholar] [CrossRef]
- Houlsby, G. Potential particles: A method for modelling non-circular particles in DEM. Comput. Geotech. 2009, 36, 953–959. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Cylindrical object contact detection for use in discrete element method simulations. Part II—Experimental validation. Chem. Eng. Sci. 2010, 65, 5863–5871. [Google Scholar] [CrossRef]
- Lin, X.; Ng, T.T. Contact detection algorithms for three-dimensional ellipsoids in discrete element modelling. Int. J. Numer. Anal. Methods Geomech. 1995, 19, 653–659. [Google Scholar] [CrossRef]
- Fraige, F.Y.; Langston, P.A.; Chen, G.Z. Distinct element modelling of cubic particle packing and flow. Powder Technol. 2008, 186, 224–240. [Google Scholar] [CrossRef]
- Matuttis, H.; Luding, S.; Herrmann, H. Discrete element simulations of dense packings and heaps made of spherical and non-spherical particles. Powder Technol. 2000, 109, 278–292. [Google Scholar] [CrossRef]
- Nezami, E.G.; Hashash, Y.M.; Zhao, D.; Ghaboussi, J. A fast contact detection algorithm for 3-D discrete element method. Comput. Geotech. 2004, 31, 575–587. [Google Scholar] [CrossRef]
- Nolan, G.T.; Kavanagh, P.E. Random packing of nonspherical particles. Powder Technol. 1995, 84, 199–205. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Rickelt, S.; Wirtz, S.; Scherer, V. A study on the validity of the multi-sphere Discrete Element Method. Powder Technol. 2008, 188, 153–165. [Google Scholar] [CrossRef]
- Rakotonirina, A.D.; Delenne, J.Y.; Radjai, F.; Wachs, A. Grains3D, a flexible DEM approach for particles of arbitrary convex shape—Part III: Extension to non-convex particles modelled as glued convex particles. Comput. Part. Mech. 2019, 6, 55–84. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef]
- Boon, C.W.; Houlsby, G.; Utili, S. A new algorithm for contact detection between convex polygonal and polyhedral particles in the discrete element method. Comput. Geotech. 2012, 44, 73–82. [Google Scholar] [CrossRef]
- Džiugys, A.; Peters, B. An approach to simulate the motion of spherical and non-spherical fuel particles in combustion chambers. Granul. Matter 2001, 3, 231–266. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K. Penalty function method for combined finite–discrete element systems comprising large number of separate bodies. Int. J. Numer. Methods Eng. 2000, 49, 1377–1396. [Google Scholar] [CrossRef]
- Marquardt, J.E.; Römer, U.J.; Nirschl, H.; Krause, M.J. A discrete contact model for complex arbitrary-shaped convex geometries. Particuology 2023, 80, 180–191. [Google Scholar] [CrossRef]
- Nassauer, B.; Kuna, M. Contact forces of polyhedral particles in discrete element method. Granul. Matter 2013, 15, 349–355. [Google Scholar] [CrossRef]
- van der Haven, D.L.H.; Fragkopoulos, I.S.; Elliott, J.A. A physically consistent Discrete Element Method for arbitrary shapes using Volume-interacting Level Sets. Comput. Methods Appl. Mech. Eng. 2023, 414, 116165. [Google Scholar] [CrossRef]
- Zhang, H.; Trias, F.X.; Oliva, A.; Yang, D.; Tan, Y.; Shu, S.; Sheng, Y. PIBM: Particulate immersed boundary method for fluid–particle interaction problems. Powder Technol. 2015, 272, 1–13. [Google Scholar] [CrossRef]
- Maier, M.L.; Milles, S.; Schuhmann, S.; Guthausen, G.; Nirschl, H.; Krause, M. Fluid flow simulations verified by measurements to investigate adsorption processes in a static mixer. Comput. Math. Appl. 2018, 76, 2744–2757. [Google Scholar] [CrossRef]
- Bukreev, F.; Simonis, S.; Kummerländer, A.; Jeßberger, J.; Krause, M.J. Consistent lattice Boltzmann methods for the volume averaged Navier–Stokes equations. J. Comput. Phys. 2023, 490, 112301. [Google Scholar] [CrossRef]
- Höcker, S.; Trunk, R.; Dörfler, W.; Krause, M. Towards the simulations of inertial dense particulate flows with a volume-averaged lattice Boltzmann method. Comput. Fluids 2018, 166, 152–162. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815. [Google Scholar] [CrossRef] [PubMed]
- Trunk, R.; Henn, T.; Dörfler, W.; Nirschl, H.; Krause, M. Inertial dilute particulate fluid flow simulations with an Euler–Euler lattice Boltzmann method. J. Comput. Sci. 2016, 17, 438–445. [Google Scholar] [CrossRef]
- Marquardt, J.E.; Arlt, C.R.; Trunk, R.; Franzreb, M.; Krause, M.J. Numerical and experimental examination of the retention of magnetic nanoparticles in magnetic chromatography. Comput. Math. Appl. 2021, 89, 34–43. [Google Scholar] [CrossRef]
- Marchisio, D.L.; Fox, R.O. Solution of population balance equations using the direct quadrature method of moments. J. Aerosol Sci. 2005, 36, 43–73. [Google Scholar] [CrossRef]
- McGraw, R. Description of aerosol dynamics by the quadrature method of moments. Aerosol Sci. Technol. 1997, 27, 255–265. [Google Scholar] [CrossRef]
- Krause, M.J.; Klemens, F.; Henn, T.; Trunk, R.; Nirschl, H. Particle flow simulations with homogenised lattice Boltzmann methods. Particuology 2017, 34, 1–13. [Google Scholar] [CrossRef]
- Trunk, R.; Marquardt, J.; Thäter, G.; Nirschl, H.; Krause, M.J. Towards the simulation of arbitrarily shaped 3D particles using a homogenised lattice Boltzmann method. Comput. Fluids 2018, 172, 621–631. [Google Scholar] [CrossRef]
- Łukaszewicz, G.; Kalita, P. Navier–Stokes Equations: An Introduction with Applications; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to Continuum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Spaid, M.A.A.; Phelan, F.R. Lattice Boltzmann methods for modeling microscale flow in fibrous porous media. Phys. Fluids 1997, 9, 2468–2474. [Google Scholar] [CrossRef]
- Simonis, S.; Hafen, N.; Jeßberger, J.; Dapelo, D.; Thäter, G.; Krause, M.J. Homogenized lattice Boltzmann methods for fluid flow through porous media—Part I: Kinetic model derivation. arXiv 2023, arXiv:2310.14746. [Google Scholar]
- Guo, Z.; Zhao, T.S. Lattice Boltzmann model for incompressible flows through porous media. Phys. Rev. E 2002, 66, 036304. [Google Scholar] [CrossRef]
- Trunk, R.A. Numerical Investigation of the Settling Behavior of Non-Spherical Particles—Application of Homogenized Lattice Boltzmann Methods. Ph.D. Dissertation, Karlsruhe Institute of Technologie (KIT), Karlsruhe, Germany, 2021. [Google Scholar] [CrossRef]
- Carvalho, A.S.; Martins, J.M. Exact restitution and generalizations for the Hunt–Crossley contact model. Mech. Mach. Theory 2019, 139, 174–194. [Google Scholar] [CrossRef]
- Hafen, N.; Marquardt, J.E.; Dittler, A.; Krause, M.J. Simulation of Dynamic Rearrangement Events in Wall-Flow Filters Applying Lattice Boltzmann Methods. Fluids 2023, 8, 213. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Graduate Texts in Physics; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling: An introduction for Geoscientists and Engineers, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Haussmann, M.; Hafen, N.; Raichle, F.; Trunk, R.; Nirschl, H.; Krause, M.J. Galilean invariance study on different lattice Boltzmann fluid–solid interface approaches for vortex-induced vibrations. Comput. Math. Appl. 2020, 80, 671–691. [Google Scholar] [CrossRef]
- Trunk, R.; Weckerle, T.; Hafen, N.; Thäter, G.; Nirschl, H.; Krause, M.J. Revisiting the Homogenized Lattice Boltzmann Method with Applications on Particulate Flows. Computation 2021, 9, 11. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Ditscherlein, R.; Furat, O.; Löwer, E.; Mehnert, R.; Trunk, R.; Leißner, T.; Krause, M.J.; Schmidt, V.; Peuker, U.A. PARROT: A Pilot Study on the Open Access Provision of Particle-Discrete Tomographic Datasets. Microsc. Microanal. 2022, 28, 350–360. [Google Scholar] [CrossRef] [PubMed]
- Kummerländer, A.; Avis, S.; Kusumaatmaja, H.; Bukreev, F.; Crocoll, M.; Dapelo, D.; Hafen, N.; Ito, S.; Jeßberger, J.; Marquardt, J.E.; et al. OpenLB Release 1.6: Open Source Lattice Boltzmann Code. 2023. Available online: https://zenodo.org/records/7773497 (accessed on 19 August 2024).
- Hafen, N.; Dittler, A.; Krause, M.J. Simulation of particulate matter structure detachment from surfaces of wall-flow filters applying lattice Boltzmann methods. Comput. Fluids 2022, 239, 105381. [Google Scholar] [CrossRef]
- Kupershtokh, A.; Medvedev, D.; Karpov, D. On Equations of State in a Lattice Boltzmann Method. Comput. Math. Appl. 2009, 58, 965–974. [Google Scholar] [CrossRef]
- Wen, B.; Zhang, C.; Tu, Y.; Wang, C.; Fang, H. Galilean invariant fluid–solid interfacial dynamics in lattice Boltzmann simulations. J. Comput. Phys. 2014, 266, 161–170. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Marquardt, J.E.; Hafen, N.; Krause, M.J. A novel model for direct numerical simulation of suspension dynamics with arbitrarily shaped convex particles. Comput. Phys. Commun. 2024, 304, 109321. [Google Scholar] [CrossRef]
- Dapelo, D.; Trunk, R.; Krause, M.J.; Bridgeman, J. Towards Lattice-Boltzmann modelling of unconfined gas mixing in anaerobic digestion. Comput. Fluids 2019, 180, 11–21. [Google Scholar] [CrossRef]
- Bretl, C.; Trunk, R.; Nirschl, H.; Thäter, G.; Dorn, M.; Krause, M.J. Preliminary Study of Particle Settling Behaviour by Shape Parameters via Lattice Boltzmann Simulations. In High Performance Computing in Science and Engineering’20; Nagel, W., Kröner, D., Resch, M., Eds.; Springer: Cham, Switzerland, 2021; pp. 245–259. [Google Scholar] [CrossRef]
- Hafen, N.; Thieringer, J.R.; Meyer, J.; Krause, M.J.; Dittler, A. Numerical investigation of detachment and transport of particulate structures in wall-flow filters using lattice Boltzmann methods. J. Fluid Mech. 2023, 956, A30. [Google Scholar] [CrossRef]
- Hafen, N.; Marquardt, J.E.; Dittler, A.; Krause, M.J. Simulation of Particulate Matter Structure Detachment from Surfaces of Wall-Flow Filters for Elevated Velocities Applying Lattice Boltzmann Methods. Fluids 2023, 8, 99. [Google Scholar] [CrossRef]
- Marquardt, J.E.; Hafen, N.; Krause, M.J. A novel particle decomposition scheme to improve parallel performance of fully resolved particulate flow simulations. J. Comput. Sci. 2024, 78, 102263. [Google Scholar] [CrossRef]
- Marquardt, J.E.; Eysel, B.; Sadric, M.; Rauh, C.; Krause, M.J. Potential for damage to fruits during transport through cross-section constrictions. arXiv 2024, arXiv:2408.09167. [Google Scholar]
- Krause, M.J.; Kummerländer, A.; Avis, S.J.; Kusumaatmaja, H.; Dapelo, D.; Klemens, F.; Gaedtke, M.; Hafen, N.; Mink, A.; Trunk, R.; et al. OpenLB—Open source lattice Boltzmann code. Comput. Math. Appl. 2021, 81, 258–288. [Google Scholar] [CrossRef]
- Schäfer, M.; Turek, S.; Durst, F.; Krause, E.; Rannacher, R. Benchmark Computations of Laminar Flow Around a Cylinder. In Notes on Numerical Fluid Mechanics (NNFM); Vieweg+Teubner Verlag: Braunschweig/Wiesbaden, Germany, 1996; pp. 547–566. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B.; Malaspinas, O.; Deville, M.; Michler, A. Straight velocity boundaries in the lattice Boltzmann method. Phys. Rev. E 2008, 77, 056703. [Google Scholar] [CrossRef]
- ten Cate, A.; Nieuwstad, C.H.; Derksen, J.J.; Van den Akker, H.E.A. Particle imaging velocimetry experiments and lattice-Boltzmann simulations on a single sphere settling under gravity. Phys. Fluids 2002, 14, 4012–4025. [Google Scholar] [CrossRef]
- Ginzbourg, I.; d’Humières, D. Local second-order boundary methods for lattice Boltzmann models. J. Stat. Phys. 1996, 84, 927–971. [Google Scholar] [CrossRef]
- Hayakawa, Y.; Oguchi, T. Evaluation of gravel sphericity and roundness based on surface-area measurement with a laser scanner. Comput. Geosci. 2005, 31, 735–741. [Google Scholar] [CrossRef]
- Hofmann, H.J. Grain-shaped indices and isometric graphs. J. Sediment. Res. 1994, 64, 916–920. [Google Scholar] [CrossRef]
- Pearson, K. VII. Mathematical contributions to the theory of evolution—III. Regression, heredity, and panmixia. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1896, 187, 253–318. [Google Scholar] [CrossRef]
- Henn, T.; Thäter, G.; Dörfler, W.; Nirschl, H.; Krause, M.J. Parallel dilute particulate flow simulations in the human nasal cavity. Comput. Fluids 2016, 124, 197–207. [Google Scholar] [CrossRef]
- Park, J. Modeling the Dynamics of Fabric in a Rotating Horizontal Drum. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2003. [Google Scholar]
- Li, X. An Experimental and Numerical Study of Normal Particle Collisions in a Viscous Liquid. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2010. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G.; Skaperdas, E.; Warren, J.; Allansson, R. Optimized Filter Design and Selection Criteria for Continuously Regenerating Diesel Particulate Traps. J. Fuels Lubr. 1999, 108, 279–288. [Google Scholar] [CrossRef]
- Dittler, A. Ash Transport in Diesel Particle Filters. In Proceedings of the SAE 2012 International Powertrains, Fuels & Lubricants Meeting, Malmo, Sweden, 18–20 September 2012. [Google Scholar] [CrossRef]
- Kimura, K.; Lynskey, M.; Corrigan, E.R.; Hickman, D.L.; Wang, J.; Fang, H.L.; Chatterjee, S. Real World Study of Diesel Particulate Filter Ash Accumulation in Heavy-Duty Diesel Trucks. In Proceedings of the Powertrain & Fluid Systems Conference and Exhibition, Toronto, ON, Canada, 16–19 October 2006. [Google Scholar] [CrossRef]
- Schiller, L.; Neumann, A. Über die grundlegenden Berechnungen bei der Schwerkraftaufbereitung. Z. Vereines Dtsch. Ingenieure 1933, 77, 318–321. [Google Scholar]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid-Z 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Bouzidi, M.; Firdaouss, M.; Lallemand, P. Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 2001, 13, 3452–3459. [Google Scholar] [CrossRef]
- Metzner, A.B.; Reed, J.C. Flow of non-newtonian fluids—Correlation of the laminar, transition, and turbulent-flow regions. AIChE J. 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Faust, E.; Schlüter, A.; Müller, H.; Steinmetz, F.; Müller, R. Dirichlet and Neumann boundary conditions in a lattice Boltzmann method for elastodynamics. Comput. Mech. 2023, 73, 317–339. [Google Scholar] [CrossRef]
- Maquart, T.; Noël, R.; Courbebaisse, G.; Navarro, L. Toward a Lattice Boltzmann Method for Solids—Application to Static Equilibrium of Isotropic Materials. Appl. Sci. 2022, 12, 4627. [Google Scholar] [CrossRef]
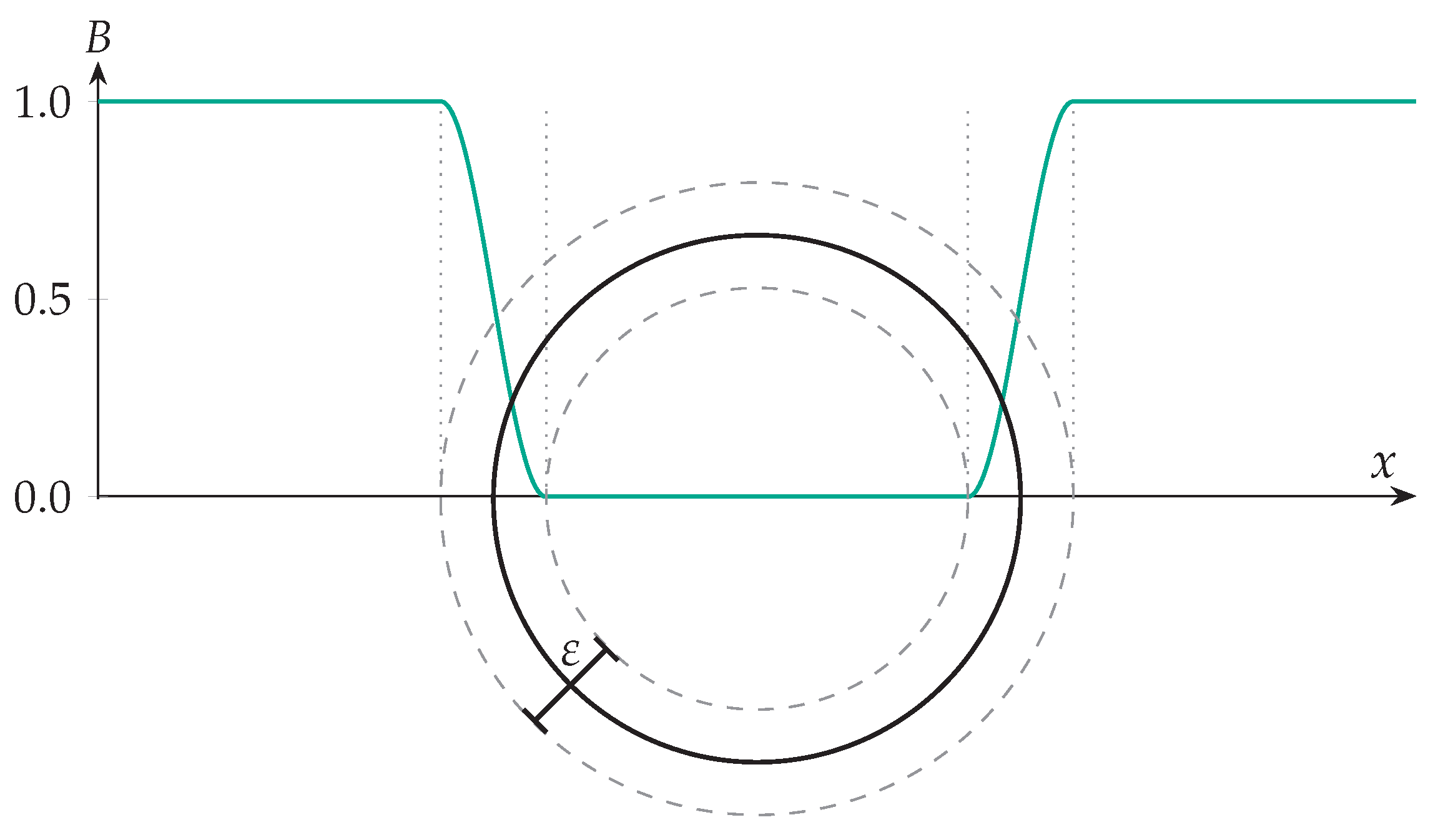

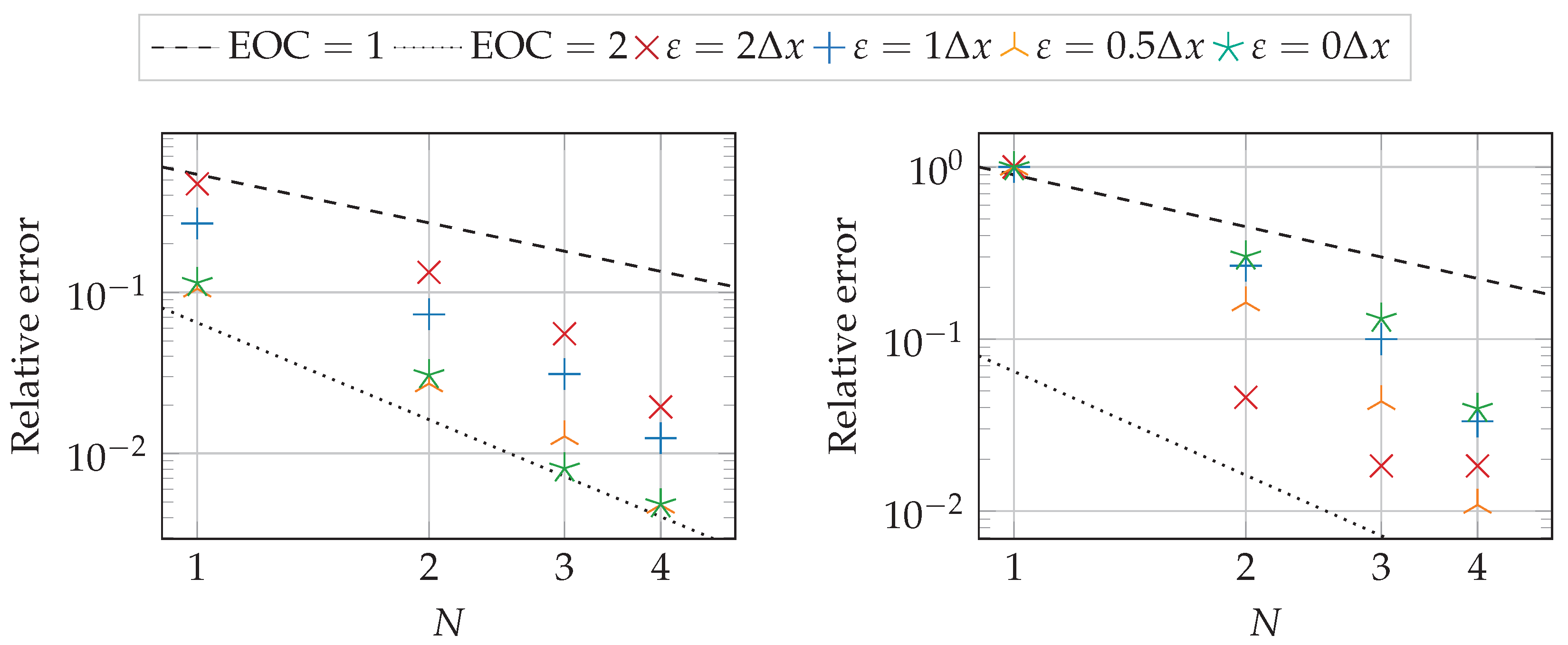



| Drag Coefficient | Lift Coefficient () | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| = 1 | = 2 | = 3 | = 4 | = 5 | = 1 | = 2 | = 3 | = 4 | = 5 | |
| Schäfer et al. [85] | – | – | ||||||||
| Case | Fluid Density in kg | Dynamic Viscosity in Pa s | Grid Spacing in mm | Time Step Size in ms |
|---|---|---|---|---|
| 1 | 970 | |||
| 2 | 965 | |||
| 3 | 962 | |||
| 4 | 960 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marquardt, J.E.; Krause, M.J. A Review of the Homogenized Lattice Boltzmann Method for Particulate Flow Simulations: From Fundamentals to Applications. Powders 2024, 3, 500-530. https://doi.org/10.3390/powders3040027
Marquardt JE, Krause MJ. A Review of the Homogenized Lattice Boltzmann Method for Particulate Flow Simulations: From Fundamentals to Applications. Powders. 2024; 3(4):500-530. https://doi.org/10.3390/powders3040027
Chicago/Turabian StyleMarquardt, Jan E., and Mathias J. Krause. 2024. "A Review of the Homogenized Lattice Boltzmann Method for Particulate Flow Simulations: From Fundamentals to Applications" Powders 3, no. 4: 500-530. https://doi.org/10.3390/powders3040027
APA StyleMarquardt, J. E., & Krause, M. J. (2024). A Review of the Homogenized Lattice Boltzmann Method for Particulate Flow Simulations: From Fundamentals to Applications. Powders, 3(4), 500-530. https://doi.org/10.3390/powders3040027






