Multidimensional Characterization and Separation of Ultrafine Particles: Insights and Advances by Means of Froth Flotation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
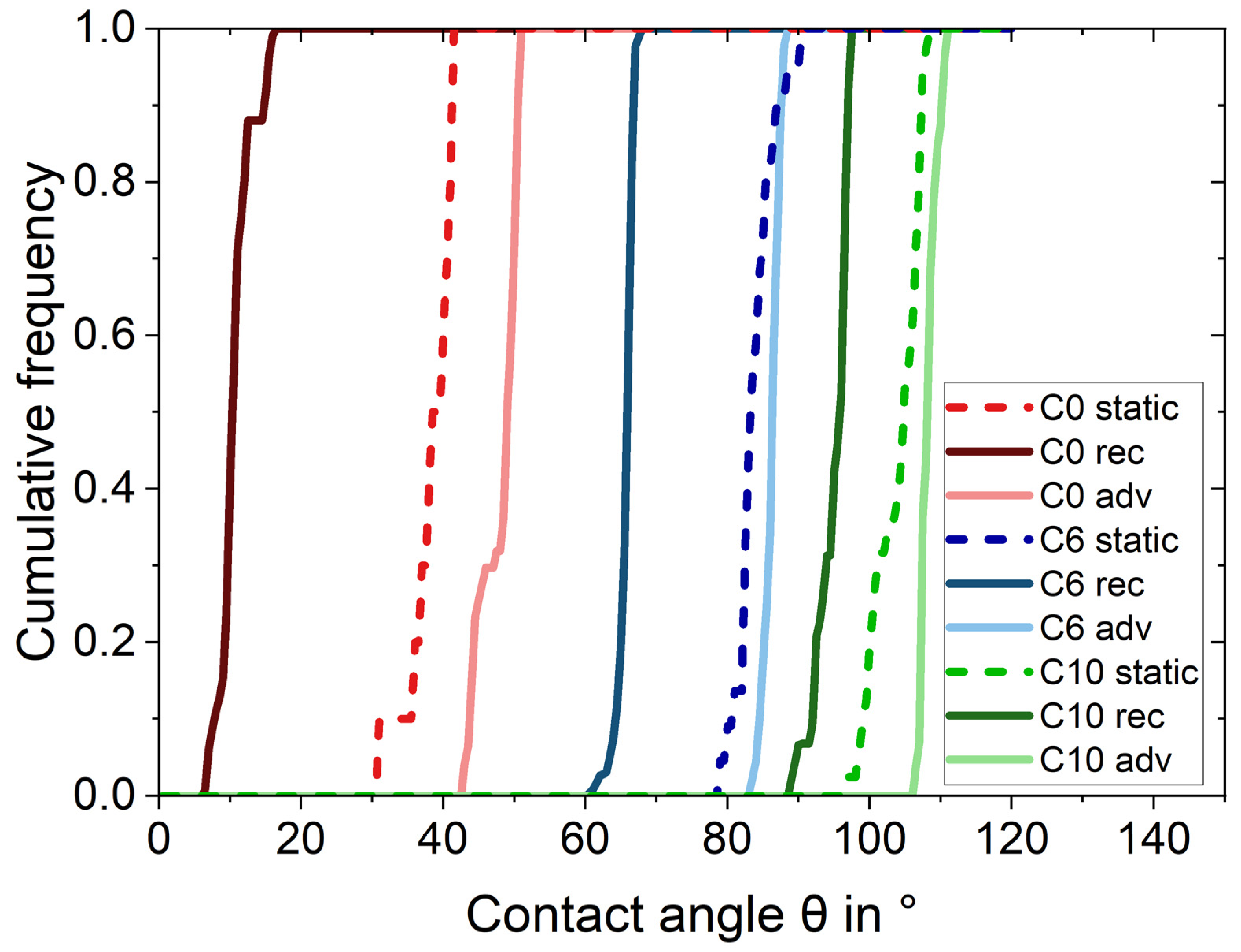
2.2. Contact Angle Measurements
2.3. Inverse Gas Chromatography
2.4. Flow Cytometry
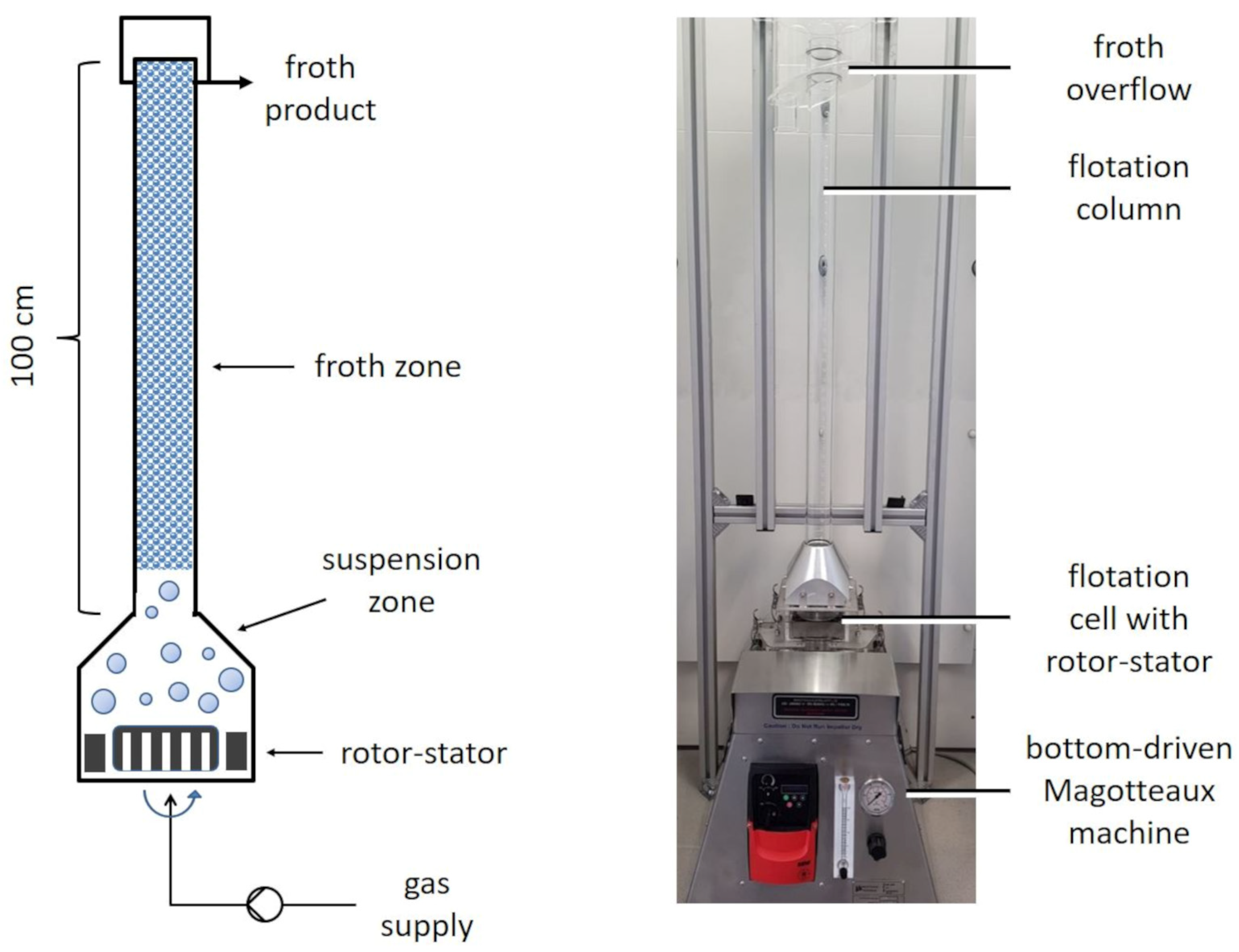
2.5. Flotation-Based Separation
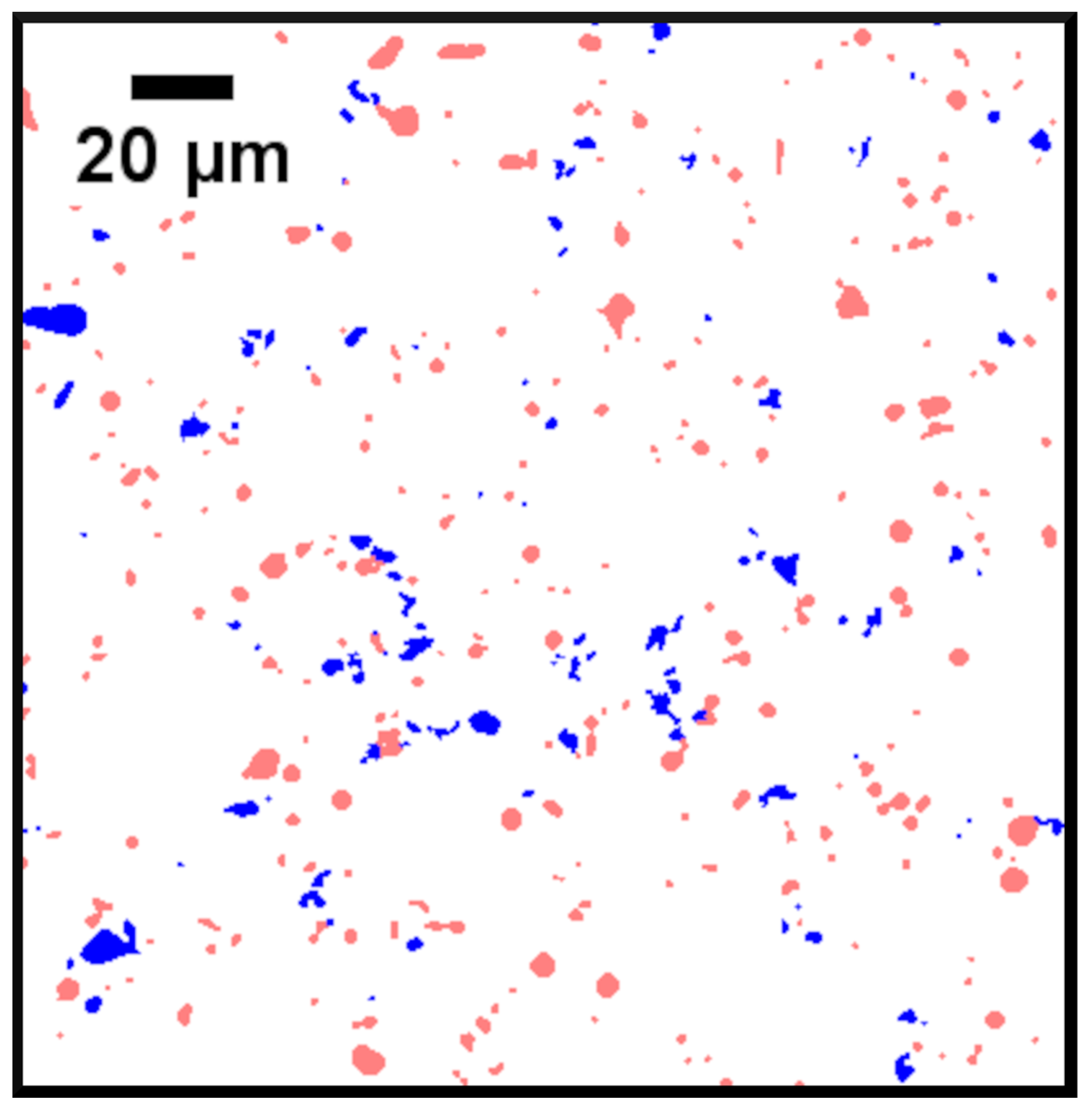
2.6. Mineral Liberation Analysis
3. Results and Discussion
3.1. Characterization of Ultrafine Particles
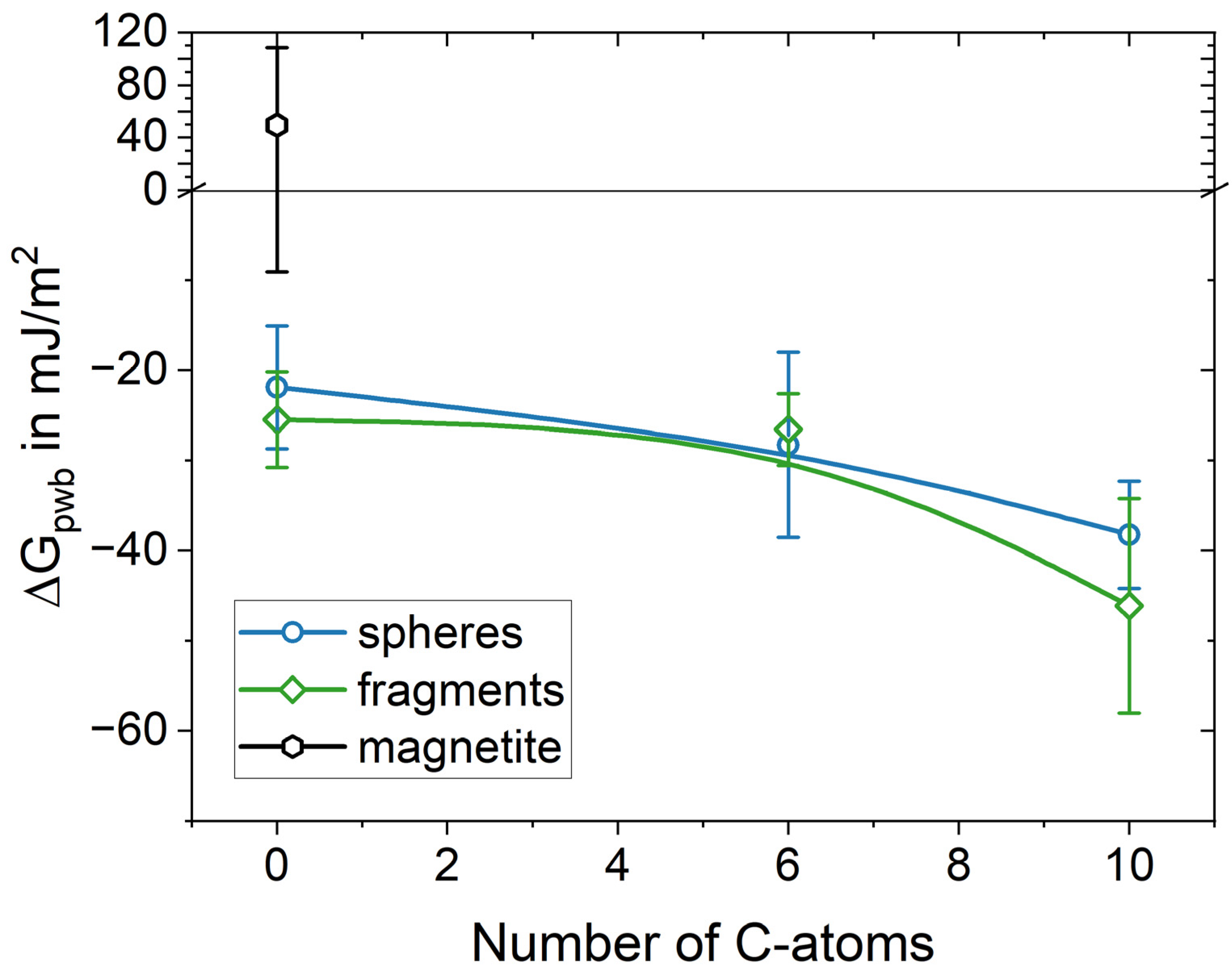
3.1.1. Characterizing (de)Wetting(Ability)
3.1.2. Characterizing Shape and Size
3.2. Separation of Ultrafine Particles
3.2.1. Separation Based on Wettability of Particles with the Same Shape
3.2.2. Separation Based on Shape of Particles with Similar Wettability States
3.2.3. Separation Based on Multiple Particle Properties
3.3. General Discussion
4. Conclusions
- The wettability of glass particles and glass slides can be modified via an esterification reaction using n-alcohols, whereby the length of the alkyl chain controls the resulting level of hydrophobicity.
- The particle wettability is influenced by the particle shape.
- The commonly used contact angle is not sufficient to accurately describe particle wettability.
- The particle-specific characterization of size and shape is challenging for ultrafine particles, as analytical techniques are not well-equipped for these size ranges.
- A novel separation apparatus was introduced, combining the advantages of mechanical and column flotation to enhance the separation of ultrafine particles.
- Different separation behaviors are observed, especially with regard to the particle shape, but also depending on the particle wettability.
- Differently shaped particles seem to exhibit different optimum levels of wettability.
- A multivariate approach was demonstrated for the multidimensional evaluation of the separation process, offering the possibility to show the combined influence of particle shape and size for different wettability scenarios.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sokolović, J.M.; Miskovic, S. The effect of particle size on coal flotation kinetics: A review. Physicochem. Probl. Miner. Process. 2018, 54, 1172–1190. [Google Scholar] [CrossRef]
- Xia, W. Role of particle shape in the floatability of mineral particle: An overview of recent advances. Powder Technol. 2017, 317, 104–116. [Google Scholar] [CrossRef]
- Sun, Y.; Bu, X.; Ulusoy, U.; Guven, O.; Hassas, B.V.; Dong, X. Effect of surface roughness on particle-bubble interaction: A critical review. Miner. Eng. 2023, 201, 108223. [Google Scholar] [CrossRef]
- Vallejos, P.; Yianatos, J.; Vinnett, L. A Model Structure for Size-by-Liberation Recoveries in Flotation. Minerals 2021, 11, 194. [Google Scholar] [CrossRef]
- Trahar, W.J.; Warren, L.J. The flotability of very fine particles—A review. Int. J. Miner. Process. 1976, 3, 103–131. [Google Scholar] [CrossRef]
- Dai, Z.; Fornasiero, D.; Ralston, J. Particle-bubble collision models—A review. Adv. Colloid Interface Sci. 2000, 85, 231–256. [Google Scholar] [CrossRef]
- De Gontijo, C.F.; Fornasiero, D.; Ralston, J. The limits of fine and coarse particle flotation. Can. J. Chem. Eng. 2007, 85, 739–747. [Google Scholar] [CrossRef]
- Konopacka, Z.; Drzymala, J. Types of particles recovery—Water recovery entrainment plots useful in flotation research. Adsorption 2010, 16, 313–320. [Google Scholar] [CrossRef]
- Miettinen, T.; Ralston, J.; Fornasiero, D. The limits of fine particle flotation. Miner. Eng. 2010, 23, 420–437. [Google Scholar] [CrossRef]
- Leistner, T.; Peuker, U.A.; Rudolph, M. How gangue particle size can affect the recovery of ultrafine and fine particles during froth flotation. Miner. Eng. 2017, 109, 1–9. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Hao, F.P.; Smith, L.K.; Chau, T.T.; Bruckard, W.J. The effect of particle shape and hydrophobicity in flotation. Int. J. Miner. Proc. 2009, 93, 128–134. [Google Scholar] [CrossRef]
- Vaziri Hassas, B.; Caliskan, H.; Guven, O.; Karakas, F.; Cinar, M.; Celik, M.S. Effect of roughness and shape factor on flotation characteristics of glass beads. Colloids Surf. A Physicochem. Eng. Asp. 2016, 492, 88–99. [Google Scholar] [CrossRef]
- Verrelli, D.I.; Bruckard, W.J.; Koh, P.T.L.; Schwarz, M.P.; Follink, B. Particle shape effects in flotation. Part 1: Microscale experimental observations. Miner. Eng. 2014, 58, 80–89. [Google Scholar] [CrossRef]
- Ma, G.; Bu, X.; Ulusoy, U.; Xie, G. Effect of particle shape on bubble-particle attachment behavior: Roles of surfaces, edges, and vertexes. J. Clean. Prod. 2023, 429, 139606. [Google Scholar] [CrossRef]
- Chen, W.; Chen, X.; Wang, P.; Zhang, Z.; Zhang, J. Influence of particle shape on the interaction processes of coal particles and bubbles in saline solution. Colloids Surf. A Physicochem. Eng. Asp. 2023, 656, 130434. [Google Scholar] [CrossRef]
- Sygusch, J.; Stefenelli, N.; Rudolph, M. Ultrafine Particle Flotation in a Concept Flotation Cell Combining Turbulent Mixing Zone and Deep Froth Fractionation with a Special Focus on the Property Vector of Particles. Minerals 2023, 13, 1099. [Google Scholar] [CrossRef]
- Kursun, H.; Ulusoy, U. Influence of shape characteristics of talc mineral on the column flotation behavior. Int. J. Miner. Process. 2006, 78, 262–268. [Google Scholar] [CrossRef]
- Little, L.; Wiese, J.; Becker, M.; Mainza, A.; Ross, V. Investigating the effects of particle shape on chromite entrainment at a platinum concentrator. Miner. Eng. 2016, 96–97, 46–52. [Google Scholar] [CrossRef]
- Kupka, N.; Tolosana-Delgado, R.; Schach, E.; Bachmann, K.; Heinig, T.; Rudolph, M. R as an environment for data mining of process mineralogy data: A case study of an industrial rougher flotation bank. Miner. Eng. 2020, 146, 106111. [Google Scholar] [CrossRef]
- Wiese, J.; Becker, M.; Yorath, G.; O’connor, C. An investigation into the relationship between particle shape and entrainment. Miner. Eng. 2015, 83, 211–216. [Google Scholar] [CrossRef]
- Johansson, G.; Pugh, R.J. The influence of particle size and hydrophobicity on the stability of mineralized froths. Int. J. Miner. Process. 1992, 34, 1–21. [Google Scholar] [CrossRef]
- Drelich, J.W.; Marmur, A. Meaningful contact angles in flotation systems: Critical analysis and recommendations. Surf. Innov. 2017, 6, 19–30. [Google Scholar] [CrossRef]
- Ata, S.; Ahmed, N.; Jameson, G.J. A study of bubble coalescence in flotation froths. Int. J. Miner. Process. 2003, 72, 255–266. [Google Scholar] [CrossRef]
- Lu, S.; Pugh, R.J.; Forssberg, E. Interfacial Separation of Particles; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Dippenaar, A. The destabilization of froth by solids. I. The mechanism of film rupture. Int. J. Miner. Process. 1982, 9, 1–14. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Runge, K.; Bradshaw, D. A review of entrainment: Mechanisms, contributing factors and modelling in flotation. Miner. Eng. 2015, 70, 77–91. [Google Scholar] [CrossRef]
- Smith, P.G.; Warren, L.J. Entrainment of Particles into Flotation Froths. Miner. Process. Extr. Metall. Rev. 1989, 5, 123–145. [Google Scholar] [CrossRef]
- Butt, H.J.; Graf, K.; Kappl, M. Physics and Chemistry of Interfaces, 3rd ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013. [Google Scholar]
- Binks, B.P.; Horozov, T.S. Colloidal Particles at Liquid Interfaces; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Frank, U.; Uttinger, M.J.; Wawra, S.E.; Lübbert, C.; Peukert, W. Progress in Multidimensional Particle Characterization. KONA Powder Part. J. 2021, 39, 3–28. [Google Scholar] [CrossRef]
- Fandrich, R.; Gu, Y.; Burrows, D.; Moeller, K. Modern SEM-based mineral liberation analysis. Int. J. Miner. Process. 2007, 84, 310–320. [Google Scholar] [CrossRef]
- Kupka, N.; Rudolph, M. Evaluation of the performance of an industrial rougher flotation bank of a scheelite ore through automated mineralogy. In Procemin GEOMET 2018; Gecamin: Santiago, Chile; p. A15 1–8.
- Schach, E.; Buchmann, M.; Tolosana-Delgado, R.; Leißner, T.; Kern, M.; Gerald van den Boogaart, K.; Rudolph, M.; Peuker, U.A. Multidimensional characterization of separation processes—Part 1: Introducing kernel methods and entropy in the context of mineral processing using SEM-based image analysis. Miner. Eng. 2019, 137, 78–86. [Google Scholar] [CrossRef]
- Pereira, L.; Frenzel, M.; Hoang, D.H.; Tolosana-Delgado, R.; Rudolph, M.; Gutzmer, J. Computing single-particle flotation kinetics using automated mineralogy data and machine learning. Miner. Eng. 2021, 170, 107054. [Google Scholar] [CrossRef]
- McKinnon, K.M. Flow Cytometry: An Overview. Curr. Protoc. Immunol. 2018, 120, 5.1.1–5.1.11. [Google Scholar] [CrossRef] [PubMed]
- Buchwald, T.; Schach, E.; Peuker, U. A framework for the description of multidimensional particle separation processes. Powder Technol. 2023, 433, 119165. [Google Scholar] [CrossRef]
- Wilhelm, T.; Sygusch, J.; Furat, O.; Bachmann, K.; Rudolph, M.; Schmidt, V. Parametric Stochastic Modeling of Particle Descriptor Vectors for Studying the Influence of Ultrafine Particle Wettability and Morphology on Flotation-Based Separation Behavior. Powders 2023, 2, 353–371. [Google Scholar] [CrossRef]
- Sygusch, J.; Wilhelm, T.; Furat, O.; Bachmann, K.; Schmidt, V.; Rudolph, M. Application of multivariate Tromp functions for evaluating the joint impact of particle size, shape and wettability on the separation of ultrafine particles via flotation. Powders 2024, 3, 338–366. [Google Scholar] [CrossRef]
- Schach, E.; Buchwald, T.; Leißner, T.; Peuker, U.; Delgado, R.T. Concepts of entropy for raw materials. Powder Technol. 2024, 435, 119398. [Google Scholar] [CrossRef]
- Sygusch, J.; Rudolph, M. A contribution to wettability and wetting characterisation of ultrafine particles with varying shape and degree of hydrophobization. Appl. Surf. Sci. 2021, 566, 150725. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Interfacial Lifshitz-van der Waals and polar interactions in macroscopic systems. Chem. Rev. 1988, 88, 927–941. [Google Scholar] [CrossRef]
- Schultz, J.; Lavielle, L.; Martin, C. The Role of the Interface in Carbon Fibre-Epoxy Composites. J. Adhes. 1987, 23, 45–60. [Google Scholar] [CrossRef]
- Della Volpe, C.; Siboni, S. Some Reflections on Acid–Base Solid Surface Free Energy Theories. J. Colloid Interface Sci. 1997, 195, 121–136. [Google Scholar] [CrossRef]
- van Oss, C.J.; Giese, R.F.; Docoslis, A. Hyperhydrophobicity of the water-air interface. J. Dispers. Sci. Technol. 2005, 26, 585–590. [Google Scholar] [CrossRef]
- Heinig, T.; Bachmann, K.; Tolosana-Delgado, R.; Van den Boogaart, K.G.; Gutzmer, J. Monitoring gravitational and particle shape settling effects on MLA sampling preparation. In Proceedings of the IAMG, Freiberg, Germany, 5–13 September 2015. [Google Scholar]
- Schulz, B.; Sandmann, D.; Gilbricht, S. SEM-Based Automated Mineralogy and Its Application in Geo- and Material Sciences. Minerals 2020, 10, 1004. [Google Scholar] [CrossRef]
- Bachmann, K.; Frenzel, M.; Krause, J.; Gutzmer, J. Advanced Identification and Quantification of In-Bearing Minerals by Scanning Electron Microscope-Based Image Analysis. Microsc. Microanal. 2017, 23, 527–537. [Google Scholar] [CrossRef] [PubMed]
- Ralston, J.; Fornasiero, D.; Hayes, R. Bubble–particle attachment and detachment in flotation. Int. J. Miner. Process. 1999, 56, 133–164. [Google Scholar] [CrossRef]
- Hewitt, D.; Fornasiero, D.; Ralston, J. Bubble particle attachment efficiency. Miner. Eng. 1994, 7, 657–665. [Google Scholar] [CrossRef]
- Ulusoy, U.; Hiçyılmaz, C.; Yekeler, M. Role of shape properties of calcite and barite particles on apparent hydrophobicity. Chem. Eng. Process. Process Intensif. 2004, 43, 1047–1053. [Google Scholar] [CrossRef]
- Maes, T.; Jessop, R.; Wellner, N.; Haupt, K.; Mayes, A.G. A rapid-screening approach to detect and quantify microplastics based on fluorescent tagging with Nile Red. Sci. Rep. 2017, 7, 44501. [Google Scholar] [CrossRef]
- Guckenberger, D.J.; Berthier, E.; Young, E.W.; Beebe, D.J. Fluorescence-based assessment of plasma-induced hydrophilicity in microfluidic devices via Nile Red adsorption and depletion. Anal. Chem. 2014, 86, 7258–7263. [Google Scholar] [CrossRef]
- Sackett, D.L.; Wolff, J. Nile Red as a polarity-sensitive fluorescent probe of hydrophobic protein surfaces. Anal. Biochem. 1987, 167, 228–234. [Google Scholar] [CrossRef]
- Barbery, G. Liberation 1, 2, 3: Theoretical analysis of the effect of space dimension on mineral liberation by size reduction. Miner. Eng. 1992, 5, 123–141. [Google Scholar] [CrossRef]
- Spencer, S.; Sutherland, D. Stereological correction of mineral liberation grade distributions estimated by single sectioning of particles. Image Anal. Stereol. 2011, 19, 175–182. [Google Scholar] [CrossRef]
- Ditscherlein, R.; Furat, O.; de Langlard, M.; Martins de Souza, E.S.J.; Sygusch, J.; Rudolph, M.; Leissner, T.; Schmidt, V.; Peuker, U.A. Multiscale Tomographic Analysis for Micron-Sized Particulate Samples. Microsc. Microanal. 2020, 26, 676–688. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, S.; Grano, S. Effect of particle hydrophobicity on particle and water transport across a flotation froth. Colloids Surf. A Physicochem. Eng. Asp. 2005, 256, 157–164. [Google Scholar] [CrossRef]

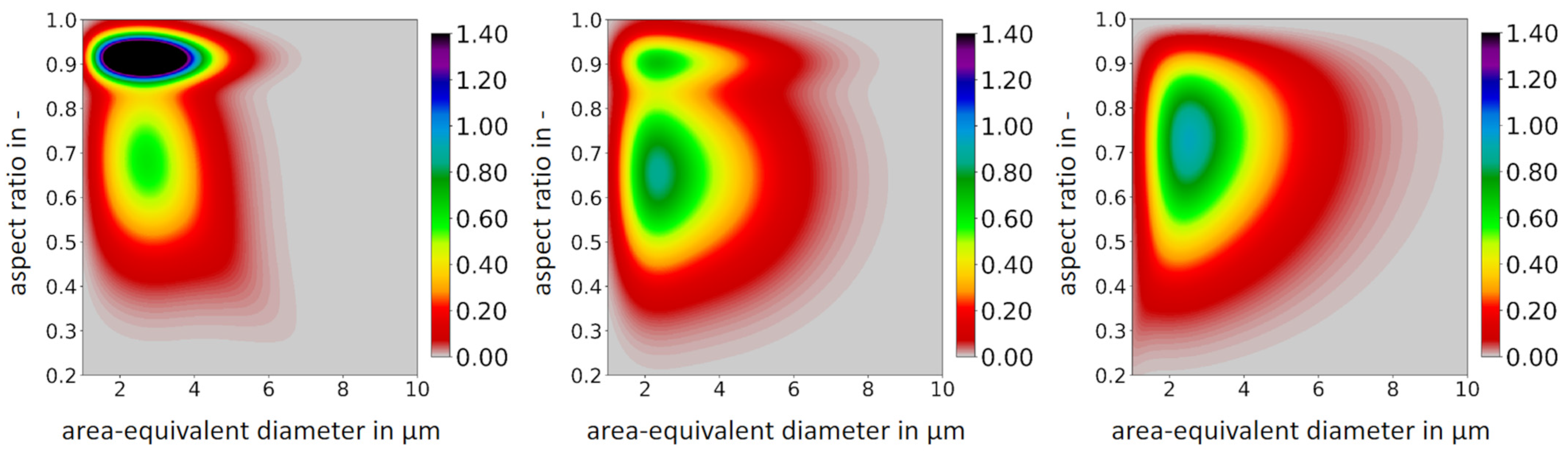
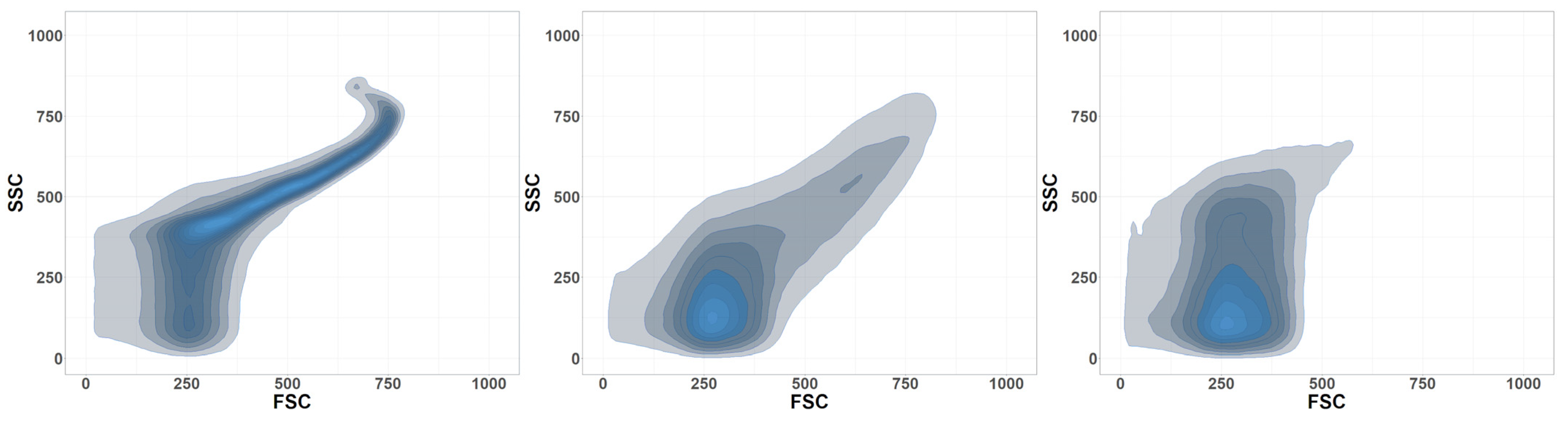
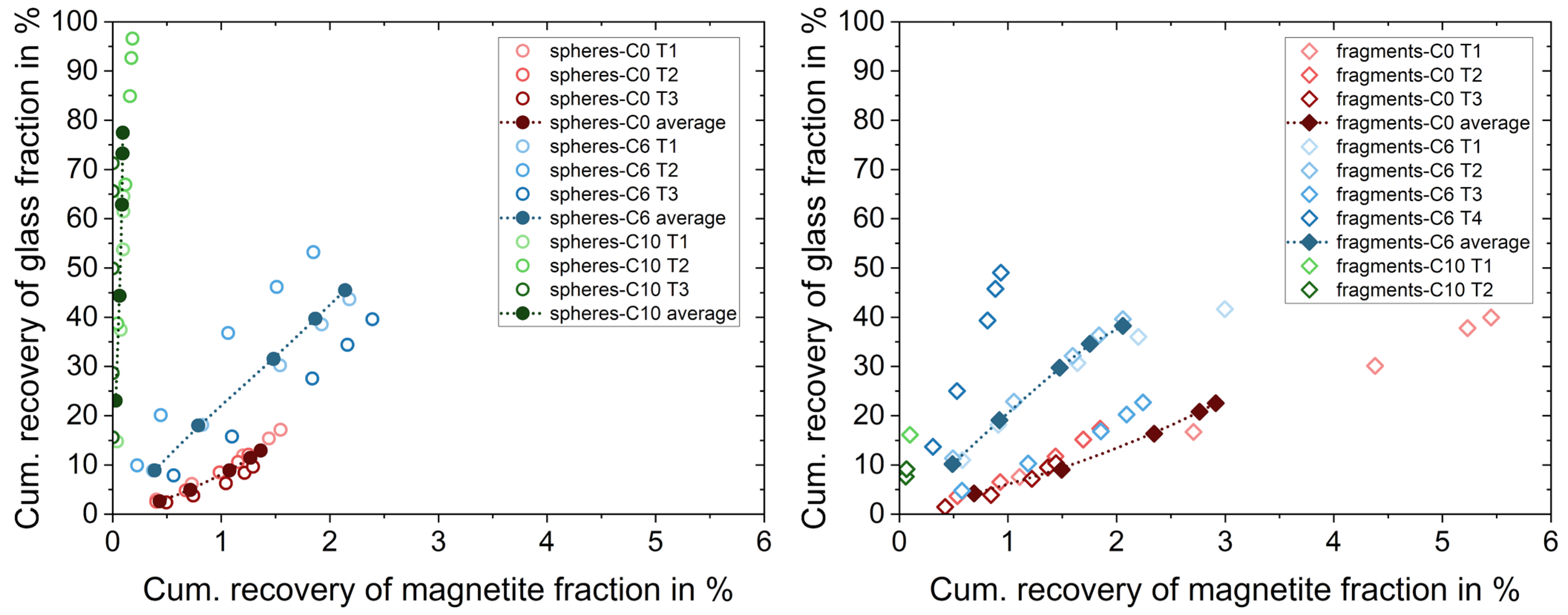
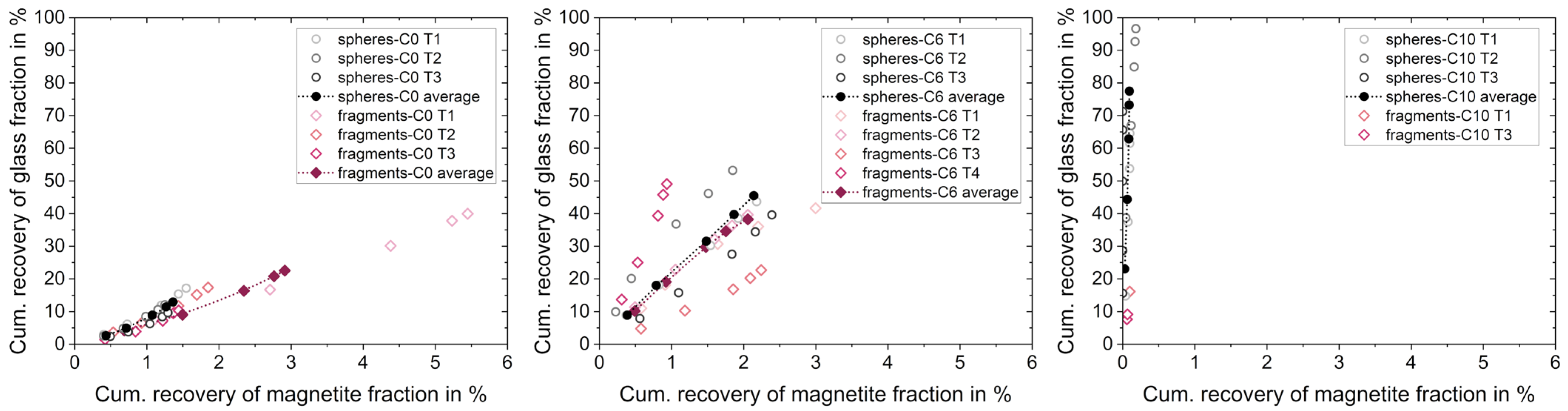
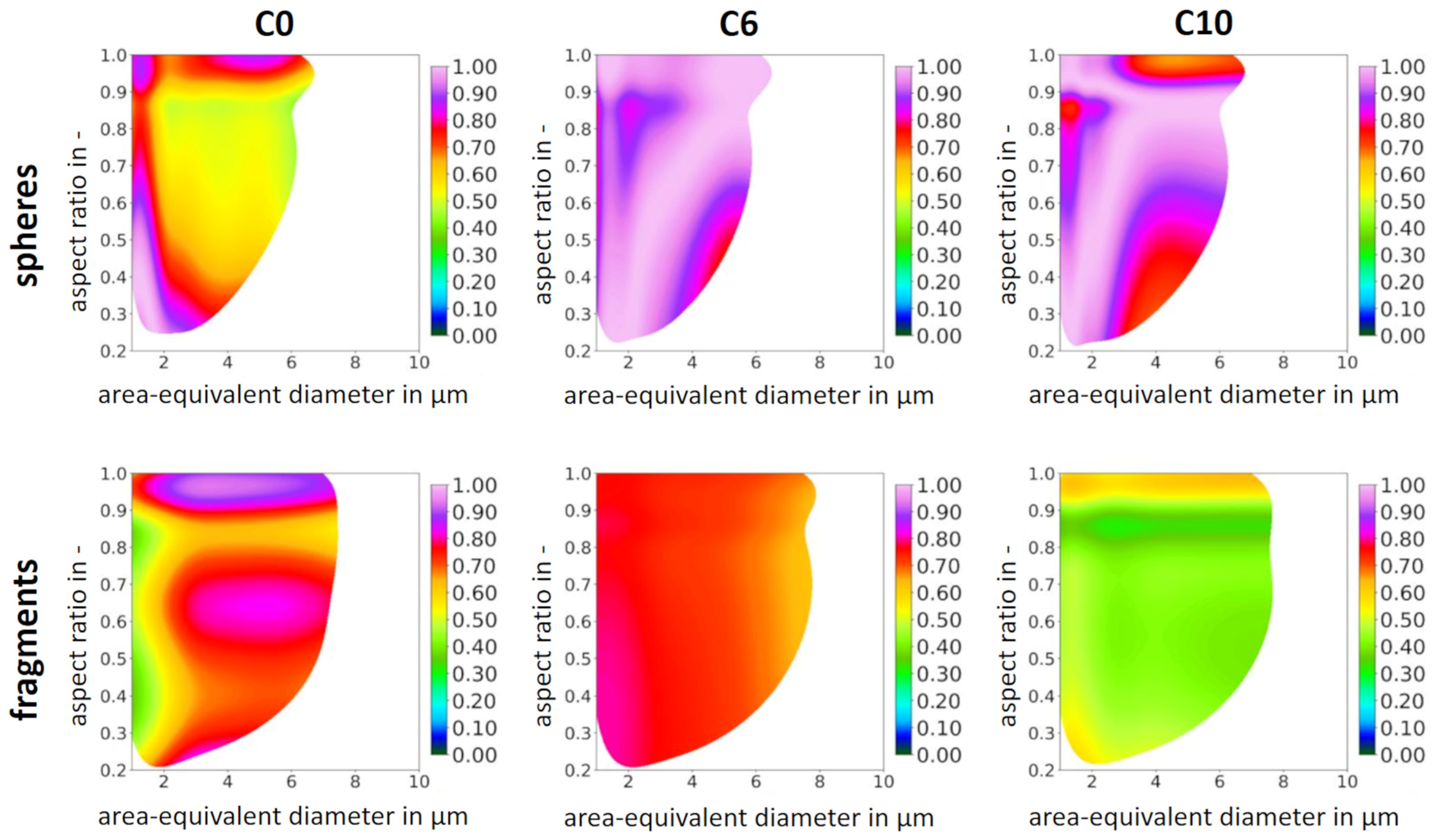

| Particle Size in µm | Spheres | Fragments | Magnetite |
|---|---|---|---|
| x10 | 0.62 | 0.81 | 0.73 |
| x50 | 2.68 | 3.21 | 2.53 |
| x90 | 5.06 | 7.41 | 6.72 |
| Fluid | T in K | γd in mJ/m2 | γ− in mJ/m2 | γ+ in mJ/m2 |
|---|---|---|---|---|
| Water | 293 | 21.8 | 65.0 | 10.0 |
| Bubble | - | 0.0 | 0.0 | 0.0 |
| Wettability Level | Static CA in ° | Receding CA in ° | Advancing CA in ° |
|---|---|---|---|
| C0 | 38.2 ± 2.4 | 10.6 ± 0.4 | 47.9 ± 0.8 |
| C6 | 83.7 ± 1.2 | 65.6 ± 0.1 | 86.2 ± 0.1 |
| C10 | 103.9 ± 1.0 | 94.8 ± 0.2 | 108.2 ± 0.1 |
| Particle System | γdspheres in mJ/m2 | γdfragments in mJ/m2 | γdmagnetite in mJ/m2 |
|---|---|---|---|
| C0 | 53.9 ± 3.1 | 44.9 ± 2.3 | 156.6 ± 40.0 |
| C6 | 48.7 ± 3.8 | 47.1 ± 2.1 | - |
| C10 | 39.5 ± 1.5 | 36.8 ± 1.5 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sygusch, J.; Rudolph, M. Multidimensional Characterization and Separation of Ultrafine Particles: Insights and Advances by Means of Froth Flotation. Powders 2024, 3, 460-481. https://doi.org/10.3390/powders3030025
Sygusch J, Rudolph M. Multidimensional Characterization and Separation of Ultrafine Particles: Insights and Advances by Means of Froth Flotation. Powders. 2024; 3(3):460-481. https://doi.org/10.3390/powders3030025
Chicago/Turabian StyleSygusch, Johanna, and Martin Rudolph. 2024. "Multidimensional Characterization and Separation of Ultrafine Particles: Insights and Advances by Means of Froth Flotation" Powders 3, no. 3: 460-481. https://doi.org/10.3390/powders3030025
APA StyleSygusch, J., & Rudolph, M. (2024). Multidimensional Characterization and Separation of Ultrafine Particles: Insights and Advances by Means of Froth Flotation. Powders, 3(3), 460-481. https://doi.org/10.3390/powders3030025







