Abstract
Cylindrical packed beds of spheres are found in many industrial and practical applications where heat and mass transfer and fluid flow occur. A proper understanding of the porous structure is imperative for the analysis and design of the performance of packed beds. The porosity of the packed bed and in particular the radial variation in porosity is of interest. When the positions and sizes of the spheres in the packed bed are known, the areas of the intersections between the spheres and selected cylindrical planes can be used to obtain the radial variation in porosity. The aim of the study is to evaluate the performance of approximate expressions that had been derived to calculate the intersection areas. Firstly, the ability of the approximate expressions to calculate the intersection area is evaluated by considering several typical sphere–cylindrical plane configurations. Secondly, the application of the approximate expressions to obtain the radial variation in porosity for a selection of cylindrical packed beds is evaluated. It is concluded that the approximate expressions should only be applied to packed beds with aspect ratios larger than 6 and for radial positions larger than 1.5 sphere diameters from the centre line of the cylindrical packed bed.
1. Introduction
Cylindrical packed beds containing spherical particles can be found in many industrial applications involving the flow of fluids and heat and mass transfer such as catalytic reactors [1], pebble bed nuclear reactors [2], and packed beds for thermal energy storage [3]. A thorough understanding of the porous structure of cylindrical packed beds and how the structure affects the transfer and flow phenomena is required for the design, analysis, and operation of packed bed reactors [4]. The most notable characteristic of the porous structure affecting the flow and transfer phenomena is the porosity or void fraction [4].
Physical experiments having destructive [5,6] and non-destructive [7,8] natures were performed to determine the variation in porosity directly. The porosity was also determined directly from images using various imaging techniques [4,9,10,11,12,13]. The images were otherwise analyzed to obtain the coordinates of the centers and the diameters of the spheres [4,9,10]. Numerical models of packed beds were also generated employing packing algorithms [14,15] and the discrete element method (DEM) [2,16], from which the coordinates of the centers of the spheres can be obtained directly. When the positions of the centers of spheres and the diameters of the spheres are known, the variation in porosity can be calculated numerically employing approaches based on volume-based formulations [9,17,18], area-based formulations [19,20,21,22], and line-based formulations [23,24,25].
It has been found that the wall of the cylindrical container and the ratio between the diameter of the cylindrical container and the diameter of the spheres, namely the aspect ratio, have a marked influence on the packing structure [6,26]. Benenati and Brosilow [5] and Goodling et al. [6] observed that the radial porosity varies in a damped oscillatory manner from a value of one at the wall to a bulk value some distance from the wall depending on the aspect ratio. Two categories of empirical correlations have been derived from the experimental and numerical data to predict the radial variation in porosity, namely exponential correlations [27,28,29] and oscillatory correlations [9,30,31,32].
In this study, the area-based methods are under the spotlight. In a previous study, Du Toit [33] considered the analytical integral expressions of Mariana et al. [19], Du Toit [20,21], and Mueller [22] to calculate the area of the intersection between a sphere and a cylindrical plane. Because of the fact that the analytical integral expressions cannot be integrated analytically, Du Toit [33] used Simpson’s Rule [34] to evaluate the analytical integrals expressions numerically. Du Toit [33] showed that for the selected sphere–cylindrical plane configurations, the results obtained for the areas of the intersections between the spheres and the cylindrical planes were in excellent agreement with the corresponding areas obtained using the Measuring Geometry Tool in the finite element code COMSOL Multiphysics [35] and the computer-aided design (CAD) codes SOLIDWORKS [36] and NX [37]. It was, therefore, concluded that the methodologies of Mariana et al. [19], Du Toit [20,21], and Mueller [22] calculate the area of the intersection between a sphere and a cylindrical plane correctly.
In addition to the analytical integral expression, Mueller [22] also derived approximate expressions to calculate the area of the intersection between a sphere and a cylindrical plane. The aim of this study is to evaluate the performance of the approximate expressions that had been derived to calculate the intersection areas. Firstly, the ability of the approximate expressions to calculate the intersection area is evaluated by considering several typical sphere-cylindrical plane configurations that can be encountered in packed beds. Secondly, the application of the approximate expressions to obtain the radial variation in porosity for a selection of cylindrical packed beds is evaluated.
2. Theoretical Overview
2.1. Intersection of Cylindrical Plane and Sphere
As the container wall has a significant effect on the porous structure in the near-wall region, a proper understanding of the radial variation in the porosity in cylindrical packed beds is important [4,6,32]. Numerical methodologies [17,18,19,20,21,22,23,24,25] can be used to obtain the radial variation in porosity when the coordinates of the centers of spheres and the diameters of the spheres are known. Mariana et al. [19], Du Toit [20,21], and Mueller [22] employed area-based formulations and considered the areas of the intersections between the spheres in a packed bed and selected cylindrical planes to obtain the radial variation in porosity.
If we define the radius of the sphere to be , the radial position of the sphere to be , and the radial position of the cylindrical plane to be , the cylindrical plane intersects the sphere; that is, it cuts through the sphere or is inside the sphere when
Figure 1a shows a top view of the case where the cylindrical plane cuts through the sphere and Figure 1b shows a side view depicting the resulting curved elliptical intersection surface. Note that the -direction is defined by the radial line connecting the centerline of the cylinder and the center of the sphere.
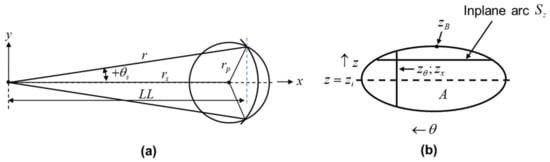
Figure 1.
Cylindrical plane cutting through the sphere: (a) top view of plane at and (b) side view.
The cylindrical plane cuts through the sphere when
where is the radius of the cylindrical container. The angular limits of the elliptical intersection surface are defined by the intersections of the cylindrical plane and the circumference of the center plane of the sphere at and . The upper limit of the elliptical surface is at relative to the axial position of the center of the sphere.
Figure 2a shows a top view when the cylindrical surface is inside the sphere and Figure 2b shows the resulting intersection surface. The cylindrical plane is inside the sphere when
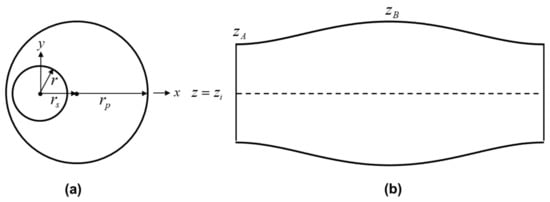
Figure 2.
Cylindrical plane inside the sphere: (a) top view of plane at , (b) side view.
The intersection plane lies between . The lower limit of the curve defining the upper edge of the intersection surface is at relative to the axial position of the center of the sphere. In the case of Figure 1b, we have that .
The integrals to calculate the area of the intersection between a sphere and a cylindrical plane can be formulated in terms of the axial z-direction, angular -direction, or the radial -direction depicted in Figure 1a,b.
2.2. Axial Integration
Mariani et al. [19] has shown that the area of the intersection surface can be obtained by integrating in the axial direction. The area is given as follows:
where the upper integration limit (axial integration height) is given as follows:
and the lower integration limit is given as follows:
The first condition in Equation (6) occurs when Equation (3) is satisfied and the cylindrical plane remains inside the sphere, as shown in Figure 2, and the second condition occurs when Equation (2) is satisfied and the cylindrical plane cuts through the sphere, as shown in Figure 1. To enable the integration of Equation (4), Mariani et al. [19] have shown that the integral expression can be transformed to the following:
where the factor is defined as follows:
Substituting Equation (5) in Equation (8), it can be shown that, when Equation (2) is valid, then and, when Equation (3) is valid, then . is the Legendre complete elliptic integral of the first kind and is defined as follows:
while is the Legendre complete elliptic integral of the second kind and is defined as follows:
The Legendre complete elliptic integrals, Equation (9) and (10), cannot be calculated analytically, and Du Toit [33] has demonstrated how the elliptic integrals can be integrated numerically employing Simpson’s Rule [34].
2.3. Angular Integration
Du Toit [20,21] has shown that the area of the intersection surface can also be obtained by integrating in the angular direction, as indicated in Figure 1b. The area is given as follows:
The factor 2 accounts for the parts of the axial height shown in Figure 1b above and below . The integration limit (intersection angle) is given as follows:
When the cylindrical plane cuts through the sphere and when cylindrical plane remains inside the sphere . The integral Equation (11) cannot be calculated analytically and Du Toit [33] has demonstrated how the integral can be integrated numerically using Simpson’s Rule [34].
2.4. Radial Integration
Mueller [22] has shown that the area of the intersection surface can also be obtained by integrating in the radial direction, as indicated in Figure 1a. The area is given as follows:
The factor 2 accounts for the parts of the axial height shown in Figure 1b above and below . The lower integration limit and the integration constant are defined as follows:
when the cylindrical plane cuts through the sphere and the conditions in Equation (2) are applicable. When the cylindrical plane remains within the sphere and the conditions in Equation (3) are applicable, then the lower integration limit and the integration constant are as follows:
Lastly, when and , then the lower integration limit and the integration constant are defined as follows:
The integral Equation (13) cannot be calculated analytically and Du Toit [33] has demonstrated how the integral can be integrated numerically using Simpson’s Rule [34]. Du Toit [33] has also shown how the singular points at and can be accounted for.
2.5. Approximate Expressions
As Equation (13) cannot be integrated analytically, Muller [22] derived approximate expressions, based on an analysis of Equation (13), to the obtain the area of the intersection surface. When the cylindrical plane cuts through the sphere, the area of the intersection is given as follows:
when
or when
where the cylindrical plane remains inside the sphere, the area of the intersection plane is given as follows:
when
or
when
3. Results
Du Toit [33] considered four representative sphere–cylindrical plane test configurations to demonstrate that the numerical integration of the analytical integral formulations developed by Mariani et al. [19], Du Toit [20,21], and Mueller [22] obtain the correct areas for the intersections between the spheres and cylindrical planes. The integral formulations of Mariani et al. [19], Du Toit [20,21], and Mueller [22] can thus be used to evaluate the validity of other proposed methods to calculate the area of the intersection between a sphere and a cylindrical plane.
In this study, the ability of the approximate expressions, Equations (17)–(22), to predict the area of the intersection between a sphere and a cylindrical plane is evaluated. This is done by first considering the four representative sphere–cylindrical plane configurations defined by Du Toit [33]. The analysis is then extended by considering an additional eight representative sphere–cylindrical plane configurations. A more detailed error analysis is further performed of the approximate expression Equation (17). Finally, the application of the approximate expressions to obtain the radial variation in porosity for a selection cylindrical packed beds is evaluated.
3.1. Primary Test Configurations
The primary test configurations selected for the analyses are summarized in Table 1.

Table 1.
Primary test configurations.
For cases 1c and 2c, the cylindrical plane remained within the sphere with for case 1c and for case 2c. For cases 3c and 4c, the cylindrical plane cuts through the sphere with and for case 3c and for case 4c. The same sphere radius of 30 mm was used for all of the cases reported in this study.
Comparison of Areas
Table 2 is a summary of the comparison between the results of the intersection areas for the primary test configurations obtained by the approximate expressions and the corresponding results obtained by the methodologies of Mariani et al. [19] and Du Toit [20,21], as well as the corresponding results obtained by COMSOL [35]. The results obtained by the approximate expressions differ by 3.78% for case 1c, –0.88% for case 2c, –24.58% for case 3c, and 0.79% for case 4c, respectively, from the other results.

Table 2.
Results of intersection areas for primary test configurations.
3.2. Extended Test Configurations
An extended set of eight cases defined to evaluate the performance of the approximate expressions further are listed in Table 3.

Table 3.
Extended test configurations.
Each case considered three positions for the cylindrical plane. For cases 5 and 6, the positions of the cylindrical planes were taken as , , and , respectively. For cases 7 to 12, the positions of the cylindrical planes were taken as , , and , respectively. In case 5, all three of the cylindrical planes are inside the sphere, with and satisfying the conditions in Equation (21), while satisfies the conditions in Equation (23). For case 6, the cylindrical planes associated with and are inside the sphere and both satisfy the conditions in Equation (21), while the cylindrical plane associated with cuts through the sphere and satisfies the conditions in Equation (19). The cylindrical planes in cases 7 to 12 all cut through the sphere and satisfy Equation (18).
Comparison of Areas
The results for the intersection areas for the extended test configurations are summarized in Table 4.

Table 4.
Summary of the results for intersection areas for extended test configurations.
In Table 4, it can be observed that, for (cases 7–12), the areas predicted by Equation (17) are symmetric around , independent of the radial position and that, as the radial position of the sphere increases, the areas predicted by Equation (17) asymptotically approach the corresponding areas predicted by Equations (7) and (11). It can also be observed that, for , Equation (17) over-predicts the intersection area, while for , Equation (17) under-predicts the intersection area. A careful study of Equation (17) reveals that it predicts the area of a circular surface, which is because of a flat plane, namely a cylindrical plane with a curvature of zero, at the given radial position cutting through a sphere. In case 6 , the areas predicted by Equations (20) and (22) differ by more than 20% from the corresponding values predicted by Equations (4) and (11). In cases 5 and 6, the remainder of the areas differ by less than 3% from the corresponding areas predicted by Equations (4) and (11).
3.3. Area Error Analysis
A more detailed error analysis was subsequently performed for Equation (17). Firstly, the asymptotic behaviour of Equation (17) was studied for and , , and . The results are depicted in Figure 3, where Am/A(r1), Am/A(r2), and Am/A(r3) are the ratios between the areas predicted by Equation (17) and the corresponding areas obtained by Equations (4) and (11). The area predicted by Equation (17) differs by less than 1% from the corresponding area obtained by Equations (4) and (11) for . However, for the areas and predicted by Equation (17) to differ by less than 1% from the corresponding areas obtained by Equations (4) and (11), it is found that .
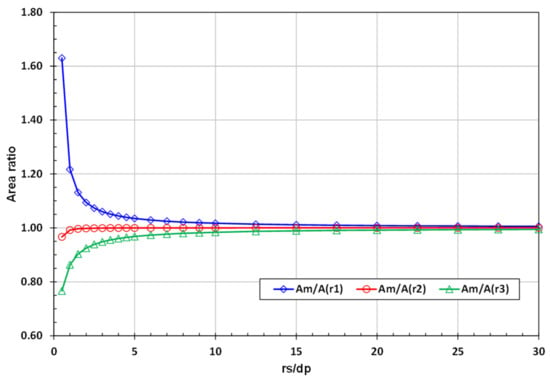
Figure 3.
Results of the analysis of asymptotic behavior of Equation (17) for .
Secondly, the behaviour of Equation (17) was studied for for spheres placed at in a cylindrical container with a radius of . This provides a more detailed analysis of the results associated with the range in Figure 3. The results are depicted in Figure 4 where the area ratio is the ratio between the area predicted by the approximate expression Equation (17) and the area predicted by Equations (4) and (11).
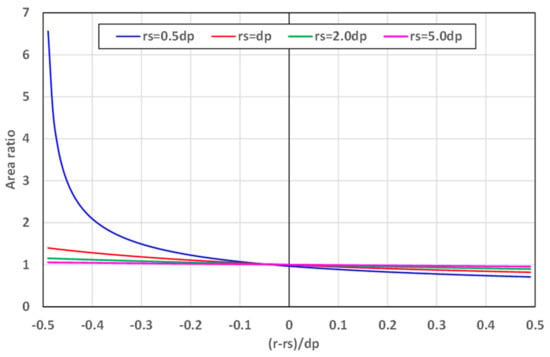
Figure 4.
Results of the analysis of asymptotic behavior of Equation (17) for .
The results in Figure 4 show the variation in the area ratio in the radial direction over the diameters of the relevant spheres. The green triangles in Figure 3 correspond to in Figure 4, the red circles to , and the blue diamonds to . It can be seen in Figure 4 that, for , Equation (17) under-predicts the area for and, for , Equation (17) over-predicts the area. This is in accordance with what is observed in Table 4 for cases 7 to 12. The under-prediction changes almost linearly with , while the over-prediction increases exponentially with . The error increases exponentially as the curvature of the cylindrical plane becomes larger. The under- and over-prediction of the areas by Equation (17) decreases as the radial positions of the spheres increase. The over-prediction in particular decreases significantly. It can thus be expected that, when the approximate expressions are used to calculate the radial variation in the porosity for a cylindrical packed bed, large errors may occur in the region between the centre line of the cylindrical packed bed and half a sphere diameter from the centre line, where the curvature of the cylindrical plane is the largest.
3.4. Radial Variation in Porosity
To evaluate the effect of using the approximate expressions, Equations (17), (20) and (22), to obtain the radial porosity profiles, cylindrical packed beds with aspect ratios of of 2.0, 3.0, 3.96, 5.96, 7.99, 15.0, and 30.0 were considered. is the diameter of the cylindrical packed bed. The data for the packed bed with the aspect ratio of 2.0 were obtained from Du Toit [38]; those with aspect ratios of 3.96, 5.96, and 7.99 from Mueller [14]; and those with aspect ratios of 15.0 and 30.0 from Bester and Du Toit [25].
The radial porosity at the radial position is given by the ratio between the sum of the areas of all the spheres intersected by the cylindrical plane with the radius and the area of the cylindrical plane between the axial levels and and is defined as follows:
is typically taken at bottom of the cylindrical packed bed and at the top of the highest sphere in the cylindrical packed bed. If the intersection areas at a given radial position are consistently over-predicted, the radial porosity at the radial position will be under-predicted. It can be deduced from Figure 4 that this will occur for cylindrical planes cutting through the half of the sphere facing the centre line of the cylindrical packed bed. Similarly, when the intersection areas at a given radial position are consistently under-predicted, the radial porosity at the radial position will be over-predicted. It can be deduced from Figure 4 that this will occur for cylindrical planes cutting through the half of the sphere facing the wall of the cylindrical packed bed.
3.4.1. Radial Porosity Profiles for an Aspect Ratio of 2.0
Figure 5a shows the positions of the centres of the spheres projected on a horizontal plane and Figure 5b shows the radial variations in porosity obtained based on Equations (11) and (17) for a cylindrical packed with an aspect ratio of 2.
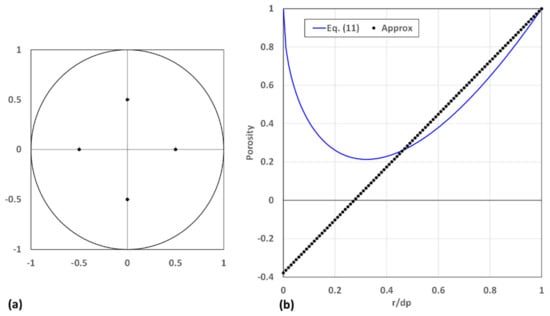
Figure 5.
(a) Positions of centres of the spheres and (b) the radial variations in porosity based on Equation (11) and the approximate expressions for .
The packed bed consists of 32 spheres each with a diameter of 0.02 m in a cylindrical container with a diameter of 0.04 m and a height of 0.23213 m. The radial position of all the spheres is . This results in Equation (18) being satisfied, thus Equation (17) was used in the calculation of the radial variation in porosity. For , the porosity based on Equation (17) is larger than the porosity based on Equation (11) because the calculated intersection areas are too small. This is supported by Figure 4. For , the porosity based on Equation (17) is significantly smaller than the porosity based on Equation (11) because the calculated intersection areas are too large. This is again supported by Figure 4. For this configuration, the porosity should also be 1.0 at the centre line based on Equation (17). The reason for this not being the case is that, in the calculations, a minimum radius of is specified for the cylindrical planes to avoid a singularity in the calculation of the porosity.
3.4.2. Radial Porosity Profiles for an Aspect Ratio of 3.0
Figure 6 shows the positions of the centres of the spheres and the radial variation in porosity as based on Equation (11) and the approximate expressions Equations (17), (20), and (22) for a packed bed with an aspect ratio of .
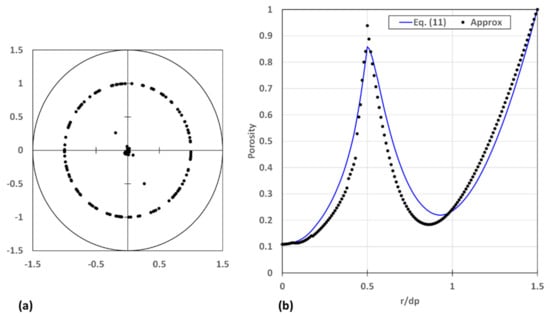
Figure 6.
(a) Positions of centres of the spheres and (b) the radial variations in porosity based on Equation (11) and the approximate expression for .
The packed bed consists of 139 spheres each with a diameter of 0.025 m in a cylindrical container with a diameter of 0.075 m and a height of 0.496 m. It can be seen in Figure 6 that there is a distinct ring of spheres near the wall, , and a small cluster of spheres around the centre line of the cylindrical container. This is corroborated by the two troughs or minima in the radial porosity profile. As a result of the ring of spheres, only Equation (17) was used to obtain the radial variation in porosity for . For , the porosity based on Equation (17) is larger than the porosity based on Equation (11) because the calculated intersection areas are too small, as supported by Figure 4. For , the porosity based on Equation (17) is smaller than the porosity based on Equation (11), because the calculated intersection areas are too large, as again supported by Figure 4. The over-prediction of the porosity by the approximate expressions for is mainly due to the application of Equation (17) to the sphere with and the cluster of spheres around the centre line because the associated intersection areas are too small. The intersection area associated with the sphere at will have little effect on the over-prediction of the porosity. For , the approximate expressions under-predict the porosity. This is because of the application of Equation (17) to the sphere with and the application of Equation (22) to the cluster of spheres around the centre line. The areas obtained by both approximate expressions are too large. Lastly, for , only Equation (20) is used to calculate the intersection areas, leading to very good prediction of the porosity.
3.4.3. Radial Porosity Profiles for an Aspect Ratio of 3.96
The positions of the centres of the spheres and the radial variation in porosity based on Equation (11) and the approximate expressions Equations (17) and (20) for a packed bed with an aspect ratio of are shown in Figure 7. The packed bed consists of 350 spheres each with a diameter of 1.0 m in a cylindrical container with a diameter of 3.96 m and a height of 28.308 m. It can be seen in Figure 7 that there is again a distinct ring of spheres near the wall at and a more diffuse ring of spheres at . This is corroborated by the two troughs or minima in the radial porosity profile.
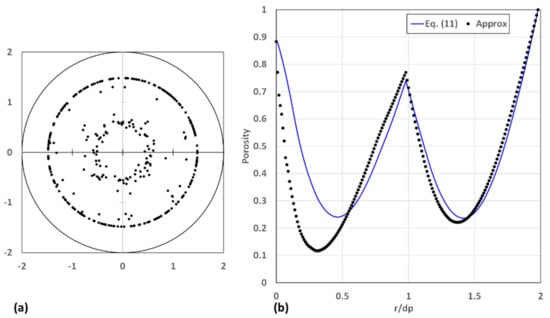
Figure 7.
(a) Positions of centres of the spheres and (b) the radial variations in porosity based on Equation (11) and the approximate expression for .
There are no spheres located in the vicinity of the centre line. However, for a number of spheres of , which means that the cylindrical planes close to the centre line will remain in these spheres, Equations (20) will be used in the calculation of the porosity. For all of the spheres with , Equation (17) will be used in the calculation of the porosity. It is observed that, for and , Equation (17) over-predicts the porosity compared with that obtained using Equation (11), while for and , the approximate expressions under-predict the porosity compared with that obtained using Equation (11). In case of the range , Equation (17) was employed in the calculation of the porosity and, for the range , primarily Equation (17), as well as Equation (20), were used. It is only at the centre line that the approximate expressions predict the porosity correctly. The significant under-prediction of the porosity and the smaller over-prediction of the porosity associated with the diffuse ring of spheres is supported by the line rs = 0.5dp in Figure 4, while the small under- and over-prediction of the porosity associated with the ring of near the cylinder wall is supported by the lines rs = dp and rs = 2.0dp in Figure 4.
3.4.4. Radial Porosity Profiles for an Aspect Ratio of 5.96
Figure 8 shows the positions of the centres of the spheres and the radial variation in porosity based on Equation (11) and the approximate expressions Equations (17), (20), and (22) for a packed bed with an aspect ratio of . The packed bed consists of 1660 spheres each with a diameter of 1.0 m in a cylindrical container with a diameter of 5.96 m and a height of 57.018 m. In Figure 8, three rings of spheres can be distinguished, namely a distinct ring of spheres near the wall at , a diffuse ring of spheres at , and a diffuse ring of spheres at , as well as a few scattered spheres in the vicinity of the centre line.
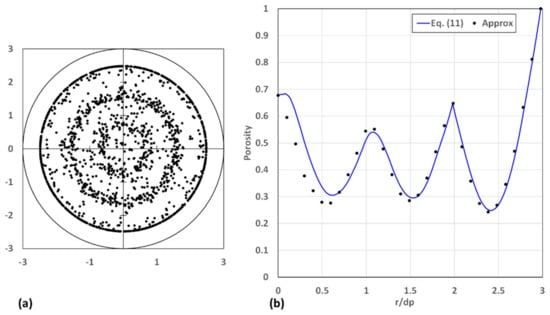
Figure 8.
(a) Positions of centres of the spheres and (b) the radial variations in porosity based on Equation (11) and the approximate expression for .
Note that, for , Equation (17) will be applicable, while for , Equations (17), (20), and (22) will be applicable. It can be observed in Figure 8 that, for , the agreement between the results obtained using Equation (11) to calculate the porosity and the results obtained using Equation (17) to calculate the porosity is very good. Between , Equation (17) under-predicts the porosity slightly compared with the porosity obtained using Equation (11) and, between , Equation (17) over-predicts the porosity slightly compared with the porosity obtained using Equation (11). For the range , the approximate expressions Equations (17), (20), and (22) under-predict the porosity markedly compared with the porosity obtained using Equation (17), except at the centre line, where the porosities are in agreement. These results are corroborated by the trends depicted in Figure 3 and Figure 4.
3.4.5. Radial Porosity Profiles for an Aspect Ratio of 7.99
The positions of the centres of the spheres and the radial variation in porosity based on Equation (11) and the approximate expressions Equations (17), (20) and (22) for a packed bed with an aspect ratio of are shown in Figure 9. Also included in Figure 9 are the corresponding porosity results obtained by Mueller [23] using a line-based approach. The packed bed consists of 6290 spheres each with a diameter of 1.0 m in a cylindrical container with a diameter of 7.99 m and a height of 116.053 m. It can be observed in Figure 9 that there are four rings of spheres and that a cluster of spheres is also located in the vicinity of the centre line of the cylindrical packed bed. A distinct ring of spheres occurs near the wall, , and three more diffuse rings of spheres are found at , , and , respectively. Note again that, for , Equation (17) will be applicable, while for , Equations (17), (20), and (22) will be applicable.
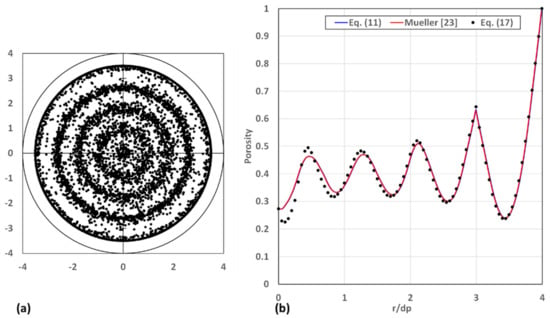
Figure 9.
(a) Positions of centres of the spheres and (b) the radial variations in porosity based on Equation (11) and the approximate expression and obtained by Mueller [23] for .
It can be observed in Figure 9b that, for , the agreement between the results obtained by Mueller [23], the results obtained using Equation (11) to calculate the porosity, and the results obtained using Equation (17) to calculate the porosity is very good, although slight differences between the three sets of results can be observed between the second and third troughs from the wall. The deviation between the results obtained by the approximate expressions and the results obtained by Mueller [23] and Equation (11) become more distinct for . It is observed in Figure 9 that, for and , Equation (17) over-predicts the porosity compared with the porosity obtained using Equation (11). In contrast, for , , and , the approximate expressions under-predict the porosity, becoming progressively worse. It is only at the centre line that the approximate expressions predict the porosity correctly. In the case of the first two ranges, Equation (17) is used to obtain the porosity, while in the case of the last range, Equations (20) and (22) are used to obtain the porosity. The application of the approximate expression Equation (20) does not have the same effect, as in the case of the packed bed shown in Figure 6. The results are again in accordance with the trends depicted in Figure 3 and Figure 4.
3.4.6. Radial Porosity Profiles for an Aspect Ratio of 15.0
The second-last case considered is a cylindrical packed bed with an aspect ratio of . The packed bed consists of 3550 spheres each with a diameter of 0.02 m in a cylindrical container with a diameter of 0.30 m and a height of 0.360 m. The positions of the centres of the spheres and the radial variation in porosity as based on Equation (11) and the approximate expressions Equations (17), (20) and (22) for the packed bed are shown in Figure 10. It can be seen in Figure 10 that there is again a distinct ring of spheres near the wall at and two more very diffuse rings of spheres at and , respectively. Throughout the remainder of the inner part of the packed bed, the spheres are scattered randomly. Note again that, for , Equation (17) will be applicable, while for , Equations (17), (20) and (22) will be applicable. It can be observed in Figure 10 that, for , the agreement between the results using Equation (11) to calculate the porosity and the results obtained using Equation (17) to calculate the porosity is very good. Between , Equation (17) slightly over-predict the porosity compared with the porosity obtained using Equation (11) and, for , Equations (17), (20), and (22) under-predict the porosity significantly compared with that based on Equation (11). It is again only at the centre line that the approximate expressions predict the porosity correctly. The application of the approximate expression Equation (20) does not have the same effect as in the case of the packed bed shown in Figure 6. The results are again in accordance with the trends depicted in Figure 3 and Figure 4.
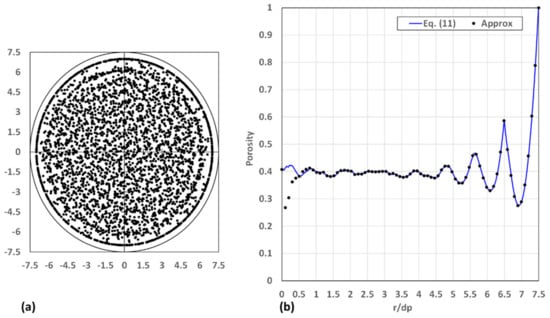
Figure 10.
(a) Positions of centres of the spheres and (b) the radial variations in porosity based on Equation (11) and the approximate expression for .
3.4.7. Radial Porosity Profiles for an Aspect Ratio of 30.0
The final cylindrical packed bed considered is one with an aspect ratio of . The packed bed consists of 21,245 spheres each with a diameter of 0.06 m in a cylindrical container with a diameter of 1.8 m and a height of 1.585 m. The positions of the centres of the spheres and the radial variation in porosity as based on Equation (11) and the approximate expressions Equations (17), (20), and (22) for the packed bed are shown in Figure 11. It can be seen in Figure 11 that there is again a distinct ring of spheres near the wall at and two more very diffuse rings of spheres at and , respectively. The radial profile in Figure 11b shows a third very diffuse ring at , which is difficult to distinguish in Figure 11a, showing the positions of the centres of the spheres. Throughout the remainder of the inner part of the packed bed, the spheres are scattered randomly. Note again that, for , Equation (17) will be applicable, while for , Equations (17), (20) and (22) will be applicable. It can be observed in Figure 11 that, for , the agreement between the porosity results obtained using Equation (11) and the porosity results obtained using Equation (17) is very good. Between , Equations (17), (20) and (22) under-predict the porosity significantly compared with the porosity based on Equation (11). It is again only at the centre line that the approximate expressions predict the porosity correctly. The application of the approximate expression Equation (20) does not have the same effect as in the case of the packed bed shown in Figure 6. The results are again in accordance with the trends shown in Figure 3 and Figure 4.
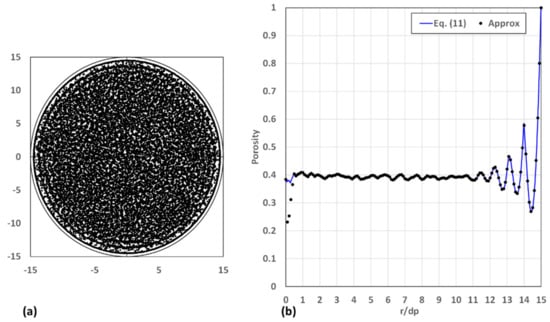
Figure 11.
(a) Positions of centres of the spheres and (b) the radial variations in porosity based on Equation (11) and the approximate expression for .
3.4.8. Summary
A careful scrutiny of the radial porosity profiles shown in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 reveals that, as the cylindrical packed aspect ratio increases, and thus the curvature of the wall of the cylindrical container decreases, the agreement between the porosity based on Equation (17) and the porosity based on Equation (11) for progressively becomes better. Further, as the aspect ratio increases, the randomness of the packing increases, and it can be expected that, at a given radial position, the over- and under-predicted areas will average out to give a good prediction of the total intersection area to be used for calculating the porosity. It is only in the case of the aspect ratios of 3 and 6 that the approximate expressions predict the porosity reasonably well for spheres with . For all other aspect ratios, the approximate expressions under-predict the porosity markedly for spheres with .
4. Conclusions
Cylindrical packed beds containing spherical particles can be found in many industrial applications involving the flow of fluids and heat and mass transfer [1,2,3]. A thorough understanding of the porous structure of cylindrical packed beds, in particular the radial variation in porosity or void fraction, and how the structure affects the transfer and flow phenomena is required for the design, analysis, and operation of packed bed reactors [4].
When the positions of the centers of spheres and the diameters of the spheres are known, the variation in the radial porosity can be calculated numerically employing approaches based on volume-based formulations [9,17,18], area-based formulations [19,20,21,22], and line-based formulations [23,24]. In this study, the area-based methods of Mariani et al. [19], Du Toit [20,21], and Mueller [22] were under the spotlight. In a previous study by Du Toit [33], it was shown that, when the integral expressions of Mariani et al. [19], Du Toit [20,21], and Mueller [22] are integrated numerically, they provide the correct results.
The focus in this study was the evaluation of the approximate expressions derived by Mueller [22] to calculate the area of the intersection between a sphere and a cylindrical plane. Firstly, the ability of the approximate expressions to calculate the intersection area was evaluated by considering several typical sphere–cylindrical plane configurations encountered in packed beds. The four configurations defined by Du Toit [33] were first considered. When it was found that differences of up to 24% between the areas predicted by the approximate expressions and the corresponding values obtained by Mariani et al. [19] and Du Toit [20,21] occurred, an additional set of configurations were defined. Based on that, an error analysis was performed that showed that large errors can occur in the case of spheres located near the centre line of the cylindrical packed bed and cylindrical planes with a large curvature.
Secondly, the application of the approximate expressions to obtain the radial variation in porosity for a selection of cylindrical packed beds was evaluated. Cylindrical packed beds with aspect ratios of 2.0, 3.0, 3.96, 5.96, 7.99, 15.0, and 30.0 were considered. The radial porosities predicted using the approximate expressions Equations (17), (20), and (22) were compared with the corresponding porosities obtained using Equation (11). For spheres with , only Equation (17) is applicable, and it was found that, as the cylindrical packed aspect ratio increases, the agreement between the porosity based on Equation (17) and the porosity based on Equation (11) progressively becomes better. For spheres with , only in the case of packed beds with aspect ratios of 3 and 6 do the approximate expressions predict the porosity reasonably well. For all other aspect ratios, the approximate expressions under-predict the porosity markedly for spheres with .
Based on the current results, it can be concluded that the approximate expressions Equations (17), (20), and (22) should be applied with the necessary care when considering packed beds with an aspect ratio less than 6. When dealing with packed beds with aspect ratios larger than 6, the approximate expression Equation (17) should only be applied to radial positions to calculate the porosity. For the radial positions , Equation (7), (11), or (13) should be employed to calculate the porosity.
Because of the fact that the approaches of Mariani et al. [19] and Du Toit [20,21] and the approximate expressions of Mueller [22] consider individual particles when calculating the intersection areas, packed beds being analysed may consist of mixtures of spheres of different sizes. Lastly, it should be noted that the approach of Mariani et al. [19] and the approximate expressions of Mueller [22] can only be employed when the full height of a packed bed is considered because of the fact that they can only be applied to full spheres. In the case where it is desired to only consider an axial segment of a packed bed with above the bottom of the packed bed and below the top of the packed bed, the approach of Du Toit [20,21] or the analytical integration procedure of Mueller [22] should be employed.
Funding
This work is based on research supported by the South African Research Chairs Initiative of the Department of Science and Technology and the National Research Foundation of South Africa (Grant No 61059). Any opinion, finding, and conclusion or recommendation expressed in this material is that of the author and the NRF of South Africa do not accept any liability in this regard.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author would like to thank N.J. Mariani for the COMSOL results.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Niu, M.; Akiyama, T.; Takahashi, R.; Yagi, J. Reduction of the wall effect in a packd bed by a hemispherical lining. AIChE J. 1996, 42, 1181–1186. [Google Scholar] [CrossRef]
- Suikkanen, H.; Ritvanen, J.; Jalali, P.; Kyrki-Rajamki, R. Discrete element modelling of pebble packing in pebble bed reactors. Nucl. Eng. Des. 2014, 273, 24–32. [Google Scholar] [CrossRef]
- Gavino, D.; Cortes, E.; Garcia, J.; Calderon-Vasquez, I.; Cardemil, J.; Estay, D.; Barraza, R. A discrete element approach to mode packed bed thermal storage. Appl. Energy 2022, 325, 119821. [Google Scholar] [CrossRef]
- Von Seckendorff, J.; Achterhold, K.; Pfieffer, F.; Fischer, R.; Hindrichsen, O. Experimental and numerical analysis of void structure in random packed beds of spheres. Powder Technol. 2021, 380, 613–628. [Google Scholar] [CrossRef]
- Benenati, R.F.; Brosilow, C.B. Void fraction distribution in beds of spheres. AIChE J. 1962, 8, 359–361. [Google Scholar] [CrossRef]
- Goodling, J.S.; Vachon, R.I.; Stelpflug, W.S.; Ying, S.J.; Khader, M.S. Radial porosity distribution in cylindrical beds packed with spheres. Powder Technol. 1983, 35, 23–29. [Google Scholar] [CrossRef]
- Giese, M.; Rottschäfer, K.; Vortmeyer, D. Measured and modeled superficial flow profiles in packed beds with liquid flow. AIChE J. 1998, 44, 484–490. [Google Scholar] [CrossRef]
- Guo, Z.; Sun, Z.; Zhang, N.; Ding, M.; Cao, X. Radial porosity peak at the centreline of packed beds with small tube to particle diameter ratios. Powder Technol. 2017, 319, 445–451. [Google Scholar] [CrossRef]
- Mueller, G.E. Radial void fraction distribution in randomly packed fixed beds of uniformly sixed spheres in cylinders. Powder Technol. 1992, 72, 269–275. [Google Scholar] [CrossRef]
- Reimann, J.; Vicente, J.; Ferrero, C.; Gan, Y.; Rack, A. X-ray tomography investigations of mono-sized sphere packing structures in cylindrical containers. Powder Technol. 2017, 318, 471–483. [Google Scholar] [CrossRef]
- Auwerda, G.J.; Kloosterman, J.L.; Winkelman, A.J.M.; Groen, J.; Van Dijk, A. Comparison of experiments and calculations of void fraction distributions in randomly stacked pebble beds. In Proceedings of the PHYSOR 2010—Advances in Reactor Physics to Power the Nuclear Renaissance, Pittsburgh, PA, USA, 9–14 May 2010. [Google Scholar]
- Al Falahi, F.; Al-Dahhan, M. Experimental investigation of the pebble bed structure by using gamma ray tomography. Nucl. Eng. Des. 2016, 310, 231–246. [Google Scholar] [CrossRef]
- Sederman, A.J.; Alexander, P.; Gladden, L.F. Structure of packed beds probed by Magnetic Resonance Imaging. Powder Technol. 2001, 117, 255–269. [Google Scholar] [CrossRef]
- Mueller, G.E. Numerically packing spheres in cylinders. Powder Technol. 2005, 159, 105–110. [Google Scholar] [CrossRef]
- Jerier, J.F.; Richefeu, V.; Imbault, D.; Donzé, F.D. Packing spherical discrete elements for large scale simulations. Comput. Methods Appl. Mech. Eng. 2010, 199, 1668–1676. [Google Scholar] [CrossRef]
- Theuerkauf, J.; Witt, P.; Schwesig, D. Analysis of particle porosity distribution in fixed beds using the discrete element method. Powder Technol. 2006, 165, 92–99. [Google Scholar] [CrossRef]
- Lamarche, F.; Leroy, C. Evaluation of the volume intersection of a sphere with a cylinder by elliptic integrals. Comput. Phys. Commun. 1990, 59, 359–369. [Google Scholar] [CrossRef]
- Govindarao, V.M.H.; Subbanna, M.; Rao, A.V.S.; Ramrao, K.V.S. Voidage profile in packed beds by multi-channel model: Effects of curvature of the channels. Chem. Eng. Sci. 1990, 45, 362–364. [Google Scholar] [CrossRef]
- Mariani, N.J.; Massa, G.D.; Martinez, O.M.; Barreto, G.F. Evaluation of radial voidage profiles in packed beds of low-aspect ratios. Can. J. Chem. Eng. 2000, 78, 1133–1137. [Google Scholar] [CrossRef]
- Du Toit, C.G. Numerical determination of the variation in the porosity of the pebble-bed core. In Proceedings of the 1st International Topical Meeting on High Temperature Reactor Technology, Petten, The Netherlands, 22–24 April 2002. [Google Scholar]
- Du Toit, C.G. Analysing the porous structure of packed beds of spheres using a semi-analytical approach. Powder Technol. 2019, 342, 475–485. [Google Scholar] [CrossRef]
- Mueller, G.E. Radial porosity in packed beds of spheres. Powder Technol. 2010, 203, 626–633. [Google Scholar] [CrossRef]
- Mueller, G.E. A simple method for determining sphere packed bed radial porosity. Powder Technol. 2012, 229, 90–96. [Google Scholar] [CrossRef]
- Feng, Y.; Gong, B.; Cheng, H.; Luo, X.; Wang, L.; Wang, X. Effects of bed dimension, friction coefficient and pebble size distribution on the packing structures of the pebble bed for solid tritium breeder blanket. Fusion Eng. Des. 2021, 163, 112156. [Google Scholar] [CrossRef]
- Bester, P.M.; Du Toit, C.G. A methodology to analyze the angular, radial and regional porosities of a cylindrical packed bed of spheres. Nucl. Eng. Des. 2022, 392, 111766. [Google Scholar] [CrossRef]
- Dixon, A.G. Correlations for wall and particle shape effects on fixed bed bulk voidage. Can. J. Chem. Eng. 1988, 66, 705–708. [Google Scholar] [CrossRef]
- White, S.M.; Tien, C.L. Analysis of flow channeling near the wall in packed beds. Wärme Stoffübertrag. 1987, 21, 291–296. [Google Scholar] [CrossRef]
- Vortmeyer, D.; Schuster, J. Evaluation of steady flow profiles in rectangular and circular packed beds by a variational method. Chem. Eng. Sci. 1983, 38, 1691–1699. [Google Scholar] [CrossRef]
- Hunt, M.L.; Tien, C.L. Non-Darcian flow, heat and mass transfer in catalytic packed-bed reactors. Chem. Eng. Sci. 1990, 45, 55–63. [Google Scholar] [CrossRef]
- Martin, H. Low Peclet number partice-to-fluid heat and mass transfer in packed beds. Chem. Eng. Sci. 1978, 33, 913–919. [Google Scholar] [CrossRef]
- Cohen, Y.; Metzner, A.B. Wall effects in laminar flow of fluids through packed beds. AIChE J. 1981, 8, 359–361. [Google Scholar] [CrossRef]
- De Klerk, A. Voidage variation in packed beds at small column to particle diameter ratio. AIChE J. 2003, 49, 2022–2029. [Google Scholar] [CrossRef]
- Du Toit, C.G. Area of the intersection between a sphere and a cylindrical plane. Math. Comp. Appl. 2022, 27, 79. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics, 8th ed.; John Wiley & Sons: New York, NY, USA, 1999; pp. 872–875. [Google Scholar]
- Mariani, N.J. (Universidad Nacional del La Plata, La Plata, Argentina). Personal communication, 2022.
- Potgieter, M.C. (M-Tech Industrial, Potchefstroom, North-West Province, South Africa). Personal communication, 2022.
- Bester, P.M. (M-Tech Industrial, Potchefstroom, North-West Province, South Africa). Personal communication, 2022.
- Du Toit, C.G. Porous structure of cylindrical packed beds with aspect ratios between 1 and 2. Nucl. Eng. Des. 2020, 359, 110451. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).