CanStoc: A Hybrid Stochastic–GCM System for Monthly, Seasonal and Interannual Predictions
Abstract
:1. Introduction
2. The Models
2.1. StocSIPS
2.2. CanSIPS
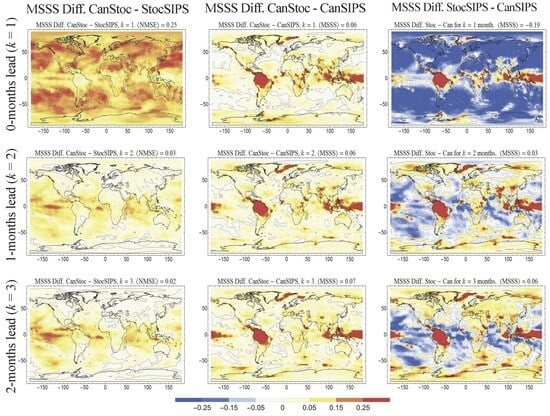
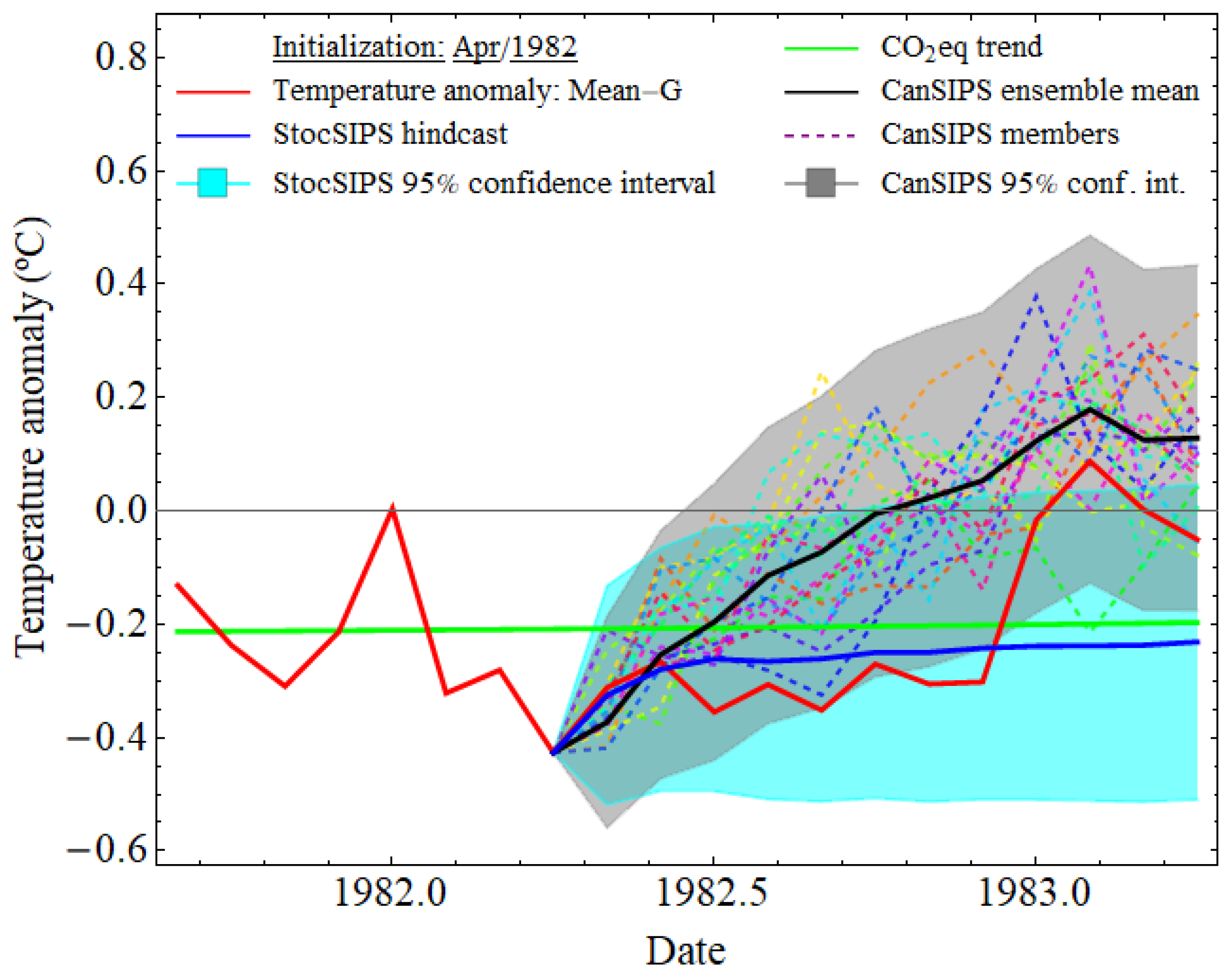
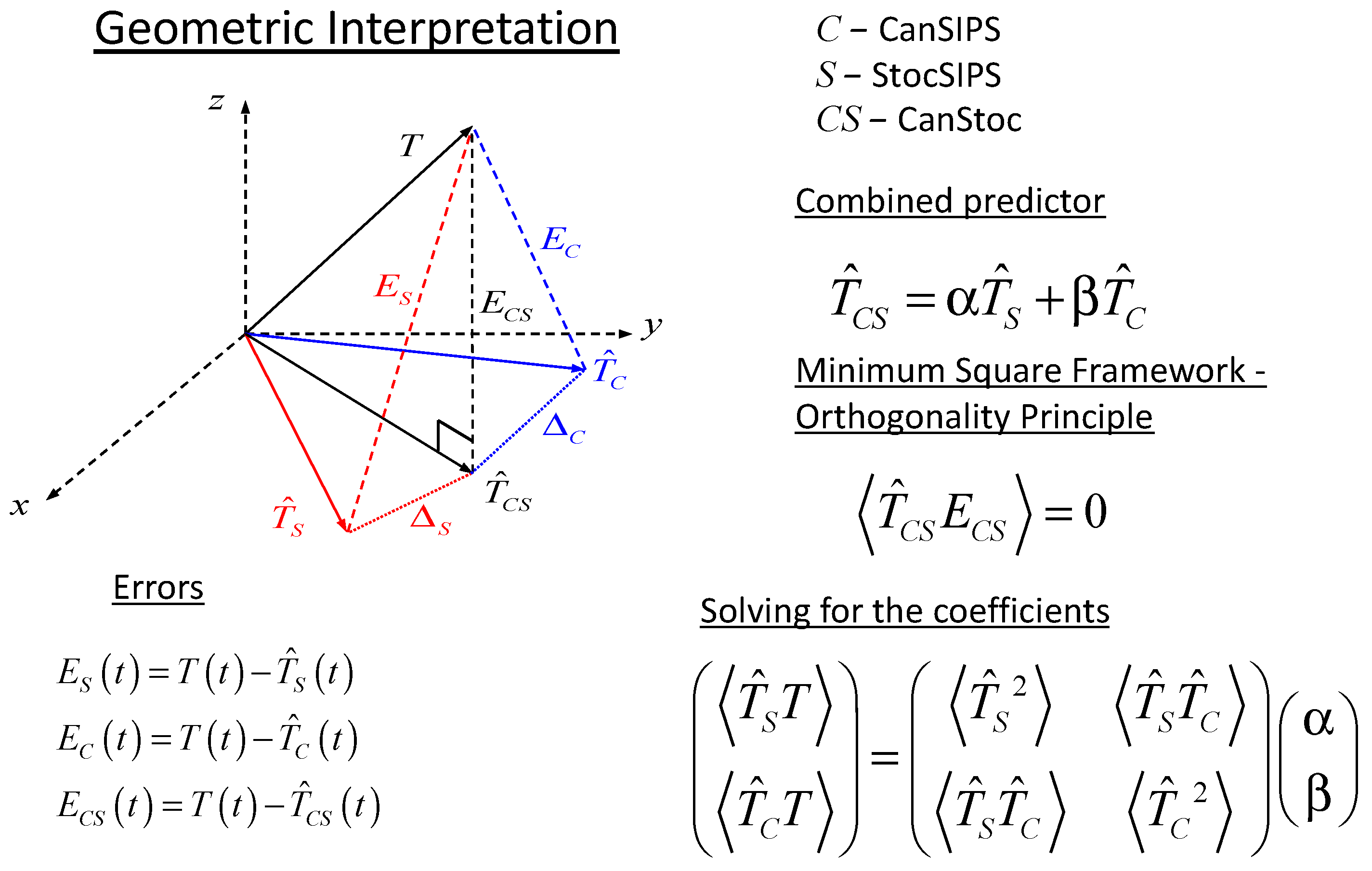
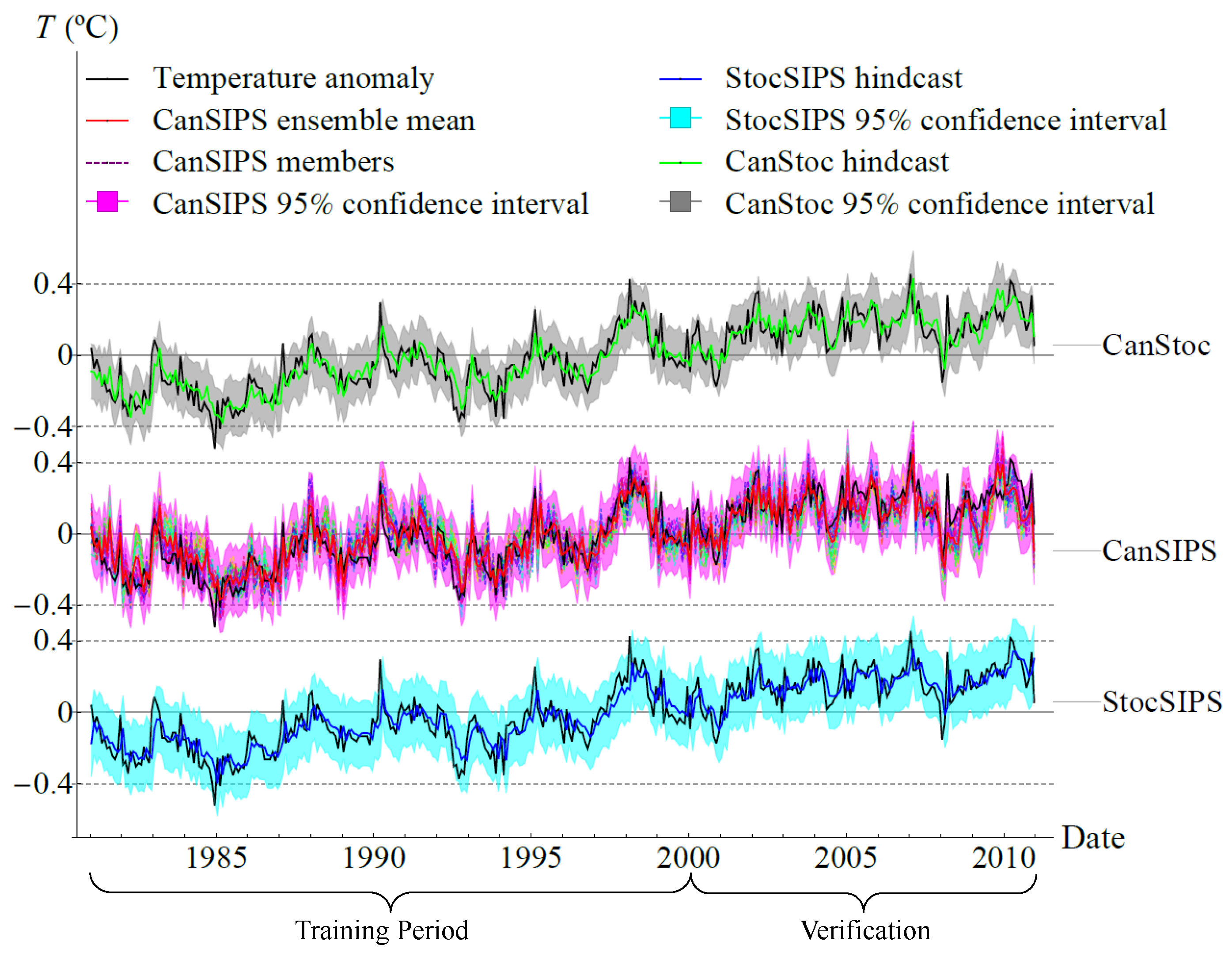
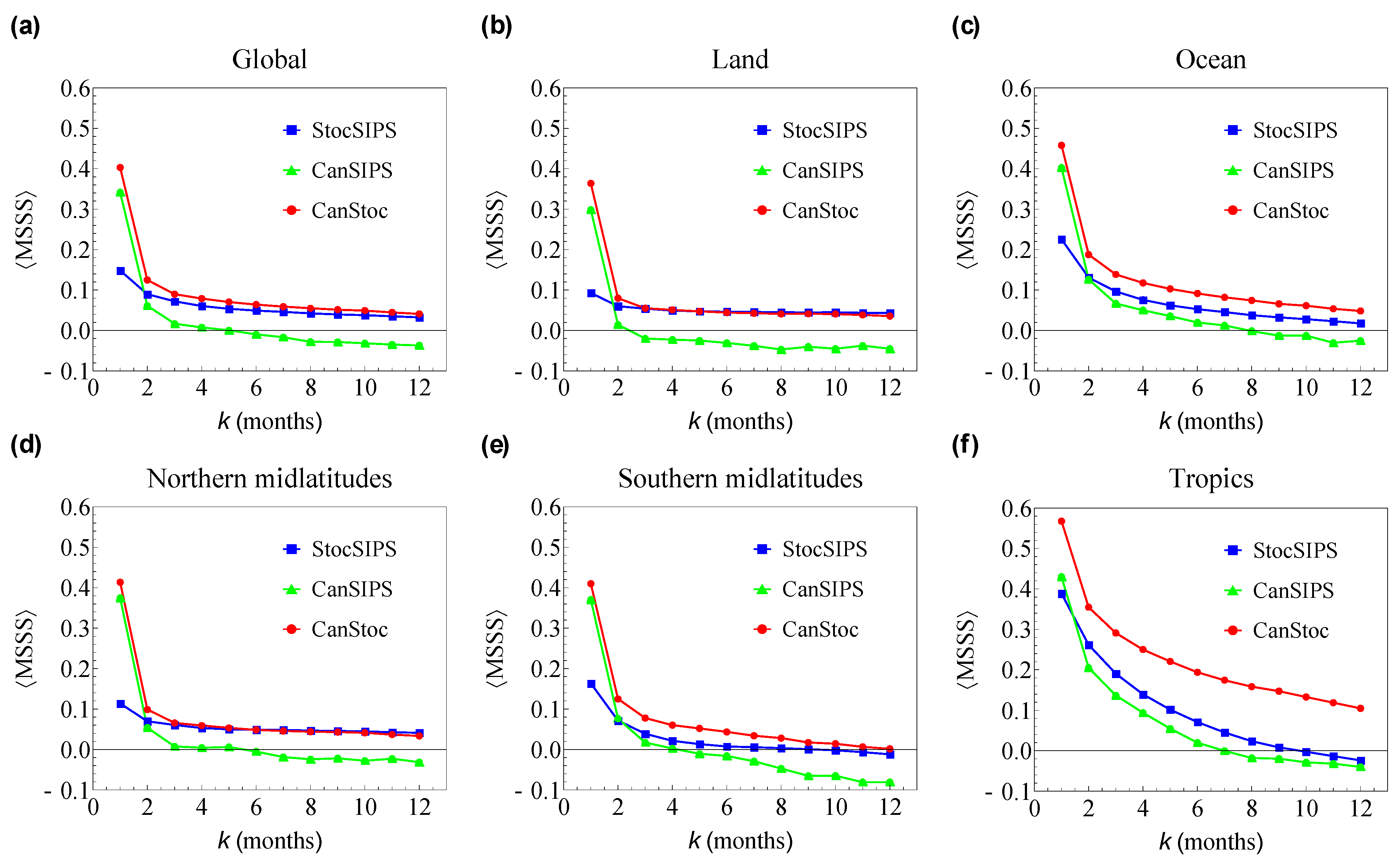
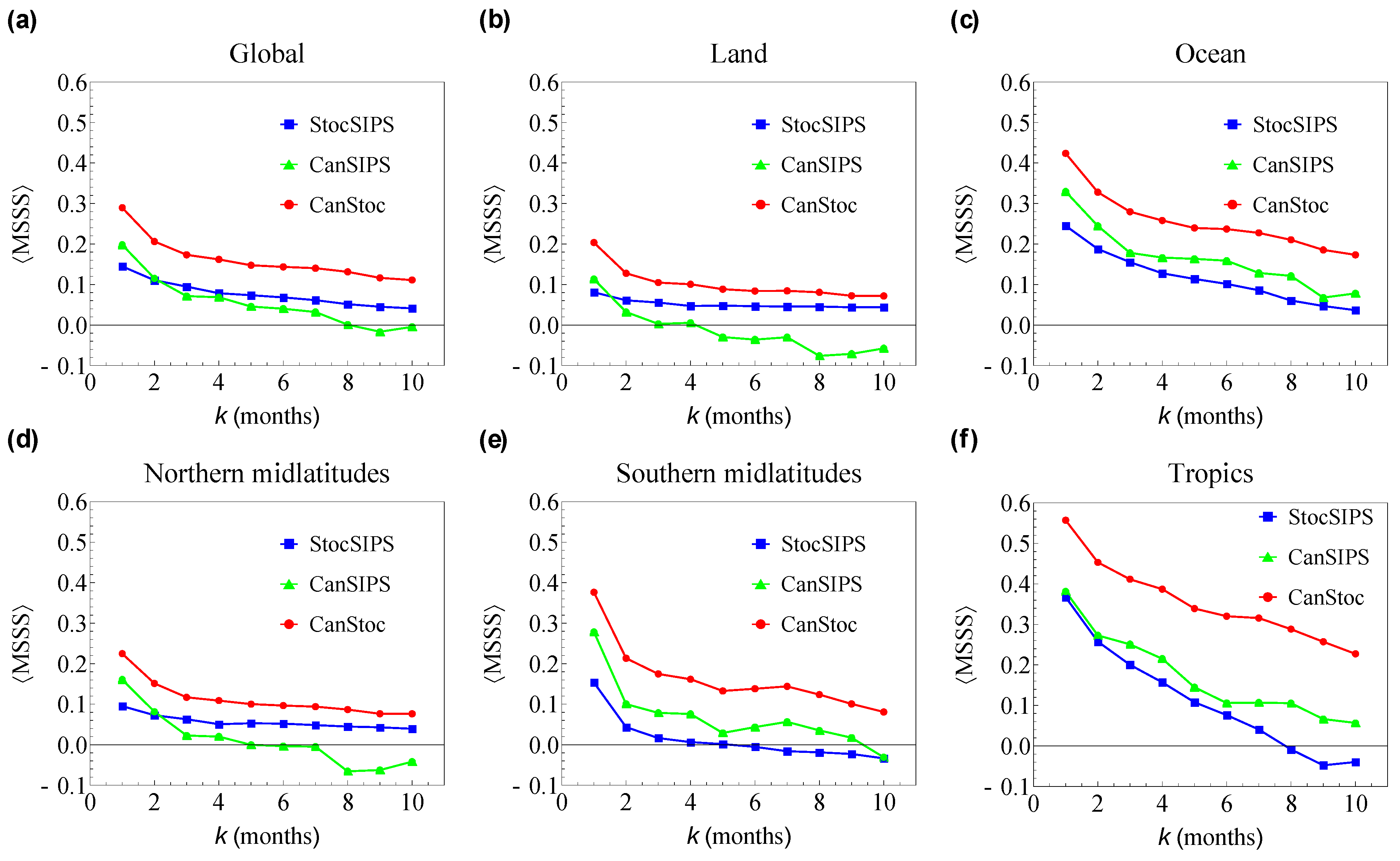
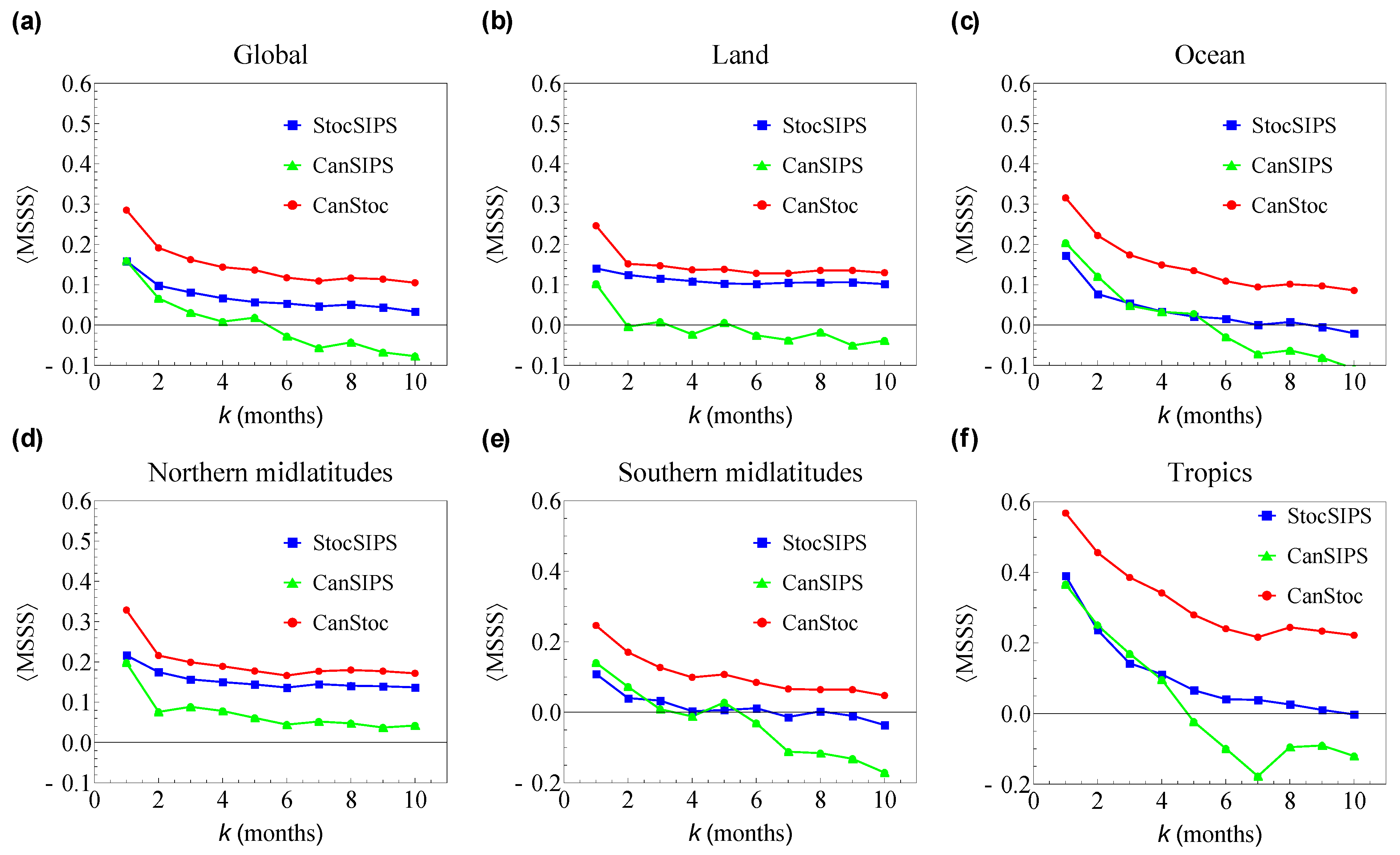
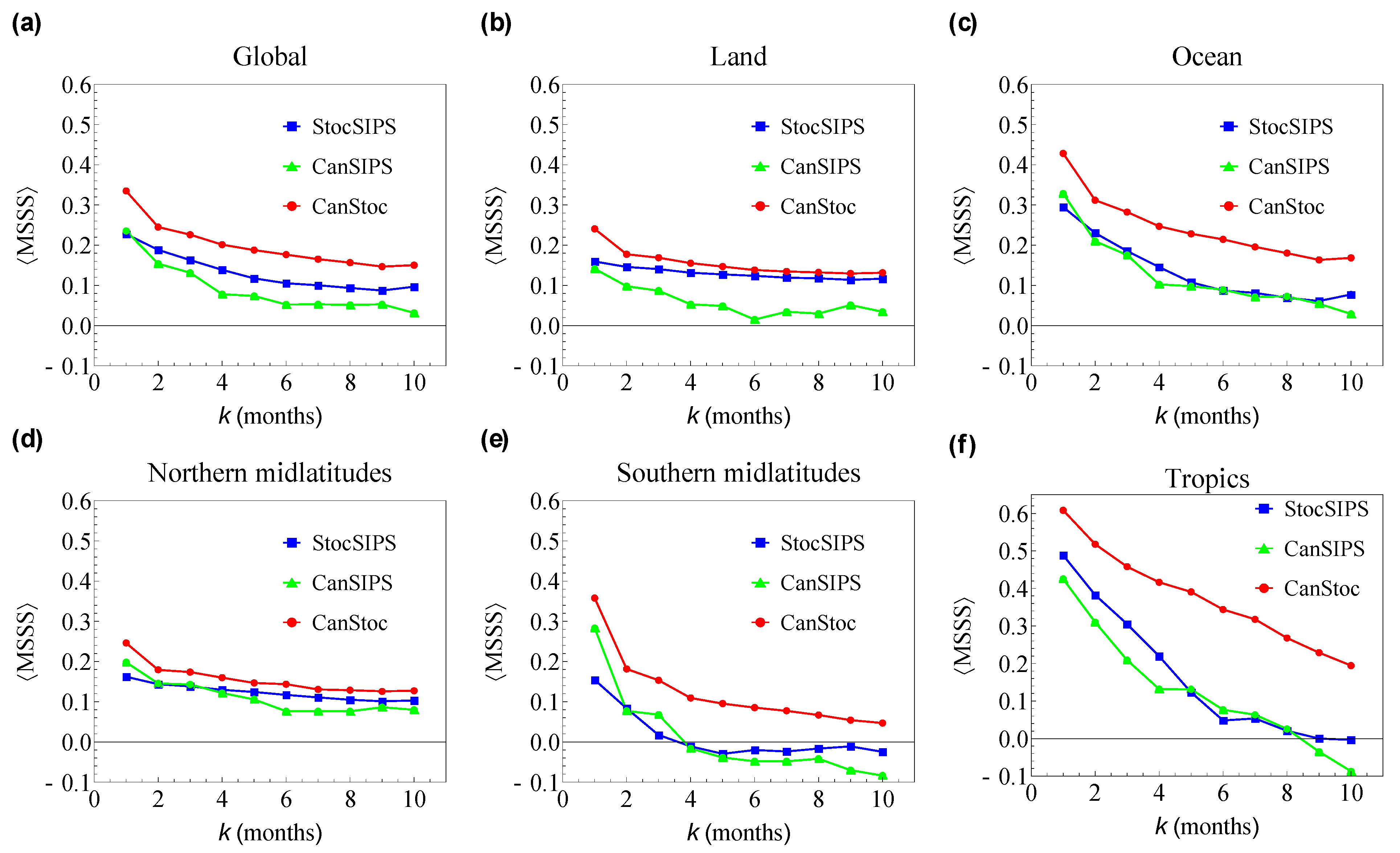
2.3. CanStoc
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lovejoy, S.; Schertzer, D. The Weather and Climate: Emergent Laws and Multifractal Cascades; Cambridge University Press: Cambridge, UK, 2013; p. 496. [Google Scholar]
- Lovejoy, S. What is climate? EOS 2013, 94, 1–2. [Google Scholar] [CrossRef]
- Lovejoy, S. A voyage through scales, a missing quadrillion and why the climate is not what you expect. Clim. Dyn. 2015, 44, 3187–3210. [Google Scholar] [CrossRef]
- Williams, P.D. Climatic impacts of stochastic fluctuations in air-sea fluxes. Geophys. Res. Lett. 2012, 39, L10705. [Google Scholar] [CrossRef]
- Christensen, H.; Berner, J.; Coleman, D.R.B.; Palmer, T.N. Stochastic Parameterization and El Niño–Southern Oscillation. J. Clim. 2017, 30, 17–38. [Google Scholar] [CrossRef]
- Berner, J.; Achatz, U.; Batté, L.; Bengtsson, L.; de la Cámara, A.; Christensen, H.M.; Colangeli, M.; Coleman, D.R.B.; Crommelin, D.; Dolaptchiev, S.I.; et al. Stochastic Parameterization: Toward a New View of Weather and Climate Models. Bull. Am. Meteorol. Soc. 2017, 98, 565–588. [Google Scholar] [CrossRef]
- Davini, P.; von Hardenberg, J.; Corti, S.; Christensen, H.M.; Juricke, S.; Subramanian, A.; Watson, P.A.G.; Weisheimer, A.; Palmer, T.N. Climate SPHINX: Evaluating the impact of resolution and stochastic physics parameterisations in the EC-Earth global climate model. Geosci. Model. Dev. 2017, 10, 1383–1402. [Google Scholar] [CrossRef]
- Rackow, T.; Juricke, S. Flow-dependent stochastic coupling for climate models with high ocean-to-atmosphere resolution ratio. Q. J. R. Meteorol. Soc. 2020, 146, 284–300. [Google Scholar] [CrossRef]
- Franzke, C.L.E.; O’Kane, T.J.; Berner, J.; Williams, P.D.; Lucarini, V. Stochastic climate theory and modeling. Wiley Interdiscip. Rev. Clim. Chang. 2015, 6, 63–78. [Google Scholar] [CrossRef]
- Palmer, T. Stochastic weather and climate models. Nat. Rev. Phys. 2019, 1, 463–471. [Google Scholar] [CrossRef]
- Hasselmann, K. Stochastic Climate models, part I: Theory. Tellus 1976, 28, 473–485. [Google Scholar]
- Penland, C.; Magorian, T. Prediction of Nino 3 sea surface temperatures using linear inverse modeling. J. Clim. 1993, 6, 1067–1076. [Google Scholar] [CrossRef]
- Penland, C. A stochastic model of IndoPacific sea surface temperature anomalies. Phys. D Nonlinear Phenom. 1996, 98, 534–558. [Google Scholar] [CrossRef]
- Sardeshmukh, P.; Compo, G.P.; Penland, C. Changes in probability assoicated with El Nino. J. Clim. 2000, 13, 4268–4286. [Google Scholar] [CrossRef]
- Newman, M. An Empirical Benchmark for Decadal Forecasts of Global Surface Temperature Anomalies. J. Clim. 2013, 26, 5260–5269. [Google Scholar] [CrossRef]
- Lovejoy, S. Using scaling for macroweather forecasting including the pause. Geophys. Res. Lett. 2015, 42, 7148–7155. [Google Scholar] [CrossRef]
- Lovejoy, S.; del Rio Amador, L.; Hébert, R. The ScaLIng Macroweather Model (SLIMM): Using scaling to forecast global-scale macroweather from months to Decades. Earth Syst. Dynam. 2015, 6, 1–22. [Google Scholar] [CrossRef]
- Del Rio Amador, L.; Lovejoy, S. Predicting the global temperature with the Stochastic Seasonal to Interannual Prediction System (StocSIPS). Clim. Dyn. 2019, 53, 4373–4411. [Google Scholar] [CrossRef]
- Lovejoy, S. Weather, Macroweather and Climate: Our Random Yet Predictable Atmosphere; Oxford University Press: New York, NY, USA, 2019; p. 334. [Google Scholar]
- Lovejoy, S.; Procyk, R.; Hébert, R.; del Rio Amador, L. The Fractional Energy Balance Equation. Q. J. R. Meteorol. Soc. 2021, 147, 1964–1988. [Google Scholar] [CrossRef]
- Lovejoy, S. The Half-order Energy Balance Equation, Part 1: The homogeneous HEBE and long memories. Earth Syst. Dyn. 2021, 12, 469–487. [Google Scholar] [CrossRef]
- Lovejoy, S. The Half-order Energy Balance Equation, Part 2: The inhomogeneous HEBE and 2D energy balance models. Earth Sys. Dyn. 2021, 12, 489–511. [Google Scholar] [CrossRef]
- Hébert, R.; Lovejoy, S.; Tremblay, B. An Observation-based Scaling Model for Climate Sensitivity Estimates and Global Projections to 2100. Clim. Dyn. 2021, 56, 1105–1129. [Google Scholar] [CrossRef] [PubMed]
- Procyk, R.; Lovejoy, S.; Hébert, R. The Fractional Energy Balance Equation for Climate projections through 2100. Earth Syst. Dyn. 2022, 13, 81–107. [Google Scholar] [CrossRef]
- Lovejoy, S. The future of climate modelling: Weather Details, Macroweather stochastics—Or both? Meteorology 2022, 1, 414–449. [Google Scholar] [CrossRef]
- Lovejoy, S. The spectra, intermittency and extremes of weather, macroweather and climate. Nat. Sci. Rep. 2018, 8, 12697. [Google Scholar] [CrossRef] [PubMed]
- StocSIPS. Available online: http://www.physics.mcgill.ca/StocSIPS/ (accessed on 21 November 2023).
- Del Rio Amador, L.; Lovejoy, S. Using regional scaling for temperature forecasts with the Stochastic Seasonal to Interannual Prediction System (StocSIPS). Clim. Dyn. 2021, 57, 727–756. [Google Scholar] [CrossRef]
- Del Rio Amador, L. The Stochastic Seasonal to Interannual Prediction System: Exploiting the Atmosphere’s Memory for Long-Term Forecasts; McGill: Montreal, QC, Canada, 2021. [Google Scholar]
- Del Rio Amador, L.; Lovejoy, S. Long-range Forecasting as a Past Value Problem: Untangling Correlations and Causality with scaling. Geophys. Res. Lett. 2021, 48, e2020GL092147. [Google Scholar] [CrossRef]
- Tsonis, A.A.; Swanson, K.L.; Roebber, P.J. What Do Networks Have to Do with Climate? Bull. Am. Meteorol. Soc. 2006, 87, 585–596. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. The backbone of the climate network. Europhys. Lett. 2009, 87, 48007. [Google Scholar] [CrossRef]
- Ludescher, J.; Gozolchiani, A.; Bogachev, M.I.; Bunde, A.; Havlin, S.; Schellnhuber, H.J. Very early warning of next El Niño. Proc. Natl. Acad. Sci. USA 2014, 111, 2064–2066. [Google Scholar] [CrossRef]
- Brown, P.T.; Caldeira, K. Empirical Prediction of Short-Term Annual Global Temperature Variability. Earth Space Sci. 2020, 7, e2020EA001116. [Google Scholar] [CrossRef]
- Eden, J.M.; van Oldenborgh, G.J.; Hawkins, E.; Suckling, E.B. A global empirical system for probabilistic seasonal climate prediction. Geosci. Model. Dev. 2015, 8, 3947–3973. [Google Scholar] [CrossRef]
- Kim, G.; Ahn, J.; Kryjov, V.; Woo-Seop, L.; Dong-Joon, K.; Arun, K. Assessment of MME methods for seasonal prediction using WMO LC-LRFMME hindcast dataset. Int. J. Climatol. 2020, 41 (Suppl. S1), E2462–E2481. [Google Scholar] [CrossRef]
- Crochemore, L.; Ramos, M.-H.; Pappenberger, F. Bias correcting precipitation forecasts to improve the skill of seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 2016, 20, 3601–3618. [Google Scholar] [CrossRef]
- Kharin, V.V.; Merryfield, W.J.; Boer, G.J.; Lee, W.S. A Postprocessing Method for Seasonal Forecasts Using Temporally and Spatially Smoothed Statistics. Mon. Weath. Rev. 2017, 145, 3545–3561. [Google Scholar] [CrossRef]
- Van Schaeybroeck, B.; Vannitsem, S. Postprocessing of Long-Range Forecasts. In Statistical Postprocessing of Ensemble Forecasts; Elsevier: Amsterdam, The Netherlands, 2018; pp. 267–290. [Google Scholar]
- Pasternack, A.; Bhend, J.; Liniger, M.A.; Rust, H.W.; Müller, W.A.; Ulbrich, U. Parametric decadal climate forecast recalibration (DeFoReSt 1.0). Geosci. Model. Dev. 2018, 11, 351–368. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Towards a new synthesis for atmospheric dynamics: Space-time cascades. Atmos. Res. 2010, 96, 1–52. [Google Scholar] [CrossRef]
- Lovejoy, S. Scaling, dynamical regimes and stratification: How long does weather last? How big is a cloud? Nonlinear Process. Geophys. 2023, 30, 311–374. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–450. [Google Scholar] [CrossRef]
- Hebert, R. A Scaling Model for the Forced Climate Variability in the Anthropocene. Master’s Thesis, McGill University, Montreal, QC, Canada, 2017. [Google Scholar]
- Lovejoy, S. Fractional relaxation noises, motions and the fractional energy balance equation. Nonlinear Proc. Geophys. 2022, 29, 93–121. [Google Scholar] [CrossRef]
- Hirchoren, G.A.; Arantes, D.S. Predictors For The Discrete Time Fractional Gaussian Processes. In Proceedings of the Telecommunications Symposium, 1998. ITS’98 Proceedings, SBT/IEEE International, Sao Paulo, Brazil, 9–13 August 1998; pp. 49–53. [Google Scholar]
- Gripenberg, G.; Norros, I. On the Prediction of Fractional Brownian Motion. J. Appl. Prob. 1996, 33, 400–410. [Google Scholar] [CrossRef]
- Merryfield, W.J.; Denis, B.; Fontecilla, J.-S.; Lee, W.-S.; Kharin, S.; Hodgson, J.; Archambault, B. The Canadian Seasonal to Interannual Prediction System (CanSIPS) An Overview of Its Design and Operational Implementation; Environment Canada: Gatineau, QC, Canada, 2011; p. 51. [Google Scholar]
- Merryfield, W.J.; Lee, W.S.; Boer, G.J.; Kharin, V.V.; Scinocca, J.F.; Flato, G.M.; Ajayamohan, R.S.; Fyfe, J.C.; Tang, Y.; Polavarapu, S. The Canadian Seasonal to Interannual Prediction System. Part I: Models and Initialization. Mon. Weather. Rev. 2013, 141, 2910–2945. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables and Stochastic Processes; Mc Graw Hill: New York, NY, USA, 1965. [Google Scholar]
- Shepherd, T.G.; Boyd, E.; Calel, R.A.; Chapman, S.C.; Dessai, S.; Dima-West, I.M.; Fowler, H.J.; James, R.; Maraun, D.; Martius, O.; et al. Storylines: An alternative approach to representing uncertainty in physical aspects of climate change. Clim. Chang. 2018, 151, 555–571. [Google Scholar] [CrossRef]
- Climate Research Board. Carbon Dioxide and Climate: A Scientific Assessment; US National Academy of Science: Washington, DC, USA, 1979.
- Shukla, J.; Palmer, T.N.; Hagedorn, R.; Hoskins, B.; Kinter, J.; Marotzke, J.; Miller, M.; Slingo, J.S. Toward a new generation of world climate research and computing facilities. Bull. Am. Meteorol. Soc. 2009, 91, 1407–1412. [Google Scholar] [CrossRef]
- Slingo, J.; Bauer, P.; Bony, S.; Flato, G.; Hegerl, G.; Christensen, J.H.; Hurrell, J.; Jakob, C.; Voeikov, V.K.; Kimoto, M.; et al. Briefing 1, Next Generation Climate Models: Building Strong Foundations for Climate Action; The Royal Society: London, UK, 2021. [Google Scholar]
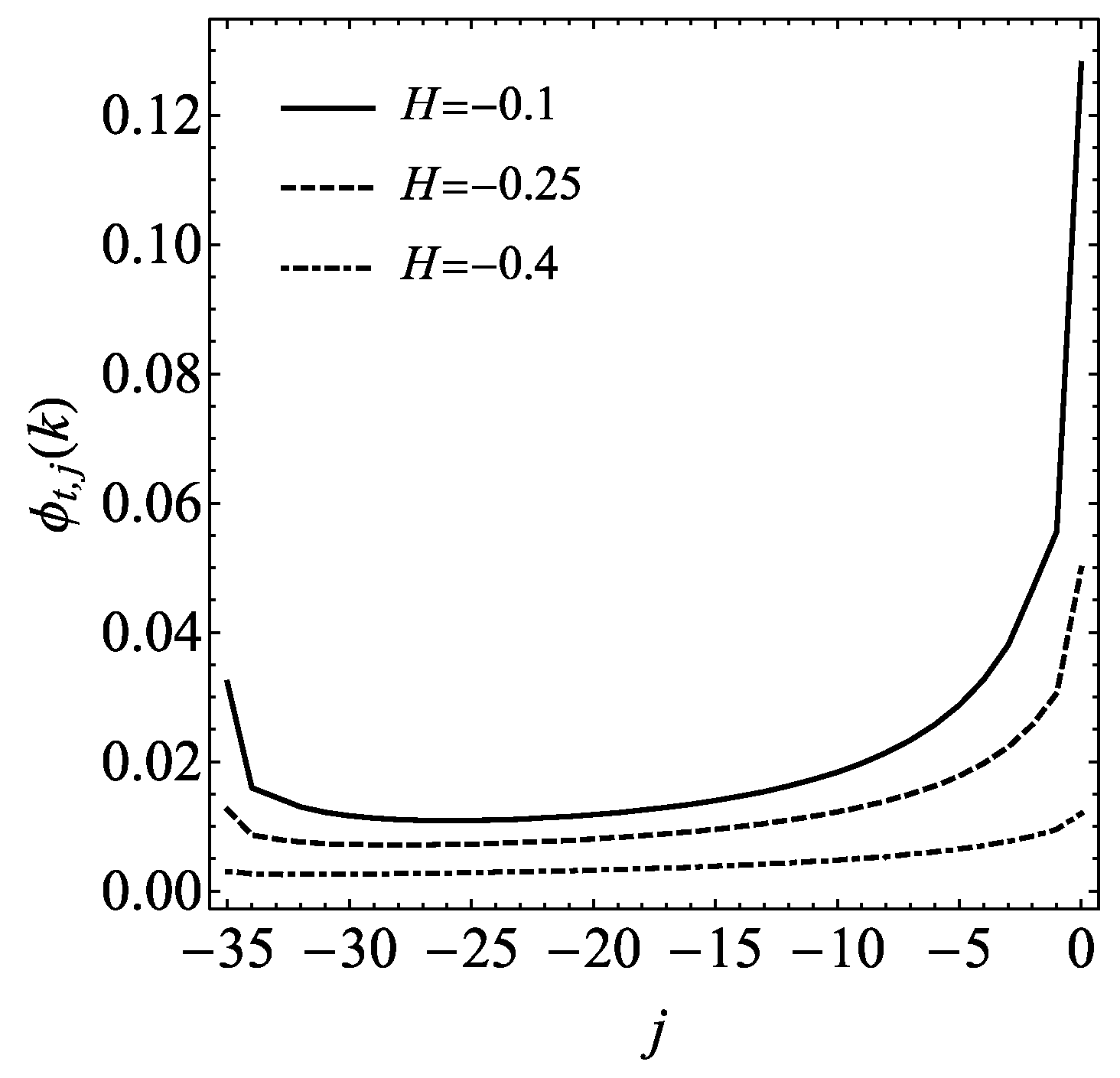




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovejoy, S.; Del Rio Amador, L. CanStoc: A Hybrid Stochastic–GCM System for Monthly, Seasonal and Interannual Predictions. Meteorology 2023, 2, 509-529. https://doi.org/10.3390/meteorology2040029
Lovejoy S, Del Rio Amador L. CanStoc: A Hybrid Stochastic–GCM System for Monthly, Seasonal and Interannual Predictions. Meteorology. 2023; 2(4):509-529. https://doi.org/10.3390/meteorology2040029
Chicago/Turabian StyleLovejoy, Shaun, and Lenin Del Rio Amador. 2023. "CanStoc: A Hybrid Stochastic–GCM System for Monthly, Seasonal and Interannual Predictions" Meteorology 2, no. 4: 509-529. https://doi.org/10.3390/meteorology2040029
APA StyleLovejoy, S., & Del Rio Amador, L. (2023). CanStoc: A Hybrid Stochastic–GCM System for Monthly, Seasonal and Interannual Predictions. Meteorology, 2(4), 509-529. https://doi.org/10.3390/meteorology2040029