Biogas Purification by Intensified Absorption in a Micromixer
Abstract
1. Introduction
2. Results and Discussions
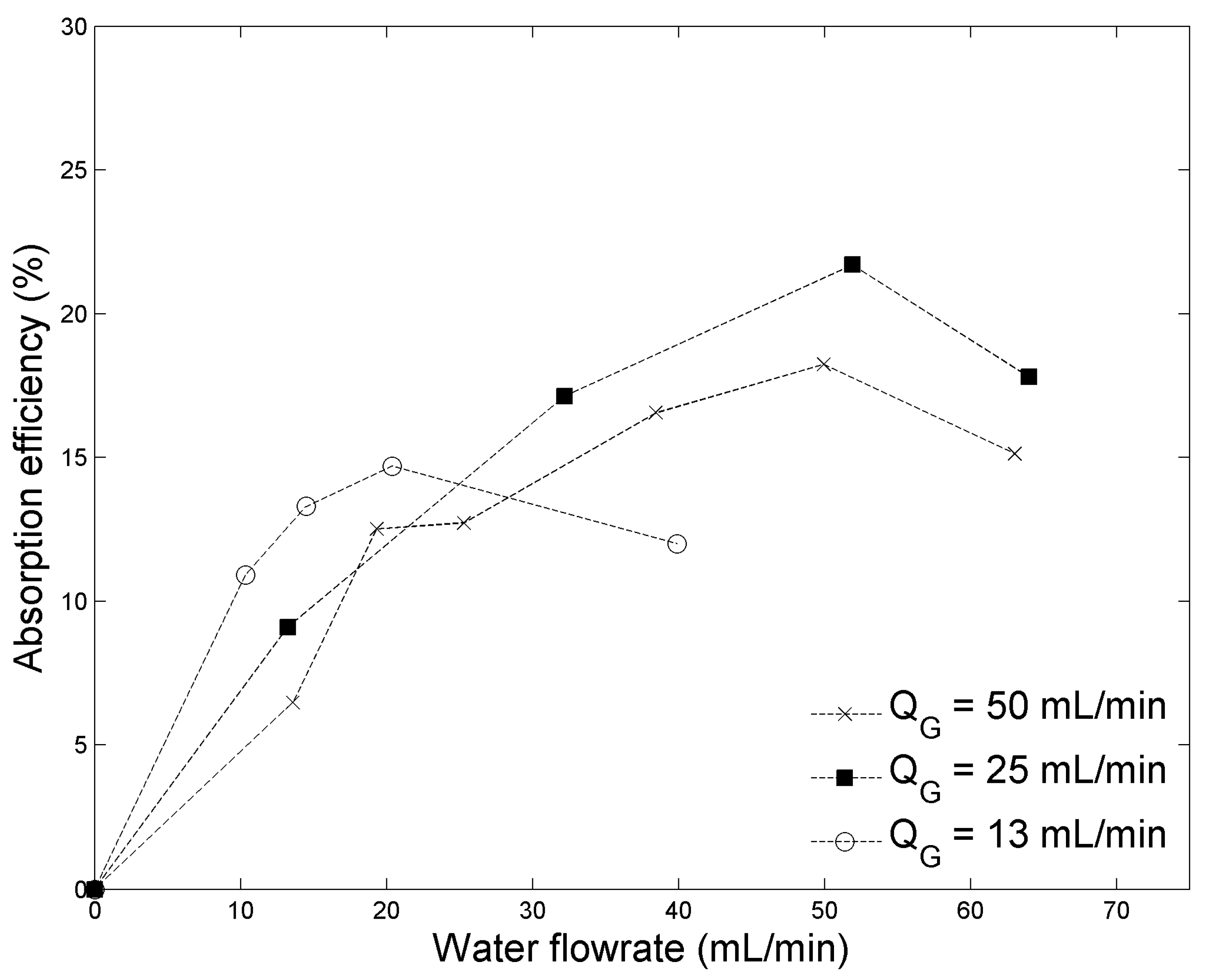
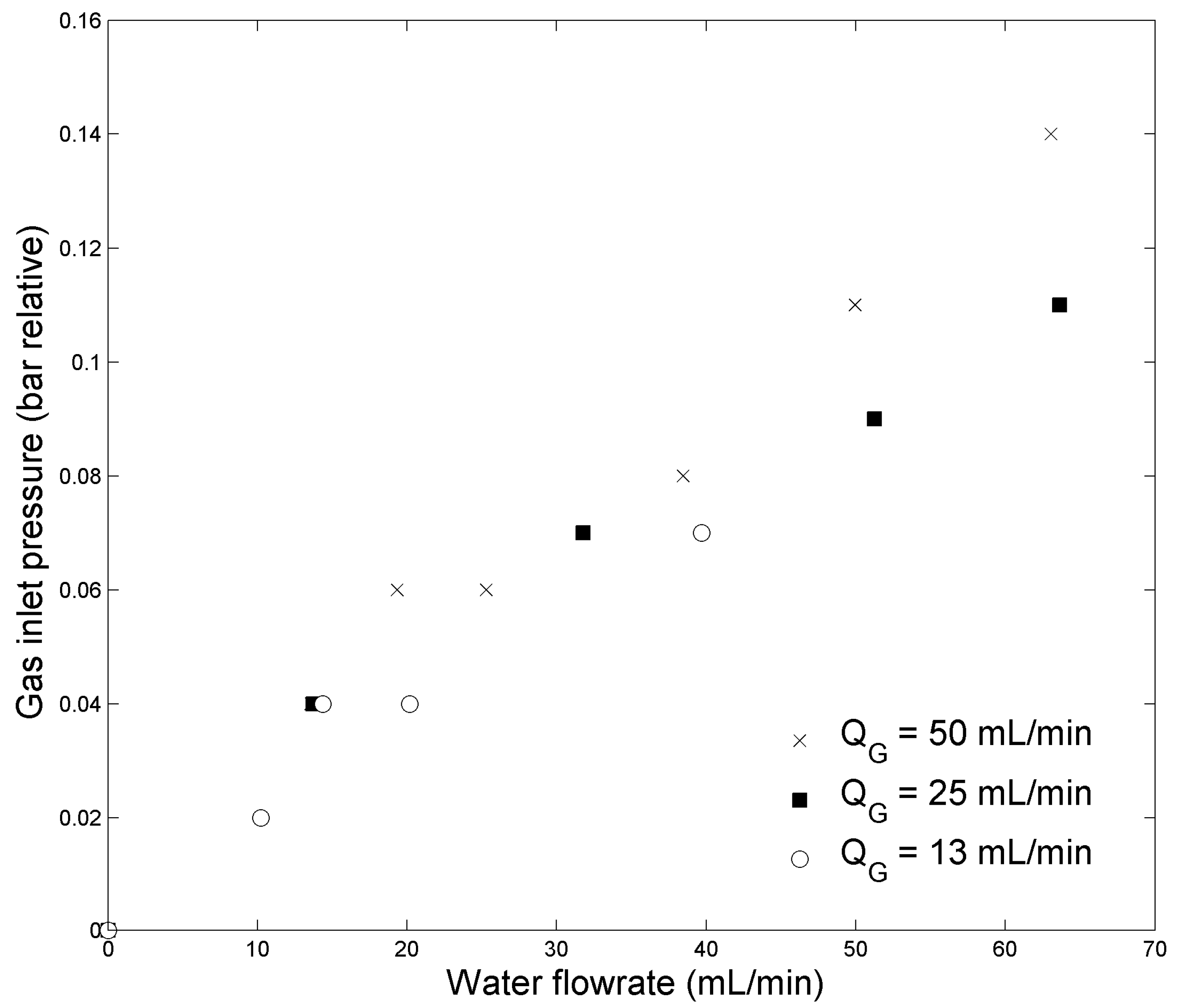
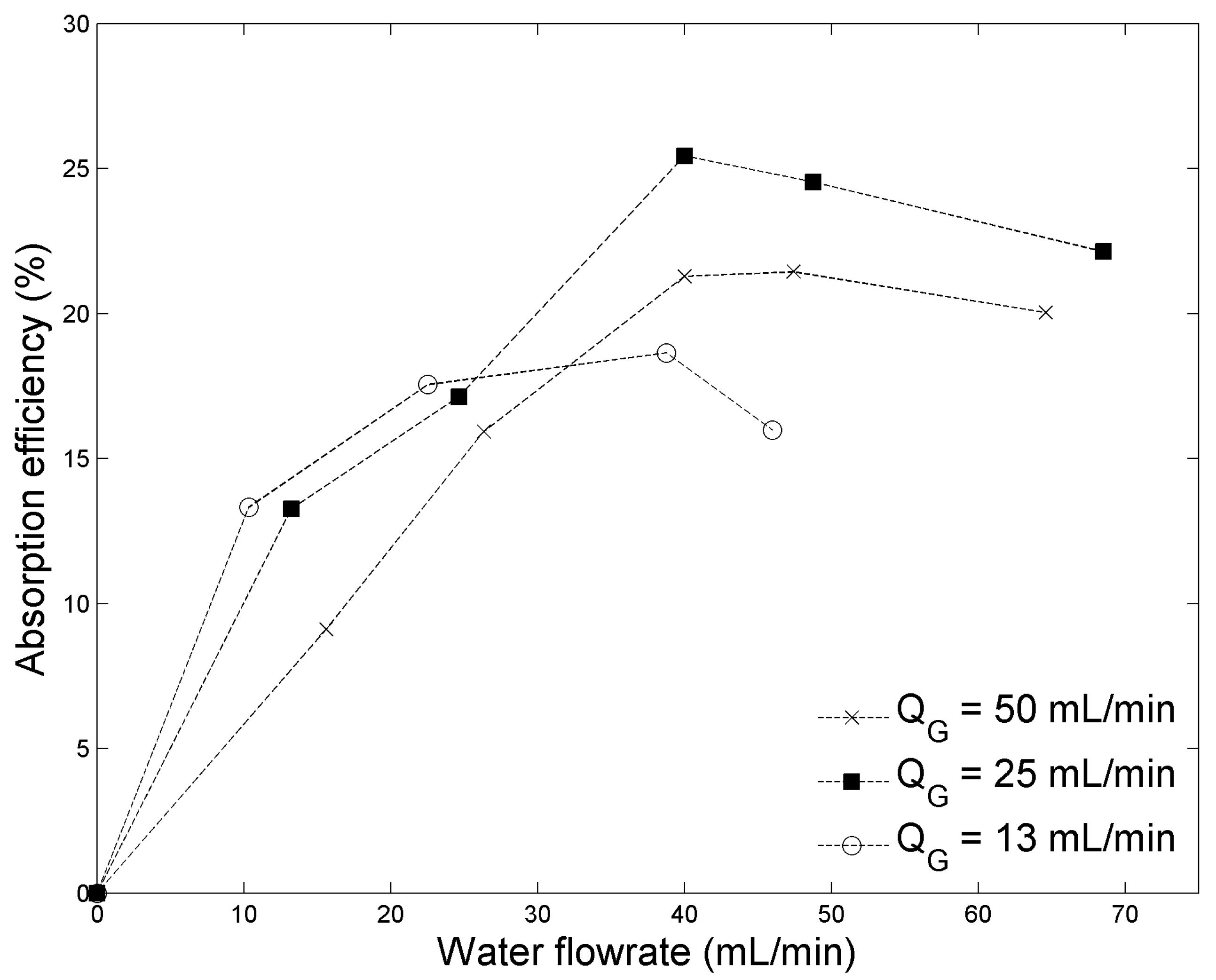
2.1. Absorption Efficiency
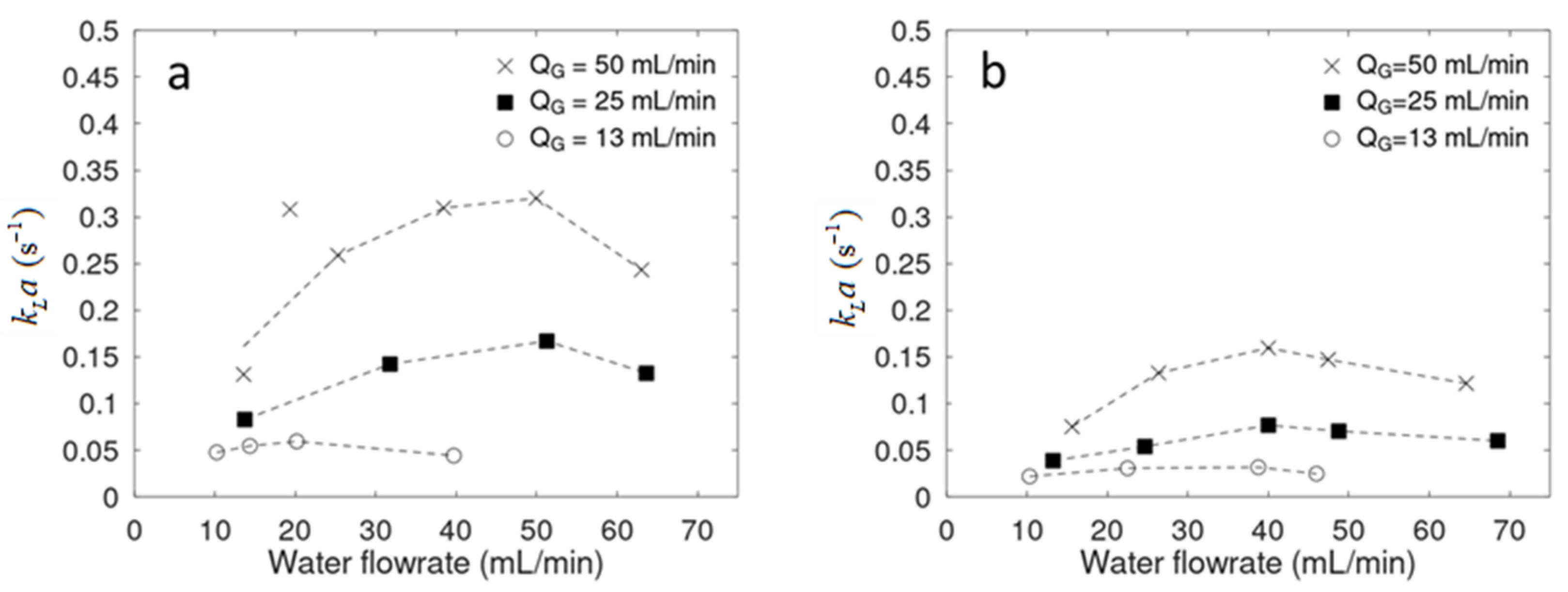
2.2. Mass Transfer Coefficients
2.2.1. Physical Absorption
2.2.2. Chemical Absorption
3. Materials and Methods
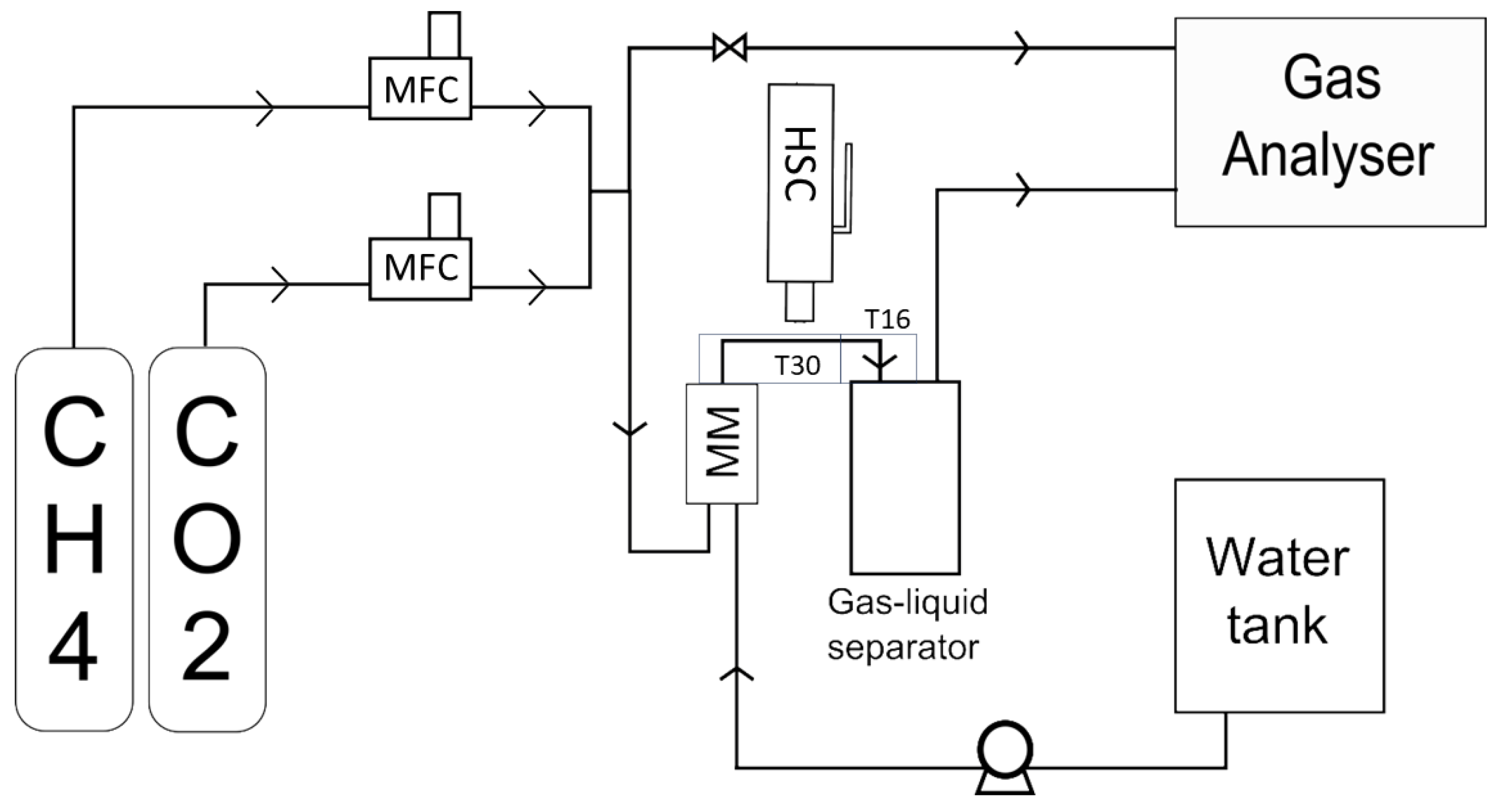
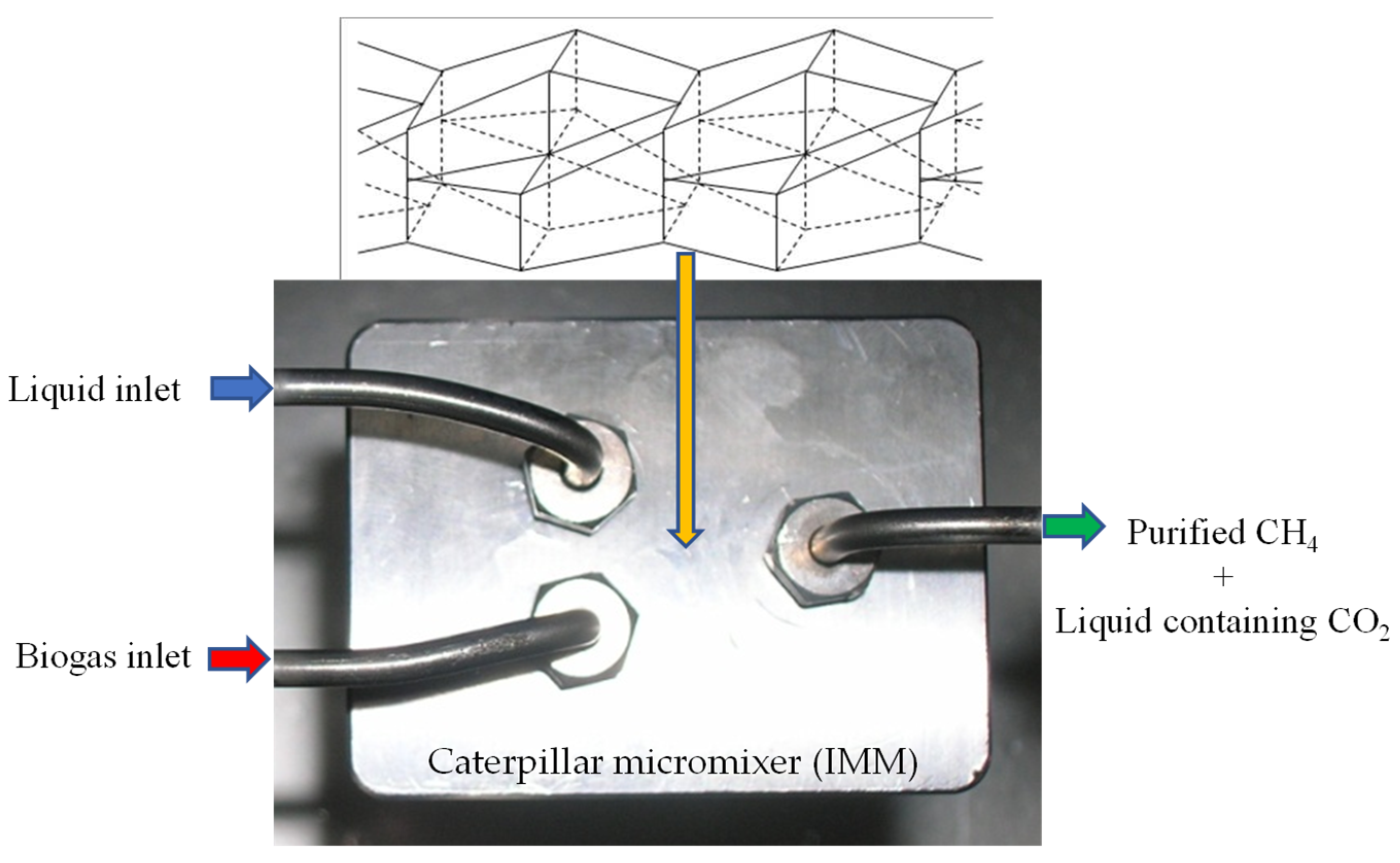
3.1. Experimental Set-Up
3.2. Definition of Absorption Efficiency
3.3. Mass Transfer Model
3.3.1. Physical Absorption Schemes
3.3.2. Chemical Absorption Schemes
3.4. Multiphase Hydrodynamics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| MM | micromixer |
References
- Aghel, B.; Behaein, S.; Wongwises, S.; Shadloo, M.S. A review of recent progress in biogas upgrading: With emphasis on carbon capture. Biomass Bioenergy 2022, 160, 106422. [Google Scholar] [CrossRef]
- Wu, H.; Liao, J.; Chen, X.; Ren, X.; Zhou, J.; Jiang, M. Decarbonization of simulated biogas with microchannel mixer by pressurized water scrubbing. J. Clean. Prod. 2024, 457, 142230. [Google Scholar] [CrossRef]
- Chalermthai, P.; Akkarawatkhoosith, N.; Kaewchada, A.; Jaree, A. Carbon dioxide Removal via Absorption using Artificial Seawater in a Microchannel for the Case of CO2-Rich Gas. Chem. Eng. Process.-Process Intensif. 2022, 175, 108928. [Google Scholar] [CrossRef]
- Ryckebosch, E.; Drouillon, M.; Vervaeren, H. Techniques for transformation of biogas to biomethane. Biomass Bioenergy 2011, 35, 1633–1645. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, L.; Ding, Y.; Zhu, X.; Liao, Q. Flow pattern and CO2 absorption in a falling film reactor with mixed aqueous solution of ionic liquid and MEA. Appl. Therm. Eng. 2018, 138, 583–590. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, G.; Yue, J.; Yuan, Q. Hydrodynamics and mass transfer of gas–liquid flow in a falling film microreactor. AIChE J. 2009, 55, 1110–1120. [Google Scholar] [CrossRef]
- Zanfir, M.; Gavriilidis, A.; Wille, C.; Hessel, V. Carbon Dioxide Absorption in a Falling Film Microstructured Reactor: Experiments and Modeling. Ind. Eng. Chem. Res. 2005, 44, 1742–1751. [Google Scholar] [CrossRef]
- Sun, X.Y.; Gavriilidis, A. Experimental Evaluation of a Micromesh Gas/Liquid Reactor for Catalytic Asymmetric Transfer Hydrogenation. Chem. Eng. Technol. 2009, 32, 1318–1325. [Google Scholar] [CrossRef]
- Constantinou, A.; Gavriilidis, A. CO2 absorption in a microstructured mesh reactor. Ind. Eng. Chem. Res. 2010, 49, 1041–1049. [Google Scholar] [CrossRef]
- Chen, G.; Yue, J.; Yuan, Q. Gas-Liquid Microreaction Technology: Recent Developments and Future Challenges. Chin. J. Chem. Eng. 2008, 16, 663–669. [Google Scholar] [CrossRef]
- Yue, J.; Boichot, R.; Luo, L.; Gonthier, Y.; Chen, G.; Yuan, Q. Flow distribution and mass transfer in a parallel microchannel contactor integrated with constructal distributors. AIChE J. 2010, 56, 298–317. [Google Scholar] [CrossRef]
- Sobieszuk, P.; Pohorecki, R.; Cygański, P.; Grzelka, J. Determination of the interfacial area and mass transfer coefficients in the Taylor gas–liquid flow in a microchannel. Chem. Eng. Sci. 2011, 66, 6048–6056. [Google Scholar] [CrossRef]
- Wang, X.; Yong, Y.; Yang, C.; Mao, Z.S.; Li, D. Investigation on pressure drop characteristic and mass transfer performance of gas–liquid flow in micro-channels. Microfluid. Nanofluidics 2014, 16, 413–423. [Google Scholar] [CrossRef]
- Ganapathy, H.; Shooshtari, A.; Dessiatoun, S.; Ohadi, M.M.; Alshehhi, M. Hydrodynamics and mass transfer performance of a microreactor for enhanced gas separation processes. Chem. Eng. J. 2015, 266, 258–270. [Google Scholar] [CrossRef]
- Hessel, V.; Hardt, S.; Löwe, H.; Schönfeld, F. Laminar mixing in different interdigital micromixers: I. Experimental characterization. AIChE J. 2003, 49, 566–577. [Google Scholar] [CrossRef]
- Schönfeld, F.; Hessel, V.; Hofmann, C. An optimised split-and-recombine micro-mixer with uniform “chaotic” mixing. Lab Chip 2004, 4, 65–69. [Google Scholar] [CrossRef]
- Zhang, H.; Li, X.; Chuai, R.; Zhang, Y. Chaotic Micromixer Based on 3D Horseshoe Transformation. Micromachines 2019, 10, 398. [Google Scholar] [CrossRef]
- Ghanem, A.; Lemenand, T.; Della Valle, D.; Peerhossaini, H. Static mixers: Mechanisms, applications, and characterization methods—A review. Chem. Eng. Res. Des. 2014, 92, 205–228. [Google Scholar] [CrossRef]
- Carrier, O.; Funfschilling, D.; Debas, H.; Poncin, S.; Löb, P.; Li, H.Z. Pressure drop in a split-and-recombine caterpillar micromixer in case of newtonian and non-newtonian fluids. AIChE J. 2013, 59, 2679–2685. [Google Scholar] [CrossRef]
- Choe, J.; Seo, J.H.; Kwon, Y.; Song, K.H. Lithium–halogen exchange reaction using microreaction technology. Chem. Eng. J. 2008, 135, S17–S20. [Google Scholar] [CrossRef]
- Kashid, M.N.; Renken, A.; Kiwi-Minsker, L. Gas–liquid and liquid–liquid mass transfer in microstructured reactors. Chem. Eng. Sci. 2011, 66, 3876–3897. [Google Scholar] [CrossRef]
- Vandu, C.O.; Liu, H.; Krishna, R. Mass transfer from Taylor bubbles rising in single capillaries. Chem. Eng. Sci. 2005, 60, 6430–6437. [Google Scholar] [CrossRef]
- Berčič, G.; Pintar, A. The role of gas bubbles and liquid slug lengths on mass transport in the Taylor flow through capillaries. Chem. Eng. Sci. 1997, 52, 3709–3719. [Google Scholar]
- Yue, J.; Chen, G.; Yuan, Q.; Luo, L.; Gonthier, Y. Hydrodynamics and mass transfer characteristics in gas–liquid flow through a rectangular microchannel. Chem. Eng. Sci. 2007, 62, 2096–2108. [Google Scholar] [CrossRef]
- Roudet, M.; Loubière, K.; Gourdon, C.; Cabassud, M. Hydrodynamic and mass transfer in inertial gas–liquid flow regimes through straight and meandering millimetric square channels. Chem. Eng. Sci. 2011, 66, 2974–2990. [Google Scholar] [CrossRef]
- Tan, J.; Lu, Y.C.; Xu, J.H.; Luo, G.S. Mass transfer performance of gas–liquid segmented flow in microchannels. Chem. Eng. J. 2012, 181–182, 229–235. [Google Scholar] [CrossRef]
- Nock, W.J.; Walker, M.; Kapoor, R.; Heaven, S. Modeling the Water Scrubbing Process and Energy Requirements for CO2 Capture to Upgrade Biogas to Biomethane. Ind. Eng. Chem. Res. 2014, 53, 12783–12792. [Google Scholar] [CrossRef]
- Cents, A.H.G. Mass Transfer and Hydrodynamics in Stirred Gas-Liquid-Liquid Contactors. Ph.D. Thesis, Universiteit Twente, Enschede, The Netherlands, 2003. [Google Scholar]
- Danckwerts, P.V.; Sharma, M.M. The absorption of carbon dioxide into solutions of alkalis and amines (with some notes on hydrogen sulphide and carbonyl sulphide). Chem. Eng. 1966, CE8, 244–278. [Google Scholar]
- Weisenberger, S.; Schumpe, A. Estimation of gas solubilities in salt solutions at temperatures from 273 K to 363 K. AIChE J. 1996, 42, 298–300. [Google Scholar] [CrossRef]
- Joosten, G.E.H.; Danckwerts, P.V. Solubility and diffusivity of nitrous oxide in equimolar potassium carbonate-potassium bicarbonate solutions at 25.deg. and 1 atm. J. Chem. Eng. Data 1972, 17, 452–454. [Google Scholar] [CrossRef]
- Pinsent, B.R.W.; Roughton, F.J.W. The kinetics of combination of carbon dioxide with water and hydroxide ions. Trans. Faraday Soc. 1951, 47, 263–269. [Google Scholar] [CrossRef]
- Benadda, B.; Prost, M.; Ismaily, S.; Bressat, R.; Otterbein, M. Validation of the gas-lift capillary bubble column as a simulation device for a reactor by the study of CO2 absorption in Na2CO3/NaHCO3 solutions. Chem. Eng. Process. Process Intensif. 1994, 33, 55–59. [Google Scholar] [CrossRef]
- Pohorecki, R.; Moniuk, W. Kinetics of reaction between carbon dioxide and hydroxyl ions in aqueous electrolyte solutions. Chem. Eng. Sci. 1988, 43, 1677–1684. [Google Scholar] [CrossRef]
- Danckwerts, P.V. Gas-Liquid Reactions; McGraw-Hill Book Co.: New York, NY, USA, 1970. [Google Scholar]

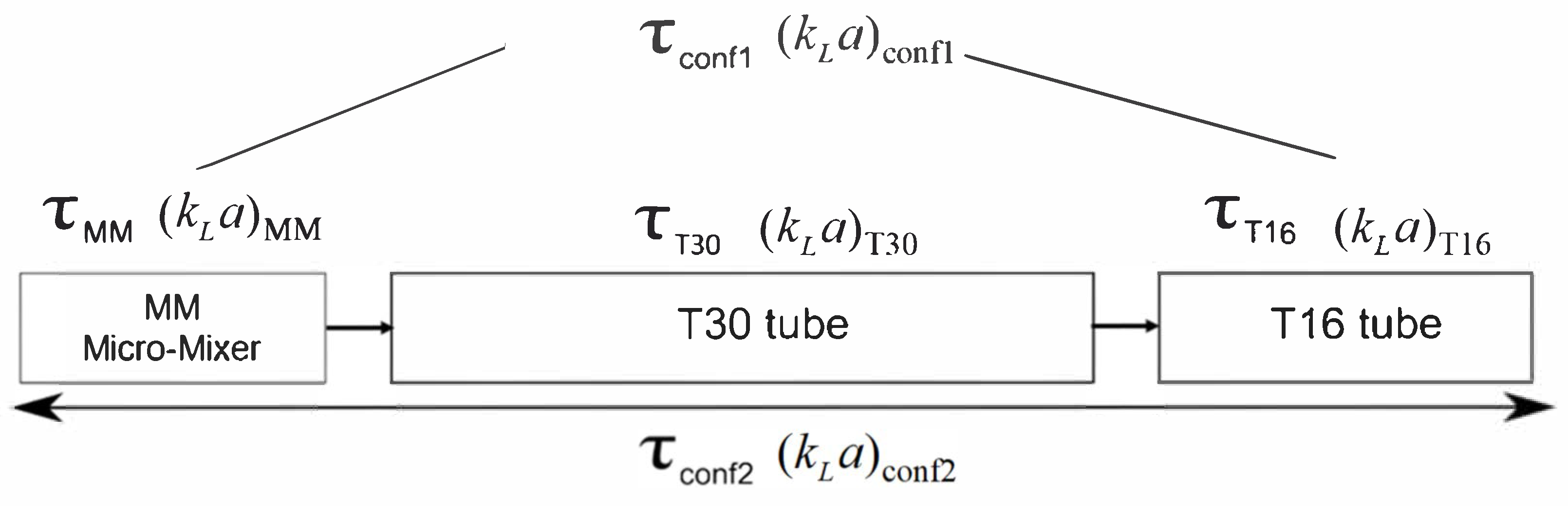

| Element | Volume (m3) | (s) | (s−1) | |
|---|---|---|---|---|
| Config. 2 | 3.3 × 10−6 | 2.2 | 0.35 | 0.16 |
| Config. 1 | 1.2 × 10−6 | 0.81 | 0.24 | 0.3 |
| T30 | 2.1 × 10−6 | 1.4 | 0.11 | 0.078 |
| T16 | 1.1 × 10−6 | 0.75 | 0.059 | 0.078 |
| MM | 7.9 × 10−8 | 0.052 | 0.18 | 3.5 |
| Configuration | CNaOCl (mol·m−3) | kapp (s−1) | Outlet yCO2 | Absorption Efficiency (%) |
|---|---|---|---|---|
| 1 | 20.5 | 31.6 | 0.120 | 76 |
| 1 | 40.2 | 62.0 | 0.130 | 74 |
| 1 | 59.1 | 91.3 | 0.087 | 83 |
| 1 | 77.4 | 119 | 0.059 | 88 |
| 2 | 10.3 | 16.0 | 0.159 | 68 |
| 2 | 20.5 | 31.6 | 0.131 | 73 |
| 2 | 30.4 | 47.0 | 0.080 | 84 |
| 2 | 40.2 | 62.0 | 0.059 | 88 |
| Auteur | Gas | System | kL × 10−4 (m·s−1) | a (m−1) | kLa (s−1) |
|---|---|---|---|---|---|
| Vandu et al. [22] | Air | Capillaries d = 1, 2, 3 mm | / | / | 0.08–0.8 |
| Berčič and Pintar [23] | CH4 | Capillaries d = 1.5, 2.5, 3.1 mm | / | / | 0.006–0.3 |
| Yue et al. [24] | CO2 | Rectangular micro-channel dH = 667 µm | 5–15 | 3000–9000 | 0.2–21 |
| Sobieszuk et al. [12] | CO2 | Circular microchannel d = 0.4 mm | / | / | 2–6 |
| Roudet et al. [25] | Air | Square microchannel dH = 2 mm | 1–5 | 200–1600 | 0.05–0.7 |
| Tan et al. [26] | CO2 | Rectangular micro-channel 0.4 × 0.5 mm | 1–7 | / | / |
| Ganapathy et al. [14] | CO2 | Circular microchannel d = 254, 508, 762 µm | 90–300 | 4500–15,000 | 25–400 |
| This study | CO2 | Microstructrured static micromixer dH = 1, 2 mm | 2 | 600 | 0.14 |
| Parameter | Value | Unit |
|---|---|---|
| 0.02 | s−1 | |
| 1.54 | m3·mol−1·s−1 | |
| 2.16 | m3·mol−1·s−1 | |
| D | 1.48 × 10−9 | m2·s−1 |
| H | 3.83 × 10−4 | mol·m−3·Pa−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wedraogo, T.N.; Djerid, S.; Wu, J.; Li, H.Z. Biogas Purification by Intensified Absorption in a Micromixer. Methane 2025, 4, 14. https://doi.org/10.3390/methane4030014
Wedraogo TN, Djerid S, Wu J, Li HZ. Biogas Purification by Intensified Absorption in a Micromixer. Methane. 2025; 4(3):14. https://doi.org/10.3390/methane4030014
Chicago/Turabian StyleWedraogo, Tarsida N., Souhila Djerid, Jing Wu, and Huai Z. Li. 2025. "Biogas Purification by Intensified Absorption in a Micromixer" Methane 4, no. 3: 14. https://doi.org/10.3390/methane4030014
APA StyleWedraogo, T. N., Djerid, S., Wu, J., & Li, H. Z. (2025). Biogas Purification by Intensified Absorption in a Micromixer. Methane, 4(3), 14. https://doi.org/10.3390/methane4030014








