Radio Pulsars Resonantly Accelerating Electrons
Abstract
1. Introduction
2. Brief Outline of Theory
- (1)
- The rate of energy gain stems from a quantum effect;
- (2)
- It requires the perpendicular momentum to be nonzero;
- (3)
- It is resonantly enhanced.
3. Theory in the Pulsar Context
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGN | Active galactic nuclei |
| EM | Electromagnetic |
| IC | Inverse Compton |
| KG | Klein–Gordon |
| KN | Klein–Nishina |
| LC | Light cylinder |
| MA | Magneto-centrifugal acceleration |
| VHE | Very high energy |
References
- Mahajan, S.M.; Asenjo, F.A. A statistical model for relativistic quantum fluids interacting with an intense electromagnetic wave. Phys. Plasmas 2016, 23, 056301. [Google Scholar] [CrossRef]
- Baade, W.; Zwicky, F. On Super-novae. Proc. Natl. Acad. Sci. USA 1934, 20, 254. [Google Scholar] [CrossRef] [PubMed]
- Sekido, Y.; Masuda, T.; Yoshida, S.; Wada, M. The Crab Nebula as an Observed Point Source of Cosmic Rays. Phys. Rev. 1951, 83, 658. [Google Scholar] [CrossRef]
- Gunn, J.E.; Ostriker, J.P. Acceleration of high-energy cosmic rays by pulsars. Phys. Rev. Lett. 1969, 22, 728. [Google Scholar] [CrossRef]
- Bednarek, W.; Protheroe, R.J. Contribution of nuclei accelerated by gamma-ray pulsars to cosmic rays in the Galaxy. APh 2002, 16, 397. [Google Scholar] [CrossRef]
- Lemoine, M.; Kotera, K.; Pétri, J. On ultra-high energy cosmic ray acceleration at the termination shock of young pulsar winds. Phys. Rev. Lett. 1969, 22, 728. [Google Scholar] [CrossRef]
- Osmanov, Z.; Rieger, F.M. On particle acceleration and very high energy γ-ray emission in Crab-like pulsars. Astron. Astrophys. 2009, 502, 15–20. [Google Scholar] [CrossRef]
- Osmanov, Z.; Rieger, F.M. Pulsed VHE emission from the Crab Pulsar in the context of magnetocentrifugal particle acceleration. Mon. Not. R. Astron. Soc. 2017, 463, 1347. [Google Scholar] [CrossRef]
- Mahajan, S.; Machabeli, G.; Osmanov, Z.; Chkheidze, N. Ultra High Energy Electrons Powered by Pulsar Rotation. Sci. Rep. 2013, 3, 1262. [Google Scholar] [CrossRef]
- Osmanov, Z.; Mahajan, S.; Machabeli, G.; Chkheidze, N. Millisecond newly born pulsars as efficient accelerators of electrons. Sci. Rep. 2015, 5, 14443. [Google Scholar] [CrossRef] [PubMed]
- Protheroe, R.J.; Szabo, A.P. High energy cosmic rays from active galactic nuclei. Phys. Rev. Lett. 1992, 69, 2885. [Google Scholar] [CrossRef] [PubMed]
- Peér, A.; Murase, K.; Mészáros, P. Radio-quiet active galactic nuclei as possible sources of ultrahigh-energy cosmic rays. Phys. Rev. D 2009, 80, 123018. [Google Scholar] [CrossRef]
- Schady, P. Gamma-ray bursts and their use as cosmic probes. Royal Soc. Op. Sc. 2017, 4, 170304. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, R.; Wang, X. Acceleration of ultrahigh-energy cosmic rays in the early afterglows of gamma-ray bursts: Concurrence of jet dynamics and wave-particle interactions. Phys. Rev. D 2021, 104, 103005. [Google Scholar] [CrossRef]
- Marcowith, A.; van Marle, A.J.; Plotnikov, I. The cosmic ray-driven streaming instability in astrophysical and space plasmas. Phys. Plasmas 2021, 28, 080601. [Google Scholar] [CrossRef]
- Globus, N.; Blandford, R. Ultra High Energy Cosmic Ray Source Models: Successes, Challenges and General Predictions. In Proceedings of the 6th International Symposium on Ultra High Energy Cosmic Rays (UHECR2022), L’Aquila, Italy, 3–7 October 2022. [Google Scholar]
- Owen, E.R. Cosmic ray processes in galactic ecosystems. Galaxies 2023, 11, 86. [Google Scholar] [CrossRef]
- Fermi, E. On the origin of the cosmic radiation. Phys. Rev. 1949, 75, 1169. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts—I. Mon. Not. R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Catanese, M.; Weeks, T.C. Very High Energy Gamma-Ray Astronomy. Publ. Astron. Soc. Pac. 1999, 111, 1193. [Google Scholar] [CrossRef]
- Rieger, F.M.; Matthaeus, W.H. Relativistic particle transport and acceleration in structured plasma turbulence. Astrophys. J. 2022, 928, 25. [Google Scholar]
- Osmanov, Z.; Mahajan, S.; Machabeli, G.; Chkheidze, N. Extremely efficient Zevatron in rotating AGN magnetospheres. Mon. Not. R. Astron. Soc. 2015, 445, 4155. [Google Scholar] [CrossRef][Green Version]
- Mahajan, S.M.; Osmanov, Z.N. Resonant energization of particles by radio AGN. Astron. Astrophys. 2022, 664, 4. [Google Scholar] [CrossRef]
- Greisen, K. End to the cosmic-ray spectrum? Phys. Rev. Lett. 1966, 16, 748. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuzmin, V.A. Upper limit of the spectrum of cosmic rays. JETP Lett. 1966, 4, 78. [Google Scholar]
- Mahajan, S.M.; Asenjo, F.A. Interacting quantum and classical waves: Resonant and non-resonant energy transfer to electrons immersed in an intense electromagnetic wave. Phys. Plasmas 2022, 29, 022107. [Google Scholar] [CrossRef]
- Machabeli, G.Z.; Usov, V.V. Cyclotron instability in the magnetosphere of the Crab Nebula pulsar, and the origin of its radiation. Sov. Astron. Lett. 1979, 5, 445–449. [Google Scholar]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Ruderman, A.; Sutherland, P.G. Theory of pulsars-Polar caps, sparks, and coherent microwave radiation. Astrophys. J. 1975, 196, 51–72. [Google Scholar] [CrossRef]
- Stollman, G.V. The radio luminosity of pulsars. Astron. Astrophys. 1987, 171, 152–156. [Google Scholar]
- Ochelkov, Y.P.; Usov, V.V. Curvature radiation of relativistic particles in the magnetosphere of pulsars: I: Theory. Astrophys. Space Sci. 1980, 69, 439–460. [Google Scholar] [CrossRef]
- Goldreich, P.; Julian, W.H. Pulsar Electrodynamics. Astrophys. J. 1999, 157, 869. [Google Scholar]
- Zhang, B.; Harding, A.K. Full polar cap cascade scenario: Gamma-ray and X-ray luminosities from spin-powered pulsars. Astrophys. J. 2000, 532, 1150. [Google Scholar] [CrossRef]
- Schaab, C.; Sedrakian, A.; Weber, F.; Weigel, M.K. Impact of internal heating on the thermal evolution of neutron stars. Astron. Astrophys. 1999, 346, 465–480. [Google Scholar]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 1970, 42, 237. [Google Scholar] [CrossRef]
- Aharonian, F.A. Very High Energy Cosmic Gamma Radiation—A Crucial Window on the Extreme Universe; World Scientic Publishing Co. Pte. Ltd.: Singapore, 2004. [Google Scholar]
- Gunn, J.E.; Ostriker, J.P. Magnetic dipole radiation from pulsars. Nature 1969, 221, 454–456. [Google Scholar] [CrossRef]
- Kegel, W.H.; Herold, H.; Ruder, H.; Leinemann, R. The radiation of charged particles accelerated in strong electromagnetic waves. Astron. Astrophys. 1995, 297, 369. [Google Scholar]
- Pétri, J. Particle acceleration and radiation reaction in strong spherical electromagnetic waves. Mon. Not. R. Astron. Soc. 2021, 503, 2123–2136. [Google Scholar] [CrossRef]

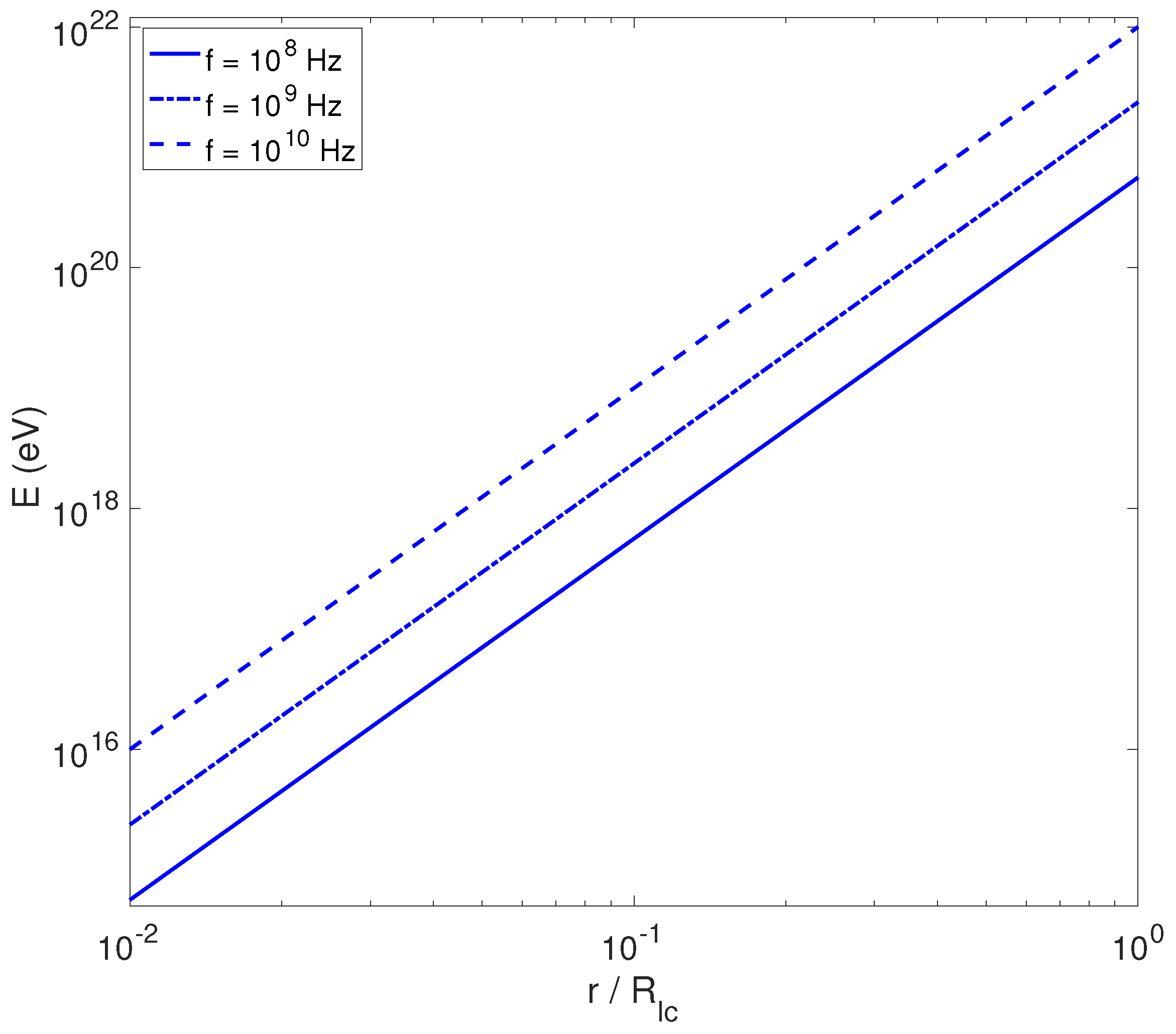
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osmanov, Z.N.; Mahajan, S.M. Radio Pulsars Resonantly Accelerating Electrons. Astronomy 2023, 2, 226-234. https://doi.org/10.3390/astronomy2040016
Osmanov ZN, Mahajan SM. Radio Pulsars Resonantly Accelerating Electrons. Astronomy. 2023; 2(4):226-234. https://doi.org/10.3390/astronomy2040016
Chicago/Turabian StyleOsmanov, Zaza N., and Swadesh M. Mahajan. 2023. "Radio Pulsars Resonantly Accelerating Electrons" Astronomy 2, no. 4: 226-234. https://doi.org/10.3390/astronomy2040016
APA StyleOsmanov, Z. N., & Mahajan, S. M. (2023). Radio Pulsars Resonantly Accelerating Electrons. Astronomy, 2(4), 226-234. https://doi.org/10.3390/astronomy2040016




