1. Introduction
The last decade of research in string theory, and quantum gravity in general, has witnessed a remarkable breadth of progress and novel ideas. A variety of connections between fundamental interactions of microscopic degrees of freedom and the breakdown of the corresponding low-energy effective field theory (EFT) dynamics have been proposed and thoroughly investigated. As a result, the existing network of swampland criteria [
1]
1 to determine consistent EFTs has been expanded and enriched. In particular, numerous insights have been collected about infinite-distance asymptotic regions of moduli space in EFTs coupled to gravity [
5,
6,
7] in support of the distance conjecture [
8] and its extensions [
9,
10,
11,
12,
13,
14,
15].
The emerging picture appears to be intimately tied to string dualities, and suggests that quantum-gravitational consistency entails a very specific breakdown of EFT. Namely, an infinite tower of massive states would become parametrically light at an exponential rate in the proper distance in moduli space, and furthermore, the states would pertain either to a Kaluza-Klein (KK) tower or higher-spin excitations of tensionless strings. These towers of states signal, respectively, the presence of extra dimensions of space or extended objects in the spectrum.
Despite many advances, investigations have focused on supersymmetric settings. In order to achieve a deeper understanding, and ultimately connect these ideas with phenomenology, it is paramount to address supersymmetry breaking, which at present, lacks a comprehensive guiding principle. Among the wide variety of mechanisms that have been proposed, string-scale supersymmetry breaking appears to provide a natural setting to seek instructive lessons beyond the current “lamppost” [
16,
17,
18,
19]. To wit, naïve dimensional arguments have been recently supplemented by additional considerations [
20,
21] on the (in)consistency of light gravitini within low-energy supersymmetry breaking, and the gravitino mass appears to play an important role reminiscent of “brane supersymmetry breaking” (BSB) [
22], as discussed in [
23].
Given the present state of affairs, we are compelled to attempt at extending the investigation of swampland proposals to non-supersymmetric settings, and to this end, the
heterotic model of [
24,
25], the
“type
” model of [
26,
27] and the
model of [
28] stand as promising candidates
2. In particular, the latter features a simple realization of BSB, whereby the closed-string sector remains supersymmetric while supersymmetry is broken in the open-string sector. The appearance of a Goldstino singlet in the perturbative spectrum hints at a spontaneous breaking, and the low-energy physics feature the expected interactions
à la Volkov–Akulov [
32,
33], but a satisfactory description of the corresponding super-Higgs mechanism in ten-dimensions remains elusive [
34,
35].
Various swampland conjectures have been studied in these models [
36,
37] and in other settings with supersymmetry breaking [
38]. In particular, some hints regarding light towers of states have been discussed in [
36]. In this paper, we shall focus on infinite-distance limits. In this respect, one expects supersymmetry breaking to dramatically affect vacua [
39,
40] and destroy exact moduli spaces. A milder counterpart of this scenario would involve potentials lifting the moduli, and their role has been discussed in [
13]. In order to circumvent these limitations, we shall investigate generalized notions of distance using holography. A similar proposal has been put forth in [
14,
15] using the Zamolodchikov metric [
41]. This approach to the geometry of theory space has been extended by O’Connor and Stephens [
42] in the context of the quantum information theory, and by Anselmi [
43] in the context of renormalization group (RG) flows. The former metric has been recently revisited by Stout [
44], and in this work, we shall employ both metrics to explore infinite-distance limits in the absence of supersymmetry.
Our findings reveal that the breakdown of EFT at an infinite distance involves either a KK tower arising from compact extra dimensions or higher-spin excitations of a D1-brane. The latter lies in a stringy regime that we approach holographically, and arises as the endpoint of a cascade of flux tunneling processes in unstable brane configurations driven by weak gravity [
37,
45]. Remarkably, in the Sugimoto model of [
28], supersymmetry is restored, thereby granting stability as expected from the considerations of [
46].
After discussing in detail our setup from the bulk and holographic perspectives, we compute the (generalized) distances associated to the endpoints of the tunneling cascade, finding that they diverge. Then, we compute anomalous dimensions of scalar operators and (single-trace) higher-spin currents in the dual field theory, and we entertain the possibility of a novel heterotic-orientifold S-duality in the final state. While our results hold in more general settings, the asymptotic scalings specific to the string models of interest
exponentially suppress the anomalous dimensions in a precise sense that we discuss. Furthermore, these novel realizations of the emergent string proposal [
9,
10,
11], supersymmetric protection and heterotic-orientifold duality [
47] exhibit a tantalizing interplay via
triality.
2. Brane Dynamics and Weak Gravity
Our starting point is to investigate the vacua of the string models that we have introduced in the preceding section. In more familiar settings, these comprise the trivial configuration where spacetime is flat and all fields vanish. However, in the present models, the low-energy EFT contains the (Einstein-frame) dilaton potential [
29,
30,
31,
32,
33]:
where the parameter
for the orientifold models and the heterotic model, respectively. For the former, the coefficient
can be interpreted as the residual tension of the
-branes and the O9-plane, while for the latter, it can be interpreted as the one-loop vacuum energy (density). This potential, absent of a balancing act, drives the vacuum to a runaway, where
. Therefore, the standard string perturbation theory is compromised by a
dynamical tadpole, whose dramatic gravitational backreaction is yet to be understood completely. In the pioneering work of [
34]
3, it was found that the most symmetric solutions appear to entail a spontaneous compactification of one spatial dimension into an interval, which however hosts curvature and/or coupling singularities at its endpoints
4. These solutions have been generalized to families [
30,
31,
45,
50,
51], strongly suggesting that geometries of these type are sourced by branes, whose presence breaks the isometry group accordingly. On the one hand, the resulting geometries feature a universal finite-distance “pinch-off” singularity [
45], which dovetails nicely with the recent considerations of [
52,
53] in the context of the swampland.
On the other hand, the backreaction of extremal charged branes is somewhat milder, since the finite-distance “pinch-off” is accompanied by a near-horizon throat which is weakly curved and weakly coupled when the number of branes is large. The resulting geometry is depicted in
Figure 1. The string models that we have discussed in the introduction contain a variety of such branes, whose presence can be ascertained from the consistency of their perturbative spectra [
35,
54] via orientifold techniques applied to one-loop vacuum amplitudes. In particular, the USp(32) model of Sugimoto [
28] contains charged D1-branes and D5-branes, while the
type
model [
26,
27] also contains charged D3-branes and D7-branes. While D5-branes and D7-branes are more subtle in this respect, D3-branes source a quasi-
near-horizon throat [
55,
56], while D1-branes source a
bona fide throat [
30,
37,
45,
57]. Similarly, NS5-branes in the heterotic model source an
throat
5. All of these geometries have no scale separation, and for a large number
N of branes, where the EFT regime is expected to be reliable, the string coupling
and the radius
R of the internal
scale according to [
30,
37,
45,
57]
The resulting geometries are unstable, both perturbatively [
60] and non-perturbatively [
45]. In the former case, field fluctuations violating the Breitenlohner–Freedman bound [
61] can potentially be avoided by replacing the internal
with a suitable Einstein manifold
, which is expected to arise by placing branes on a conical singularity [
62], or performing a suitable orbifold projection. In the heterotic model, this is readily achieved by an antipodal
projection as shown in [
60]. Other instances of perturbatively stable vacua have been found in [
63,
64]. On the other hand, the orientifold models are subtler and no explicit projection has been found. However, since the dangerous mass values lie in an interval [
60], any replacement of the sphere with a scalar Laplacian gap sufficient to skip the interval would remove perturbative instabilities. At any rate, the considerations in this paper are general and apply to any such
brane construction. In the latter case, the non-perturbative instability cannot be avoided, and flux tunneling occurs with a probability
per unit volume per unit time which is schematically of order [
45,
65,
66]:
for
in the semiclassical limit
. After nucleation branes expand, one can determine what forces they exert on each other, computing static interaction potentials between parallel stacks [
37,
45]. One finds that branes with the same charges repel, consistently with the weak gravity [
67] and repulsive force [
68] conjectures. The net repulsion is mediated by the supersymmetry-breaking dynamical tadpole, which renormalizes the effective charge-to-tension ratio by the
factor
as shown in
Figure 2.
3. Bubble Nucleation and Holography
According to our preceding discussion, the
vacua at stake undergo flux tunneling, nucleating charged branes. Although the corresponding decay rates are parametrically exponentially suppressed
6, eventually this non-perturbative instability drives the vacua to progressively lower values of
N, at least until the low-energy EFT ceases to be reliable. This process points to a dynamically generated trajectory in the (discrete) landscape of flux vacua. One is thus naturally led to investigate whether the endpoints of this trajectory, located at
and
, lie at an infinite distance in some sense, and whether towers of light states emerge.
The former large
N limit, already considered in [
36], is considerably simpler, since it lies fully within the low-energy description, where the masses of KK states can be reliably computed. Dimensionally reducing the ten-dimensional gravitational EFT yields an effective action for the dilaton
and the (canonically normalized) radion
[
30,
36]. The kinetic metric is canonical, and the masses of KK excitations around the
flux compactifications scale according to
in units of the
dimensionally reduced Planck mass [
36,
45]. The vacuum values of the dilaton and radion pertaining to a given flux number
N are given by [
36,
45,
57]
for large fluxes, so that the masses scale as the inverse radius of the internal space
measured in the
-dimensional Einstein frame [
45]. In particular, the squared KK masses scale as
and
for the orientifold models and the heterotic models, respectively.
Clearly, the KK tower becomes massless as . However, our main aim is to understand whether this limit lies at an infinite distance, and whether the decay of KK masses is precisely exponential in the distance. Although the landscape of (metastable) vacua at stake is discrete, the flux tunneling process is realized by solitonic bubble profiles that continuously interpolate between the vacua. One could thus define a discrete-landscape distance via the metric in the scalar field space defined by the effective action along such profiles.
This procedure would
a priori raise the issues of finding the relevant instanton solutions and minimizing the total distance along the many possible interpolations between two flux numbers
. Actually, one can circumvent these obstacles bounding the distance from above and from below as follows, in such a way that the result is independent on the particular solitonic profile. From (
6), along any interpolating profile, one can bound the metric via the inequalities
which imply that the distance between
and
is bounded by
where
are the
constants that arise from (
6). Therefore, the distance scales logarithmically, and accordingly, the tower of KK masses decays exponentially fast in the distance, with a rate bounded by (
8) combined with (
5). Let us emphasize that this result holds independently of the specific field profile induced by the bubble. In the following, we will argue that this is dual to an RG flow along the lines of [
71]. In addition to supporting the distance conjecture in the absence of supersymmetry, as we have discussed, this result resonates with the absence of scale separation in
vacua [
12,
72,
73,
74,
75]. Furthermore, since the KK masses are proportional to a positive power of the
cosmological constant, the
version of the distance conjecture [
12] holds as well.
Let us now focus on the opposite limit where
is small. The EFT description is not trustworthy in this regime, since the string coupling and the curvatures are not negligible. In order to obtain an alternative description, we appeal to holography, and in particular to the proposal of [
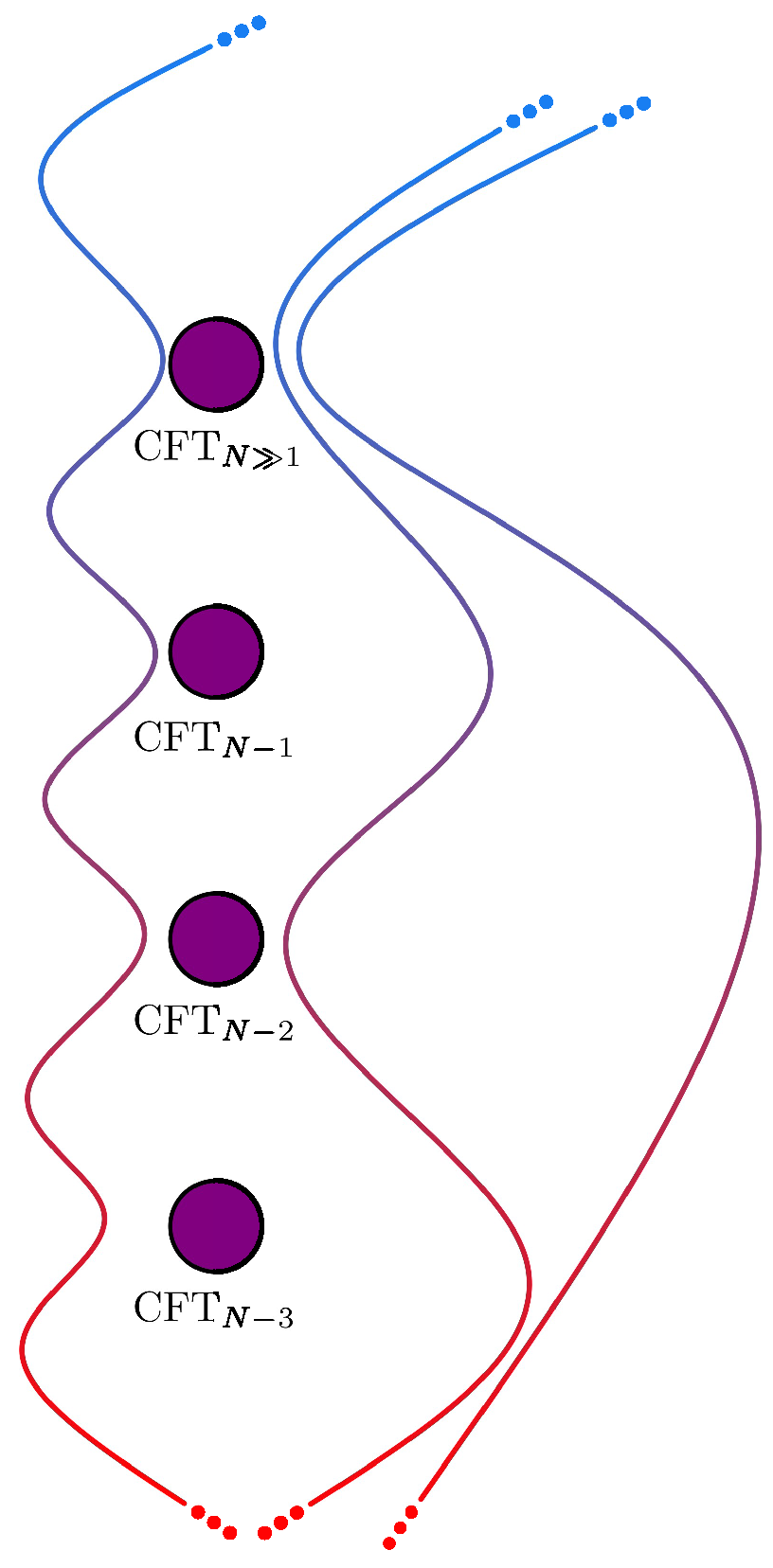
71]: the cascade of tunneling processes would be dual to a RG flow in the dual field theory, as depicted in
Figure 3. Importantly, the flows can only approach a fixed point for a large
N, since the
vacua become more stable in this limit. As we shall find, the flow eventually reaches an endpoint for
, where for the BSB Sugimoto model, supersymmetry is actually recovered. The existence of fixed points for the intermediate values of
N can be argued for from the exponentially fast vanishing of the bulk decay rate; the dual RG flow is (parametrically) slow, suggesting an approach to a fixed point which becomes closer and closer as depicted in
Figure 3. Since a fixed point also exists for
, as we shall discuss in detail, and the standard proposal for the dual field theory involves open-string dynamics on D-branes, we expected these fixed points to exist at least for
N large or close to one, if not for all
N. From these considerations, any potential window of non-conformality would involve intermediate values of
N where the theory is strongly coupled. In any case, we only need the two extrema of the flow to derive the results of this paper on infinite-distance limits.
In the string models that we consider, the dual conformal field theory (CFT) for each
N ought to arise from the infrared (IR) regime of the worldvolume gauge theory that lives on a stack of
N parallel branes, following the original construction of [
76], and suitable deformations encoding flux tunneling. In particular, in the remainder of this paper, we shall focus on D1-branes in the orientifold models, since heterotic NS5-branes are considerably more difficult to deal with in this respect. Moreover, since the resulting field theories are two-dimensional, it is conceivable that progress can be achieved despite the absence of supersymmetry. As a minor technicality, we shall consider D1-branes in the parametrically controlled and flat region of the Dudas–Mourad background [
30,
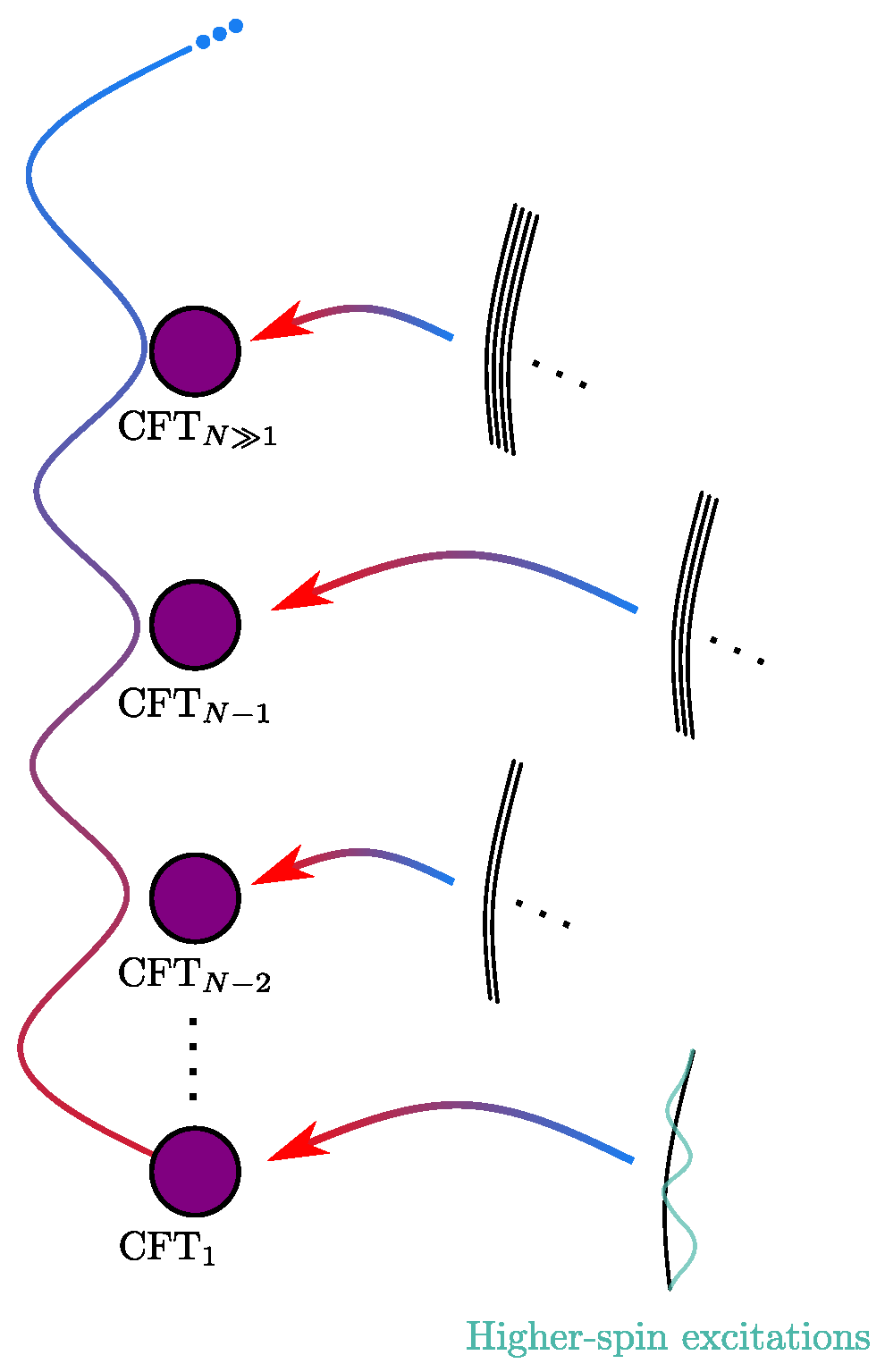
37], since there is no ten-dimensional Minkowski background. This holographic setup is shown in
Figure 4, where now each CFT arises from a worldvolume gauge theory in the IR, and the repulsion between branes triggers an RG flow. The corresponding operators arise by integrating out the brane separation modes, analogously to the more familiar case of supersymmetric D3-branes, where Higgsing generates Born–Infeld operators [
77,
78,
79,
80,
81,
82,
83].
The massless field content of the worldvolume gauge theory of
N D1-branes in the Sugimoto model comprises [
28,
35] a
gauge field
A, scalars
in the vector representation
of the transverse isometry group
and the
antisymmetric representation of the gauge group and Majorana–Weyl fermions
in the spinor representations
of
belonging to the symmetric (
) and antisymmetric (
) representations of the gauge group. Finally, bi-fundamental
fermions
arise from the
open-string sector. On the other hand, in the type
model, a stack of
N D1-branes carries a
gauge group, and the scalars
are in the
adjoint, while the Weyl fermion representations are unchanged [
54]. One can verify that the worldvolume gauge anomalies cancel, since for the characteristic classes pertaining to the (anti)symmetric representations [
54],
and thus, one obtains a net contribution of
from the chiral fermions. However, the gravitational anomaly does not cancel on the worldvolume without an inflow mechanism, which suggests that the theories are, in general, gapless [
84]. This is indeed what we find for the theories at stake. Two-dimensional gauge theories are amenable to a variety of methods, including light-cone techniques, such as those pioneered in the original ’t Hooft model [
85] and (chiral) bosonization [
86,
87,
88]. The presence of scalars complicates matters to some extent, but one can expect, due to the quartic potential, for the IR dynamics to be described by a non-linear
model (NL
M) [
89]. We shall return to this point later. For the time being, we shall focus on the last step of the cascade of decays,
. Since we are interested in the asymptotic behavior of the distance, this is the only relevant step of the RG flow. We shall begin from the endpoint
itself, the CFT dual to the final state of the tunneling process.
Emergent Supersymmetry and WZW Cosets
Among the various simplifications, crucially for
, the scalars
decouple, as we shall now explain. This is expected, since they describe transverse fluctuations of a single D1-brane in spacetime. As we shall see shortly, the remaining degrees of freedom in the worldvolume theories ought to flow to WZW coset models [
84,
90], which can be constructed by means of non-Abelian bosonization.
In detail, in the Sugimoto model, the scalars and the fermions in the antisymmetric representation decouple because they belong to a singlet. Furthermore, the scalar potential and the Yukawa term vanish identically. Therefore, a free sector comprised of eight pairs of a real scalar and a chiral fermion appears. These fields rearrange into a
Wess–Zumino multiplet, displaying
emergent supersymmetry at the endpoint of the tunneling cascade. This resonates with the considerations of [
46,
71] and shows that the
configuration is the stable final state of this process, protected by the restored supersymmetry. Let us observe that this remarkable phenomenon occurs due to
triality, by virtue of the isomorphism
. This remarkable occurrence in turn requires eight transverse dimensions. In the present setting, this is only possible for (D-)
strings, realizing the proposal of [
9,
10,
11] in a novel and peculiar fashion. Indeed, as we shall see, emergent strings are also the only case in which the (generalized) distance to the
configuration is infinite. On the other hand, the antisymmetric fermions in the type
model disappear for
, and thus only a non-supersymmetric free-boson CFT decouples. This is compatible with the non-supersymmetric origin of the theory. We now turn to the sectors that remain coupled to the gauge field.
For the Sugimoto model, the remaining degrees of freedom rearrange into the chiral WZW coset:
whose central charges read,
is compatible with the same gravitational anomaly
. Interestingly, the
total central charges of this model, including the free
SCFT sector, can be recast in the form
which is tempting to identify with the central charges of (the transverse degrees of freedom of) a dual ten-dimensional heterotic string, plus a “correction” due to supersymmetry breaking. While this is at best an amusing hint, the prospect of a strong-weak duality in the absence of supersymmetry remains tantalizing [
91,
92,
93,
94], and we shall elaborate on this point shortly. Furthermore, the correction to the left-moving supersymmetric sector is compatible with a Gepner model built by two copies of the
,
minimal models. The deviation
from the free
SCFT is also compatible with Gepner models of this type. The relation between this WZW coset model and the
transition is depicted in
Figure 5.
These considerations on the worldsheet theory of a D-string in the Sugimoto model, which answer the question originally posed in [
28], can be complemented by arguments based on the low-energy effective action, in the spirit of the supersymmetric heterotic-type I duality [
47]. Performing a naïve S-duality transformation on the spacetime metric and dilaton fields, the tadpole potential of (
1) translates into the string-frame contribution
. Intriguingly, this structure mirrors the presence of two decoupled sectors of the worldsheet theory; quantizing it on disjoint unions of two Riemann surfaces, with the free geometric sector on one connected component and the non-geometric WZW coset on the other, would seem to reproduce this effect while being consistent with a single heterotic-like string in physical spacetime. In particular, the leading contribution to the string perturbation theory would stem from a surface with topology
, and a scale precisely as
. Notably, only one sector is geometric, preserving the standard interpretation of a connected worldsheet in physical spacetime, while the other sector is non-geometric. Let us emphasize that disconnected worldsheets have already appeared in the literature, in the context of D-instantons and non-perturbative effects [
95,
96,
97]. All in all, the emergent superconformal free heterotic-like sector, together with a non-geometric sector and the corresponding leading contribution to an S-dual EFT, seem to point to a novel heterotic-orientifold duality, although the arguments that we have presented are but compelling indications for the time being. As we shall discuss in the following section, this configuration arises from an infinite-distance emergent-string limit, which is also a smoking gun of dualities of this type [
8]. It would be interesting to attempt to construct a Polyakov quantization of such a heterotic string.
For the type
model, the
worldvolume gauge theory is Abelian, and bosonization simplifies accordingly [
87,
98] in a slight generalization of the (chiral) Schwinger model [
99]. The upshot is that a single linear combination of the bosonized chiral scalars becomes gapped in the IR, resulting in one less massless fermion for both chiralities [
98]. Since the photon acquires a dynamical mass, the resulting CFT is free. It would be interesting to assess whether emergent supersymmetry can arise in this model in terms of two-dimensional
Fermi supermultiplets.
4. Infinite Distances and Emergent Strings
Having described the endpoint of the tunneling process holographically, we can now turn to the RG flow. In both orientifold models, the CFT dual to the final state contains a free sector, and thus single-trace higher-spin currents that are conserved. On general grounds, one expects that the higher-spin symmetry be broken along the flow, and that the anomalous dimensions vanish continuously at the endpoint. Similarly to our analysis of KK masses, one is thus led to seek a suitable generalization of the Zamolodchikov metric, since there is no exact conformal manifold. Such a notion was introduced by O’Connor and Stephens on information-theoretic grounds [
42], explored by Dolan [
100,
101] and subsequently revisited in numerous settings, most recently by Stout in the context of the distance conjecture [
44].
Parametrizing the theory space by operators
with couplings
, the metric reads
up to a volume factor, in a special coordinate system in which the action is linear in the couplings, so that
g is also the negative Hessian of the vacuum energy density [
42]. While this metric was developed by applying the tools of quantum information theory to RG flows, a similar metric was defined by Anselmi in the context of Lorentz-breaking field theories [
43]. This metric trades the integral over spacetime in (
14) for an energy scale
, which appears in a timelike position argument
. The metric reads
and in both metrics, the correlators are connected. In the following, we shall compute distances along the RG flow using both metrics. While the results coincide up to a constant in this case, the metrics differ in general. Before moving on to the computation, let us comment on the connection with the bulk description. To begin with, as discussed in [
44], the field-space metric that we employed in the bulk computation is the quantum information metric of the bulk EFT in the perturbative limit in which the field space is weakly curved, and thus we are using the same underlying notion of the metric in different guises. Furthermore, the following holographic computation is dual to the bulk (according to the proposal of [
71]) in a variation of the well-understood correspondence between bulk domain walls and certain types of boundary RG flows. In the conformal limit, the field-space metric of the bulk EFT also matches the information metric of the holographic dual, which reduces to the Zamolodchikov metric for marginal couplings.
As we have anticipated, it is natural to expect that the IR regime of the RG flow be dominated by a NL
M deformation of the free (S)CFT, as shown in
Figure 5. Indeed, in two dimensions, these are the only (classically) marginal ones, since the IR fixed point is Gaussian and classical power counting applies. On the one hand, from the point of view of the renormalization group, these deformations are present during a generic flow. On the other hand, as we shall discuss, they arise from the repulsion of branes in the specific models that we consider. In fact, such deformations are marginally irrelevant, and the distance along the flow can diverge only in this case. This stems from the exponential decay
of strictly irrelevant deformations as the RG time
in the IR, so that the integral
computing the total distance converges. Once again, this peculiar fact dovetails nicely with the emergent string proposal of [
9,
10,
11], namely the infinite distance limit at stake only exists when the extended object that becomes tensionless is a (D-)string. Indeed, in contrast, one can verify that, were an analogous Gaussian fixed point present for NS5-branes, there would not be any marginally irrelevant deformations preserving the symmetries, and hence, no corresponding infinite-distance limit.
Here, we shall focus on the bosonic sector, defined by the action
for a suitable constant
7, although by power counting, one does not expect that the fermionic sector yield different results. The deformation of the NL
M effectively turns on the tension of the D-string, and takes the general form
where we shall take
with
transverse target-space dimensions. In the string perturbation theory, (
17) would be (part of) a graviton vertex operator. While this terminology is useful, one ought to keep in mind that in this holographic CFT, its meaning is different, and in particular, there is no on-shell constraint. Although (
17) is quite general, we shall derive a more concrete expression for the string models that we consider.
The corresponding one-loop Ricci flow for transverse-traceless
is
so that the Fourier modes of
run according to
. Thus, the perturbation of (
17) is indeed marginally irrelevant in the IR. In the ensuing discussions, we shall consider modes of this type, in order to simplify the computations. However, the qualitative results should be unaffected in the general case.
The “Stout-O’Connor-Stephens” (SOS) quantum information distance along the RG flow in the deep IR is then asymptotically given by
where the subscript indicates free correlators, since the theory is free in the IR. In the following, all asymptotic signs refer to the IR limit
. To compute the correlator in (
20), we shall employ the general Gaussian formula
for free correlators, where normal ordering is understood and
. Functionally differentiating with respect to the auxiliary source
and differentiating with respect to the worldsheet position, one can obtain normal-ordered correlators subtracting the contact terms and setting the insertion points equal at the end of the calculation. Applying this technique to (
20), taking into account the connected contributions and the transverse-traceless “graviton”, one finds
in the IR, where
. Therefore, as
, the relevant contributions arise from the
region of integration. The integrated correlator thus has the IR behavior
where we have evaluated the integral at
using a lattice regulator
8, which here amounts to the replacement
. The resulting asymptotic SOS distance is
where the dependence on the RG time
t has been factored out for clarity. Taking into account the volume factor in (
14), this differs by a factor of
from the “intensive” metric of [
44], which is thus finite. At this point, the
asymptotics of the Fourier modes of
h are needed in order to evaluate the IR distance. As we shall see, it seems reasonable to assume that, schematically,
as
, for some,
. Indeed, we shall shortly verify this assumption in the string models that we consider. Then, up to an irrelevant constant,
so that the distance is infinite insofar as
.
As one can see from (
22), the metric of (
15) actually coincides with the SOS metric up to a constant, since multiplying by
leaves
when evaluated at the RG-scale insertion
. This reconstructs the RG flow of the “graviton vertex” operator, as expected from the Callan–Symanzik equation.
4.1. Graviton Vertex from Brane Separation
From the preceding discussion, one can expect that the IR regime of the
configuration be encoded, at least partly, in the NL
M described by the minima of the scalar potential, i.e., mutually commuting matrices. In order to describe the geometry of the resulting manifold, let us begin from the simpler case of the type
model, where the scalars belong to the adjoint representation of
. Mutually commuting Hermitian matrices
can be parametrized in terms of their eigenvalues
and of a unitary matrix
U that simultaneously diagonalizes them according to
. The canonical kinetic-term metric
is thus pulled back to
where
can be interpreted as the transverse position vector of the
kth brane and
is the Maurer–Cartan form. For
, one can express (
26) in terms of the center-of-mass and relative positions
,
, which yields
Integrating out the center-of-mass position does not affect the relative dynamics, while integrating out
U, which encodes the interaction between the branes in this sector, generates an effective action for
that describes fluctuations of the remaining brane. We are interested in the target-space metric, encoded in the kinetic term, at the large brane separation
, which translates into the
asymptotics of (
25). Parametrizing
U with local coordinates
and writing the kinetic term corresponding to the last term of (
27) as
up to a constant, one recognizes a NL
M coupled to a “dilaton”
in the sense of [
102]. Large separations intuitively correspond to the semiclassical limit, since the branes interact weakly, and thus a one-loop analysis is expected to be reliable. In order to see this more clearly, one can choose normal coordinates to perform a covariant background-field expansion about a point,
which we take as the origin of the coordinates. One can then canonically redefine
to absorb the “dilaton” in the quadratic term in the fluctuations, while all the other terms are suppressed in the large
limit. As a result, one can indeed perform a one-loop computation along the lines of [
102]. Integrating by parts, one can recast the quadratic term as
so that the heat-kernel expansion [
102,
103] yields a single local two-derivative term that corrects the field-space metric. This term is proportional to the first heat-kernel coefficient
, and the corrected metric reads
with IR and UV cutoffs
.
For the Sugimoto model, the scalars belong to the antisymmetric representation of
, and mutually commuting matrices of this type can be parametrized by a rotation
and block-diagonal matrices built as linear combinations
, where
and
Then, writing
, the canonical metric
pulls back to
and one can check that the dependence on the center-of-mass and relative coordinates separate, with no mixed terms. The resulting expression for the trace in (
33),
encodes two pull-backs on the hyperplanes
in the space of the antisymmetric matrices, since these combinations do not appear in (
35). Hence, introducing local coordinates
, one arrives at kinetic terms of the type
Once again, one can reabsorb the “dilaton” with a field redefinition
, and integrating out
yields terms that are subleading at a large
. Repeating the above argument for the type
model yields a corrected metric of the form of (
31), albeit with a halved prefactor
in front of the logarithm due to the constraints of (
35).
The scaling
of (
31) can be compared with a bulk calculation. In Poincaré coordinates, the near-horizon
throat warp factor for D1-branes scales as
, and according to our setup, one expects that the background metric be fixed by the D8-branes in the controlled region. As a result, when all of the branes have repelled each other, one expects the correction to the transverse-space metric of the remaining brane located at
to be well-approximated by a linear superposition of the form
for large separation
r, which reproduces the overall scaling
of the correction in (
31).
All in all, comparing with (
25), one finds
from which the asymptotic distance is proportional to the RG time,
where the (regularization-dependent, but calculable) proportionality constant
has been reinstated. As a result, exponential decay in
t in the IR is tantamount to exponential decay in the distance
ℓ at large distances. This asymptotic scaling is crucial in order to establish such a behavior of anomalous dimensions as the distance diverges. We would like to stress that the result of (
39) is not generic in the space of marginally irrelevant deformations; rather, it appears to be specific to our settings arising from string theory.
4.2. Anomalous Dimensions of Scalar Operators
We are now ready to compute anomalous dimensions along the RG flow, using the scheme in (
23). One can then translate the dependence on the RG time
t, which appears consistently with the Callan–Symanzik equation, into a dependence on the distance
ℓ. The resulting behavior turns out to be precisely consistent with the distance conjecture, as we shall see below. Since our approach is holographic, we mostly refer to the CFT counterpart of the distance conjecture [
14,
15], according to which, in two dimensions, the quantity of interest is the gap in the spectrum of scalar primaries
. In order to find a non-trivial scalar gap, one can compactify the target space in a
D-torus with quantized “momenta”
. Then, we shall turn to single-trace higher-spin currents, which ought to describe higher-spin single-particle states in the bulk.
For scalar operators, the first-order conformal perturbation theory suffices to obtain the leading-order asymptotics. The first-order contribution to the correlator of the scalar primaries is
and extracting the divergent part, which is logarithmic for the small
, which have the least decreasing anomalous dimensions, entails separating the contributions of the integration regions
and
, according to
Evaluating the integrals with a lattice regulator, for the small
, one finds the logarithmic divergence
up to a scheme-dependent positive multiplicative constant and a factor of
. The prefactor reflects the tree-level correlator
while the exponent in (
42) reconstructs the one-loop Ricci flow evaluated at the RG time
, as expected from the Callan–Symanzik equation
Therefore the (“matrix” of) anomalous dimensions
, obtained by differentiating the anomalous contribution with respect to
, scales according to
up to a (scheme-dependent) constant, where
denotes the Fourier modes of the (linearized) Ricci tensor. This expression shows that “graviton” zero-modes do not result in anomalous dimensions, which is indeed the case since they are exactly marginal deformations leaving the theory free.
All in all, (
45) highlights an exponential decay of the scalar gap with the distance, on account of (
39). As anticipated, this result supports the distance conjecture, and its various refinements, in the absence of (linear) supersymmetry. In particular, the emergent string scenario is realized in a novel fashion, since the
configuration lies at an infinite distance only in two dimensions.
4.3. Anomalous Dimensions of Higher-Spin Currents
The free-boson CFT defined by the action of (
16) also possesses single-trace (anti-)holomorphic higher-spin currents of the form [
104,
105]
with suitable coefficients
, such that they generate a
algebra. We shall focus on the
singlets
for simplicity, which only exist for even
s [
105], retracing the computation for scalar operators. The leading-order correction to the correlator
now arises at second order in
h. Taking into account normal ordering, for transverse-traceless
h, one finds
at second order in
h, where we have defined
Once again, a lattice regulator is understood, and in order to extract the anomalous dimensions, one ought to extract the (quasi-)logarithmic divergences at the small
k. In order to do so, one can rescale
,
, so that the overall dependence is
. The holomorphic denominator reflects the tree-level result
while the numerator carries the leading quasi-logarithmic divergence
9 and, indeed, reconstructs the one-loop Ricci flow evaluated at the RG time
as in the preceding case. The remainder of (
47) contains, in general, at most, power-like divergences. When the dust settles, the (matrix of) anomalous dimensions
scales, in the IR, according to
up to a (scheme-dependent) constant
, where once again, we have factored out the dependence on the RG time for clarity.
As for (
45), the result in (
50) highlights a decay of the anomalous dimensions, and thus of the masses of higher-spin particles, which is precisely exponential in the distance
ℓ, rather than power-like or exponential in a power of
ℓ. Strictly speaking, this is the case for quantized “momenta”
k, as for the case of scalar operators. However, even without compactifying each Fourier mode of the “graviton vertex”, deformation contributes an exponential decay, albeit the full integral in (
50) will, in general, scale as a negative power of
ℓ in this case. This result lends further support to the various incarnations of the distance conjecture and to the (S-)duality arguments that we have presented in
Section 3, remarkably with broken supersymmetry.
5. Conclusions
The results that we have discussed point to an intriguing mechanism for the consistency of string-scale supersymmetry breaking, as well as a novel realization of a number of swampland proposals. The tunneling cascade that we have discussed in
Section 2 is closely connected to the weak gravity conjecture [
37,
45], and leads to two infinite-distance limits controlled by the flux number
N. As we have discussed in
Section 3, in the regime where ten-dimensional EFT is expected to be reliable
, the absence of scale separation is reflected by the emergence of a KK tower whose mass scale is exponentially suppressed in the “discrete-landscape” distance defined by bubble profiles. The opposite regime, where
, appears strongly coupled within the EFT description, while the holographic description that we have developed features a decoupled free sector at an infinite distance along the dual RG flow.
The free sector restores (super)conformal symmetry, thereby granting stability for the Sugimoto model, and describes a tensionless D-string via conserved single-trace higher-spin currents, whose anomalous dimensions decay in the IR with individual contributions that are exponentially suppressed in the generalized distance, which we have introduced in
Section 4. Tantalizingly, emergent supersymmetry appears deeply tied to the proposal of [
9,
10,
11] via
triality, and points to a peculiar instance of S-duality. As a result, we are led to speculate that string theory with broken supersymmetry contains the ingredients to remain in the landscape, despite numerous instabilities plaguing its EFT counterpart. Although the present work constitutes but a first step in this direction, and more potential obstacles lurk around the corner, we find the results that we have presented encouraging in this respect. The approach that we have undertaken can, in principle, be applied to milder supersymmetric settings, in order to provide further evidence in a controlled setup. The simplest example that comes to mind involves computing distances between type IIB
vacua for different values of
N, using the known backreacted geometry sourced by separated D3-branes. This should match the quantum information distance along the dual RG flow driven by the brane separation mode. This computation is underway, but it would also be interesting to further ground the framework that we have proposed in this paper in the absence of supersymmetry, in order to sharpen the quantitative grasp of the pressing issues that we have discussed. Ultimately, the endgoal of this endeavor is to understand whether string theory can be consistent in the absence of (spacetime) supersymmetry. If the elusive S-duality hinted at in this paper does emerge for the Sugimoto model but not for the 0′B model, and if the latter turned out to have some inconsistency at the non-perturbative level, it would mean that perhaps supersymmetry, even if nonlinearly realized, is needed to some extent. However, no evidence to this effect besides the line of reasoning that we have presented in this paper is available at present. Another promising avenue to explore the consistency of non-supersymmetric string theory is the study of anomalies, of which many new aspects have come to light in the recent years.