Modernizing Wind Load Standards for Ireland
Abstract
1. Introduction
2. Identification of Important Changes Between the Codes of Practice
- Changes in the determination of the structural factor, CsCd;
- The calculation of peak velocity pressures, qp(z).
- Net pressure coefficients, focusing on the effects of the proposed global pressure coefficients, Cpeg;
- Pressure coefficients for roofs.
- Pressure coefficients for façade elements.
- The treatment of upwind terrain transitions.
3. Case Studies for Comparison
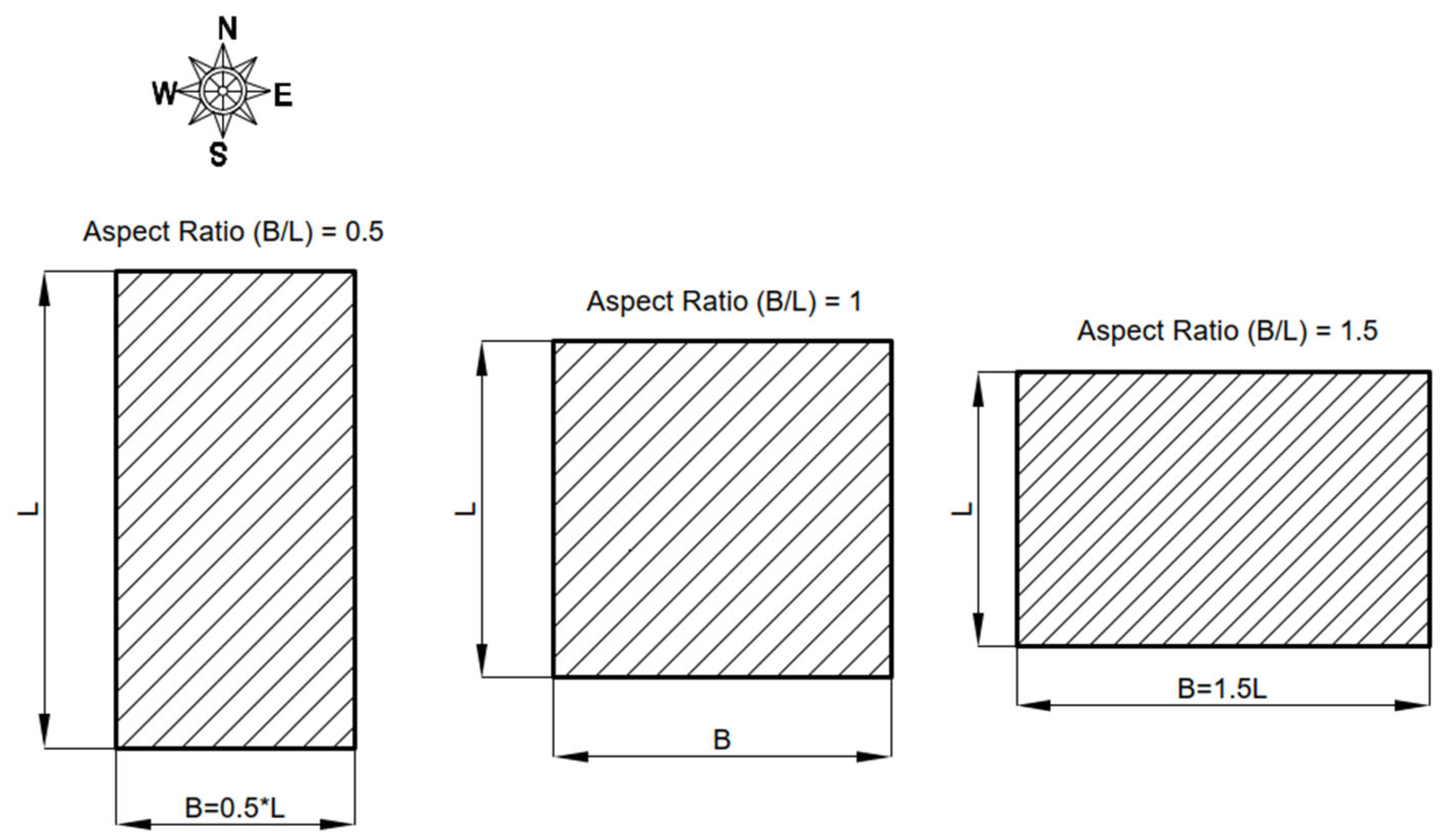
3.1. Building Types
3.2. Site Locations
3.3. Data Extraction and Interpolation from Code Charts and Tables
4. Structural Factor (CsCd)
4.1. Introduction
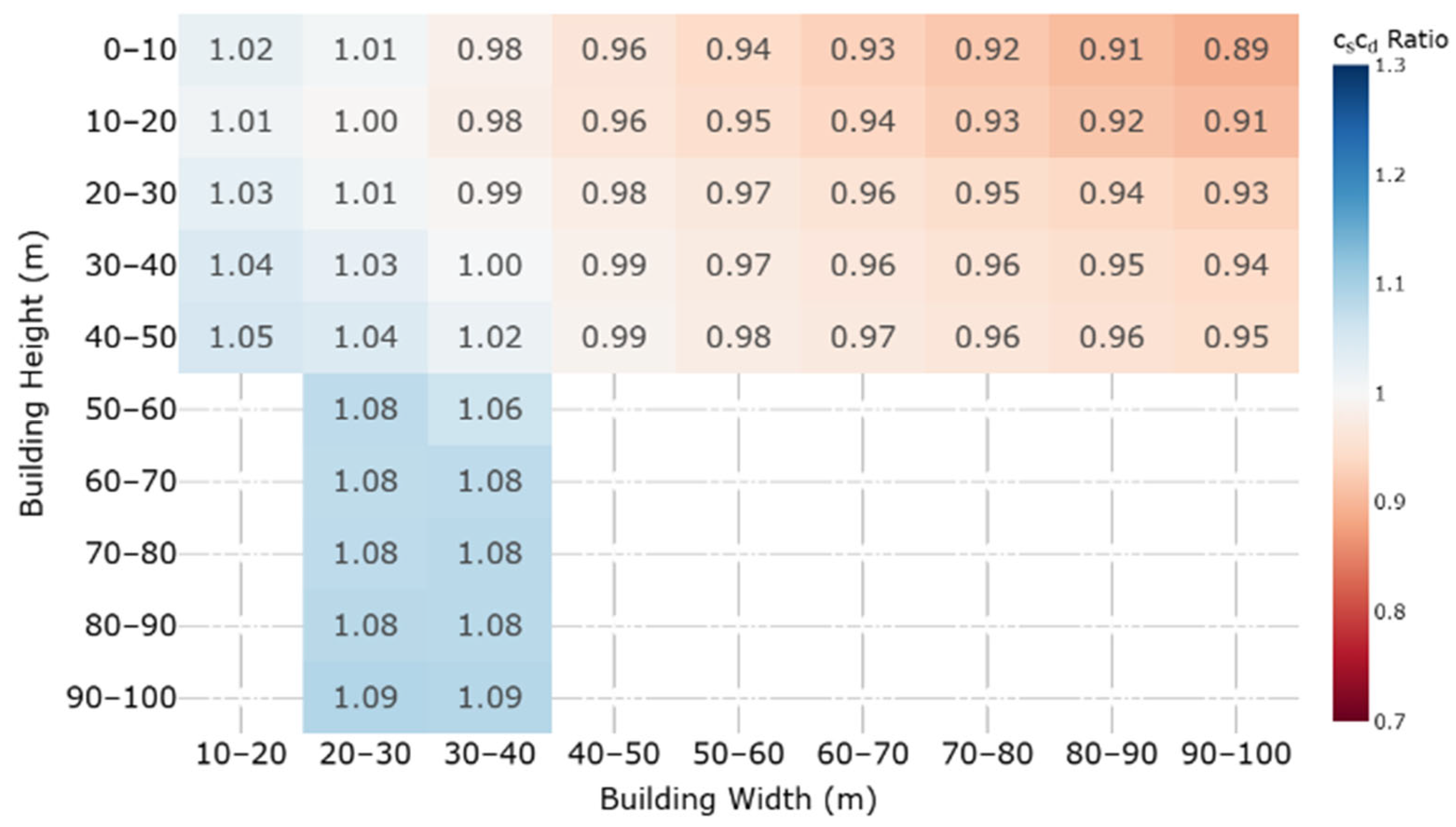
4.2. Comparison of CsCd Values: City Sites
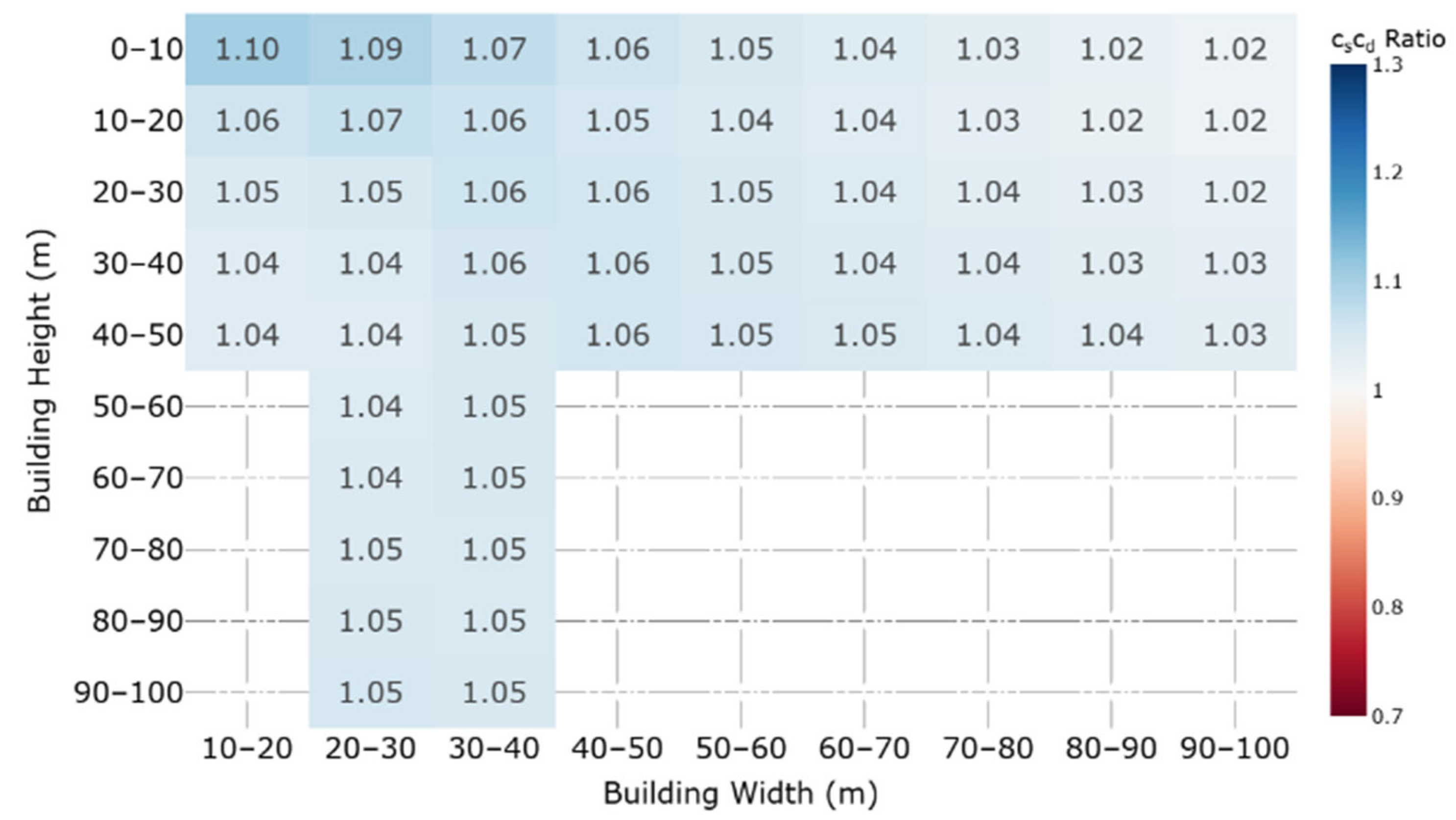
4.3. Comparison of CsCd Values: Country Sites
5. Pressure Coefficients
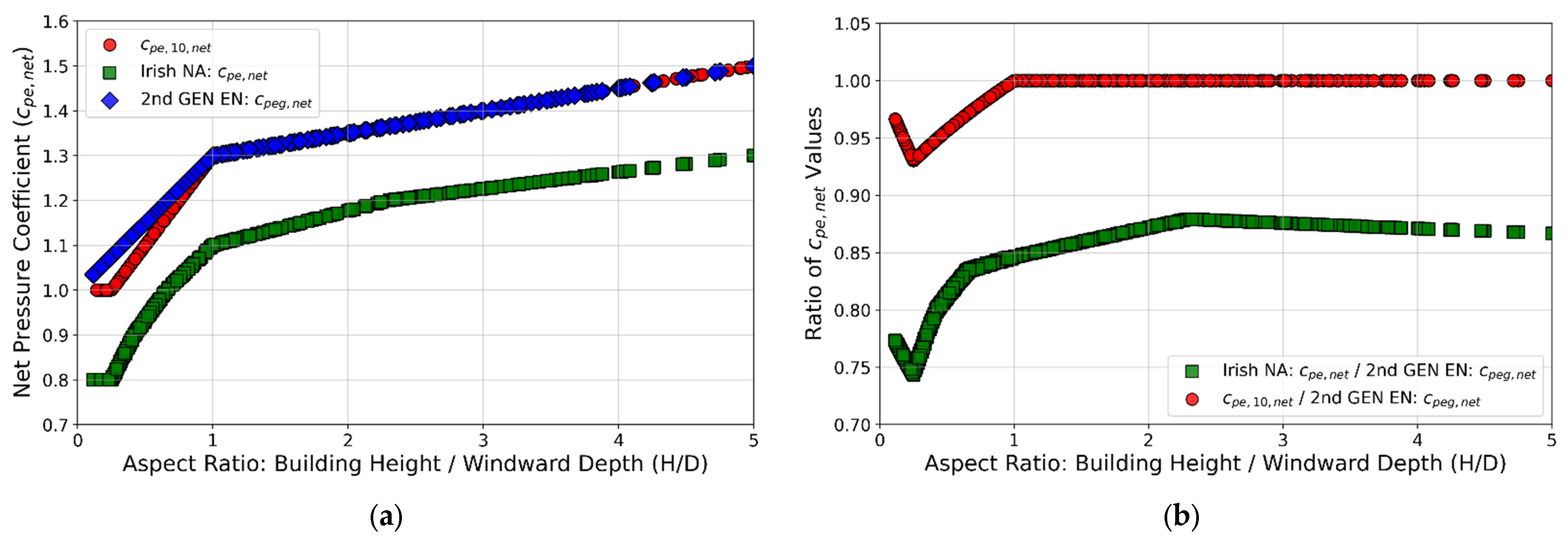
5.1. Net Pressure Coefficients
5.2. Flat Roofs
5.3. Façade Elements
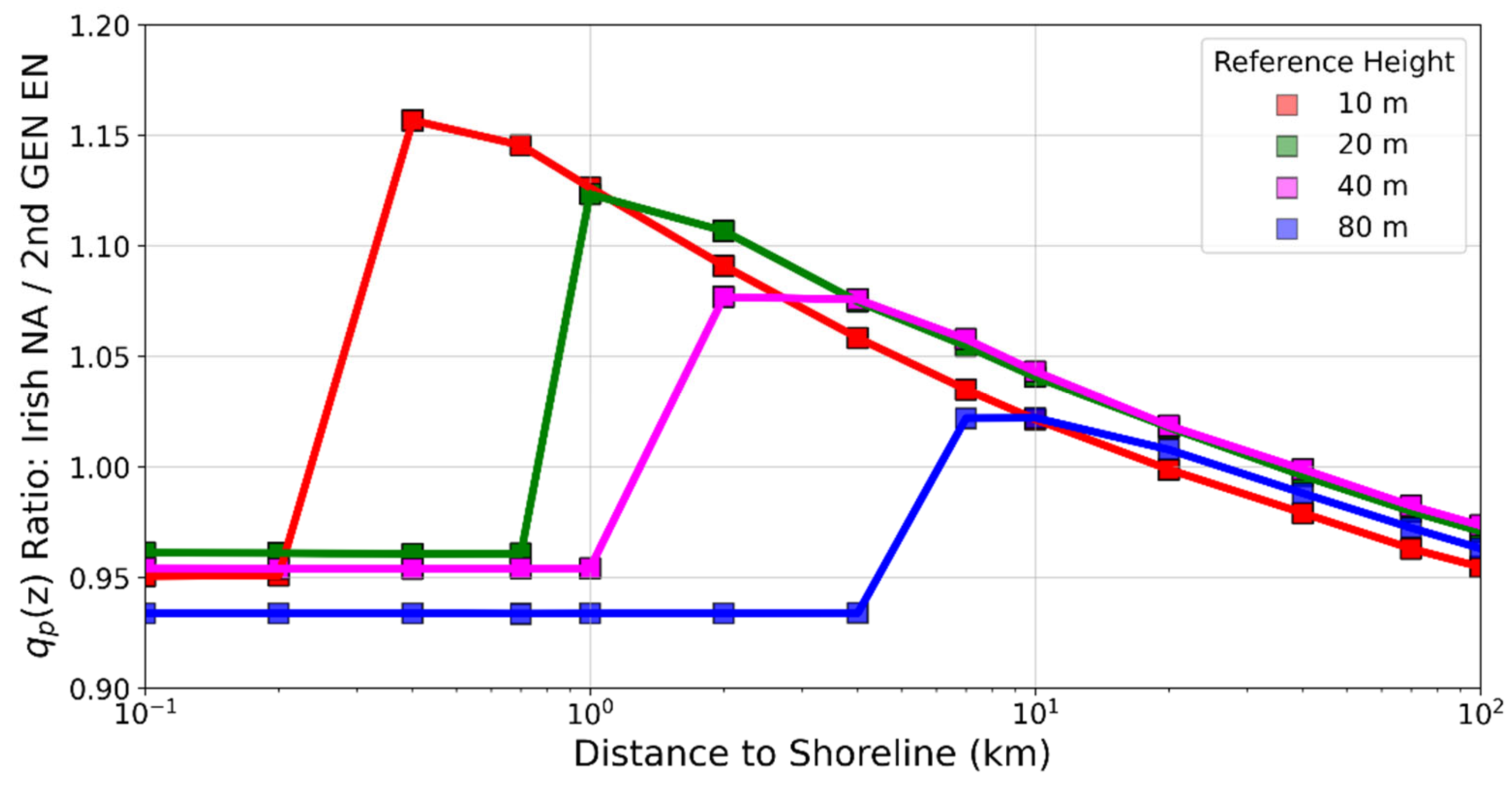
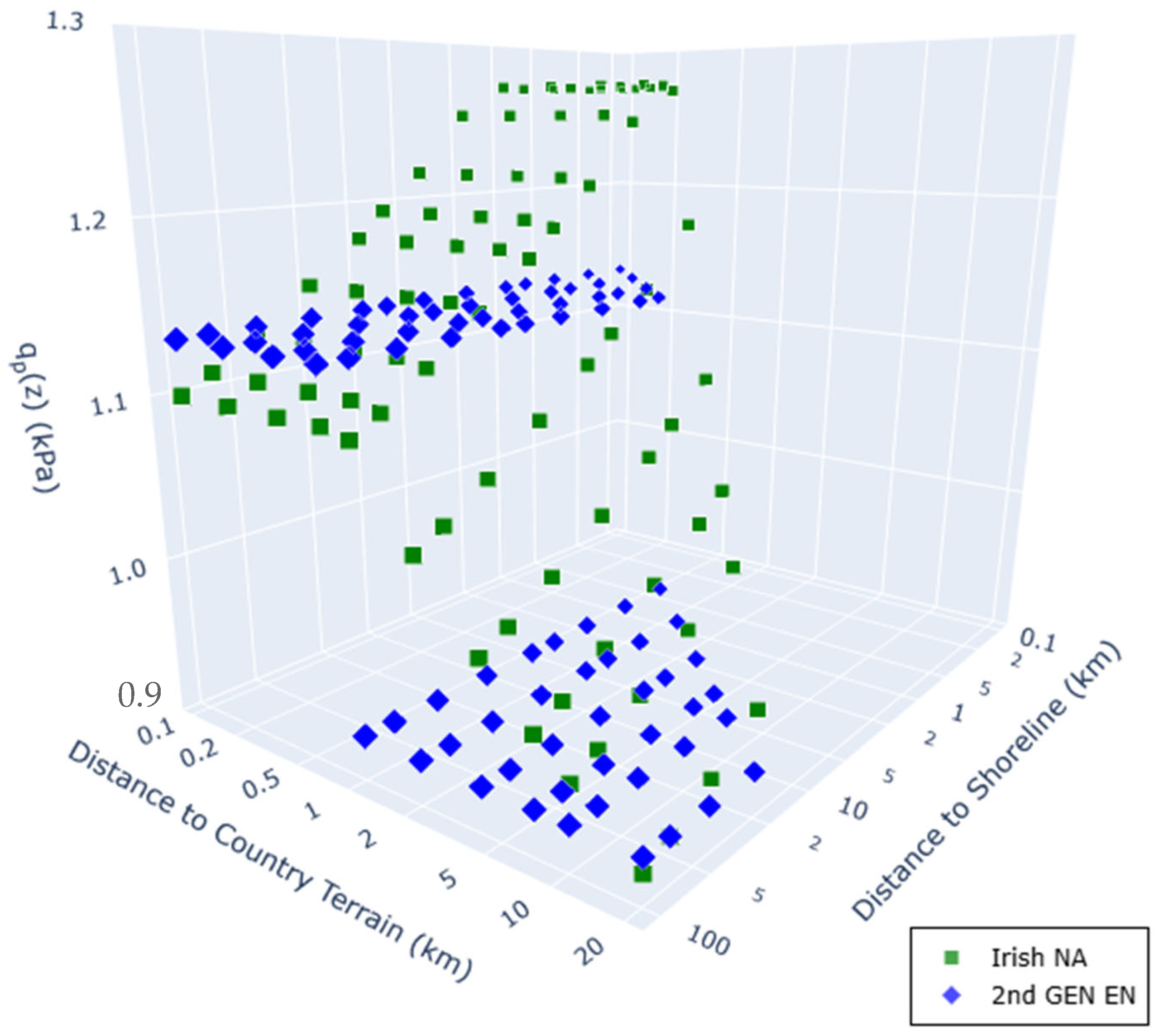
6. Terrain Roughness Transitions and Peak Velocity Pressure
6.1. Peak Velocity Pressure Profiles
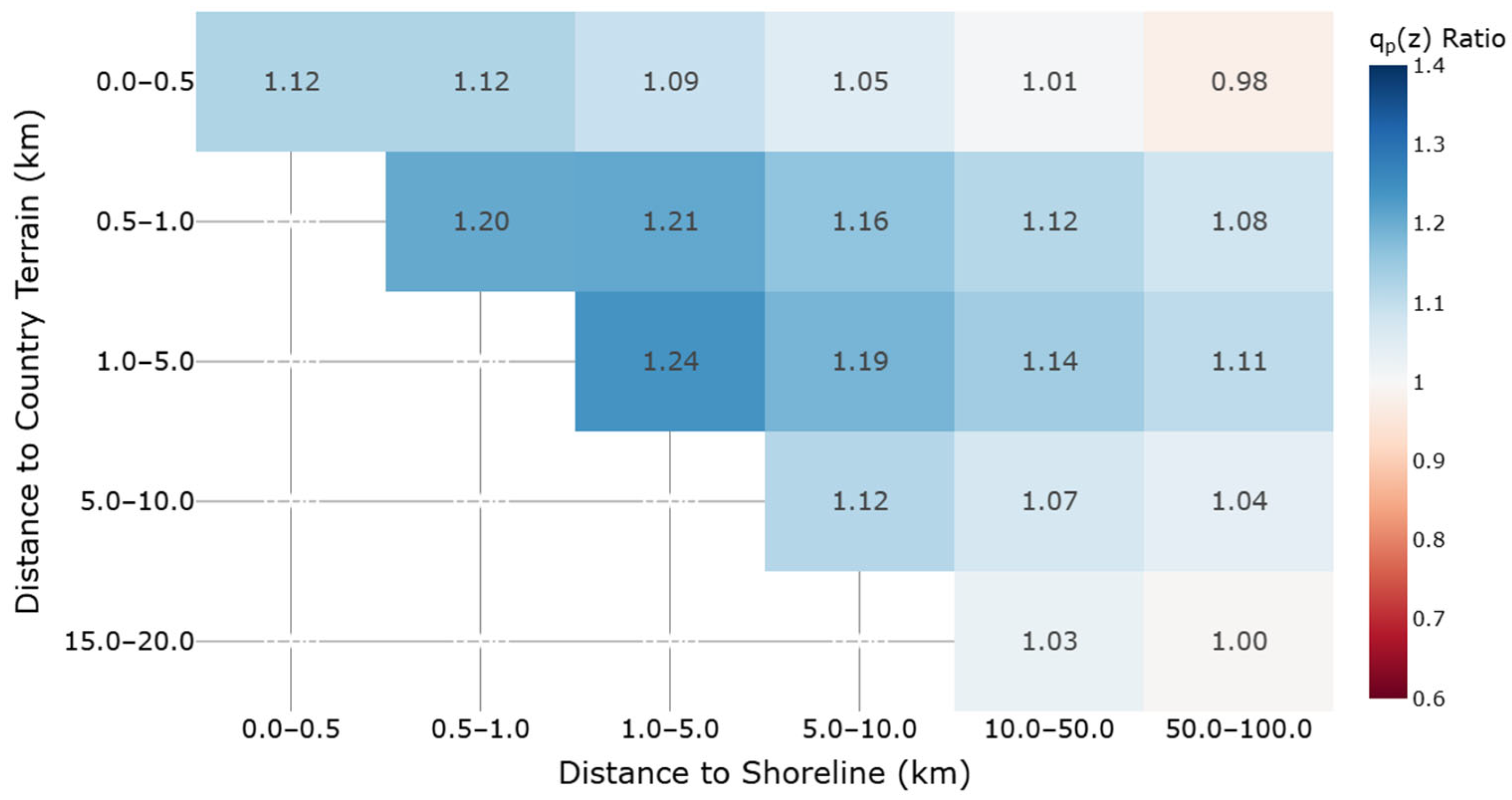
6.2. Upwind Terrain Transitions: Country Sites
6.3. Upwind Terrain Transitions: City Sites
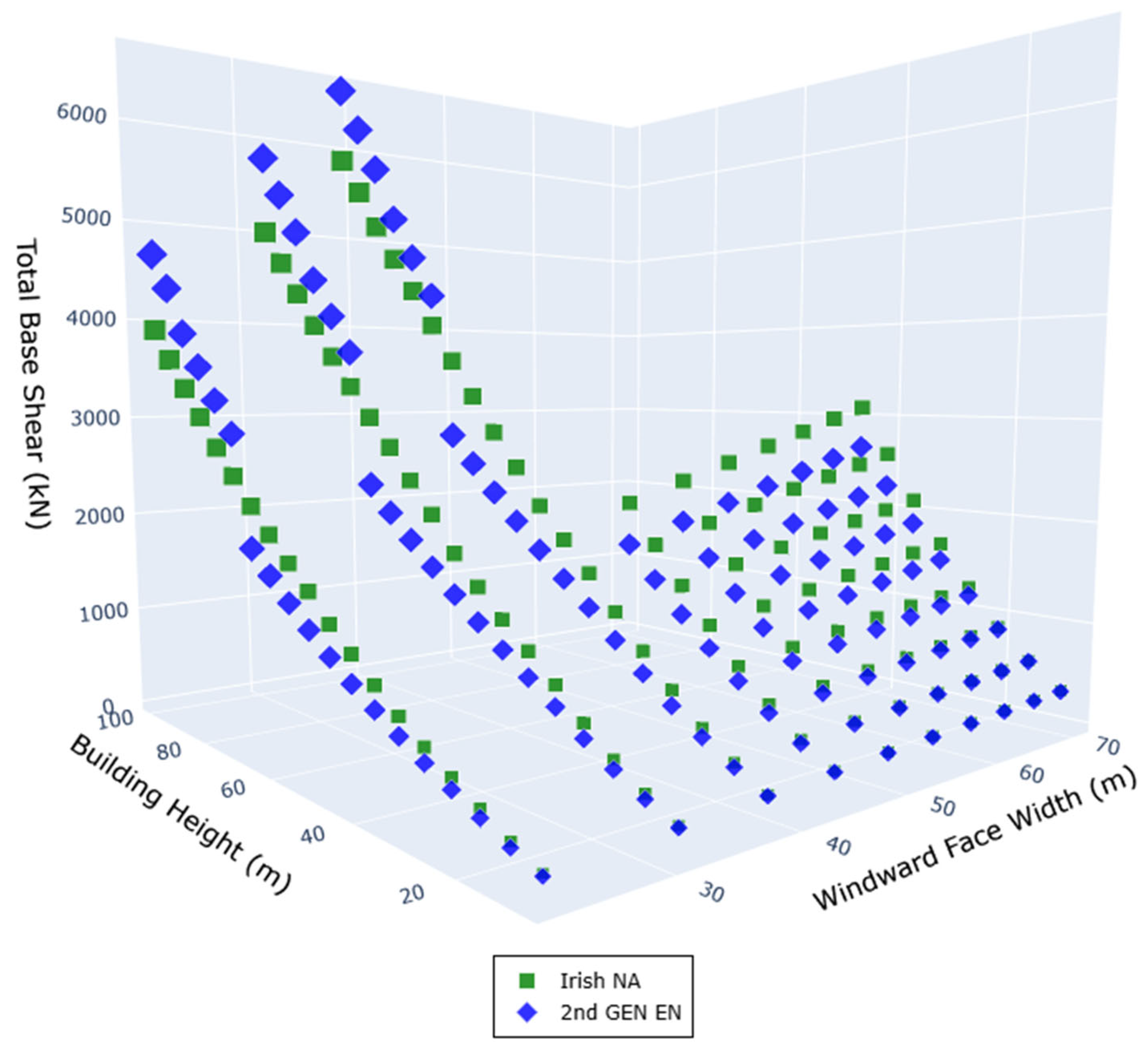
7. Wind Loads
7.1. City Sites
7.2. Country Sites
7.3. Conceptual Implications of Discrete Terrain Transitions
7.4. Historical Context and Comparison with First-Generation Transition
7.5. Practical Structural Implications for Design
8. Conclusions
9. Recommendations for the National Annex Drafting Committee and Irish Practitioners
- Issue national guidance to smooth terrain-threshold discontinuities by prescribing exposure assessment and sensitivity bracketing across the xs rule, sector-based fetch mapping and a conservative continuity rule for mixed exposures.
- Clarify when to use Cpeg versus Cpe,10 for global actions; for low rise, large plan industrial forms (aspect ratios < 1), verify with Cpe,10 where Cpeg proves more conservative (up to ~7% in these cases).
- Either retain Cpe,10 for façade areas > 1 m2 as an acceptable method or set criteria for adopting logarithmic interpolation, noting typical ~5% higher panel pressures and procurement and fixings implications.
- Provide guidance for urban sites influenced by smoother upwind sectors, noting > 20% qp(z) and 30–45% base shear differences at continuities; prioritize consistency across adjacent plots and phases.
- Clarify whether to retain the 0.85 lower bound for chart-derived structural factors or permit the detailed method without it where large windward widths would otherwise be penalized.
- For flat roof coefficients (normative annex), provide national advice on parapets, zone application, and verification to avoid unintended reductions in safety margins as practice moves away from BS 6399-2 [1].
- Near terrain thresholds, run sensitivity checks with the 2nd GEN EN rule, bracket sector distances, and adopt the governing envelope for qp(z), net/global coefficients, and base shear.
- For low-rise industrial buildings in rural terrain, budget for ~30% higher base shear and proportional increases in bracing, section moduli, and foundation dimensions.
- On urban sites downstream of smoother terrain (e.g., Cork, Waterford, Limerick), anticipate 30–45% higher base shear for common 3–5-storey forms and plan corresponding upsizing unless rougher exposure can be robustly justified.
- For 1–10 m2 façade elements, plan for logarithmic interpolation and allow ~5% higher design pressures for common 4–6 m2 panels.
- For flat roofs with parapets, note that 2nd GEN EN coefficients are lower than BS 6399-2 [1]; verify any increases in purlin spacing or reductions in fastening against performance in Zones F and G.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EN | European Norm |
| CFD | Computational Fluid Dynamics |
| NBCC | National Building Code of Canada |
| ASCE | American Society of Civil Engineers |
| AIJ | Architectural Institute of Japan |
| ISO | International Standards Organization |
| AS/NZS | Australian/New Zealand Standards |
| NA | National Annex (local adaptions of the Eurocode for Ireland) |
| BS | British Standard |
| NAO | North Atlantic Oscillation |
| 2nd GEN EN | Second generation Eurocode |
| CsCd | Structural factor |
| qp(z) | Peak velocity pressure at height z (kPa) |
| Cpeg | Global external pressure coefficient (dimensionless) |
| Cpe,10 | External pressure coefficient for areas > 10 m2 (dimensionless) |
| Cpe,1 | External pressure coefficient for areas < 1 m2 (dimensionless) |
| Cpi | Internal pressure coefficient (dimensionless) |
| Zo | Surface roughness length (m) |
| B | Plan breadth (windward width)—(m) |
| L | Plan length (perpendicular to B)—(m) |
| H/D | Aspect ratio |
| B/L | Plan aspect ratio—dimensionless |
| Z | Height above ground where quantities are evaluated (m) |
| Vm(z) | Mean wind speed at height z (m/s) |
| Vb | Basic wind speed (m/s) |
| Vb,0 | Reference basic wind speed (m/s) |
| Cdir | Directional factor (dimensionless) |
| Cseason | Seasonal factor (dimensionless) |
| Cprob | Probability factor (dimensionless) |
| Cr,(z) | Roughness factor at height z (dimensionless) |
| Co(z) | Orography factor at height z (dimensionless) |
| Iv(z) | Turbulence intensity at height z (dimensionless) |
| k1 | Terrain/turbulence parameter (dimensionless) |
| Kp | Peak factor used in gust formulation (dimensionless |
| Cs | Size (lack-of-correlation) factor (dimensionless) |
| Cd | Dynamic factor (dimensionless). |
| Csd | Structural factor in 2nd GEN EN (dimensionless). |
| CsCd | Structural factor (size × dynamic) in Irish NA (dimensionless). |
| A | Gross steel member area (brace)—mm2 |
| h0 | Reference height parameter in xs expression (m). |
| xs | Threshold fetch distance for terrain-change consideration (m). |
| x0 | Length parameter in xs expression (1000) (m). |
| ρ | Air density (taken as 1.25) (kg/m3). |
| qmax | Maximum bearing pressure under foundations (kPa). |
| calt | Altitude factor (dimensionless). |
| cseason | Seasonal factor (dimensionless). |
| cprob | Probability factor (dimensionless). |
| cdir | Directional factor (dimensionless). |
| Vb,map | Value of fundamental basic wind velocity (m/s). |
| vb | Basic wind velocity (m/s). |
| qb | Basic velocity pressure (kPa). |
| ce(z) | Exposure factor at height z (dimensionless). |
| ce,T(z) | Exposure correction factor for sites in town terrain at height z (dimensionless). |
| Aref | Reference area for wind force calculation (m2). |
| kr | Terrain factor (dimensionless). |
| z0 | Surface roughness length (m). |
| z0,II | Surface roughness length for terrain category II terrain (m). |
| vp(z) | Peak wind velocity at height z (m/s). |
| d | Depth of the building plan measured parallel to the wind direction |
| b | Breadth of the building plan measured perpendicular to the wind direction |
| e | Zone-extent parameter used to size the roof perimeter zones |
Appendix A
- Irish NA
- 2nd GEN EN
References
- BS6399-2:1997; Loading for Buildings—Part 2: Code of Practice for Wind Loads. British Standard Institute: London, UK, 1997.
- Arup. Wind Loading Calibration Study; Arup: London, UK, 2009. [Google Scholar]
- Holmes, J.D. Wind Loading of Structures; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Davenport, A.G. The application of statistical concepts to the wind loading of structures. Proc. Inst. Civ. Eng. 1961, 19, 449–472. [Google Scholar] [CrossRef]
- Simiu, E.; Yeo, D. Wind Effects on Structures: Modern Structural Design for Wind; John Wiley and Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Kareem, A.; Zhou, Y. Gust loading factor—Past, present and future. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1301–1328. [Google Scholar] [CrossRef]
- Zhou, Y.; Kareem, A. Gust loading factor: New model. J. Struct. Eng. 2001, 127, 168–175. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, B.; Wu, Y.; Tamura, Y. Wind-induced response and equivalent static wind load of long-span roof structures by combined Ritz-proper orthogonal decomposition method. J. Struct. Eng. 2013, 139, 997–1008. [Google Scholar] [CrossRef]
- Pierre, L.S.; Kopp, G.; Surry, D.; Ho, T. The UWO contribution to the NIST aerodynamic database for wind loads on low buildings: Part 2. Comparison of data with wind load provisions. J. Wind Eng. Ind. Aerodyn. 2005, 93, 31–59. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Alrawashdeh, H. Wind loads on buildings: A code of practice perspective. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104338. [Google Scholar] [CrossRef]
- Uematsu, Y.; Isyumov, N. Wind pressures acting on low-rise buildings. J. Wind Eng. Ind. Aerodyn. 1999, 82, 1–25. [Google Scholar] [CrossRef]
- Chen, F.; Zhu, Y.; Wang, W.; Shu, Z.; Li, Y. A review on aerodynamic characteristics and wind-induced response of flexible support photovoltaic system. Atmosphere 2023, 14, 731. [Google Scholar] [CrossRef]
- Tamura, Y.; Kareem, A.; Solari, G.; Kwok, K.; Holmes, J.D.; Melbourne, W.H. Aspects of the dynamic wind-induced response of structures and codification. Wind Struct. 2005, 8, 251–268. [Google Scholar] [CrossRef]
- Cook, N.J. The Deaves and Harris ABL model applied to heterogeneous terrain. J. Wind Eng. Ind. Aerodyn. 1997, 66, 197–214. [Google Scholar] [CrossRef]
- Khanduri, A.; Stathopoulos, T.; Bédard, C. Wind-induced interference effects on buildings—A review of the state-of-the-art. Eng. Struct. 1998, 20, 617–630. [Google Scholar] [CrossRef]
- Caracoglia, L.; Crisman, D.; Noè, S. Wind Pressure and Load Analysis on Large Building Roofs: Applicability of Database-Assisted Design to Eurocode 1 and Italian Standards. J. Struct. Eng. 2025, 151, 04025193. [Google Scholar] [CrossRef]
- Zheng, X.; Montazeri, H.; Blocken, B. CFD simulations of wind flow and mean surface pressure for buildings with balconies: Comparison of RANS and LES. Build. Environ. 2020, 173, 106747. [Google Scholar] [CrossRef]
- Fernández-Cabán, P.L.; Masters, F.J.; Phillips, B.M. Predicting roof pressures on a low-rise structure from freestream turbulence using artificial neural networks. Front. Built Environ. 2018, 4, 68. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.-H.; Kopp, G.A. A method to estimate peak pressures on low-rise building models based on quasi-steady theory and partial turbulence analysis. J. Wind Eng. Ind. Aerodyn. 2021, 218, 104785. [Google Scholar] [CrossRef]
- ASCE/SEI 7-22; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2022.
- PrEN 1991-1-4; Second Generation Eurocode Draft: Eurocode 1: Actions on Structures—Part 1–4: General Actions—Wind Actions. CEN: Brussels, Belgium, 2025.
- National Research Council of Canada. National Building Code of Canada 2020; NRC: Ottawa, ON, Canada, 2020. [Google Scholar]
- Architectural Institute of Japan. Recommendations for Loads on Buildings; AIJ: Tokyo, Japan, 2015. [Google Scholar]
- AS/NZS 1170.2:2021, Amd 1:2023; Structural Design Actions—Part 2: Wind Actions. Standards Australia: Sydney, Australia; Standards New Zealand: Wellington, New Zealand, 2021.
- Zhou, Y.; Kijewski, T.; Kareem, A. Along-wind load effects on tall buildings: Comparative study of major international codes and standards. J. Struct. Eng. 2002, 128, 788–796. [Google Scholar] [CrossRef]
- Jayasundara, H.; Koliyabandara, S.; Wijesundara, K. Wind loads on tall buildings: A comparative study of the international wind codes and numerical simulation. Eng. J. Inst. Eng. Sri Lanka 2018, 51, 31–45. [Google Scholar] [CrossRef]
- Weerasuriya, A.; Jayasinghe, M. Wind loads on high-rise buildings by using five major international wind codes and standards. Eng. J. Inst. Eng. Sri Lanka 2014, 47, 13–25. [Google Scholar] [CrossRef]
- Lee, S.; Kim, S.; Kwon, S.-D. A Comparative Study of Wind Tunnel Tests and Design Codes in Evaluation of Along-Wind Effects on Towers. Shock Vib. 2021, 2021, 8818057. [Google Scholar] [CrossRef]
- Moore, N.; Keenahan, J. Wind Forces on Medium-Span Bridges: A Comparison of Eurocode 1 Part 4 and Computational Fluid Dynamics. CivilEng 2022, 3, 794–808. (In English) [Google Scholar] [CrossRef]
- Outten, S.; Sobolowski, S. Extreme wind projections over Europe from the Euro-CORDEX regional climate models. Weather Clim. Extrem. 2021, 33, 100363. [Google Scholar] [CrossRef]
- Donat, M.; Leckebusch, G.; Wild, S.; Ulbrich, U. Future changes in European winter storm losses and extreme wind speeds inferred from GCM and RCM multi-model simulations. Nat. Hazards Earth Syst. Sci. 2011, 11, 1351–1370. [Google Scholar] [CrossRef]
- Haylock, M. European extra-tropical storm damage risk from a multi-model ensemble of dynamically-downscaled global climate models. Nat. Hazards Earth Syst. Sci. 2011, 11, 2847–2857. [Google Scholar] [CrossRef]
- Outten, S.; Esau, I. Extreme winds over Europe in the ENSEMBLES regional climate models. Atmos. Chem. Phys. 2013, 13, 5163–5172. [Google Scholar] [CrossRef]
- Nolan, P.; Lynch, P.; McGrath, R.; Semmler, T.; Wang, S. Simulating climate change and its effects on the wind energy resource of Ireland. Wind Energy 2012, 15, 593–608. [Google Scholar] [CrossRef]
- Pinto, J.G.; Raible, C.C. Past and recent changes in the North Atlantic oscillation. Wiley Interdiscip. Rev. Clim. Change 2012, 3, 79–90. [Google Scholar] [CrossRef]
- Irish National Annex to EN1991-1-4; NSAI: Dublin, Ireland, 2010.
- EN 1991-1-4:2005; Eurocode 1: Actions on Structures—Part 1–4: General Actions—Wind Actions. CEN: Brussels, Belgium, 2005.
- Department of Housing. Building Regulations 2014—Technical Guidance Document K—Stairways, Ladders, Ramps and Guards; Department of Housing, Local Government and Heritage: Dublin, Ireland, 2014. [Google Scholar]
- Dyrbye, C.; Hansen, S.O. Static Wind Load. In Wind Loads on Structures; European Union—The CEN: Brussels, Belgium, 1996; Chapter 4; pp. 49–73. [Google Scholar]
- Davenport, A.G. Note on the distribution of the largest value of a random function with application to gust loading. Proc. Inst. Civ. Eng. 1964, 28, 187–196. [Google Scholar] [CrossRef]
- PD6688-1-4:2015; Background Information to the National Annex to BS EN 1991-1-4 and Additional Guidance. British Standard Institute: London, UK, 2015.
- Harris, R. The structure of strong winds. In Proceedings of the CIRIA Conference on Wind Engineering in the Eighties, Edinburgh, UK, 12–13 November 1981. [Google Scholar]
- EN 1993-1-1:2022; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2022.
- EN 1997-1:2024; Eurocode 7: Geotechnical Design—Part 1: General Rules. European Committee for Standardization (CEN): Brussels, Belgium, 2024.

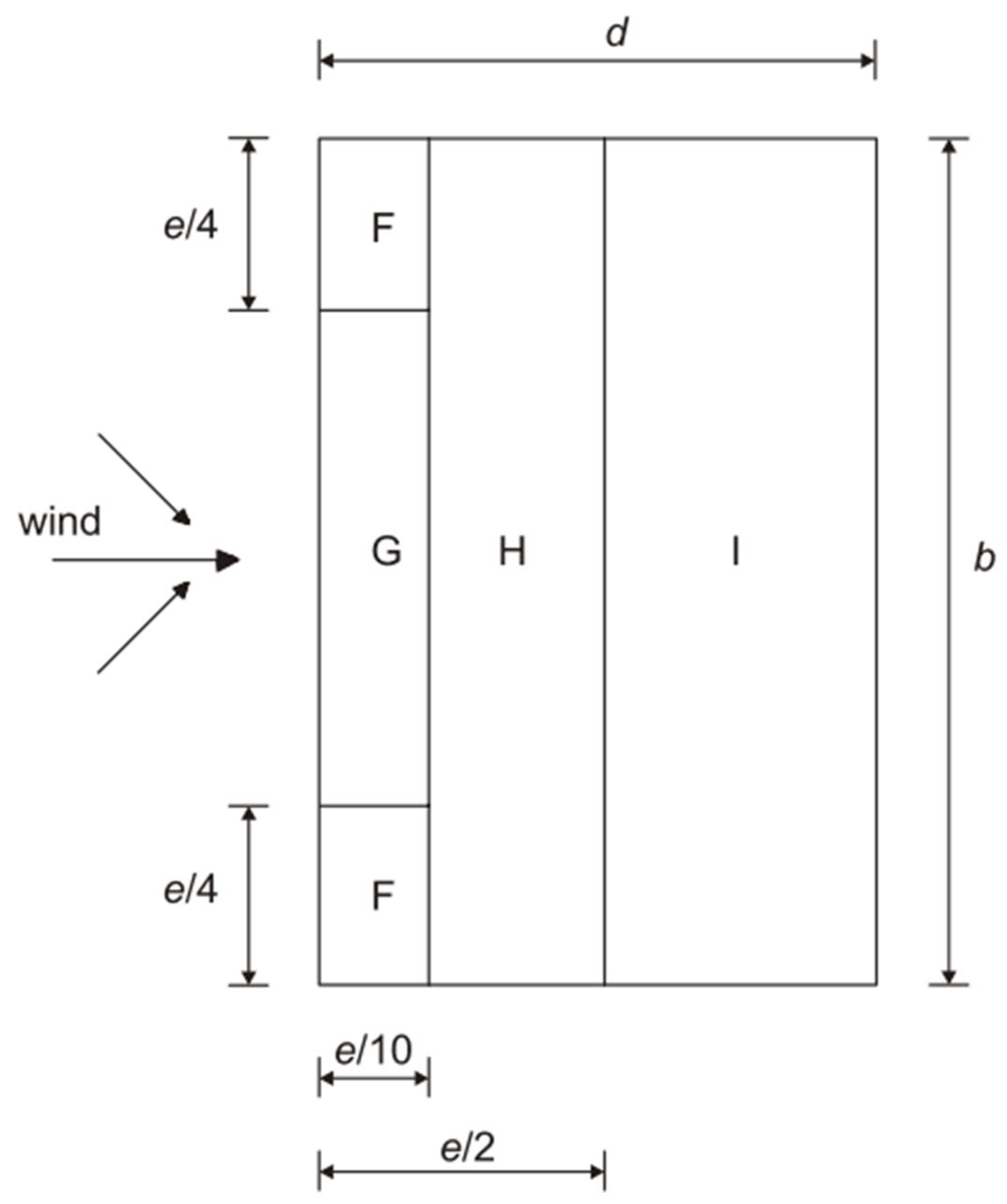
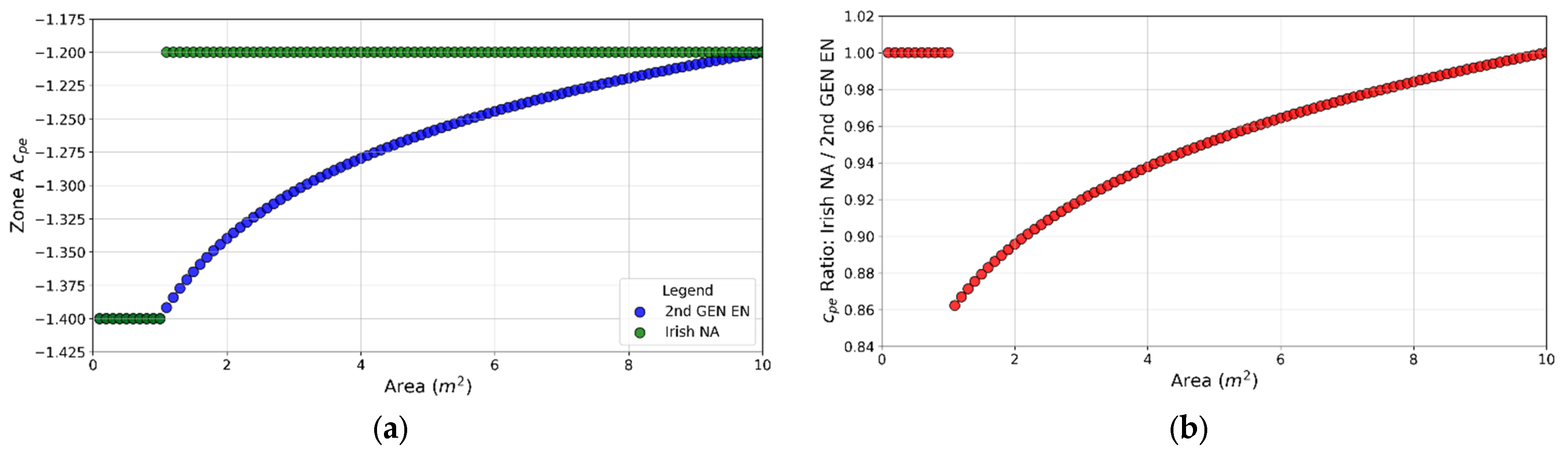
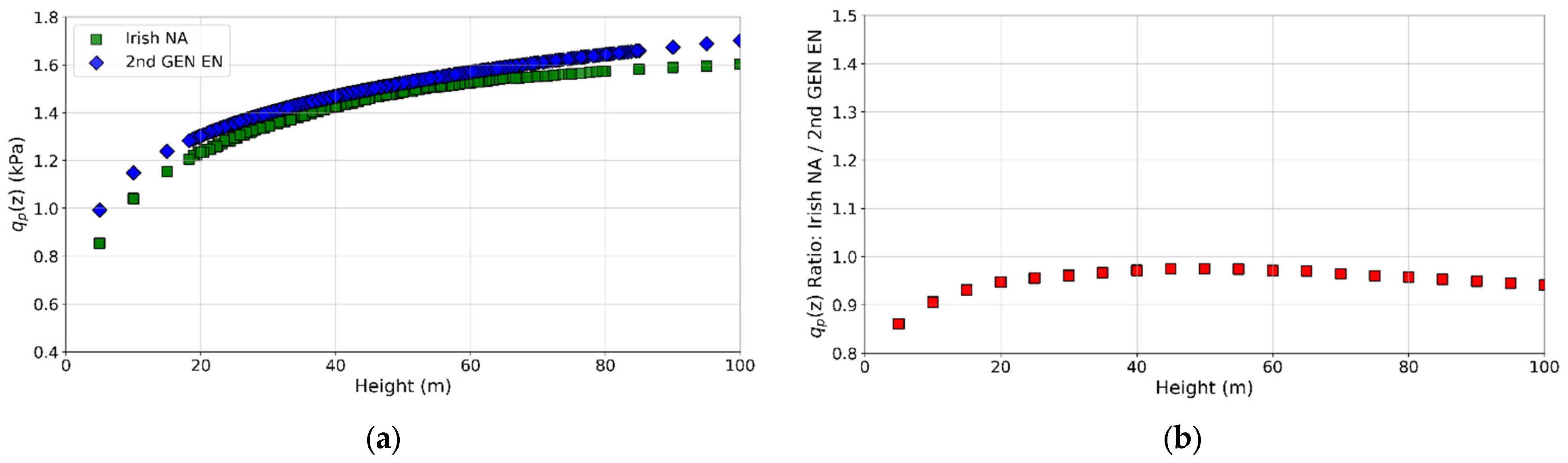
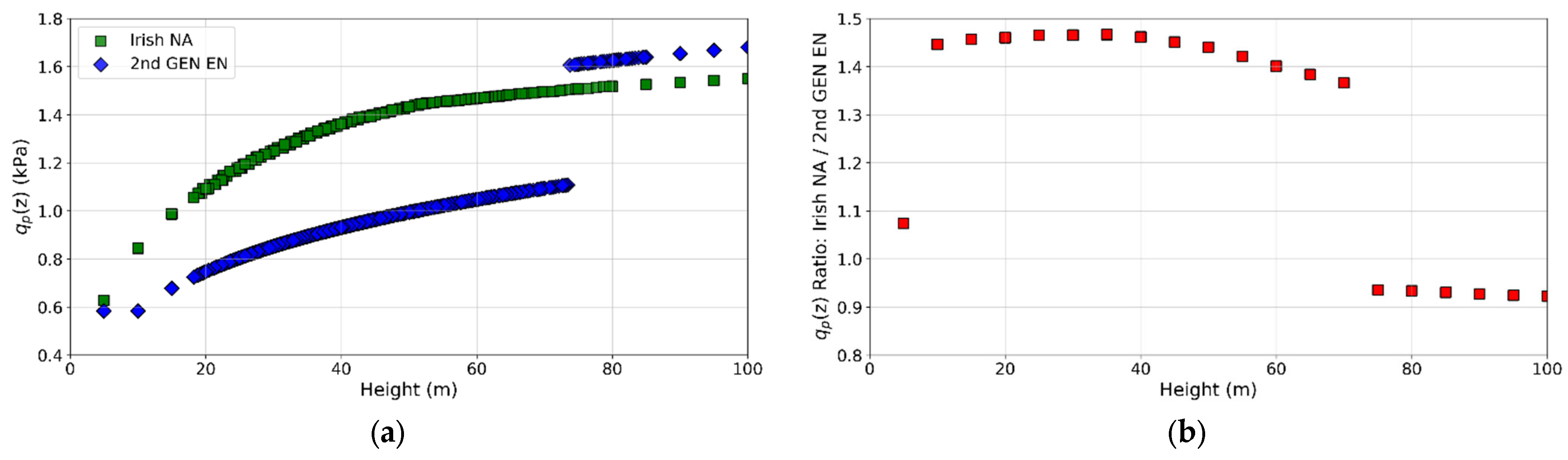
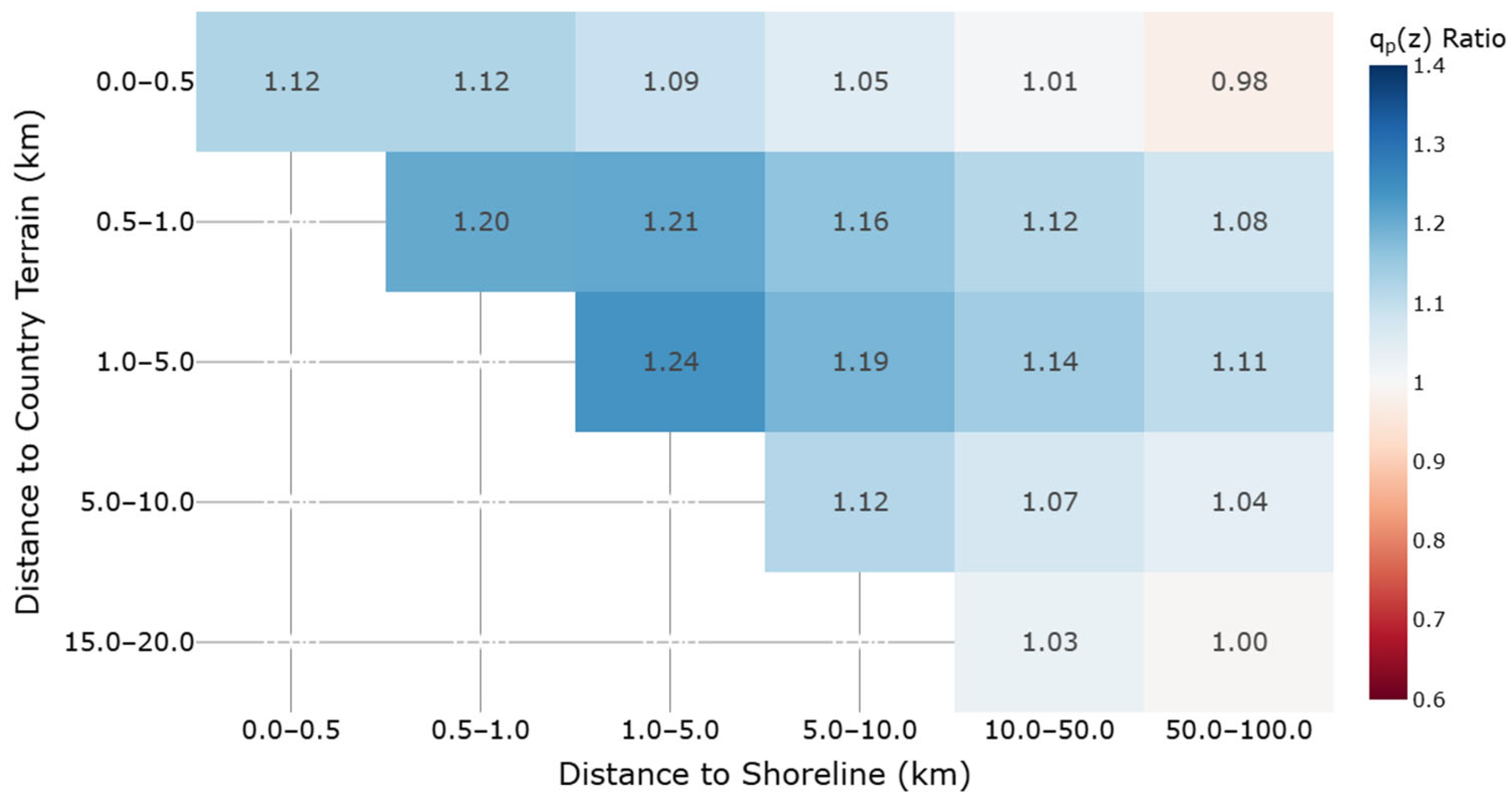

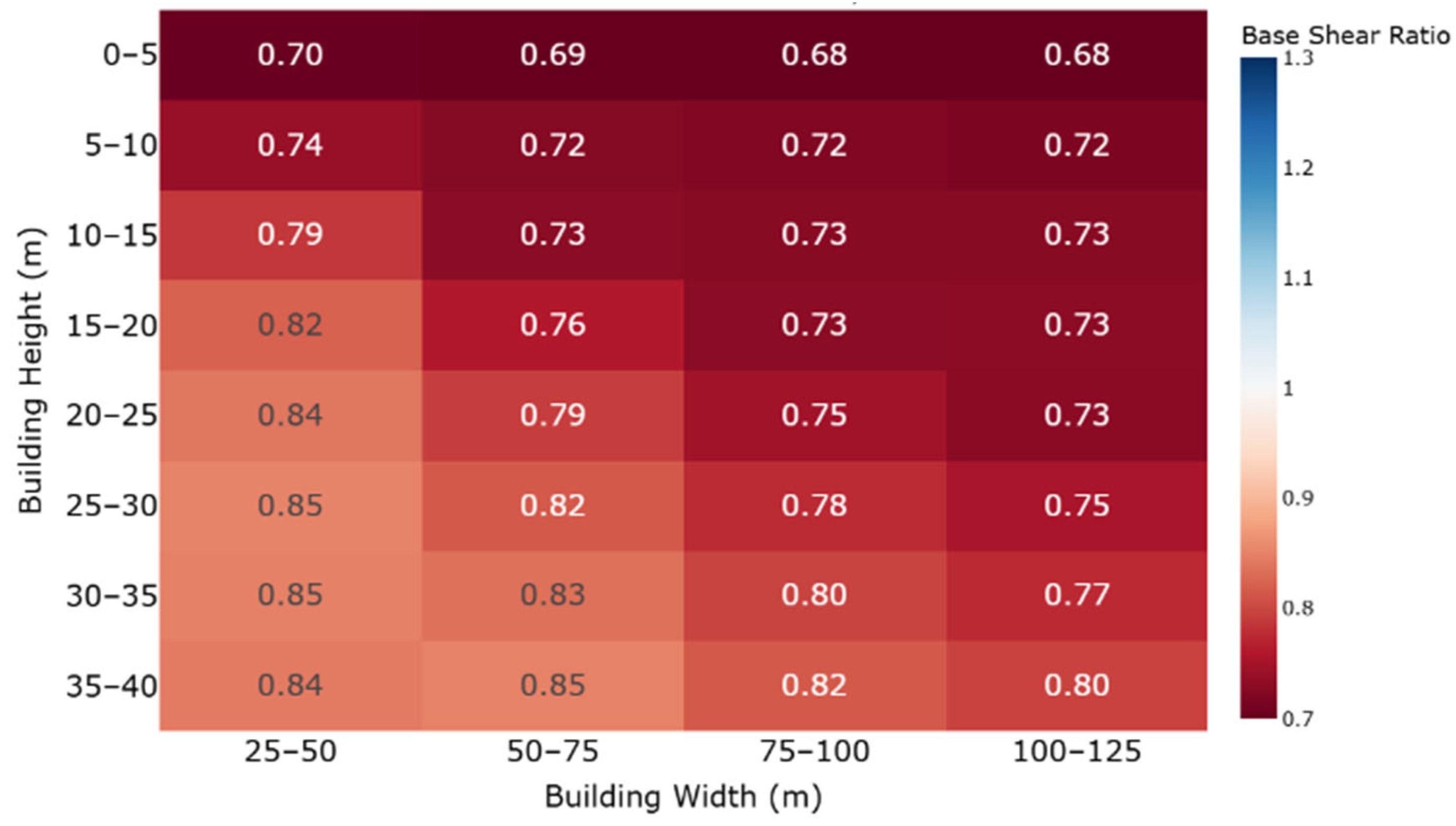
| Location | Site | Critical Wind Direction | Distance to Shoreline (km) | Distance to Town Edge (km) | Site Terrain Category | Smoother Upstream Terrain Category |
|---|---|---|---|---|---|---|
| Cork | City | West | 130 | 0.2 | 4 | 3 |
| Waterford | City | East | 9 | 45 | 4 | 0 |
| Dublin | City | East | 4.5 | 4.5 | 4 | 0 |
| Limerick | City | West | 70 | 0.4 | 4 | 3 |
| Galway | City | South | 1.7 | 1.7 | 3 | 0 |
| Cork | Country | South | 45 | 1 | 0 | |
| Waterford | Country | South | 9 | 1 | 0 | |
| Dublin | Country | East | 6.8 | 1 | 0 | |
| Limerick | Country | West | 70 | 2 | 1 | |
| Galway | Country | East | 150 | 2 | 1 |
| Site | Max. Ratio | Min. Ratio | Ratios > 1 | Ratios < 1 | ||
|---|---|---|---|---|---|---|
| % of Domain | Mean | % of Domain | Mean | |||
| Cork | 1.56 | 1.08 | 100 | 1.22 | 0 | |
| Waterford | 1.63 | 1.00 | 97 | 1.20 | 3 | 0.99 |
| Dublin | 1.47 | 0.92 | 74 | 1.42 | 26 | 0.94 |
| Limerick | 1.56 | 1.04 | 100 | 1.22 | 0 | |
| Galway | 1.30 | 0.92 | 61 | 1.22 | 39 | 0.94 |
| Height (m) | Max. Ratio | Min. Ratio | Ratios > 1 | Ratios < 1 | ||
|---|---|---|---|---|---|---|
| % of Domain | Mean | % of Domain | Mean | |||
| 10 | 1.4 | 0.95 | 82 | 1.13 | 18 | 0.97 |
| 20 | 1.37 | 0.97 | 84 | 1.13 | 16 | 0.98 |
| 40 | 1.27 | 0.97 | 82 | 1.10 | 18 | 0.98 |
| 80 | 1.17 | 0.96 | 75 | 1.04 | 25 | 0.97 |
| Site | Max. Ratio | Min. Ratio | Ratios > 1 | Ratios < 1 | ||
|---|---|---|---|---|---|---|
| % of Domain | Mean | % of Domain | Mean | |||
| Cork | 1.38 | 0.92 | 62 | 1.05 | 38 | 0.98 |
| Waterford | 1.45 | 0.81 | 11 | 1.25 | 89 | 0.91 |
| Dublin | 1.30 | 0.84 | 68 | 1.19 | 32 | 0.93 |
| Limerick | 1.27 | 0.93 | 79 | 1.04 | 21 | 0.98 |
| Galway | 1.17 | 0.81 | 21 | 1.09 | 79 | 0.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cunningham, D.; Ramponi, R.; MacReamoinn, R.; Keenahan, J. Modernizing Wind Load Standards for Ireland. Wind 2025, 5, 26. https://doi.org/10.3390/wind5040026
Cunningham D, Ramponi R, MacReamoinn R, Keenahan J. Modernizing Wind Load Standards for Ireland. Wind. 2025; 5(4):26. https://doi.org/10.3390/wind5040026
Chicago/Turabian StyleCunningham, David, Rubina Ramponi, Reamonn MacReamoinn, and Jennifer Keenahan. 2025. "Modernizing Wind Load Standards for Ireland" Wind 5, no. 4: 26. https://doi.org/10.3390/wind5040026
APA StyleCunningham, D., Ramponi, R., MacReamoinn, R., & Keenahan, J. (2025). Modernizing Wind Load Standards for Ireland. Wind, 5(4), 26. https://doi.org/10.3390/wind5040026







