Lift-Based Rotor Optimization of HAWTs via Blade Element Momentum Theory and CFD
Abstract
1. Introduction
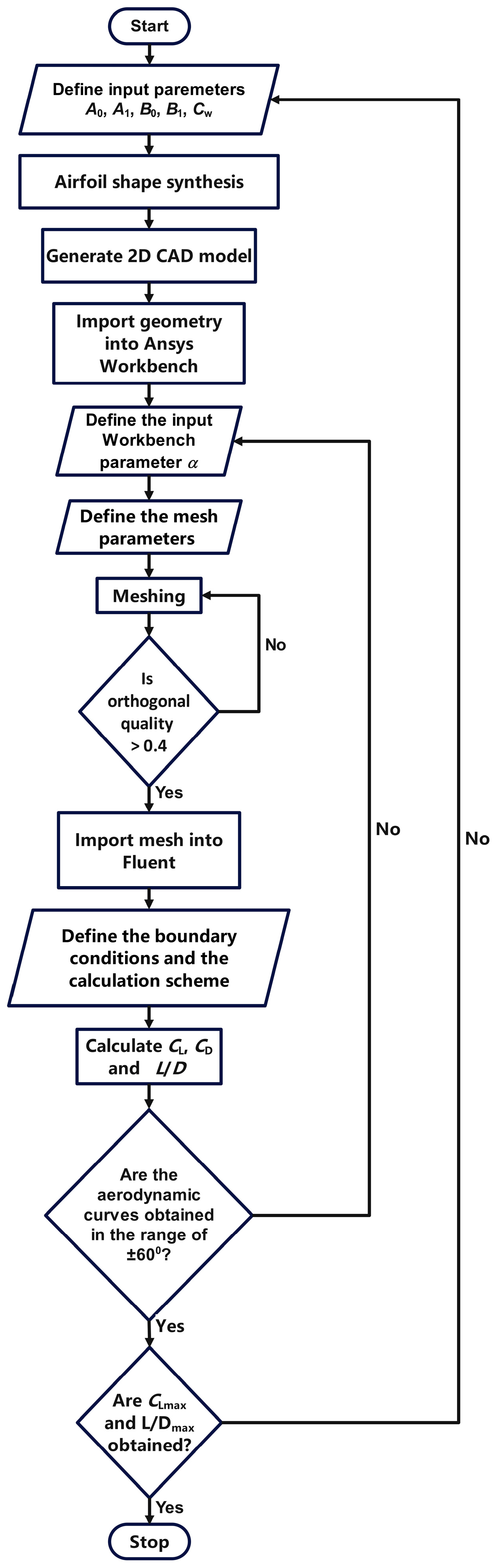
2. Airfoil Shape Optimization
2.1. Optimization Methodology
2.2. CFD Setup for Profile Evaluation
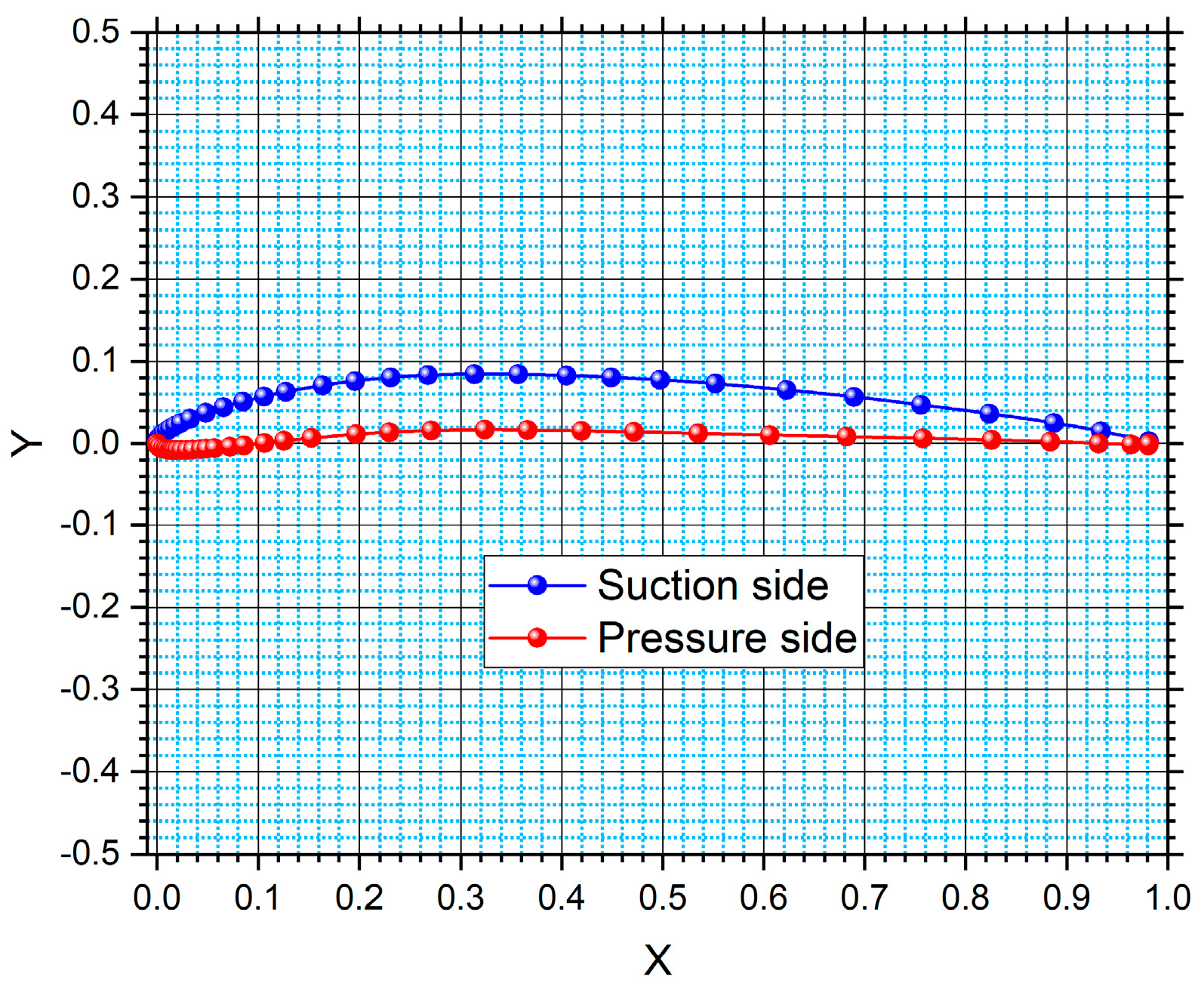
2.3. Results of Airfoil Optimization
3. Blade Design and Rotor Synthesis
3.1. Blade Geometry Generation
3.2. Synthesized Blade Geometry
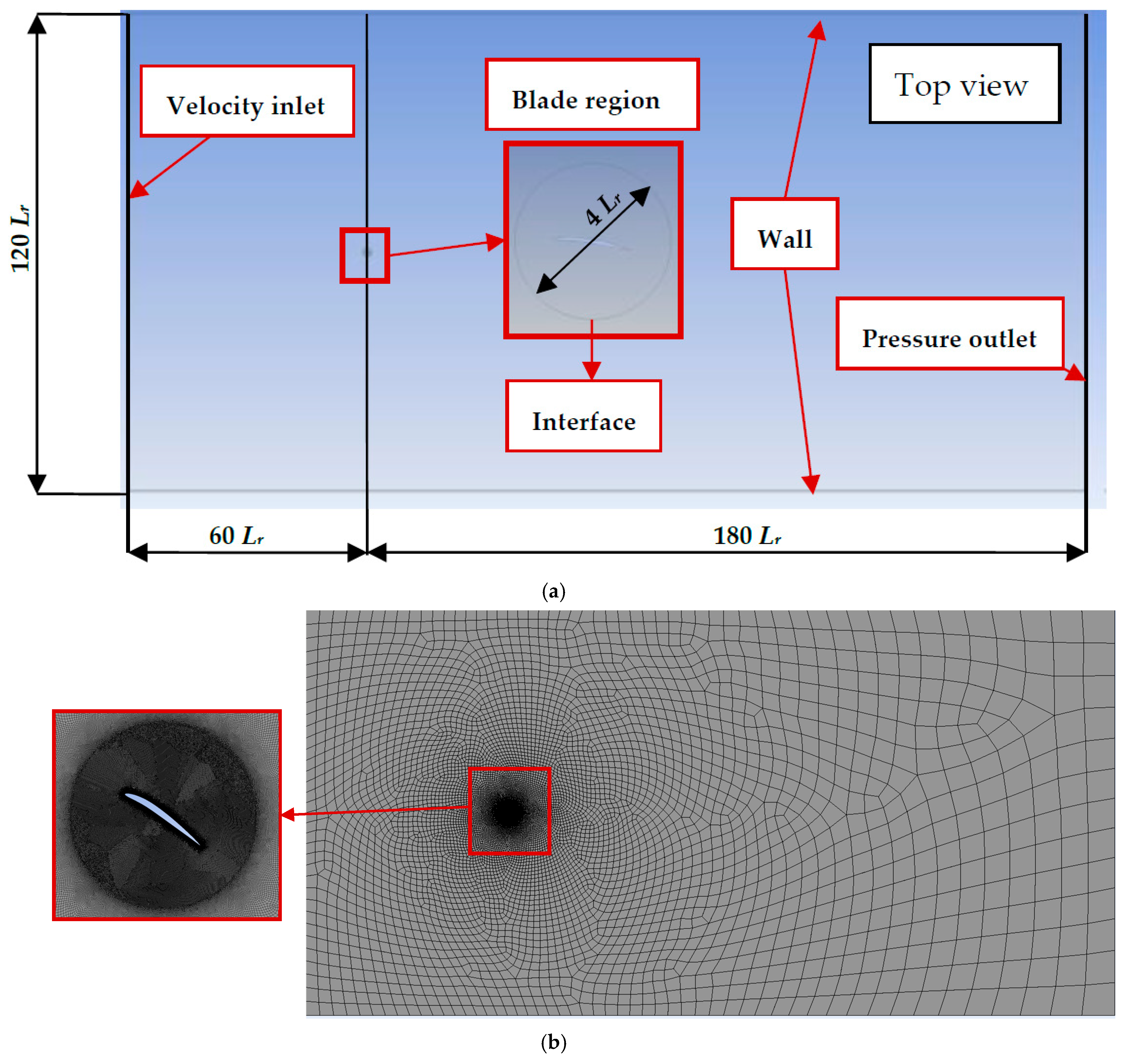
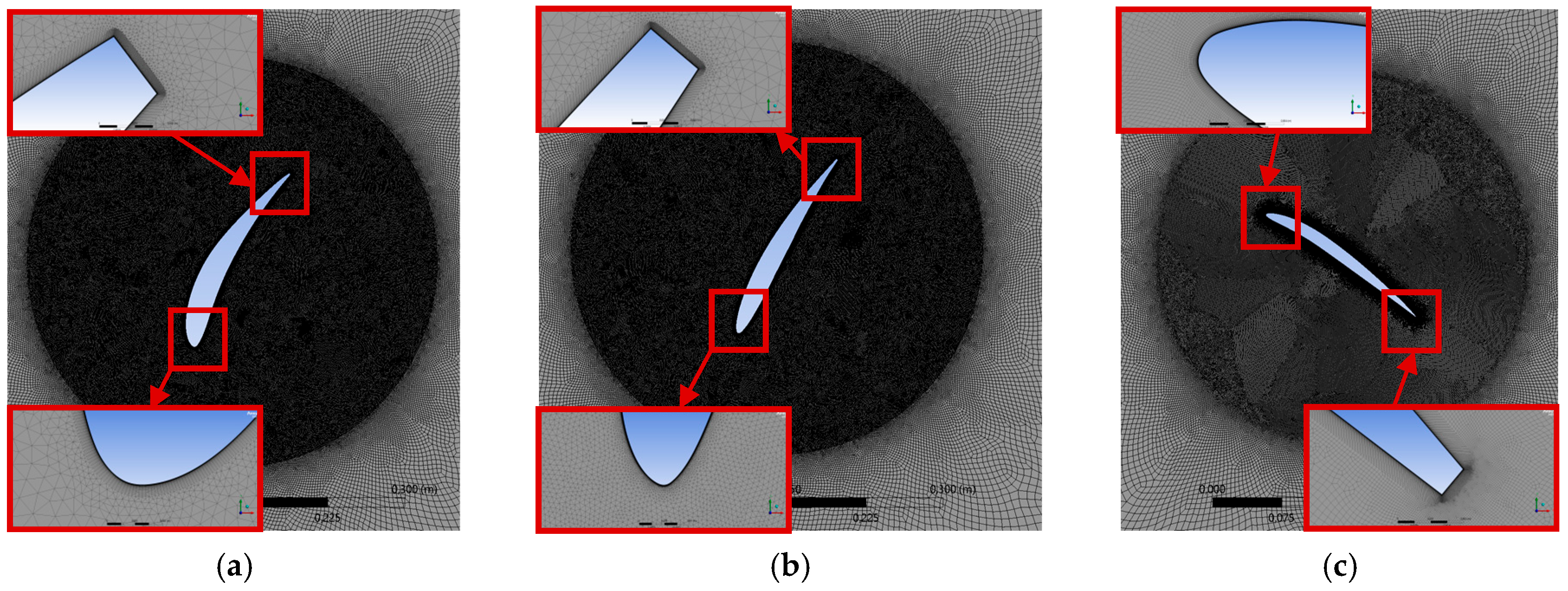
3.3. CFD Setup for Turbine Simulations
4. Experimental Validation
4.1. Test Bench Description
4.2. Experimental Procedure
4.3. Data Processing
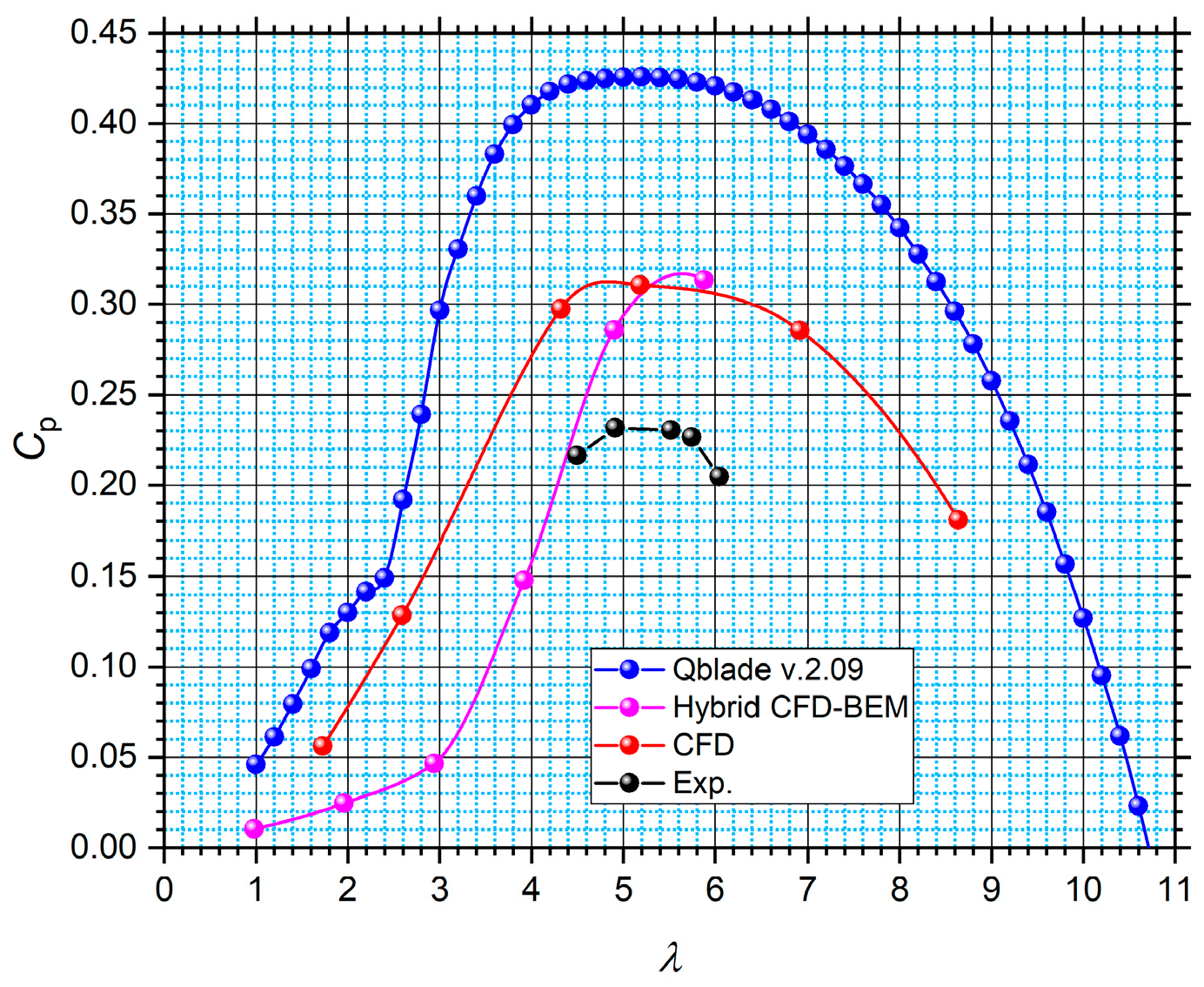
4.4. Validation of CFD Results
5. Discussion
6. Conclusions
- The hybrid CFD-BEM methodology accurately predicts the power coefficient and optimal operating point of small-scale wind turbines.
- It provides better accuracy than commonly used IBL methods at low Reynolds numbers. It is also faster and cost-effective than modern optimization methods like ROMs and adjoint solvers. The implemented two-dimensional CFD model does not require prior training and higher computational resources;
- The validation of the presented methodology is performed on small-scale wind turbines, which are relevant for supplying electricity to farms, residential areas, and households;
- Future studies will focus on expanding this methodology for larger wind turbines, which operate at higher Reynolds numbers.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BET | Blade Element Theory |
| BEM | Blade Element Momentum theory |
| BGA | Binary-Coded Genetic Algorithm |
| B. L. | Boundary Layer |
| CGA | Cellular Genetic Algorithm |
| CFD | Computer Fluid Dynamics |
| CS | Command System |
| DoE | Design of Experiment |
| FI | Frequency Inverter |
| GA | Genetic Algorithm |
| HAWT | Horizontal-Axis Wind Turbine |
| PC | Personal computer |
| SST | Shear Stress Transport |
| VAWT | Vertical-Axis Wind Turbine |
Nomenclatures
| Symbol | Description |
| A0 | Coefficient of Glauert Fourier series related to the camber line maximum curvature |
| A1 | Coefficient of Glauert Fourier series related to the location of the maximum curvature of the camber line |
| a‘ | Axial induction factor |
| B0 | Coefficient of Glauert Fourier series related to the maximum thickness of the blade |
| B1 | Coefficient of Glauert Fourier series related to the thickness distribution of the blade |
| b‘ | Tangential induction factor |
| CL | Lift coefficient |
| CL * | Normalized lift coefficient |
| CD | Drag coefficient |
| CN | Normal force coefficient |
| CT | Tangential force coefficient |
| Cw [m/s] | Far field velocity |
| Cp | Power coefficient |
| Cp,init | Power coefficient before the optimization |
| Cp,max | Maximum power coefficient |
| Cp,opt | Power coefficient after the optimization |
| D1r [m] | Main diameter of the turbine |
| Dp [m] | Inner diameter of the aerodynamic tube |
| [N] | Drag force |
| [N] | Lift force |
| [N] | Normal force |
| [N] | Tangential force |
| [m2/s] | Total bound circulation from the leading edge up to the position defined by the angle θ |
| [m/s] | Vortex sheet strength per unit length |
| I [A] | Current |
| L/D | |
| Lr [m] | Chord length |
| Lopt [m] | Optimal chord length |
| Lhub [m] | Chord length at the hub |
| Ltip [m] | Chord length at the tip |
| Mdry air [g/mol] | Molar mass of dry air |
| Mvapor [g/mol] | Molar mass of vapor |
| Nsec | Number of blade sections used in the BEM calculation |
| n [min−1] | Rotational speed |
| Δn [min−1] | Rotational speed increment step |
| ncalc [min−1] | Design rotational speed |
| nmax [min−1] | Maximum rotational speed |
| P [W] | Mechanical power |
| Pel [W] | Electric power |
| pa [hPa] | Atmospheric pressure |
| pv [hPa] | Vapor pressure of water |
| ps [hPa] | Saturation pressure of water |
| ) [m] | |
| ) [m2/s] | Source strength per unit length, derived from the thickness distribution. |
| Rgas [J/Kmol] | Ideal gas constant |
| R [m] | Radius at a specific blade section |
| Rhub [m] | Hub radius |
| Rtip [m] | Tip radius |
| Re | Radius at a specific blade section |
| Reynolds number based on rotor diameter | |
| Reynolds number based on airfoil chord length | |
| Sr [m2] | Rotor flow area |
| T [K] | Air temperature |
| Tτ [Nm] | Torque of the rotor |
| U [m/s] | Peripheral speed of the rotor |
| U1r [m/s] | Peripheral speed at rotor tip |
| Uel [V] | Voltage |
| [m/s] | The x-component of the velocity induced at given point by a distribution of singularities |
| ut [m/s] | Tangential velocity component on the streamlined surface |
| [m/s] | The x-component of the velocity induced by thickness source distribution |
| [m/s] | The y-component of the velocity induced at given point by a distribution of singularities |
| [m/s] | The y-component of the velocity induced by thickness source distribution |
| W [m/s] | Relative velocity |
| Wa [m/s] | Axial component of relative velocity |
| Wu [m/s] | Tangential component of the relative velocity |
| X | Dimensionless coordinate in horizontal direction |
| x [m] | X-coordinate of the point where velocity is evaluated |
| x‘ [m] | X-coordinate of the singularity point where the vortex or source is located |
| Y | Dimensionless coordinate in vertical direction |
| y [m] | Y-coordinate of the point where velocity is evaluated |
| y‘ [m] | Y-coordinate of the singularity point where the vortex or source is located |
| y+ | Dimensionless wall distance |
| ywall [m] | Normal distance from the streamlined surface |
| Zr | Number of blades |
| α [rad] | Angle of attack |
| αopt [rad] | Optimal angle of attack |
| θ [rad] | An angular coordinate that maps points along the airfoil contour |
| Tip speed ratio | |
| opt | Optimal tip speed ratio |
| [m2/s] | Kinematic viscosity of air |
| ξ1 | Tolerance for convergence in the calculation of induction factors in the optimal regime |
| ξ2 | Tolerance for convergence in the calculation of induction factors outside the optimal regime |
| ρair [kg/m3] | Density of air |
| Rotor solidity | |
| φr [rad] | Pitch angle at a specific blade section |
| φflow [rad] | Flow angle at a specific blade section |
| Relative humidity of the air | |
| ωcalc [rad/s] | Design angular velocity |
References
- Sultan, K.; Elshabli, A.; Kashbour, A.; Atega, S.B. Performance assessment of the vortex panel method. Libyan J. Sci. Technol. 2019, 9, 122–128. [Google Scholar] [CrossRef]
- Cox, C. Linear Strength Vortex Panel Method for a Two Element Airfoil. Senior Bachelor’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2011. Available online: https://digitalcommons.calpoly.edu/aerosp/28/ (accessed on 1 July 2025).
- Bristow, D. A New Surface Singulatity Method for Multi-Element Airfoil Analysis and Design. In Proceedings of the 14th Aerospace Sciences Meeting, Washington, DC, USA, 26–28 January 1976. [Google Scholar] [CrossRef]
- Bottai, A.; Jonson, L.; Campbell, R. Singularity Based Method for Small Peturbation Unsteady Aerodynamics Using Higher Fidelity Steady State Pressure Profiles. In Proceedings of the ASME 2023 International Mechanical Engineering Congress and Exposition, New Orleans, LA, USA, 29 October–2 November 2023. [Google Scholar] [CrossRef]
- Sørensen, J.; Ramos-García, N.; Okulov, V. Analysis and Validation of Glauert Rotor Design. J. Phys. Conf. Ser. 2022, 2265, 032047. [Google Scholar] [CrossRef]
- Abedi, H. Development of Vortex Filament Method for Aerodynamic Loads on Rotor Blades. Licentiate of Engineering. Bachelor’s Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2013. Available online: https://www.tfd.chalmers.se/~lada/postscript_files/Licentiate_thesis_Hamid.pdf (accessed on 26 June 2025).
- Queipo, N.; Haftka, R.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, K. Real-World Applications of Genetic Algorithms; IntechOpen: London, UK, 2012; pp. 333–362. [Google Scholar] [CrossRef]
- Agrawal, R.; Bose, S.; Griffin, K.; Moin, P. An extension of Thwaties’ method for turbulent boundary layers. Flow 2024, 4, E25. [Google Scholar] [CrossRef]
- Mason, W. Aerodynamic Calculation Methods for Programmable Calculators & Personal Computers; Huntington: New York, NY, USA, 1981; Available online: https://archive.aoe.vt.edu/mason/Mason_f/AerocalPak4.pdf (accessed on 29 June 2025).
- Hwang, P.; Wu, J.; Chang, Y. Optimization Based on Computational Fluid Dynamics and Machine Learning for the Performance of Diffuser-Augmented Wind Turbines with Inlet Shrouds. Sustainability 2024, 16, 3648. [Google Scholar] [CrossRef]
- Kenway, G.; Mader, C.; He, P.; Martins, J. Effective adjoint approaches for computational fluid dynamics. Prog. Aerosp. Sci. 2019, 110, 100542. [Google Scholar] [CrossRef]
- Amoignon, O. Adjoint-Based Aerodynamic Shape Optimization. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2003. Licentiate of Technology in Numerical Analysis. [Google Scholar]
- Dhert, T.; Ashuri, T.; Martins, J. Aerodynamic Shape Optimization of Wind Turbine Blades Using a Reynolds-Averaged Navier-Stokes Model and an Adjoint Method. Wind Energy 2017, 20, 909–926. [Google Scholar] [CrossRef]
- Vardhan, H.; Hyde, D.; Timalsina, U.; Volgyesi, P.; Sztipanovits, J. Sample-efficient and surrogate-based design optimizxation of underwater vehicle hulls. Ocean Eng. 2024, 311, 118777. [Google Scholar] [CrossRef]
- Saalfield, B.; Rutten, M.; Saalfiield, S.; Kunemund, J. Improved Mesh Morphing Based on Radial Basis Functions. In Proceedings of the 6th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Vienna, Austria, 10–14 September 2012; Available online: https://www.researchgate.net/publication/225026002_Improved_Mesh_Morphing_Based_on_Radial_Basis_Functions (accessed on 18 July 2025).
- Airfoil Tools. Available online: http://airfoiltools.com/ (accessed on 16 July 2025).
- Schmitz, S.; Maniaci, C. Methodology to determine a tip-loss factor for highly loaded wind turbines. AIAA 2017, 55, 341–351. [Google Scholar] [CrossRef]
- Zhao, D.; Han, N.; Goh, E.; Cater, J.; Reinecke, A. Wind Turbines and Aerodynamics Energy Harvesters, 1st ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 373–400. [Google Scholar]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics; Springer: Berlin/Heidelberg, Germany, 1989; Volume 54, pp. 1–12. [Google Scholar] [CrossRef]
- Marten, D.; Wendler, J.; Pechivanoglou, G.; Nayeri, C.; Paschereit, C. Qblade: An open source tool for design and simulation of horizontal and vertical axis Wind turbines. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 264–269. [Google Scholar]
- PROPAN—Propeller Panel Code. Available online: https://www.researchgate.net/publication/356556813_PROPAN_-_Propeller_Panel_Code (accessed on 15 June 2025).
- Eppler, R. Airfoil Design and Data; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Romani, G.; Grande, E.; Avallone, F.; Ragni, D.; Casalino, D. Performance and Noise Prediction of Low-Reynolds Number Propellers Using the Lattice-Boltzmann Method. Aerosp. Sci. Technol. 2022, 125, 107086. [Google Scholar] [CrossRef]
- Klose, B.F.; Spedding, G.R.; Jacobs, G.B. Flow Separation, Instability and Transition to Turbulence on a Cambered Airfoil at Reynolds Number 20000. J. Fluid Mech. 2025, 1009, A9. [Google Scholar] [CrossRef]
- Cantwell, B.J.; Bilgin, E.; Needels, J.T. A New Boundary Layer Integral Method Based on the Universal Velocity Profile. Phys. Fluids 2022, 34, 075130. [Google Scholar] [CrossRef]
- Rapp, B. Microfluidics: Modelling, Mechanics and Mathematics, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 273–289. [Google Scholar]
- Quarona, E. Design Loading Optimization of a Horizontal Axis Turbine with Lifting Line and Panel Methods. Master’s Thesis, Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal, 2019. [Google Scholar]
- Goates, C.D.; Hunsaker, D.F. Practical Implementation of a General Numerical Lifting-Line Method. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–21 January 2021; American Institute of Aeronautics and Astronautics: Reston, VA, USA. [Google Scholar] [CrossRef]
- Koc, E.; Gunel, O.; Yavuz, T. Comparison of QBlade and CFD Results for Small-Scaled Horizontal Axis Wind Turbine Analysis. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; IEEE: New York, NY, USA, 2016; pp. 204–209. [Google Scholar] [CrossRef]
- Pourrajabian, A.; Dehghan, M.; Rahgozar, S. Genetic Algorithms for the Design and Optimization of Horizontal Axis Wind Turbine (HAWT) Blades: A Continuous Approach or a Binary One? Sustain. Energy Technol. Assess. 2021, 44, 101022. [Google Scholar] [CrossRef]
- Poole, S.; Phillips, R. Optimization of a Mini H.A.W.T. Blade to Increase Energy Yield during Short Duration Wind Variations. J. New Gener. Sci. 2016, 14, 47–59. [Google Scholar]
- Bekkai, R.; Mdouki, R.; Laouar, R. Aerodynamic Optimization of 3D Micro HAWT Blade via RSM. J. Appl. Fluid Mech. 2025, 18, 504–517. [Google Scholar] [CrossRef]
- Ansys Fluent Software. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 23 July 2025).
- Radi, J.; Sierra-García, J.; Santos, M.; Armenta-Déu, C.; Djebli, A. Metaheuristic Optimization of Wind Turbine Airfoils with Maximum-Thickness and Angle-of-Attack Constraints. Energies 2024, 17, 6440. [Google Scholar] [CrossRef]
- Boudis, A.; Hamane, D.; Guerri, O.; Bayeul-Laine, A. Airfoil Shape Optimization of a Horizontal Axis Wind Turbine Blade Using a Discrete Adjoint Solver. J. Appl. Fluid Mech. 2023, 16, 724–738. [Google Scholar] [CrossRef]
- Kriswanto; Setiawan, M.; Al-Janan, D.; Naryanato, R.; Roziquin, A.; Firmansyah, H.; Setiadi, R.; Darsono, F.; Setiyawan, A.; Jamari; et al. Power Optimization of The Horizontal Axis Wind Turbine Capacity of 1 MW on Various Parameters of The Airfoil, an Angle of Attack, and a Pitch Angle. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 103, 141–156. [Google Scholar] [CrossRef]
- Antony, J. Taguchi or Classical Design of Experiments: A Perspective from a Practitioner. Sens. Rev. 2006, 26, 227–230. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mohammadi, A.; Farahat, S. A New Method for Horizontal Axis Wind Turbine (HAWT) Blade Optimization. Int. J. Renew. Energy Dev. 2016, 5, 1–8. [Google Scholar] [CrossRef]
- Al-Abadi, A.; Ertunç, Ö.; Beyer, F.; Delgado, A. Torque-Matched Aerodynamic Shape Optimization of HAWT Rotor. J. Phys. Conf. Ser. 2014, 555, 012003. [Google Scholar] [CrossRef]
- Shen, X.; Zhu, X.; Du, Z. Optimization of Wind Turbine Blades Using Lifting Surface Method and Genetic Algorithm. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 841–847. [Google Scholar]
- Lee, K.-J.; Hoshino, T.; Lee, J.-H. A Lifting Surface Optimization Method for the Design of Marine Propeller Blades. Ocean. Eng. 2014, 88, 472–479. [Google Scholar] [CrossRef]
- Umar, D.A.; Yaw, C.T.; Koh, S.P.; Tiong, S.K.; Alkahtani, A.A.; Yusaf, T. Design and Optimization of a Small-Scale Horizontal Axis Wind Turbine Blade for Energy Harvesting at Low Wind Profile Areas. Energies 2022, 15, 3033. [Google Scholar] [CrossRef]
- Devlin, K.; Miller, M. High Reynolds Number Wind Turbine Testing in the Compressed Air Wind Tunnel. In Proceedings of the 2024 Regional Student Conferences; American Institute of Aeronautics and Astronautics AIAA: Reston, VA, USA, 2024. [Google Scholar] [CrossRef]
- Cunningham, J. Field Testing the Effects of Low Reynolds Number on the Power Performance of the Cal Poly Wind Power Research Center Small Wind Turbine. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2020. Available online: https://digitalcommons.calpoly.edu/theses/2249 (accessed on 16 July 2025).
- Peters, N.; Silva, C.; Ekaterinaris, J. A Data-Driven Reduced-Order Model for Rotor Optimization. Wind Energ. Sci. 2023, 8, 1201–1223. [Google Scholar] [CrossRef]
- Popov, M. Hydrodynamics, 1st ed.; State Publishing House “Technika”: Sofia, Bulgaria, 1973. [Google Scholar]
- Mohamed, O.; Ibrahim, A.; Etman, E.; Abdelfatah, A.; Elbaz, A. Numerical Investigation of Darrieus Wind Turbine with Slotted Airfoil Blades. Energy Convers. Manag. X 2020, 5, 100026. [Google Scholar] [CrossRef]
- Adam, N.; Attia, O.; Al-Sulttani, A.; Mahmood, H.; As’arry, A.; Md Rezali, K. Numerical Analysis for Solar Panel Subjected with an External Force to Overcome Adhesive Force in Desert Areas. CFD Lett. 2020, 12, 60–75. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent User’s Guide, Version 2022; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Durmuş, S.; Ulutaş, A. Numerical Analysis of NACA 6409 and Eppler 423 Airfoils. J. Polytech. 2023, 26, 39–47. [Google Scholar] [CrossRef]
- White, M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Menter, F.R. Zonal Two Equation Kappa-Omega Turbulence Models for Aerodynamic Flows. In Proceedings of the AIAA Fluid Dynamics Conference (No. AIAA Paper 93-2906), Orlando, FL, USA, 6–9 July 1993; AIAA: Reston, VA, USA, 1993. [Google Scholar]
- Hansen, M. Aerodynamics of Wind Turbines, 3rd ed.; Routledge: Oxford, UK, 2015. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2nd ed.; Wiley: Chichester, UK, 2009. [Google Scholar]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook, 2nd ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
- Saldana, M.; Gallegos, S.; Gálvez, E.; Castillo, J.; Salinas-Rodríguez, E.; Cerecedo-Sáenz, E.; Hernández-Ávila, J.; Navarra, A.; Toro, N. The Reynolds Number: A Journey from Its Origin to Modern Applications. Fluids 2024, 9, 299. [Google Scholar] [CrossRef]
- Wußow, S.; Sitzki, L.; Hahm, T. 3D-Simulation of the Turbulent Wake behind a Wind Turbine. J. Phys. Conf. Ser. 2007, 75, 012033. [Google Scholar] [CrossRef]
- Kao, J.-H. Developing the Process in Matching a Wind Turbine System to Attain Optimal Performance. Adv. Mech. Eng. 2016, 8, 1687814016674697. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. Towards Accurate CFD Simulations of Vertical Axis Wind Turbines at Different Tip Speed Ratios and Solidities: Guidelines for Azimuthal Increment, Domain Size and Convergence. Energy Convers. Manag. 2018, 156, 301–316. [Google Scholar] [CrossRef]
- Tsilingiris, P. Thermophysical and Transport Properties of Humid Air at Temperature Range between 0 and 100 °C. Energy Convers. Manag. 2008, 49, 1098–1110. [Google Scholar] [CrossRef]
- Alduchov, O.; Eskridge, R. Improved Magnus Form Approximation of Saturation Vapor Pressure. J. Appl. Meteor. 1996, 35, 601–609. [Google Scholar] [CrossRef]

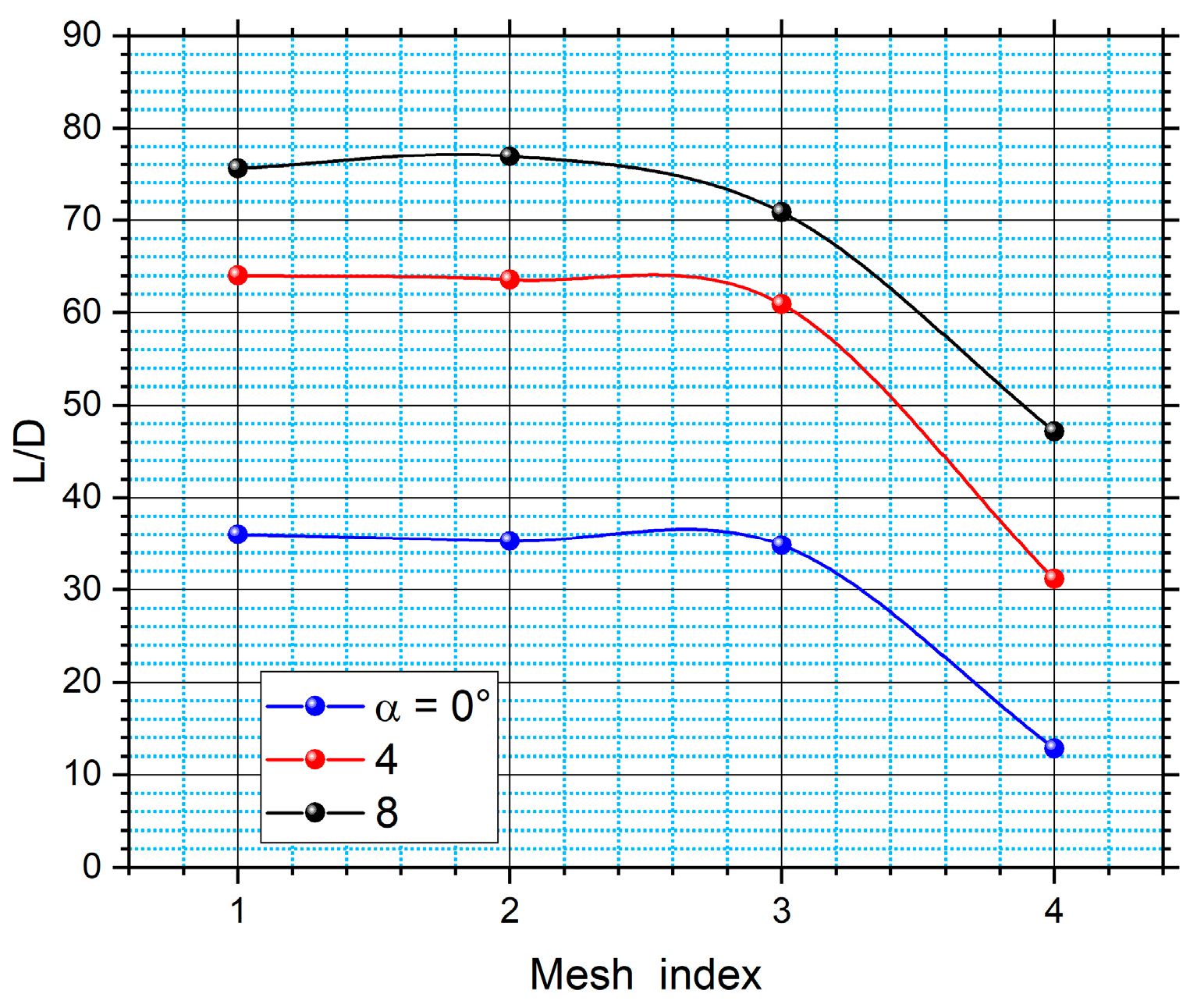
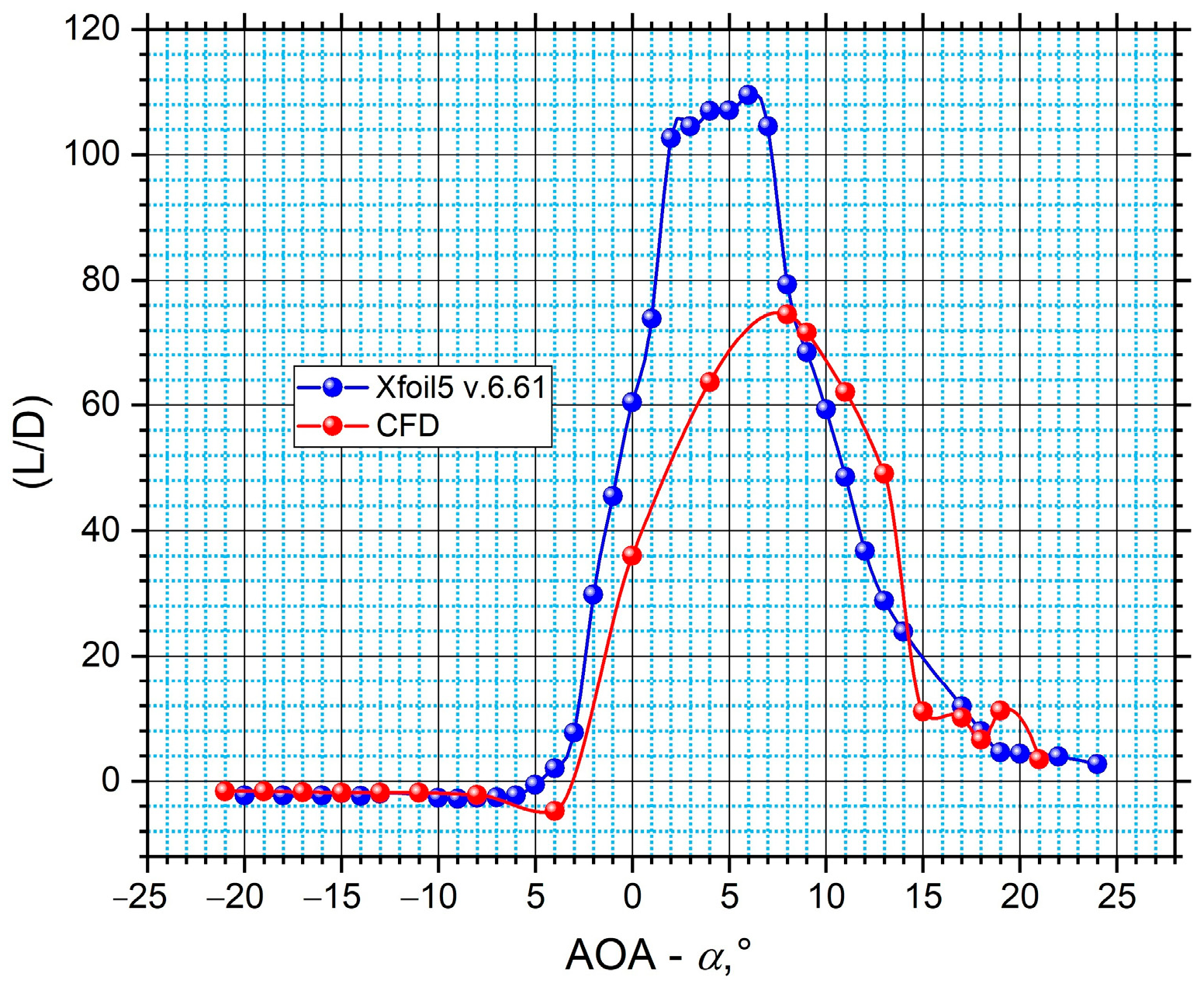

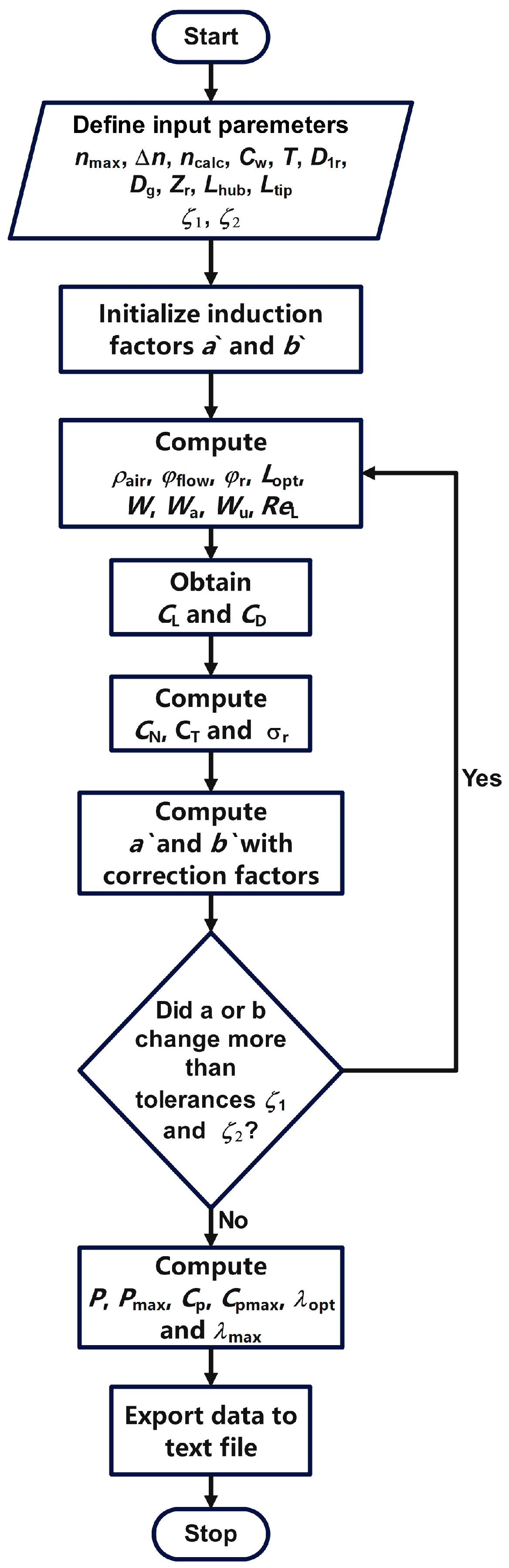
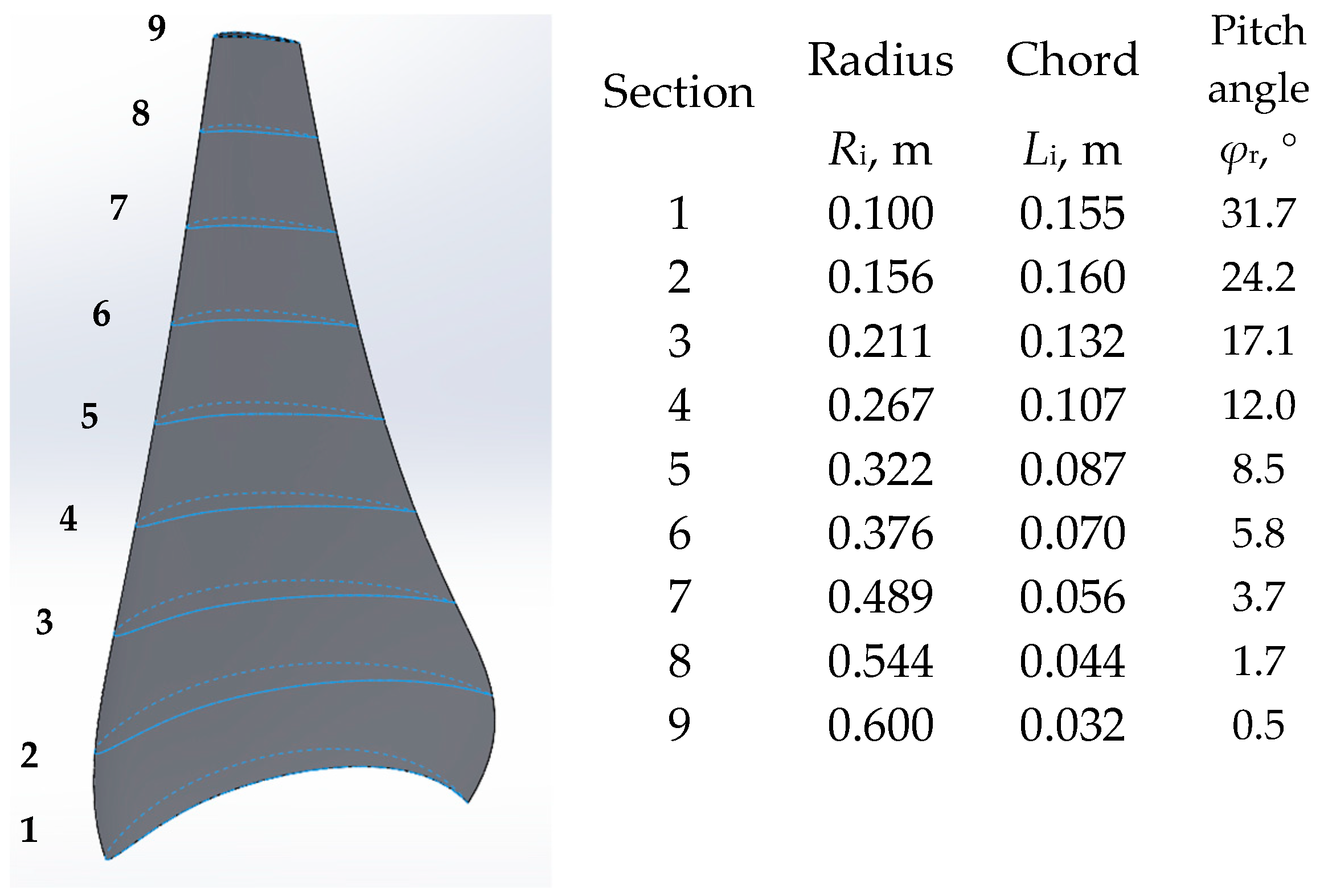
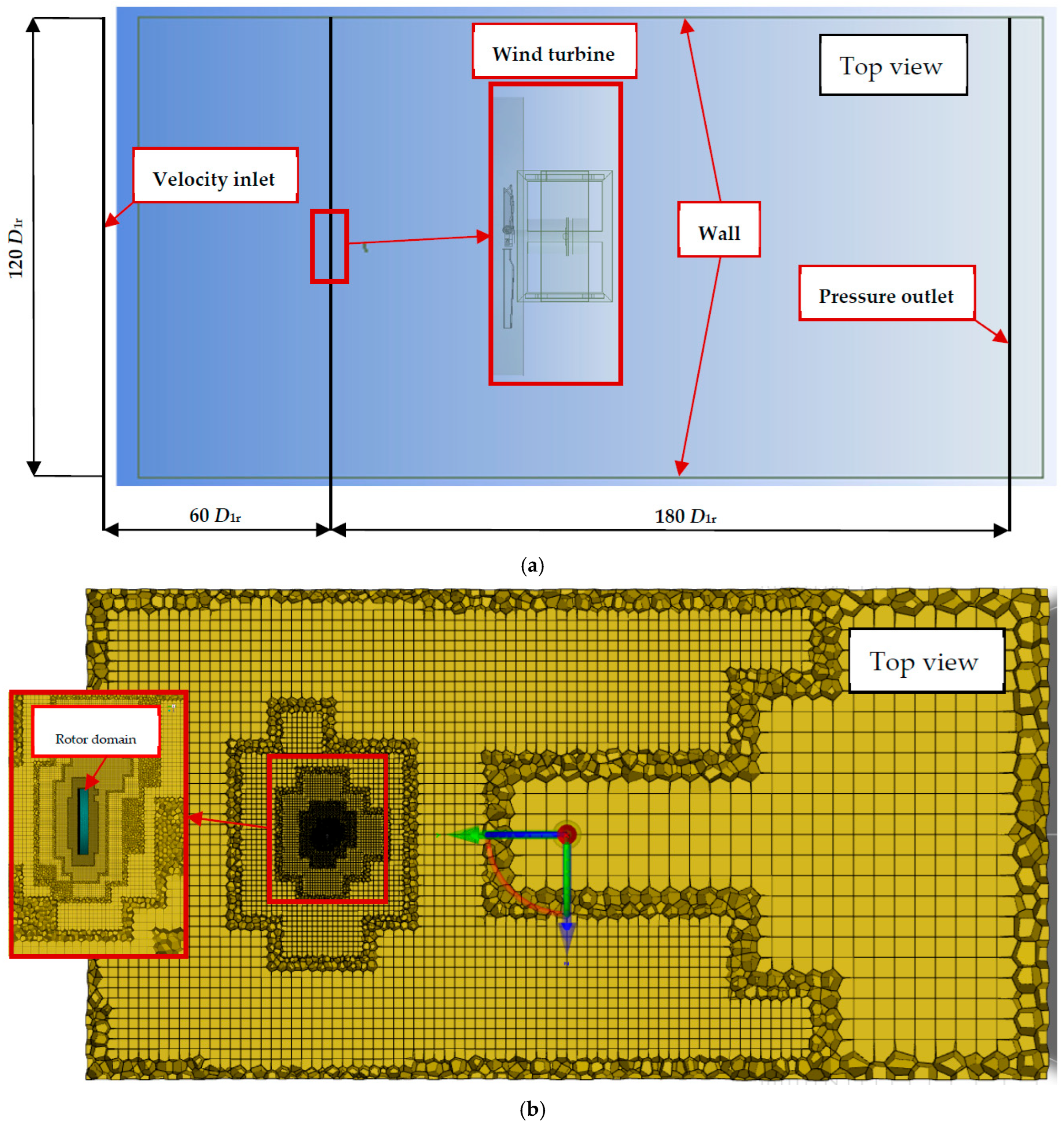

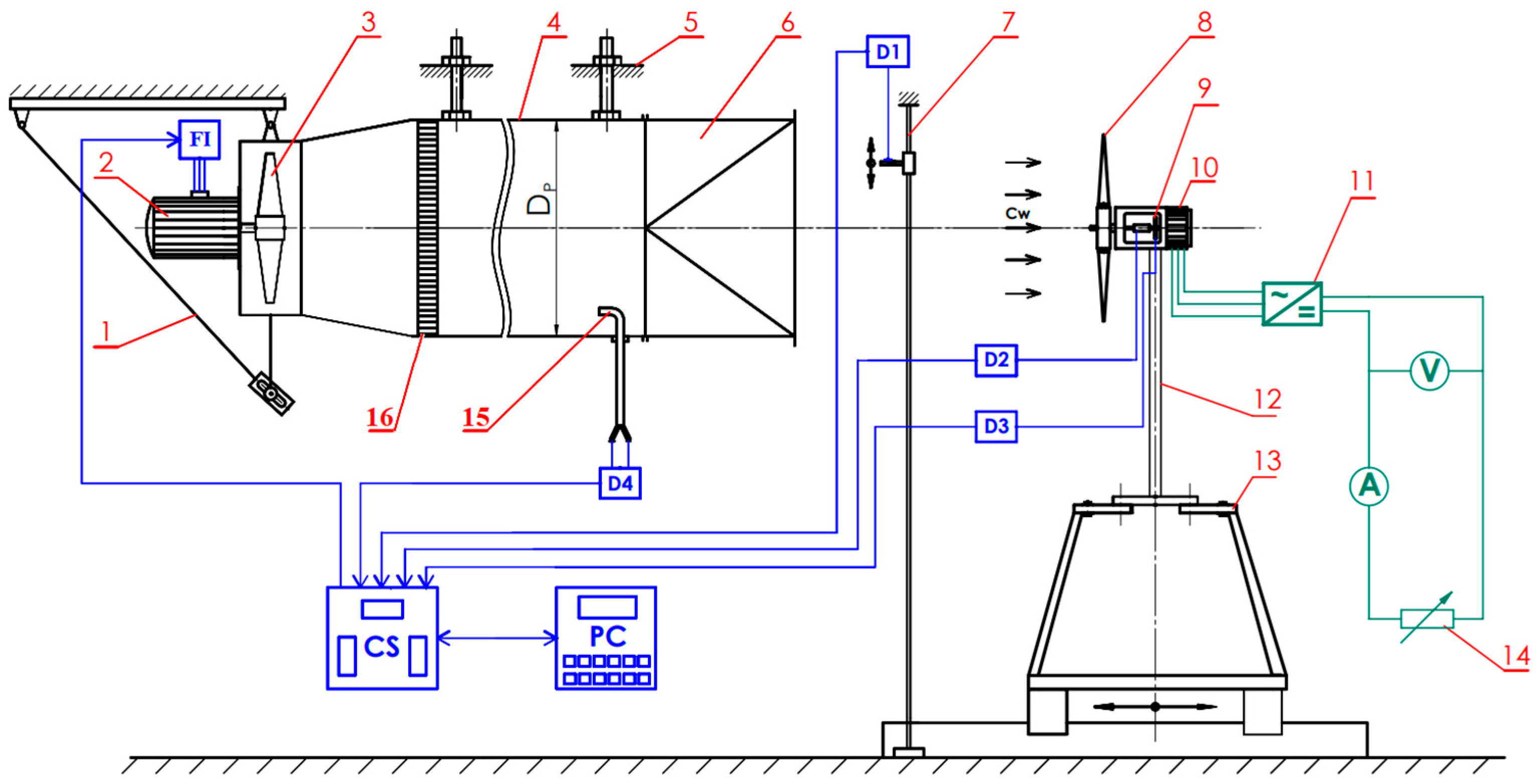



| No. | Authors | Optimization Method | Cp,init | Cp,opt | Used Blade Profile | Used Software | Based on Potential Flow? | I. B. L.? | Reynolds |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Bekkai et al. [33] (2024) | DOE, RSM, and MOGA | 0.400 | 0.450 | SG6043 | QBlade, Ansys Fluent | Yes (QBlade) | No | 4 × 104 |
| 2 | Radi et al. [35] (2024) | Generetic algorithm | 0.440 | 0.470 | NACA2424 | XFoil | Yes (XFoil) | Yes (XFoil) | 1 × 106 |
| 3 | A. Boudis et al. [36] (2023)) | Discrete adjoint solver and BEM | 0.450 | 0.470 | S809 | QBlade, Ansys Fluent v.2020 | Yes (QBlade) | No | 3 × 105, 4.8 × 105, 1 × 106 |
| 4 | Kriswanto et al. [37] (2023) | Taguchi DOE | - | 0.405 | NACA4412, NACA2412-4 | QBlade | Yes (QBlade) | No | 9 × 107 |
| 5 | Umar et al. [43] (2022) | BEMT | - | 0.450 | NACA4412, SG6043 | Matlab, QBlade, XFoil | Yes (QBlade, XFoil) | No | 1 × 10−3 × 105 |
| 6 | Pourrajabian et al. [31] (2021) | CGA&BGA and BEM | 0.450 | 0.500 | NACA4412 | Matlab | Yes (BEM) | No | 1.61 × 106 |
| 7 | Quarona [28] (2019) | Lifting line and ProPan | - | 0.560 | - | ProPan | Yes | No | - |
| 8 | Koç et al. [30] (2017) | BEM | 0.450 | 0.500 | NACA4412 | Matlab | Yes (BEM) | No | 1.60 × 106 |
| 9 | Mohammadi et al. [39] (2016) | BEM | - | 0.410 | 43 different profiles | Matlab | Yes (BEM) | No | 4.8 × 105–2.25 × 106 |
| 10 | S. Poole et al. [32] (2016) | BEM | - | 0.510 | NACA4412 | XFoil | Yes (BEM, XFoil) | Yes (XFoil) | 8 × 105 |
| 11 | Al-Abadi et al. [40] (2014) | Schmitz and BEM | 0.410 | 0.440 | NREL, S809 | Matlab, Star-CCM+ v. 7.02 | Yes (Schmitz, BEM) | No | 6.65 × 105 |
| 12 | Xin Shen et al. [41] (2011) | Lifting surface and GA | 0.370 | 0.390 | S809 | - | Yes (Lifting surface) | No | 1.67–5 × 106 |
| Max. Cell Size | Min. Cell Size | Wall Distance | Min. Orth. Quality | Max. Aspect Ratio | Layers | Growth Rate |
|---|---|---|---|---|---|---|
| 1 mm | 0.5 mm | 1 μm | 0.771 | 168 | 42 | 1.1 |
| Max. Cell Size | Min. Cell Size | Min. Orth. Quality | Max. Aspect Ratio | Growth Rate |
|---|---|---|---|---|
| Fluid domain | ||||
| 2680 mm | 1 mm | 0.975 | 9.4 | 1.08 |
| Airfoil domain | ||||
| 1 mm | 0.5 mm | 0.53 | 2.62 | 1.08 |
| Parameter | Value |
|---|---|
| Orthogonal quality | >0.10 [49] |
| Aspect ratio | <30 [50] |
| Aspect ratio at the boundary layer | <100 [50] |
| Growth rate | <1.2 [50] |
| Growth rate at the boundary layer | <1.1 [50] |
| Gradient | Last Square Cell Based |
|---|---|
| Pressure | Second Order |
| Momentum | Second Order Upwind |
| Turbulent Kinetic Energy | Second Order |
| Dissipation Rate | Second Order Upwind |
| Transient Formulation | Second Order Implicit |
| Camber Line Coefficients | Thickness Distribution Coefficients | ||
|---|---|---|---|
| A0 | A1 | B0 | B1 |
| 0.065 | 0.08 | 0.1 | 0.08 |
| Max. curvature location | Max. thickness location | ||
| X | Y | X | Y |
| 0.3400 | 0.0503 | 0.3550 | 0.0502 |
| Max. Cell Size | Min. Cell Size | Min. Orth. Quality | Max. Aspect Ratio | Max. Volume Ratio | Growth Rate |
|---|---|---|---|---|---|
| Fluid domain | |||||
| 235 mm | 10 mm | 0.41 | 22 | 13 | 1.1 |
| Rotor domain | |||||
| 32 mm | 1 mm | 0.31 | 25 | 15 | 1.1 |
| Max. Cell Size | Min. Cell Size | Wall Distance | Min. Orth. Quality | Max. Aspect Ratio | Max. Volume Ratio | Layers | Growth Rate |
|---|---|---|---|---|---|---|---|
| 10 mm | 1 mm | 6 μm | 0.25 | 142 | 1.26 | 40 | 1.1 |
| No. | Parameters | Model | Range | Accuracy |
|---|---|---|---|---|
| 1 | Voltmeter | M4430 | 0.00–100.00 V | ±1% |
| 2 | Ammeter | M4430 | 0.000–10.000 A | ±1% |
| 3 | Wind speed | VT 210 F | 0.00–25.00 m/s | ±3% |
| 4 | Torque | Wobit DFM22-2.5 | 0.0–2.5 Nm | ±0.02% |
| 5 | Rotational speed | FUA 9192 | 1–12,000 min−1 | ±0.02% |
| 6 | Air temperature | 2/12BTH | −30 to +50 °C | ±0.4% |
| 7 | Air Humidity | 0.00–100% | ±2% | |
| 8 | Atmospheric pressure | 910–1050 hPa | ±0.3% |
| Quantity | Equation | No. |
|---|---|---|
| Power coefficient | (34) | |
| Tip speed ratio | (35) | |
| Generator electric power | (36) | |
| Air density | (37) | |
| Vapor pressure of water | (38) | |
| Saturation pressure of water | (39) | |
| Reynolds number | (40) |
| QBlade | Hybrid CFD-BEM | CFD | Experiments | Wind Tunnel Experiments [44] |
|---|---|---|---|---|
| 0.426 | 0.314 | 0.311 | 0.232 | 0.329 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iliev, R. Lift-Based Rotor Optimization of HAWTs via Blade Element Momentum Theory and CFD. Wind 2025, 5, 25. https://doi.org/10.3390/wind5040025
Iliev R. Lift-Based Rotor Optimization of HAWTs via Blade Element Momentum Theory and CFD. Wind. 2025; 5(4):25. https://doi.org/10.3390/wind5040025
Chicago/Turabian StyleIliev, Rossen. 2025. "Lift-Based Rotor Optimization of HAWTs via Blade Element Momentum Theory and CFD" Wind 5, no. 4: 25. https://doi.org/10.3390/wind5040025
APA StyleIliev, R. (2025). Lift-Based Rotor Optimization of HAWTs via Blade Element Momentum Theory and CFD. Wind, 5(4), 25. https://doi.org/10.3390/wind5040025






