Abstract
Wind energy is a renewable energy resource that can be harnessed to generate electrical energy. In this paper, a novel Artificial Neural Network (ANN) approach using wavelet analysis for wind energy forecasting is proposed and tested with wind data from Kanyakumari, India, for different seasons. The wavelet decomposition is used to decom-pose the wind power time series data into different frequency components. The model simulates the complex mapping of historical wind power to allow the forecasting of wind power data for the next 3 h or the next 24 h. The predicted components are then reconstructed to obtain the overall predicted wind energy time series. The proposed models give more promising prediction results than the model without the use of wavelets. The regression coefficient and Mean Square Error (MSE) are computed and observed in order to assess the model’s performance.
1. Introduction
Wind power is mostly determined by wind speed. Wind kinetic energy is proportional to the cube of its velocity, so even slight variations in wind speed can affect power generation [1]. Forecasting wind power requires wind speed estimation. To effectively harness wind energy resources, it is imperative to gather precise information about the wind characteristics specific to each location. Factors like local climate, regional weather patterns, topography, and obstacles like buildings all play significant roles in determining the viability and efficiency of wind power generation in a given area.
The requirement for wind farms in India to perform short-term wind energy forecasting with a 15 min interval, as per the India Electricity Grid Code (IEGC) [2], reflects the importance of accurately predicting wind power generation to ensure grid stability and reliability. By mandating such forecasts, regulatory bodies aim to minimize deviations between predicted and actual wind power output, thereby optimizing grid operations and minimizing economic losses for wind farm operators.
Scholars have proposed four types of prediction models based on historical wind speed time records in recent decades: statistical, intelligence learning, hybrid, and physical models [3,4,5]. The complexities involved in accurately predicting wind power output highlight the necessity of comprehensive understandings and data gathering of the various factors influencing wind patterns and energy generation. The classification of wind power prediction models into physical, statistical, intelligent learning, and hybrid models reflects the diverse approaches researchers have explored to address this challenge. Each type of model leverages different methodologies and data inputs to forecast wind power output.
Physical models utilize principles of fluid dynamics and atmospheric physics to simulate wind behavior. They consider factors such as atmospheric pressure, temperature gradients, and terrain features to predict wind patterns. They provide extensive insights but are computationally costly and may require accurate input data. Statistical models analyze historical wind speed data to identify patterns and correlations. These models are often more straightforward to implement and can provide reasonable predictions, especially in stable wind conditions. Intelligent learning models employ advanced machine learning and artificial intelligence techniques to learn from historical data and make predictions. Neural networks, support vector machines, and ensemble methods are examples of approaches used in intelligent learning models. They excel in capturing complex relationships but may require extensive data and computational resources for training. Hybrid models combine elements of multiple approaches to leverage their respective strengths. For example, a hybrid model might integrate physical principles with statistical techniques or combine machine learning algorithms with empirical data. By synergizing different methodologies, hybrid models aim to improve prediction accuracy and robustness. These modeling techniques must be researched and developed to improve wind power prediction reliability and efficiency, enabling wind energy resource use. Models for prediction are complicated and require a large number of historical datasets, because many of the aforementioned approaches combine historical wind energy data with numerical weather prediction (NWP) data. This research proposes a simple and robust wind forecasting model that can estimate wind power with minimal historical data. Wind power may be accurately predicted in the short term using a single prediction model using a wavelet-based neural network (WNN).
In the literature on time series forecasting for a variety of applications, including wind power, decomposition-based hybrid models are becoming more prevalent [6,7].
The fact that wind power time series data are typically noisy, nonlinear, and non-stationary is a major contributing factor to this. As a result, modeling such time series data using a single statistical model is challenging. Non-stationary time series data may be broken down into a collection of component sequences with varying frequencies using decomposition techniques [8]. Subsequently, simpler patterns within the sub-series data can be extracted by statistical approaches. Furthermore, in order to increase forecasting accuracy, decomposition approaches function well with combination technologies, that is, the use of several forecasting methods to anticipate distinct sub-series [9,10,11,12]. Studies of decomposition-based models often concentrate on the forecasting and decomposition modules, which fall into two groups: the direct method and multicomponent approach [13,14].
A hybrid deep learning approach that integrates transformers, convolutional neural networks (CNNs), and recurrent neural networks (RNNs) to handle multiple time series simultaneously is proposed in [15]. This model achieved an R2 value of 0.99 for short-term forecasts and maintained an R2 of 0.50 for 96 h predictions, demonstrating its robustness in various forecasting horizons. The study published in [16] introduced two novel hybrid models: CNN-ABiLSTM and CNN-Transformer-MLP. The CNN component captures short-term patterns in wind and solar power data, while ABiLSTM and Transformer-MLP address long-term dependencies. These models outperformed standalone CNN, BiLSTM, and Transformer models in day-, week-, and month-ahead forecasting, with the CNN-Transformer-MLP hybrid excelling in short-term predictions and the CNN-ABiLSTM hybrid leading in long-term forecasts. DEWP is introduced in [17], a deep learning framework that models complex dependencies in wind power data. DEWP employs variable and time expansion blocks to capture multi-level dependencies and utilizes multi-head self-attention mechanisms for feature extraction. Experiments on real-world datasets demonstrated its effectiveness in handling intricate temporal and spatial relationships in wind power forecasting. In [18], the authors proposed a medium-term wind power forecasting model combining Temporal Convolutional Networks (TCNs) and Gated Recurrent Units (GRUs) with dual-stage attention mechanisms. The model was optimized using White Shark Optimization (WSO) and achieved a maximum Mean Absolute Percentage Error (MAPE) of 8.07% for week-ahead forecasts, outperforming traditional methods in terms of accuracy and computational efficiency. SD-STGNN, a model that decomposes wind power data into seasonal and trend components, has also been developed. The seasonal component is processed using Gated Temporal Convolutional Networks and Graph Convolutional Networks to capture spatiotemporal relationships, while the trend component is enhanced using a Temporal Feature Enhancement module. The model demonstrated a reduction in Mean Absolute Error by approximately 6.26% and improved the coefficient of determination by about 4.74% compared to baseline methods [19]. A comparative study on different types of models, i.e., statistical, machine learning, physical, and hybrid models, is summarized in Table 1. A comparison between current state-of-the-art hybrid models such as LSTM, CNNs, and SVMs is presented in Table 2.

Table 1.
A comparative study on different types of models.

Table 2.
Comparison of current state-of-the-art hybrid models.
In this paper, a novel machine learning (ML) approach using wavelet analysis for wind energy forecasting is proposed and tested with wind data from Kanyakumari, India, for different seasons. It gives good results for all the seasons, hence proving it to be a robust model. Two approaches have been proposed in this paper: a direct-approach WNN and multiple-component-approach WNN. It was concluded that the multiple-component-approach WNN gives the best accuracy for the short-term prediction of wind power.
2. Artificial Neural Network (ANN)
As they can predict complicated nonlinear input–output interactions without explicitly specifying them, ANNs are useful forecasting tools in many industries, including wind power generation [20,21]. ANNs, which are formed by layers of connected nodes or neurons, are modeled after the structure of the human brain. Every neuron performs a nonlinear modification after performing a weighted sum to process its inputs. The neurons of the ANN are trained using actual data, and the results are predicted based on the training.
Mathematically it is described as in Equation (1).
where vk is the output, wkj is the weight, and xj is the input.
Usually, the structure consists of the following:
- Input Layer: Receives the raw data.
- Hidden Layers: Perform computations using neurons that process previous layer inputs.
- Output Layer: Produces the final forecast or prediction.
2.1. Data Preparation
Before training an ANN, data must be properly prepared as follows:
- Data Collection: Assemble historical data (e.g., wind speed, direction, temperature, pressure).
- Normalization: Scale the data (often between 0 and 1) to improve the training process.
- Segmentation: Convert time series data into a format suitable for ANN training, often involving the creation of moving windows of inputs and corresponding outputs.
2.2. Designing the Network
- Architecture Selection: Choose the number of hidden layers and neurons. More complex patterns may require deeper networks.
- Activation Functions: Common choices include ReLU for hidden layers and linear or sigmoid functions for the output layer, depending on the nature of the prediction (continuous or binary).
2.3. Training the Network
- Backpropagation: Adjust the weights to minimize the difference between the expected and actual outputs to train the network.
- Loss Function: Regression tasks often use MSE.
- Optimizer: Use techniques like SGD (Stochastic Gradient Descent), Adam, or RMS prop to improve model convergence.
3. Wavelet Theory
The wavelet transform analyses the time–frequency domain. Multi-resolution approximation by wavelet basis functions represents a function on several scales using scaled and translated mother wavelets [22]. The signal Continuous Wavelet Transform (CWT) is mathematically shown in Equation (2).
The scaling parameter s and the translation parameter τ determine the transformed signal, XWT (τ, s). The mother wavelet is represented by ψ; the * shows that the complex conjugate is used in the case of a complex wavelet. Each scale signal energy is modified by dividing the wavelet coefficients by . This implies that the wavelets have the same energy at all scales.
Changes in scale parameters contract and dilate the mother wavelet. Scale s affects wavelet center frequency fc and window length. Thus, wavelet analysis findings are represented by scale s instead of frequency. The translation parameter τ indicates the wavelet’s position in time; by varying τ, the wavelet can be moved across the signal. The time-scale plane rows are filled for constant scale s and variable translation τ, while the columns are filled for varied scale s and constant translation τ. Wavelet coefficients are the elements in XWT (τ, s) that are linked to a frequency scale and a time domain point, correspondingly [23].
In practice, the discrete wavelet transform (DWT) is utilized instead of CWT. This approach is implemented through the use of filters and the computation of ‘details’ and ‘approximations’. For a discrete signal x[n], DWT can be represented as in Equation (3).
Here, ϕj0,k [n] and φj,k [n] are the scaling and wavelet functions, and cj0[k] and dj[k] are the approximations and detail coefficients, respectively.
There are several types of wavelet filters, also referred to as mother wavelets; these include the Haar, Daubechies (db), Coiflets (coif), Biorthogonal (bior), and Reverse Biorthogonal wavelet filters. A series of daughter wavelets with different frequencies and locations will be obtained after a certain mother wavelet is employed to modify the original data signal. The coefficient of each daughter wavelet indicates the contribution of the daughter wavelet at a certain frequency to the parent signal at a specific location. These coefficients can therefore be utilized as future inputs for neural networks and save information about the original signal.
This paper implements the Haar wavelet with eight-level decomposition.
DWT Algorithm
- Filter Design
- Design a pair of filters: A low-pass filter h[n] and a high-pass filter g[n], as shown in Equations (4) and (5). These filters are used to decompose the signal into approximations and details, respectively.
- The filters should be designed such that they satisfy certain mathematical properties, e.g., orthogonality and biorthogonality.
- 2.
- Decomposition
- Convolution: Convolve the input signal x[n] with the low-pass filter h[n] to obtain the approximate coefficients c[n], as shown in Equation (6).
- Detail Coefficients d[n]: Convolve the input signal x[n] with the high-pass filter g[n] to obtain the detail coefficient d[n], as shown in Equation (7).
- 3.
- Downsampling:
- Downsample the filtered signal by a factor of 2 to reduce the number of data points, as shown in Equation (8).
- 4.
- Recursive Decomposition:
- Repeat the decomposition process on the approximation coefficients cdownsampled to further break down the signal into different frequency bands until the desired level of decomposition is achieved. The approximation coefficients at level 8 represent the low-frequency components of the signal after eight levels of decomposition.
4. Methodology
4.1. Wavelet Neural Network
An important development with applications for smart grid emergency response systems has been the incorporation of wavelet decomposition into neural networks for short-term wind power forecast models. The wind power time series data are decomposed into different frequency components using wavelet analysis. This decomposition separates the signal into its low-frequency approximate part and high-frequency random part, providing a multi-resolution representation of the data. Each frequency component obtained through wavelet decomposition is analyzed separately to understand its characteristics and predictability.
The low-frequency components may capture long-term trends and periodic patterns, while the high-frequency components may represent short-term fluctuations and noise [24,25]. A WNN model can be constructed to predict each decomposed component separately. WNNs combine the capabilities of wavelet analysis of handling multi-resolution data with the learning ability of neural networks. These models can efficiently capture the local and global patterns of data. The predicted components are then reconstructed to obtain the overall predicted wind power time series. This reconstructed signal represents the short-term wind power forecast, which can be utilized for emergency response planning and grid management in smart grids. Due to its ability to divide an original signal into numerous time series with smaller frequency components, the wavelet transform (WT) has been applied effectively in the fields of data analysis and signal processing [26,27,28].
In order to estimate wind power generation, this research provided a hybrid model that combined an ANN and wavelet transform based on detailed and approximation coefficients. The ANN parameters chosen were learning rate = 0.01, hidden layers = 2, neurons = 10, and the activation function was tanh.
The wind speed in m/s was the original signal. Pre-processing was performed on the data to fill in any missing values. The wind power time series was divided into numerous detail components di(t) (i = 1, …, n) and an approximate component Cn(t) using a wavelet technique. Each component was examined to determine its energy level, followed by the autocorrelation between the original signal and the coefficients.
4.2. Proposed Direct-Approach WNN
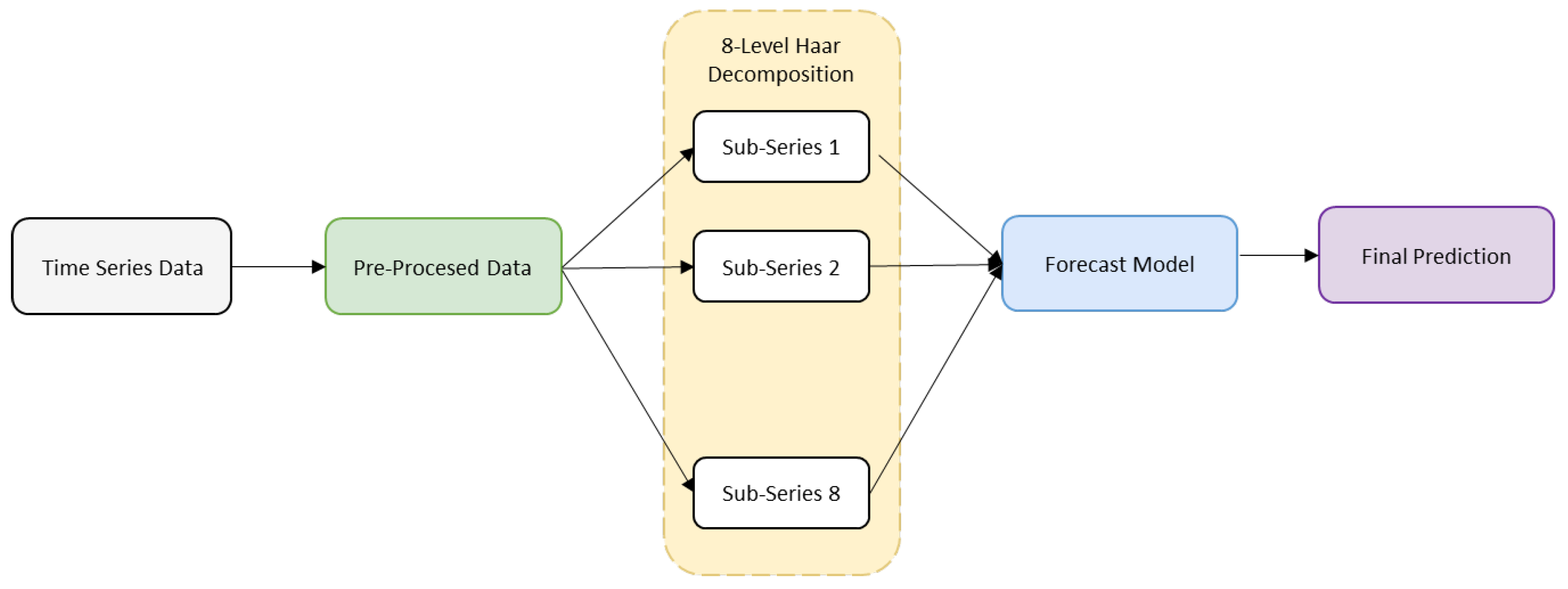
This approach decomposed the original signal into sub-series using 8-level Haar wavelet decomposition. These were then used as input features for a single forecasting model. The architecture of this model is presented in Figure 1.
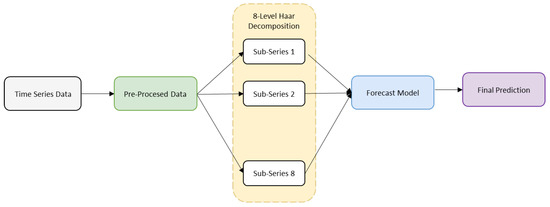
Figure 1.
Architecture of proposed direct-approach WNN.
Algorithm:
- Pre-process the original signal to fill in the missing values.
- Decompose the signal into approximate and detail coefficients using the wavelet transform.
- Calculate the energy of each level of decomposition and discard the zero or low energy levels.
- Set the remaining coefficients as input features for the neural network.
- Train the feedforward network and predict the results.
- Calculate the regression coefficient and Mean Square Error.
4.3. Proposed Multiple-Component-Approach WNN
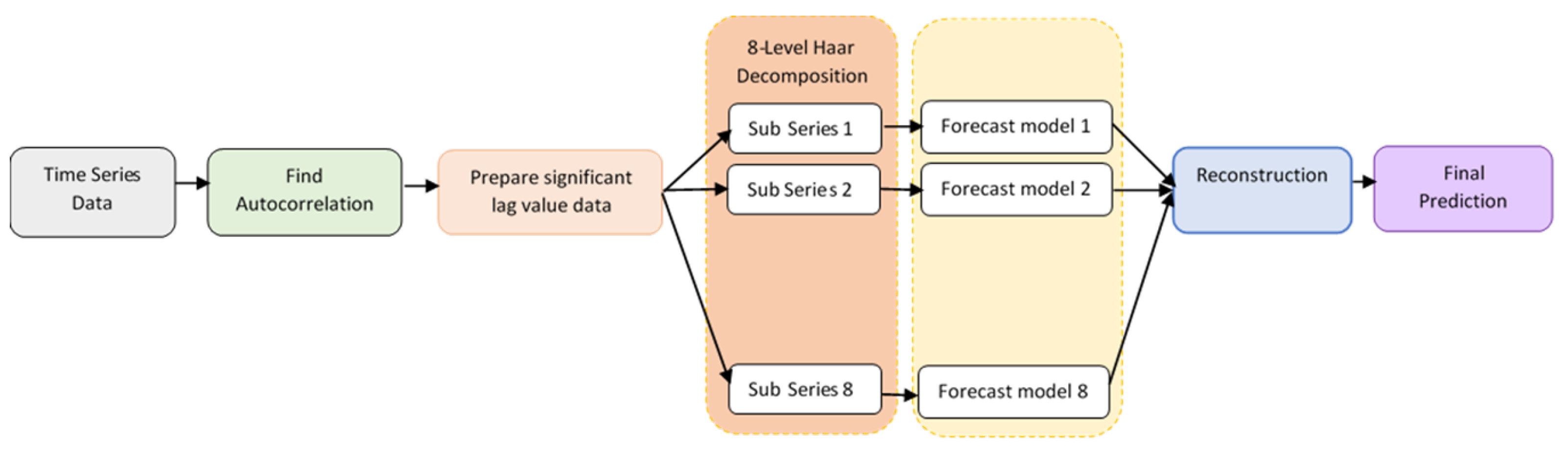
In this proposed model, the autocorrelation factor of the original signal was observed in order to arrive at the number of significant past lags, and the training dataset was prepared. This series was decomposed, and different models were implemented for each sub-series. The predictions were then reconstructed into the target prediction. The architecture of this model is presented in Figure 2.
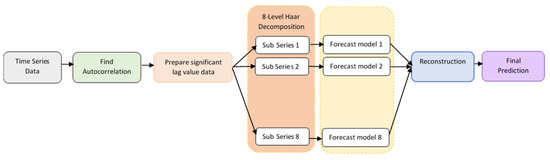
Figure 2.
Architecture of proposed multiple-component-approach WNN.
Algorithm:
- Pre-process the original signal to fill in the missing values.
- Find the correlation of the time series and its lagged version over time.
- Decide the number of past values to be taken to predict the future values and prepare the data, e.g., past 10 h data are used to predict 11th-hour data.
- Decompose these data into approximate and detailed coefficients using wavelet transform.
- Calculate the energy of each level of decomposition and discard the zero or low energy levels.
- Set the remaining coefficients as input features for the neural network.
- Train the feedforward network and predict the results for the next 3 h and for the next 24 h.
- Calculate the regression coefficient and Mean Square Error.
- Compare the results with the neural network model without use of wavelet decomposition and also with proposed WNN model 1.
- Compare the results with those in the literature.
4.4. Dataset and Analysis
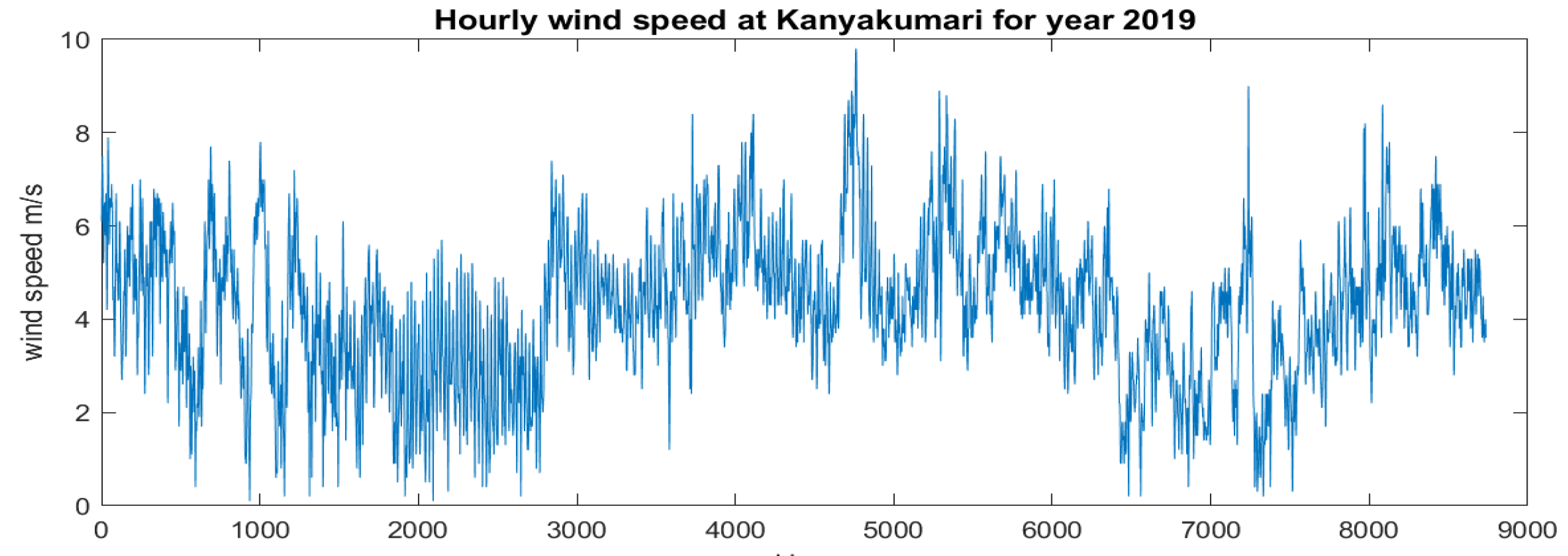
A dataset containing wind speed measurements gathered from a wind farm in Kanyakumari, India, over a period of one year, with data recorded at 60 min intervals was considered. A graphical visualization of this wind speed sequence, showing how wind speed fluctuates over time, is shown in Figure 3. Before analysis, it was essential to pre-process the data, which may involve cleaning any missing or erroneous values and potentially converting timestamps into a standardized format if necessary. It was important to visualize the wind speed sequence to explore its temporal patterns, trends, and seasonal variations.
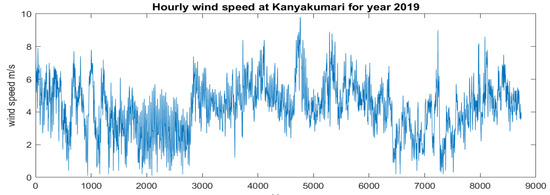
Figure 3.
Hourly wind speed at Kanyakumari for 2019.
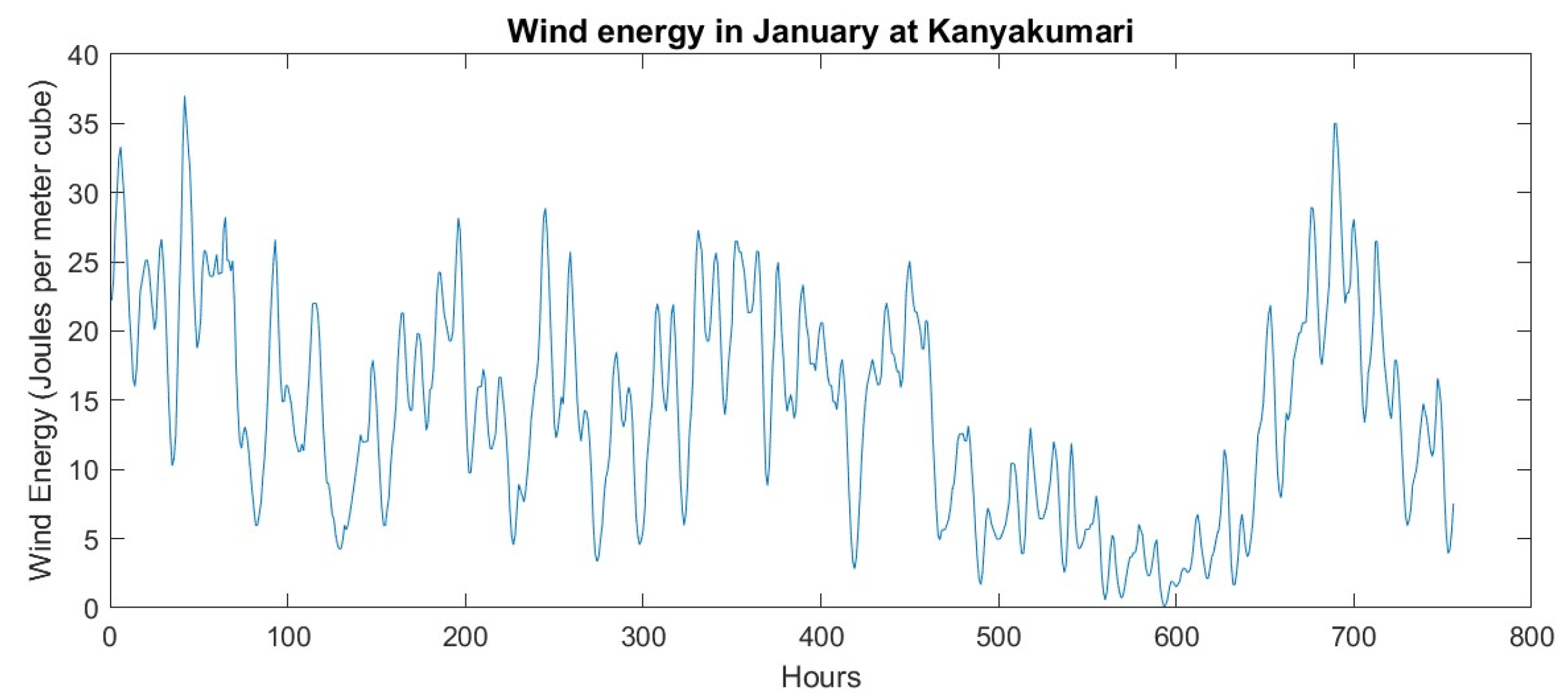
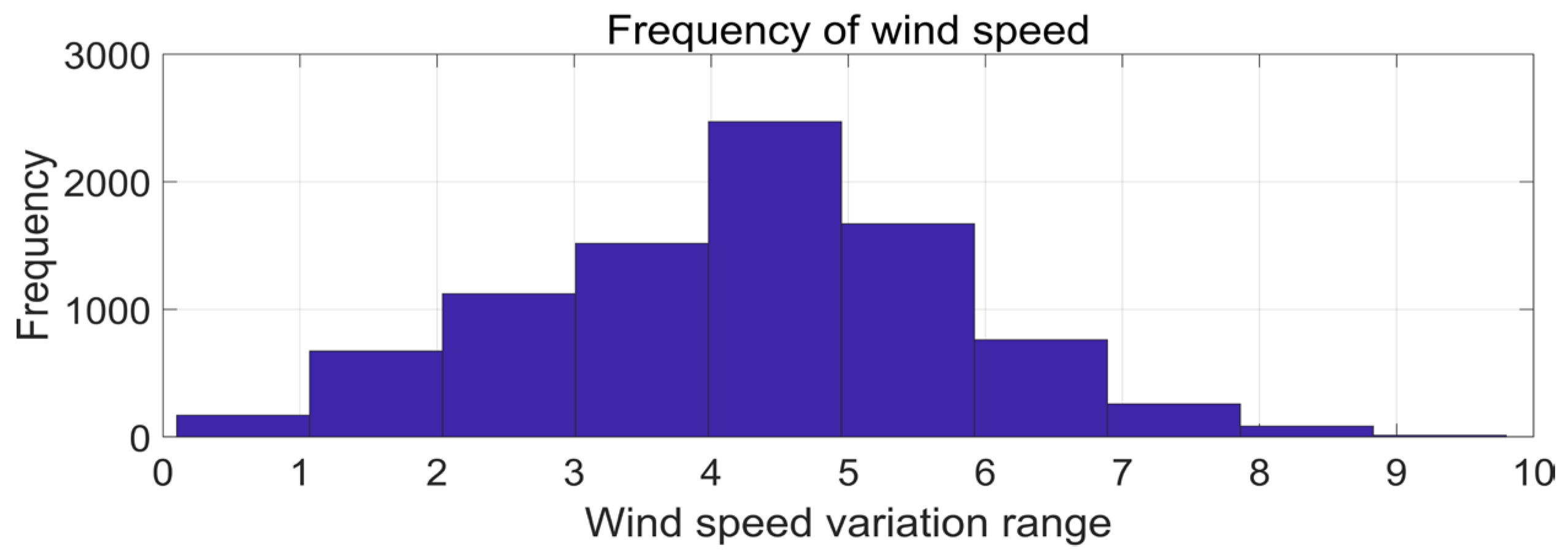
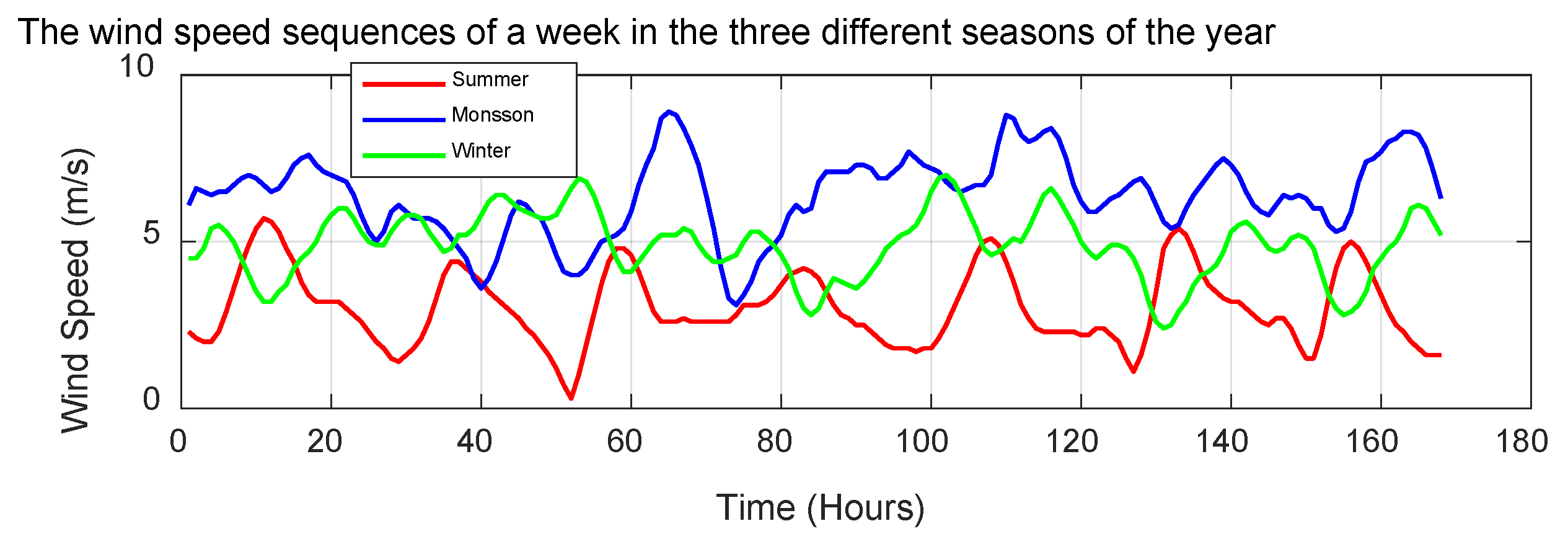
The wind energy for the month of January is displayed in Figure 4 and the frequency of speed plot is shown in Figure 5. Wind speed variations throughout a week in each of the four seasons, offering insights into the fluctuating nature of wind energy resources over different time periods, are shown in Figure 6.
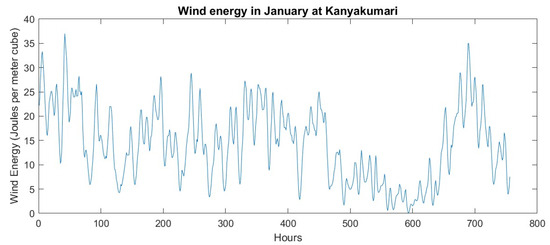
Figure 4.
Wind energy in January at Kanyakumari.
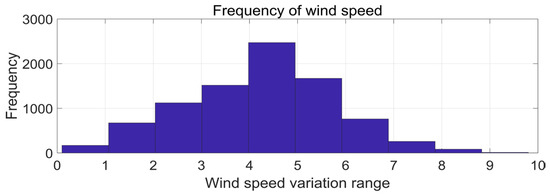
Figure 5.
Frequency of wind speed.
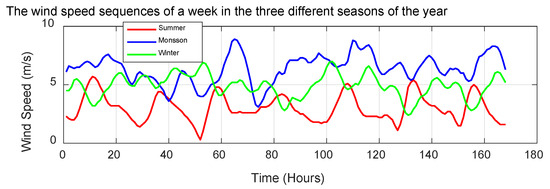
Figure 6.
Wind speed sequences of a week in the three different seasons of the year.
4.5. Autocorrelation Function
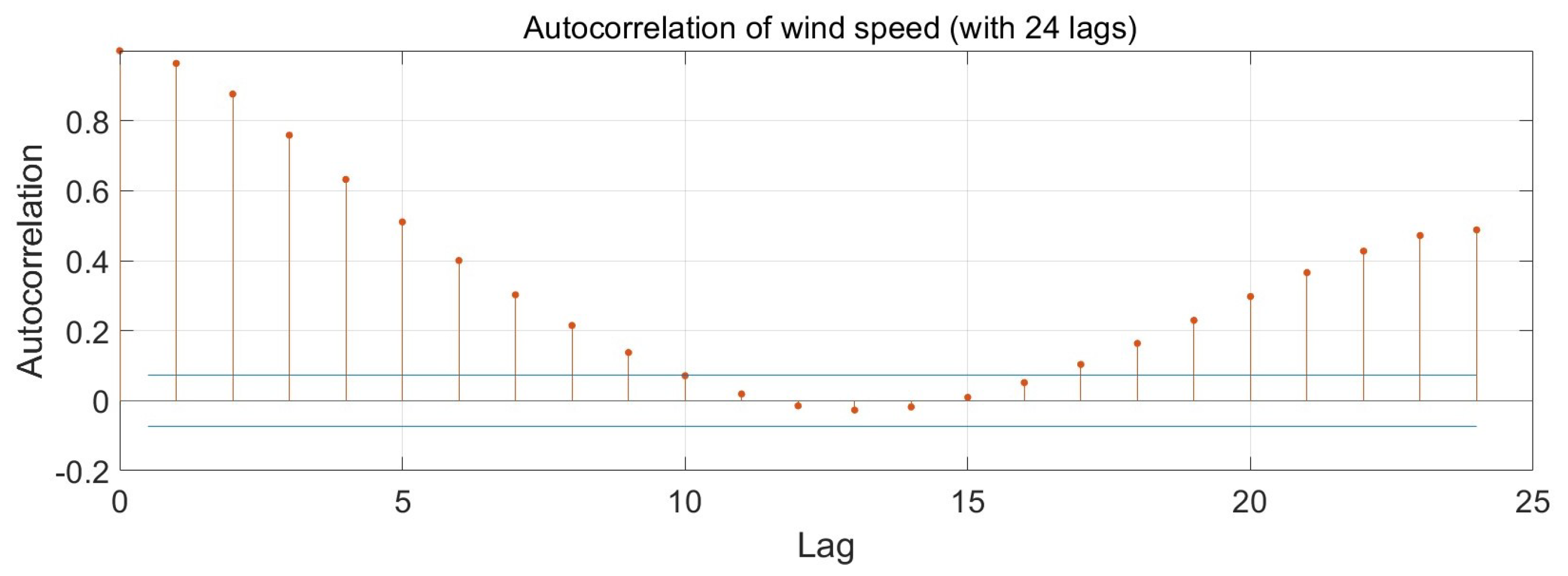
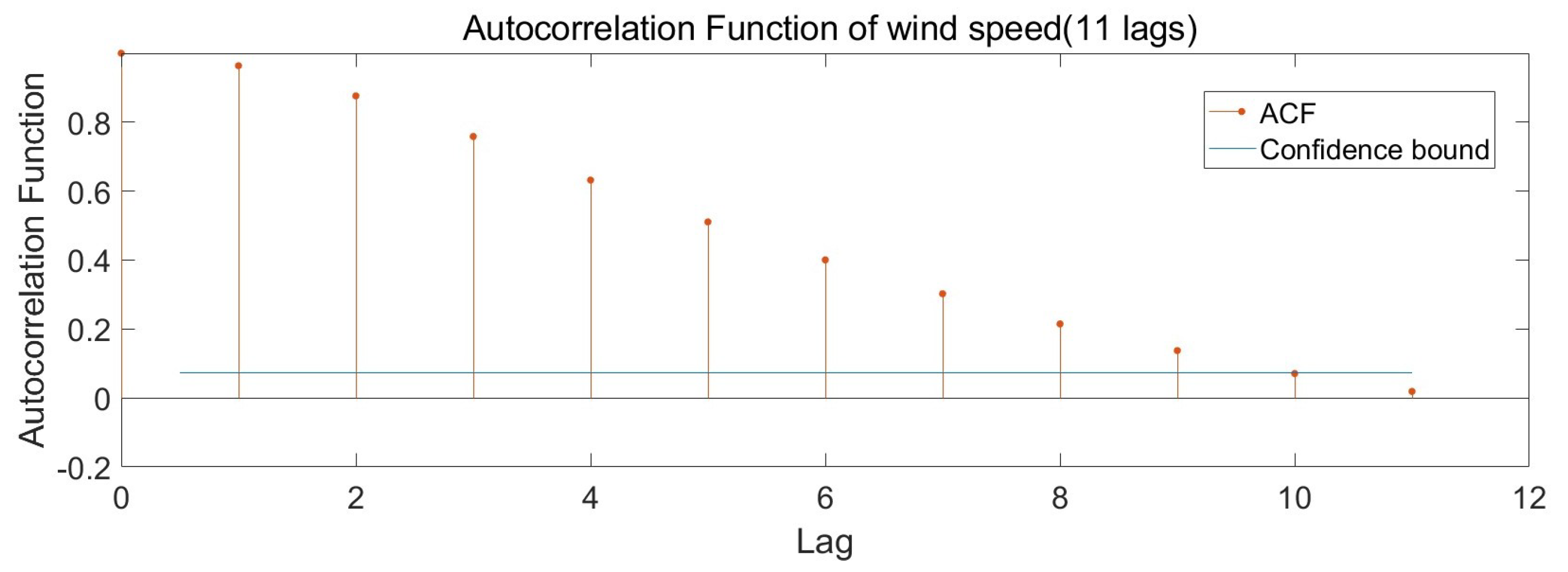
Autocorrelation functions (ACFs) with 24 lags and 11 lags are shown in Figure 7 and Figure 8, respectively. The ACF plots demonstrate that the lags t − 1 up to t − 11 have stronger relationships with the wind speed than the other lag periods. Additionally, the other lags are close to the confidence level for the interval. Hence, the data could be prepared with the last 11 data points.
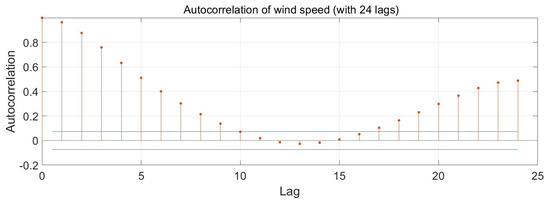
Figure 7.
Autocorrelation of wind speed (with 24 lags).
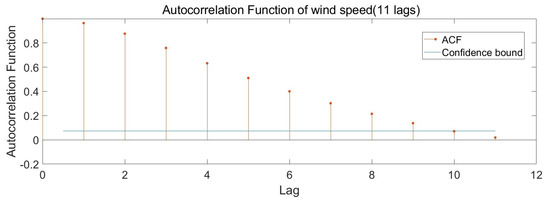
Figure 8.
Autocorrelation function of wind speed (11 lags).
4.6. Wavelet Decomposition
The signal was decomposed using Haar as the mother wavelet, with 8 levels of decomposition. The number of energy levels and the type of wavelet was decided by the trial-and-error method. The approximate and detail coefficients were given as the features to the feedforward ANN. To verify the robustness of the model, it was tested for all seasons, i.e., winter, summer, and monsoon.
5. Results and Discussions
5.1. Proposed Wavelet Neural Network (WNN) Model 1
The WNN model that has been given was utilized for day-ahead prediction with an hourly interval for all twelve months of 2019. For the wavelet neural network model, the 24 data points were decomposed into low and high-frequency components. Then, the detail coefficients with an energy level of zero were omitted, and the remaining coefficients were given as input features for the WNN model. The model uses the data from prior days to forecast the 30th day of January because the data for the 30th day was not available for day-ahead prediction. Among them, nine days of data (216 data points) were used for neural network validation, and twenty days of data (480 data points) were used for training.
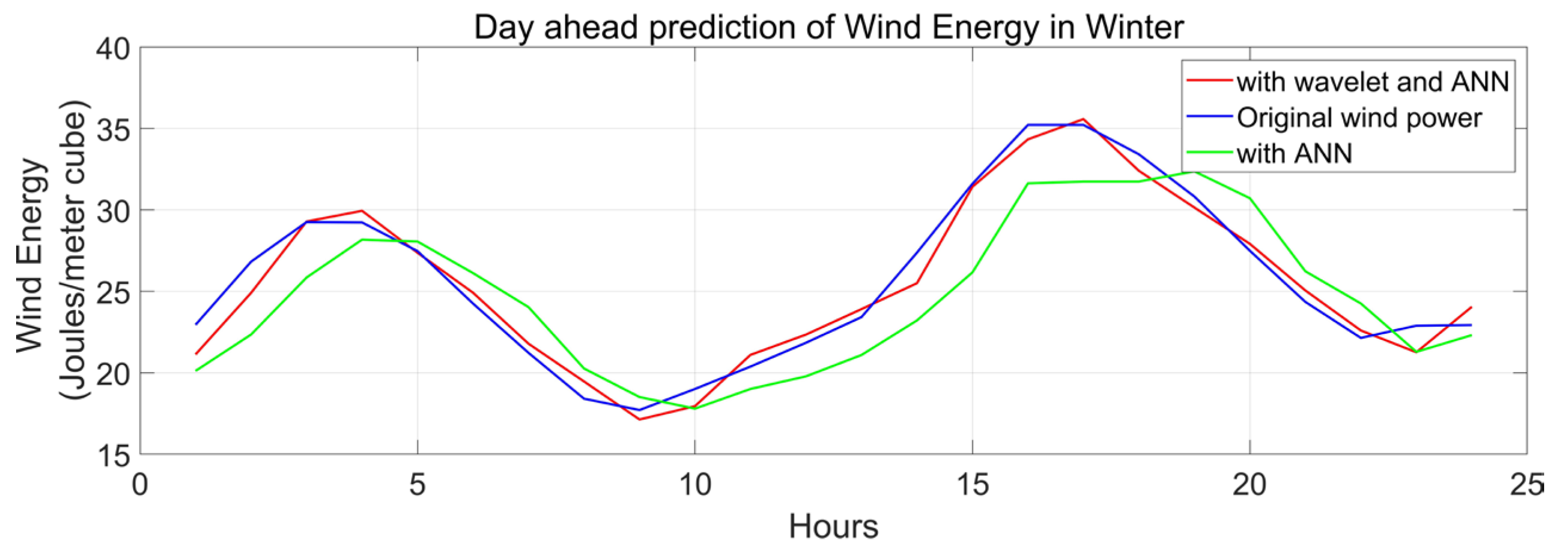
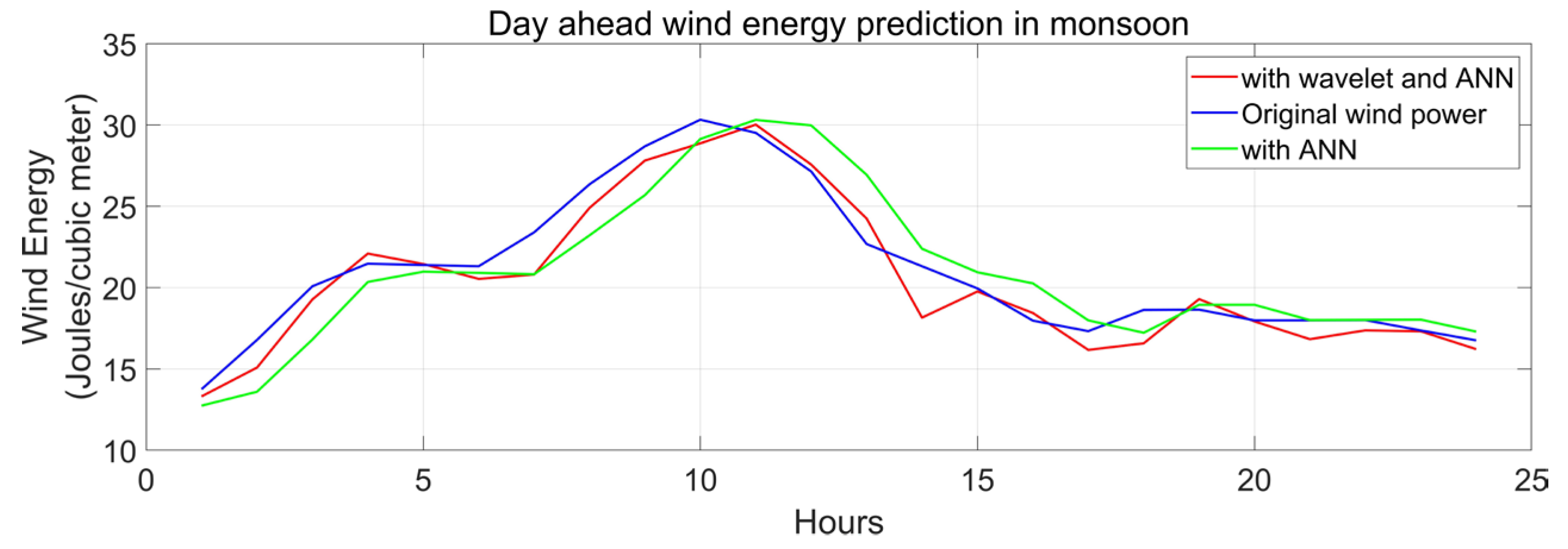
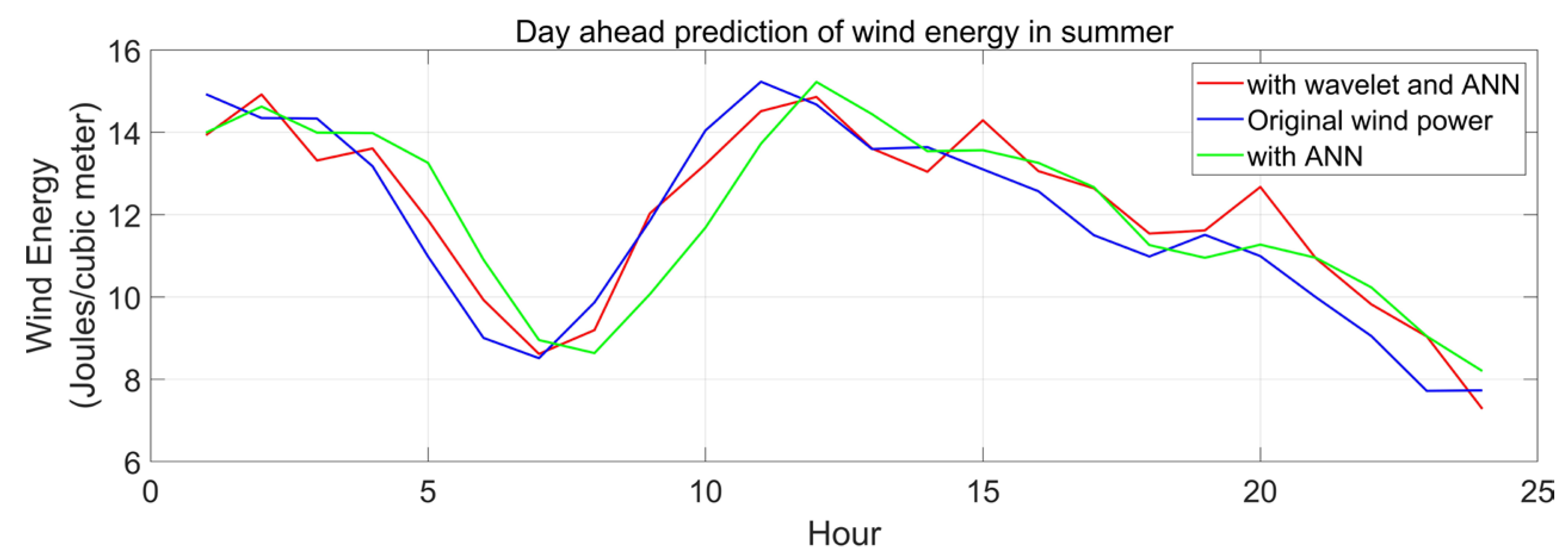
This algorithm for wind energy forecasting is assessed for the Kanyakumari district of Tamil Nadu. The regression coefficient and MSE are computed and observed to assess the model’s performance. The WNN and NN (neural network) model performances have been compared. For both models, the input data and the prediction horizon remained constant. The regression coefficient and MSE are computed and observed to assess the models’ performance. The WNN model’s performance has been compared to the NN model, which is shown in Table 1. The prediction horizon and the input data for both models remain the same. Figure 9, Figure 10 and Figure 11 depict a one-day forward forecast with a 60 min interval for the months of January, August, and April in 2019. The three seasons are represented by the three months. It is noted that wind generation may be predicted with a high degree of accuracy using the same model.
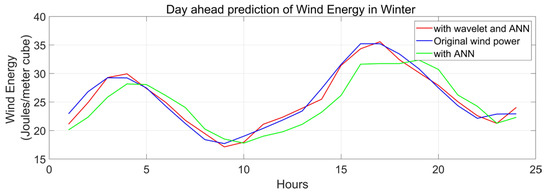
Figure 9.
Day-ahead prediction of wind energy in winter season.
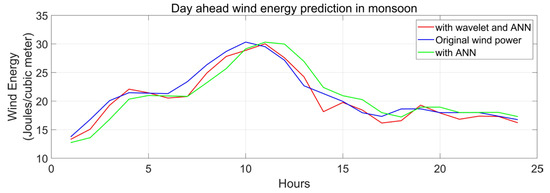
Figure 10.
Day-ahead prediction of wind energy in monsoon season.
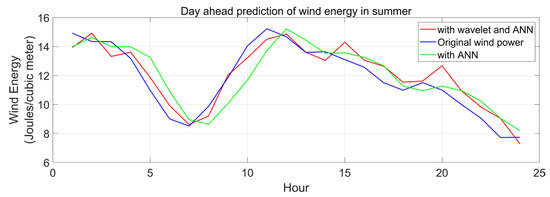
Figure 11.
Day-ahead prediction of wind energy in summer season.
5.2. Proposed WNN Model 2
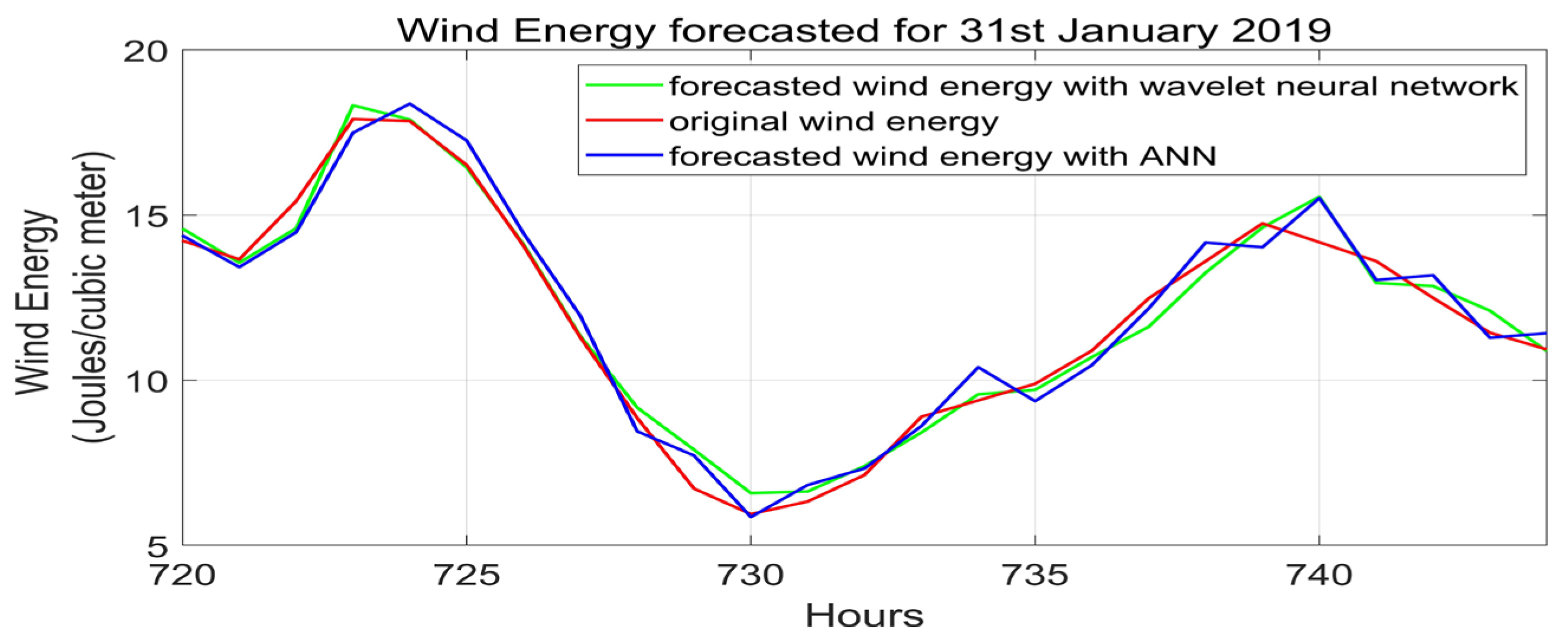
Data from the last 24 h is employed to prepare the data for this model. The wind speed for the first hour of the following day is predicted by the ANN model using 24 h of data. There are 24 input features. For the wavelet neural network, the previous 24 h of data points are decomposed into low- and high-frequency components. After wavelet decomposition, all the coefficients are given to the respective ANN model and then the signal is reconstructed to obtain the forecasted output. The model utilized the data from the past 30 days to forecast the 31st day of January because the data for the 31st day was not available for day-ahead prediction. Nine days of data (216 data points) were utilized for neural network validation, while the remaining 21 days of data (504 data points) were employed for training. An evaluation of the provided wind energy forecasting algorithm model is conducted for the Tamil Nadu district of Kanyakumari.
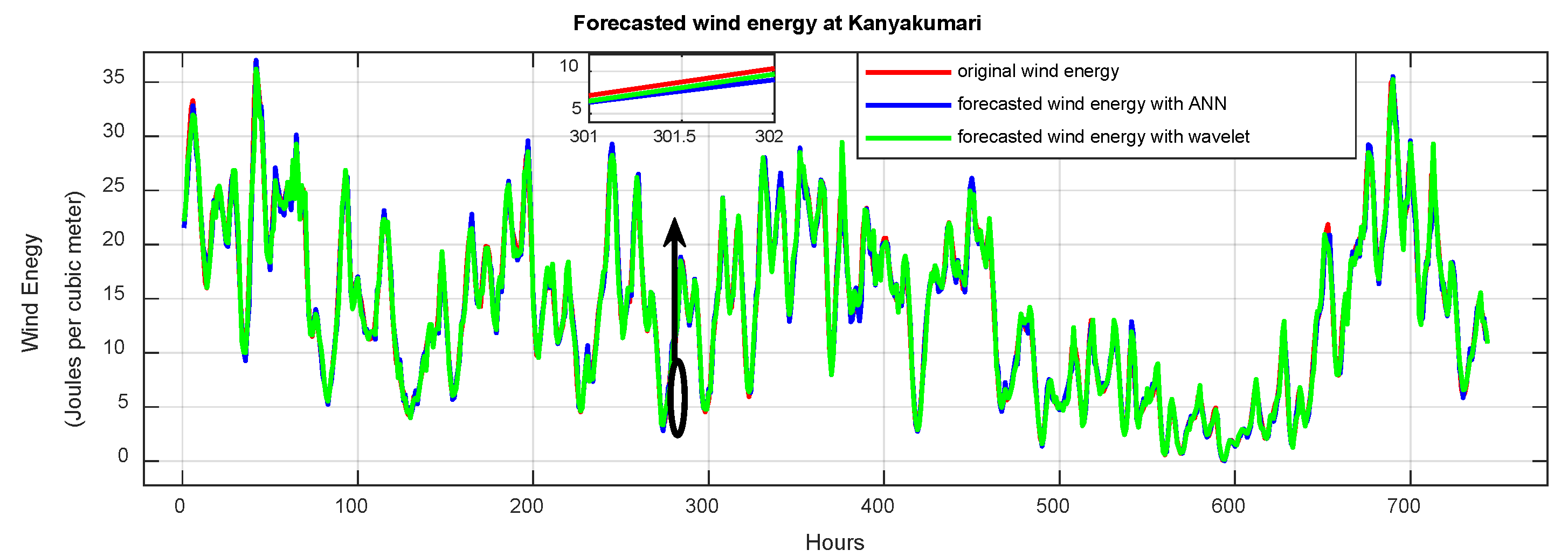
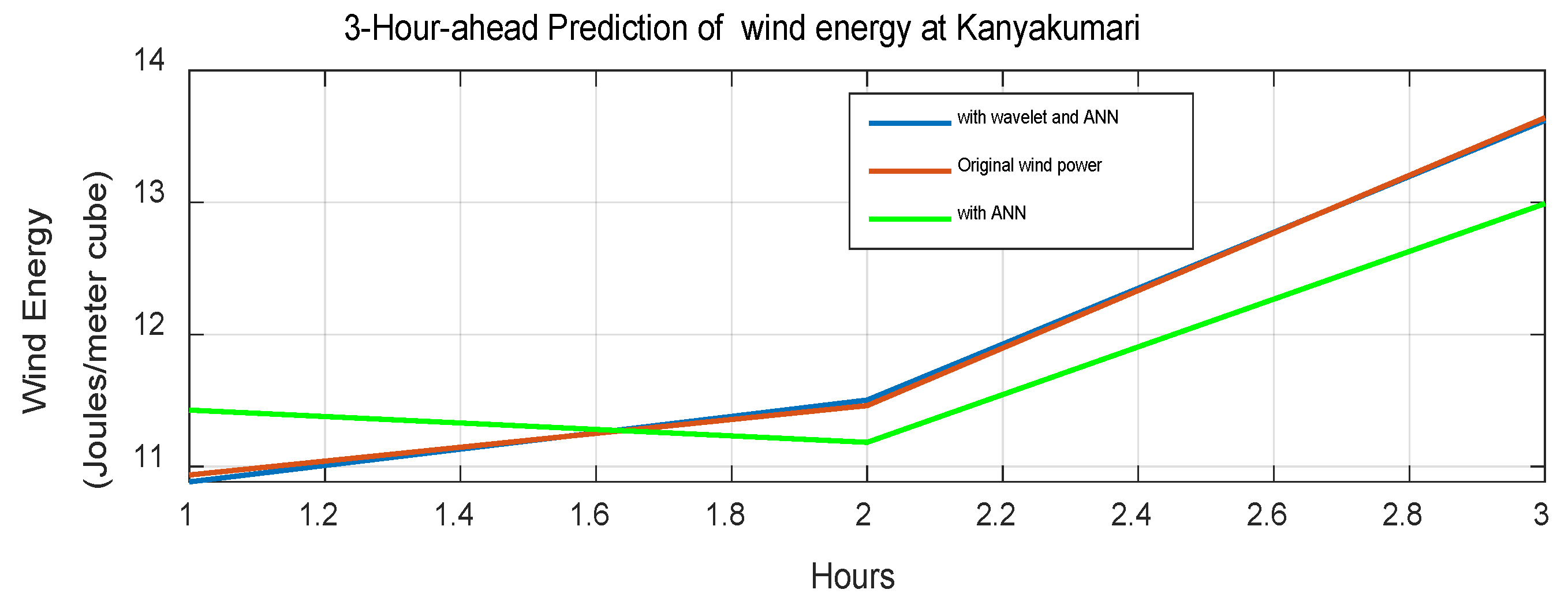
The forecasted wind energy with proposed model 2 for the month of January is shown in Figure 12, and the prediction for 31 January is shown in Figure 13. It was compared with the ANN model without wavelet decomposition. The MSE values for the day-ahead prediction and 3 h prediction are presented in Table 2. The MSE obtained using proposed model 2 for 3 h prediction is less than those shown in [1,29]. The three-hour prediction graph is shown in Figure 14. Comparison of wavelet neural network and feedforward neural network with proposed model 1 is shown in Table 3 and Comparison of ANN model and proposed multiple-component-approach WNN is shown in Table 4.
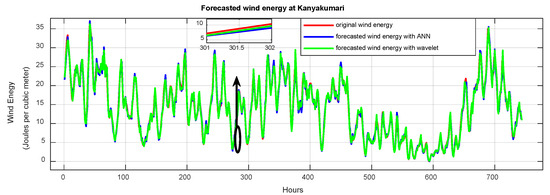
Figure 12.
Forecasted wind energy at Kanyakumari.
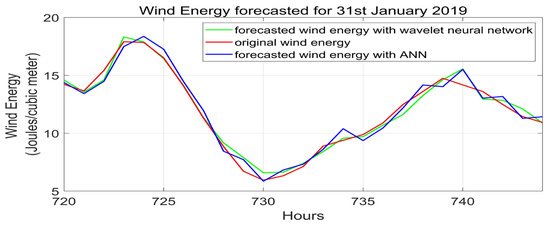
Figure 13.
Wind energy forecasted for 31 January 2019.
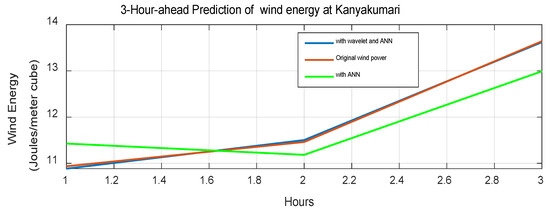
Figure 14.
3-hour-ahead-prediction of wind energy at Kanyakumari.

Table 3.
Comparison of wavelet neural network and feedforward neural network with proposed model 1.

Table 4.
Comparison of ANN model and proposed multiple-component-approach WNN.
6. Conclusions
In both the proposed wavelet-based models, it can be observed that the ANN with wavelet transform gives a lower Mean Square Error and a better regression coefficient than the ANN model without wavelet transform, which means it achieves better accuracy. The MSEs (Mean Square Errors) for the direct-approach ANN in the summer, monsoon, and winter seasons are 0.024295, 0.032753 and 0.01657, respectively, which are less than those achieved using an ANN without wavelet transform: 0.0482, 0.072641 and 0.11288, respectively. Using the multiple-component-approach WNN, the 3 h prediction and 24 h prediction MSEs are 0.000105 and 0.3005, which are less than those achieved without using wavelet transform, which have respective values of 0.0188 and 0.4022. If we compare the direct approach and the multiple component approach, the latter gives the best accuracy for 3 h prediction. Hence, this approach of using a WNN can be used for short-term prediction with high accuracy. Using autocorrelation, the number of lagged values can be determined and used as the features to a wavelet neural network. The direct approach can be applied to all seasons with significant accuracy and proves to be a robust model.
Author Contributions
Conceptualization, F.L.D. and A.J.N.; methodology, F.L.D.; software, F.L.D. and A.J.N.; validation, F.L.D. and A.J.N.; formal analysis, F.L.D.; investigation, F.L.D.; resources, F.L.D. and A.J.N.; data curation, F.L.D.; writing—original draft preparation, F.L.D.; writing—review and editing, F.L.D.; visualization, F.L.D.; supervision, F.L.D. and A.J.N.; project administration, F.L.D. and A.J.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon substantiated request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the existing affiliation information. This change does not affect the scientific content of the article.
References
- Dias, F.; Naik, A.J. Wind Power Prediction Model Using Artificial Neural Network. In Proceedings of the E3S Web of Conferences, International Conference on Renewable Energy, Green Computing and Sustainable Development, Bangkok, Thailand, 15–18 December 2024; EDP Sciences: Les Ulis, France; Volume 472. [Google Scholar]
- Indian Electricity Grid Code. Compendium of CERC Regulations. Available online: https://allaboutrenewables.com (accessed on 28 April 2025).
- Cristea, P.; Tuduce, R.; Cristea, A. Time series prediction with wavelet neural networks. In Proceedings of the 5th Seminar on Neural Network Applications in Electrical Engineering, Belgrade, Yugoslavia, 25–27 September 2000. [Google Scholar]
- Taylor, J.W.; McSharry, P.E.; Buizza, R. Wind power density forecasting using ensemble predictions and time series models. IEEE Trans. Energy Convers. 2009, 24, 775–782. [Google Scholar] [CrossRef]
- Alexiadis, M.C.; Dokopoulos, P.S.; Sahsamanoglou, H.S. Wind speed and power forecasting based on spatial correlation models. IEEE Trans. Energy Convers. 1999, 14, 836–842. [Google Scholar] [CrossRef]
- Mbuli, N.; Mathonsi, M.; Seitshiro, M.; Pretorius, J.-H.C. Decomposition forecasting methods: A review of applications in power systems. Energy Rep. 2020, 6, 298–306. [Google Scholar] [CrossRef]
- Li, Z.; Luo, X.; Liu, M.; Cao, X.; Du, S.; Sun, H. Wind power prediction based on EEMD-Tent-SSA-LS-SVM. Energy Rep. 2020, 8, 3234–3243. [Google Scholar] [CrossRef]
- Wu, Y.P.; Wu, W.B. Analysis of wavelet decomposition properties of wind turbine signal. Energy Rep. 2021, 7, 873–879. [Google Scholar] [CrossRef]
- Salles, R.; Belloze, K.; Porto, F.; Gonzalez, P.H.; Ogasawara, E. Nonstationary time series transformation methods: An experimental review. Knowl.-Based Syst. 2019, 164, 274–291. [Google Scholar] [CrossRef]
- Clemen, R.T. Combining forecasts: A review and annotated bibliography. Int. J. Forecast. 1989, 5, 559–583. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, X.; Pan, K.; Liu, Y. A novel wind speed forecasting based on hybrid decomposition and online sequential outlier robust extreme learning machine. Energy Convers. Manag. 2019, 180, 338–357. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, H.; Zhang, J.; Yan, Y.; Zhang, L.; Wu, C.; Hua, X.; Wang, Y. Wind power prediction based on variational mode decomposition multi-frequency combinations. J. Mod. Power Syst. Clean Energy 2019, 7, 281–288. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Nabney, I.T. Short-term electricity demand and gas price forecasts using wavelet transforms and adaptive models. Energy 2010, 35, 3674–3685. [Google Scholar] [CrossRef]
- Qian, Z.; Pei, Y.; Zareipour, H.; Chen, N. A review and discussion of decomposition-based hybrid models for wind energy forecasting applications. Appl. Energy 2019, 235, 939–953. [Google Scholar] [CrossRef]
- Akbal, Y.; Ünlü, K.D. A hybrid deep learning methodology for wind power forecasting based on attention. Int. J. Green Energy 2024, 21, 3713–3722. [Google Scholar] [CrossRef]
- Bashir, T.; Wang, H.; Tahir, M.; Zhang, Y. Wind and solar power forecasting based on hybrid CNN-ABiLSTM, CNN-transformer-MLP models. Renew. Energy 2025, 239, 122055. [Google Scholar] [CrossRef]
- Fan, W.; Fu, Y.; Zheng, S.; Bian, J.; Zhou, Y.; Xiong, H. Dewp: Deep expansion learning for wind power forecasting. ACM Trans. Knowl. Discov. Data 2024, 18, 1–21. [Google Scholar] [CrossRef]
- Priya, C.B.; Arulanand, N. Enhancing Medium Term Wind Power Forecasting Accuracy with Dual Stage Attention Based TCN-GRU Model and White Shark Optimization. Electr. Power Compon. Syst. 2024, 1–18. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, J.; Zheng, W.; Zhang, F. Long-term wind power forecasting with series decomposition and spatio-temporal graph neural network. Int. J. Green Energy 2024, 21, 3470–3484. [Google Scholar] [CrossRef]
- Mwaura, J.I.; Kenduiywo, B.K. County level maize yield estimation using artifcial neural network. Model. Earth Syst. Environ. 2020, 7, 1417–1424. [Google Scholar] [CrossRef]
- Wagh, V.M.; Panaskar, D.B.; Muley, A.A.; Mukate, S.V.; Lolage, Y.P.; Aamalawar, M.L. Prediction of groundwater suitability for irrigation using artificial neural network model: A case study of Nanded tehsil, Maharashtra, India. Model. Earth Syst. Environ. 2016, 2, 1–10. [Google Scholar] [CrossRef]
- Feng, Q.; Qian, S. Research on the prediction of short-term wind power based on wavelet neural networks. Energy Rep. 2022, 8, 553–559. [Google Scholar] [CrossRef]
- Gao, X.; Xiao, F.; Zhang, J.; Cao, C. Short-term prediction of chaotic time series by wavelet networks. In Proceedings of the Fifth World Congress on Intelligent Control and Automation, Hangzhou, China, 15–19 June 2004; Volume 3, pp. 1931–1935. [Google Scholar]
- Abhinav, R.; Pindoriya, N.M.; Wu, J.; Long, C. Short-term wind power forecasting using wavelet-based neural network. Energy Procedia 2017, 142, 455–460. [Google Scholar] [CrossRef]
- Kio, A.E.; Xu, J.; Gautam, N.; Ding, Y. Wavelet decomposition and neural networks: A potent combination for short term wind speed and power forecasting. Front. Energy Res. 2024, 12, 1277464. [Google Scholar] [CrossRef]
- Shafaei, M.; Adamowski, J.; Fakheri-Fard, A.; Dinpashoh, Y.; Adamowski, K. A wavelet-SARIMA-ANN hybrid model for precipitation forecasting. J. Water Land Dev. 2016, 28, 27–36. [Google Scholar] [CrossRef]
- Amirat, Y.; Benbouzid, M.E.H. Survey paper generators for wind energy conversion systems: State of the art and coming attractions. J. Electr. Syst. 2007, 3, 26–38. [Google Scholar]
- Essandoh, E.O. Wind Data Collection and Analysis in Kumasi. Ph.D. Thesis, Kwame Nkrumah University of Science and Technology, Kumasi, Ghana, 2012. [Google Scholar]
- Mohammed, M.A.; Ahmed, L.A. Forecasting wind speed using the proposed wavelet neural network. Discret. Dyn. Nat. Soc. 2023, 2023, 9940038. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).