Turbulent Flow over a Rough Surface in a Wind Tunnel
Abstract
1. Introduction
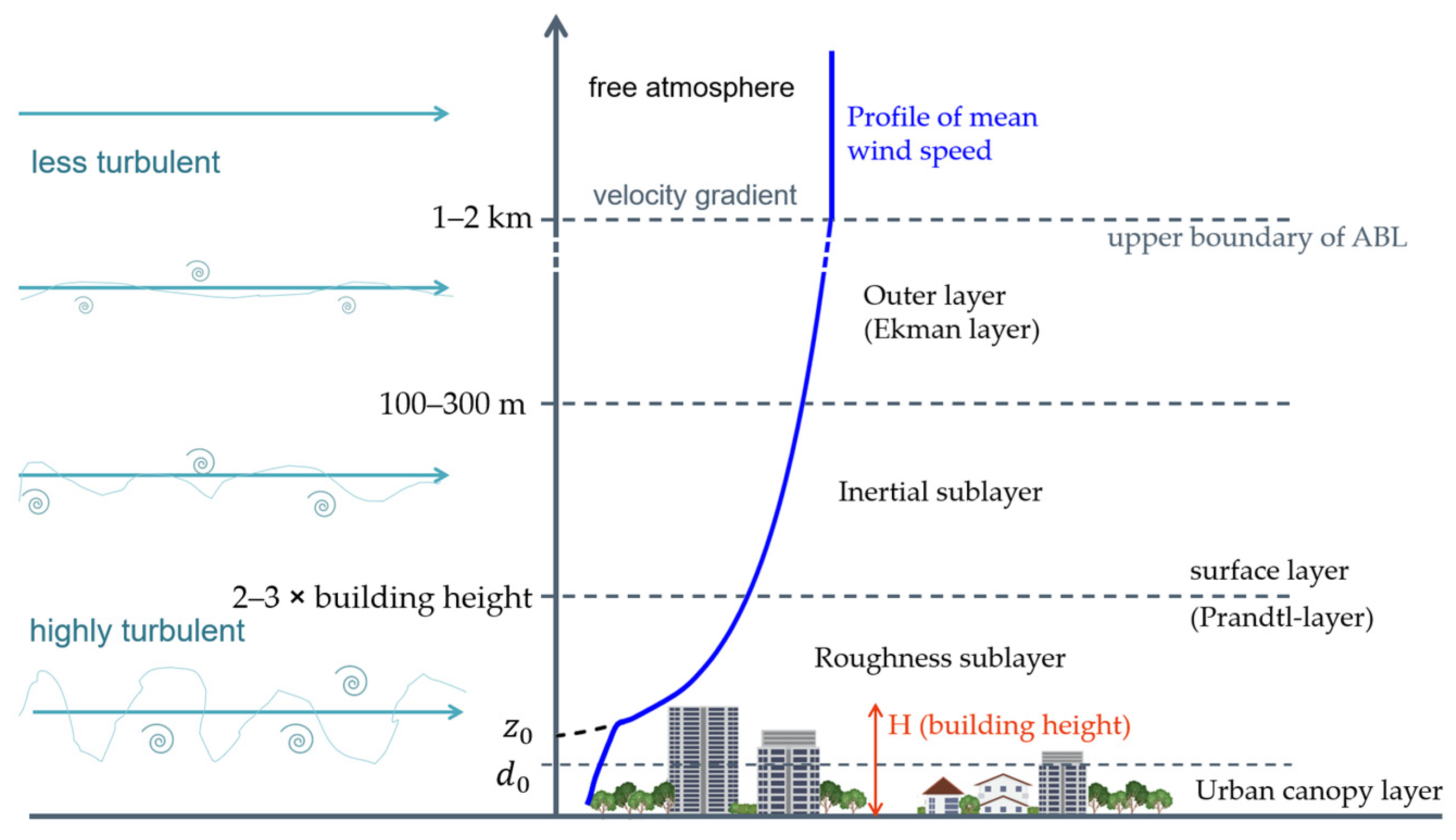
2. Flow over a Rough Surface
2.1. Turbulent Flow over a Rough Surface
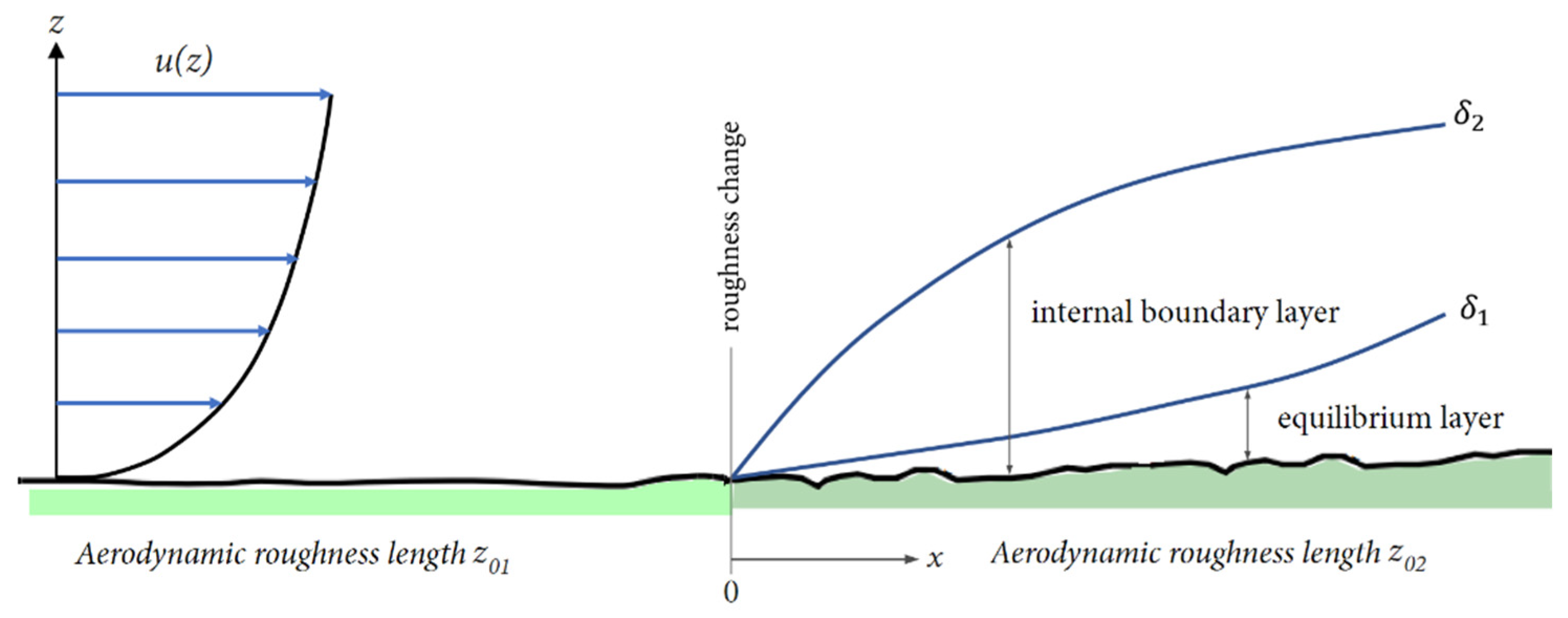
2.2. Flow over a Terrain Change
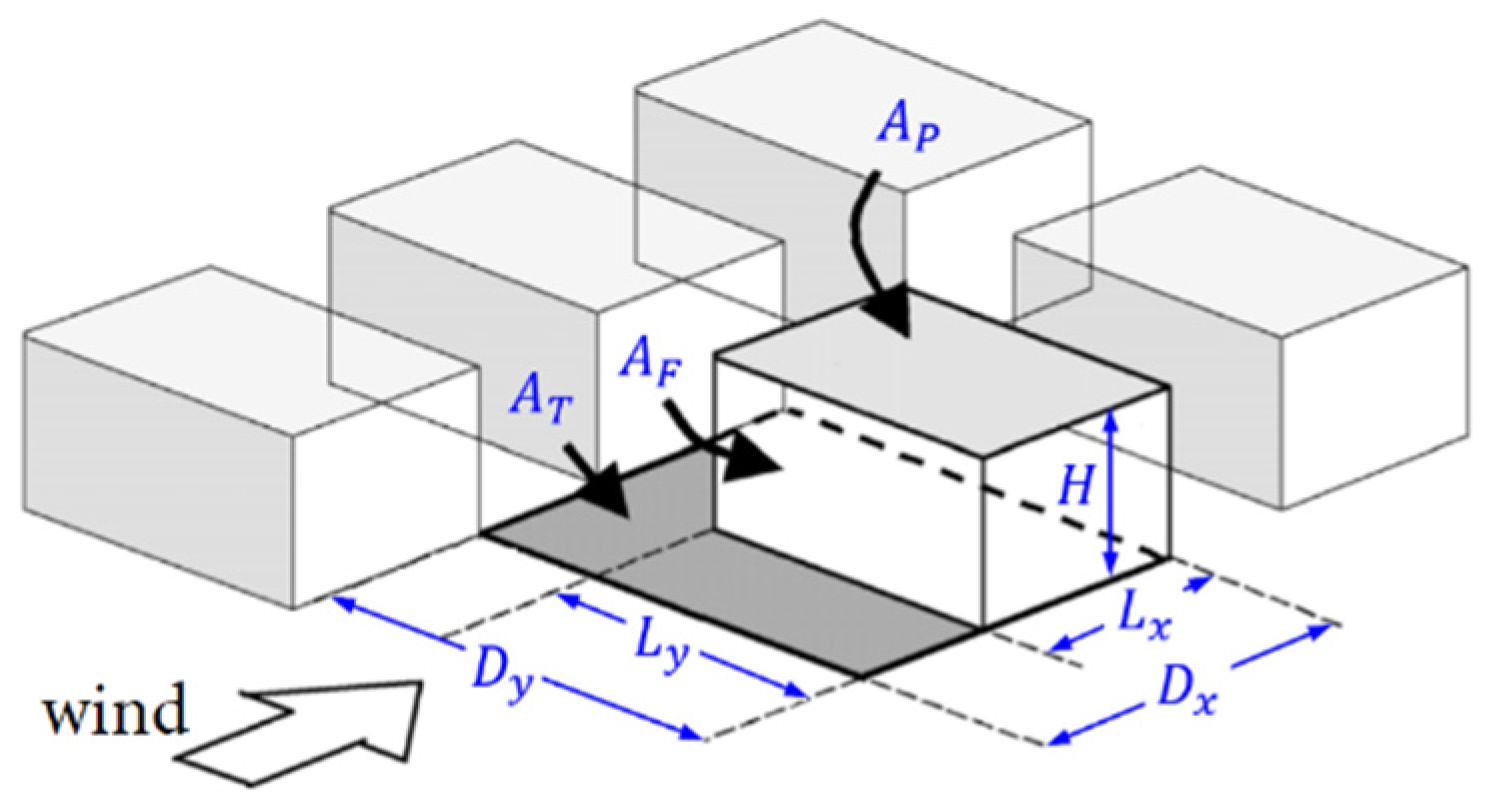
3. Morphometric Analysis
- Based on roughness height: ;
- Based on the ratio of the plan area of the obstacles to the lot area: ;
- Based on the ratio of the frontal area of the obstacles to the lot area: .
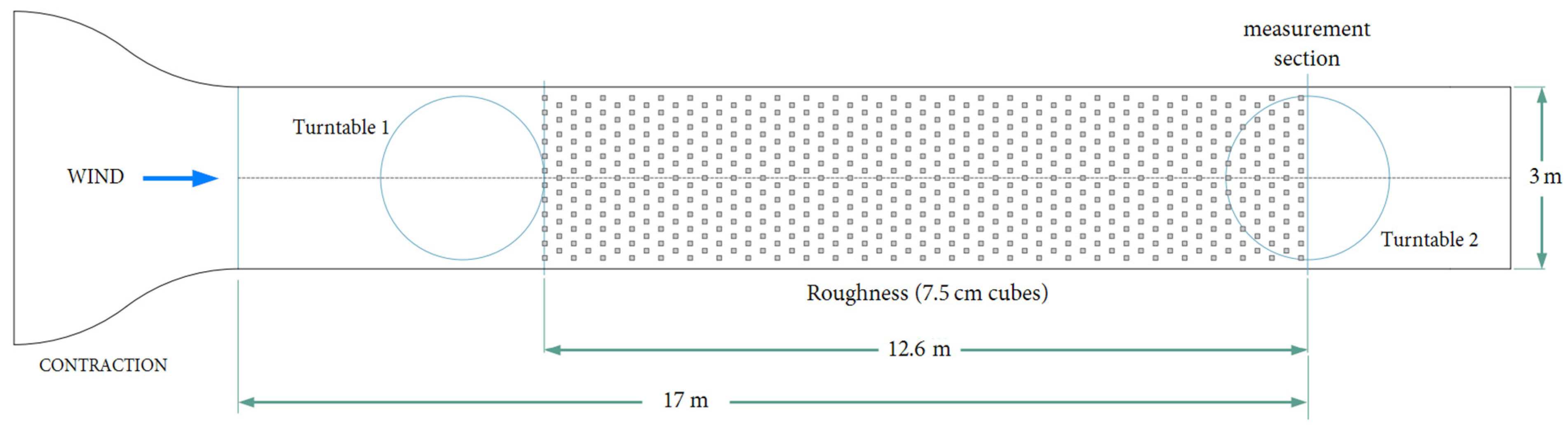
4. Experimental Study in Wind Tunnel
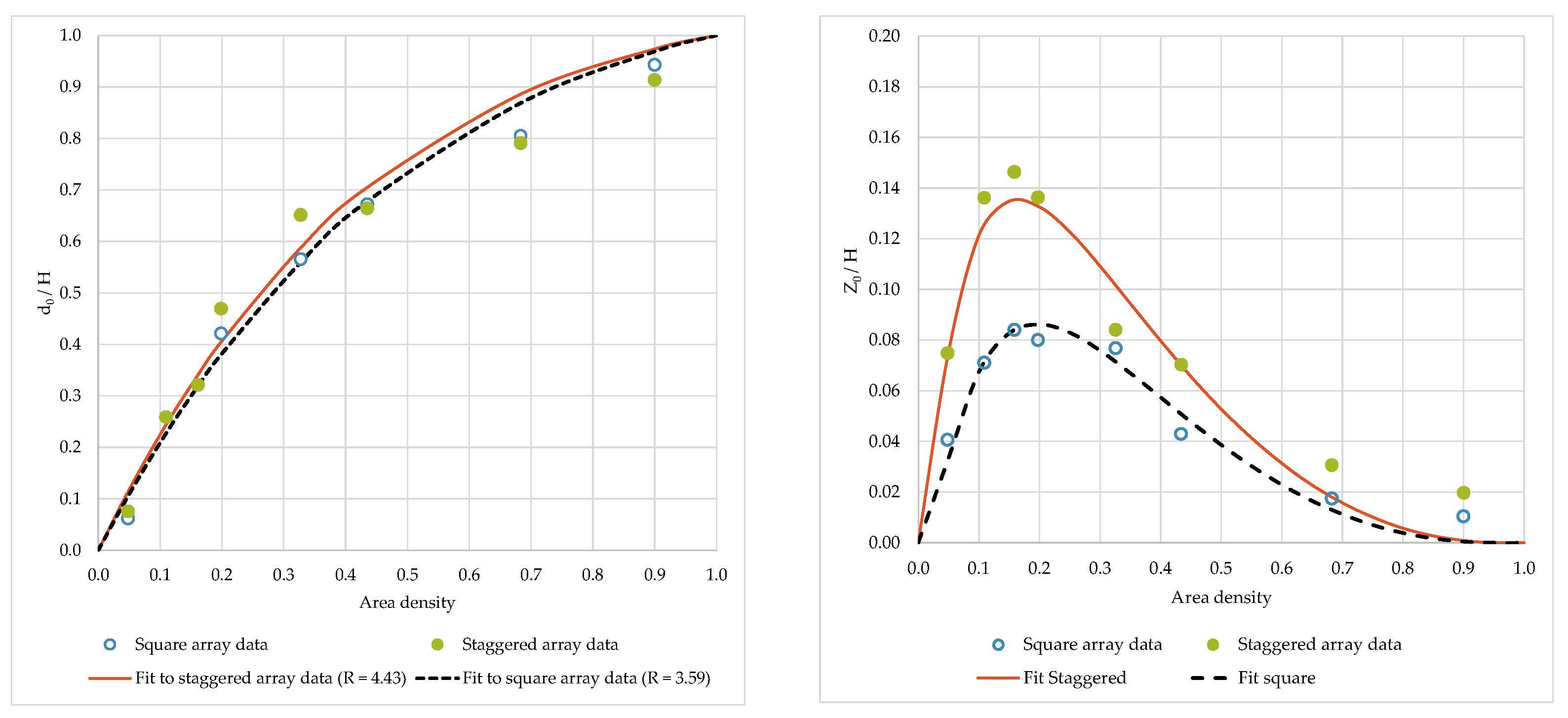
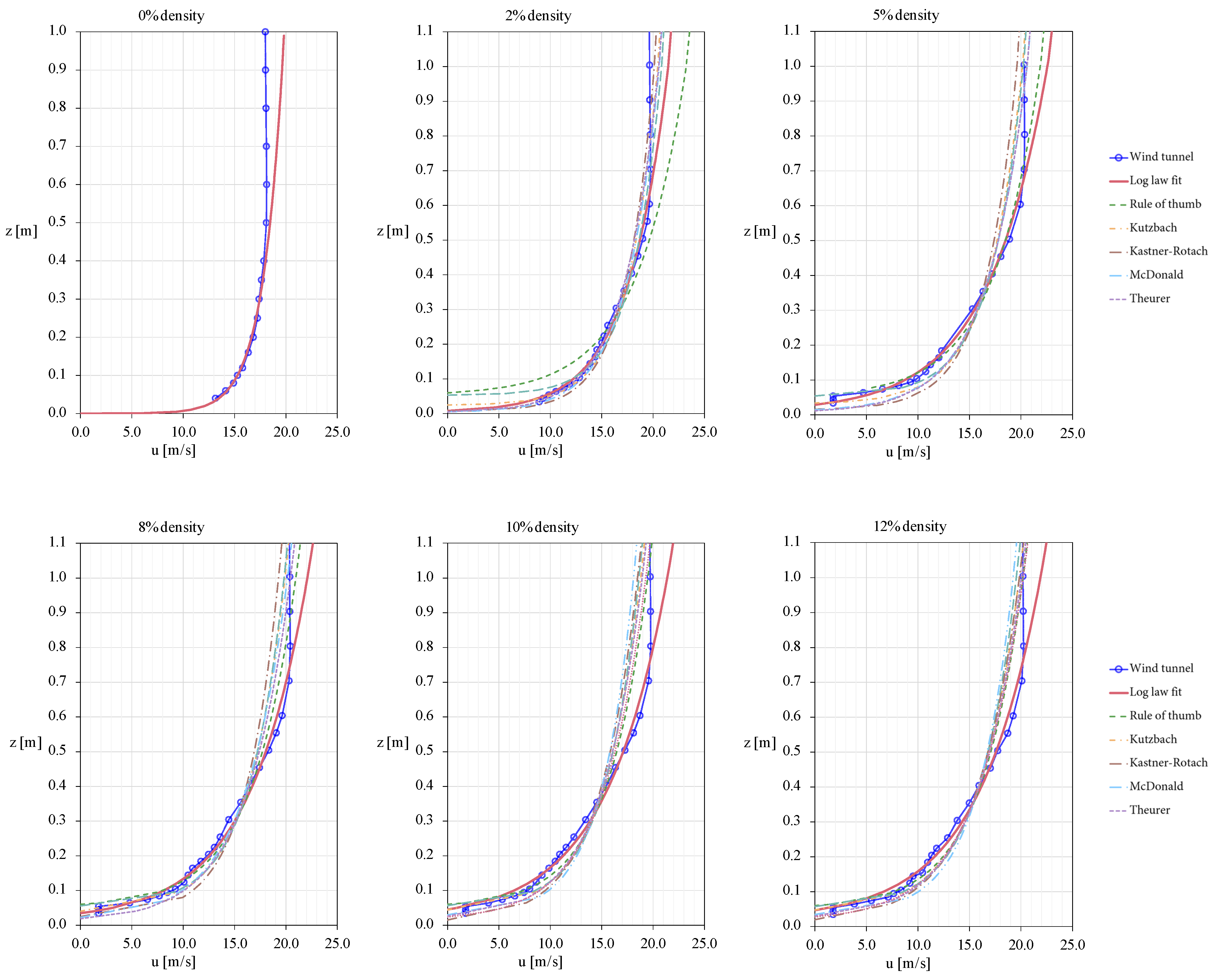
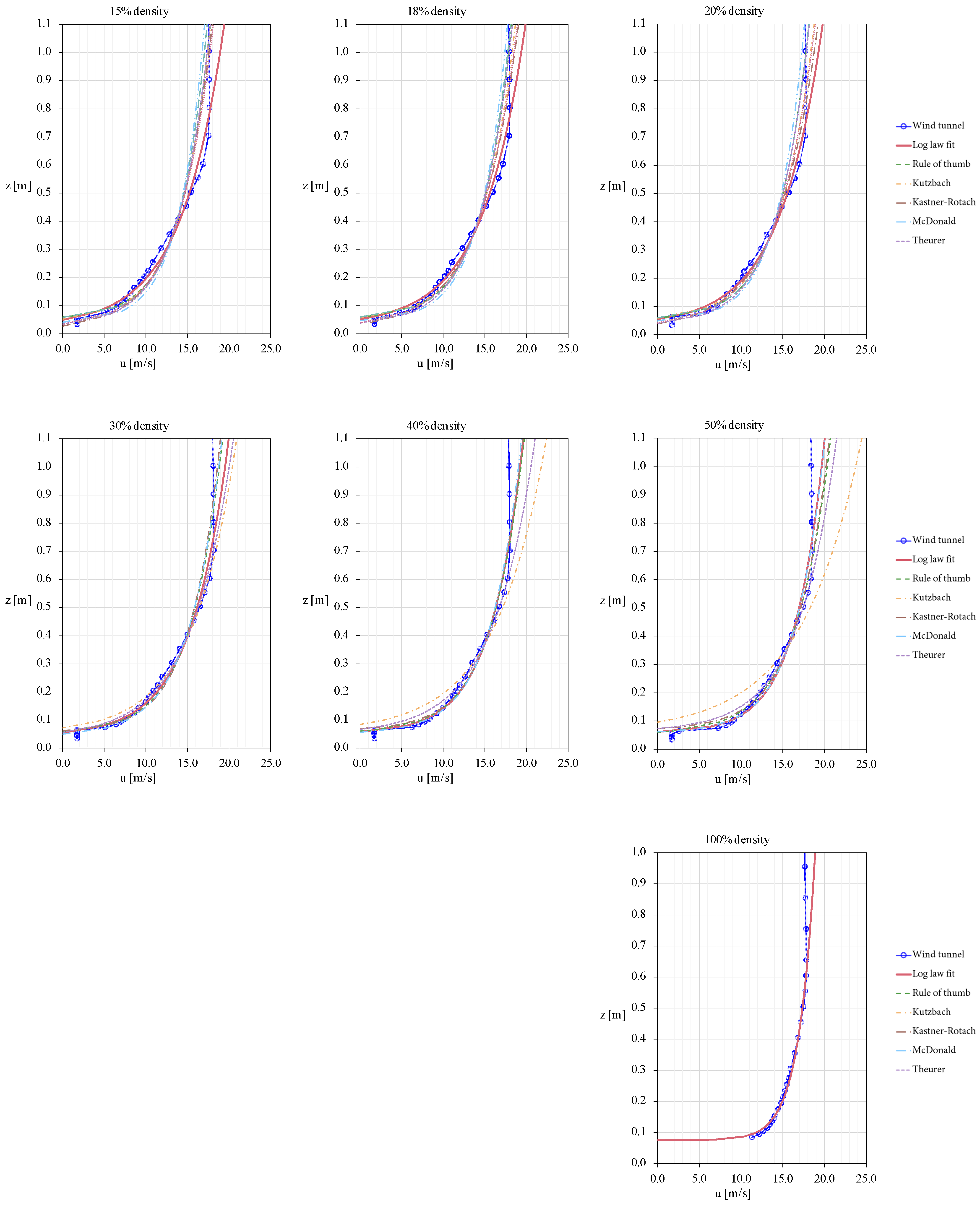
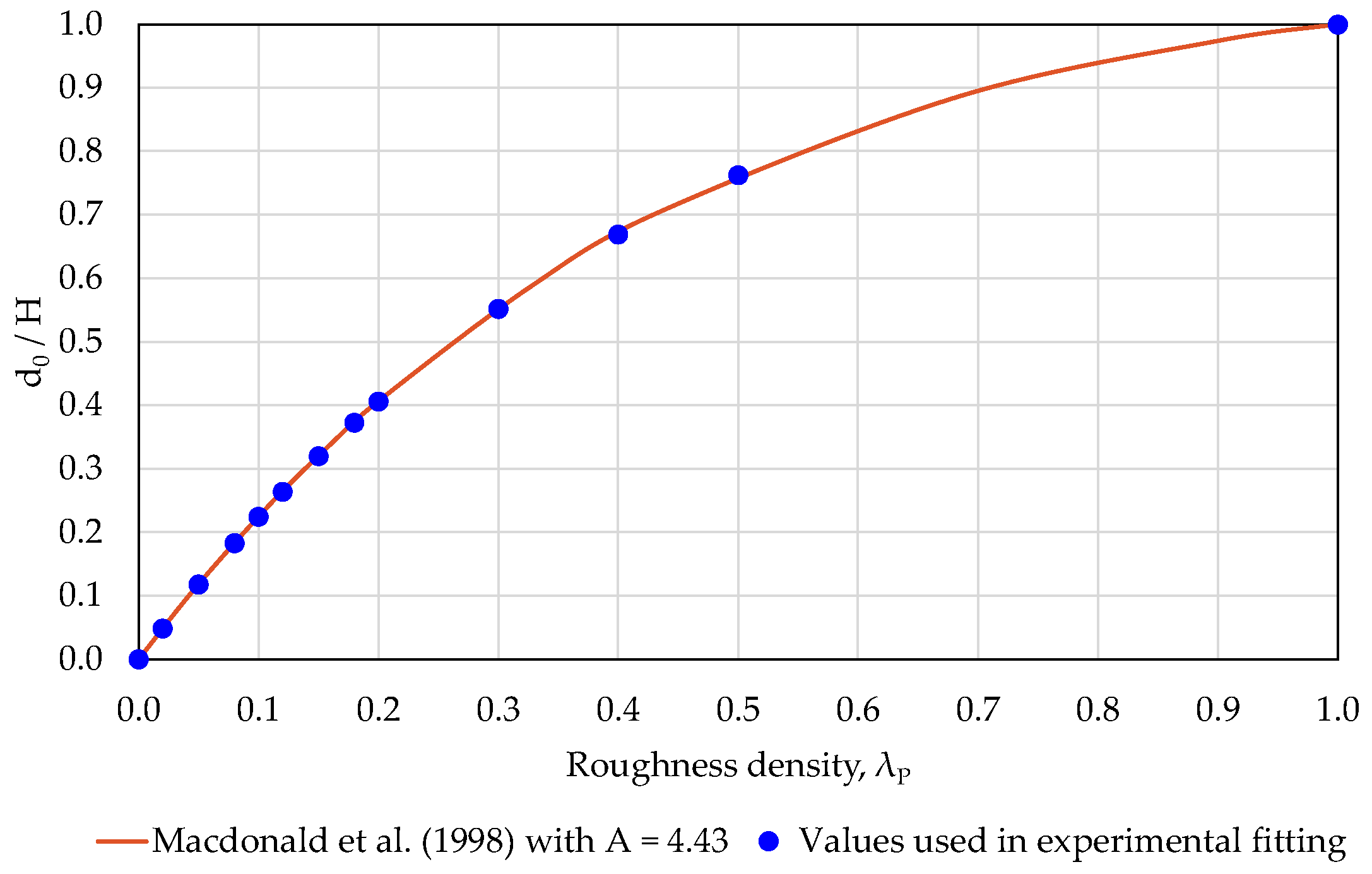
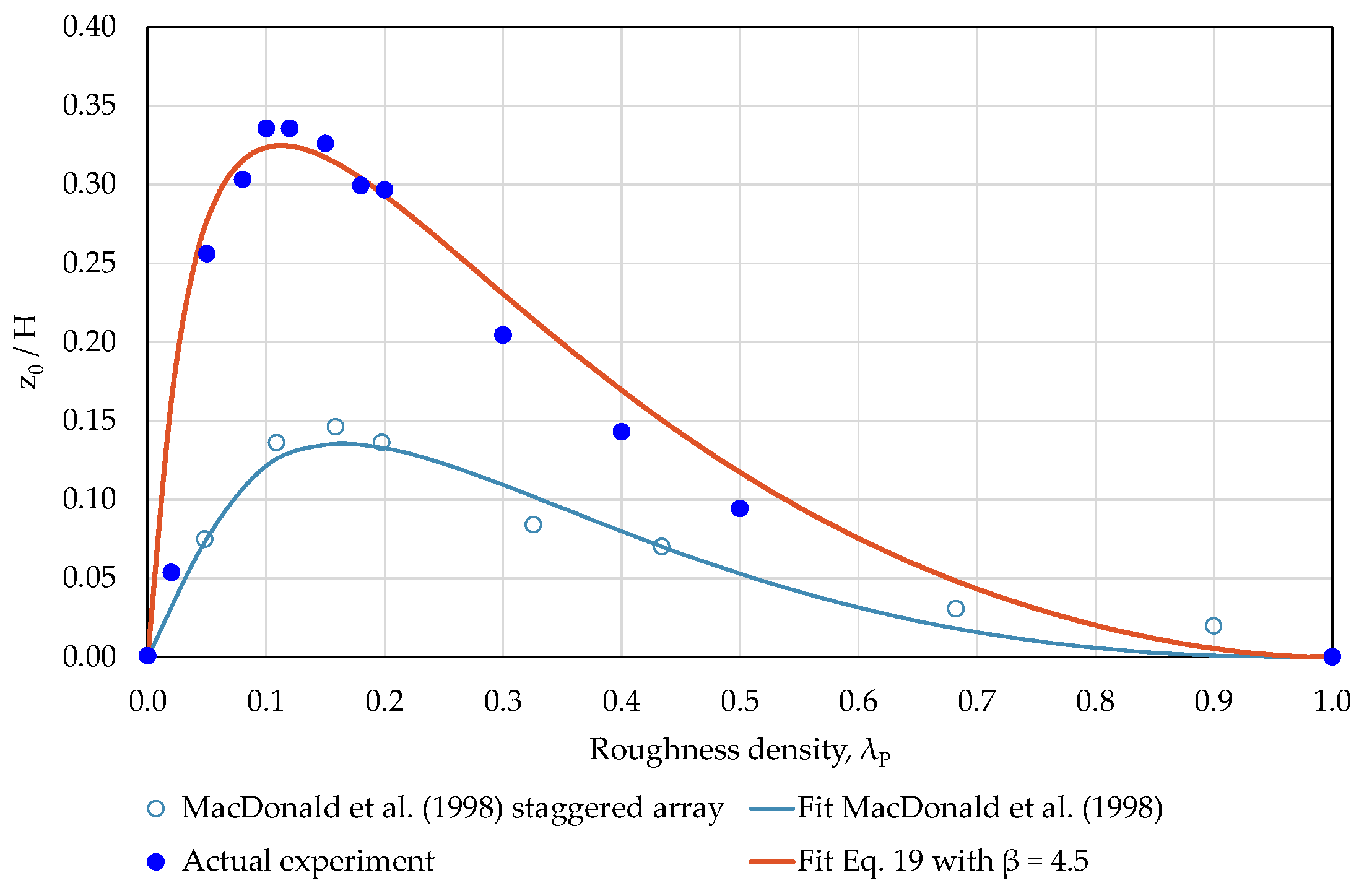
4.1. Fitting of Aerodynamic Surface Characteristics
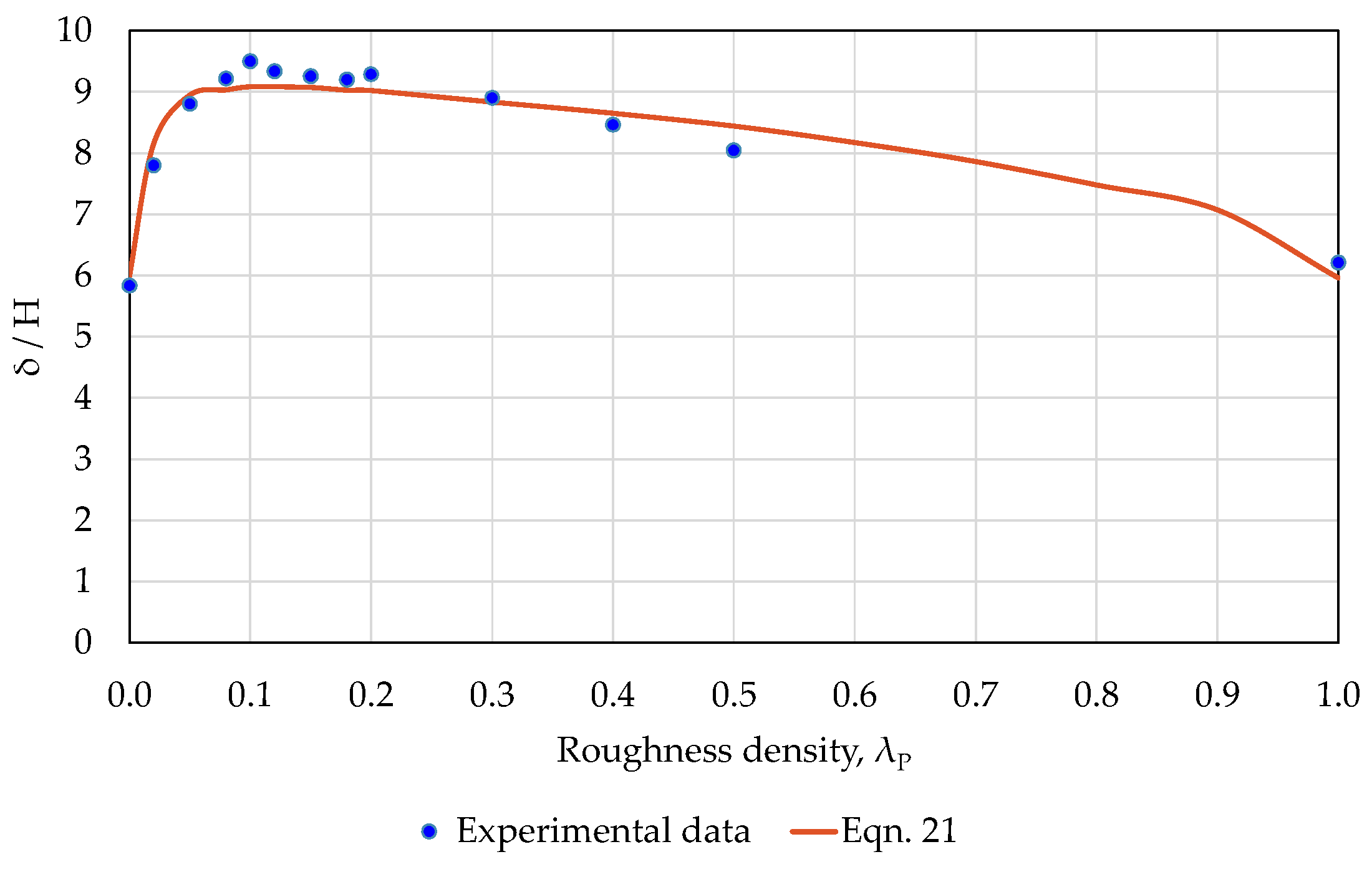
4.2. Boundary Layer Depth
4.3. Turbulence Intensity
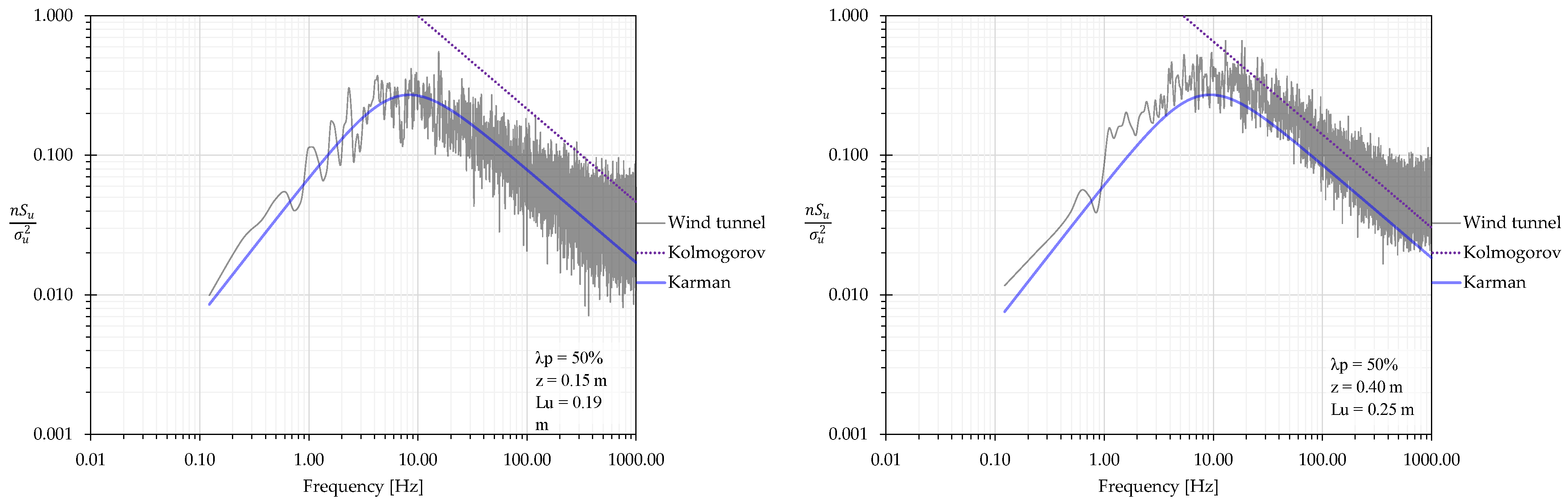
4.4. Spectral Density Function
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van der Hoven, I. Power spectrum of horizontal wind speed in the frequency range from 0.0007 to 900 cycles per hour. J. Meteorol. 1957, 14, 160–164. [Google Scholar] [CrossRef]
- Solari, G. Wind Science and Engineering: Origins, Developments, Fundamentals and Advancements; Springer: Basel, Switzerland, 2019. [Google Scholar]
- Davenport, A.G. A Statistical Approach to the Treatment of Wind Loading on Tall Masts and Suspension Bridges. Ph.D. Thesis, University of Bristol, Bristol, UK, 1961. [Google Scholar]
- Hu, W.; Yang, Q.; Peng, L.; Liu, L.; Zhang, P.; Li, S.; Wu, J. Non-stationary modeling and simulation of strong winds. Heliyon 2024, 10, e35195. [Google Scholar] [CrossRef] [PubMed]
- Hangan, H.; Romanic, D.; Jubayer, C. Three-dimensional, non-stationary and non-Gaussian (3D-NS-NG) wind fields and their implications to wind–structure interaction problems. J. Fluids Struct. 2019, 91, 102583. [Google Scholar] [CrossRef]
- Huang, M.; Li, Q.; Xu, H.; Lou, W.; Lin, N. Non-stationary statistical modeling of extreme wind speed series with exposure correction. Wind. Struct. 2018, 26, 129–146. [Google Scholar] [CrossRef]
- Jiang, F.; Zhang, M.; Li, Y.; Zhang, J.; Qin, J.; Wu, L. Field measurement study of wind characteristics in mountain terrain: Focusing on sudden intense winds. J. Wind. Eng. Ind. Aerodyn. 2021, 218, 104781. [Google Scholar] [CrossRef]
- Liu, Y.X.; Hong, H.P. Analyzing, modelling, and simulating nonstationary thunderstorm winds in two horizontal orthogonal directions at a point in space. J. Wind. Eng. Ind. Aerodyn. 2023, 237, 105412. [Google Scholar] [CrossRef]
- Tubino, F.; Solari, G. Time varying mean extraction for stationary and nonstationary winds. J. Wind. Eng. Ind. Aerodyn. 2020, 203, 104187. [Google Scholar] [CrossRef]
- Su, Y.; Huang, G.; Xu, Y. Derivation of time-varying mean for non-stationary downburst winds. J. Wind Eng. Ind. Aerodyn. 2015, 141, 39–48. [Google Scholar] [CrossRef]
- Zhang, S.; Solari, G.; Burlando, M.; Yang, Q. Directional decomposition and properties of thunderstorm outflows. J. Wind Eng. Ind. Aerodyn. 2019, 189, 71–90. [Google Scholar] [CrossRef]
- Hui, Y.; Li, B.; Kawai, H.; Yang, Q. Non-stationary and non-Gaussian characteristics of wind speeds. Wind. Struct. 2017, 24, 59–78. [Google Scholar] [CrossRef]
- Counihan, J. An Improved Method of Simulating an Atmospheric Boundary Layer in a Wind Tunnel. Atmos. Environ. 1969, 3, 197–214. [Google Scholar] [CrossRef]
- Counihan, J. Wind tunnel determination of the roughness length as a function of the fetch and the roughness density of three-dimensional roughness elements. Atmos. Environ. 1971, 5, 637–642. [Google Scholar] [CrossRef]
- Counihan, J. Simulation of an Adiabatic Urban Boundary Layer in the Wind Tunnel. Atmos. Environ. 1973, 7, 673–689. [Google Scholar] [CrossRef]
- Standen, N.M. A Spire Array for Generating Thick Turbulent Shear Layers for Natural Wind Simulation in Wind Tunnels; Report of National Aeronautical Establishment; National Research Council Canada: Ottawa, OT, Canada, 1972; LTR-LA-94. [Google Scholar]
- Cook, N.J. Wind-Tunnel Simulation of the Adiabatic Atmospheric Boundary Layer by Roughness, Barrier and Mixing Device Methods. J. Ind. Aerodyn. 1978, 3, 157–176. [Google Scholar] [CrossRef]
- Gartshore, I.S.; De Croos, K.A. Roughness element geometry required for wind tunnel simulations of the atmospheric wind. Transactions of the ASME, New York. J. Fluids Eng. 1977, 99, 480–485. [Google Scholar] [CrossRef]
- Cermak, J.E. Wind-Simulation Criteria for Wind-Effect Tests. J. Struct. Eng. 1984, 110, 328–339. [Google Scholar] [CrossRef]
- Irwin, H.P.A.H. The Design of Spires for Wind Simulation. J. Wind. Eng. Ind. Aerodyn. 1981, 7, 361–366. [Google Scholar] [CrossRef]
- Ohya, Y. Wind-Tunnel study of atmospheric stable boundary layers over a rough surface. Bound.-Layer Meteorol. 2001, 98, 57–82. [Google Scholar] [CrossRef]
- Kozmar, H. Truncated vortex generators for part-depth wind tunnel simulations of the atmospheric boundary layer flow. J. Wind Eng. Ind. Aerodyn. 2011, 99, 130–136. [Google Scholar] [CrossRef]
- Dyrbye, C.; Hansen, S.O. Wind Loads on Structures; Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Cheng, H.; Castro, I.P. Near wall flow over urban-like roughness. Bound.-Layer Meteorol. 2002, 104, 229–259. [Google Scholar] [CrossRef]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows, Their Structure and Management; Oxford University Press: Oxford, UK, 1994; 289p. [Google Scholar]
- ESDU 85020; Characteristics of Atmospheric Turbulence Near the Ground. Part II: Single Point Data for Strong Winds (Neutral Atmosphere). ESDU International: London, UK, 1985.
- Savelyev, S.A.; Taylor, P.A. Internal boundary layers: I. Height formulae for neutral and diabatic flows. Bound.-Layer Meteorol. 2005, 115, 1–25. [Google Scholar] [CrossRef]
- Savelyev, S.A.; Taylor, P.A. Notes on Internal Boundary-Layer Height Formula. Bound.-Layer Meteorol. 2001, 101, 293–301. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Dutton, J.A. Atmospheric Turbulence; Wiley (Interscience): New York, NY, USA, 1984; 397p. [Google Scholar]
- Grimmond, C.S.B.; Oke, T.R. Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 1999, 38, 1262–1292. [Google Scholar] [CrossRef]
- Macdonald, R.W.; Griffiths, R.F.; Hall, D.J. An improved method for estimation of surface roughness of obstacle arrays. Atmos. Environ. 1998, 32, 1857–1864. [Google Scholar] [CrossRef]
- Kutzbach, J. Investigations of the Modification of Wind Profiles by Artificially Controlled Surface Roughness. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 1961. [Google Scholar]
- Lettau, H. Note on aerodynamic roughness parameter estimation on the basis of roughness element description. J. Appl. Meteorol. 1969, 8, 828–832. [Google Scholar] [CrossRef]
- Theurer, W. Dispersion of Ground-Level Emissions in Complex Built-Up Areas. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, 1993. (In German). [Google Scholar]
- Kastner-Klein, P.; Rotach, M.W. Mean flow and turbulence characteristics in an urban roughness sublayer. BLM 2004, 111, 55–84. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and testing of a GRG code for nonlinear optimization. ACM Tran. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Introduction to Spectral Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1997. [Google Scholar]
- Trush, A.; Pospisil, S.; Kozmar, H. Comparison of Turbulence Integral Length Scale Determination Methods; WIT Press: Southampton, UK, 2020; pp. 113–123. [Google Scholar] [CrossRef]



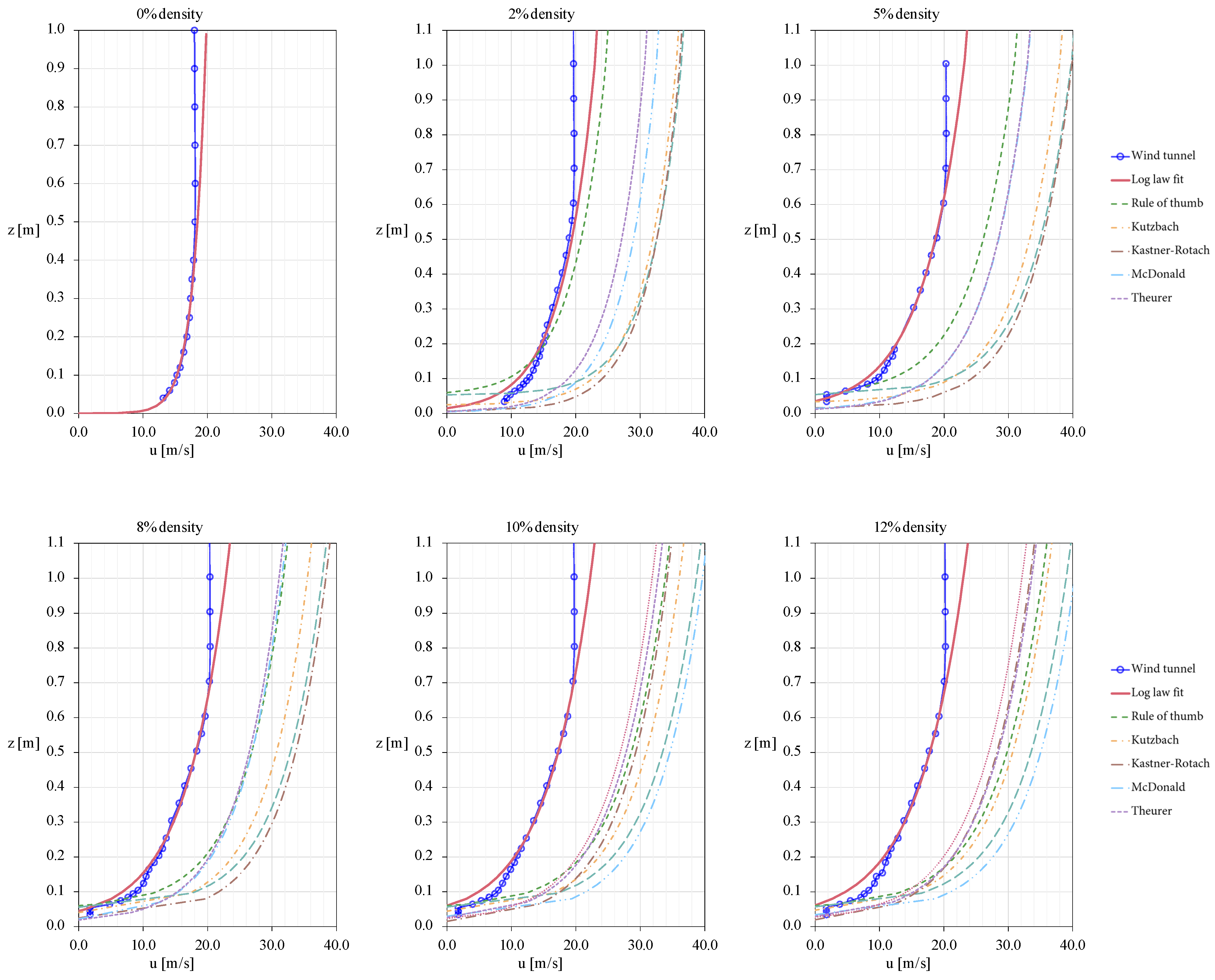
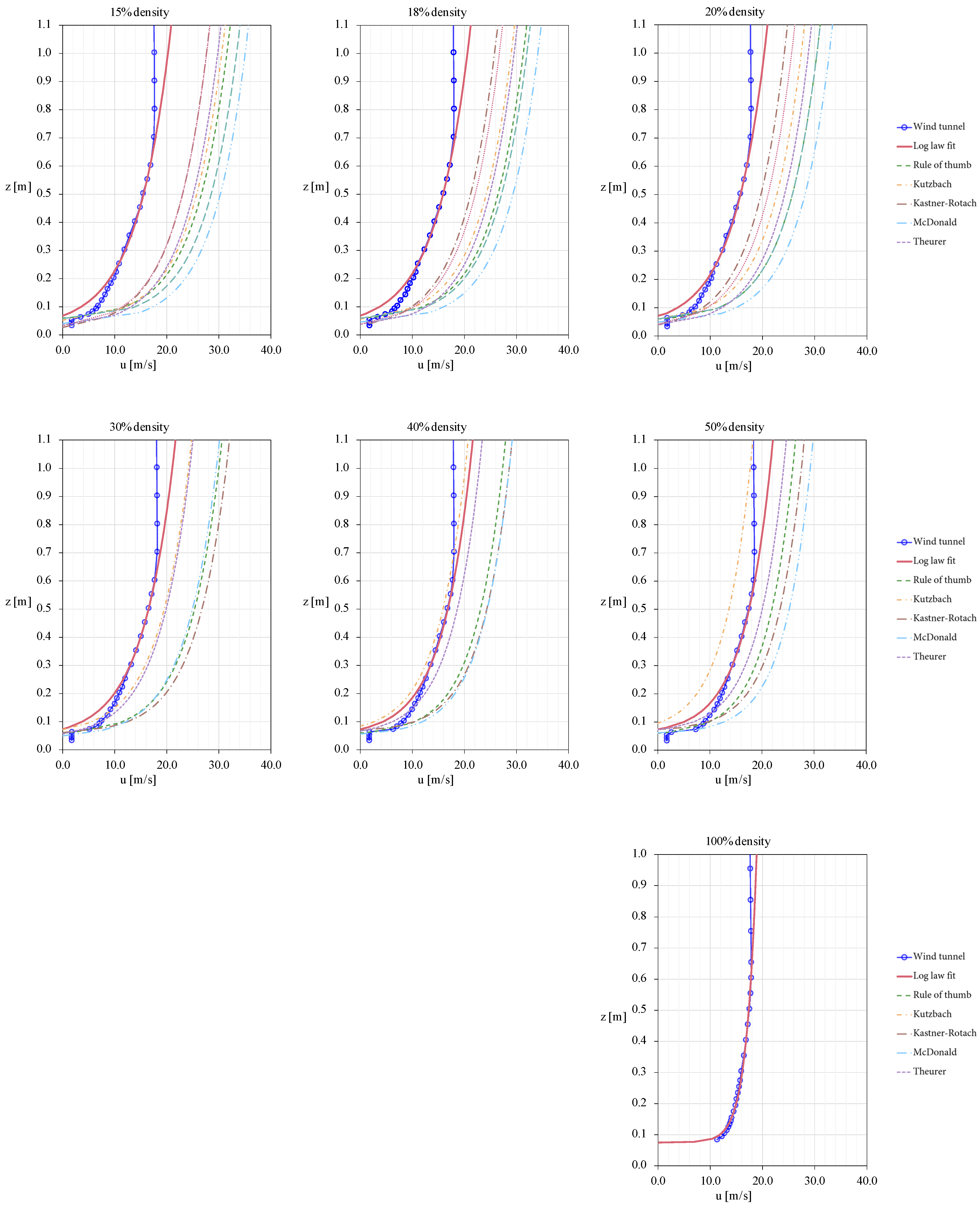
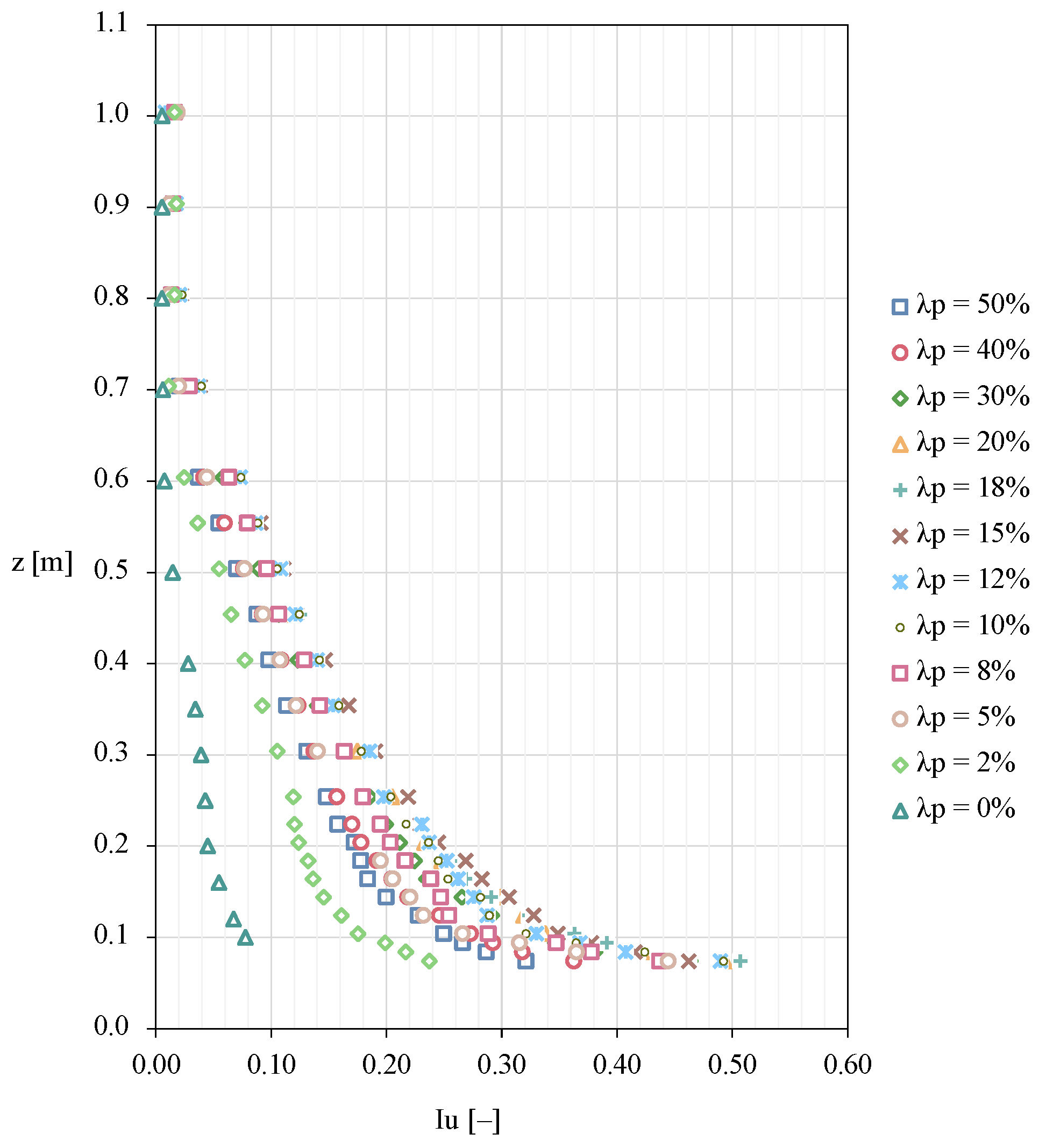

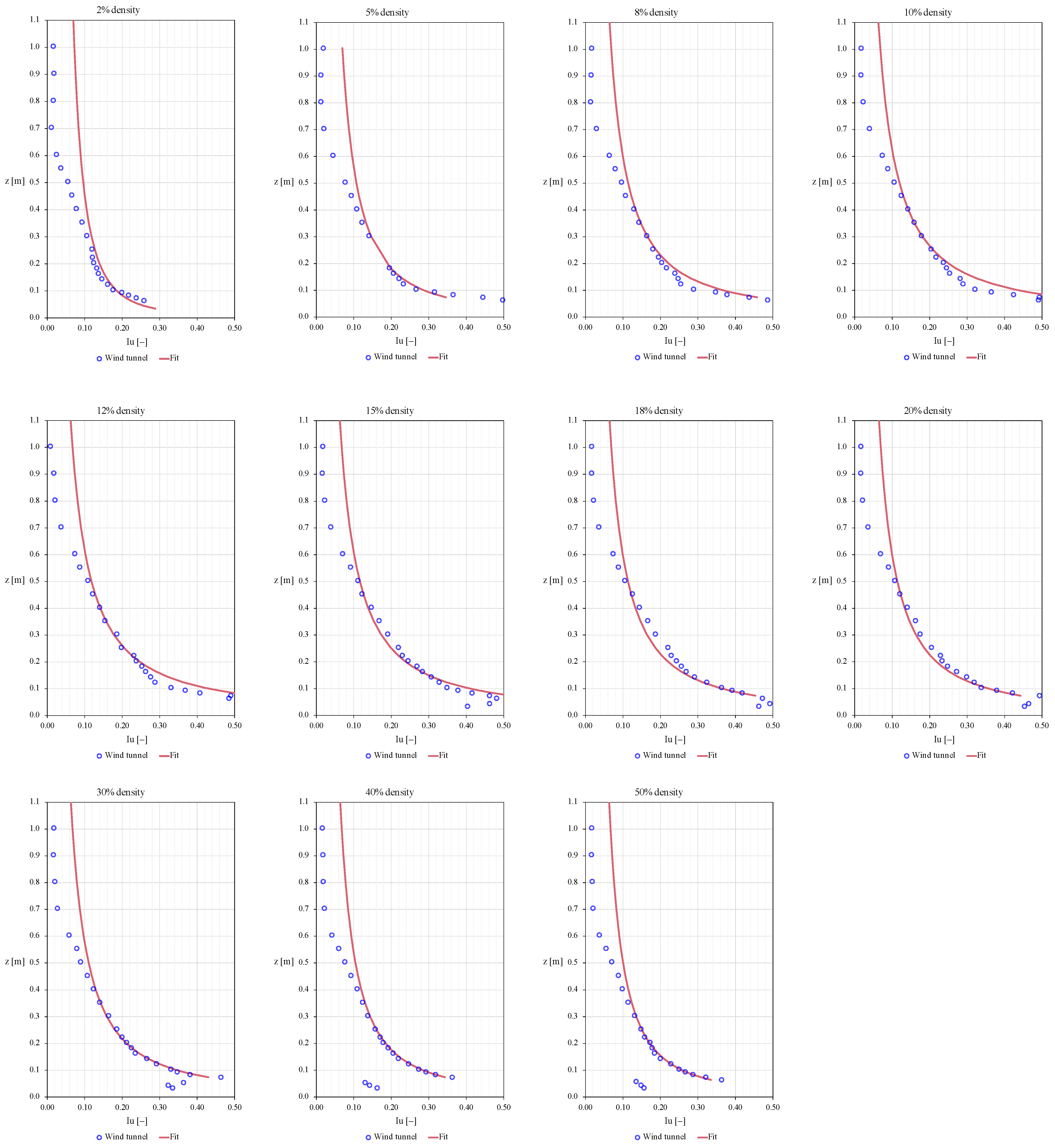
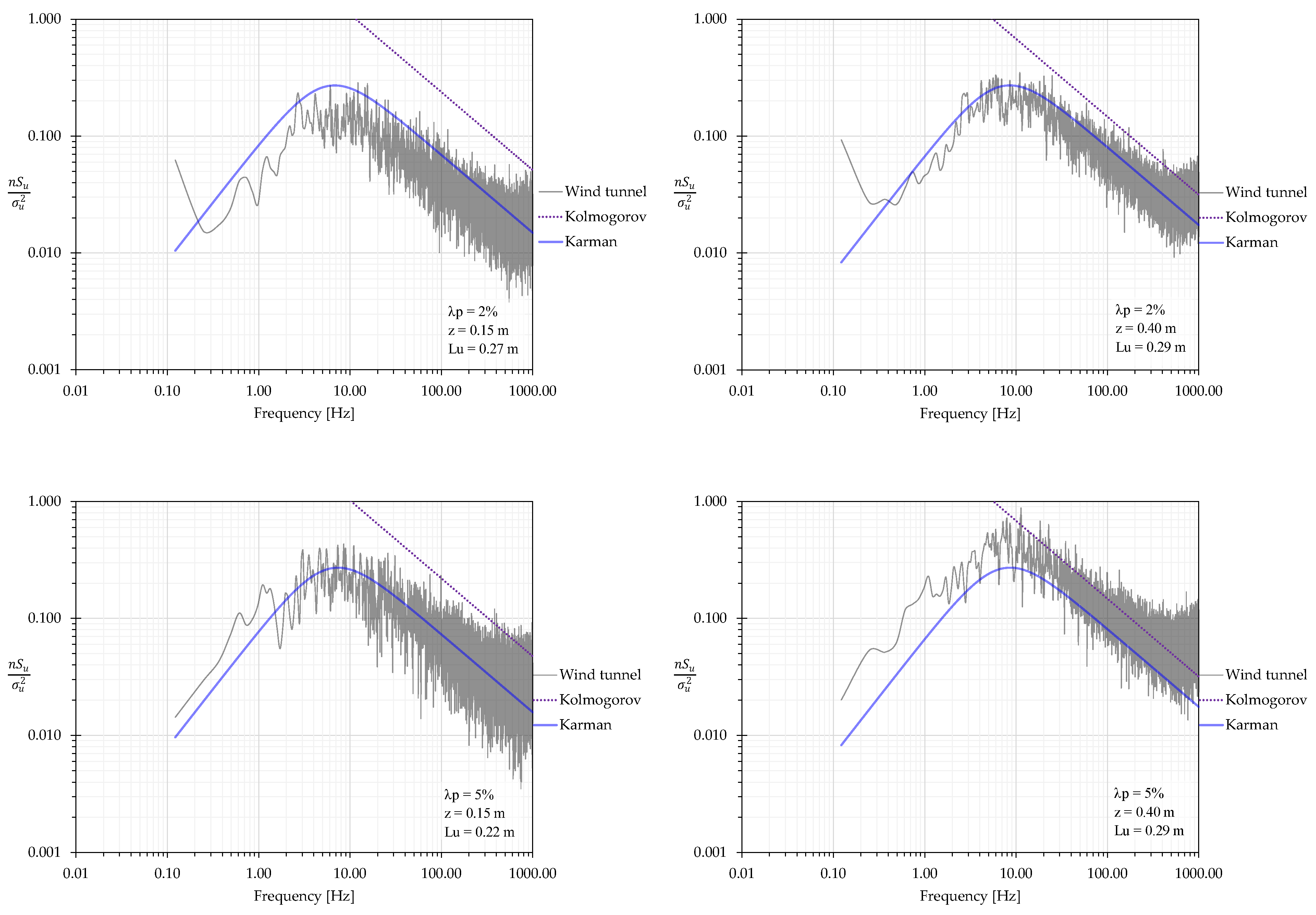
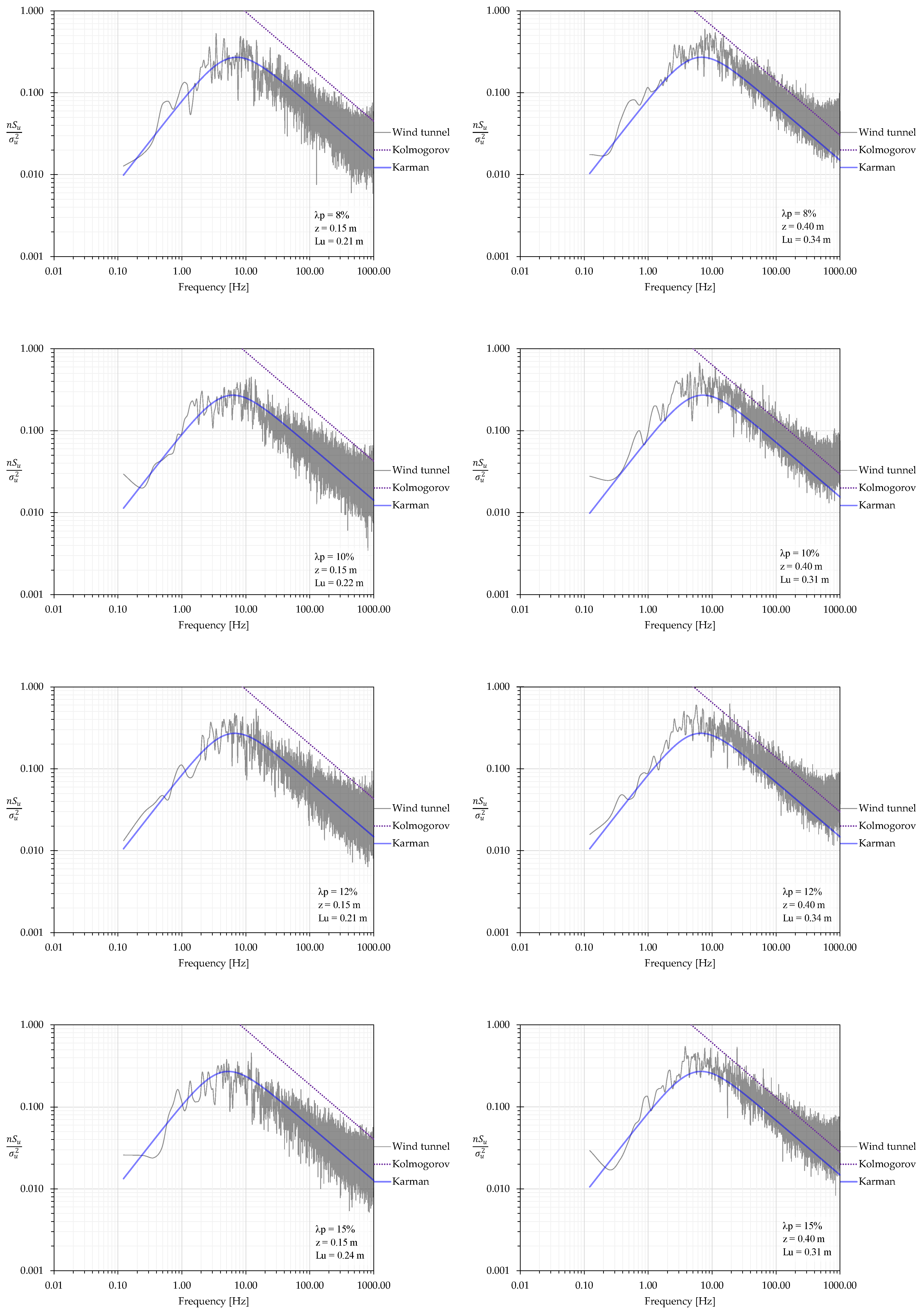

| Experimental Fit | Rule of Thumb | Kutzbach | Lettau | Counihan | McDonald | Kastner-Rotach | Theurer | ||
|---|---|---|---|---|---|---|---|---|---|
| 0.0000 | - | - | - | - | - | - | - | ||
| 0% | 4.38 × 10−5 | - | - | - | - | - | - | - | |
| 0.79 | - | - | - | - | - | - | - | ||
| 0.0037 | 0.0525 | 0.0241 | 0.0525 | - | 0.0037 | 0.0061 | 0.0025 | ||
| 2% | 0.0110 | 0.0075 | 0.0009 | 0.0008 | - | 0.0017 | 0.0008 | 0.0024 | |
| 2.04 | 2.04 | 2.04 | 2.04 | - | 2.04 | 2.04 | 2.04 | ||
| 0.0089 | 0.0525 | 0.0315 | 0.0525 | - | 0.0089 | 0.0144 | 0.0063 | ||
| 5% | 0.0265 | 0.0075 | 0.0025 | 0.0019 | - | 0.0057 | 0.0019 | 0.0057 | |
| 2.55 | 2.55 | 2.55 | 2.55 | - | 2.55 | 2.55 | 2.55 | ||
| 0.0137 | 0.0525 | 0.0361 | 0.0525 | - | 0.0137 | 0.0218 | 0.0100 | ||
| 8% | 0.0304 | 0.0075 | 0.0043 | 0.0030 | - | 0.0081 | 0.0028 | 0.0087 | |
| 2.62 | 2.62 | 2.62 | 2.62 | - | 2.62 | 2.62 | 2.62 | ||
| 0.0168 | 0.0525 | 0.0385 | 0.0525 | 0.0073 | 0.0168 | 0.0262 | 0.0125 | ||
| 10% | 0.0410 | 0.0075 | 0.0056 | 0.0038 | 0.0075 | 0.0091 | 0.0034 | 0.0104 | |
| 2.80 | 2.80 | 2.80 | 2.80 | 2.80 | 2.80 | 2.80 | 2.80 | ||
| 0.0198 | 0.0525 | 0.0406 | 0.0525 | 0.0094 | 0.0198 | 0.0304 | 0.0150 | ||
| 12% | 0.0417 | 0.0075 | 0.0068 | 0.0045 | 0.0102 | 0.0097 | 0.0038 | 0.0120 | |
| 2.92 | 2.92 | 2.92 | 2.92 | 2.92 | 2.92 | 2.92 | 2.92 | ||
| 0.0240 | 0.0525 | 0.0433 | 0.0525 | 0.0127 | 0.0240 | 0.0359 | 0.0188 | ||
| 15% | 0.0439 | 0.0075 | 0.0088 | 0.0056 | 0.0143 | 0.0101 | 0.0044 | 0.0141 | |
| 2.61 | 2.61 | 2.61 | 2.61 | 2.61 | 2.61 | 2.61 | 2.61 | ||
| 0.0280 | 0.0525 | 0.0456 | 0.0525 | 0.0159 | 0.0280 | 0.0409 | 0.0225 | ||
| 18% | 0.0404 | 0.0075 | 0.0108 | 0.0068 | 0.0183 | 0.0101 | 0.0049 | 0.0158 | |
| 2.59 | 2.59 | 2.59 | 2.59 | 2.59 | 2.59 | 2.59 | 2.59 | ||
| 0.0304 | 0.0525 | 0.0470 | 0.0525 | 0.0181 | 0.0304 | 0.0439 | 0.0251 | ||
| 20% | 0.0382 | 0.0075 | 0.0122 | 0.0075 | 0.0210 | 0.0100 | 0.0052 | 0.0167 | |
| 2.52 | 2.52 | 2.52 | 2.52 | 2.52 | 2.52 | 2.52 | 2.52 | ||
| 0.0414 | 0.0525 | 0.0529 | 0.0525 | - | 0.0414 | 0.0555 | 0.0376 | ||
| 30% | 0.0320 | 0.0075 | 0.0192 | 0.0113 | - | 0.0082 | 0.0059 | 0.0187 | |
| 2.48 | 2.48 | 2.48 | 2.48 | - | 2.48 | 2.48 | 2.48 | ||
| 0.0502 | 0.0525 | 0.0575 | 0.0525 | - | 0.0502 | 0.0629 | 0.0501 | ||
| 40% | 0.0230 | 0.0075 | 0.0266 | 0.0150 | - | 0.0060 | 0.0059 | 0.0166 | |
| 2.26 | 2.26 | 2.26 | 2.26 | - | 2.26 | 2.26 | 2.26 | ||
| 0.0572 | 0.0525 | 0.0613 | 0.0525 | - | 0.0572 | 0.0676 | 0.0626 | ||
| 50% | 0.0168 | 0.0075 | 0.0343 | 0.0188 | - | 0.0040 | 0.0054 | 0.0103 | |
| 2.14 | 2.14 | 2.14 | 2.14 | - | 2.14 | 2.14 | 2.14 | ||
| 0.0750 | - | - | - | - | - | - | - | ||
| 100% | 6.09 × 10−5 | - | - | - | - | - | - | - | |
| 0.78 | - | - | - | - | - | - | - |
| Experimental Fit | Rule of Thumb | Kutzbach | Lettau | Counihan | McDonald | Kastner-Rotach | Theurer | ||
|---|---|---|---|---|---|---|---|---|---|
| 0.0000 | - | - | - | - | - | - | - | ||
| 0% | 4.38 × 10−5 | - | - | - | - | - | - | - | |
| 0.79 | - | - | - | - | - | - | - | ||
| 0.0037 | 0.0525 | 0.0241 | 0.0525 | - | 0.0037 | 0.0061 | 0.0025 | ||
| 2% | 0.0040 | 0.0075 | 0.0009 | 0.0008 | - | 0.0017 | 0.0008 | 0.0024 | |
| 1.56 | 1.92 | 1.17 | 1.17 | - | 1.29 | 1.13 | 1.37 | ||
| 0.0089 | 0.0525 | 0.0315 | 0.0525 | - | 0.0089 | 0.0144 | 0.0063 | ||
| 5% | 0.0192 | 0.0075 | 0.0025 | 0.0019 | - | 0.0057 | 0.0019 | 0.0057 | |
| 2.27 | 1.80 | 1.35 | 1.29 | - | 1.58 | 1.25 | 1.59 | ||
| 0.0137 | 0.0525 | 0.0361 | 0.0525 | - | 0.0137 | 0.0218 | 0.0100 | ||
| 8% | 0.0228 | 0.0075 | 0.0043 | 0.0030 | - | 0.0081 | 0.0028 | 0.0087 | |
| 2.36 | 1.73 | 1.47 | 1.38 | - | 1.68 | 1.32 | 1.73 | ||
| 0.0168 | 0.0525 | 0.0385 | 0.0525 | 0.0073 | 0.0168 | 0.0262 | 0.0125 | ||
| 10% | 0.0252 | 0.0075 | 0.0056 | 0.0038 | 0.0075 | 0.0091 | 0.0034 | 0.0104 | |
| 2.29 | 1.61 | 1.46 | 1.35 | 1.51 | 1.62 | 1.28 | 1.70 | ||
| 0.0198 | 0.0525 | 0.0406 | 0.0525 | 0.0094 | 0.0198 | 0.0304 | 0.0150 | ||
| 12% | 0.0252 | 0.0075 | 0.0068 | 0.0045 | 0.0102 | 0.0097 | 0.0038 | 0.0120 | |
| 2.39 | 1.67 | 1.60 | 1.46 | 1.73 | 1.74 | 1.39 | 1.83 | ||
| 0.0240 | 0.0525 | 0.0433 | 0.0525 | 0.0127 | 0.0240 | 0.0359 | 0.0188 | ||
| 15% | 0.0245 | 0.0075 | 0.0088 | 0.0056 | 0.0143 | 0.0101 | 0.0044 | 0.0141 | |
| 2.05 | 1.44 | 1.48 | 1.33 | 1.66 | 1.52 | 1.25 | 1.67 | ||
| 0.0280 | 0.0525 | 0.0456 | 0.0525 | 0.0159 | 0.0280 | 0.0409 | 0.0225 | ||
| 18% | 0.0226 | 0.0075 | 0.0108 | 0.0068 | 0.0183 | 0.0101 | 0.0049 | 0.0158 | |
| 2.07 | 1.48 | 1.63 | 1.44 | 1.87 | 1.57 | 1.32 | 1.79 | ||
| 0.0304 | 0.0525 | 0.0470 | 0.0525 | 0.0181 | 0.0304 | 0.0439 | 0.0251 | ||
| 20% | 0.0222 | 0.0075 | 0.0122 | 0.0075 | 0.0210 | 0.0100 | 0.0052 | 0.0167 | |
| 2.03 | 1.47 | 1.68 | 1.47 | 1.95 | 1.56 | 1.33 | 1.81 | ||
| 0.0414 | 0.0525 | 0.0529 | 0.0525 | - | 0.0414 | 0.0555 | 0.0376 | ||
| 30% | 0.0153 | 0.0075 | 0.0192 | 0.0113 | - | 0.0082 | 0.0059 | 0.0187 | |
| 1.91 | 1.56 | 2.09 | 1.75 | - | 1.58 | 1.47 | 2.03 | ||
| 0.0107 | 0.0075 | 0.0266 | 0.0150 | - | 0.0060 | 0.0059 | 0.0166 | ||
| 40% | 1.7600 | 1.5984 | 2.4426 | 1.9671 | - | 1.5031 | 1.5168 | 2.0307 | |
| 0.00 | 0.00 | 0.00 | 0.00 | - | 0.00 | 0.00 | 0.00 | ||
| 0.0572 | 0.0525 | 0.0613 | 0.0525 | - | 0.0572 | 0.0676 | 0.0626 | ||
| 50% | 0.0072 | 0.0075 | 0.0343 | 0.0188 | - | 0.0040 | 0.0054 | 0.0103 | |
| 1.67 | 1.68 | 2.87 | 2.23 | - | 1.44 | 1.57 | 1.86 | ||
| 0.0750 | - | - | - | - | - | - | - | ||
| 100% | 6.09 × 10−5 | - | - | - | - | - | - | - | |
| 0.78 | - | - | - | - | - | - | - |
| % | m | m | m/s | m |
|---|---|---|---|---|
| 0 | 0.00 | 3.37 × 10−5 | 0.766 | 0.44 |
| 2 | 0.0037 | 0.0040 | 1.556 | 0.58 |
| 5 | 0.0089 | 0.0192 | 2.274 | 0.66 |
| 8 | 0.0137 | 0.0228 | 2.358 | 0.69 |
| 10 | 0.0168 | 0.0252 | 2.289 | 0.71 |
| 12 | 0.0198 | 0.0252 | 2.389 | 0.70 |
| 15 | 0.0240 | 0.0245 | 2.053 | 0.69 |
| 18 | 0.0280 | 0.0226 | 2.068 | 0.69 |
| 20 | 0.0304 | 0.0222 | 2.030 | 0.70 |
| 30 | 0.0414 | 0.0153 | 1.912 | 0.67 |
| 40 | 0.0502 | 0.0107 | 1.760 | 0.63 |
| 50 | 0.0572 | 0.0072 | 1.671 | 0.60 |
| 100 | 0.0750 | 6.09 × 10−5 | 0.785 | 0.47 |
| (%) | 1 | ||
|---|---|---|---|
| 0 | 0.000 | 0.000 | 5.84 |
| 2 | 0.049 | 0.054 | 7.80 |
| 5 | 0.118 | 0.256 | 8.81 |
| 8 | 0.183 | 0.303 | 9.22 |
| 10 | 0.224 | 0.336 | 9.50 |
| 12 | 0.264 | 0.336 | 9.34 |
| 15 | 0.320 | 0.326 | 9.26 |
| 18 | 0.373 | 0.302 | 9.20 |
| 20 | 0.406 | 0.296 | 9.29 |
| 30 | 0.552 | 0.205 | 8.90 |
| 40 | 0.669 | 0.143 | 8.46 |
| 50 | 0.762 | 0.096 | 8.04 |
| 100 | 1.000 | 0.001 | 6.21 |
| % | m | m | – | – |
|---|---|---|---|---|
| 2 | 0.0040 | 0.585 | 0.057 | 171.1 |
| 5 | 0.0192 | 0.661 | 0.058 | 46.5 |
| 8 | 0.0228 | 0.691 | 0.076 | 33.4 |
| 10 | 0.0252 | 0.713 | 0.084 | 29.8 |
| 12 | 0.0252 | 0.700 | 0.087 | 29.4 |
| 15 | 0.0245 | 0.694 | 0.096 | 28.7 |
| 18 | 0.0226 | 0.690 | 0.090 | 33.5 |
| 20 | 0.0222 | 0.697 | 0.088 | 33.9 |
| 30 | 0.0153 | 0.668 | 0.078 | 51.6 |
| 40 | 0.0107 | 0.635 | 0.074 | 68.6 |
| 50 | 0.0072 | 0.603 | 0.073 | 100.3 |
| % | – |
|---|---|
| 2 | 101.4 |
| 5 | 34.2 |
| 8 | 29.5 |
| 10 | 28.5 |
| 12 | 28.7 |
| 15 | 30.3 |
| 18 | 33.4 |
| 20 | 33.3 |
| 30 | 46.3 |
| 40 | 58.2 |
| 50 | 81.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-García, R.; Gómez-Martínez, R. Turbulent Flow over a Rough Surface in a Wind Tunnel. Wind 2025, 5, 13. https://doi.org/10.3390/wind5020013
Sánchez-García R, Gómez-Martínez R. Turbulent Flow over a Rough Surface in a Wind Tunnel. Wind. 2025; 5(2):13. https://doi.org/10.3390/wind5020013
Chicago/Turabian StyleSánchez-García, Raúl, and Roberto Gómez-Martínez. 2025. "Turbulent Flow over a Rough Surface in a Wind Tunnel" Wind 5, no. 2: 13. https://doi.org/10.3390/wind5020013
APA StyleSánchez-García, R., & Gómez-Martínez, R. (2025). Turbulent Flow over a Rough Surface in a Wind Tunnel. Wind, 5(2), 13. https://doi.org/10.3390/wind5020013





