Evaluation of Regional Elevation and Blade Density Effects on the Efficiency of a 1-kW Wind Turbine for Operation in Low-Wind Counties in Iran

Abstract

This research investigates the effect of blade density and elevation above sea level on the startup time (T_s) and power coefficient (C_p) of a 1-kW two-bladed wind turbine. The study uses three Iranian hardwoods as the blade material and four counties of Iran with low wind speeds and different elevations as the case studies. The BW-3 airfoil is considered as the blade profile. A multi-objective optimization process with the aid of the differential evolution (DE) algorithm is utilized to specify the chord length and twist angle. The findings demonstrate that, while the maximum C_p of the optimal blades designed with all three types of wood is high and equal to 0.48, the average T_s of the optimal blades designed with oak and hornbeam wood is 84% and 108% higher than that of alder wood, respectively. It is also observed that, while raising the elevation to 2250 m decreases the C_p by only 2.5%, the ideal blade designed to work at sea level could not manage to start rotating at a height of 1607 m and above. Finally, an improvement in the T_s and C_p was observed by performing optimization based on the local atmospheric conditions associated with the incrementing blade chord length at high elevations.

1. Introduction

After the oil crisis and the spike in fossil fuel prices in the 1970s, the next big shock to the global energy market was undoubtedly the Russia–Ukraine conflict. Efforts to accelerate the shift towards renewable energy have never been more serious [1]. Thus, the possibility of the prominence of renewable energies, especially wind energy, and the phasing out of fossil fuels has been greatly strengthened [2]. In this regard, Germany, which is the third-most producer of wind power in the world, presented a plan to produce 100% of its energy from renewable sources by 2035 [3]. Moreover, the European Union aims to meet 50% of its energy demand through wind by 2050 [4]. With a straightforward structure, minimalistic design, easy portability, and reduced noise, small wind turbines (SWTs) have become indispensable tools for harnessing wind energy in rural, suburban, and even densely populated urban areas, where installing large wind turbines (LWTs) is impractical due to limited space and noise concerns [5].

Different methods have been developed to analyze the flow around wind turbine (WT) blades, calculate the aerodynamic torque (M), and as a result, compute the output power of turbines, the most important of which are experimental testing in the wind tunnel, the blade element momentum (BEM) method, and the computational fluid dynamics (CFD) simulations. While the first technique provides real data, it is often time-consuming and costly. In contrast, both the BEM theory and CFD technique offer the advantage of generating varied and trustable results at a reduced expense. Refan and Hangan [6] conducted both experimental and theoretical assessments on the aerodynamic behavior of a small 2.2-m diameter upwind three-bladed horizontal axis wind turbine (HAWT) rotor. Their comparison of the theoretical and experimental findings indicated that the overall predictions of the BEM theory fall within an acceptable accuracy range. Plaza et al. [7] carried out an aerodynamic evaluation of the MEXICO WT rotor, comparing the data from the BEM theory, CFD analysis, and experimental tests. Their findings revealed that, at lower wind speeds (V), the BEM theory presents more reliable data than the the CFD analysis.

The wind is turbulent by nature, and its turbulence is considered to be the result of friction with the Earth’s topography and the nonuniform heating of different air layers above the ground. Turbulence refers to the variation in wind speed around its average value over a particular period. This period can be annually, daily, or for periods less than 10 min. It is a complex phenomenon to describe accurately, so it is usually represented by a statistical property known as turbulence intensity. Turbulence intensity (I) can be computed by dividing the standard deviation (σ) of wind speeds by the mean wind speed (U) over a particular period (Equation (1)) [8]:

$$I=\frac{\sigma }{U}$$

(1)

This intensity varies from about 0.1 (10%) for smooth terrain to more than 0.2 (20%) for rough terrain [9]. It has been shown that high turbulence intensity is the main factor that shortens the fatigue life of a turbine structure [10], and it also affects the furling behavior [11]. Many mathematical models can describe atmospheric turbulence. Some models, like those usually used in CFD simulations, are time-dependent. Other techniques work based on the frequency domain [12,13].

The influence of turbulence on the power output is challenging to generalize, since furling/power limiting, airfoil performance, and wind alignment are influenced by turbulent gusts. Winds with higher turbulence intensities have higher power than winds with less turbulence but the same mean wind speed because of the cubic variation of power with the wind speed.

The research studies by Churchfield et al. [14] and Nandi et al. [15] showed that, in large wind turbines, the oncoming atmospheric turbulence can result in considerable fluctuations in the local angles of attack and their aerodynamic performance. However, based on research studies on small wind turbines with operating Reynolds numbers less than 500,000, the influence of atmospheric turbulence on their aerodynamic performance is not significant [9,16]. In this regard, Lubitz [17] experimentally evaluated the influence of atmospheric turbulence on the output power of a Bergey XL.1 1-kW small wind turbine. This turbine, which used a BW-3 airfoil as its blade profile, was installed 18 m above the ground. The results of this study showed that the turbulence levels had an insignificant influence on the overall power output at wind speeds between the startup and furling. Based on their findings for the normal operating range (4 m/s to 7 m/s), while a low turbulence intensity (I < 0.14) resulted in only a 2% reduction in the power output relative to the power output over all turbulence conditions, medium and high turbulence intensities (I > 0.14) led to a power rise of around 2%. In another research, Wood [9] assessed the influence of atmospheric turbulence on the performance of a small wind turbine. For this purpose, he analyzed the daily output of two identical Skystream 2.4-kW small wind turbines over 16 days (30 April–15 May). These turbines were installed on towers 11 m in the city of Calgary, Canada, at a distance 8 km from each other. The first turbine was installed on flat ground around 80 m away from a large two-story house, and the second turbine was installed at the same distance from a similarly sized house but on a ridge. Despite the differences in these sites and the variation in atmospheric turbulence they caused, the average power outputs of these turbines were found to be 12.62 kWh and 12.91 kWh, respectively (2.24% difference). Therefore, overall, the literature review indicates that, unlike large wind turbines [13,14,15], atmospheric turbulence does not have a significant influence on the output power of small wind turbines with Reynolds numbers less than 500,000 [9,17], and it mostly affects the structure fatigue life [10] and furling behavior [11] in these turbines.

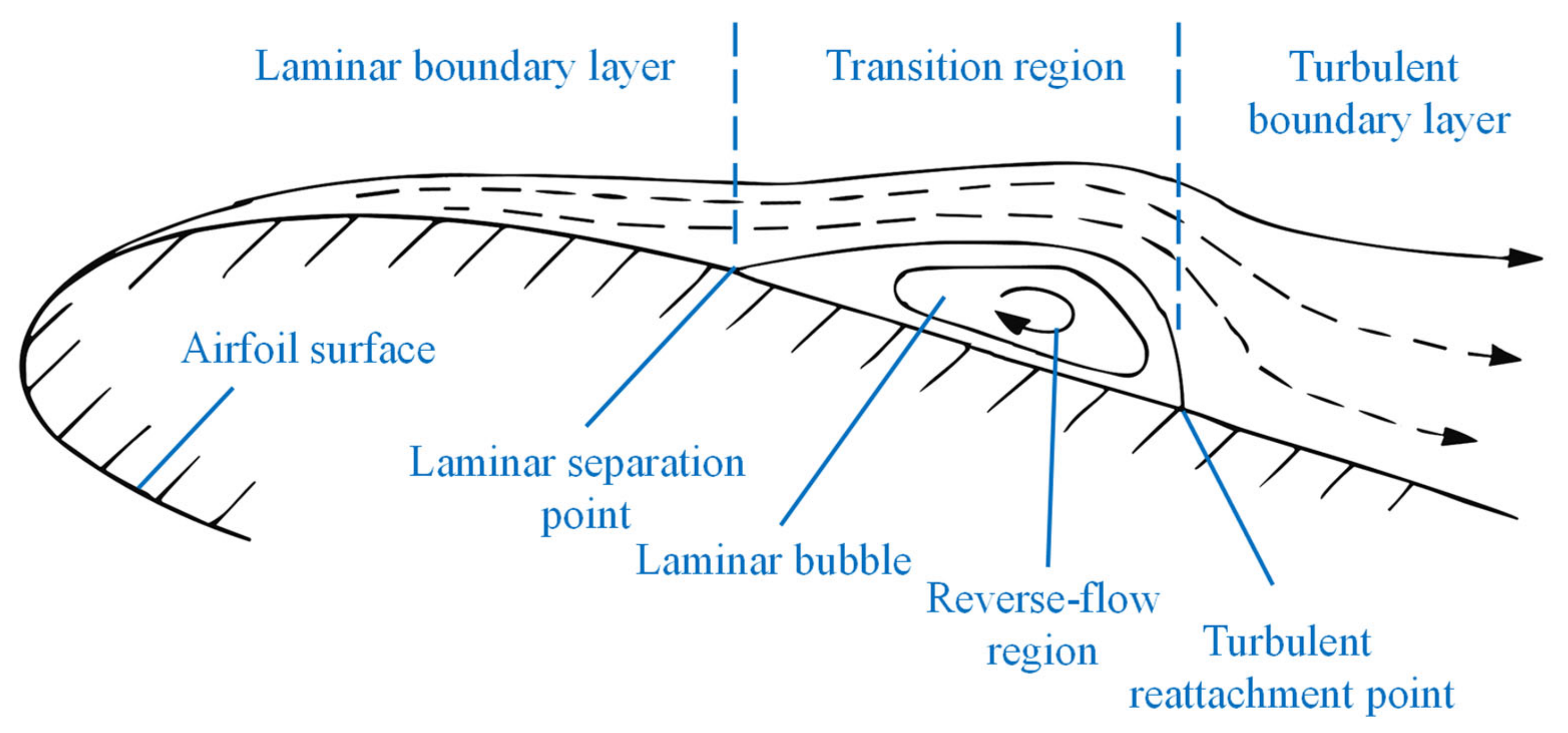
Due to the laminar separation that occurs at low Reynolds numbers, the aerodynamics of wind turbines operating at low wind speeds is challenging. At Reynolds numbers below 5 × 10⁵, the flow around an airfoil might separate while the boundary layer is still laminar and before the transition to turbulent. This laminar separation might lead to the formation of air bubbles, which are known as laminar separation bubbles. These bubbles result in extra drag in airfoils, which is defined by the bubble drag. Figure 1 shows a schematic of laminar separation bubbles. A typical airfoil not designed for operating at low Reynolds numbers will suffer from a loss in performance in this condition; however, some thin airfoils are designed to operate at low Reynolds numbers and reduce the impact of the separation bubble. The BW-3 airfoil is one of these airfoils [18].

In this regard, the design and optimization of small wind turbine blades with the help of the BEM method using the experimental lift and drag coefficients of thin airfoils has provided accurate results and has received much attention from researchers in recent years [19,20,21]. The current research is based on this method as well.

To enhance the lift-to-drag coefficient and elevate the performance of an airfoil with applications in wind turbines, Liu et al. [22] worked on the transition of the boundary layer and its effects on the stall performance. They made use of the CFD method for simulating the transition over an airfoil in pitching movement. They stated that the transition model exhibits more accurate predictions than the conventional turbulence model in light dynamic stalls. Nandi et al. [23] used a numerical method based on the BEM and the unsteady Reynolds-averaged Navier–Stokes (URANS) to focus on the transitional boundary layers to investigate the influence of transient atmospheric conditions that are exerted on the turbine blades. The capability of this method was compared against the SST k-ω model. According to the findings, the transition model was more successful in predicting the dynamics of the boundary layer. Also, this method outperformed the SST k-ω model for capturing the lift curve.

Not using pitch and yaw control mechanisms is the most important difference between SWTs and LWTs [24]. With the aid of the pitch mechanism, the blade rotates around its longitudinal axis, and by changing the twist angle, efforts are made to keep the value of the angle of attack (AOA) at the desired level. The yaw mechanism rotates the turbine when the direction of the wind changes, and it puts the turbine directly in front of the wind [25]. Unlike LWTs, SWTs do not have the yaw mechanism. In SWTs, a mechanical system called a tail fin is used instead. It should be explained that, based on standards, an SWT has a rated power of less than 50 kW, which corresponds to a blade length of less than 8 m [26]. In a more detailed classification, SWTs are classified into three groups: micro (≤1 kW), medium (≤5 kW), and mini (≤50 kW) [18]. The second difference between SWTs and LWTs is the number of airfoils used in the blade. To reduce the manufacturing cost of SWT blades, only one airfoil is used all over the blade, but in LWT blades, the operating conditions of the root and tip sections are completely different from each other. In the root section of LWT blades, considerable bending moments occur, which requires the use of thick airfoils. Thinner airfoils, which have superior aerodynamic behavior, are utilized in the middle and tip sections to harness more energy from the wind [27]. Since the main goal of designing a WT is to acquire the maximum power output, the way that this parameter is considered in the blade design process can be counted as the third main difference between SWTs and LWTs. LWTs are installed in windy regions, so their design and optimization are not based on a specific speed but based on reaching the maximum annual energy production (AEP) in a range of various speeds. On the other hand, SWTs are installed in places that do not have good wind potential [28], requiring maximum efficiency for the turbine during the limited instances in which the wind is blowing. Thus, the power coefficient (C_p) is employed to design the blades of these turbines [29].

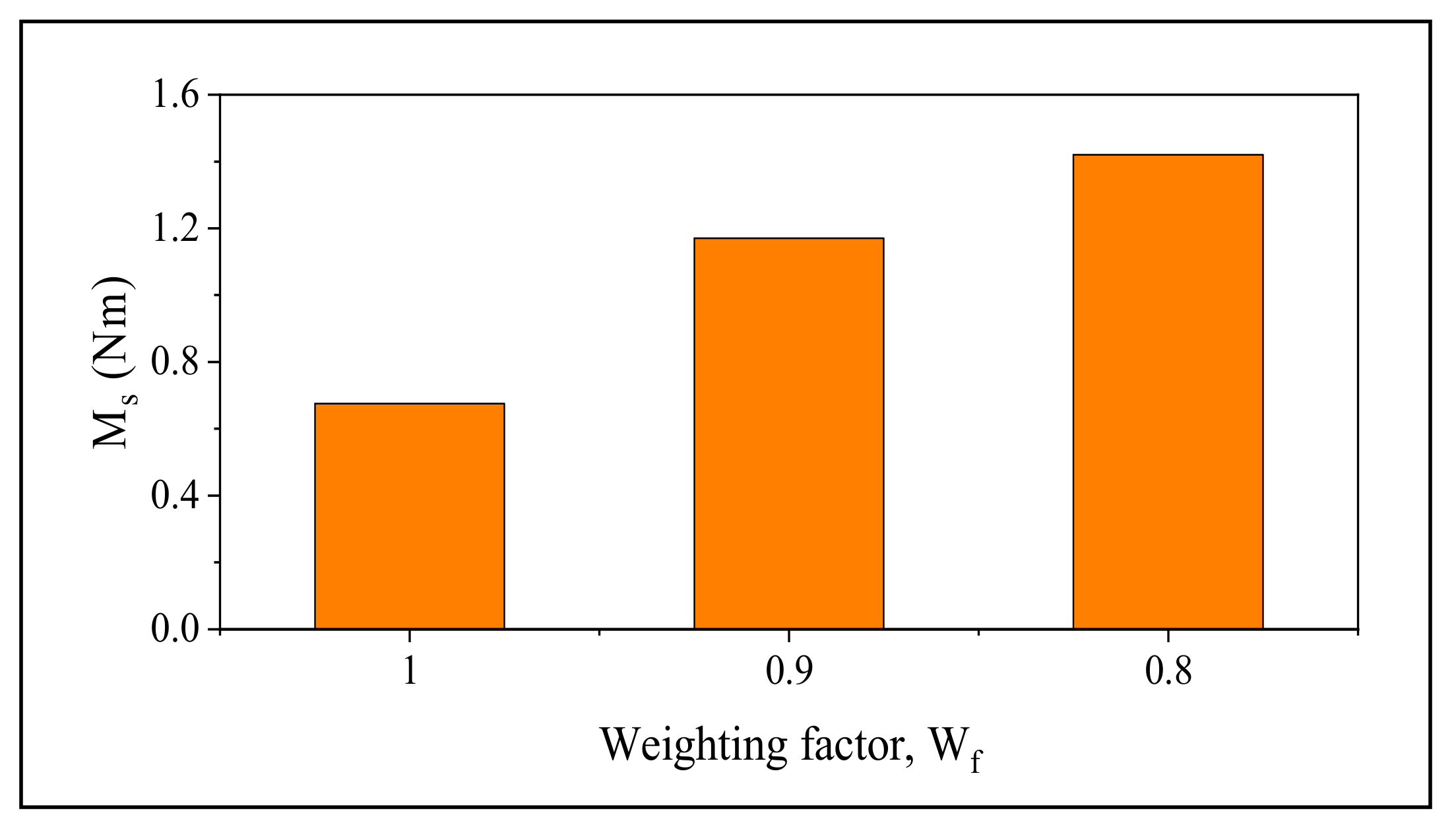
At low V values, the startup process of SWTs is delayed, and the generation of power is more idle [30]. The main reason is the absence of a pitch control mechanism. Also, permanent magnet generators (PMGs) used in SWTs have a high cogging torque (M_c) that must be overcome by the generated startup torque (M_s) [19]. Studies have shown that the M values generated by the root elements of the blade have a vital role in starting the blade rotation from the stationary state, and the startup process of the blade is mostly contributed by these elements. As the rotational speed of the turbine rises, the AOA along the blade reduces, so that the aerodynamic moment generated by the elements near the blade tip is much larger than that of the root elements. Thus, these elements have a greater contribution to the amount of power output from the turbine.

In SWTs, after choosing the airfoil type utilized in the blade, the twist angle (β) and the chord length (c) in each blade element can be computed by the Schmitz equations [31]:

$$\beta =\frac{2}{3}{\tan }^{-1}\left(\frac{1}{{\lambda }_r}\right)-\alpha$$

(2)

$$c=\frac{16\pi r}{B{C}_l}{\sin }^2\left(\frac{1}{3}{\tan }^{-1}\left(\frac{1}{{\lambda }_r}\right)\right)$$

(3)

In these equations, λ_r is the local tip speed ratio, α is the AOA in which the lift-to-drag ratio is the maximum, B is the number of blades, and C_l is the lift coefficient. Research studies have suggested that, while using the nonlinear distribution obtained from Equations (2) and (3) provides the maximum C_p, it causes a significant reduction in the M_s and therefore leads to an increment in the rotor startup time [32]. Similar results have been presented for the application of the ideal equations provided by Burton et al. [33] for the design of SWT blades [34]. Thus, if any other objectives besides the C_p are considered for the blade design, optimization methods should be employed [35]. In general, optimization techniques fall into two groups: gradient, and nongradient [36]. In gradient techniques, the derivative of the objective function with respect to the design variables is acquired, and then, the optimization process is carried out using them. The solving techniques of adjoint [37] and second-order sequential quadratic equations [38], as well as the finite difference method [39], are some of the gradient techniques. Nongradient methods are independent from the objective function characteristics, such as continuity and differentiability. In this regard, the optimal solution is determined by calculating the values of the objective function and comparing to with each other in an evolutionary process. Genetic algorithm (GA) [40], differential evolution (DE) [41], and particle swarm optimization (PSO) [42] are among the most famous nongradient algorithms. Robustness, rapidness, and convergence rate are the most fundamental features of the optimization methods, in which evolutionary algorithms, especially the DE algorithm, have been very successful [43].

Akbari et al. [32] designed and optimized the blades of an SWT with a blade length of 1.5 m by using the NACA4412 airfoil as the blade section to increase the M_s. By raising the β and the c at r/R < 0.52 and following the Schmitz formula at r/R ≥ 0.52, they managed to obtain a 140% increment in the M_s by losing only 1.5% of the C_p value. This resulted in reducing the startup speed from 6 to 4 m/s. Pourrajabian et al. [44] investigated the chord and twist variables in three SWTs with power outputs of 0.5, 0.75, and 1 kW. They focused on enhancing the turbines’ operation during low wind conditions at the startup time. Enlarging the c and β values at the root section of the blades was found to be essential for reaching a better performance in low-wind scenarios. Their findings indicate that using more blades or enlarging the existing ones contributes to both a better startup process and greater power generation. Abdelsalam et al. [45] conducted experimental research on the aerodynamic efficiency of two distinct small HAWT rotors. The first rotor possessed nonlinear chord and twist distributions, while the second one had a novel linearized pattern that was designed using the BEM theory. The RISØ-A-24 airfoil was used as the blade profile. The findings exhibited that the maximum C_p of the nonlinear model was higher; however, the linear model had a better startup performance. In the study carried out by Rahgozar et al. [21], a one-meter wooden HAWT blade was developed by taking both the startup time and power output into account. They tested four potential combinations of linear/nonlinear c and β distributions utilizing the BEM theory. They made use of the SG6043 airfoil as the uniform profile along the blade. They concluded that employing a linear distribution enhances the startup performance with a minimal impact on the power output. By choosing ten airfoils that are prominently used in the SWT industry, Akbari et al. [34] recommended the application of Bergey BW-3 and SG6043 airfoils as blade profiles for use in less and more windy regions, respectively. The reduced inertia presented in the blades featuring the Bergey BW-3 profile, along with the impressive lift-to-drag proportion exhibited by the SG6043 design, represent some of the noteworthy benefits of these aerodynamic structures.

As compared to LWTs, the blades of SWTs are manufactured from more diverse materials and methods. Glass fiber and carbon fiber reinforcement embedded in epoxy are the most prevalent materials that are used for manufacturing LWTs [46]. Although the material technology of large blades can be applied to small blades, they are typically costly and are associated with a substantial growth of manufacturing expenses. Studies have shown that paying attention to fatigue is cardinal in SWTs [47]. Wood is used as a stable, green, inexpensive, and durable engineering material in a wide range of devices, such as airplane propellers and SWT blades. The fatigue resistance of wood is excellent, and the strength-to-density ratio of this material is very satisfactory [48]. 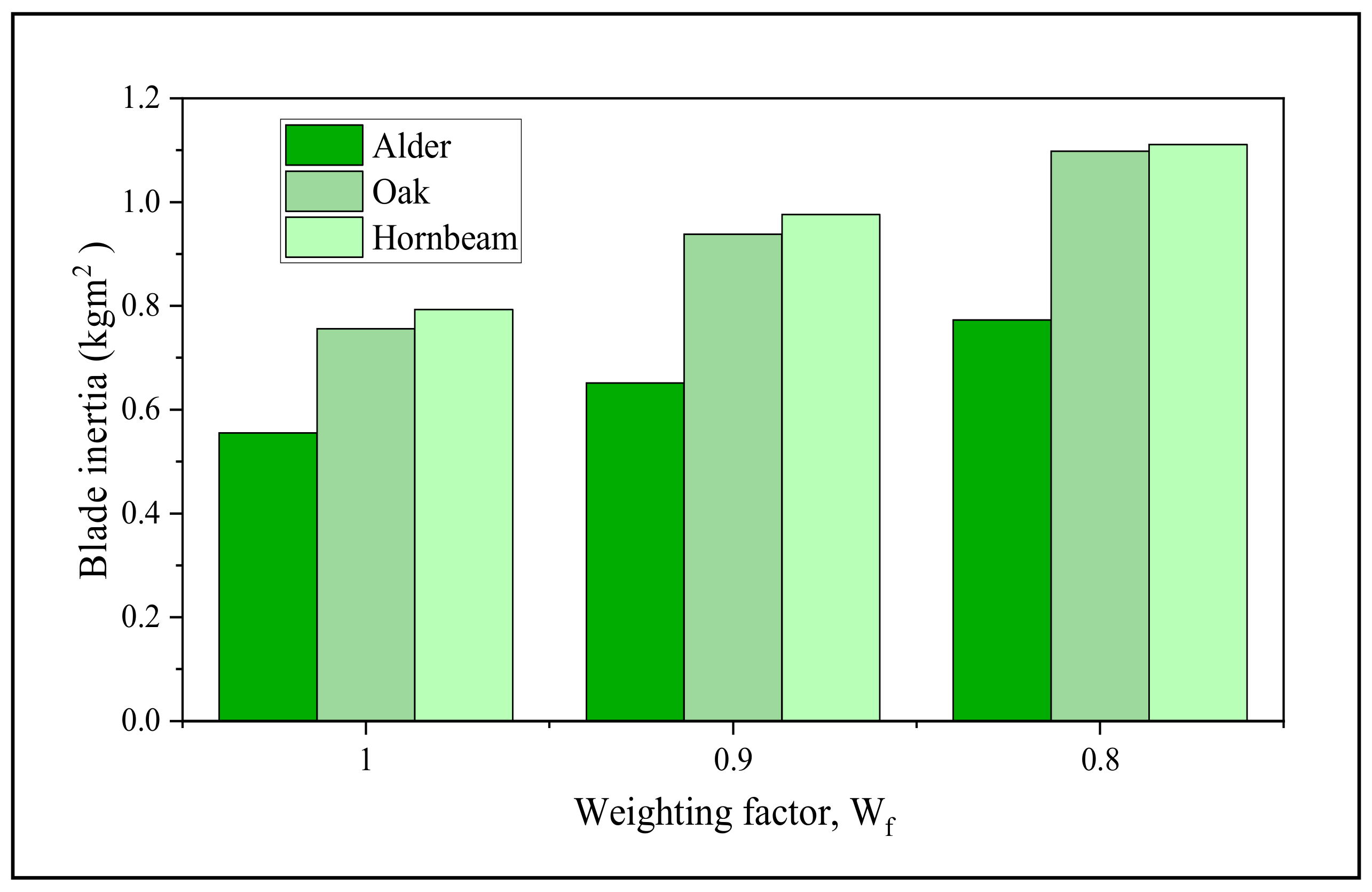In this regard, research has shown that wood has applications for manufacturing SWT blades that have a capacity of 5 kW or less and a length of no more than 2.5 m [49]. Blade and air densities are important parameters in the startup behavior of SWTs, which affect the blade inertia and the M_s, respectively. On the other hand, with the rise in elevation and the kinematic viscosity of the air, the Reynolds number (Re) on the blade is reduced and can decrease the lift value and, as a result, decrease the C_p of the turbine. Considering the increase in the application of SWTs and the requirement to improve their performance, especially at low V values, the importance of these parameters can be well perceived. For this purpose, in the current study, three hardwoods with different densities that grow in Iran and also four low-wind counties with different elevations from the sea level up to 2250 m were selected as case studies. In the subsequent sections of the study, by designing and optimizing a low-cost two-bladed SWT, the impact of the blade density and elevation on the startup behavior and the power extraction coefficient will be investigated.

2. Wind and Timber Resources in Iran

Iran, a historic nation in the Middle East, is placed between Africa, Europe, and Asia. As the 17th largest nation globally, Iran shares borders with Afghanistan and Pakistan to the east; Armenia, Turkmenistan, and Azerbaijan to the north (and the Caspian Sea); Iraq, and Turkey to the west; and the Sea of Oman, as well as the Persian Gulf, to the south.

Iranians are pioneers in using wind energy to pump water and grind grains. The first windmill was used around 644 B.C. in Sistan, Iran [50]. Despite being situated in a wind-rich region and possessing substantial wind energy potential, Iran has merely harnessed 342 MW of its wind capacity by 2023, which is a small contribution to supplying Iran’s 90 GW electricity requirement [51]. Natural gas is the largest source of electricity supply in Iran, which includes about 81% of the total production, followed by oil and hydro at 14 and 4%, respectively [51]. While the conducted studies show the potential of at least 18 GW of wind energy in Iran [52], the share of wind energy in Iran’s energy portfolio has always been less than 0.5% [52], while the corresponding average value in the world is virtually 6.5% [53]. Therefore, it is evident that further efforts are required to tap into Iran’s wind energy resources. The wind energy potential has been investigated in some regions of Iran, including Bushehr [54], Zahedan [55], Tabriz and Ardabil [56], Tehran [57], Zanjan [58], Chalus [59], and Semnan [60]. Also, Mostafaeipour [61] evaluated the practicality of deploying offshore WTs in the Persian Gulf and the Caspian Sea.

To assess the impact of elevation on the aerodynamic efficiency of SWTs, four counties with different elevations were considered, according to

Table 1. Specifications of the considered counties.

Case Study	County	Elevation (m)	Air Density (kg/m3)	Air Kinematic Viscosity (m2/s)	Coordinate E–N
Sea level	-	0	1.225	1.460 × 10−5	-
1	Dalgan	392	1.1795	1.525 × 10−5	59°32′–27°26′
2	Maku	1182	1.0919	1.624 × 10−5	44°38′–39°29′
3	Asadabad	1607	1.0468	1.680 × 10−5	48°8′–34°47′
4	Sisakht	2250	0.9814	1.771 × 10−5	51°45′–30°86′

. In this table, the air properties are determined based on the International Standard Atmosphere (ISA) [62].

The locations of the selected cities are shown in Figure 2a, with numbers 1 to 4 for Delgan, Maku, Asadabad, and Sisakht, respectively. Iran is home to various forest types, particularly in the western and northern regions. The Caspian Hyrcanian forests in Northern Iran span 1.8 million hectares, extending from the Caspian Sea coastline to an elevation of 2800 m above sea level on the northern slopes of the Alborz Mountain Range (Figure 2b). Due to the mild, humid climate and suitable soil, these forests produce more than 900,000 m³ of wood annually [63]. In the present study, three types of hardwood grown in this area, namely alder, oak, and hornbeam, which physical properties were presented in the work of Kiaei and Samariha [64], were used for the SWT blades.

3. Aerodynamic Analysis

In the current research, the BEM model [65] was employed for computing the $C_p$. To do so, the blade was segmented into multiple distinct regions (elements), which exhibit aerodynamics behaviors similar to two-dimensional airfoils. Then, the aerodynamic forces were computed according to the local flow circumstances [66].

For computing the $C_p$ value, initially, the blade was segmented into multiple distinct regions. For this purpose, based on previous works in this field, 10–20 regions were selected for the blade so that the aerodynamic forces applied to each of these regions and the distribution of these forces could be computed. Subsequently, an iterative process was employed to compute the tangential force coefficient ($C_{a^{\prime }}$), the tip loss factor (F), the axial ($a$) and rotational induction coefficients ($a^{\prime }$), the inflow angle ($\varphi$), the axial force coefficient ($C_a$), and the solidity rate ($\sigma$). Following the computation of $a^{\prime }$ and $a$, the power (dp), as well as tangential ($d{F}_y)$ and axial forces ($d{F}_x$), were computed for the blade sections. After the integration of these derivatives for the entire blade, the values of P, $F_y$, and $F_x$ along the blade were acquired, respectively [65]. 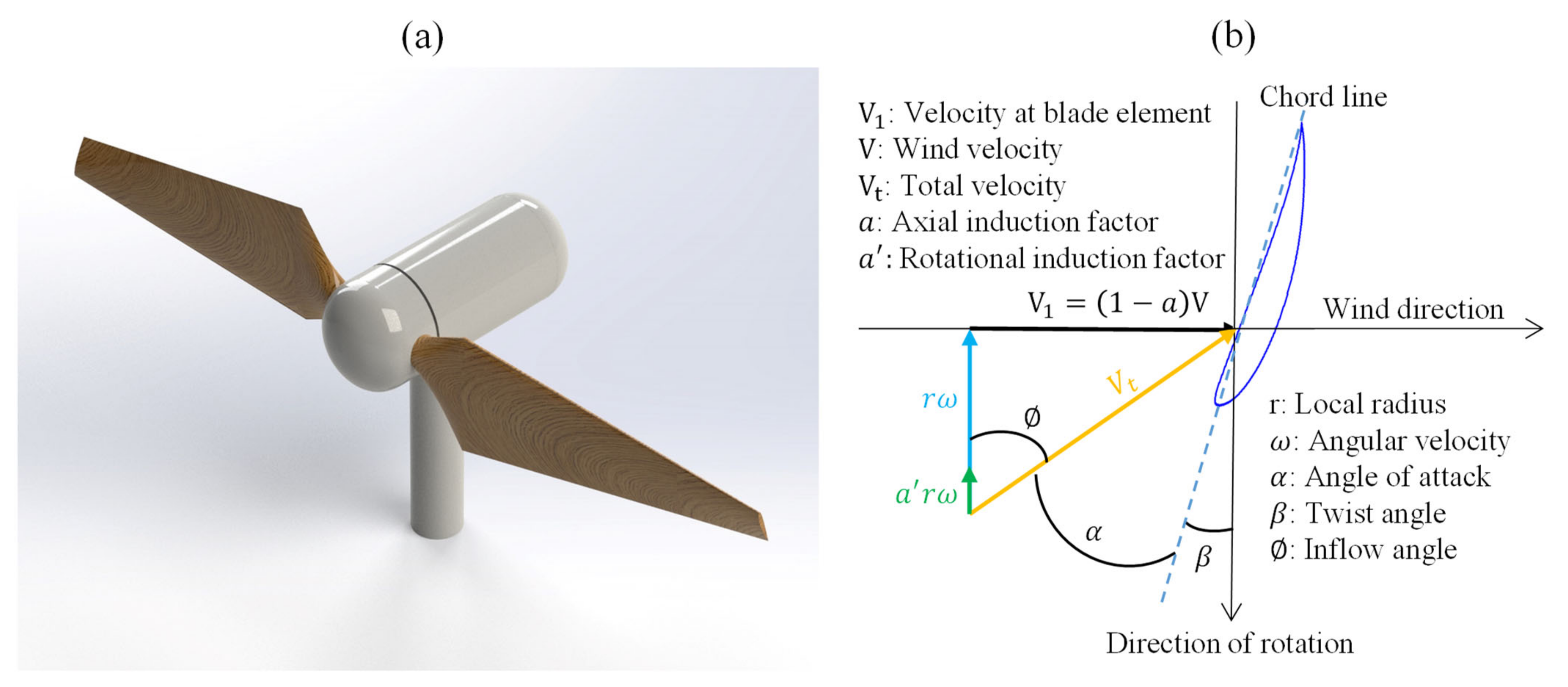Figure 3 depicts an SWT with timber blades and also the velocities on a blade element positioned at a radial distance of r from the center of the rotation.

To compute the $C_p,$ the following measures were implemented:

Initially, a value of 0 was applied to both $a^{\prime }$ and $a,$ and the algorithm was initiated by computing the α and the inflow angle:

$$\varphi ={\tan }^{-1}\left(\frac{\left(1-a\right)V}{\left(1+a^{\prime }\right)r\omega }\right)$$

(4)

$$C_a=C_l\cos \varphi +C_d\sin \varphi$$

(5)

in which $\omega$, r, and V represent the rotational velocity, radius, and wind speed, respectively.

The following equations were employed to compute the $C_{a^{\prime }}$ and $C_a$:

$$C_a=C_l\cos \varphi +C_d\sin \varphi$$

(6)

$$C_{a^{\prime }}=C_l\sin \varphi -C_d\cos \varphi$$

(7)

Subsequently, the Prandtl model was utilized to compute the blade tip losses:

$$F=\frac{2}{\pi }{\cos }^{-1}\left[\exp \left(-\frac{B\left(R-r\right)}{2(r-\sin \varphi }\right)\right]$$

(8)

where R and B indicate the blade length and number, respectively.

After that, the induction terms were calculated:

$$a=\frac{1}{\frac{4F{\sin }^2\varphi }{\sigma C_a}+1}$$

(9)

$$a^{\prime }=\frac{1}{\frac{4F\sin \varphi \cos \varphi }{\sigma C_{a\prime }}-1}$$

(10)

where $\sigma =\raisebox{1ex}{$Bc$}\!\left/ \!\raisebox{-1ex}{$2\pi r$}\right.$ represents the solidity factor, in which c is the chord length.

At this stage, the computed induction terms were substituted in Equation (4), and the previous steps were repeated as long as these convergence criteria were not met:

$$\left|a_{n+1}-a_n\right|<{10}^{-5}$$

(11)

$$\left|{a^{\prime }}_{n+1}-{a^{\prime }}_n\right|<{10}^{-5}$$

(12)

After the determination of the induction term values, $d{F}_y$, $d{F}_x$, and the total velocity ($V_t$) could be computed using the following correlations:

$$V_t=\sqrt{{\left[\left(1-a\right)V\right]}^2+{\left[\left(1+a^{\prime }\right)r\omega \right]}^2}$$

(13)

$$d{F}_x=\left(\frac{1}{2}\rho V_t{}^{2}cdr\right) C_a$$

(14)

$$d{F}_y=\left(\frac{1}{2}\rho V_t{}^{2}cdr\right) C_{a\prime }$$

(15)

in which ρ represents the air density.

Next, the power ($dP$) and torque ($dM$) for each blade section were computed from:

$$dM=r d{F}_y$$

(16)

$$dP=\omega dM$$

(17)

Considering B, the total power ($P$) and aerodynamic moment ($M$) were acquired:

$$M=B{\displaystyle \sum }_{i=1}^n{\left(dM\right)}_i$$

(18)

$$P=B{\displaystyle \sum }_{i=1}^n{\left(dP\right)}_i$$

(19)

In these correlations, n indicates the number of blade sections (elements).

The $C_p$ value was then computed using:

$$C_p=\frac{M\omega }{0.5\rho S{V}^3}$$

(20)

where S represents the surface swept by the rotor.

Since the V value in the selected places was relatively low, to reduce the inertia and improve the startup behavior of the blades, the Bergey BW-3 airfoil, which geometry is shown in Figure 4, was used as the blade profile. Having a high lift-to-drag ratio and possessing good aerodynamic performance in the presence of roughness were some features of this airfoil.

Figure 5 shows the aerodynamic coefficients extracted from the experimental data conducted with the Bergey BW-3 airfoil. In the current research, these coefficients were tabulated and coded, so that the corresponding aerodynamic coefficient was calculated and called during the computations considering the Re and the AOA of every individual element.

4. Analyzing the Startup Time

When the turbine blades start to rotate, the AOA is high. Studies show that, at high AOAs, the aerodynamic behavior of airfoils is analogous to a flat plate. In this regard, Wood [9] presented the following correlation to calculate the startup torque (M_s) generated by the blade during the startup process:

$$M_S=B\rho V^2{R}^3{\displaystyle {\int }_{r_h}^1{\left(1+{\lambda }_r^2\right)}^{1/2}}\mathrm{c} \mathrm{r}\sin \beta \left(\cos \beta -{\lambda }_r\sin \beta \right)dr$$

(21)

In this equation, r_h is the hub radius. It is also worth noting that all speeds and lengths in this equation have been nondimensionalized by V and R, respectively. The important point in Equation (21) is the independence of the M_s from the Re, which is due to using generic flat plate expressions to determine the aerodynamic coefficients at high AOAs. Also, c and r represent the chord length and the radial coordinate along the blade, respectively. During the startup process of the blade from a static condition, the changes in the tip speed ratio (λ) with time can be written as follows:

$$\frac{d\lambda }{dt}=\frac{R\left(M_s-M_c\right)}{JV}$$

(22)

where J is the blade inertia [9]:

$$J=B{\rho }_{b}A{R}^5\left[{\displaystyle \int {(c r)}^2}dr+\frac{1}{12}\left({\displaystyle \int c^4}{\cos }^2\beta dr+A^2{\displaystyle \int c^4}{\sin }^2\beta dr\right)\right]$$

(23)

In this correlation, ρ_b is the blade density, and A is the area of the airfoil by assuming c = 1. Solving the differential Equation (22) from the static condition λ = 0 to λ = 1 determines the turbine startup time. Experimental studies have affirmed the reliability of Equation (22), and this correlation has been used by many researchers for computing the startup time of SWTs [9,21].

5. Multi-Objective Optimization and Input Parameters

The absence of any constraints such as continuity and derivability for the objective function, as well as demonstrating its effectiveness in solving multi-objective optimization problems, are two prominent characteristics of the DE algorithm, which was established by Storn and Price [68] in 1997. For this algorithm, there is no limit to the number of variables in the objective function, and this method only needs the objective function for execution, and its complexity does not impede the process. To find the optimal solution, three operators, including mutation, crossover, and selection, are used in the DE algorithm. In this technique, first, a random initial population (which is the blades in this study) is created based on the constraints considered for the design variables (β and c for this research); then, with the aid of the mutation and crossover operators, offsprings (new blades) are produced, and each child is compared against its parent with the aid of the selection operator. In case the child has a better objective value, it substitutes its parent, and the next generation is created. This process continues until reaching a global solution. In this regard, the steps taken in the DE algorithm in this study are briefly described as follows:

• Initialization of the population and selecting the algorithm settings, including evolution administration and termination criterion.
• Arbitrarily generating the population and computing objective function value for each member of the population.
• Continuing these substeps unless the termination criteria are reached:

  3.1

  Mutating with the difference vectors ($x_{r1.g}$, $x_{r2.g},$ and $x_{r3.g}$) according to the mutation factor (F) and generating another vector ($V_G=x_{r1.g}+F\left(x_{r2.g}-x_{r3.g}\right)$).

  3.2

  Crossing over based on the crossover constant (C_r).

  3.3

  Computing the objective function for the members of the population after the evolution.

  3.4

  Selecting the optimal members based on the greatest value of the objective function.

• Returning to the third step.

The two design goals considered in the present study, i.e., the C_p and startup time, are different. While the C_p has a numerical value of less than one, the startup time can possess any value. Thus, by nondimensionalizing and using the weighting coefficients method, which is one of the techniques for determining the Pareto front, the following objective function was considered for the optimization process, so that the DE algorithm tried to maximize this function [16]:

$$\mathrm{Maximize} \left(W_f\frac{C_P}{\max \left(C_P\right)}+(1-W_f)\frac{\min \left(T_s\right)}{T_s}\right)$$

(24)

where 0 ≤ W_f ≤ 1 is the weighting ratio that specifies the contribution of each of the design goals. Moreover, C_P is the power coefficient corresponding to the blades in the population matrix, and max(C_P) is the highest power coefficient in each generation. On the other hand, T_s is the startup time corresponding to the blades in the population matrix, and min(T_s) is the minimum startup time in each generation. With the aid of this objective function, the C_p and startup time in each generation are nondimensionalized, and the value of the objective function is between zero and one. The objective function constants, max(C_P) and min(T_s), are variable during the execution of the algorithm, and therefore, the objective function also changes. The input parameters of the DE algorithm are given in

Table 2. The values chosen for the DE algorithm variables.

Parameter	Population	Generation	Mutation Factor	Crossover Constant
Value	3000	500	0.8	0.1

. It is necessary to explain that, in the present study, a numerical code written using MATLAB R2014a software was used for the optimization.

The geometry of the WT blade is determined by three parameters, including the airfoil type and the β and c distributions. By choosing the Bergey BW-3 airfoil as the blade profile, the objective function variables are the β and the c. In the BEM theory, it is suggested to use between 10 and 20 elements along the blade [9]. In the present study, 15 elements were considered, and with this selection, the problem had 30 variables.

Table 3. Input values for design and optimization.

Parameter	Value	Parameter	Value	Parameter	Value
Output Power	1000 W	Vs	4 m/s	Rh	0.125 m
B	2	Vrated	8 m/s	ω	450 rpm
Min c/R	0.01	Max c/R	0.2	Mc	0.5 Nm
Min β	−5	Max β	25	Generator inertia	0.01 kg·m2

shows the input parameters and their values, along with the range of the design variables.

The range considered for the c parameter is determined by the requirements of the manufacturing and machining process. To avoid excessive alternations while connecting the aerodynamic part of the blade to the root section, a maximum value of 25° was considered for the twist angle. Also, machining restrictions recommend a value of −5° for the minimum twist angle. The considered M_c values, as well as its inertia, are among the characteristics of the selected one-kilowatt generator [44]. Since the selected counties do not have a significant wind potential [69], the startup wind speed (V_s) of the turbine was selected to be 4 m/s. On the other hand, it is suggested that the rated speed in the design should not be less than twice the V_s value [9]. Thus, the design wind speed was chosen to be 8 m/s. The multi-objective optimization algorithm used in the present study is shown in Figure 6 in the form of a flowchart.

6. Validation

In this part, the accuracy of the developed in-house code is assessed. In this regard, in the first section, the C_p results, and in the second part, the startup time (T_s) values, are validated.

6.1. Validation of the C_p

In this section, the results of the current code are compared with the experimental data presented in Reference [70]. In this reference, the experimental data of a small two-blade WT with the NACA4412 airfoil as the blade profile and a rotor diameter of 3 m were presented at V = 10 m/s. The aerodynamic coefficients of the related airfoil at diverse Re and AOAs [9] were tabulated, coded, and used in the relevant computations. The C_p values calculated from the numerical code have been compared against the experimental values in Figure 7. It can be perceived that the numerical results are in agreement with the reference data, having a maximum deviation of less than 6.5%.

6.2. Validation of the T_s

To ensure that the startup results of the present code are valid, the numerical results of a small three-blade WT presented in Reference [16] were used. Considering the c and β values presented in this reference for ash blades with a density of 590 kg/m³, the T_s was calculated. It is necessary to explain that, in Reference [16], the V_s was considered to be 5 m/s, and the SG6043 airfoil was used as the blade profile.

Table 4. Comparison of the T_s from the developed code and Reference [16].

Parameter	Reference [16]	Current Research	Deviation (%)
Startup time (s)	5.1	5.2	1.96

compares the T_s results. It is conspicuous that the results are significantly close to an absolute error of less than 2%.

7. Results and Discussion

In this section, two optimization processes are followed. In the first part, an SWT is designed for the elevation of the sea level; then, the influence of the selected timbers on its performance is evaluated, and the best blade is selected. Subsequently, the efficiency of the selected blade at various elevations is investigated. In the second part, to ameliorate the performance of the selected blade at each elevation, the blade is reconstructed. In this regard, the blade design will be based on the kinematic viscosity and air density of each region.

7.1. Designing a Blade for Operating at Sea Level and Evaluating Its Efficiency in the Selected Counties

According to Table 3, the generator considered in the current research generates 1000 W of power at a rated speed of 450 rpm, and its efficiency is 75% [44]. Therefore, by choosing a V of 8 m/s, which was explained in the previous section, the C_p and tip speed ratio of the turbine design can be acquired in terms of the blade length:

$$C_p=\frac{P/\eta }{0.5\rho S{V}^3}=\frac{1000/0.75}{0.5\times 1.225\times \pi R^2\times 8^3}=\frac{1.35}{R^2}$$

(25)

$$\lambda =\frac{R\omega }{V}=\frac{450\times 2\pi }{8\times 60}R=5.89R$$

(26)

By choosing any value for R, the corresponding values for C_p and λ are acquired. However, it should be noted that the value of C_p cannot exceed the Betz–Joukowsky limit ($\frac{16}{27}$). The achievable C_p value in SWTs is reported to be 0.48 [9]. Considering this value for the C_p, the corresponding λ and R values are found to be 9.9 and 1.68 m, respectively (Figure 8). As was stated before, for the current research, a two-bladed turbine was chosen, the reasons for which are presented as follows:

1. In the design and optimization of wind turbines, it is necessary to select the number of blades based on the rated tip speed ratio (λ). As explained by Manwell et al. [71] for the rated λ values higher than 4, one to three blades offer the best performance for a wind turbine. Considering that, in the current work, the rate λ is 9.9, the number of blades should be between one and three.

2. Changes in the power coefficient at various tip speed ratios in wind turbines with different numbers of blades show that, at high tip speed ratios, selecting more than two blades does not lead to a significant effect on the turbine power coefficient [71].

3. As discussed in the work of Tang et al. [72], the manufacturing cost of wind turbine blades accounts for around 15 to 20% of the total cost of the turbine. Therefore, to reduce manufacturing and maintenance costs as much as possible, the selection of a turbine with fewer blades seems reasonable.

According to these points, it can be concluded that a two-bladed turbine is ideal for the present study. Now, it is possible to conduct the optimization process with the aid of the other input parameters (Table 2 and Table 3).

The optimum values of the β and the c are provided in Figure 9 for the blade made of alder timber. Also,

Table 5. The optimal C_p and T_s values for the blades made of each selected hardwood.

Timber	ρb (kg/m3)	Wf = 1		Wf = 0.9		Wf = 0.8
		Cp	Ts (s)	Cp	Ts (s)	Cp	Ts (s)
Alder	490	0.480	8.08	0.469	2.75	0.446	2.12
Oak	600	0.479	17.86	0.469	3.39	0.444	2.61
Hornbeam	707	0.480	19.83	0.469	3.98	0.445	3.09

summarizes the values of the C_p and optimal T_s for each of the selected timbers.

The density of these timbers is also given in this table. As can be observed, by diminishing the values of W_f in the objective function (Equation (24)), both the C_p and the T_s are decreased, but the reduction of the T_s is more considerable than the decrement in the C_p, so that, for the blade made of alder timber, by reducing the C_p by 7%, a 74% enhancement in the T_s is observed. The improvement of the T_s for the blades designed to be made of oak and hornbeam timbers is around 85%. This point underlines the significance of considering the T_s in the design of SWT blades, which do not possess a pitch control mechanism. According to Table 5, even though the blade density does not influence the turbine C_p, it substantially affects the T_s. Figure 10 depicts the average T_s of the optimal blades made of the selected timbers.

As can be observed, the time for the blades made of oak and hornbeam timbers is 84 and 108% more than the blades designed with alder wood, respectively. The reason for this is the low density of alder and, consequently, the lower inertia of the blades designed using this timber (Figure 11).

It is necessary to explain, besides the M_c, the M_s and the blade inertia are two factors that affect the startup behavior of SWTs. Based on Figure 9, as the value of W_f is reduced, the β and c values increase in the root elements. Raising the β values reduces the AOA of the root elements and increases the lift coefficient. On the other hand, based on Equation (21), the increment of the c also raises the M_s. In this regard, Figure 12 demonstrates that, for the blades made of alder timber, by reducing the value of W_f, the M_s increases.

Regarding the increase in the c, it is essential to mention that, although raising this parameter causes an increase in the M_s, it also increases the blade inertia, which can hurt the turbine T_s; thus, there is a conflict between the inertia and the M_s, for which the optimization algorithm tries to come up with a compromise by determining the optimal value for the c.

According to Table 5, the optimal blades made from alder timber have better performance than those made of the other selected timbers. Therefore, the aerodynamic behavior of these blades (designed with different W_f values) was investigated in the selected cities (Table 1), and the results are tabulated in

Table 6. The performance of the optimal blades for the sea level (made of alder timber) at different elevations.

Case Study	Wf = 1		Wf = 0.9		Wf = 0.8
	Cp	Ts (s)	Cp	Ts (s)	Cp	Ts (s)
Dalgan (392 m)	0.477	20.71	0.466	2.95	0.443	2.26
Maku (1182 m)	0.475	61.67	0.462	3.42	0.441	2.58
Asadabad (1607 m)	0.471	-	0.460	3.72	0.439	2.77
Sisakht (2250 m)	0.470	-	0.457	4.26	0.436	3.11

.

It can be perceived that, as the elevation increases, the C_p is reduced while the T_s rises. Even though the decrease in the C_p due to the reduction in the Re (because of the increase in kinematic viscosity) can be up to 2.5%, the increase in the T_s is notable, so that the ideal blade (W_f = 1), which was designed to work at the sea level, cannot start to spin at V = 4 m/s in the cities of Asadabad and Sisakht, and it practically loses its performance. In these regions, the generated M_s cannot conquer the M_c, which has a meaningful value in SWTs (as compared to the M_s generated in these turbines). This point affirms that, in the design and selection of SWT blades, the parameter of elevations above sea level should be considered.

7.2. Redesigning the Blades for Each County

In this section, the blades are redesigned for each elevation based on the standard air conditions presented in Table 1, and the findings are given in

Table 7. The performance of the optimal blades for the sea level (made of alder timber) at different elevations.

Case Study	Wf = 1		Wf = 0.9		Wf = 0.8
	Cp	Ts (s)	Cp	Ts (s)	Cp	Ts (s)
Dalgan (392 m)	0.479	6.73	0.468	2.95	0.446	2.28
Maku (1182 m)	0.479	9.35	0.467	3.39	0.444	2.58
Asadabad (1607 m)	0.479	11.89	0.466	3.67	0.444	2.78
Sisakht (2250 m)	0.478	17.76	0.465	4.22	0.442	3.27

.

It can be perceived that, by accounting for the effect of elevation in the design, the overall performance of the blades has improved compared to the results in Table 6, so that the redesigned ideal blades can start rotating and be employed to generate power in Asadabad and Sisakht Counties. To investigate the reason for this issue, the geometry of the optimized blade redesigned for the highest elevation, i.e., Sisakht County, along with the optimized blade geometry designed to work at sea level, are compared in Figure 13. It can be perceived that, while the β values are almost the same in both blades, the c of the blade redesigned to work at a higher elevation is generally greater than that of the blade designed to work at sea level. Indeed, with the rise in elevation (increase in the kinematic viscosity), the Re on the blade decreases, which will lead to a decrement in the lift coefficient of the blade. Therefore, the optimization algorithm tries to raise the lift coefficient and, as a result, the energy harnessed from the wind to improve the C_p and prevent its drastic reduction by raising the c. On the other hand, as mentioned before, the increase in the c also results in an increment in the M_s, which enables the blades to rotate at V = 4 m/s.

8. Conclusions

Wood is a stable, cheap, and durable engineering material that has good fatigue resistance. This material has been an interesting choice for application in SWT blades in recent years. Moreover, SWTs are installed in areas with different elevations. This study examines the impacts of wood density and elevations above sea level on the performance of a small 1-kW wind turbine. For this purpose, the usage of three hardwoods—namely, alder, oak, and hornbeam—which grow abundantly in the Hyrcanian forests of Iran as the materials of SWT blades and four low-wind counties, including Delgan, Maku, Asadabad, and Sisakht, with different elevations above sea level were selected as the case studies. To reduce the blade inertia, the Bergey BW-3 airfoil, which has a smaller area compared to other airfoils used in the SWT industry, was used as the blade profile. Additionally, to reduce the cost, a rotor with two blades was selected. Considering that the wind speed is not high in the selected counties, minimizing the startup time (T_s) was added to the main design goal, which was maximizing the power coefficient (C_p) of the turbine. Then, based on these objectives, the geometric shape of the blades was determined with the aid of the DE algorithm. The BEM model (along with the Prandtl model for accounting for the blade tip losses) was utilized to compute the C_p, and a quasi-steady version of the BEM model was employed to calculate the T_s. The findings showed that the hardwood type utilized in the blade has no impact on the C_p, but it utterly influences the T_s, so that the average T_s of the blades made of oak and hornbeam timbers are 84 and 108% higher than the average T_s of the optimized blades made of alder timber. It is highly recommended to consider the T_s for the design and optimization of wind turbine blades in less windy regions, because the results demonstrate that, with only about a 7% reduction in the C_p, the T_s of the blades made of alder improves by 74%, and the enhancement of the T_s for the blades made of oak and hornbeam timbers is around 85%. This undeniable improvement stems from raising the twist angle and chord length in the root elements of the blades. In addition, it was observed that the performance of the turbine that was designed to work at sea level was weakened at greater elevations. Although the change in the C_p can be ignored, the startup performance is prone to more severe impacts, and the reduction in the startup torque (M_s) can be so drastic that it practically stops the turbine from operating in these regions, since the rotor cannot conquer the generator cogging torque (M_c) and start rotating. In this case, the turbine loses its performance and cannot be used to generate power. This phenomenon was observed for the two-bladed turbine of the current research in Asadabad and Sisakht Counties, with elevations of 1607 and 2250 m above sea level. To solve this problem, the blade was redesigned based on the local atmospheric conditions in which the turbine was intended to be used, and improvements were observed in the C_p and T_s of the blades, especially the ideal blades.