Validation of Wind Turbine Models Based on Test Bench Measurements: A System for Theoretical Representation of the Grid Replica

Abstract

In recent years, nacelle test benches for wind turbines have been developed internationally. New standards are currently being developed that explicitly refer to the measurement of the electrical properties of wind turbines on these test benches. Thus, they are suitable for measuring the electrical properties required for certification. Another part of the certification is the creation and validation of suitable models of the wind turbine, which are used for stability analyses of the utility grid. Validation requires a suitable model of grid replication on the test benches, which is not yet covered by any applicable standard. Such models should be as simplified a representation of the artificial grid replication as possible to ensure that they are accessible to certification bodies. A model of the grid emulator installed at the CWD of RWTH Aachen University, which was validated with real measurement data, serves as a reference. A step-by-step reduction of the model’s depth up to the system’s technical representation is followed by a model evaluation with respect to the level of detail and an analysis of time and frequency. The evaluation shows that even a highly simplified model consisting of a reference voltage and an impedance replica meets the requirements for the validation of wind turbine models according to IEC 61400-27-2.

1. Introduction

Classically, the type of testing performed on wind turbines, which verifies compliance with the grid’s code, is usually conducted in the field. In most cases, these also represent the first tests performed with the complete wind turbine. This approach is highly dependent on prevailing wind conditions, and therefore, they are not plannable and are potentially time-consuming. The costs for the field tests are difficult to estimate in advance and increase with testing duration. Furthermore, a reproduction of the tests is not possible, as different conditions always prevail in the field. Another issue with the existing test procedures is that problems caused by the respective influences of the individual components are only detected during the field tests [1].

In order to validate the interactions of the individual components with each other in advance, new test procedures have emerged in recent years. These include virtual testing, which examines the interactions of the individual components in advance [2], and system test benches, on which the complete nacelle is tested in advance under laboratory conditions [3]. These were first described by Jansen [4,5]. One of the goals of these procedures is to reproduce real field behavior on the system test benches, also called nacelle test benches, to make them usable for certification [1,6,7]. For this purpose, emulator systems reproduce both the behavior of the rotor on the test bench and an artificial grid connection [8]. The grid emulators on the system test benches consist of several parallel converter systems connected via the under-voltage winding of a transformer [7,9]. The transformer raises the voltage to the required level [7,9,10]. Grid emulators are required to have dynamics that satisfy the requirements of the Under Voltage Ride Through (UVRT) tests [11]. At the same time, the required tests on power system responses demand consistent high voltage quality [12]. To meet these two requirements, advanced control algorithms have been developed, such as feed-forward control [9], interleaved switching of the converters [13], and modulators with optimized pulse patterns [7].

UVRT is one of the most complex tests, as it requires additional test equipment [14]. As a controllable voltage source, the grid emulators are capable of executing the voltage dip themselves. Comparisons with field measurements prove that the results obtained from field testing are verifiable on the test bench, and thus, they confirm the high accuracy of the tests on nacelle test benches [15]. A crucial criterion for comparability is the replication of the fault impedance in the context of a PHiL simulation [16]. Due to this impedance control, the complete behavior patterns of voltage divider-based test equipment can be reproduced on the test bench [17].

The aforementioned work proves that the grid emulators currently used on test benches enable UVRT measurement with accuracy comparable to field tests. However, impedance emulation is necessary [16]. In addition to the measurement of the UVRT characteristics of the wind turbine, certification also requires the validation of a wind turbine model when using UVRT [18]. The exact requirements for the validation of a wind turbine model are described in Section 2. In addition to the wind turbine model, a model of the voltage dip generator itself is required for the validation. Compared to the previous state-of-the-art voltage divider-based test method [12], the modeling effort for grid emulators is increased because they represent an actively controlled voltage source. Section 3 presents a grid emulator model based on a 4 MW system test bench at the Center for Wind Power Drives (CWD) at RWTH Aachen University [10]. The main focus of the model is the mapping of the control strategy, as this significantly defines the voltage at the point of connection (PoC). This is validated in Section 4 using real measured data. The real measured PoC voltage of the wind turbine can be reproduced in the simulation. In combination with a generic wind turbine model, it is shown that the validation of wind turbine models based on test bench results is possible. In Section 5, the previous grid emulator model is further simplified, and the limits to its validity are examined. The validation against the previous grid emulator model shows that the exclusive mapping of the impedance replication within the simulation is sufficient to validate the wind turbine models according to the criteria of [18].

2. Wind Model Validation According to Standards

Wind turbine manufacturers are required to provide models of their turbines. The models are used to simulate power systems in order to perform stability analyses with respect to long-term disturbances and short-term stability phenomena. In addition to changes in the set point, frequency interferences and symmetrical voltage dips due to a short circuit are among the aspects to be investigated. Wind turbine models are also required to represent both the control of the wind turbine and its limits. Consideration of the fundamental frequency component is sufficient. The Thévenin equivalent is sufficient to represent the electrical grid. UVRT tests additionally require mapping the test equipment used to generate the voltage dips. An exact specification of the model of the voltage dip generator is currently not available [19].

Validation is performed by directly comparing measured values of defined tests with simulation results. The difference between simulation and measurement in the positive sequence results in different error values [18]. With respect to UVRT tests, a subdivision is first made into five windows, three semi-stationary and two transient. Figure 1 shows the individual windows. Transient areas, which are not considered in detail in the validation, include the first 140 ms after fault occurrence and the first 500 ms after fault clearance. The three semi-stationary ranges describe a pre-fault range from the start of the measurement to the beginning of the fault, the fault range from time $t_{QS}$ to fault declaration, and the post-fault range from time $t_{clearQS}$ to the end of the measurement. $t_{QS}$ and $t_{clearQS}$ each describe the time at which the transient ranges end [20]. For each of the three ranges, the mean error $x_E$ (Equation (1)), maximum error $x_{ME}$ (Equation (2)), and mean absolute error $x_{MAE}$ (Equation (3)) are calculated [18].

$$x_E\left(n\right)=x_{sim}\left(n\right)-x_{mea}\left(n\right)$$

(1)

$$x_{ME}=\frac{{\sum }_{n=0}^N{x}_E\left(n\right)}{N}$$

(2)

$$x_{MAE}=\frac{{\sum }_{n=0}^N\left|x_E\left(n\right)\right|}{N}$$

(3)

3. Grid Emulator Representation in the Simulation

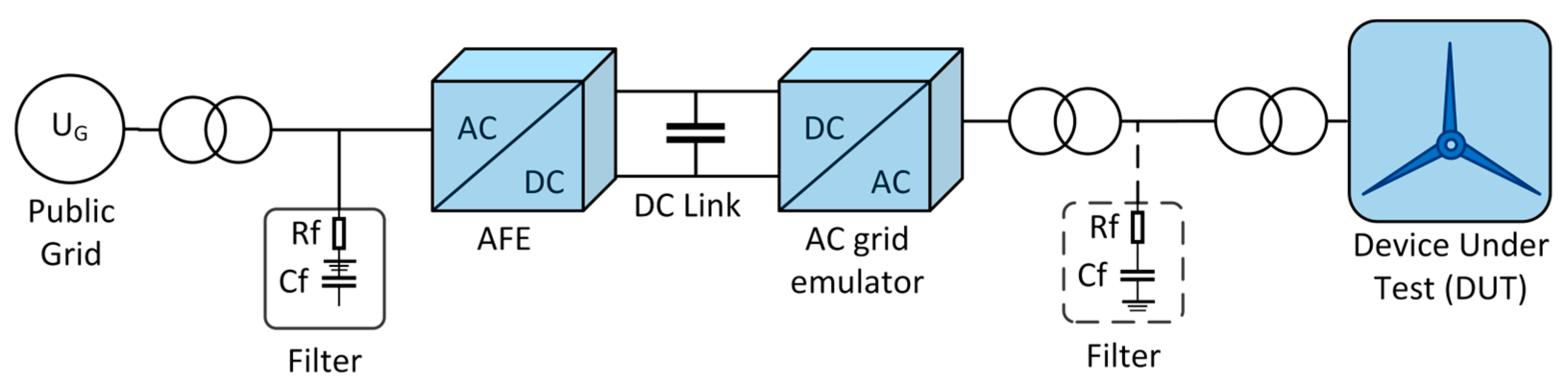
Grid emulators comprising a back-to-back converter system replicate the electrical grid at the nacelle test benches. The first converter, referred to as the active front end (AFE), is connected to the power grid via a transformer. It controls the DC link voltage. The second converter, called the AC grid emulator, simulates realistic dynamic and steady-state grid conditions by acting as a controlled voltage source. The device under test (DUT) is connected to this converter via a transformer [8]. To reproduce realistic grid conditions, the grid emulators have in addition to the voltage control an impedance emulator [16]. Figure 2 shows the general setup of a grid emulator to which a wind turbine is connected as a DUT. The AFE has a filter to avoid stressing the voltage in the upstream grid. A filter may be installed on the side of the AC grid emulator to ensure voltage quality at the emulated connection point of the DUT. However, there are also configurations that use advanced voltage control algorithms to be able to omit a filter [7].

The AC grid emulator represents the artificial grid as a regulated voltage source. Thus, this converter is decisive for the grid-side response of the DUT; consequently, only the AC grid simulator is relevant for the validation of the wind turbine model. The grid emulator at the CWD, presented in Figure 3, serves as reference.

This emulator consists of three parallel medium-voltage converters and a five-winding transformer. One converter each is connected to a separate winding on the low voltage side of the transformer. The fourth winding represents the point of connection (PoC) of the wind turbine. The rated voltage at the PoC is 20 kV. An RC low-pass is connected to the fifth winding. Together with the leakage inductance of the transformer, this forms the filter of the grid emulator [10]. The AC grid emulator has a voltage control to specify the phase, amplitude, and frequency of the voltage. An impedance control is included as a second control, allowing the DUT to be tested under various grid characteristics [16].

Figure 4 represents a highly simplified illustration of the control relationship as it exists on the test bench. The wind turbine as DUT is shown as the current source, and the grid emulator is the voltage source. Both the grid emulator and the DUT perform a control function related to the PoC. Due to this linkage, there is a direct influence between the grid emulator and the DUT. The transfer functions G1(s) and G2(s) correspond to the calculation of the grid impedance of the grid emulator and the power calculation of the wind turbine, respectively. The controlled system results from the real impedance Z_G on the grid emulator side and the impedance of the wind turbine Z_DUT on the DUT side. Both impedances are mainly determined by their respectively connected transformers.

3.1. Voltage Control

The voltage control of the grid emulator aims to provide the reference voltage at the PoC. Figure 5 schematically shows the control of the grid emulator, with the blue box showing the voltage control.

The set point of the reference voltage U_Ref* results from the preset voltage and the voltage correction due to the impedance control (see Section 3.2). To represent both three-phase symmetrical and two-phase asymmetrical voltage dips, the control is implemented in alpha–beta coordinates. It offers the advantage of two separately controllable coordinates and facilitates the control of the three-phase grid. The structure of the control of both coordinates is identical. As a disadvantage, the alpha–beta transformation still deals with sinusoidal variables. To be able to follow the changing set point, a proportional and resonance controller (PR) is used. PR controllers, as shown in Figure 6, follow oscillating input variables without a remaining controller deviation. In addition, the control of individual, defined harmonics is possible [22].

The validation of the wind turbine models according to the criteria of [18,24] explicitly neglects harmonic and transient effects. Consequently, only control of the first harmonic and the fundamental frequency component is implemented in the model. The generation of pulse width modulation (PWM), which typically controls the converter [25], is, therefore, also negligible. The modeled converters, which are represented as an ideal voltage source, directly represent the control signal U_act. Nevertheless, unrealizable voltages, e.g., those exceeding the maximum converter voltage, are not permitted to occur. Violating the system limits otherwise leads to non-linarites. A set point limitation ensures that only permissible voltages appear, but this can lead to the so-called windup effect. In the control context, it describes a type of misbehavior triggered by the manipulated variable’s limit, which is to be prevented via an anti-windup control. Figure 7 displays the voltage control. In the alpha coordinate, the reference voltage $U\_ref\_alpha$ and the voltage correction due to the impedance control $dU\_alpha$ serve as input parameters. A PR controller controls the PoC voltage as described above. The anti-windup is applied subsequent to the PR controller. The anti-windup feedback is subtracted from the measured actual voltage $U\_POC\_alpha$ transformed into the alpha coordinate. This prevents windup due to the manipulated variable’s limit. Thus, the controller receives a continuous sinusoidal voltage as input again even if the manipulated variable is exceeded. At the same time, it is not possible to exceed the manipulated variable limit at the controller output. The anti-windup thereby prevents overshooting of the PoC voltage and ensures stable operation. For transforming back to abc coordinates, the beta coordinate is still necessary; it is controlled identically to the alpha coordinate, and therefore, it is not shown in the figure [21].

During uninterrupted grid operation, the transformer of the grid emulator increases the voltage to 20 $\mathrm{kV}$. At the same time, it represents the controlled system. The PoC voltage is subsequently fed back to the controller [21].

3.2. Impedance Control

The mutual influence of PoC voltage and injected wind current strongly depends on the height and angle of the grid impedance. Therefore, a device in the loop control of the grid impedance is implemented on the grid emulator [21]. The PHiL setup for the impedance control is well described in [16,26].

The voltage drop across impedance depends equally on the absolute value $I_{abs}$ and phase $\varphi I$ of the measured wind current. For these reasons, the input signal of the current is further processed with a second-order generalized integrator (SOGI). In addition to the absolute value and phase, the SOGI determines the DC component $I_{DC}$ and filters the input signal [27]. Equation (4) describes the transfer function of a SOGI. To calculate the voltage change across virtual impedance, the magnitude $Z_{ref,abs}$ and the phase $Z_{ref,angle}$ of a preset impedance are required as input parameters. It is calculated in alpha and beta coordinates to facilitate the addition of the resulting voltage change to the reference voltage $U_{Ref}$ [21].

$$G\left(s\right)=\frac{k_i · s}{s^2+w_n^2}$$

(4)

The voltage drop is determined with a zero-phase angle of 0 to neglect phase differences between current and voltage. Equation (5) indicates separate calculations of the real and imaginary parts of the voltage drop. The combination of the two values results in the complex quantities $d{U}_{alpha}$ and $d{U}_{beta}$, which are added to the corresponding reference voltage $U_{ref,alpha/beta}$ in the voltage controller. Considering the virtual impedance modifies both the magnitude and the phase of the set input voltage [21].

$$\begin{gathered} d{U}_{alpha,real}=\cos \left({\phi }_{Z,ref}+{\phi }_{I,alpha}\right) · Z_{ref,abs} · I_{abs,alpha} \\ d{U}_{alpha,imag}=\sin \left({\phi }_{Z,ref}+{\phi }_{I,alpha}\right) · Z_{ref,abs} · I_{abs,alpha} \\ d{U}_{beta,real}=\cos \left({\phi }_{Z,ref}+{\phi }_{I,beta}\right) · Z_{ref,abs} · I_{abs,beta} \\ d{U}_{beta,imag}=\sin \left({\phi }_{Z,ref}+{\phi }_{I,beta}\right) · Z_{ref,abs} · I_{abs,beta} \end{gathered}$$

(5)

3.3. Wind Turbine Model

Both the wind turbine as DUT and the grid emulator exercise control with reference to the PoC. Due to the direct influence of the two controllers, the modeling of the DUT is also necessary for the stability analysis of the grid emulator model. For this purpose, a simplified wind turbine model is integrated into the simulation. The DUT is a full converter turbine, which is also referred to as a type 4 turbine [19]. Figure 8 shows the model of the wind turbine as a modification of the general model of a type 4 turbine as shown in [19]. The focus is exclusively on the grid characteristics. The full converter decouples the mechanical system from the electrical system so that the mechanical components are not modeled. Therefore, the implemented model consists of the generator, which provides the power, and the power electronic components, which transmit the power to the grid. In the generic models, a separation is made between protection and control. The validation of the grid emulator model requires both the provision of a defined power in steady-state operation (“control”) and a specific behavior during a voltage dip (“protection”). Switching between the control module and the protection module is done according to the voltage level [19].

In protection mode, the wind turbine provides voltage support. For this purpose, it feeds in a reactive current I_DUT;reac, the level of which depends on the voltage difference $\Delta u$ and a preset proportionality constant $k$, as shown in Equation (6).

$$\Delta i_{DUT,reac}=k · \Delta u$$

(6)

$$\Delta u=\frac{U_N-U_{rms}}{U_N}$$

(7)

Determining the requested reactive current injection requires the RMS value of the measured voltage $U_{rms}$. The conversion of the RMS voltage into per unit (pu) allows the calculation of the voltage difference $\Delta u$ according to Equation (7). The active current that the wind turbine delivers in the UVRT case $I_{DUT,act}$ depends on the maximum possible current $I_{DUT}$ and the reactive current just calculated. Equation (8) describes the calculation of the active current injection.

$$I_{DUT,act}=\sqrt{I_{DUT}^2-I_{DUT,reac}^2}$$

(8)

The current control enables the compliance with the power specification. Wind turbines are classically controlled in dq-coordinates, which allow direct determination of the active and reactive power [28]. A phase-locked loop (PLL) is used to calculate the dq coordinates from the measured current. The control of the two components is done independently based on a pre-sampled reference value. In the UVRT case, the reference value is calculated as described previously. In steady state mode, the reference value is a predefined parameter. For real wind turbines, this results from the available wind power and the reactive power feed-in specified by the grid operator. The selection of the reference value first requires information about the current operating mode. In the simulation, the level of reactive current is the decisive criterion to define the mode. If the required reactive current is higher than the reactive current injection specified in the steady-state operating mode, it indicates a UVRT case, and hence, protection mode is enabled. Figure 9 shows the control mode of the DUT current controller.

3.4. Simulink Model

Figure 10 shows the complete setup of the grid emulator model in the simulation. MATLAB/Simulink is chosen as the simulation environment. Simscape^TM, which is integrated in the Simulink environment, transfers the variables into a physical system. This model is referred to as the complex grid emulator model henceforth and consists of three parts: The control of the grid emulator, the model of the hardware components, and the wind turbine control. Although the control of the grid emulator and the wind turbine are presented as completely as possible, the model of the hardware components allows some simplifications. The validation of the wind turbine models according to the criteria of [18,24] prescribes fundamental frequency models. Accordingly, the simulation does not include the real switching behavior, the interleaved switching, and the parallel connection of the three converter systems. Consequently, the filter needed to reduce the harmonics generated by the real converters is not necessary. An ideal voltage source represents the converter system of the grid emulator. These receive the three-phase voltage signal U_PoC,abc generated by the grid emulator’s controller. Before that, a manipulated variable limiter verifies the signal for the limits of the converter system to avoid excess voltages. The ideal voltage sources generate an electrical voltage that is applied to the lower voltage side of the grid emulator’s transformer. By neglecting the filter, the tertiary winding is omitted. The transformer is modeled as a three-phase transformer. The power rating is 8 MVA. The high voltage (HV) winding represents the PoC. The measured PoC current is used just like the measured PoC voltage for the control of the grid emulator as well as for the control of the DUT [21].

The wind turbine is also represented as a voltage source in the simulation. Connecting the wind turbine to the PoC is again done with a three-phase transformer.

4. Validation of the Complex Grid Emulator Model

The first step is to validate the complex grid emulator model by comparing it with real measurement data. The measurement data results from the research project CertBench, which is presented in [6,15]. A further detailed overview of the measurements is included in the final report. The final report in [29] of the project also contains a detailed overview of the measurements, the measurement equipment used, and the measurements’ accuracy. A turbine from the manufacturer Enercon served as the DUT. The test bench measurements were validated with real field data within the research project. To ensure comparability, the parameters in the simulation have to correspond to the parameters set in the test bench measurement. This applies equally to the wind turbine and the grid emulator. For the settings at the grid emulator, the significant parameters are the short-circuit power and the X/R ratio at the PoC. The dip depth, fault duration, and starting time are also critical factors. For the wind turbine, the model must represent the active and reactive power injection and the predefined k-factor.

Table 1. Parameters of the tests used for validation.

Test Nr.	Upos,f in pu	tfault in s	X/R	SSC in MVA	PDUT in pu	k-Factor
1	0.01	0.402	12.5	2000	0.323	2
2	0.01	0.402	12.5	2000	0.323	2
3	0.01	0.401	12.5	2000	1.014	2
4	0.25	1.497	12.5	56	1.015	1.8
5	0.25	1.497	12.5	56	1.015	1.8
6	0.25	1.497	12.5	56	0.323	1.8
7	0.25	1.497	12.5	56	0.323	1.8
8	0.25	1.497	12.5	56	0.323	1.8
9	0.47	2.991	15.6	30	1.015	1.7
10	0.47	2.991	15.6	30	0.328	1.7
11	0.47	2.991	15.6	30	0.328	1.7
12	0.73	2.991	14.4	19	1.019	1.6
13	0.73	2.991	14.4	19	0.328	1.8
14	0.73	2.991	14.4	19	0.328	1.8

describes the parameters of the tests used for the validation.

4.1. Evaluation of the Complex Grid Emulator Model

The analysis of the validity and accuracy of the grid emulator model requires the exact replication of the wind turbine behavior in the simulation. The model described above is a standard model of a wind turbine. In order to exclude possible deviations from the wind turbine model, the validation was first performed using the so-called playback variant [18]. In this case, real measurements of the current injected by the wind turbine $I_{PoC}$ replaced the wind turbine model. Low-resistance resistors connected between the simulated current source and the PoC increased the stability of the overall simulation. In the playback variant, the current injected by the wind turbine is no longer able to react to the voltage within the simulation. However, a changed angle between voltage and current leads directly to a deviation of the active and reactive power. For this reason, the playback variant requires that the phase angle of the voltage in the simulation matches the phase angle of the measured PoC voltage [21].

The established standards and technical guidelines prescribe the evaluation of the positive sequence system component. The comparison between measured data and simulation result was carried out for the pre-fault, fault, and post-fault areas, as can be seen in Figure 11. The two transient areas of no relevance in the validation are also indicated. The measured and simulated voltages indicate high agreement before and after the error. The deviation in these ranges is always less than 1%, which is negligible considering the measurement accuracy [21].

This result is confirmed in Figure 12. Figure 12a presents the mean error of the three ranges for all tests. This is always less than one percent. The maximum error, shown in Figure 12b, is also below one percent in 10 of 14 measurements. Only the three tests with a 0% voltage and the full-load test with 0.73% fault voltage are between 1 and 2 percent deviation [21].

Figure 13 exemplifies the instantaneous values for test number 10. Although the current measurement which replaces the wind turbine model contains harmonic distortions, the simulated voltages, in contrast to the measured voltages, did not exhibit harmonic distortions. The input filter of the grid emulator’s controller eliminates them completely within the simulation. The quasi-stationary regions before, during, and after the fault again demonstrate high agreement among the respective phase voltages. The transient area shows deviations, which refer during the voltage dip exclusively to the time of the dip itself. After only half of a period, no more deviations remain. The voltage dip continued to be sinusoidal in the simulation. The real measurement shows a more abrupt change of the voltage, which briefly leaves the sinusoidal curve. A similar behavior was observed during voltage recovery. The measured voltage contains a short overshoot of the voltage, which did not appear in the simulation. Responsible for this is the filter of the current input signal as well as the taken linearization. Moreover, especially non-linear effects of the transformers, e.g., saturation effects, cannot be represented by the simulation. The evaluation shows that the developed model of the grid emulator reproduces the measured data in the simulation with high accuracy. Only the transient regions show deviations, and those are mostly within the first period after the voltage change. Because the validation of the wind turbine models does not consider these areas further, the grid emulator model provides a high level of accuracy, and therefore, it is suitable for validation purposes [21].

4.2. Complex Grid Emulator Model in Combination with a Generic Wind Turbine Model

The previous evaluation refers exclusively to simulations in which the wind turbine model is replaced by real measured data. The control of the wind turbine itself has not yet been integrated into the simulation. Because the PoC is the reference point of the control for both the grid emulator and the wind turbine, it can have mutually strong influence on both. To further analyze the effects of this mutual influence, the validated simulation results of the playback variant were compared with simulations of a complete model. Figure 14 and Figure 15 are examples of the instantaneous voltages of a simulation in the playback (PB) variant and a simulation with the complete model of the wind turbine. Figure 14 shows a full-load test to a resulting voltage of 0.25 pu, and Figure 15 presents a partial-load test with 0.47 pu nominal voltage.

The generic wind turbine model describes the behavior of the measured turbine very accurately for the full-load test to 0.25 pu residual voltage. There were no deviations in the instantaneous voltages. The transient range during the voltage dip similarly reveals consistent agreement between the two simulations. It can be concluded that the voltage behavior during the dip is significantly influenced by the model of the grid emulator. During the voltage return, the simulation with the full model of the wind turbine showed slightly higher dynamics. This may be due to the neglect of the non-linear effects (e.g., saturation of the transformer) in the generic wind turbine model. The two controllers did not influence each other.

The partial-load test likewise showed no deviations between the two simulations in the pre-fault and post-fault regions. Within the fault region, the amplitude was higher in the variant with the generic wind turbine model than in the playback version. This indicates that the generic wind turbine model does not accurately represent the fault current of the real turbine in partial-load mode. The wind model injected a higher reactive current to support the voltage during the fault. This effect occurred over the entire fault range, but it was clearly due to the wind turbine model. During the voltage dip, the transient ranges show a consistent pattern, indicating that there was no negative influence from the two controllers here, either.

In summary, the grid emulator model accurately represents the behavior of the wind turbine in the simulation. This is valid for the playback version as well as for simulations with the complete model of the wind turbine. Therefore, the developed model of the grid emulator is suitable for validating wind turbine models using test bench tests.

5. Transfer Function of the Grid Emulator Control

The grid emulator model should be accessible to all stakeholders involved in the certification process. In addition to the manufacturer, who tests its turbine on the test bench, this refers above all to the certification body, which ultimately validates the wind turbine model against the measurement results. Therefore, the model needs to have an open interface to be integrated into a wide range of grid simulation software available on the market. For this reason, further simplification of the grid emulator model is necessary.

5.1. Transfer Function of the Grid Emulator Controller Derivation from the Impedance Replica

Exceeding the maximum converter voltage is less critical in the simulation model, as damage to the hardware is excluded. Consequently, voltage limits are not included further in the simulation. The validity limit of the simulation must be considered critically accordingly. The simulation results are only valid as long as the nominal voltage is within the real limits of the grid emulator. Removing the manipulated variable limit avoids saturation of the controller. Therefore, the anti-windup is no longer active [21].

The control is done directly for the instantaneous voltages and not as before in alpha/beta coordinates. Both the wind turbine models to be validated and, in the playback application, the power fed in by the wind turbine refer to the PoC. Therefore, the PoC is defined as the interface to the wind turbine. The controlled variable is directly the PoC voltage so that the connecting transformer as a controlled system is not further represented in the model. Furthermore, an ideal RL impedance substitutes the existing virtual impedance representation separated into alpha/beta components. This also eliminates the need to divide the measured PoC current into absolute, phase, and DC components [21].

Figure 16 presents the overall simplified design of the grid simulation model, which is composed of only the PR controller and an ideal impedance. The less complex structure of the model allows description of a transfer function between current and voltage. This nevertheless consists of two parts, the impedance replica and the resonance controller, as the reference voltage $U_{ref}$ is added after calculating the grid impedance [21].

An ideal R-L element represents the impedance, resulting in Equation (9) describing the relationship between current and voltage [21].

$$U\left(s\right)=\left(R_{ref}+s · L_{ref}\right) · I\left(s\right)$$

(9)

To set up the transfer function, the auxiliary constant $L_{in}=1/f_{mes}$ is introduced to replace $s$ with $s/\left(s · L_{in}+1\right)$. In the simulation, $f_{mes}$ corresponds to the encoder sampling rate of 10 kHz. On one hand, the auxiliary constant compensates the polynomial with a higher denominator so that the denominator and numerator have the same degree. On the other hand, the derivative of a continuous system in the Laplace domain requires the form given by Equation (10) [21].

$$ℒ\left\{f^{\prime }\left(s\right)\right\}=s · F\left(s\right)-f\left(0\right)$$

(10)

As a result, Equation (11) describes the transfer function of the impedance replica $G_{IR}$ [21].

$$G_{IR}=\frac{\left(L_{ref}+L_{in} · R_{ref}\right) · s+R_{ref}}{L_{in} · s+1}$$

(11)

To set up the transfer function of the PR controller, Figure 17 shows the corresponding block diagram. $P_{Volt}$ and $I_{Volt}$ describe the control parameters of the PR controller. The angular frequency $\omega =2\pi f$ corresponds to a 50 Hz system. Establishing the closed-loop transfer function $G_{CL}$ according to Equation (12) first requires the analysis of the two control loops $G_2$ and $G_{inner}$ [21].

$$G_{CL}\left(s\right)=\frac{G_2\left(s\right)}{1+G_2\left(s\right)}$$

(12)

The transfer function $G_2$ is calculated according to Equation (14) and depends on the transfer function of the inner control loop $G_{inner}$, described by Equation (13) [21].

$$G_{inner}\left(s\right)=\frac{\frac{1}{s}}{1+\frac{1}{s} · \frac{\omega }{s}}$$

(13)

$$G_2\left(s\right)=P_{Volt}+2 · I_{Volt} · G_{inner}\left(s\right)$$

(14)

Substituting Equations (13) and (14) into Equation (12) results in the transfer function of the PR controller defined by Equation (15) [21].

$$G_{CL}\left(s\right)=\frac{P_{Volt} · s^2+2 · I_{Volt} · s+\omega }{\left(P_{Volt}+1\right) · s^2+2 · I_{Volt} · s+2 · \omega }$$

(15)

A Bode plot of the transfer function is shown in Figure 18. The comparison with an ideal grid impedance, which consists of an RL resistor, shows the validity of the grid emulator model. Deviations from the ideal impedance response become apparent at high frequencies. Obviously, these are a result of the system’s sampling rate and the controller’s limited power. The sampling rate of 10 kHz sets a defined upper limit. In addition to the amplitude, the deviation of the phase angle also increases at both higher and lower frequencies. Accordingly, the grid parameters deviate at higher frequencies with an increased amount of real resistance. The grid emulator model is not capable of reproducing the response of defined impedances at high frequencies. The validity is limited to the range around the fundamental frequency. Therefore, for the validation of wind turbine models according to the criteria of [18,24], the model is suitable, but higher frequency effects cannot be analyzed [21].

In addition to the complete transfer function, Figure 18 presents the transfer function of the impedance replica. Especially at low frequencies, the agreement with the ideal frequency response is higher than with the full transfer function. The exclusive impedance replica reproduces the ideal frequency response up to a frequency of 600 Hz. Consequently, it is concluded that the grid emulator model can be further reduced. The exclusive consideration of the impedance replication is suitable for the validation of wind turbine models [21].

5.2. Transfer Function of the Grid Emulator Control

Figure 19, Figure 20, Figure 21 and Figure 22 exemplify the comparison of the full grid emulator model with the mapping of the grid emulator as a transfer function of the grid impedance replica. Figure 19 shows the instantaneous voltage for a voltage dip to 0 pu of the nominal voltage. The wind turbine is in partial-load operation. The two simulations’ results agree in all areas. During the voltage dip, the simulations’ results completely overlap even in the transient range. Only the active current has a slightly higher overshoot in the transient region in the model with the transfer function. Figure 20 presents the corresponding active and reactive current. Both the reactive and active positive-sequence currents have a high degree of agreement between the two grid emulator models. Only the transient region shows short-term deviations; however, these are outside the windows to be considered. The active current has a slightly higher overshoot during the voltage dip in the model with the transfer function. For the voltage recovery period, it is the other way around: here, the active current has a slightly higher overshoot in the complex model.

Figure 21 and Figure 22 confirm these results. They show the positive sequence voltage and currents for a voltage dip to 0.25 pu of the nominal voltage. The wind turbine is operating at full load. The high agreement between the two simulation results confirms that the reduction of the grid emulator model to the representation of a simplified impedance replica is sufficient for the validation of wind turbine models.

6. Discussion

An initially complex grid emulator model was validated against real measurement data with a type 4 wind turbine. The required accuracy according to [18,24] is exceeded in the so-called playback version. Furthermore, its stable operation in combination with a wind turbine model, which interacts with the grid emulator model in terms of control, is proven. The grid emulator model was simplified step by step and validated against the full model. Ultimately, the grid emulator model was replaced by an exclusive representation of a complex impedance as a Thévenin equivalent. The validation against the full grid emulator model reveals a match of the voltage and current behavior at the PoC. Moreover, because the standards require the consideration of the fundamental frequency component of the positive sequence voltage, the discrepancy is further reduced. All short-term effects in which the models differ were not further considered in this representation. Plotting and examining the frequency response of the simplified model using the Bode plot restricted its validity to the range around the fundamental frequency component. This is equally valid for the full grid emulator model, as both the switching behavior of the converters and the filters were not modeled. Therefore, the harmonic distortion of a wind turbine cannot be evaluated with any of the developed models. For this purpose, the complex grid emulator model must be extended to include real switching characteristics. The Bode plot gives a first indication that the model can be used to evaluate flicker values. However, this has to be proven in separate investigations which still have to be conducted.