Numerical Investigation of Aerodynamic Performances for NREL 5-MW Offshore Wind Turbine

Abstract

As one of the preferred types of renewable energy, wind energy is rapidly growing. The purpose of this study is to provide a comprehensive and in-depth numerical analysis on the National Renewable Energy Lab (NREL) 5-MW offshore wind turbine to help understand the wind turbine’s aerodynamic features. In this research, the preprocessing was conducted by using SolidWorks modeling, and a realizable k-ε viscous model from ANSYS/FLUENT was used as the solver in the CFD simulation. Eight test cases were developed, and fixed inlet velocity 9 m/s was set as the baseline case. After the initial mesh independent study and model validation, a detailed numerical analysis was carried out. The results of near wake flow features, torque and thrust, pressure and pressure coefficient distribution, limiting streamline along wind turbine blades, power coefficient as a function of tip speed ratio were evaluated. Whenever possible, simulation results were compared with data in the literature (numerical or experimental), and good agreement was observed. The detailed wind turbine aerodynamic analysis results are expected to provide valuable input to wind turbine design and thus to improve the effectiveness of harnessing wind energy. Research is on the way to further understanding the influence of different inflow conditions on the aerodynamic characteristics.

1. Introduction

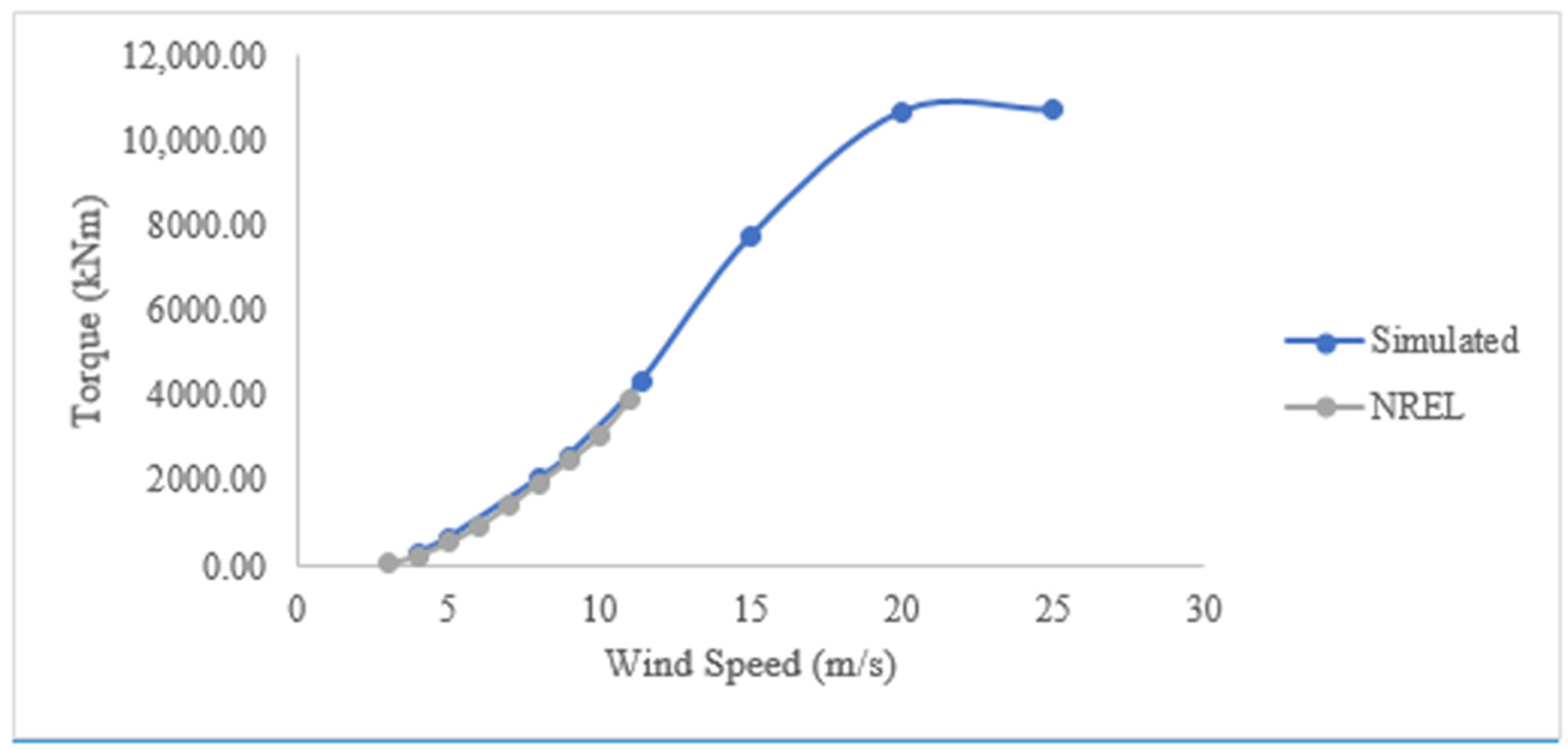
With the rapid growth of the world’s population, the use of fossil fuels as a conventional energy is in a foreseeable shortage. Wind energy is becoming one of the most common and preferred forms of renewable energy [1,2,3,4,5,6,7,8]. The capabilities of offshore wind energy show increasing promise, with the abundance of wind resources and more uniform wind features. To better design wind turbines and more effectively harness wind energy, a solid understanding of the aerodynamics features of wind turbines is needed. As such, much research work has been conducted experimentally or numerically to study the aerodynamic performance of offshore wind turbines.

In 2009, the NREL created a comprehensive design of a 5-MW offshore wind turbine. Extensive experiments were also performed [9]. Since then, the NREL 5-MW offshore wind turbine has been widely used in aerodynamic research.

Coulling et al. used a 1/50-scale model of an NREL 5-MW offshore wind turbine constructed for a floating platform to verify a model of FAST [10]. Comparing test results to FAST predictions, they discovered that FAST and the test achieved a high level of agreement with the turbine’s performance in terms of elasticity, aerodynamics, and hydrodynamics. Shin et al. constructed a 1/128-scale model of a 5-MW floating offshore wind turbine in a water depth of 50 m in the University of Ulsan’s Ocean Engineering Wide Tank [11]. The response amplitude operator in natural frequency was produced and compared under various situations. Duan et al. simulated a test to examine the dynamical reaction of an OC3 model of spar floating wind turbine at 1/50 scale [12]. They also documented the reaction behavior under wind and wave conditions. These investigations were meticulously planned and carried out in order to provide references for simulation research. More recently, Chen et al. [13] conducted a review of model experimental methods for floating offshore wind turbines, addressing their development status and existing limitations. Boersma et al. [14] built a scaled-down model of the 61 m NREL 5-MW blade (30:1), and conducted a series of experiments on it. They observed coupled-mode flutter, which further proved that larger wind turbine blades are susceptible to coupled-mode flutter.

Experimental study is costly; further, simultaneously using Froude scaling and Reynolds scaling for large-scale offshore wind turbines was deemed unfeasible for satisfying platform testing. This can be attributed to the inaccuracy that occurs when the test findings are applied to full-scale wind turbines. When looking for an alternative, it was determined that numerical study would be cost efficient without compromising the integrity of the experimental findings.

Wang [15] utilized the CFD approach to describe the three-dimensional transient flow for an offshore 5-MW wind turbine at 9 m/s. The contours of velocities and pressure were presented. He calculated the wind turbine aerodynamic torque efficiency to be 72.2% using the LES model, and concluded that the LES method was a reliable tool to study complex transient turbulent flows. Cheng et al. [16] investigated the aerodynamic and hydrodynamic responses of an NREL 5-MW offshore wind turbine placed on a semi-submersible foundation using OpenFOAM. Zhou et al. [17] analyzed the aerodynamic behaviors of the 5-MW offshore wind turbine in downwind and upstream settings using the PimpleDyMFoam solver based on OpenFOAM. Wake vortices, pressure distributions on the blade, and limiting streamlines were analyzed. Cheng et al. [18] also investigated the unstable aerodynamic characteristics of the NREL 5-MW offshore wind turbine with periodic pitch and surge movements of the platform using the naoe-FOAM-SJTU technique based on OpenFOAM. They also demonstrated that, compared with surge motion, pitch motion had a greater effect on the thrust and torque of the rotor.

The multiple reference frame (MRF) technique, which is based on OpenFOAM, was used by Zhao et al. [19] to simulate a 5-MW offshore wind turbine at varying wind speeds. They obtained the aerodynamic features on the blade surfaces and got the wake vortex, rotor thrust, and torque without considering the effect of the floating structure. The aerodynamic performance of a selected 5-MW offshore baseline wind turbine at the mouth of the Chesapeake Bay was modelled by Ian et al. [20]. They calculated the lift coefficient, drag coefficient, tangential velocity, axial velocity, and AOA at different inlet wind velocities along the azimuth and blades. De Cillis et al. [21] focused on the NREL 5-MW wind turbine wake effects from the incoming turbulence influence. Unsteady wake characteristics of the NREL 5-MW wind turbine were discussed further by Xue et al. [22], based on an LBM-LES model. Arabgolarcheh et al. [23] focused on the near wake characteristics of NREL phase VI and 5-MW offshore wind turbine analysis using an actuator line method. Besides the direct modeling techniques, Fan et al. [24] conducted a numerical study on the NREL 5-MW wind turbine wake effects in yaw conditions using an improved actuator line method based on OpenFOAM.

Lienard et al. [25] used CFD to examine the aerodynamic behavior of a 5-MW offshore wind turbine under various wave movements. According to their findings, pitch and surge movements had a significant impact on boosting mean aerodynamic power among six degrees of freedom motions. Yuan et al. [26] discussed the aerodynamic characteristics of the NREL 5-MW offshore wind turbine under wind shear effects based on the Lattice–Boltzmann method; they concluded that, due to the wind shear effects, the angle of attack deviates from the theoretical optimal value, which decrease the torque generated by the wind turbine. Tran et al. [27] demonstrated a floating wind turbine device with a periodic pitch motion. They completed the spinning turbine’s unsteady aerodynamic study satisfactorily. The effects of platform movements on aerodynamic performance were examined by Lee et al. [28]. They tested the 5-MW offshore wind turbine with periodic translational and rotational movements and compared the results to the bottom-fixed simulation. The result they reached also suggests that surge and pitch motions have a major impact on thrust and power, which is similar to that obtained by Lienard et al. [21] and Cheng et al. [16]. De Oliveira et al. [29] focused on the aspects of solver configuration and discretization strategies in blade-resolved numerical simulation of the 5-MW NREL offshore wind turbine, and attempted to improve the simulation accuracy and reduce the computational cost. Further, Papi et al. [30] discussed the technical difficulties in floating offshore wind turbine upscaling based on the NREL 5-MW and IEA 15-MW wind turbines.

Although much research on the aerodynamic behavior of a 5-MW offshore baseline wind turbine has been conducted, a comprehensive analysis of the aerodynamic behavior on the NREL 5-MW offshore wind turbine is missing in the literature. The current research was carried out to obtain the aerodynamic performance on the NREL 5-MW offshore wind turbine under various inflow velocities, including: below the rated wind speed, at the rated wind speed and above the rated wind speed; developing eight test cases; conducting detailed analysis on aerodynamic properties such as the near wake flow features, torque and thrust, pressure and pressure coefficient distribution; limiting streamline along wind turbine blades, and evaluating the power coefficient as a function of tip speed ratio. The comprehensive and in-depth modeling and simulation results of the aerodynamic characteristics of the NREL 5-MW are expected to provided valuable input for wind turbine design, which will eventually contribute to efficiently harnessing wind energy.

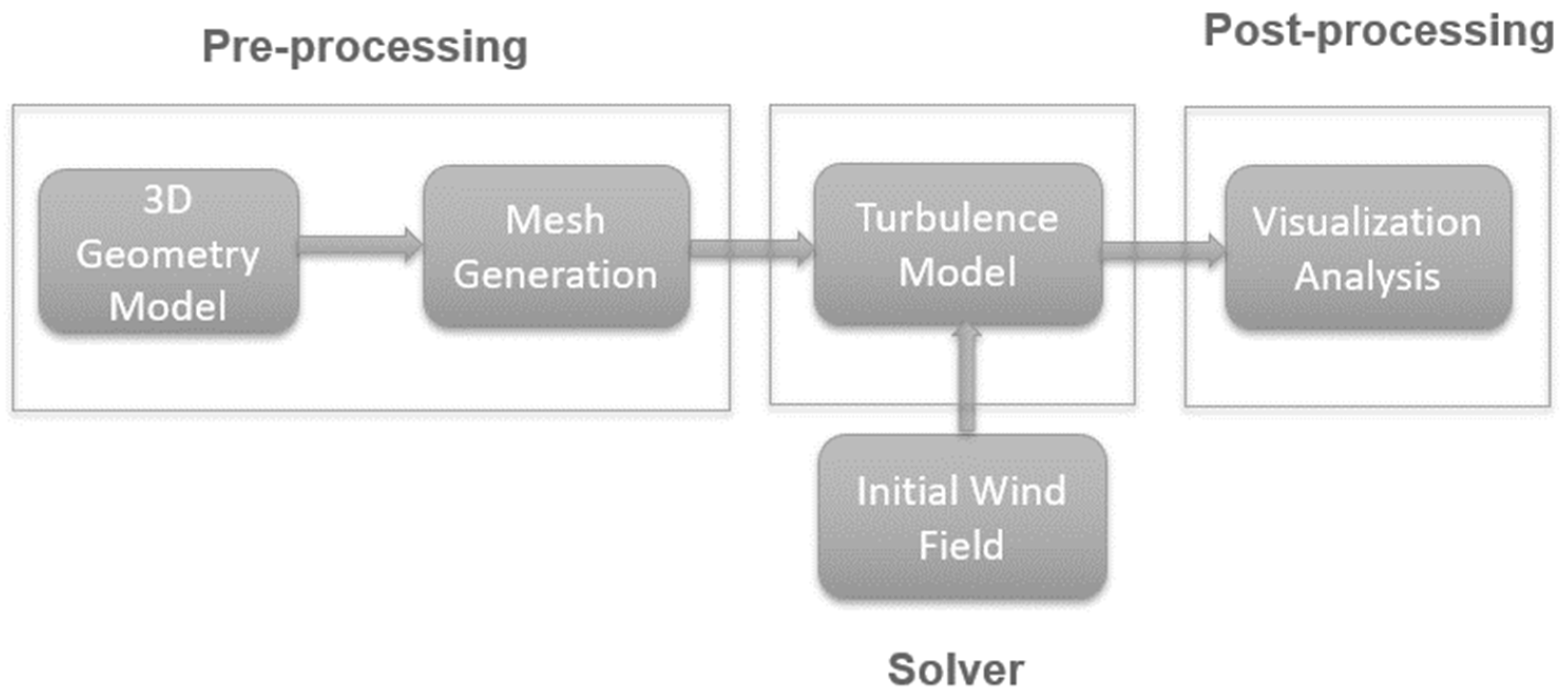
The general process of solving the problem is discussed in Section 2, which includes geometry modeling, mesh generation and turbulence modeling, followed by instructions; the results are presented in Section 3, where detailed discussion of the aerodynamic characteristics of the NREL 5-MW wind turbine is provided; and Section 4 summarizes the conclusions of the presented work along with limitations and future research recommendations.

2. Materials and Methods

2.1. Aerodynamic Features

The aerodynamic properties are discussed in this section. For the pressure coefficient:

$$C_p=\frac{2\left(P_0-P_{\infty }\right)}{\rho (U^2+{\left(\omega r\right)}^2)}$$

(1)

where $P_{\infty }$ is the pressure at infinity, which is set as 0, $P_0$ is the total pressure, and the inlet wind speed is denoted by U. $\omega$ is the angular velocity in rad/s, and r is the radial distance on the wind turbine.

Tip speed ratio, which is the ratio of tangential tip velocity to inlet wind velocity, is an essential metric in turbine design. Tangential tip velocity is described as

$$V_t=\omega r$$

(2)

The tip speed ratio can be expressed as

$$TSR=\lambda =\frac{\omega r}{v}$$

(3)

The coefficient of power is also a significant parameter in wind turbine study. It is expressed as the following equation.

$$C_p=\frac{power generated}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rho A{v}^3}$$

(4)

where A is the sweeping area of the wind turbine. A is known as

$$A=\pi R^2$$

R is the radius of the wind turbine, here R is 62.9 m.

The power generated is described as

$$Power=T\omega$$

(5)

Thus, the power coefficient is also expressed as

$$C_p=\frac{T\omega }{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\rho \pi R^2{U}^3}$$

(6)

where T is the torque, $\rho$ is the density of the air.

The power coefficient is also expressed in the following equation:

$$C_p=4a{\left(1-a\right)}^2$$

(7)

where a is the axial induction factor.

By differentiating the above equation, the maximum theoretically possible rotor power occurs at

$$\frac{d{C}_p}{da}=3a^2-4a+1=0$$

(8)

which makes a = 1/3, and $C_{pmax}=0.59$.

Thus, the maximum theoretical power coefficient should not be greater than 0.59.

2.2. General Solution Procedure

The general solution procedure is illustrated in Figure 1. The pre-processing includes the geometry model and mesh generation. The geometry model was built by using the different types of airfoil at given cross sections. ANSYS Workbench was used to generate the mesh. Mesh independent study was conducted to make sure the simulation results were not influenced by the mesh resolution. After the model validation, extensive numerical simulation was conducted by using the selected turbulence model. Once the desired simulation results were obtained, post-processing functions were chosen to better evaluate and understand the aerodynamic characteristics of the selected wind turbine.

2.3. Turbine Blade Geometry Modeling

The NREL 5-MW offshore baseline wind turbine has three blades and features a 129-m-diameter. The cut-in velocity, rated velocity, and cut-out velocity are 3 m/s, 11.4 m/s and 25 m/s, respectively. Detailed blade aerodynamic properties can be found in [9]. In the NREL 5-MW baseline turbine, three cylinders are used at the root of the blade and DU series airfoils are used in the middle part of the turbine blade. With the decrease of the chord, NACA 64 airfoil is used all along to the blade tip. The airfoil used at different cross sections in the turbine design is shown in Figure 2.

The geometry model of the wind turbine was generated using Solidworks. The airfoils at various cross sections are shown in Figure 3a, and the geometry of the wind turbine blade is shown in Figure 3b. Assembling the turbine blades and the hub together, the geometry of the 5-MW offshore wind turbine is obtained as shown in Figure 3c.

2.4. Mesh Generation

When generating the mesh, considering the big ratio of the size of the computational domain to the small size of the blade tips, body sizing was used in the whole fluid domain and rotational domain to reduce the computational cost, while edge sizing was applied on the turbine sides and tip edges to obtain finer meshes in those regions for more accurate simulation results. The medium sized mesh is shown in Figure 4. Tetrahedral meshes were applied. For spatial discretization, second order in pressure, and second order upwind in momentum were applied.

2.5. Aerodynamic Models

Blade Element Momentum theory (BEM) and the Computational Fluid Dynamic (CFD) method are commonly used to simulate the aerodynamic features of wind turbines. The BEM method is one of the oldest methods for providing reasonable estimations of turbine aerodynamic characteristics analysis [9,11]. However, since it significantly relies on the airfoil data, the accuracy of aerodynamic calculations will be affected. The CFD method is an attractive and powerful way to simulate wind turbine fluid flow and aerodynamic features. Unlike BEM theory, CFD methods solve unsteady turbulence flow. Two turbulent models are widely implemented for wind turbine simulation. Reynolds-averaged Navier–Stokes (RANS) is one of the oldest methods of turbulence model. The physical parameters of a fluid motion can be expressed as the sum of the fluctuating part and the averaging part. By substituting the new expression into the original N-S equation and then averaging it, the RANS equations can be obtained. The other commonly used turbulence model is the Large Eddy Simulation (LES), which resolves large eddies while modeling small eddies. It gives a better depiction of turbulence in the aspect of wind turbine simulation, however, a finer mesh is required for the LES model, which requires more computational resources.

In this study, commercial software ANSYS/FLUENT is used to run the simulation. The rotating motion and the dynamic performances of the wind turbine can be observed, which is a great support to wind turbine analysis.

The velocity field of a flow can be divided into a mean part and a fluctuating part:

$$u_i=\overline{u_i}+u_i^{\prime }$$

(9)

$$p_i=\overline{p_i}+p_i^{\prime }$$

(10)

The continuity equation of the incompressible Navier–Stokes equations is written as

$$\frac{\partial u_i}{\partial x_i}=0$$

(11)

And the momentum equation is expressed as

$$\rho \left(\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}\right)=-\frac{\partial p}{\partial x_i}+\mu \left(\frac{{\partial }^2{u}_i}{\partial x_j\partial x_j}\right)$$

(12)

Substituting Equation (12) with Equations (9) and (10), and after applying averaging, the RANS equation is obtained as

$$\rho \left(\frac{\partial \overline{u_i}}{\partial t}+\overline{u_j}\frac{\partial \overline{u_i}}{\partial x_j}\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left(\mu \frac{\partial \overline{u_i}}{\partial x_j}-\rho \overline{u_i^{\prime }{u}_j^{\prime }}\right)$$

(13)

RANS k-ε models consist of standard, RNG, and realizable k-ε models. The main differences in those models are the ways of estimating the turbulent viscosity. The standard k-ε model is a two-equation model. The turbulent velocity and length scales may be estimated separately with the use of two equation solutions. The difference with the RNG model is that it has an extra term in its ε formula that increases the precision for quickly strained flows. As for the realizable k-ε model, it has the enhancement where a novel formula for the turbulent viscosity is included.

$$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_j}\left(\rho k{u}_j\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k+G_b-\rho \epsilon -Y_M+S_k$$

(14)

and

$$\frac{\partial }{\partial t}\left(\rho \epsilon \right)+\frac{\partial }{\partial x_j}\left(\rho \epsilon u_j\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+\rho C_{1}S\epsilon -\rho C_2\frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}+C_{1\epsilon }\frac{\epsilon }{k}{C}_{3\epsilon }{G}_b+S_{\epsilon }$$

(15)

where

$$C_1=max\left[0.43,\frac{\eta }{\eta +5}\right],\eta =S\frac{k}{\epsilon },S=\sqrt{2S_{ij}{S}_{ij}}$$

(16)

The realizable k-ε model fulfills specific mathematical limitations in terms of Reynolds stresses, which are compatible with turbulent flow physics. In addition, it is effective for rotational flow simulation, with notable simulation efficiency compared with the LES model. It was selected for the following simulations.

3. Results

3.1. Mesh Independent Study

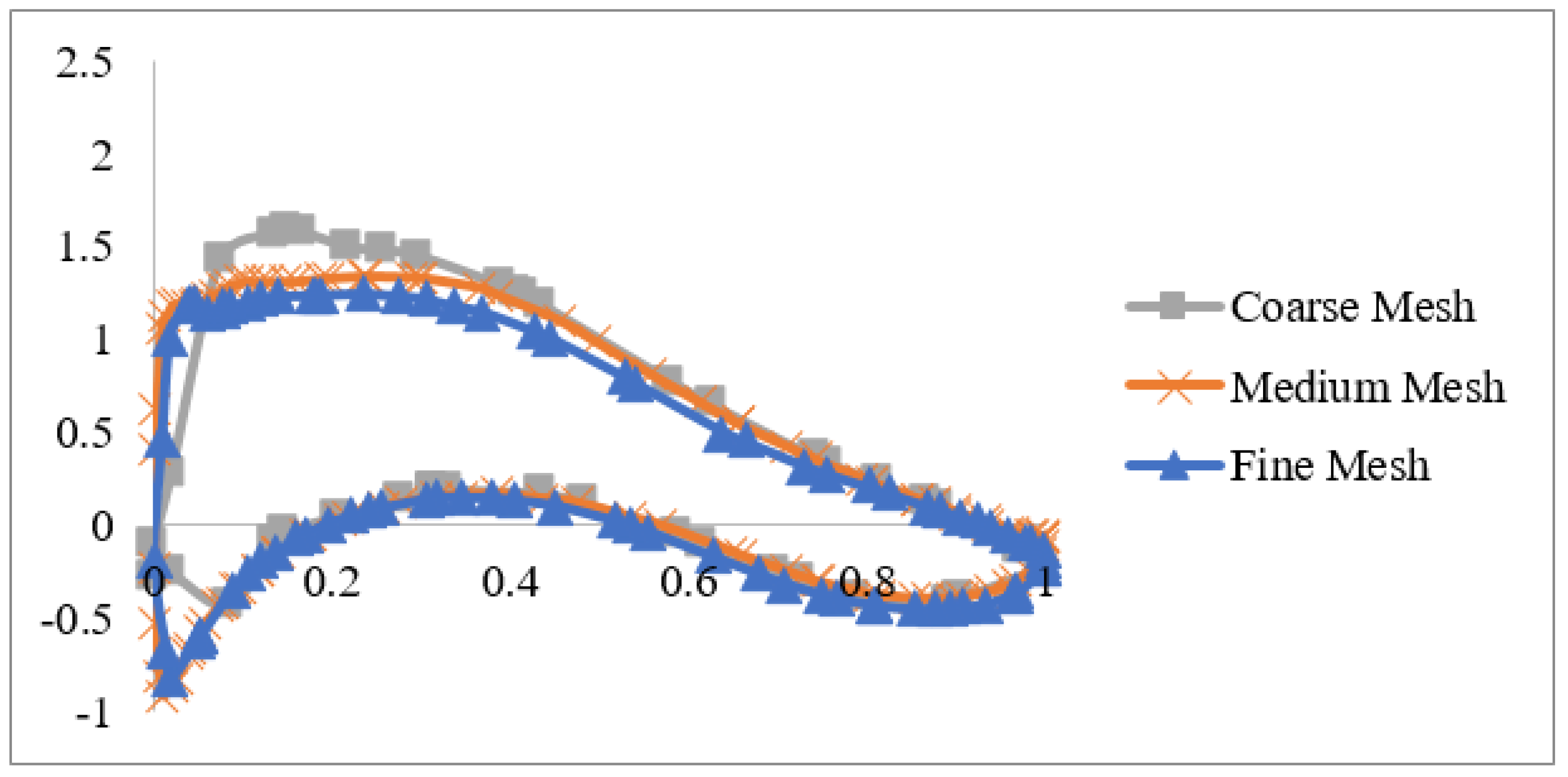
The mesh independent study was conducted to analyze the effects of mesh size on simulation results. Three different mesh settings are selected and tested: the total cell number for the coarse mesh is 1,613,463, for the medium mesh is 2,479,240 and for the fine mesh is 4,262,617.

Figure 5 shows the pressure coefficient at the location where r/R equals 0.63 when the inlet wind speed was set as 9 m/s. It is designed to identify whether the results under different mesh conditions are precise enough. The results from the coarse mesh and the fine mesh show evident differences, while a similar pressure coefficient profile was observed for both the medium mesh and the fine mesh. The medium mesh size was finally selected as it provided a good balance between the computational time and accuracy.

3.2. Computational Domain and Boundary Settings

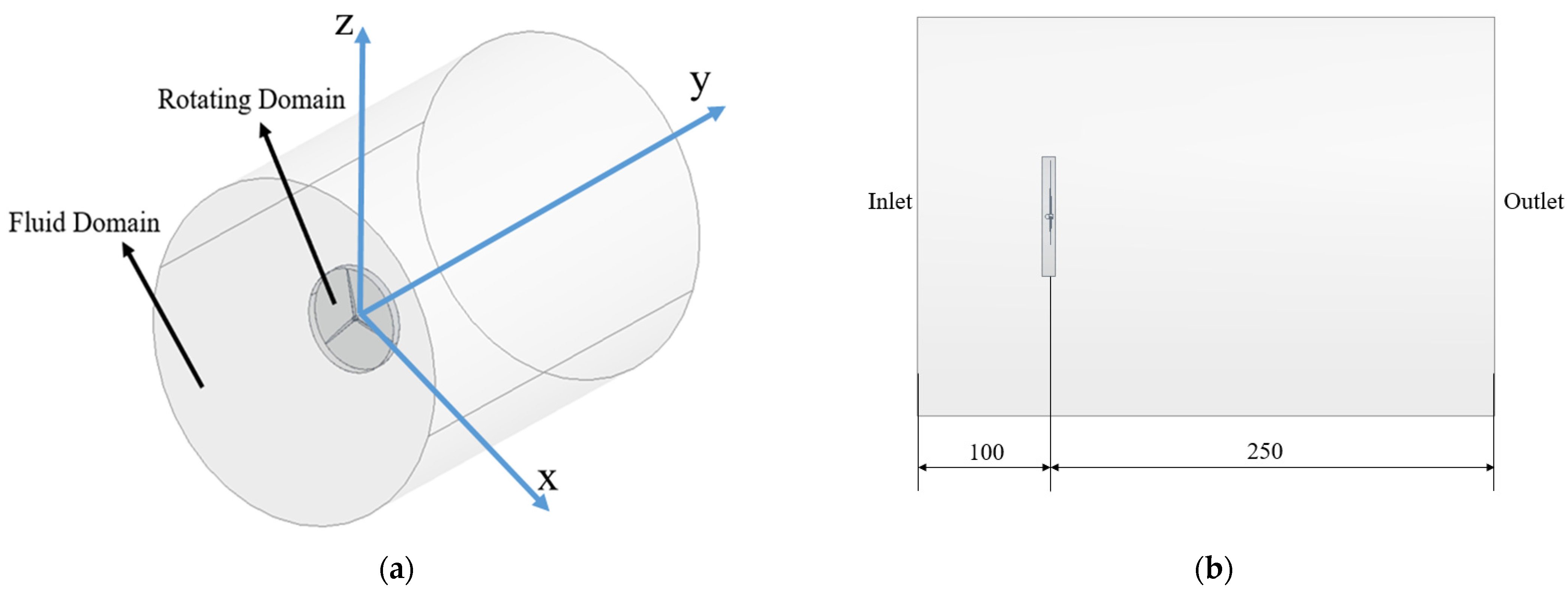
Model validation was conducted, and the results were compared with Zhao’s work [14]. The same computational domain was used; the center of the rotor blades, which is also the center of the hub, coincided with the center of global coordinates. As shown in Figure 6, two domains consisting of computational fluid and rotational region were generated. The rotating domain contains the rotor blade as a smaller cylinder with a 62.9 m in radius, while the fluid domain has a radius of 200 m. The distance from the inlet to the rotor blade is 100 m and the length between the rotor blade and the outlet is 250 m.

In this paper, the aerodynamic performances of NREL offshore 5-MW wind turbine under different fixed wind speeds in the range of 3 m/s to 25 m/s were simulated. The rotor torque, thrust, power, power coefficient, pressure coefficient, wake vortices and velocity profiles are obtained in detail. A total of eight cases were designed and are listed in

Table 1. List of simulation cases.

Simulation Cases	Inlet Velocity (m/s)	Rotational Speed (rpm)
case 1	4.00	7.18
case 2	5.00	7.39
case 3	8.00	9.16
case 4	9.00	10.30
case 5	11.40	11.89
case 6	15.00	12.10
case 7	20.00	12.10
case 8	25.00	12.10

. The rated wind speed for NREL offshore 5-MW wind turbine is 11.4 m/s. For cases 1, 2, 3 and 4, the inlet wind velocity is below the rated speed, and the inlet wind velocity in case 5 is at the rate wind speed, while in cases 6, 7 and 8 the inlet wind velocity is above the rated wind speed. First and foremost, case 4 was validated by comparing the rotor torque and efficiency to numerical results from [19] and experimental results from [9], and good agreements were observed. Then, further simulations were conducted to obtain the aerodynamic features for all the eight cases. The aerodynamic features from different cases were also compared with each other. The detailed simulation results are presented in the next section.

3.3. Model Validation Study

Validation was conducted using case 4, with the inlet wind velocity at 9 m/s. The simulated torque was compared the data in the literature for both the numerical results [19] and experimental results [9]. A summary of the comparison is given in

Table 2. Torque and power comparison.

Comparison	Current Result	Zhao [19]	Jonkman [9]
Torque (kNm)	2596.96	2682.00	2474.50
Torque Error (%)	-----	−3.17	4.94
Power (MW)	2.80	2.89	2.67
Power Error (%)	----	−3.11	4.87

.

The power generated can be determined using

$$P_0=T_{f0}\times \omega =2596.96 \mathrm{kNm}\times 1.079 \mathrm{rad}/\mathrm{s}=2.80 \mathrm{MW}$$

The percentage error of the torque can be calculated as:

$$\frac{2596.96-2474.5}{2474.5}\times 100\%=4.94\%$$

Compared with the data from the literature, the percentage errors are less than 5%, and good agreement is observed. Consequently, the current numerical model and settings are appropriate for the following case studies.

3.4. Wake Vortex Development

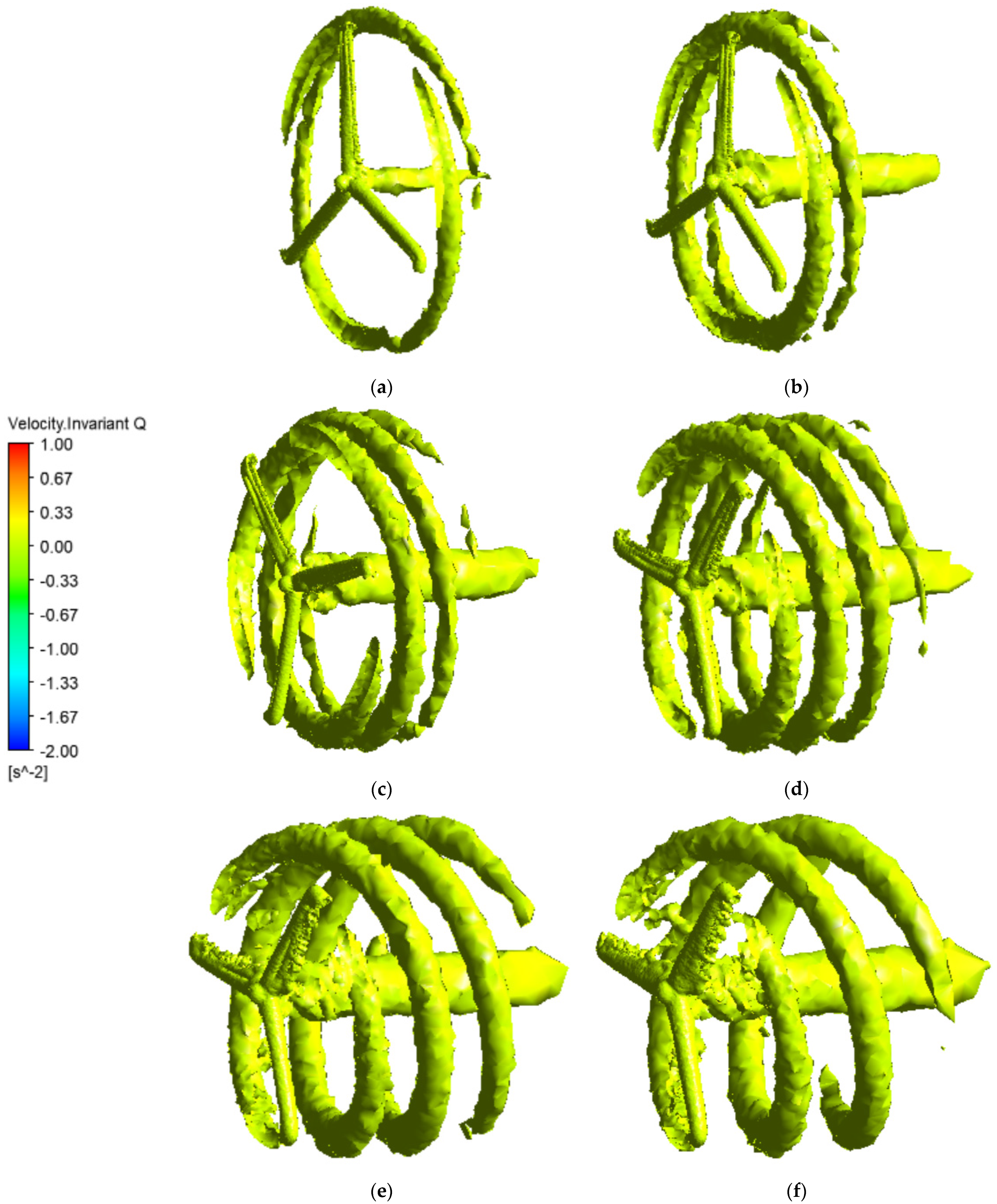
Figure 7 shows the iso-surfaces of Q = 0.008 under different uniform inlet velocities, and clearly demonstrates the wake vortices near and behind the blades. The wake vortex is one of the most significant properties for the aerodynamic analysis of the turbine blade. Additionally, Q is a second invariant velocity gradient tensor. It is used to capture the wake vortices around the blades and indicates the wake vortices. Q is expressed as

$$Q=\frac{1}{2}\left({\Omega }_{ij}\times {\Omega }_{ij}-S_{ij}{S}_{ij}\right)$$

(17)

where ${\Omega }_{ij}$ represents the vorticity tensor and $S_{ij}$ represents the rate of strain tensor.

The wake patterns at the back of the wind turbine rotor under different wind speeds are visualized in Figure 7. Since the wind turbine blades are rotating, the turbine blades and the surrounding fluid interact with each other. The vortices are generated due to this interaction. The vortices perform helically, intensely, and symmetrically, and then dissipate. With an increase of wind speed, the helical vortices could persist in a longer downstream distance. Once the inlet wind speed is greater than the rated wind speed, the distance between each tip vortex revolution apparently increases.

3.5. Near Wake Flow Features

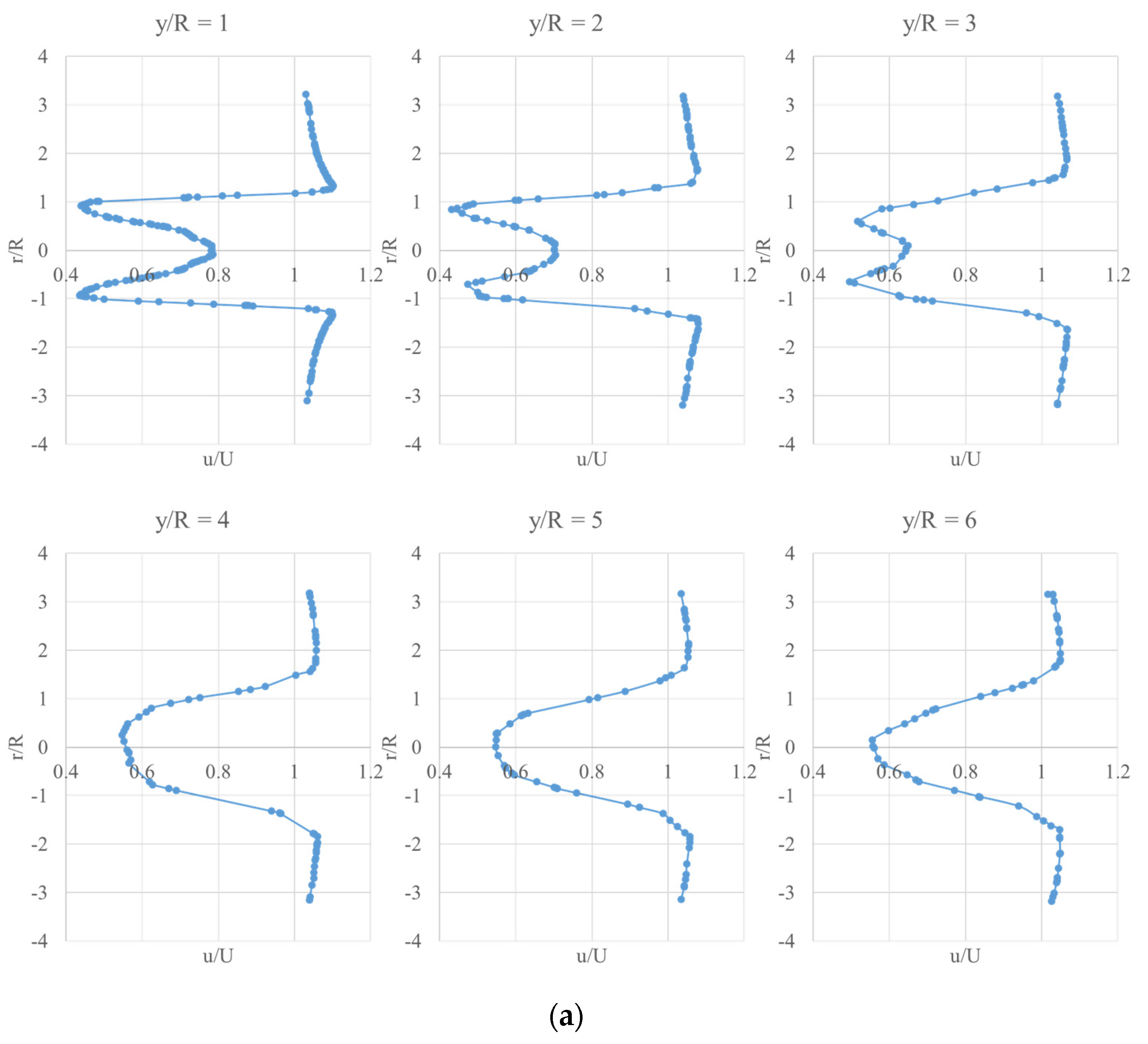
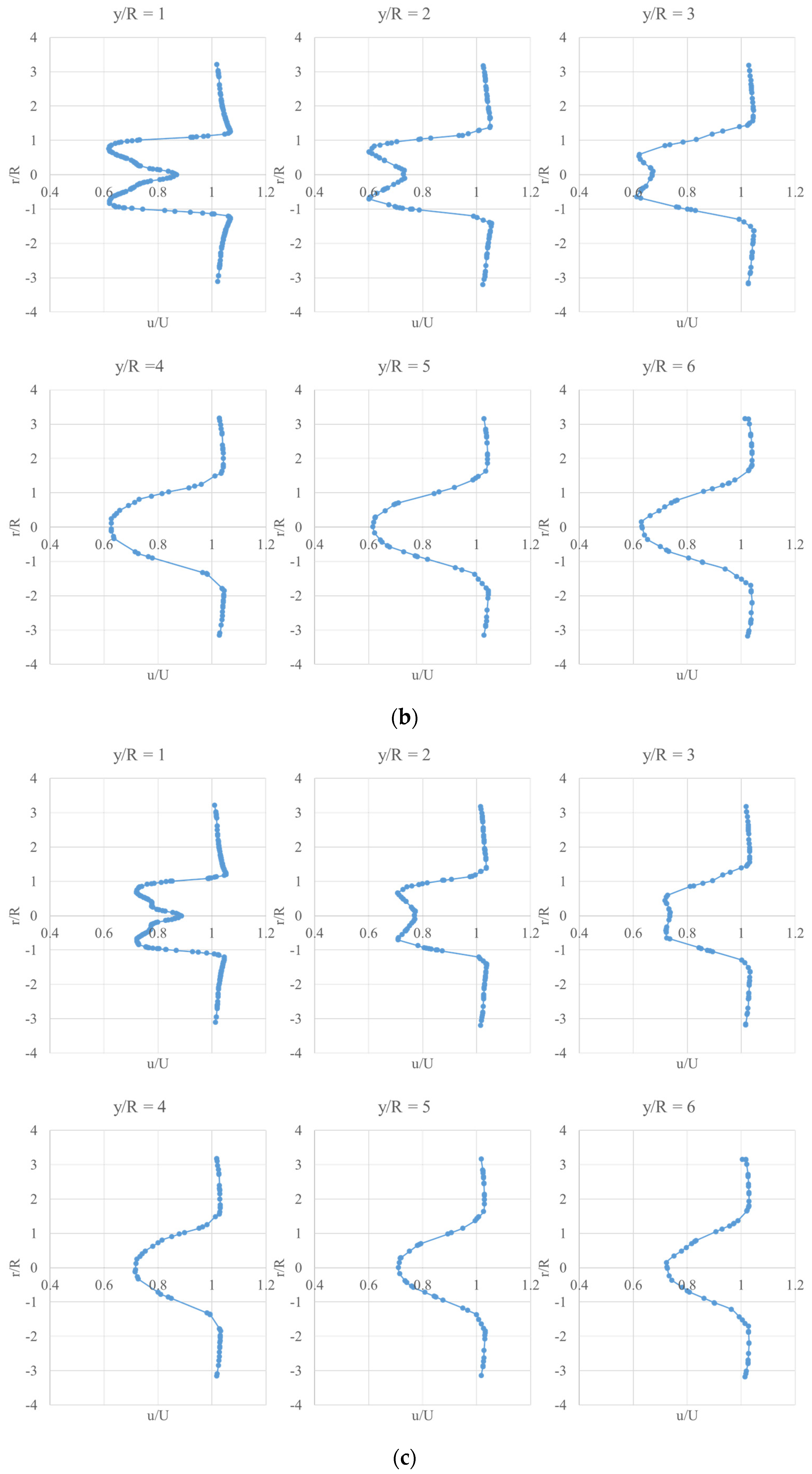
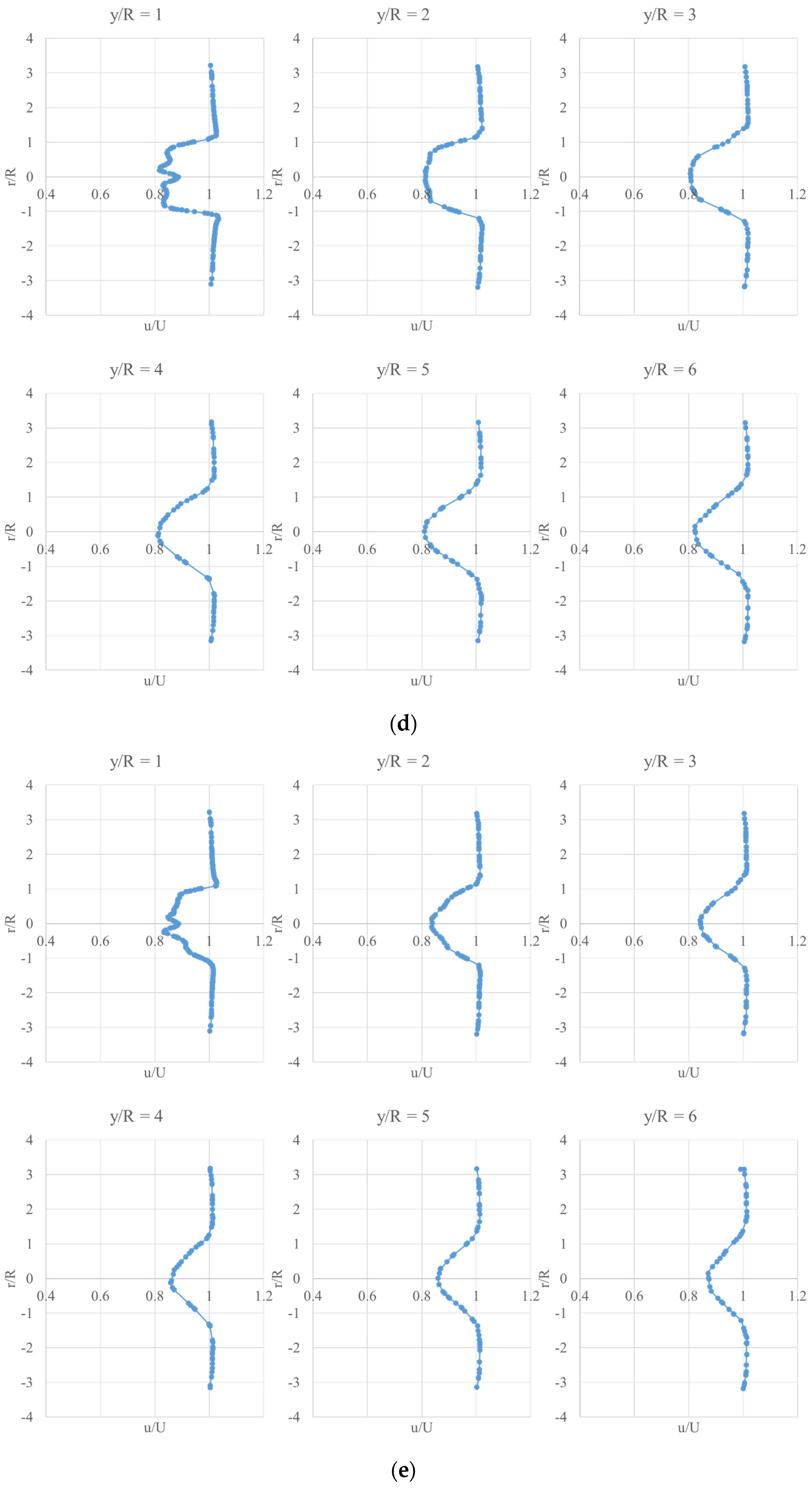
Downstream velocity profiles at various locations (y/R = 1, y/R = 2, y/R = 3, y/R = 4, y/R = 5, y/R = 6) under different inlet wind conditions are shown in Figure 8. u is local wind velocity and U is the inlet wind speed. When the inlet velocity remains the same, the velocity deficit reaches the peak at y/R = 1, which is the closest region to the wind turbine blade. With the increase of y/R, the selected locations gradually move away from the wind turbine, and the velocity deficit decreases. The center of the velocity profile may be influenced by the wind turbine hub. Focusing on the locations of y/R = 1, 2 and 3, the velocity variation around the center is big. Checking the locations of y/R = 4, 5 and 6, it is easy to find that the velocity barely changes. Thus, when the selected location is gradually further away from the hub, the influence of the wind turbine hub decreases. The velocity recovery process is vividly presented. Somewhere after a downstream of 4R, there is an apparent change from a Double-Gaussian to a Single-Gaussian distribution.

Comparing the velocity profiles under different wind speeds, it can be concluded that as the inlet wind speed increases, the influence of the hub on the velocity profile reduces. Especially when observing the velocity profile at the y/R = 1 location under different wind speeds, the velocity variation around the center when U = 5 m/s is big when compared to the velocity variation under U = 25 m/s.

3.6. Wind Flow Features near Turbine Blades

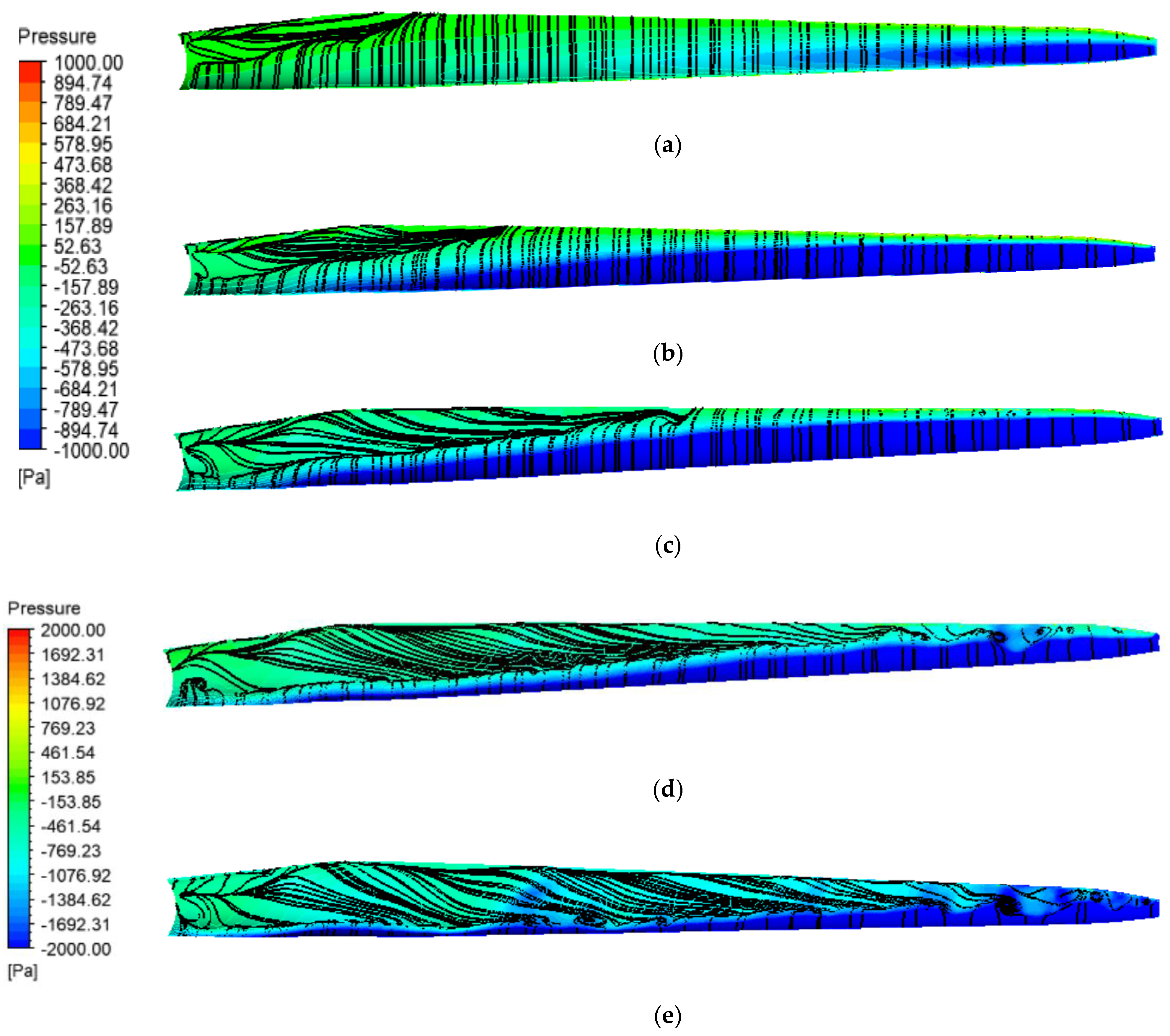
The near blade flow behavior has a big impact on the rotor, which will be discussed in this section. The limiting streamline is a streamline whose distance normal to the body surface is close to zero but not equal to zero, and it clearly shows the flow separation near the blade. The limiting streamline offers a method to exhibit detailed flow structure near the turbine blade.

The limiting streamline, along with the distribution of pressure on the suction and pressure side for various conditions, are shown in Figure 9 and Figure 10. The changes of the limiting streamline on the suction side are apparent. In Figure 9, we can see that the flow separation occurs near the root and leading edge part of the blade. This is caused by the pressure difference between the blade’s leading and following edges. Observing the following five conditions, it is easy to conclude that the near root flow separation seems to extend throughout much of the turbine blade as the wind velocity rises. This is due to the rotational centrifugal acceleration. When the inflow wind velocity is big, vortices appear at the trailing edge, while the streamline on the pressure side shows small changes with the various wind speeds. When flow is separated in a stalled region, the pressure difference between the pressure and suction sides of the root is less, leading to a small lift.

3.7. Pressure and Pressure Coefficient Distribution

Figure 11 shows the pressure distribution along the blade at r/R = 0.3, 0.63 and 0.95 under various inlet wind speeds. r/R represents the different cross sections of the turbine blade. When r/R = 0.3, Du 35 is implemented for the blade. When r/R is 0.63, Du 21 is used. When r/R = 0.95, NACA 64 is utilized. NACA 64 is more elliptical than the other two selected airfoils.

For the same inflow condition, pressure increases at the leading and the trailing edges; as the inlet velocity increases, the pressure also increases at both the leading and the trailing edges. The lifting pressure increases from the base to the tip under the same inflow condition, it also increases when the inflow velocity is below the rated wind speed; however, once the inflow velocity is above the rated wind speed, that is not the case.

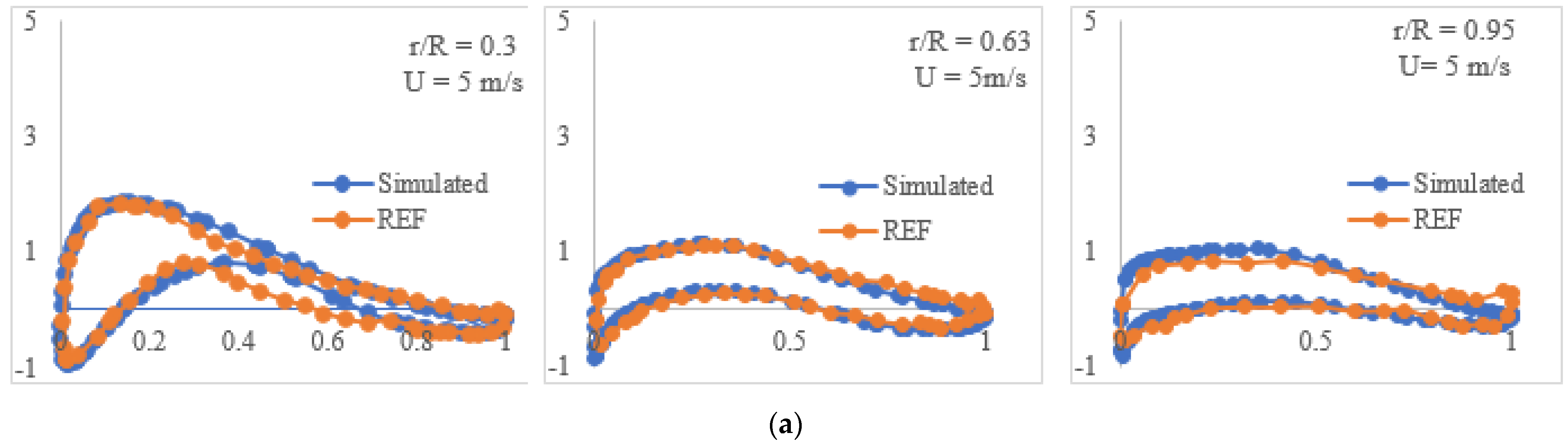
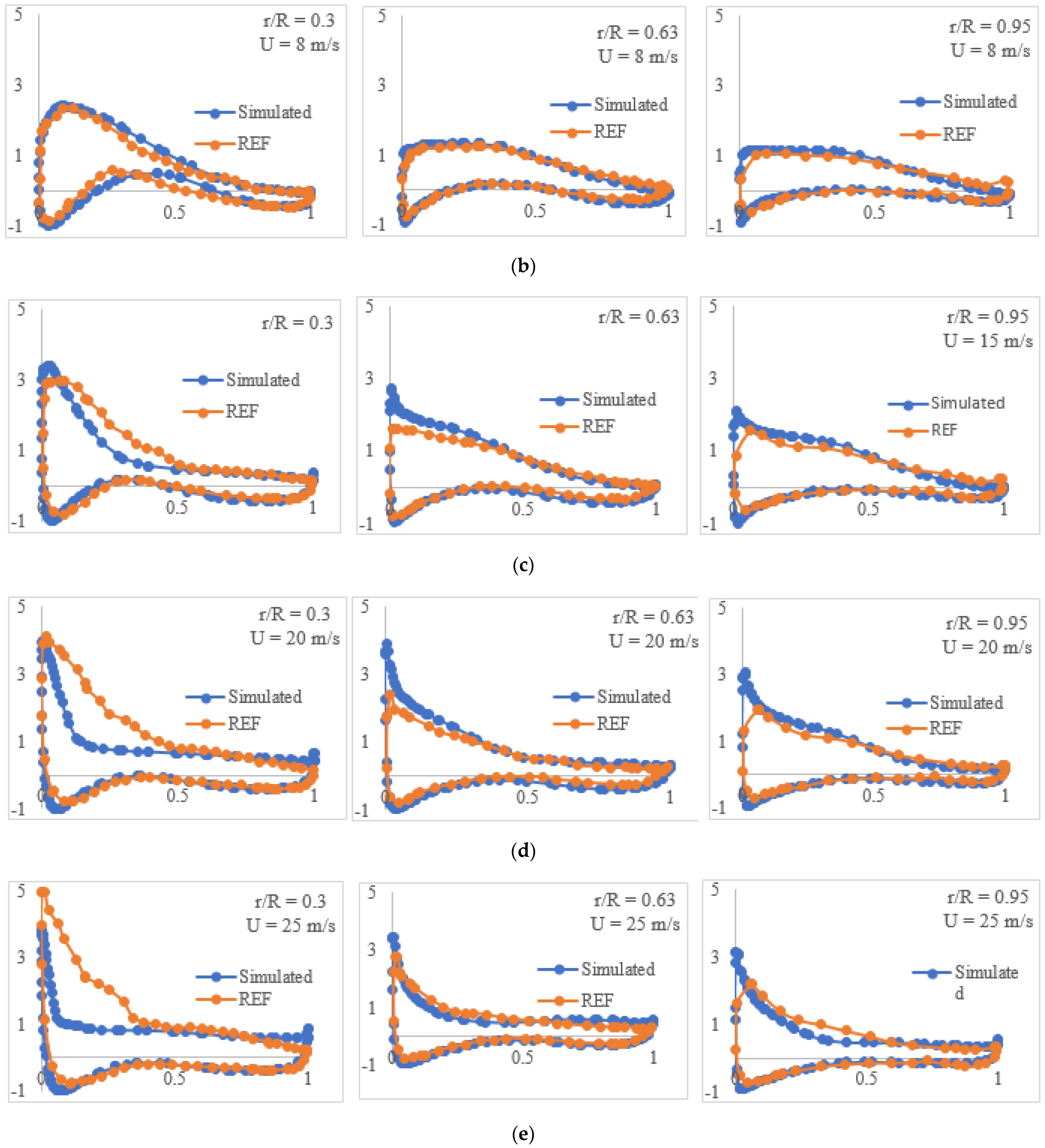
The pressure coefficient distribution of the selected airfoils, DU 35, DU 21, and NACA 64 under different inlet wind speeds is shown in Figure 12. The simulated pressure coefficient shows great consistency with the reference data, especially when the inlet wind velocity is low. As the inlet wind speed increases, it can be seen that the pressure coefficient at the same location increases. For case 1, at location r/R is 0.3, the largest pressure coefficient is around 2, but for case 8, the largest pressure coefficient is nearly equal to 4 at the same location, which is almost double the value for that at case 2. In addition, the difference of pressure coefficient increases from the root of the blade to the tip of the blade. A larger inlet velocity also leads to a more evident curvature of the pressure coefficient profile, especially when the inlet wind speed is greater than the rated value, which indicates more that structural strength design needs to be considered.

3.8. Torque and Thrust

The torque and thrust under different inflow conditions were analyzed. As mentioned, 11.4 m/s is the rated wind velocity. When the inlet wind velocity is smaller than the rated wind speed, the rotation speed rises as the wind speed increases. When the inlet wind velocity exceeds 11.4 m/s, the rotation speed remains the same even if the wind speed keeps increasing. It is obvious that when the inlet wind velocity increases, the corresponding torque and thrust increase as well.

With the increase in wind velocity, the thrust increases gradually, but the torque increases dramatically. Figure 13 shows the variation of torque as a function of the inlet wind speed. When the wind speed is smaller than the rated wind velocity, the curve from the simulation results shows great consistency with the NREL results [9]. When the inlet wind velocity exceeds 11.4 m/s, there is not enough information from NREL results. 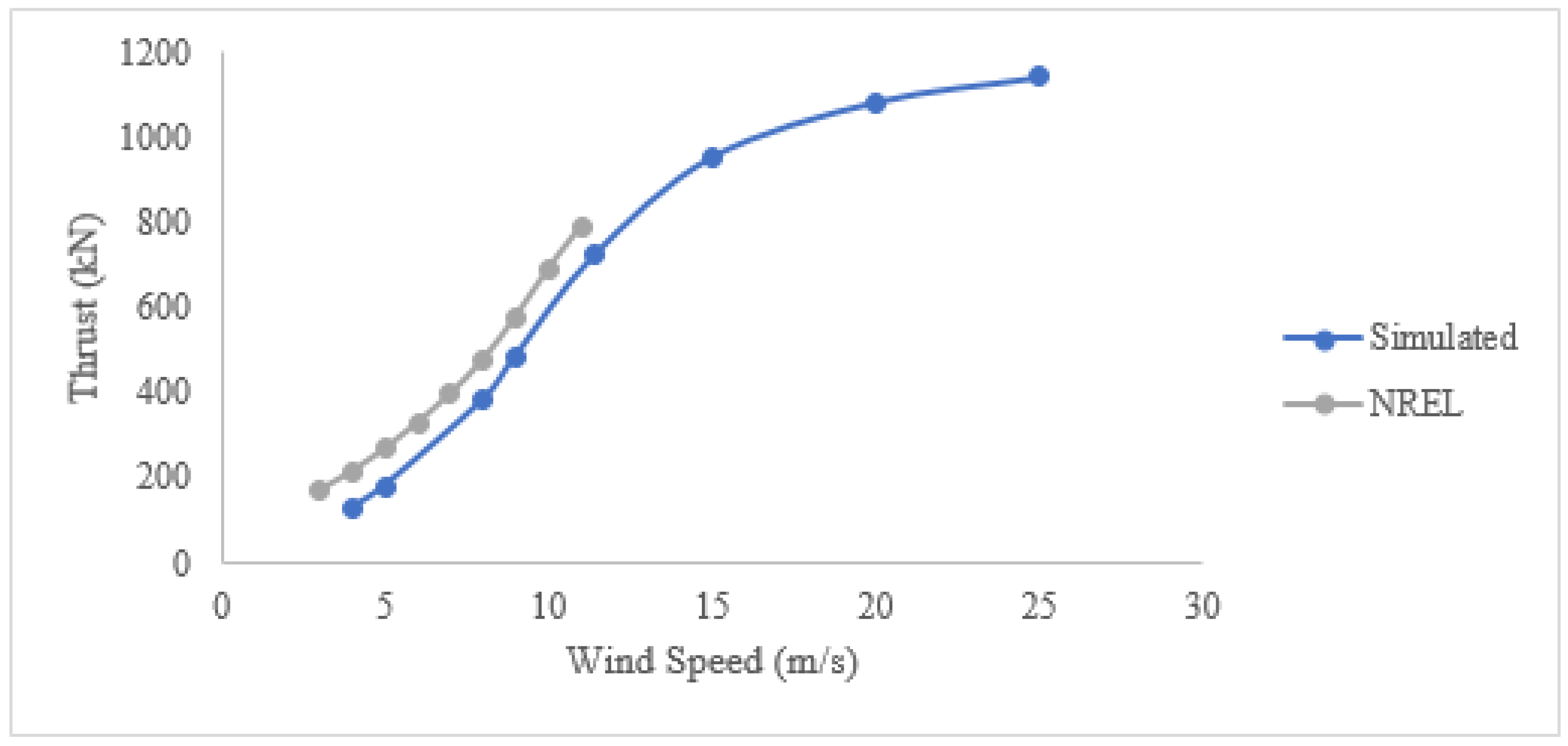Figure 14 shows the variation of thrust with wind speed. A similar trend was observed compared with available NREL data.

3.9. Power Coefficient and Tip Speed Ratio

Power coefficient is directly affected by the wind turbine tip speed ratio. If a turbine rotates very fast, the turbine blades will function like a solid wall, which may block most of the wind blowing on it and reduce the power extraction; on the other hand, if a turbine rotates very slow, most of the wind will pass through it with no or little disturbance, resulting in little power extraction from the turbine. Maximum power extraction can only be expected at the optimal tip speed ratio.

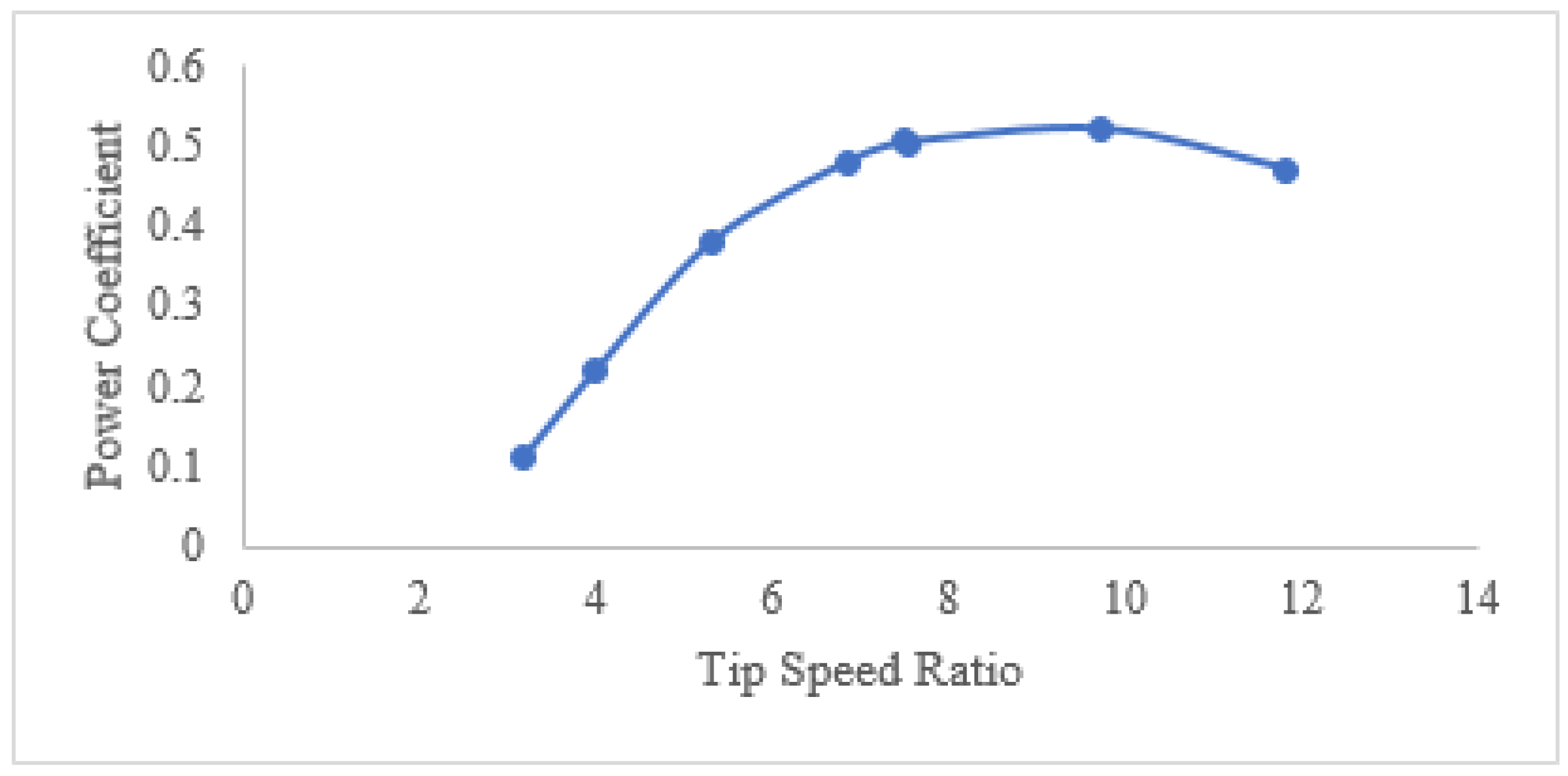
As shown in Figure 15, as the wind speed increases, the tip speed ratio increases, the power coefficient has a strong tendency to increase. After the power coefficient reaches the peak, it goes down. In addition, when TSR is between 2 and 6, the power coefficient grows rapidly. While TSR is from 6 to 10, the rate of growth of the power coefficient slows down. With TSR in the range of 10 to 12, the power coefficient goes down. To conclude based on the current simulation results, the optimum tip speed ratio for the maximum coefficient of power is around 9.

4. Discussion

A comprehensive numerical investigation was conducted for the NREL 5-MW offshore wind turbine. The numerical simulation was first validated by comparing the torque with others’ work and good agreement was observed. The error between the simulated torque and data in the literature was calculated to be less than 5%. This small error reflects that the current setting and model are feasible.

Eight test cases were developed with different inlet wind speeds: four with inlet velocity lower than the rated wind speed; one with inlet velocity equal to the rated wind speed and the remaining three with inlet velocity above the rated wind speed. The relation between torque, thrust and wind speed was then obtained. The velocity profile at various selected locations under different wind speeds was presented. When the selected location is close in proximity to the turbine hub, the influence from the hub to the velocity profile is significant. As the selected location is gradually further away from the blade, the influence of the wind turbine hub on the velocity profiles decreases. The recovery process of the velocity is presented. After comparing the velocity profiles under different wind speeds, it can be concluded that with an increase in wind speed, the influence of the hub on the velocity profile reduces.

In addition to the near wake velocity profile, limiting streamline was presented. This indicated that the flow of the whole turbine blade was smooth except for near the root area when the wind speed inlet was low. As the wind speed gradually increased, the whole turbine blade increasingly became occupied by vortices. The wake of the vortices which perform helically, intensely, and symmetrically were visualized. It was also concluded that with the growth of inlet wind velocity, the helical vortices could persist over a longer downstream distance.

Further, the pressure distribution along the blade was visualized and the pressure coefficient at cross sections of 0.3, 0.63, and 0.95 under different wind speeds were obtained. The results indicate that a larger inlet velocity led to a more evident curvature of the pressure coefficient profile. This was especially true when the inlet wind speed was greater than the rated wind velocity, which indicates that structure strength design needs to be considered further. At the end, the relation between the power coefficient and TSR were investigated. When the wind speed increased, the power coefficient increased until it reached a peak: the optimal tip speed ratio was around 9.

In conclusion, a comprehensive aerodynamic analysis of the NREL 5-MW wind turbine under various uniform inflow conditions was conducted. The variation of velocity profiles, pressure, pressure coefficient, limiting streamline, near wake flow feature, wind turbine torque, thrust and power coefficient were analyzed. The detailed wind turbine aerodynamic analysis results are expected to provide valuable input to wind turbine design and help to improve the effectiveness of harnessing wind energy. Current results are limited to uniform inflow condition; further research will be conducted by considering different inflow conditions (such as linear wind shear and linear wind shear with turbulence) effects on the wind turbine aerodynamic characteristics along with floating wind turbine settings.