Abstract
In this quick study, we estimated the Weibull distribution’s parameters using wind data collected between March 2017 and January 2018 using a twelve-meter mast meteorological station on the grounds of the National Energy Research Center in Khartoum. In order to quantify these descriptors, we relied on analytical and stochastic methods, subsequently enabling specialists from researchers, engineers, decision-makers, and policymakers to apprehend the wind characteristics in the vicinity. Hence, the computed scale and shape parameters were provided, in which the Firefly algorithm (FA) resulted in the most accuracy in terms of the coefficient of determination, which equaled 0.999, which we considered logical due to the observed nonlinearity in the wind speed numbers. On the contrary, the energy pattern factor method had the worst prediction capability depending on several goodness-of-fit metrics. This concise work is unique because it is the first to use data from Sudan to forecast local wind speeds using artificial intelligence algorithms, particularly the FA technique, which is widely used in solar photovoltaic modeling. Additionally, since classic estimating approaches act differently spatially, evaluating their efficacy becomes innovative, which was accomplished here. On a similar note, a weighted-average wind speed was found to equal and the FA average wind speed was , while the rose diagram indicated that most winds with potential energy equivalent to or more blow from the north.
1. Introduction
Sudan is an enormous reservoir of renewable energy resources, with an evident annual wind energy yield, which is verified by GIS analysis [1], as shown in in Figure 1 [2,3] and Figure 2 [4]. The government-endorsed plans that encourage the switch to clean energy generation were included in the 2015 Intended Nationally Determined Contribution (INDC) declaration that was presented to the United Nations Framework Convention on Climate Change (UNFCCC). Among them, 1000 MWp of grid-connected wind power plants is planned to be constructed in high-potential regions [5]. In 2021, the country witnessed the arrival of the first wind turbine, which will have its electricity generation fed into the national network serving 14,000 people, and has already been installed in Dongola, a rich in wind energy northern city [6].
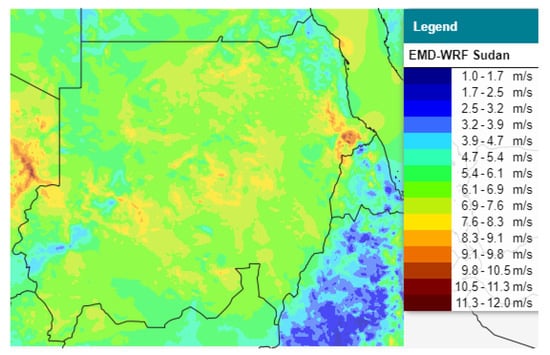
Figure 1.
Wind energy resource map for Sudan [2,3].
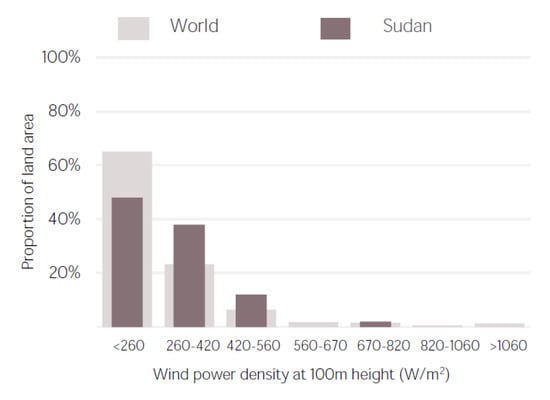
Figure 2.
Distribution of wind potential. Reprinted with permission from Ref. [4]. 2022, IRENA.
The Weibull distribution is the most commonly used statistical distribution to model wind speed [7,8,9,10,11,12,13,14,15], which served this purpose for the first time in the late 1970s. It then established many wind energy regulations worldwide and modeled software, such as WASP and HOMER [16]. The two parameters of the Weibull distribution are well-known for being straightforward and fitting the actual wind speed readings perfectly. Hence, if these two parameters are accurately predicted, the Weibull-based forecasting model will represent the exact wind speed variations [17,18]. The work of [19] depended on the Weibull distribution to obtain wind characteristics in the Alaçatı region, Turkey, and found that its shape and scale parameters equal 2.05 and 9.16, respectively. Additionally, the mean wind speed based on the dataset was . [10]. They estimated the same distribution parameters using different analytical methods and compared them with the results of other parametric and non-parametric models. In Pakistan, ref. [11] used six analytical estimation methods to identify the shape and scale estimates of the Weibull distribution and accordingly obtained an average wind speed range from for different weather mast heights. In Sudan, [20] estimated the annual average wind speeds and their corresponding Weibull shape parameters at a 10 m height. Table 1 presents the mentioned estimates for major cities in the country.

Table 1.
Wind energy potential for different cities in Sudan. Adapted with permission from Ref. [20]. 2008, Elsevier.
The wind speed prediction models provide the information needed for industry development [21]. There are four main modeling techniques. (1) Physical models show better forecasting performance with long-term data; still, the precision is low. Still, suppose the resolution is high enough, and the initialization is perfect. In that case, the accuracy can be increased. (2) Statistical models include the conventional model that relies on famous probability distributions, such as Weibull, but with a limited capacity in front of nonlinear wind speed data. (3) Third, spatial algorithms, which require a large amount of information. (4) Lastly, artificial intelligence or metaheuristic algorithms, which are gaining more popularity, especially with nonlinear data [21,22,23,24,25,26,27,28,29,30,31].
Statistical models or analytical methods are widely used to extract the parameters of the Weibull distribution [12,32]. Among these techniques, the most popular ones are the maximum likelihood method (MLM), the least square method (LSM), the method of moment (MOM), and the graphical method (GM) [15]. Additionally, the metaheuristics or stochastic processes, mainly swarm intelligence algorithms, are successively used in the literature to evaluate the wind speed Weibull parameters, including the particle swarm optimization, Cuckoo search, Gray wolf algorithm, Firefly algorithm (FA), Ant Colony optimization, and many others [33]. Since FA was put forward in this study, we have to mention that many researchers developed multiple variants of FA and applied them to estimate the parameters of the Weibull distribution effectively. Ref. [34] hybridized the FA with the support vector machine method to obtain a novel, efficient way for Weibull parameter estimation. Ref. [35] used a hybrid technique containing the FA and a back-propagation neural network to evaluate the Weibull distribution parameters for wind data in China, yielding a better prediction performance.
To link points together, our work here targets utilizing several analytical methods in addition to the FA to estimate the parameters of the Weibull distribution for the wind speed data collected in Khartoum. The importance of the city as the country’s capital and the availability of the research means from meteorological stations that save long-term data and the suitable equipment made us focus our attention on this region to help us build a model or a mathematical template that will guide similar future work for the rest of the country. The novelty in this work lies in using the FA with wind speed data in Sudan and the Weibull distribution, and then comparing the results with conventional estimation methods whose quality varies location-wise. For instance, the graphical way showed a good performance, while it has proven ineffectiveness in analyzing the data in some areas in the Republic of Korea, as claimed by [36]. We placed particular attention to the FA methodology here because if we want to obtain a powerful Weibull-based forecasting model, an accurate estimation of the shape and scale parameters is of paramount importance, and this accuracy is only obtained through stochastic algorithms, precisely the swarm-intelligence set of techniques that the FA methods belong to. Accordingly, the significance of this study is reflected in forming a solid foundation for wind speed forecasting, which will comply with different sites within the surrounding area and in a larger circle involving the whole country.
Therefore, the rest of this article is organized as follows. Section 2 presents the experimental setup, which sheds information on the meteorological mast station system, and Section 3 outlines the analysis methodology, including data filtering, missing data imputation, Weibull distribution description, parameter estimation techniques, and goodness-of-fit metrics. Section 4 delivers and discusses the results, and Section 5 concludes.
2. Experimental Setup
The measurement tower from which the data were taken is located inside the National Energy Research Center (NERC) campus in the Soba suburb, Khartoum, and has a wind monitoring tower. At the top of the tower, a first anemometer, which measures wind speed, is fixed. Right beneath it, a wind vane that detects the wind direction is placed at . Below the wind vane at , a second anemometer is fixed, which provides a separate measurement for the wind speed. Additionally, there is a second wind vane at , reading another measurement for wind direction.
A barometer, an air pressure measuring device, and a thermocouple sensor are placed at . Moreover, a hygrometer is placed at the same height to measure the water content in the air (i.e., relative humidity). Finally, a pyranometer is connected to the tower at .
All the sensors or measuring devices are connected to a data acquisition system (Model: Meteo-40L, manufactured by Ammonit (Ammonit Measurement GmbH, Berlin, Germany) or data logger, in which the data are continuously collected at a sampling rate of or higher. Each sensor measures and records its relevant reading once in a minute or less, and for every 10 min, the data logger saves the minimum, maximum, mean, and standard deviation of the set of measurements. It is worth mentioning that the analysis depended on retrieved data that belongs to the anemometer and wind vane set at a height of . Figure 3 and Figure 4 show a schematic diagram and picture of the wind mast station within the NERC premises.
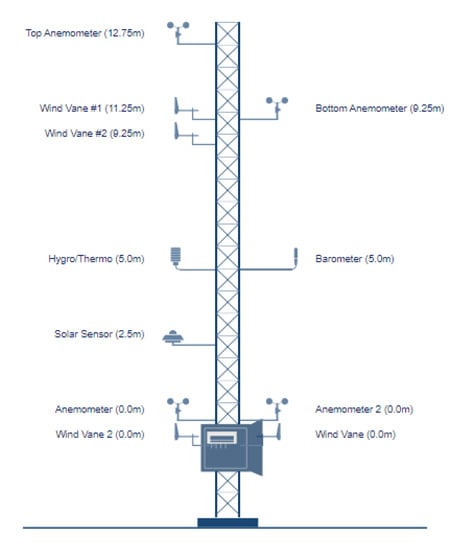
Figure 3.
Schematic diagram of the meteorological mast station.

Figure 4.
Photo of the weather mast at the NERC.
3. Analysis Methodology
3.1. Data Filtering
Filtering is the process of defining, identifying, and fixing data flaws to lessen their effect [37]. In the restored readings from the mast data logger, we discovered error codes in the form of negative wind speeds, which were successively removed, leaving behind blank spaces or empty data fields. Figure 5 displays the ten-minute interval time series graph between 18 March 2017 and 30 January 2018, and Figure 6 illustrates the same data as a frequency histogram that includes the normal curve.
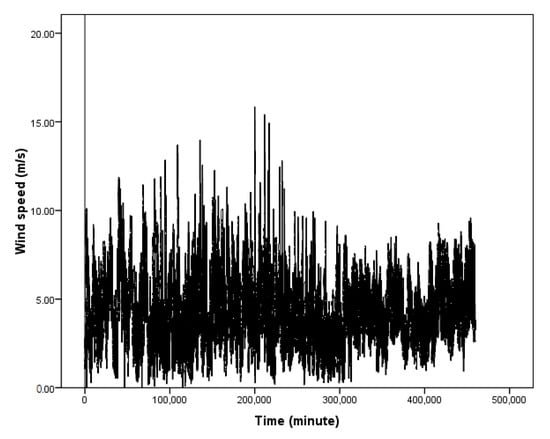
Figure 5.
Wind speed time series chart as recorded by the NERC meteorological mast station between March 2017 and January 2018.
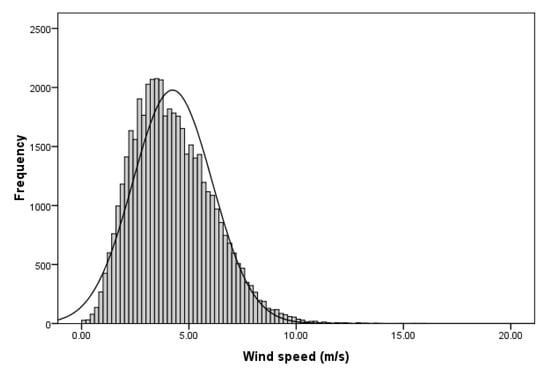
Figure 6.
Frequency histogram of wind speed as recorded by the NERC meteorological mast station between March 2017 and January 2018.
3.2. Missing Data Imputation
Missing data methods either discard data using complete and available case analysis techniques, also known as likewise and pairwise deletion [38], or retain all data using single and multiple imputation methods [39]. In our analysis, we used the single mean imputation approach seeking simplicity, as we have less than 0.05% missing data, though in general, the single imputation methods generate filled-in values infused with standard errors, causing bias in the sample [40]. However, we defend our choice by claiming that almost a trivial part of the data are missing if we consider the 5% missingness threshold over which rigorous imputation methods should be used [41].
3.3. Weibull Distribution
The two-parameter Weibull distribution best fits the wind speed data [42]. The probability density function of this distribution is given in Equation (1), the cumulative density function is provided in Equation (2) [43,44], and the mean and the variance are given in Equations (3) and (4), respectively [45]. Figure 7 and Figure 8 show graphs of the typical Weibull density functions [43].
where is the wind speed.
where .
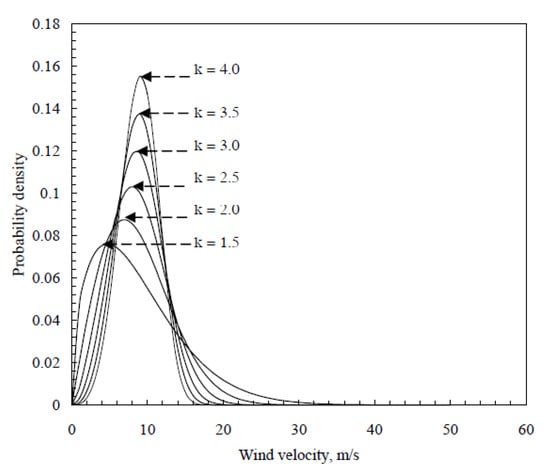
Figure 7.
Weibull probability density function at different values.Reprinted with permission from Ref. [43]. 2006, Springer Nature.
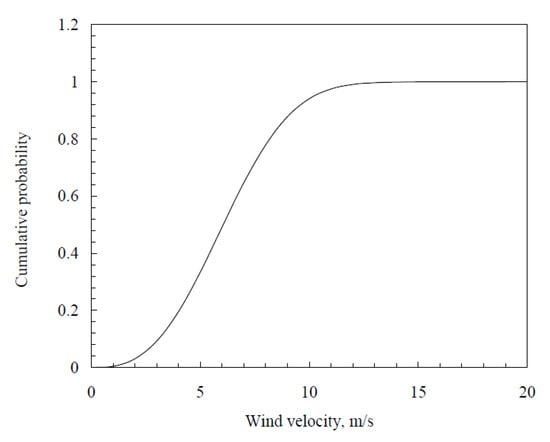
Figure 8.
Typical Weibull cumulative density function. Reprinted with permission from Ref. [43]. 2006, Springer Nature.
3.4. Parameter Estimation
The parameter estimation concept depends on the availability of measured data to statistically approximate the parameter value. The well-known estimation methods could be grouped into analytical, numerical iterative, and stochastic methods, which perfectly fit nonlinear models [46].
3.4.1. Analytical Methods
Energy Pattern Factor Method
The Energy pattern factor method (EPFM) estimates the scale and shape parameters of the Weibull distribution using Equations (5)–(7) [47].
Graphical Method
We chose to use the graphical method (GM) to estimate the scale and shape parameters, as this method is the most common one with reliable results [43,48,49]. Equations (8)–(10) present the estimators’ equations obtained by applying the natural logarithm transformation to Equation (2) to find the straight-line formula.
where is given in Equation (2).
Method of Moments
The method of moments (MOM) estimates the scale and shape parameters depending on Equations (11) and (12) [45,50].
Least Square Method
The least square method (LSM) is an analytical technique to estimate the scale and shape parameters of the Weibull distribution [45,50], employing Equations (13) and (14) [51,52].
3.4.2. Stochastic Method
Firefly Algorithm
The Firefly optimization algorithm (FA) introduced by [53,54] is a swarm-intelligence methodology that takes the Firefly position as the candidate solution. The Firefly brightness, the fitness value, is utilized by the algorithm to define the relationship between the fireflies, as the brighter ones are attractive, and the distance between them and the less-glowing fireflies is shortened. The primary benefits of the FA include the automated separation of the entire population into subgroups, the innate ability to handle multi-modal optimization, and the high ergodicity and diversity of the solutions. [53]. Equations (15)–(17) are the backbone equations for this artificial intelligence technique, while Figure 9 shows the algorithm pseudo-code.
where , , and . These parameter values are given in Table 2.

Figure 9.
FA pseudo code.

Table 2.
Parameter settings for the FA.
Objective Function
The mean square error (MSE) represented by Equation (18) is used here as an objective function for the minimization problem that is intended to be solved using the FA [24,26,28]. Hence, this work aims to minimize the MSE between the observed and estimated cumulative density functions.
where is the cumulative density function estimator.
3.5. Goodness-of-Fit
The goodness-of-fit measures used in this study are also widely applicable for testing the fit of the estimation method in use, which are the root-mean-square error (RMSE) in Equation (19) [22,45,47,55,56,57,58,59], the coefficient of determination (R2), represented by Equation (20) [19,50,55], the mean absolute error (MAE) in Equation (21) [50,55,57], and the Kolmogorov–Smirnov test (K-S) presented in Equation (22) [45,56]. If we used the cumulative density function to evaluate these metrics, the latter variants are associated with the P-P plot. On the other hand, the variants evaluated using the probability density function are associated with the Q-Q plot. However, the P-P goodness-of-fit criteria are favored because the cumulative density function generates an unbiased estimate of the Weibull parameters [60].
where is either . or and is either or .
4. Results and Discussion
Figure 10 illustrates the monthly average wind speeds at the NERC site, as drawn from the collected data. Additionally, Table 3 lists the average wind speed, frequency, frequency percentage, and cumulative frequency percentage corresponding to equal-width wind speed classes. Table 2 provides the parameters specific to the FA technique, among them the stopping criterion, which was 1000 iterations, that we used to obtain high-accuracy results. It took the FA algorithm less than 200 iterations to reach the steady state, meaning that the fitness value converges or an exact solution is reached. Figure 11 shows that the convergence to the optimal solution occurred approximately after 100 iterations. It is worth mentioning that the researchers in this study relied on Python code to execute the artificial intelligence algorithm.
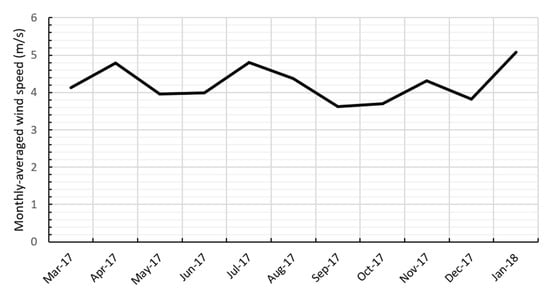
Figure 10.
Monthly averaged wind speed.

Table 3.
Frequency distribution of wind speed.
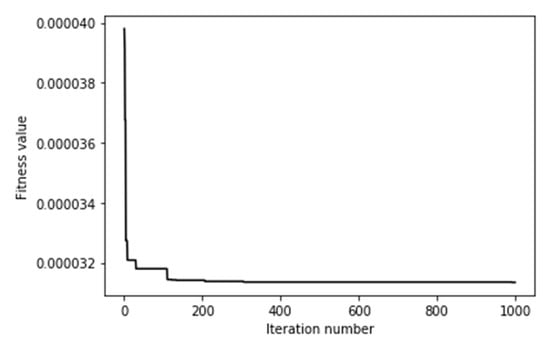
Figure 11.
FA convergence vs. iteration.
Following the statistical analysis and the parameter estimation methods described above, Table 4 delivers the shape and scale estimates associated with every technique. Consequently, it is clear from the demonstrated results that the FA has the best prediction potential regarding every testing metric used, followed by the MOM and GM. For example, using the FA method, the K–S number corresponding to the extracted shape and scale parameters is the most accurate as it tends to zero. The LSM and EPFM showed a weak performance looking at the R2PP and R2QQ. If we rely on visual comparison and inspection to determine the quality of the methods used in estimating the parameters of the Weibull distribution, then Figure 12, Figure 13, Figure 14 and Figure 15 explicitly show the superiority of the artificial intelligence technique. Additionally, these figures prove that the Weibull distribution perfectly describes the wind data at the NERC site. We can understand the dominance of the FA over the rest of the prediction methods due to the apparent nonlinearity in the wind speed data by looking at the regression analysis results in Table 5, which favors the stochastic metaheuristic methods in such cases. Moreover, the average wind speeds were evaluated by employing and to Equation (3), and are given in Table 4. The average speed corresponding to the FA method equals .

Table 4.
Analysis summary.
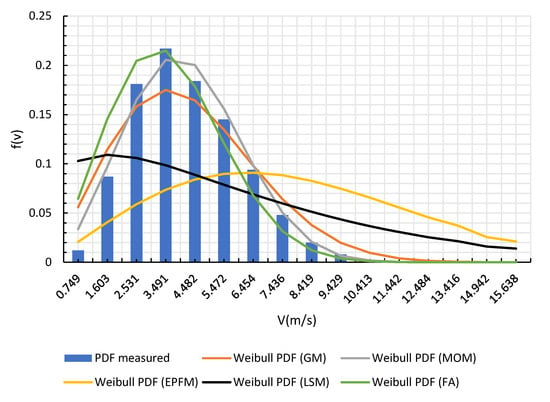
Figure 12.
The Weibull probability density function for the parameter estimation methods in use.
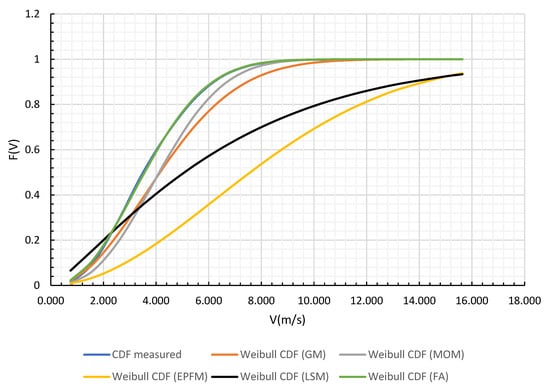
Figure 13.
The Weibull cumulative density function for the parameter estimation methods in use.
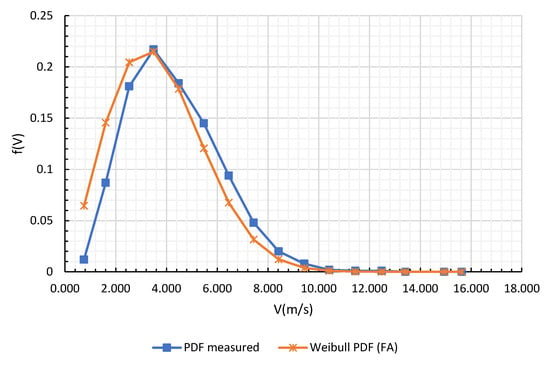
Figure 14.
The Weibull probability density functions for the measured data and the FA.
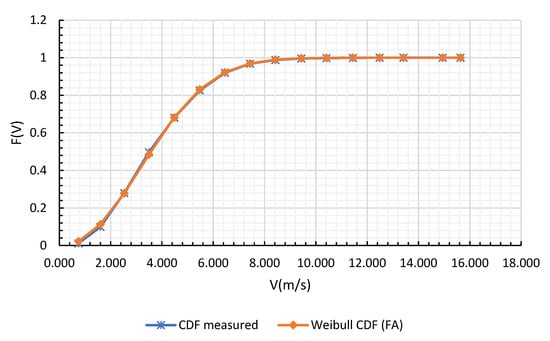
Figure 15.
The Weibull cumulative density functions for the measured data and the FA.

Table 5.
Regression analysis result of the wind speed data.
The average speed for the wind energy assessment must also consider the dataset’s power content. Hence, the weighted average expression represented by Equation (23) was used [43], and a was obtained.
It is worth mentioning that although the FA method has a high prediction accuracy, the average wind speed produced by the classic techniques (i.e., MOM and GM) are closer in magnitude to the weighted average speed. Even after the visual inspection of the wind speed data given in Figure 10, it is noticeable that the classically produced numbers rest within the region of most data points. On the other hand, looking at the frequency percentages delivered in Table 2, the wind speed class that embraces the average speed produced by the FA method has the highest frequency, making the FA values more realistic in forecasting.
where is the average wind speed, is the sample size, and are the observations or wind speeds.
Finally, the frequency percentage data in Table 6, which corresponds to the wind direction, indicates that the wind primarily blows from the north, which is again noticeable in the rose diagram in Figure 16. The wind direction illustrated in the rose diagram precisely simulates reality according to our on-field remarks that we have noticed monitoring our currently operating 2 kWp wind turbine recently installed at the NERC campus.

Table 6.
Frequency distribution of wind speed per wind direction.
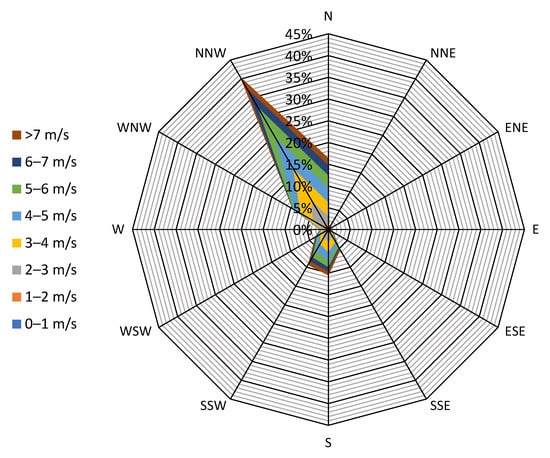
Figure 16.
Frequency distribution per direction in the rose diagram.
5. Conclusions
In this research, we presented the results of the statistical analysis performed on wind speed and direction data collected by a weather mast station installed at the NERC, Soba, Khartoum. Limited data filtering was applied to detect and remove error codes, and then filling in the gaps was performed using the simple arithmetic mean of the remaining data points, as the distorted data fields were considered trivial (i.e., ) compared to the whole dataset (i.e., ) in terms of size. Firstly, we obtained the Weibull distribution parameters using analytical and stochastic methods, shown in Table 4. In this table, the FA method outperforms the others in the goodness-of-fit. The MOM and the GM rank second and third, while the EPFM performs weakest. The best value for the shape parameter is 2.197, while the worst value is 1.918. The best value for the scale parameter is 4.211, while the worst value is 9.174. Secondly, the nonlinearity in wind speed data, which was conveyed in the regression analysis results provided in Table 5, explains the advantage of the FA method over the conventional ones, as the artificial intelligence methods best fit nonlinear data. Thirdly, the rose diagram shows wind mainly blowing from the north, which complies with the real-world scenario. Finally, the average wind speed, according to the FA results, is equal to , while the weighted average speed equals . Still, the weighted average value looks more realistic from the field measurements point of view, but the FA average figure better serves the forecasting purpose due to the high accuracy applied while obtaining this number coupled with the high frequency of occurrence of this speed. The novelty in this work is reflected in the use of data generated in Sudan to forecast local wind speeds using the FA technique, which is widely used in solar PV modeling. Additionally, since classic estimating approaches execute differently location-wise, assessing their efficacy becomes new, which was achieved here. The authors can present several recommendations regarding the assessment of the local wind energy resource and the optimal use of this potential based on the cutting-edge technologies available in the global market:
- A higher and multi-anemometer mast wind station must be installed locally to facilitate the vertical extrapolation of wind speed in heights compatible with utility-scale power production.
- Figure 15 demonstrates the high capacity of stochastic methods, in particular the swarm intelligence algorithms, in predicting the wind speed in the region, making this technique the best choice for domestic meteorological and forecasting research.
- Private sector participation in power generation from clean energy resources such as wind can fill the energy demand gap in Sudan. Hence, soft financing means provided by the stakeholders and international institutions will be the base for such contributions.
- Wind turbine manufacturers need to deploy pilot projects in the country, preferably under the supervision of the NERC, to inspect the prospects of this investment.
Author Contributions
Conceptualization, A.Y.; methodology, A.Y., A.O. and Y.Y.; software, A.Y.; validation, A.Y.; formal analysis, A.Y.; investigation, A.Y.; resources, A.Y., H.E., Y.Y. and A.O.; data curation, A.Y.; writing—original draft preparation, A.Y., H.E., D.O., G.S.-E., A.E. and E.B.; writing—review and editing, A.Y., A.O. and Y.Y.; supervision, A.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Scale parameter | |
| Scale estimator | |
| Probability density function | |
| Cumulative density function | |
| Shape parameter | |
| Shape estimator | |
| Wind speed (m/s) | |
| Arithmetic mean | |
| variance | |
| Gamma function | |
| EM | Empirical method |
| EPFM | Energy pattern factor method |
| FA | Firefly algorithm |
| GM | Graphical method |
| MLM | Maximum likelihood method |
| MMLM | Modified maximum likelihood method |
| MOM | Method of moments |
| LSM | Least square method |
| NERC | National Energy Research Center |
References
- Mentis, D.; Hermann, S.; Howells, M.; Welsch, M.; Siyal, S.H. Assessing the technical wind energy potential in africa a GIS-based approach. Renew. Energy 2015, 83, 110–125. [Google Scholar] [CrossRef]
- Sudan Soil Information System Data. Available online: https://susis.sd/data/ (accessed on 5 September 2022).
- EMD International A/S Wind Energy Resources for the Republic of Sudan. Available online: http://sudan.windprospecting.com/ (accessed on 4 September 2022).
- IRENA. Energy Profile-Sudan; IRENA: Masdar City, United Arab Emirates, 2022. [Google Scholar]
- UNFCCC: Republic of Sudan: First Intended Nationally Determined Contribution. 2015. Available online: https://unfccc.int/sites/default/files/NDC/2022-10/Sudan%20Updated%20First%20NDC-12102021.pdf (accessed on 4 April 2023).
- United Nations Development Programme Sudan’s First Wind Turbine Arrives. Available online: https://www.arabstates.undp.org/content/rbas/en/home/presscenter/pressreleases/2021/sudan_s-first-wind-turbine-arrives.html (accessed on 14 April 2022).
- Ahmed Shata, A.S.; Hanitsch, R. Evaluation of wind energy potential and electricity generation on the coast of Mediterranean Sea in Egypt. Renew. Energy 2006, 31, 1183–1202. [Google Scholar] [CrossRef]
- Bagiorgas, H.S.; Assimakopoulos, M.N.; Theoharopoulos, D.; Matthopoulos, D.; Mihalakakou, G.K. Electricity generation using wind energy conversion systems in the area of Western Greece. Energy Convers. Manag. 2007, 48, 1640–1655. [Google Scholar] [CrossRef]
- Gökçek, M.; Bayülken, A.; Bekdemir, Ş. Investigation of wind characteristics and wind energy potential in Kirklareli, Turkey. Renew. Energy 2007, 32, 1739–1752. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Ma, K. Wind speed probability distribution estimation and wind energy assessment. Renew. Sustain. Energy Rev. 2016, 60, 881–899. [Google Scholar] [CrossRef]
- Khalid Saeed, M.; Salam, A.; Rehman, A.U.; Abid Saeed, M. Comparison of six different methods of Weibull distribution for wind power assessment: A case study for a site in the Northern region of Pakistan. Sustain. Energy Technol. Assess. 2019, 36, 100541. [Google Scholar] [CrossRef]
- Guarienti, J.A.; Kaufmann Almeida, A.; Menegati Neto, A.; de Oliveira Ferreira, A.R.; Ottonelli, J.P.; Kaufmann de Almeida, I. Performance analysis of numerical methods for determining Weibull distribution parameters applied to wind speed in Mato Grosso do Sul, Brazil. Sustain. Energy Technol. Assess. 2020, 42, 100854. [Google Scholar] [CrossRef]
- Mahmood, F.H.; Resen, A.K.; Khamees, A.B. Wind characteristic analysis based on Weibull distribution of. Energy Rep. 2020, 6, 79–87. [Google Scholar] [CrossRef]
- Aslam, M. Testing average wind speed using sampling plan for Weibull distribution under indeterminacy. Sci. Rep. 2021, 11, 7532. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Wind speed distribution selection—A review of recent development and progress. Renew. Sustain. Energy Rev. 2019, 114, 109290. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramırez, P.; Velazquez, S. A review of wind speed probability distributions used in wind energy analysis Case studies in the Canary Islands. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Kadhem, A.A.; Wahab, N.I.A.; Aris, I.; Jasni, J.; Abdalla, A.N. Advanced wind speed prediction model based on a combination of Weibull distribution and an artificial neural network. Energies 2017, 10, 1744. [Google Scholar] [CrossRef]
- Wang, R.; Li, W.; Bagen, B. Development of wind speed forecasting model based on the Weibull probability distribution. In Proceedings of the International Conference on Computer Distributed Control and Intelligent Environmental Monitoring, Changsha, China, 19–20 February 2011; pp. 2062–2065. [Google Scholar]
- Ozay, C.; Celiktas, M.S. Statistical analysis of wind speed using two-parameter Weibull distribution in AlaçatI region. Energy Convers. Manag. 2016, 121, 49–54. [Google Scholar] [CrossRef]
- Omer, A.M. On the wind energy resources of Sudan. Renew. Sustain. Energy Rev. 2008, 12, 2117–2139. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, J.; Zhang, H.; Zhao, W. An advanced weighted system based on swarm intelligence optimization for wind speed prediction. Appl. Math. Model. 2021, 100, 780–804. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, S.; Xiao, L.; Fu, T. Wind speed forecasting based on multi-objective grey wolf optimisation algorithm, weighted information criterion, and wind energy conversion system: A case study in Eastern China. Energy Convers. Manag. 2021, 243, 114402. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Sanandaji, B.M.; Poolla, K.; Varaiya, P. Exploiting sparsity of interconnections in spatio-temporal wind speed forecasting using Wavelet Transform. Appl. Energy 2016, 165, 735–747. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, J. A new combined model based on multi-objective salp swarm optimization for wind speed forecasting. Appl. Soft Comput. J. 2020, 92, 106294. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.; Guo, Z.; Yang, W. Research and application of a novel hybrid forecasting system based on multi-objective optimization for wind speed forecasting. Energy Convers. Manag. 2017, 150, 90–107. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Yang, W. A novel non-linear combination system for short-term wind speed forecast. Renew. Energy 2019, 143, 1172–1192. [Google Scholar] [CrossRef]
- Zhang, K.; Qu, Z.; Dong, Y.; Lu, H.; Leng, W.; Wang, J.; Zhang, W. Research on a combined model based on linear and nonlinear features—A case study of wind speed forecasting. Renew. Energy 2019, 130, 814–830. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, C.; Zhang, G. A combined forecasting system based on modified multi-objective optimization and sub-model selection strategy for short-term wind speed. Appl. Soft Comput. J. 2020, 94, 106463. [Google Scholar] [CrossRef]
- Baran, S.; Lerch, S. Log-normal distribution based Ensemble Model Output Statistics models for probabilistic wind-speed forecasting. Q. J. R. Meteorol. Soc. 2015, 141, 2289–2299. [Google Scholar] [CrossRef]
- Gomes, P.; Castro, R. Wind Speed and Wind Power Forecasting using Statistical Models: AutoRegressive Moving Average (ARMA) and Artificial Neural Networks (ANN). Int. J. Sustain. Energy Dev. 2012, 1, 41–50. [Google Scholar] [CrossRef]
- Aasim; Singh, S.N.; Mohapatra, A. Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting. Renew. Energy 2019, 136, 758–768. [Google Scholar] [CrossRef]
- Azad, K.; Rasul, M.; Halder, P.; Sutariya, J. Assessment of wind energy prospect by weibull distribution for prospective wind sites in Australia. Energy Procedia 2019, 160, 348–355. [Google Scholar] [CrossRef]
- Guedes, K.S.; de Andrade, C.F.; Rocha, P.A.C.; Mangueira, S.; Moura, E.P. De Performance analysis of metaheuristic optimization algorithms in estimating the parameters of several wind speed distributions. Appl. Energy 2020, 268, 114952. [Google Scholar] [CrossRef]
- Gani, A.; Shamshirband, K.M.S.; Altameem, T.A.; Petkovic´, D.; Ch, S. A Combined Method to Estimate Wind Speed Distribution Based on Integrating the Support Vector Machine with Firefly Algorithm. Environ. Prog. Sustain. Energy 2016, 35, 867–875. [Google Scholar] [CrossRef]
- Gao, Y.; Qu, C.; Zhang, K. A hybrid method based on singular spectrum analysis, firefly algorithm, and BP neural network for short-term wind speed forecasting. Energies 2016, 9, 757. [Google Scholar] [CrossRef]
- Kang, S.; Khanjari, A.; You, S.; Lee, J.H. Comparison of different statistical methods used to estimate Weibull parameters for wind speed contribution in nearby an offshore site, Republic of Korea. Energy Rep. 2021, 7, 7358–7373. [Google Scholar] [CrossRef]
- Wedin, O.; Bogren, J.; Grabec, I. D3.1 Data Filtering Methods; European Commission: Brussels, Belgium, 2008. [Google Scholar]
- Peugh, J.L.; Enders, C.K. Missing data in educational research: A review of reporting practices and suggestions for improvement. Rev. Educ. Res. 2004, 74, 525–556. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Single Imputation Methods. In Statistical Analysis with Missing Data; Wiley Online Library: Hoboken, NJ, USA, 2019; pp. 67–84. [Google Scholar]
- Osman, M.S.; Abu-Mahfouz, A.M.; Page, P.R. A Survey on Data Imputation Techniques: Water Distribution System as a Use Case. IEEE Access 2018, 6, 63279–63291. [Google Scholar] [CrossRef]
- Baraldi, A.N.; Enders, C.K. An introduction to modern missing data analyses. J. Sch. Psychol. 2010, 48, 5–37. [Google Scholar] [CrossRef] [PubMed]
- Pobočíková, I.; Sedliačková, Z.; Michalková, M. Application of Four Probability Distributions for Wind Speed Modeling. Procedia Eng. 2017, 192, 713–718. [Google Scholar] [CrossRef]
- Mathew, S. Wind Energy: Fundamentals, Resource Analysis and Economics; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 3540309055. [Google Scholar]
- Wais, P. A review of Weibull functions in wind sector. Renew. Sustain. Energy Rev. 2017, 70, 1099–1107. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, J.; Wu, J.; Geng, W. Comparison of numerical methods and metaheuristic optimization algorithms for estimating parameters for wind energy potential assessment in low wind regions. Renew. Sustain. Energy Rev. 2017, 69, 1199–1217. [Google Scholar] [CrossRef]
- Da Ros, S.; Colusso, G.; Weschenfelder, T.A.; de Marsillac Terra, L.; de Castilhos, F.; Corazza, M.L.; Schwaab, M. A comparison among stochastic optimization algorithms for parameter estimation of biochemical kinetic models. Appl. Soft Comput. J. 2013, 13, 2205–2214. [Google Scholar] [CrossRef]
- Shoaib, M.; Siddiqui, I.; Rehman, S.; Khan, S.; Alhems, L.M. Assessment of wind energy potential using wind energy conversion system. J. Clean. Prod. 2019, 216, 346–360. [Google Scholar] [CrossRef]
- Tuller, S.E.; Brett, A.C. The Characteristics of Wind Velocity that Favor the Fitting of a Weibull Distribution in Wind Speed Analysis. J. Clim. Appl. Meteorol. 1984, 23, 124–134. [Google Scholar] [CrossRef]
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]
- Alrashidi, M.; Pipattanasomporn, M.; Rahman, S. Metaheuristic optimization algorithms to estimate statistical distribution parameters for characterizing wind speeds. Renew. Energy 2020, 149, 664–681. [Google Scholar] [CrossRef]
- Al-Fawzan, M.A. Methods for Estimating the Parameters of the Weibull Distribution; King Abdulaziz City for Science and Technology: Riyadh, Saudi Arabia, 2000. [Google Scholar]
- Pobočíková, I.; Sedliačková, Z. Comparison of four methods for estimating the Weibull distribution parameters. Appl. Math. Sci. 2014, 8, 4137–4149. [Google Scholar]
- Yang, X.S.; He, X. Firefly algorithm: Recent advances and applications. Int. J. Swarm Intell. 2013, 1, 36. [Google Scholar] [CrossRef]
- Younis, A.; Bakhit, A.; Onsa, M.; Hashim, M. A comprehensive and critical review of bio-inspired metaheuristic frameworks for extracting parameters of solar cell single and double diode models. Energy Rep. 2022, 8, 7085–7106. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Zhao, Y.; Dai, B.; Pei, M.; Tang, Y. Review of meta-heuristic algorithms for wind power prediction: Methodologies, applications and challenges. Appl. Energy 2021, 301, 117446. [Google Scholar] [CrossRef]
- Kollu, R.; Rayapudi, S.R.; Narasimham, S.V.L.; Pakkurthi, K.M. Mixture probability distribution functions to model wind speed distributions. Int. J. Energy Environ. Eng. 2012, 3, 27. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Shaheen, A.M.; Shalaby, A.S. Aquila Optimization Algorithm for Wind Energy Potential Assessment Relying on Weibull Parameters Estimation. Wind 2022, 2, 33. [Google Scholar] [CrossRef]
- Ali, S.; Lee, S.M.; Jang, C.M. Statistical analysis of wind characteristics using Weibull and Rayleigh distributions in Deokjeok-do Island—Incheon, South Korea. Renew. Energy 2018, 123, 652–663. [Google Scholar] [CrossRef]
- Khaled, A.; Abdelaziz, A.Y.; Ali, Z.M.; Alharthi, M.M.; Ghoneim, S.S.M.; Eskaros, M.R.; Attia, M.A. Mixture probability distribution functions using novel metaheuristic method in wind speed modeling. Ain Shams Eng. J. 2022, 13, 101613. [Google Scholar] [CrossRef]
- Shi, H.; Dong, Z.; Xiao, N.; Huang, Q. Wind Speed Distributions Used in Wind Energy Assessment: A Review. Front. Energy Res. 2021, 9, 769920. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).