Effects of Inflow Parameters and Disk Thickness on an Actuator Disk inside the Neutral Atmospheric Boundary Layer
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
2.2. Actuator Disk Model
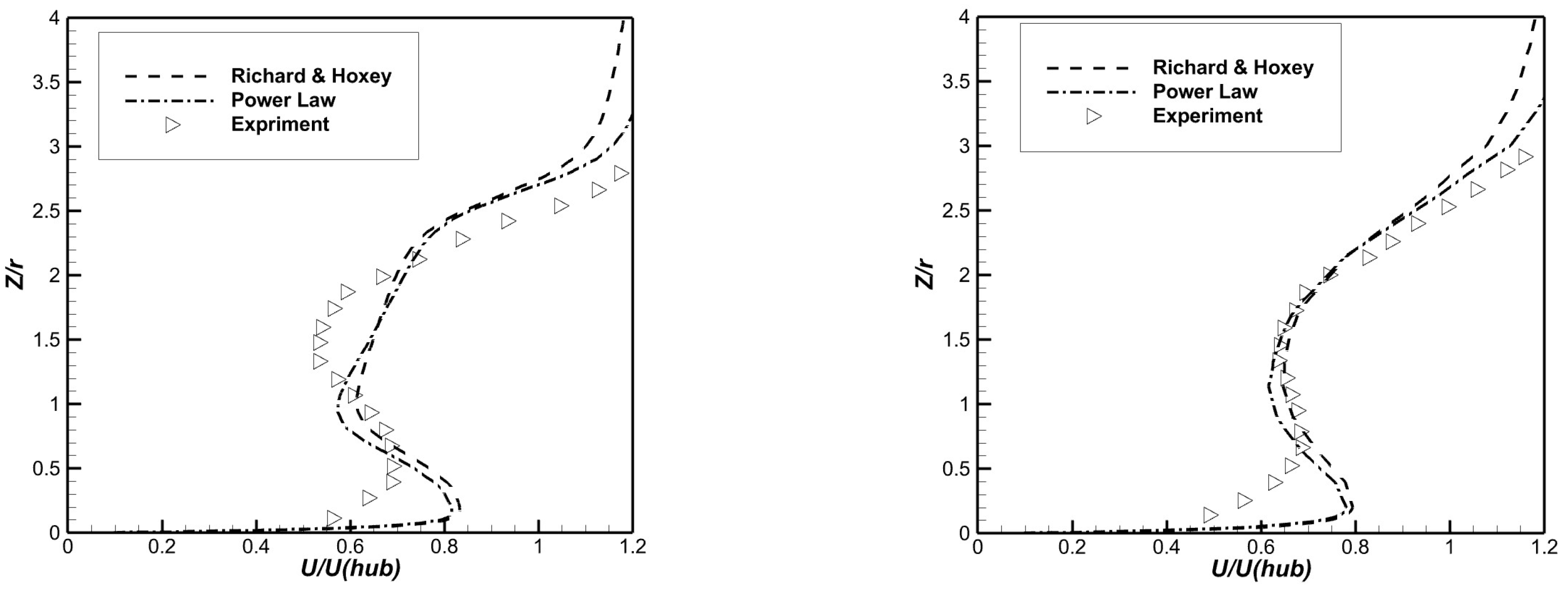
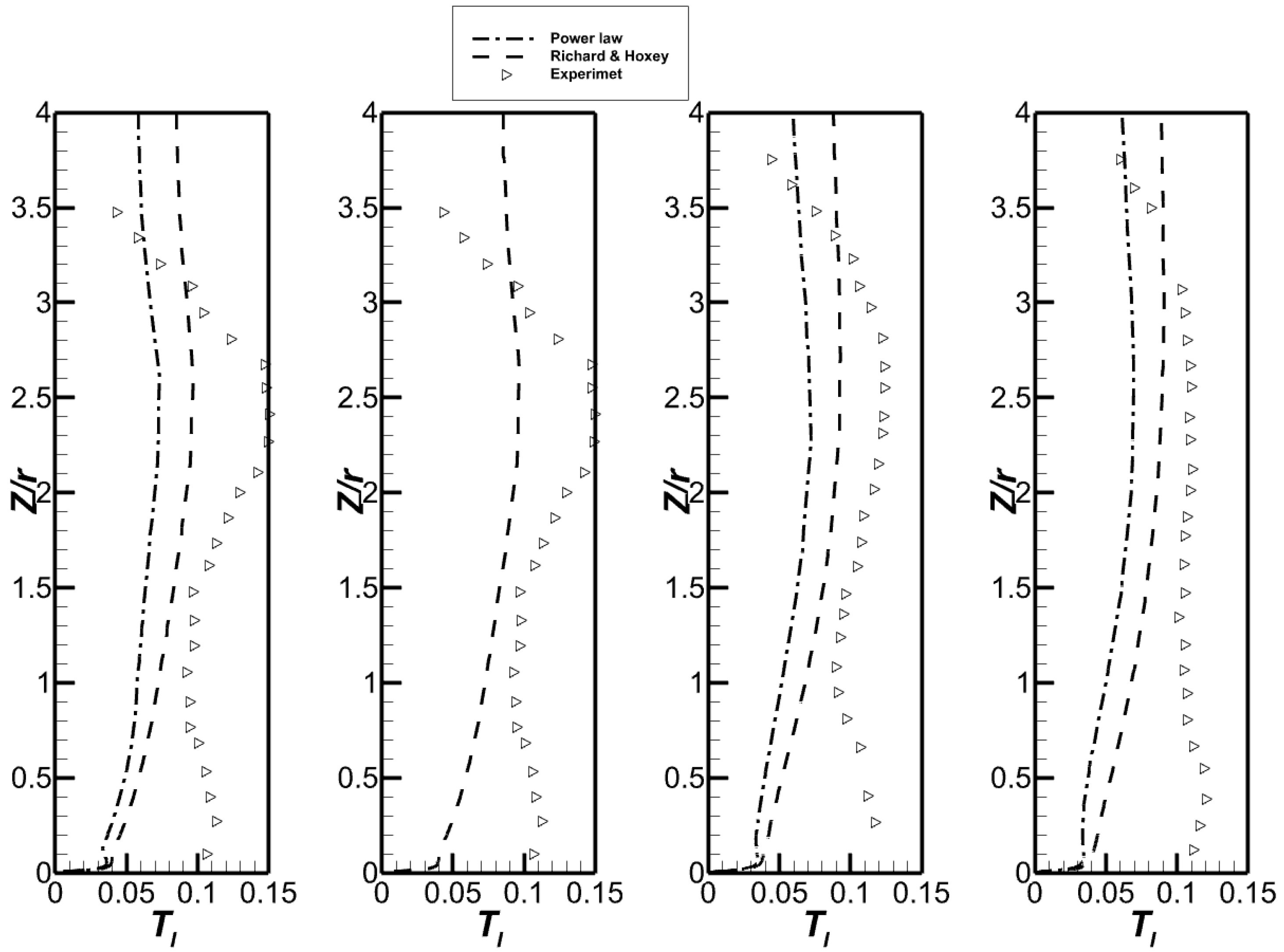
2.3. Validation Data
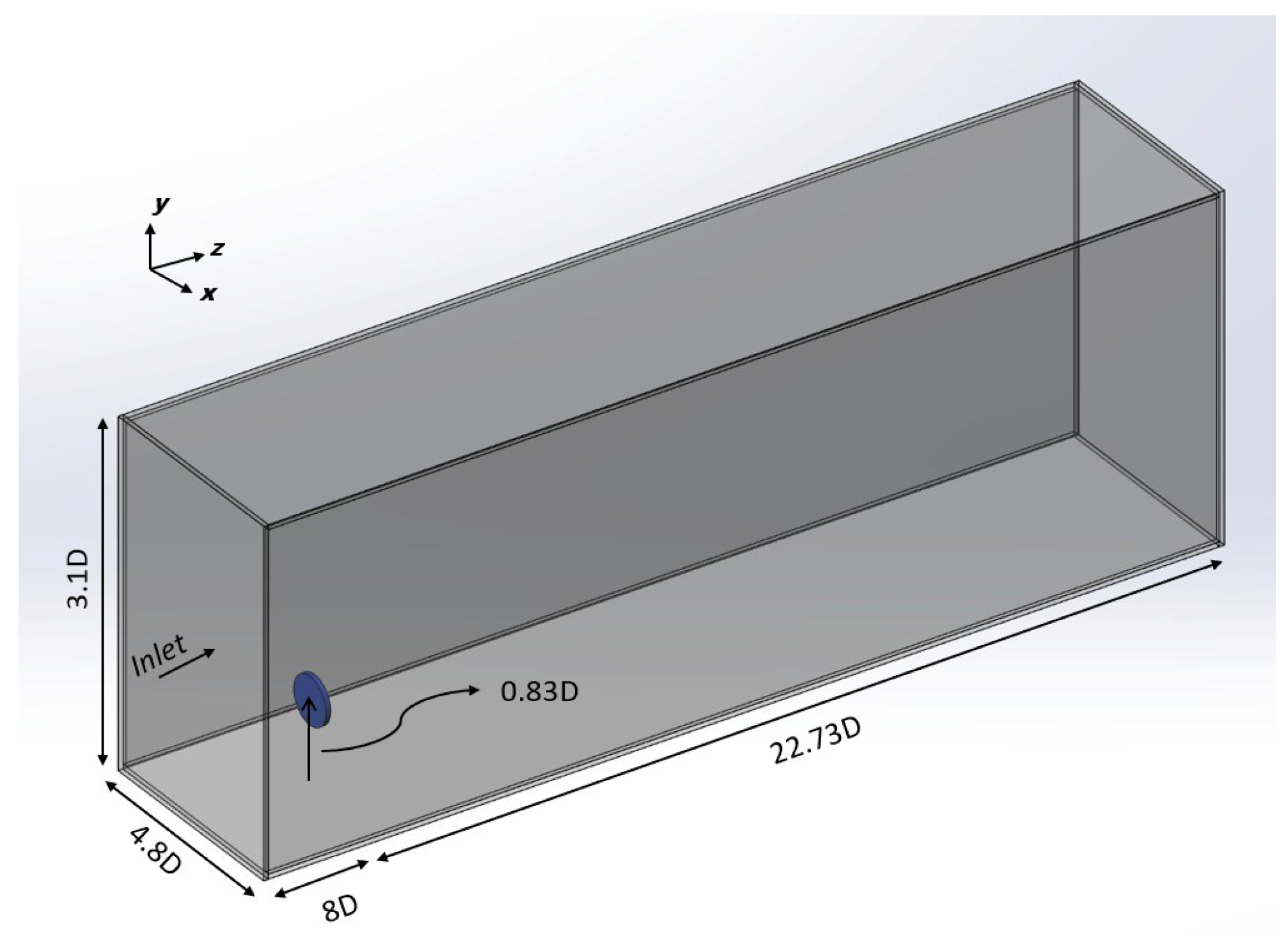
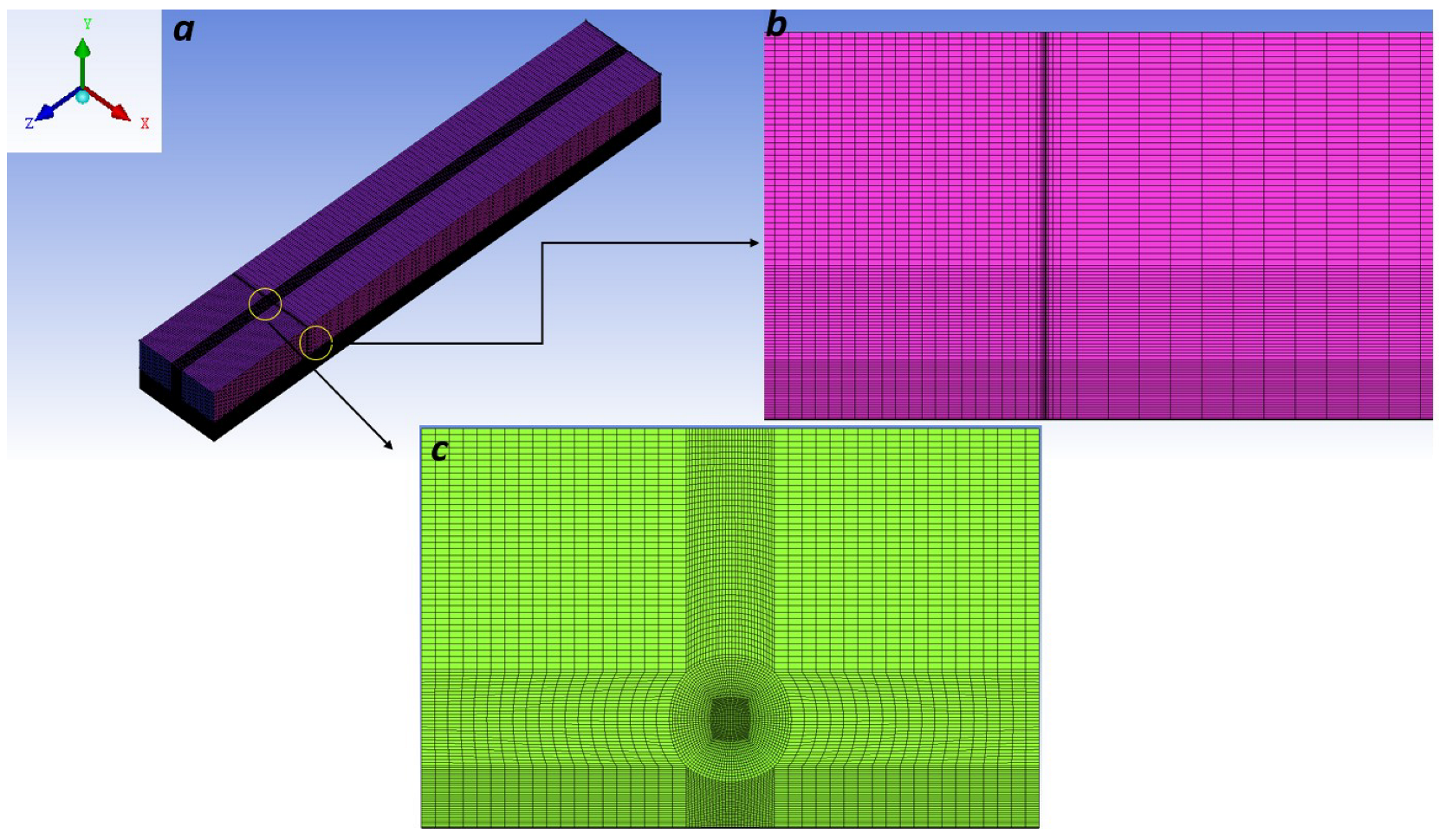
2.4. Computational Settings
2.4.1. Inflow Conditions
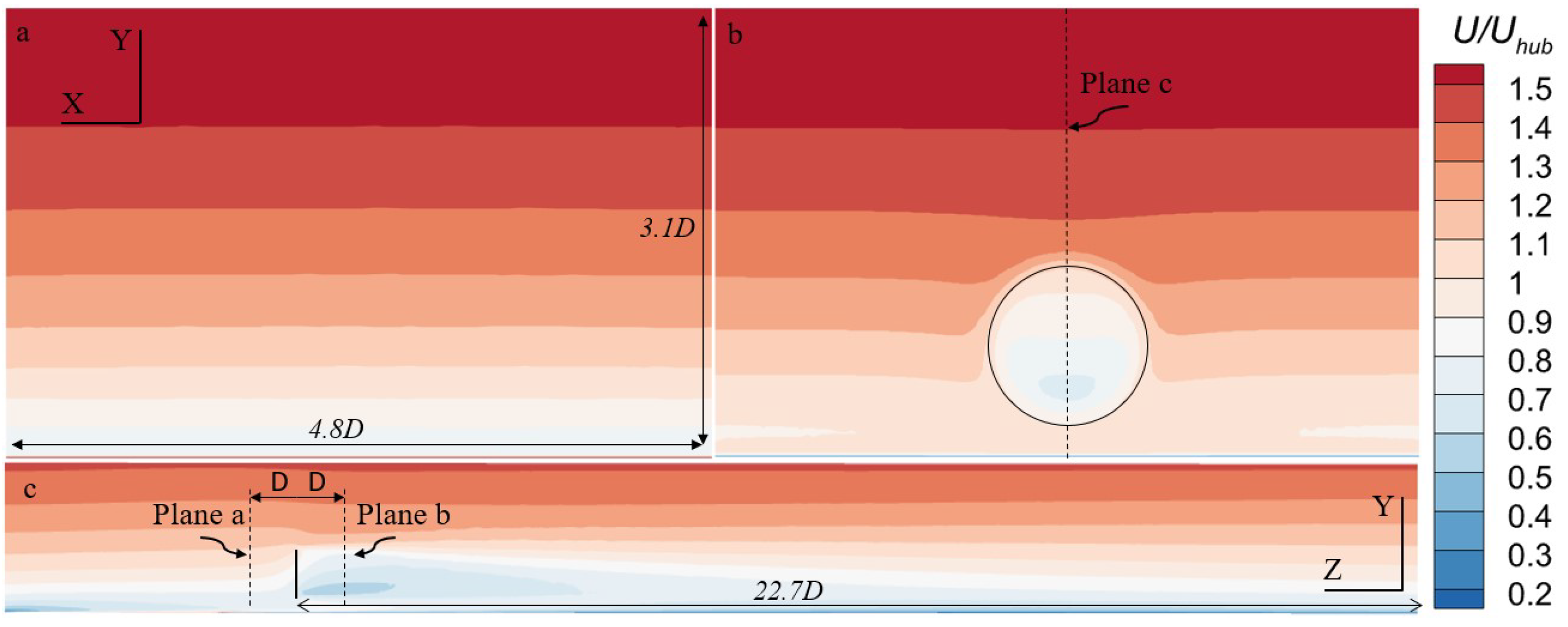
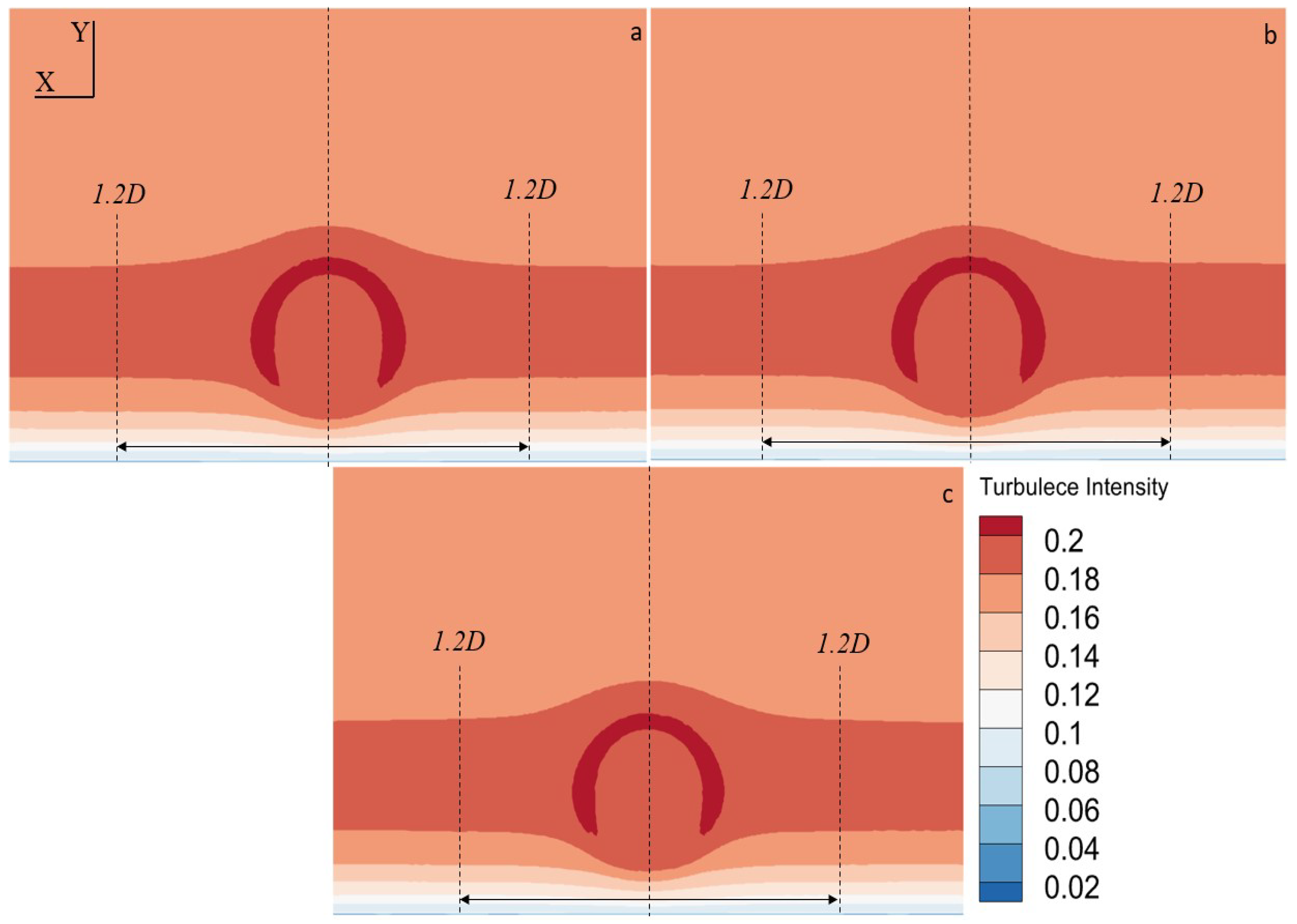
2.4.2. Horizontal Homogeneity
3. Results and Discussion
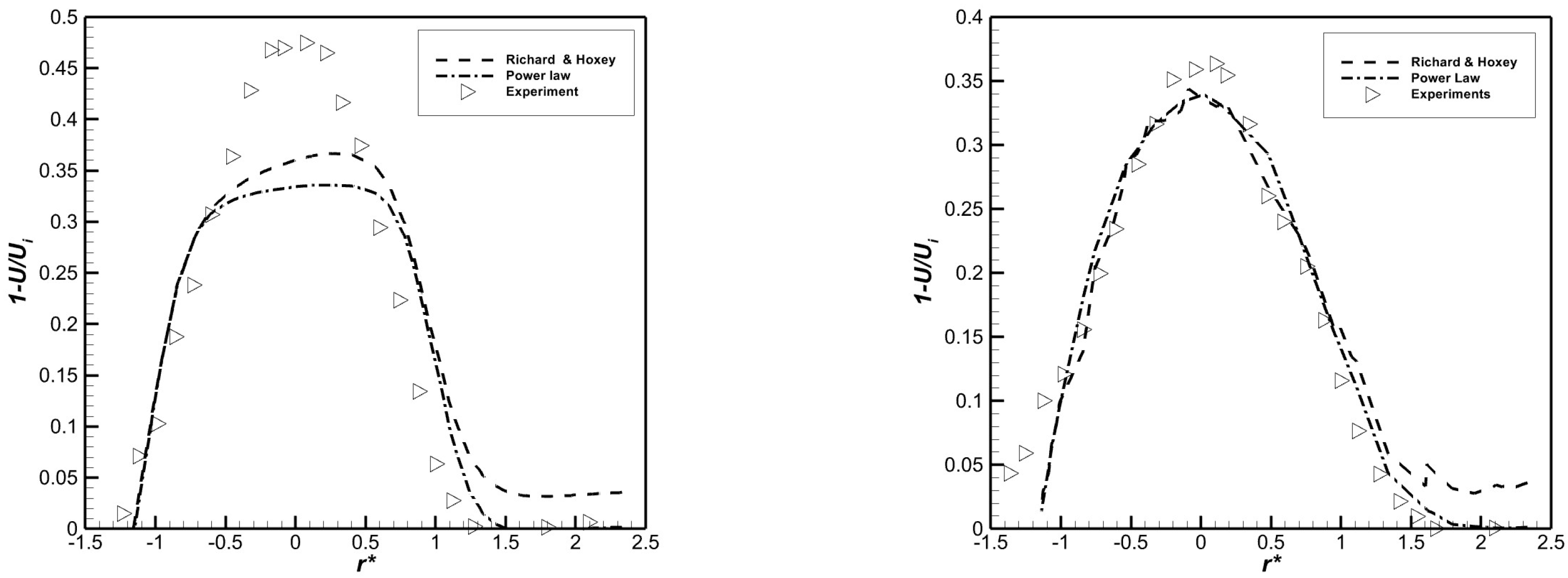
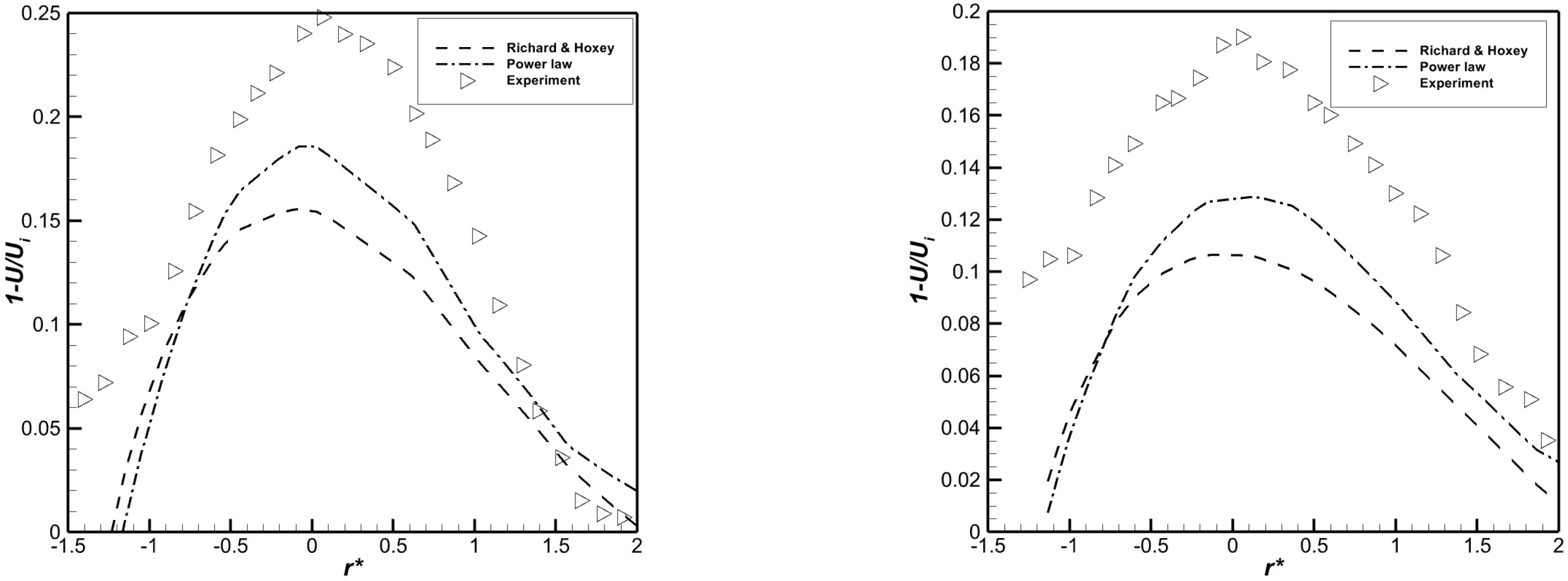
3.1. A Study of Inflow Parameters
3.2. Actuator Disk Thickness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AD | Actuator Disk |
| DRM | Direct Rotor Modelling |
| IRM | Indirect Rotor Modelling |
| BEM | Blade Element Momentum |
| AL | Actuator Line |
| AS | Actuator Surface |
| LES | Large Eddy Simulation |
| RANS | Reynolds Averaged Navier-Stokes |
| R & H | Richard & Hoxey |
| TI | Turbulence Intensity |
| Thrust Coefficient | |
| Turbine Thrust | |
| Friction Velocity | |
| Aerodynamic Surface Roughness Lengths | |
| Terrain Roughness Coefficient | |
| Boundary Layer Friction Velocity | |
| Non-dimensionalized distance from the actuator disk center | |
| Thickness Ratio | |
| Mesh size | |
| GSCR | Global Scaled Continuity Residuals |
| Continuity Residual | |
| Continuity Residual At The Current Iteration |
References
- IRENA. Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects; Report; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Froude, R.E. On the Part Played in Propulsion by Difference in Pressure. Trans. Inst. Nav. Archit. 1889, 30, 390–423. [Google Scholar]
- Sumner, J.; España, G.; Masson, C.; Aubrun, S. Evaluation of RANS/actuator disk modelling of wind turbine wake flow using wind tunnel measurements. Int. J. Eng. Syst. Model. Simul. 2013, 5, 147–158. [Google Scholar] [CrossRef]
- Antonini, E.; Romero, D.; Amon, C. Improving CFD wind farm simulations incorporating wind direction uncertainty. Renew. Energy 2018, 133, 1011–1023. [Google Scholar] [CrossRef]
- Glauert, H. Airplane Propellers. In Aerodynamic Theory: A General Review of Progress under a Grant of the Guggenheim Fund for the Promotion of Aeronautics; Durand, W.F., Ed.; Springer: Berlin/Heidelberg, Germany, 1935; pp. 169–360. [Google Scholar] [CrossRef]
- Lin, M.; Porté-Agel, F. Large-Eddy Simulation of Yawed Wind-Turbine Wakes: Comparisons with Wind Tunnel Measurements and Analytical Wake Models. Energies 2019, 12, 4574. [Google Scholar] [CrossRef]
- Lavaroni, L.; Watson, S.; Cook, M.; Dubal, M. A comparison of actuator disc and BEM models in CFD simulations for the prediction of offshore wake losses. J. Phys. Conf. Ser. 2014, 524, 012148. [Google Scholar] [CrossRef]
- Sorrensen, J.N.; Shen, W.Z. Numerical Modeling of Wind Turbine Wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2009. [Google Scholar]
- Richards, P.J.; Norris, S.E. Appropriate boundary conditions for computational wind engineering models revisited. J. Wind Eng. Ind. Aerodyn. 2011, 99, 257–266. [Google Scholar] [CrossRef]
- Richards, P.J.; Hoxey, R.P. Appropriate boundary conditions for computational wind engineering models using the k-ϵ turbulence model. J. Wind Eng. Ind. Aerodyn. 1993, 46–47, 145–153. [Google Scholar] [CrossRef]
- Japan, A.I.O. Guidebook for CFD Predictions of Urban Wind Environment; Architectural Institute of Japan: Tokyo, Japan, 2007. [Google Scholar]
- Mattar, S.J.; Kavian Nezhad, M.R.; Versteege, M.; Lange, C.F.; Fleck, B.A. Validation Process for Rooftop Wind Regime CFD Model in Complex Urban Environment Using an Experimental Measurement Campaign. Energies 2021, 14, 2497. [Google Scholar] [CrossRef]
- Kavian Nezhad, M.R.; Lange, C.F.; Fleck, B.A. Performance Evaluation of the RANS Models in Predicting the Pollutant Concentration Field within a Compact Urban Setting: Effects of the Source Location and Turbulent Schmidt Number. Atmosphere 2022, 13, 1013. [Google Scholar] [CrossRef]
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Effect of rotor–tower interaction, tilt angle, and yaw misalignment on the aeroelasticity of a large horizontal axis wind turbine with composite blades. Wind Energy 2020, 23, 1578–1595. [Google Scholar] [CrossRef]
- Syed Ahmed Kabir, I.F.; Ng, E. Effect of different atmospheric boundary layers on the wake characteristics of NREL Phase VI Wind Turbine. Renew. Energy 2018, 130, 1185–1197. [Google Scholar] [CrossRef]
- Cabezón, D.; Migoya, E.; Crespo, A. Comparison of turbulence models for the computational fluid dynamics simulation of wind turbine wakes in the atmospheric boundary layer. Wind Energy 2011, 14, 909–921. [Google Scholar] [CrossRef]
- Pichandi, C.; Pitchandi, P.; Kumar, S.; Sudharsan, N.M. Improving the performance of a combined horizontal and vertical axis wind turbine for a specific terrain using CFD. Mater. Today Proc. 2022, 62, 1089–1097. [Google Scholar] [CrossRef]
- Tian, W.; Zheng, K.; Hu, H. Investigation of the wake propagation behind wind turbines over hilly terrain with different slope gradients. J. Wind Eng. Ind. Aerodyn. 2021, 215, 104683. [Google Scholar] [CrossRef]
- Song, Y.L.; Tian, L.L.; Zhao, N. Numerical simulation and model prediction of complex wind-turbine wakes. J. Chin. Inst. Eng. 2021, 44, 627–636. [Google Scholar] [CrossRef]
- Ichenial, M.M.; Elhajjaji, A. A study of the wind turbine wake dynamics in the neutral boundary layer using large eddy simulation. Procedia Manuf. 2019, 32, 775–785. [Google Scholar] [CrossRef]
- Naderi, S.; Parvanehmasiha, S.; Torabi, F. Modeling of horizontal axis wind turbine wakes in Horns Rev offshore wind farm using an improved actuator disc model coupled with computational fluid dynamic. Energy Convers. Manag. 2018, 171, 953–968. [Google Scholar] [CrossRef]
- Sedaghatizadeh, N.; Kelso, R.; Cazzolato, B.; Ghayesh, M.; Arjomandi, M. The effect of the boundary layer on the wake of a horizontal axis wind turbine. Energy 2019, 182, 1202–1221. [Google Scholar] [CrossRef]
- Tian, L.; Song, Y.; Zhao, N.; Shen, W.; Zhu, C.; Wang, T. Effects of turbulence modelling in AD/RANS simulations of single wind and tidal turbine wakes and double wake interactions. Energy 2020, 208, 118440. [Google Scholar] [CrossRef]
- Uchida, T.; Taniyama, Y.; Fukatani, Y.; Nakano, M.; Bai, Z.; Yoshida, T.; Inui, M. A New Wind Turbine CFD Modeling Method Based on a Porous Disk Approach for Practical Wind Farm Design. Energies 2020, 13, 3197. Available online: https://www.mdpi.com/1996-1073/13/12/3197 (accessed on 1 November 2022). [CrossRef]
- Boni Cruz, L.E.; Carmo, B. Wind farm layout optimization based on CFD simulations. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 433. [Google Scholar] [CrossRef]
- Chiang, Y.C.; Hsu, Y.C.; Chau, S.W. Power Prediction of Wind Farms via a Simplified Actuator Disk Model. J. Mar. Sci. Eng. 2020, 8, 610. [Google Scholar] [CrossRef]
- Hamlaoui, M.N.; Smaili, A.; Dobrev, I.; Pereira, M.; Fellouah, H.; Khelladi, S. Numerical and experimental investigations of HAWT near wake predictions using Particle Image Velocimetry and Actuator Disk Method. Energy 2022, 238, 121660. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Micallef, D. Wake interactions of two tandem floating offshore wind turbines: CFD analysis using actuator disc model. Renew. Energy 2021, 179, 859–876. [Google Scholar] [CrossRef]
- Richmond, M.; Antoniadis, A.; Wang, L.; Kolios, A.; Al-Sanad, S.; Parol, J. Evaluation of an offshore wind farm computational fluid dynamics model against operational site data. Ocean. Eng. 2019, 193, 106579. [Google Scholar] [CrossRef]
- Tian, L.; Song, Y.; Zhao, N.; Shen, W.; Wang, T. AD/RANS Simulations of Wind Turbine Wake Flow Employing the RSM Turbulence Model: Impact of Isotropic and Anisotropic Inflow Conditions. Energies 2019, 12, 4026. [Google Scholar] [CrossRef]
- Creech, A.; Früh, W.G.; Maguire, A.E. Simulations of an Offshore Wind Farm Using Large-Eddy Simulation and a Torque-Controlled Actuator Disc Model. Surv. Geophys. 2015, 36, 427–481. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Modeling turbine wakes and power losses within a wind farm using LES: An application to the Horns Rev offshore wind farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
- Moens, M.; Duponcheel, M.; Winckelmans, G.; Chatelain, P. LES of wind farm response to transient scenarios using a high fidelity actuator disk model. J. Phys. Conf. Ser. 2016, 753, 032053. [Google Scholar] [CrossRef]
- Behrouzifar, A.; Darbandi, M. An improved actuator disc model for the numerical prediction of the far-wake region of a horizontal axis wind turbine and its performance. Energy Convers. Manag. 2019, 185, 482–495. [Google Scholar] [CrossRef]
- Simisiroglou, N.; Karatsioris, M.; Nilsson, K.; Breton, S.; Ivanell, S. The Actuator Disc Concept in Phoenics. Energy Procedia 2016, 94, 269–277. [Google Scholar] [CrossRef]
- Chamorro, L.; Porté-Agel, F. A Wind-Tunnel Investigation of Wind-Turbine Wakes: Boundary-Layer Turbulence Effects. Bound.-Layer Meteorol. 2008, 132, 129–149. [Google Scholar] [CrossRef]
- Stevens, R.; Martínez-Tossas, L.; Meneveau, C. Comparison of wind farm large eddy simulations using actuator disk and actuator line models with wind tunnel experiments Turbulence Effects. Renew. Energy 2018, 116, 470–478. [Google Scholar] [CrossRef]
- Chamorro, L.; Porté-Agel, F. Effects of Thermal Stability and Incoming Boundary-Layer Flow Characteristics on Wind-Turbine Wakes: A Wind-Tunnel Study. Bound.-Layer Meteorol. 2010, 136, 515–533. [Google Scholar] [CrossRef]
- Uchida, T. Design Wind Speed Evaluation Technique in Wind Turbine Installation Point by Using the Meteorological and CFD Models. J. Flow Control. Meas. Vis. 2018, 6, 168–184. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Bouras, I.; Ma, L.; Ingham, D.; Pourkashanian, M. An improved k-ω turbulence model for the simulations of the wind turbine wakes in a neutral atmospheric boundary layer flow. J. Wind Eng. Ind. Aerodyn. 2018, 179, 358–368. [Google Scholar] [CrossRef]
- Gargallo-Peiró, A.; Avila, M.; Owen, H.; Prieto-Godino, L.; Folc, A. Mesh generation, sizing and convergence for onshore and offshore wind farm Atmospheric Boundary Layer flow simulation with actuator discs. J. Comput. Phys. 2018, 375, 209–227. [Google Scholar] [CrossRef]
- Ansys, Inc. Ansys Fluent User’s Guide; Ansys, Inc.: Canonsburg, PA, USA, 2022; p. 5864. [Google Scholar]




| Author | Method | Inflow Condition |
|---|---|---|
| Santo et al. [15] | Direct rotor Modelling | Richard & Hoxey |
| Fazil et al. [16] | Direct rotor Modelling | Richard & Hoxey |
| Cabezón et al. [17] | Actuator Disk | Richard & Hoxey |
| Pichandi et al. [18] | Actuator Disk | Richard & Hoxey |
| Tian et al. [19] | Actuator Disk—BEM | Richard & Hoxey |
| Song et al. [20] | Actuator Disk | Richard & Hoxey |
| Ichenial et al. [21] | Direct rotor Modelling | Richard & Hoxey |
| Naderi et al. [22] | Actuator Disk—BEM | Richard & Hoxey |
| Sedaghatizadeh. [23] | Direct rotor Modelling | Power Law |
| Tian et al. [24] | Actuator Disk | Power Law |
| Uchida et al. [25] | Direct rotor Modelling | Power Law |
| Surface Type | ||
|---|---|---|
| Rough | 1.2 mm | 0.16 m/s |
| Smooth | 0.05 mm | 0.11 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
RahnamayBahambary, K.; Fleck, B.A. Effects of Inflow Parameters and Disk Thickness on an Actuator Disk inside the Neutral Atmospheric Boundary Layer. Wind 2022, 2, 733-746. https://doi.org/10.3390/wind2040038
RahnamayBahambary K, Fleck BA. Effects of Inflow Parameters and Disk Thickness on an Actuator Disk inside the Neutral Atmospheric Boundary Layer. Wind. 2022; 2(4):733-746. https://doi.org/10.3390/wind2040038
Chicago/Turabian StyleRahnamayBahambary, Khashayar, and Brian A. Fleck. 2022. "Effects of Inflow Parameters and Disk Thickness on an Actuator Disk inside the Neutral Atmospheric Boundary Layer" Wind 2, no. 4: 733-746. https://doi.org/10.3390/wind2040038
APA StyleRahnamayBahambary, K., & Fleck, B. A. (2022). Effects of Inflow Parameters and Disk Thickness on an Actuator Disk inside the Neutral Atmospheric Boundary Layer. Wind, 2(4), 733-746. https://doi.org/10.3390/wind2040038







