Abstract
Corrosion is the leading cause of failure for Offshore Wind Turbine (OWT) structures and it is characterized by a low probability of detection. With focus on uniform corrosion, we propose a corrosion detection and prognosis system coupled with a Decision Support Tool (DST) and a Graphical User Interface (GUI). By considering wall thickness measurements at different critical points along the wind turbine tower, the proposed corrosion detection and prognosis system—based on Kalman filtering, empirical corrosion models and reliability theory—estimates the Remaining Useful Life of the structure with regard to uniform corrosion. The DST provides a systematic approach for evaluating the results of the prognosis module together with economical information, to assess the different possible actions and their optimal timing. Focus is placed on the optimization of the decommissioning time of OWTs. The case of decommissioning is relevant as corrosion—especially in the splash zone of the tower—makes maintenance difficult and very costly, and corrosion inevitably leads to the end of life of the OWT structure. The proposed algorithms are illustrated with examples. The custom GUI facilitates the interpretation of results of the prognosis module and the economical optimization, and the interaction with the user for setting the different parameters and costs involved.
1. Introduction
Offshore wind energy is a fast-growing sector: in 2021, it enjoyed its best ever year (despite a second year of the COVID-19 pandemic) with a 21.1 GW commissioned worldwide, which represents three times more than the previous year. This brings the world’s total offshore capacity to 57 GW, which represents 7% of global installations. Moreover, the annual global offshore market is expected to grow from 21.1 GW in 2021 to 31.4 GW in 2026, which would result in more than 90 GW of offshore capacity to be added worldwide from 2022–2026 [1].
In comparison with onshore wind, Offshore Wind Turbines (OWTs) benefit from two main advantages for more reliable power generation: (i) higher mean wind speeds and (ii) steadier wind supply. Moreover, technology improvements and the growing maturity of the industry have driven down the total installed cost and Levelized Cost Of Electricity (LCOE) for offshore wind: between 2010 and 2019, the global weighted average LCOE of offshore wind fell 29%, from USD 0.161/kWh to USD 0.115/kWh [2].
Innovations in this industry are mostly achieved at the level of improved design and operations, to drive the LCOE down further, both by novel floating turbine designs [3,4] and improved offshore turbine foundations [5].
Nevertheless, Operation and Maintenance (O&M) costs for offshore wind farms are considerably higher than those for onshore wind due to the harsher and highly corrosive marine environment and higher costs for access to the wind site for performing maintenance (which is heavily influenced by weather conditions and the availability of skilled personnel and specialised vessels) [2].
In this context, further reducing the LCOE for offshore wind and improving its reliability becomes essential. The highly corrosive marine environment makes corrosion management and structural health monitoring a fundamental strategy for this purpose. Indeed, corrosion is a main root cause for offshore structure failure [6,7], which has the lowest probability of detection, and the biggest economical consequence in the event of failure.
Corrosion can be defined as deterioration due to electrochemical reactions between the metal and its environment. Uniform corrosion, also known as general corrosion, is defined as an evenly distributed loss of material (metal) thickness of a sheetlike, exposed surface as a function of time. It is the most frequent type of corrosion at the wind turbine base (in the splash zone), as it is augmented by the presence of both oxygen and moisture.
Although in practice some corrosion protection solutions are initially installed in offshore structures, the highly corrosive offshore conditions can still damage these solutions [8]. Hence, an improper corrosion protection follow-up and inadequate corrosion management on offshore structures can result in structural degradation, which highly impacts the achievable lifetime of OWTs and, consequently, the LCOE.
To support a systematic corrosion assessment and management of OWTs, an integrated system/solution that is able to handle corrosion monitoring data and to transform and visualize the data into actionable information is therefore required for the offshore wind energy industry. However, to the authors’ knowledge, as discussed in previous works [8,9], tools and solutions that can serve the aforementioned purpose are still very limited and not mature yet.
To remedy this gap, we propose in this paper a system that integrates a corrosion detection and prognostics system coupled with a Decision Support Tool (DST) and a Graphical User Interface (GUI). This integrated system, developed in the framework of the WATEREYE project [10], focuses on the atmospheric and splash zones of the wind turbine tower. In these zones, uniform corrosion is monitored through measurements of the wall thickness obtained by ultrasound sensors: fixed smart sensors in the splash zone, and a mobile platform in the atmospheric zone (i.e., a drone that positions a corrosion sensor on the internal side of the wall of the wind turbine) [11].
The proposed prognosis method (combining a corrosion degradation model with online measurement data) is based on Bayesian Filtering, and allows for recursive updating of the degradation model parameters and uncertainty computation of the estimated Remaining Useful Life time (RUL), in order to resolve the complexity of corrosion and, in particular, the high uncertainty of corrosion rates.
The RUL estimation (with regard to uniform corrosion) supports the decision making regarding the end of service life of the OWT, namely, life-time extension, re-powering or decommissioning. In this paper, we present an approach where the uniform corrosion RUL estimation (including its uncertainty) serves for the optimization of the decommissioning time of OWTs, considering the various costs involved and the risk related to failure.
Notably, the case of decommissioning is relevant, as corrosion (especially in the splash zone of the tower) makes maintenance (mainly focused on coating repair) difficult and very costly, and corrosion inevitably leads to End Of Life (EOL) of the OWT structure. Additionally, wind turbine decommissioning is still a largely unexplored topic mainly due to the lack of experience [12], despite the huge impact that decommissioning has on the LCOE.
Given the important challenges posed by the natural difficulties and constraints of the offshore environment, the required decisions in a wind turbine EOL scenario become more critical offshore, and the decommissioning planning should be completed years (e.g., a decade) in advance [13]. In this sense, the proposed method aims at providing a long-term to mid-term (i.e., scale of years) view of the optimal decommissioning time that enables improved preparation and planning of decommissioning. Short-term (i.e., scale of weeks) optimization of tasks (e.g., scheduling of tasks) may be addressed based on more detailed costs information and less uncertain weather forecast (e.g., [14]).
1.1. Main Contributions
The scientific contributions detailed in this paper are threefold: (1) the development and application of a methodology capable of remotely estimating the current and future corrosion both at the component level (i.e., some important locations, the tower, splash-zone, and tower-platform junction) and system level, (2) the improvement of two objective cost functions based on the total cost of ownership (TCO) and the levelised cost of energy (LCOE) taking into account the stochastic remaining useful life (RUL) estimates and risk aversion, (3) the development of a custom graphical tool for predictive maintenance decision support, which determines the economically best time for decommissioning wind turbine towers due to corrosion. This decommissioning time is obtained by the optimisation of the improved objective cost functions.
1.2. Paper Organisation
The remainder of this paper is organized as follows. The architecture overview of the developed tool is discussed in Section 2. The methodology and developed algorithms for corrosion detection and prognosis, and DST are presented in Section 3 and Section 4, respectively. Section 5 presents the design and implementation details of the GUI. Finally, the main conclusions are presented in Section 6.
2. Overview of the Developed System
The architecture of the developed system is graphically illustrated in Figure 1. This system works as follows. First, the corrosion detection and Remaining-Useful-Life (RUL) estimation are performed at different critical points along the tower. This estimation is based on Kalman filtering and an empirical corrosion model and it consists of a corrosion detection phase followed by a corrosion prognosis phase. Later, the local RUL estimates are aggregated to obtain a system-level RUL estimate, with a definition of system failure based on reliability theory.
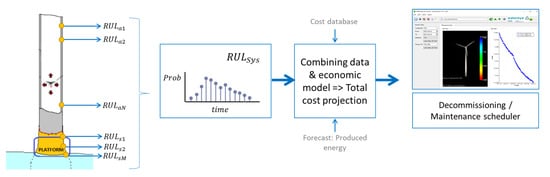
Figure 1.
Overview of the corrosion detection and prognostic system coupled with the decision support tool.
Next, the system-level prognosis information is processed by the DST, which provides a systematic approach for evaluating the results of the prognosis module together with economical information and the long-term forecast of the produced energy to assess the various possible actions and their optimal timing. For this purpose, we consider a risk-based economical optimization.
Finally, the capability of the GUI that was developed previously [9] has been extended to enable to present the results of the corrosion detection and prognosis module and the economical optimization. This extended GUI facilitates the interpretation of results using 3D visualization of the corrosion status along the wind turbine tower, and 2D graphics presenting the evolution in time of historical data and the prognostics results. This GUI also facilitates the interaction with the user for setting the different parameters and costs involved in the economical optimization.
3. Corrosion Detection and Prognosis
In this section, we first present the proposed methodology for the corrosion detection and prognosis on wind turbine structures. Later, the algorithms for the local corrosion detection and prognosis, and the system-level prognosis are discussed.
3.1. Methodology
The corrosion detection and prognosis are based on wall thickness measurements, obtained via the ultrasound technique [11], and the depletion of the Corrosion Allowance (CA). Corrosion allowance (CA) is the additional material thickness that the manufacturer includes that may be corroded away without causing structural issues, as even without it, enough material thickness is available to guarantee structural stability. The initial material thickness is the reference thickness. When the corrosion allowance is corroded away, the critical, minimal thickness of the material remains. See, e.g., [8] for a more in-depth explanation.
For primary steel structures (structures where failure has significant consequences, such as tower or flanges) the CA can be calculated as:
where is the maximum expected corrosion rate, is the expected useful design lifetime of the coating and is the design lifetime of the structure [15].
For the prognosis module, the End-Of-Life (EOL) for a given location in the tower is defined as the date on which a wall thickness smaller than the critical wall thickness, which is equal to the nominal wall thickness of which half of the corrosion allowance, is reached, where the corrosion allowance (CA) is completely lost over the full-service life without decommissioning phase (see [16]).
Indeed, this criterion is followed as the fatigue calculations for the design of wind turbine support structures are based on this critical wall thickness. This implies that a wall thickness smaller than the critical wall thickness can consequently lead to the appearance of catastrophic structural failures, depending on the chosen design philosophy (i.e., on the safety factors used for the fatigue design, see [16]). Note that this critical wall thickness should be provided by the manufacturer of the WT tower structure, as it is a parameter linked to the structural design of the tower to ensure mechanical stability.
Note that the corrosion prognosis of the wind turbine structure proposed in this work follows a distributed approach [17]: the system-level prognostics problem is decomposed into several independent local prognostics sub-problems that are solved in parallel. These local prognostic results (corresponding to the above mentioned EOL assessment for different locations in the tower) are regarded as component-level prognosis, which are then merged to obtain the system-level prognostics solution by means of reliability theory. This distributed approach facilitates the prognosis: the algorithms are simplified, providing scalability, efficiency, and flexibility for adding or removing measurement locations.
3.2. Local Detection and Prognosis
In this subsection, we discuss an approach for corrosion detection and corrosion prognosis for a fixed location of the wind turbine structure. We assume here that for this fixed location, the wall thickness is measured at least once per month using ultrasound sensors (either with fixed ultrasound sensors or with a sensor attached to a drone), in order to obtain sufficiently accurate estimates in the face of various noise sources (including measurement noise).
3.2.1. Corrosion Detection
Ultrasound sensors provide a way to measure the thickness of the steel part of a WT wall structure, but not the thickness of the coating. Since the wall thickness of the steel remains unchanged until the coating is fully degraded (after which corrosion starts), it is important to detect this onset of corrosion both reliably (no false positives) and early (few false negatives). By doing this, corrosion prognosis will be performed more accurately.
The approach we recall here (see [18]) does not assume that the initial wall thickness at the start of the commissioning of the wind turbine is known. Indeed, due to engineering tolerances the actual wall thickness might deviate from the design sufficiently to have either false positives right from the start or very late corrosion onset detection. Instead, we estimate the initial wall thickness by combing all measurements (e.g., by taking the mean) over a relatively short period of time after the start of commissioning where we may assume that the coating has not been fully degraded. In addition to the potential improvement in accuracy, it avoids the need of manually providing an initial wall thickness estimate.
Based on the estimated initial wall thickness , we set a threshold such that we consider corrosion to be detected once the wall thickness estimation drops below this threshold. More specifically, we set , where is a suitably chosen length (e.g., 1 mm), which can be tuned if either the measurement noise or historical measurement data of the ultrasound sensor is known.
The crucial aspect of this approach is the estimation of wall thickness given wall thickness measurements. Indeed, due to measurement noise, simply taking the last wall thickness measurement as the estimated wall thickness is an unreliable method, since a single measurement value might well be smaller than without the onset of corrosion. To obtain reliable results, one can employ a well-known paradigm called Bayesian filtering (e.g., Kalman filtering) to obtain an estimate that also takes into account previous measurements. Here, recent measurements have the most influence on the estimated wall thickness to be able to adapt to changes (in this case, the onset of corrosion), while the use of multiple measurements (in fact, all measurements) provides reliability.
3.2.2. Corrosion Prognosis
In the previous subsection, we recalled that Bayesian filtering is a means of providing a more accurate estimation of the current wall thickness compared to simply taking the last measurement value. In fact, Bayesian filtering allows one to not only provide an estimate of the current state, but also an estimate of the future states. The reason for this is that Bayesian filtering does not only keep track of the current wall thickness estimate, but it keeps track of a representation of the state of the system within some model which can be extrapolated into the future. More specifically, Bayesian filtering requires as input a model of the system over time, which may have unknown empirical constants. For example, consider the Pourbaix corrosion model [19] for bare steel:
where is the wall thickness at time , is (as before) the initial wall thickness, and A and p are empirical constants. In this case, Bayesian filtering does not directly keep track of an estimation the current wall thickness , but instead keeps track of the current estimates of A, t, and p, from which can be computed (we assume here that is fixed and provided by the corrosion detection method described above). Bayesian filtering uses its current state estimate at the current time to compute to a preliminary (called a priori) estimate of the next state, where and since A and p are constants and (one unit of time later). Next, the value is combined with the next measurement at time (the way to perform this computing depends on the type of Bayesian filtering), taking into account process and measurement noise estimates, to obtain a final (called a posteriori) estimate for the next state.
Various types of Bayesian filtering methods exist. For example, Kalman filtering [20] is a fast and optimal method in case the state transition function (i.e., the function mapping a state to the a priori estimate of the next state) is linear, the measurement function (i.e., the function mapping a state to its most likely measurement value) is linear, and the process noise and measurement noise are Gaussian. Extensions such as unscented Kalman filtering exist for addressing the case where the state transition function and measurement function are not necessarily linear. In [21], a performance comparison is made of corrosion prognosis algorithms resulting from using a linear corrosion model as the underlying state model and Kalman filtering compared to using an involved corrosion model, called the bimodal corrosion model [22], as the underlying state model and unscented Kalman filtering. In [18], this comparison was extended to include a corrosion prognosis algorithm using the Pourbaix corrosion model and unscented Kalman filtering. Indeed, there is a natural balance between model complexity and the ability to estimate the parameters of the model accurately given the amount of measurements available. In particular, it was observed in [18] that the prognosis algorithm that is based on the Pourbaix corrosion model (which in terms of complexity resides in between the linear corrosion model and the bimodal corrosion model) obtains highest accuracy, where the remaining useful life --accuracy metric was used.
Corrosion prognosis is achieved by extrapolation, i.e., by iteratively computing a priori estimates of next states. In the example, since A and p are constants, this amounts to using the formula . Moreover, Bayesian filtering keeps track of a probability distribution describing for each possible state the likelihood that state is the actual state of the system. In this way, we can compute, e.g., a 90% confidence interval for the current state and future states (for the latter assuming non-dominant process noise). The probability distributions computed at all monitored positions locally is used as input to the system-level prognosis step described in the next section (see Section 3.3).
Figure 2 illustrates corrosion prognosis at a particular point in time. The (simulated) wall thickness measurements (red dots) together with the Pourbaix corrosion model obtains, using Bayesian filtering (in this case unscented Kalman filtering), an estimate of the current state and indirectly an estimate of the current wall thickness (green line). Prognosis (purple line) is obtained by extrapolating the current state. By extrapolating the probability distribution of the current state, we obtain a probability distribution of the remaining useful life (bottom plot, assuming a given EOL wall thickness threshold) and the confidence interval in the top plot. The (simulated) ground truth is plotted for reference.
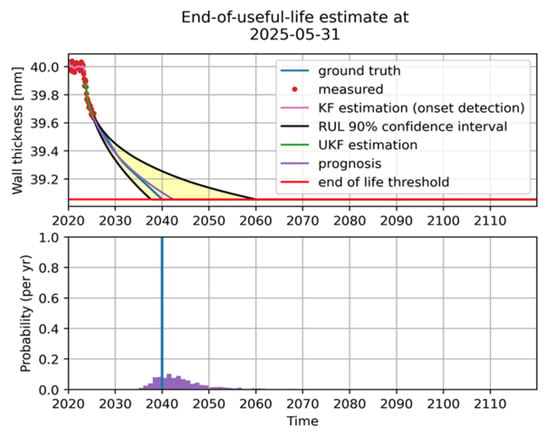
Figure 2.
Output of the corrosion prognosis algorithm based on the power-law corrosion model on (simulated) measurement data, along with the ground truth for reference.
3.3. System-Level Prognosis
The output of the Local Prognosis described in the previous subsection is a probability distribution of the RUL for a given measurement location on the tower (i.e., local RUL). It is assumed that the measurement locations are not close to each other, so that each local RUL estimation represents the status of a part or component of the monitored tower. Note that the locations may belong to areas characterized by different corrosivity (e.g., the atmospheric or splash zones) and/or different critical wall thicknesses.
This subsection presents the computation of the system-level RUL, which is derived through reliability theory. In the following, we refer to the failure probability distribution , its cumulative distribution function called unreliability (representing the probability that the component fails at or before time t), and the complementary function of is called reliability (i.e., ). Note that the information provided by the local prognosis (i.e., the probability distribution of the time of failure) corresponds to , which is called the RUL if it is referenced with respect to the present time or EOL if it is referenced with respect to a fixed time ().
In the reliability theory, a system is modelled as the interconnection of n components. The most common configuration of components is in series (i.e., the system is good if all n components are good) or parallel (i.e., the system is good if at least one component is good). However, other configurations are possible, such as k-out-of-n or weighted k-out-of-n. For the latter, each component has its own positive integer weight, such that the system is considered good if the total weight of good components is at least k [23]. Note that k-out-of-n is a special case of the weighted k-out-of-n (wherein the weight of each component is 1), 1-out-of-n is equivalent to a parallel connection, and n-out-of-n represents a series connection. The algorithm for computing the system reliability for a weighted k-out-of-n system is described in [23]. Note that for the computation of the system , it is assumed that the components are independent.
Clearly, the structure to be chosen for the system depends on the application (preserving a close relation to a physical meaning) and the definition of system failure. The series connection gives the most strict definition of system failure (the system fails if any component fails), resulting in the most conservative system-level RUL estimate. From a structural point of view, this system failure definition may be too restrictive and a more relaxed definition may be more appropriate for some purposes and partially redundant designs.
Therefore, we propose a flexible structure for defining the system reliability, namely, the system may consist of subsystems, which at the same time may consist of other subsystems, and so on (in a nested way). The reliability of a given (sub)system is then modelled by a weighted k-out-of-n structure. This is better expressed as a tree structure (see an illustration in Figure 3), where each parent node has a k value, and child nodes have an associated weight w. The leaves of such a tree correspond to the components, whose un-reliabilities are associated with the local RULs of the measurement locations. In addition to flexibility, the proposed structure allows for a systematic and easy calculation of the system reliability departing from the algorithms described in [23].
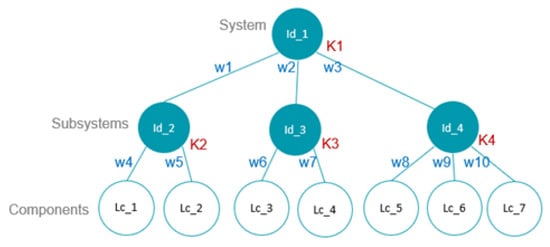
Figure 3.
Tree structure for computing the system-level reliability.
This structure supports as many branches and depth levels as necessary. However, a subsystem or component may only have one parent, since the principle of independence of components (and subsystems) must be preserved. Note that the actual tuning of the model requires a structural study of the tower. The user may define the structure of this tree according to a structural study of the tower, or they may choose the default option series configuration, which leads to a strict definition of system failure.
Examples of reliability studies for structural applications may be found in references 1–12 of [24]. Here, we present a rationale to illustrate the suitability of this flexible structure for computing the system reliability (see Figure 4). For a given measurement location, the prognosis module estimates the local RUL due to (uniform) corrosion, which characterizes the status of a delimited area of the tower. We may then define a section of the tower, for which we can measure at multiple locations, and consider the tower as an arrangement of sections with different weights or contributions to the system reliability. These weights may be related, for instance, to structural properties such as load levels.
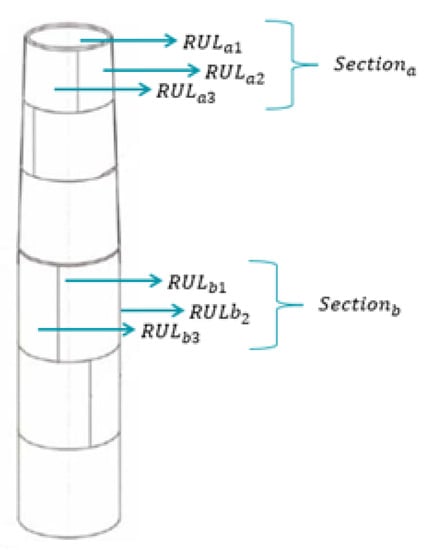
Figure 4.
Illustration of computation of system reliability for the tower.
Figure 5 illustrates the computation of the system-level unreliability for a system with five components (i.e., measured locations). The component-level unreliabilities were obtained through the algorithms described in Section 3.2 for simulated corrosion processes started at month ‘January 2010’ and described by (2) with different parameters and noise levels. The shown prognosis data correspond to the estimated EOL for the components at month ‘January 2038’. The system-level unreliability is presented for two different definitions of system failure: 3-out-of-5 and series configurations (for which the tree structures definitions of Figure 3 are straight forward). From Figure 5, it can be seen that indeed, the series configuration leads to the most conservative EOL, with a 50th percentile at month ‘2040-01’ instead of the ‘August 2040’ obtained for the 3-out-of-5 configuration.
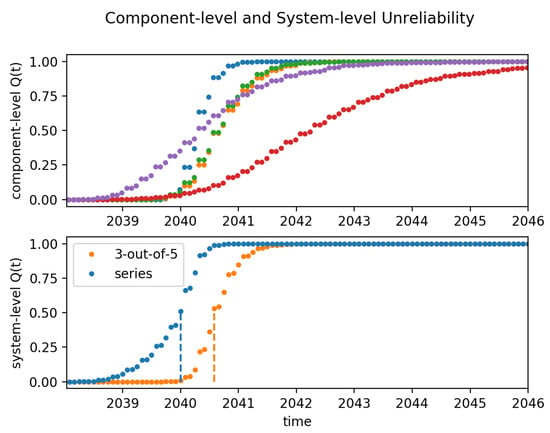
Figure 5.
Component-level Top pane: Component system Unreliabilities (top pane, 5 components each depicted with a separate colour (including: blue, purple, orange, green, and red) and Bottom pane: Resulting system-level unreliability ; with two timeseries: the series weighting of all component level unreliabilities (blue line) versus a weighting of the risk of failure of 3 out of 5 components (orange line), using the k-out-of-n: Good System Method. (blue line:) 5-out-of-5 (series connection) gives a 50th percentile at month ‘January 2040’; (orange line:) 3-out-of-5 gives a 50th percentile at month ‘August 2040’.
In the following section, the system-level prognosis distribution, resulting from the algorithms above described, is handled by the Decision Support Tool.
4. Decision Support Tool
This section presents the design of the Decision Support Tool (DST). More precisely, it presents the proposed economical optimization algorithm.
4.1. Economical Optimization
Unlike other turbine components, for practical reasons, the tower as a whole cannot be replaced, as related costs are prohibitively high, and often comparable to those of a new installation. Therefore, the RUL with regard to structural corrosion of the turbine tower is directly linked to the RUL of the wind turbine as a whole.
Most of the maintenance optimization algorithms in the literature start from the assumption that a component can be replaced or restored to an initial fault free condition (e.g., [25,26,27,28,29,30]). This is not the case for corrosion of the tower. Maintenance actions are mainly focused on repairing the corrosion protective coating, which are local solutions, very costly and even not practical in the case of an imminent failure in the splash zone. The corrosion allowance may not be restored to its initial condition, and eventually, severe corrosion can lead to the EOL of the turbine.
In this sense, the economical optimization should consider the complete lifetime and economic value of the asset, as the fault phenomena under study affect directly the total lifetime of the wind turbine. With focus on the optimization of the time of decommissioning, we describe below the proposed economical optimization based on an objective cost function that meets this evaluation criterion.
A first common metric, widely used in the wind energy sector, is the Levelized Cost of Electricity (LCOE). It corresponds to the ratio of lifetime costs to lifetime electricity generation, both of which are discounted back to a common year using a discount rate [2]. The lifetime costs may be classified as capital costs (), operational and maintenance costs (), and decommissioning costs () [31], resulting in the following expression for the LCOE:
where E is the produced energy, and , , , and are the discount rates for , , , and E respectively, which the end-user may define separately or set to a common discount rate r. Note that t corresponds to a time duration in months, as this is the time resolution set for the prognosis module. is the time of decommissioning, and is the actual time of failure (i.e., the structural end-of-life, for which an estimate is provided by the prognosis module). Here, n is the evaluation horizon for the LCOE, namely, the maximum structural lifetime of the wind turbine. In this analysis, we assume that the structural lifetime is the only active stochastic process, and all other effects of ageing are lumped in maintenance costs or income variations.
The discount rates are usually available (and provided by the user) as effective annual rates (). Therefore, the need arises to transform them into an effective monthly rate r by means of the following formula:
Alternatively to the LCOE, another possible metric is the Total Cost of Ownership (TCO), which is the estimation of the lifetime costs of an asset, over an evaluated period of time. In our methodology, the Net present value discounting method is used. We discount the TCO down to year zero, to compensate for inflation, deflation, and wage or market price changes. As the income for produced electricity () depends on the decisions made related to maintenance, we have included it as a term in the TCO metric, calculated as:
where the negative sign in the equation before the last term containing indicates it is an income, in contrast to the other terms, which are all positive cost. Consequently, an optimal economic result aims at minimizing this function.
The proposed objective cost function may be based on these metrics, according to the end-user choice
where the notation indicates the dependence of this cost function on and .
We aim at optimizing the decommissioning time , given the time of failure provided by the prognosis module. As is a stochastic variable (described by a probability distribution), the uncertainty propagation on the should be considered for the optimization. Indeed, in a deterministic scenario, with known time of failure and known economic scenarios, the optimum minimal date can be directly found; this is not, however, the case in a stochastic framework. Figure 6 illustrates this concept: the vs. graph consists of a series of lines describing a given percentile of , hence the ambiguity in the definition of the optimal .
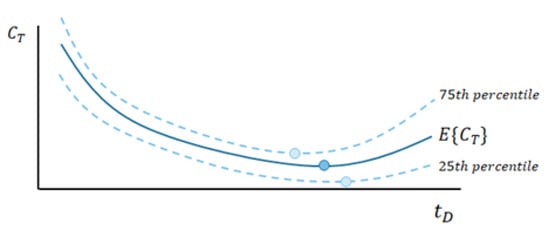
Figure 6.
Propagation uncertainty on due to the stochastic nature of .
Therefore, before the optimization, we require a function such that
so that the optimal decommissioning time can be found as
with denoting the present time. A possible choice for is, for instance, the expected value of the stochastic cost function :
From a statistical point of view, this optimization is reasonable. It represents the minimization of expected outcome of a large population of evaluations of the cost function (each one corresponding to a different realization of the stochastic variable ). However, there is a chance that, for one evaluation (i.e., one realization of ), the cost function is higher than its expected value. Aiming for the expected mean value thus entails an economical risk. This is illustrated in Figure 6: the cost may be higher than its expected value (see, for example, the 75th percentile).
Risk aversion theory [32] states that the valuation of an uncertain outcome depends not only on the expected mean outcome, but also on the personal (or company) risk-aversion factor and the distribution of potential gains or costs. To account for this, we propose an alternative function that includes a risk aversion factor as follows:
where is the k-th probability distribution percentile, and belonging to is a factor that reflects the risk aversion.
The augmentation of the objective cost function, modified through the risk aversion term , can be seen as a relative risk aversion tariff (hedging premium) that the decision maker (or company) is willing to pay, to avoid the risk of a less economically favourable scenario in case of a structural failure at (reference scenario without decommissioning action, which has a higher -assumed- incurred cost).
The hedging premium is the amount of money the asset management team should forfeit if they want to mitigate the potential impact of the risk. This premium is equal to . In this domain (wind turbine decommissioning) and for scenarios with high uncertainty, a high premium corresponds to earlier decommissioning, leading to a forfeit of potential future income.
4.2. Definitions for Economical Optimization
- Capital costs ()This cost involves the wind turbine investment (i.e., all costs related to the initial investment for bringing the wind turbine to an operable status), including the investment for implementing the monitoring and prognosis software and hardwareThese costs may be considered as a single payment or spread in time following an amortization formula, taking into account loan interest rates. Note that is a fixed cost that does not depend on or , and so it does not contribute to the optimization of . However, it does serve for the interpretation of the results.
- Operational costs ()This cost term encompasses all ongoing expenses that are inherent to the operation of the wind turbine (such as operation, maintenance, inspection, insurance, leasing and taxes costs). With regard to the impact of the failure, we split this cost aswhere is a monthly recurring cost that continues until the decommissioning or failure date, defined as:where reflects the costs before the failure, and —the incurring costs of preserving the asset, once the failure takes place, until the decommissioning (e.g., additional inspections). is a one-time-incurred cost that lumps all costs related with the failure. It is defined aswithNotably, the use of the delta Dirac function reflects the fact that if the decommissioning takes place before the failure, there are no costs associated to it. The cost includes both direct and indirect losses due to the failure occurrence. Direct losses include, for instance, fines due to inoperability of the asset and inspections or corrective actions that need to take place because of the failure. Indirect losses include environmental, human, and financial losses. Note that the production losses are included as part of , which is defined below.
- Decommissioning costs ()This one-time cost summarizes all costs related to the decommissioning of the wind turbine.with denoting the cost of decommission being defined as:which reflects the possible difference in costs depending on the occurrence of the failure (i.e., ). Note that the time dependency of these costs allows for penalizing actions that take place during months where the accessibility to the wind turbine is difficult due to, for example, weather conditions or logistics.
- Produced energy ()The produced energy is defined as:with denoting the expected produced energy in a failure-free condition (e.g., estimated from historical production data or from a wind resource characterization of the site including the expected turbine efficiency and possibly the reduction of production due to wake effects), and denoting a function that reflects the impact of the failure and the decommissioning being defined as:
- Income for produced energy ()This income is defined as:with denoting the price of energy per unit.Note that the remaining value of the asset after decommissioning is not included explicitly as a separate income term, as it is not recurrent, it is highly uncertain and difficult to estimate years in advance. However, it can be included indirectly by the users of the methodology, by merging this remaining value as an income term (thus, a negative modifier) to the decommissioning term .
4.3. Simulation
This section illustrates the economical optimization algorithm described in the previous subsections, with the corrosion prognosis used as an input for the DST estimated as discussed in Section 3.
The illustrative examples presented here are based on fictitious data. We assume that: (i) the corrosion prognosis module has estimated the system-level EOL distribution presented in Figure 5 (for the series configuration); (ii) the ground truth for the EOL is at month 2040-01 (i.e., year 30, assuming a construction date of 2010-01); (iii) the EOL of the turbine is driven by the tower corrosion (i.e., other components of the wind turbine are operating correctly, and related OPEX costs are lumped in the maintenance costs).
The economic assumptions are centralized in an Economic parameter table, which is accessible both for visualization and editing through the DST software interface that is presented in Section 5. For the example presented here, we assume the economic parameters presented in Appendix A.
Figure 7 presents the LCOE as a function of the decommissioning time for the assumptions and scenario described above. It can be seen from this figure that a higher risk aversion term leads to a more conservative optimum for . Similar results were obtained for the TCO metric. The results are summarized in Table 1.
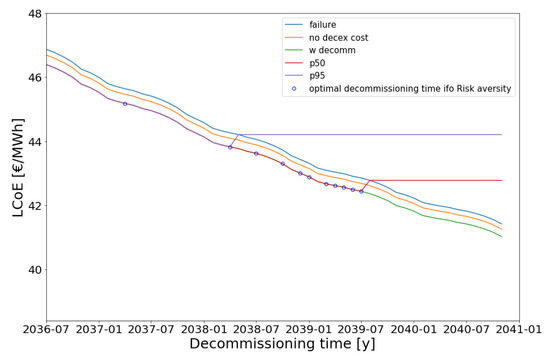
Figure 7.
LCOE as function of the decommissioning time , with system-level EOL distribution () as presented in Figure 5 (for the series configuration). The blue points indicate the economical optima for different values of the risk aversion term : from bottom right being low to top left being high (inferring earlier decommissioning advice).

Table 1.
Summary of results for different risk aversion levels.
The benefit of the corrosion prognosis is that an estimation of the EOL is available (which we assumed has a ground truth equal to January 2040). The results of Table 1 show that the decommissioning dates resulting from the economic optimization using this estimation of the EOL, typically fall before the ground truth EOL, but close to it, which result in an optimal decision that optimizes the TCO and LCOE, at the cost of an upfront investment for installing the monitoring and prognosis system. Without prognosis insight, the decommissioning time may be chosen in an sub-optimal way: either (long) before the ground truth EOL (reducing the operational lifetime and hence the income) or even after it (with a failure that already manifests before ).
Under most sets economic assumptions, this leads to a more opportune TCO and LCOE, yet under some scenarios, the upfront investment might not be completely countered by the (discounted) additional end of life benefits and avoided costs. Either way, having a monitoring system in place, at least for a few representative turbines in a wind turbine park, allows for data-driven decision making rather than performing a predetermined, blind execution of a long term decommissioning plan or making frequent on-site quality control visits.
This is further illustrated in Table 2, where the ground truth EOL is used to calculate the True TCO and LCOE for a corresponding to a premature or too late decommissioning (scenarios A and B, corresponding to a lack of prognosis information), compared to the (risk-averse optimal) values obtained with the economic optimization presented above (scenarios C1 and C2). Note that the scenarios A and B do not include the cost related to implementing the monitoring and prognosis solution (i.e., in the capital costs ), so for this scenario and these economic assumptions, the additional investment costs were compensated by the prolonged income over the lifetime. From the results, the lower and obtained for scenarios C1 and C2 illustrate how the use of prognosis information can lead to a better expected economic outcome.

Table 2.
Summary of economic outcomes, using (known) ground truth.
The results from the DST can thus support a maintenance team or owner to convince other involved parties about the beneficial economic consequences of a certain course of action, tailored to each wind turbine. This analysis enables the comparison of expected optimal and minimal costs for each action (decommissioning dates), thereby empowering maintenance teams to make informed decisions.
5. Graphical User Interface
To understand the spatial and temporal relationships in a voluminous amount of structural stability data of a wind turbine park, a Graphical User Interface (GUI) is required. For this purpose, a theoretical study of required features and a market study of currently available software was undertaken. Technical details of this process and a description of the custom development of a new 3D-visualization tool can be found in [9], with an example front-end shown in Figure 8.
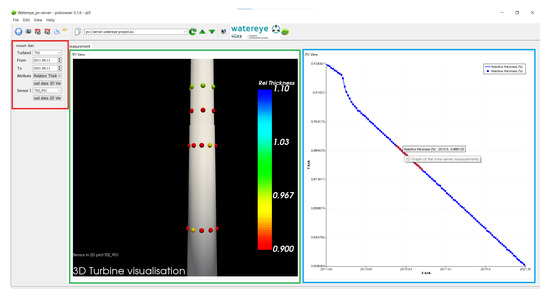
Figure 8.
Browser window of the custom visualization software-tool. It consists of three areas: user input (red box), a 3D visualization area (green box), and a 2D time series visualization (blue box). All widgets are interactive and responsive. Reused from [9] with author permission.
This 3D-visualization tool was further augmented with an user interface, which allows to parameterize and visualize the decision support methodology on (dummy or) live data. A mock-up of this DST-interface is shown in Figure 9. Other user parameters and economical assumptions (such as the yearly energy price evolution) can be entered through an integrated Economic parameter table in the visualization area (not shown in the figure). Furthermore, an interface to visualize the prognosis tool output(s) is implemented as well (not shown here). The optimal decommissioning time is calculated for a set of different values of the risk aversion term , taking into account the estimated system-level RUL, which is regularly updated using the latest measurement data.
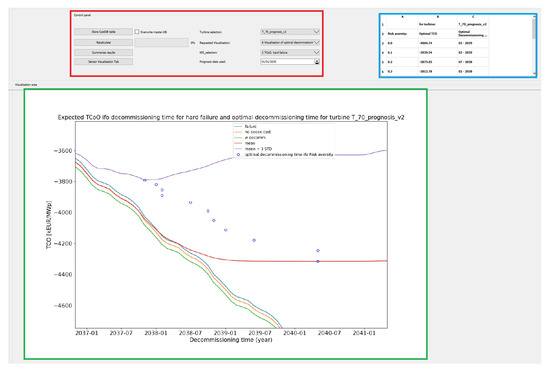
Figure 9.
Browser window of the custom visualization software-tool for decision support module. It consists of two areas: user input (software tool, top left), a visualization area (green rectangle, bottom), and a tabulated summary area (blue rectangle, top right).
Thereby, this extended GUI supports the visualization and analysis of raw data, prognosis data, and decision support metrics.
6. Conclusions
To contribute to the systematic assessment and management of corrosion in wind turbine structures, we developed an integrated corrosion detection and prognostics system coupled with a Decision Support Tool (DST) and a Graphical User Interface (GUI).
In a first step, the wall thickness at different critical locations of the tower is measured via the ultrasound technique. At each location, uniform corrosion is detected and a local RUL estimate is obtained based on the depletion of the corrosion allowance. In a next step, the local RUL estimates are aggregated to obtain an RUL estimate for the whole structure (i.e., the system-level RUL estimate). This distributed approach facilitates the prognosis: the algorithms are simplified, providing scalability, efficiency, and flexibility for adding or removing measurement locations.
On the component level, a corrosion detection and prognosis algorithm was developed based on the Bayesian filtering and the power law corrosion model. This algorithm does not assume a given initial wall thickness and is robust against the level of measurement noise that is typical for ultrasound sensors.
For the system-level prognosis, an algorithm based on reliability theory is proposed. The system failure definition is encoded in a tree structure which establishes the membership of components to (sub)systems, with the reliability of each (sub)system modelled by a weighted k-out-of-n: good structure. This flexible structure for encoding the system failure definition allows the user to choose from the default option ’series connection’, which leads to a strict definition of system failure, to more complex definitions that can be set based on the expert knowledge or know-how of the structural behaviours of the tower.
The DST processes the system-level prognosis information together with economical information and the long-term forecast of the produced energy to assess, in a systematic way, the most optimal timing for decommissioning. For this purpose, we propose a risk-based economical optimization that considers the complete lifetime of the asset. The user may choose between an objective cost function based on the Levelised Cost Of Electricity (LCOE), or based on Total Cost of Ownership (TCO).
The corrosion detection and prognosis system and the DST count with a GUI. This GUI was implemented as part of the software tool described in [9]. This GUI facilitates the visualization of actionable information retrieved from the measurement data by means of a 3D visualization of the corrosion status along the wind turbine tower, and 2D graphics presenting the results of the prognostics module and the economical optimization. This GUI also facilitates the interaction with the user for setting the different parameters and costs involved in the economical optimization.
Author Contributions
Conceptualization, S.V., J.V., R.B. and A.P.O.; methodology, S.V., J.V. and R.B.; software, S.V., J.V. and R.B.; validation, S.V., J.V. and R.B.; investigation, S.V., J.V. and R.B.; writing—original draft preparation, S.V., J.V. and R.B.; writing—review and editing, S.V., J.V., R.B. and A.P.O.; supervision, A.P.O.; project administration, A.P.O.; funding acquisition, A.P.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried within the WATEREYE project, which has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 851207.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful for the technical support of Stijn Helsen, and the project administration of Thibault Crepain during the development of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Economic Assumptions
This appendix presents the economic assumptions used for the example of Section 4.3. The default economic parameters are assumed to be known for the whole evaluation horizon (this includes known historic values and estimated future values). They are built up by concatenating parametric monthly cost values over the course of one year, with yearly multipliers. The resulting costs are presented in Figure A1. The top pane shows values without depreciation to account for wage, energy price and inflation, the bottom pane shows effects with depreciation to year 0 (2010). For both panes, the (one-time incurred) failure costs and decommissioning costs fall outside of the plotting area, as they are constant (without inflation) in function of time. They are at, respectively, plus kEUR 200/MWp and minus kEUR 200/MWp before applying inflation and depreciation.
The CAPEX investment given by the user are typically not assumed to be all paid upfront, but rather to be amortized over a period of time with a given loan interest rate, over a period of N months after the initial investment (with N a control parameter, set to 60 months by default).
Note that the effects of other required inputs, such as monetary depreciation, maintenance interval and duration (set by default to once every 12 months, with length of 0.25 months) and monthly energy production, are assumed to be constant in this fictitious input data, however, they may not be constant in our tool, they can be varied linearly or exponentially. This may have a significant impact on the outcome, especially when discounting all incomes and costs over a 30–50-year horizon to a single base year.
The interest rate values have been artificially set here, to show the possible influence of their relative value, on the slope of the cost distribution. In a real economic evaluation, the sensitivity to these economic assumptions can and should be evaluated by the operator. For these inflation parameters, the following values are assumed: monetary inflation or considered weighted average cost of capital (WACC) rate of 2.0% (effective yearly rate); loan and debt interest rate of 3.7%; yearly energy price increase of 3.0%; yearly wage inflation of 1.2%; and inflation of economic impact of risk and environmental effects of 0.0%.
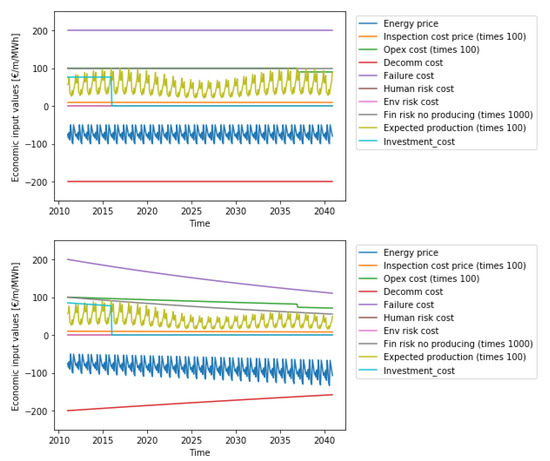
Figure A1.
Overview of the economic assumptions for the analysis, both the costs which are incurred only once (e.g., failure cost, investments, decommissioning) and monthly recurring costs (e.g., maintenance, incomes, environmental impact). All costs are normalized by turbine capacity MWp or by turbine production rate MWh. Incomes are presented as negative costs on this graph. Top pane shows monthly costs without interest impact, bottom pane shows cost discounted down to year X (here 2010), with monetary inflation and varied (linear) interest rates applied to energy price, wages, and capital cost.
References
- Global Wind Energy Council (GWEC). GWEC Global Wind Report 2022; GWEC: Brussels, Belgium, 2022. [Google Scholar]
- International Renewable Energy Agency (IRENA). Renewable Power Generation Costs in 2019; IRENA: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- Chen, J.; Kim, M.H. Review of Recent Offshore Wind Turbine Research and Optimization Methodologies in Their Design. J. Mar. Sci. Eng. 2022, 10, 28. [Google Scholar] [CrossRef]
- Failla, G.; Arena, F. New perspectives in offshore wind energy. Philos. Top. 2015, 373, 20140228. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z.; et al. Foundations of offshore wind turbines: A review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Price, S.J.; Figueira, R.B. Corrosion Protection Systems and Fatigue Corrosion in Offshore Wind Structures: Current Status and Future Perspectives. Coatings 2017, 7, 25. [Google Scholar] [CrossRef]
- Martinez-Luengo, M.; Kolios, A.; Wang, L. Structural health monitoring of offshore wind turbines: A review through the Statistical Pattern Recognition Paradigm. Renew. Sustain. Energy Rev. 2016, 64, 91–105. [Google Scholar] [CrossRef]
- Brijder, R.; Hagen, C.H.M.; Cortés, A.; Irizar, A.; Thibbotuwa, U.C.; Helsen, S.; Vásquez, S.; Ompusunggu, A.P. Review of corrosion monitoring and prognostics in offshore wind turbine structures: Current status and feasible approaches. Front. Energy Res. 2022, 10, 1433. [Google Scholar] [CrossRef]
- Verhelst, J.; Coudron, I.; Ompusunggu, A.P. SCADA-Compatible and Scaleable Visualization Tool for Corrosion Monitoring of Offshore Wind Turbine Structures. Appl. Sci. 2022, 12, 1762. [Google Scholar] [CrossRef]
- WATEREYE_H2020. O&M Tools Integrating Accurate Structural Health in Offshore Energy. 2022. Available online: https://cordis.europa.eu/project/id/851207 (accessed on 7 September 2022).
- Thibbotuwa, U.C.; Cortés, A.; Irizar, A. Ultrasound-Based Smart Corrosion Monitoring System for Offshore Wind Turbines. Appl. Sci. 2022, 12, 808. [Google Scholar] [CrossRef]
- Ortegon, K.; Nies, L.F.; Sutherland, J.W. Preparing for end of service life of wind turbines. J. Clean. Prod. 2013, 39, 191–199. [Google Scholar] [CrossRef]
- Topham, E.; Gonzalez, E.; McMillan, D.; João, E. Challenges of decommissioning offshore wind farms: Overview of the European experience. In Proceedings of the WindEurope Conference and Exhibition 2019, Journal of Physics: Conference Series, Bilbao, Spain, 2–4 April 2019; Volume 1222. [Google Scholar]
- Irawan, C.A.; Wall, G.; Jones, D. An optimisation model for scheduling the decommissioning of an offshore wind farm. OR Spectrum 2019, 41, 513–548. [Google Scholar] [CrossRef]
- DNV GL AS. DNVGL-RP-0416: Corrosion Protection for Wind Turbines; Technical Report; DNV GL AS: Høvik, Norway, 2016. [Google Scholar]
- DNV GL AS. DNVGL-ST-0126: Support Structures for Wind Turbines. Technical Report; DNV GL AS: Høvik, Norway, 2016. [Google Scholar]
- Daigle, M.; Bregon, A.; Roychoudhury, I. A Distributed Approach to System-Level Prognostics. In Proceedings of the Annual Conference of the PHM Society, Minneapolis, MN, USA, 23–27 September 2012; Volume 4. [Google Scholar] [CrossRef]
- Brijder, R.; Helsen, S.; Ompusunggu, A.P. Switching Kalman Filtering Based Corrosion Detection and Prognostics for Offshore Wind-Turbine Structures. Wind, 2022; Submitted. [Google Scholar]
- Pourbaix, M. International cooperation in the prevention of corrosion of materials. In Proceedings of the IX International Congress of Metallic Corrosion, Toronto, ON, Canada, 3–7 June 1984; Volume 1, pp. 57–100. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Brijder, R.; Helsen, S.; Ompusunggu, A.P. Corrosion Prognostics for Offshore Wind-Turbine Structures using Bayesian Filtering with Bi-modal and Linear Degradation Models. In Proceedings of the 13th International Workshop on Structural Health Monitoring (IWSHM 2021), Stanford, CA, USA, 15–17 March 2022. [Google Scholar]
- Melchers, R.E. Progress in developing realistic corrosion models. Struct. Infrastruct. Eng. 2018, 14, 843–853. [Google Scholar] [CrossRef]
- Wu, J.S.; Chen, R.J. An algorithm for computing the reliability of weighted-k-out-of-n systems. IEEE Trans. Reliab. 1994, 43, 327–328. [Google Scholar] [CrossRef]
- Chang, Y.; Mai, Y.; Yi, L.; Yu, L.; Chen, Y.; Yang, C.; Gao, J. Reliability Analysis of k-out-of-n Systems of Components with Potentially Brittle Behavior by Universal Generating Function and Linear Programming. Math. Probl. Eng. 2020, 2020, 8087242. [Google Scholar] [CrossRef]
- Louhichi, R.; Sallak, M.; Pelletan, J. A cost model for predictive maintenance based on risk-assessment. In Proceedings of the 13ème Conférence Internationale CIGI QUALITA 2019, HAL, Montreal, QC, Canada, 14 August 2019. [Google Scholar]
- Jin, T.; Tian, Z.; Huerta, M.; Piechota, J. Coordinating maintenance with spares logistics to minimize levelized cost of wind energy. In Proceedings of the 2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Chengdu, China, 15–18 June 2012; pp. 1022–1027. [Google Scholar] [CrossRef]
- Feng, J.; Cai, H.; Liu, Z.; Lee, J. A Systematic Framework for Maintenance Scheduling and Routing for Off-Shore Wind Farms by Minimizing Predictive Production Loss. In Proceedings of the E3S Web of Conferences, 2020 2nd International Academic Exchange Conference on Science and Technology Innovation, Guangzhou, China, 18–20 December 2020. [Google Scholar] [CrossRef]
- Lei, X.; Sandborn, P.; Bakhshi, R.; Kashani-Pour, A.; Goudarzi, N. PHM based predictive maintenance optimization for offshore wind farms. In Proceedings of the 2015 IEEE Conference on Prognostics and Health Management (PHM), Austin, TX, USA, 22–25 June 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Besnard, F.; Patriksson, M.; Strömberg, A.B.; Wojciechowski, A.; Bertling, L. An optimization framework for opportunistic maintenance of offshore wind power system. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2019. [Google Scholar] [CrossRef]
- Yu, Q.; Patriksson, M.; Sagitov, S. Optimal scheduling of the next preventive maintenance activity for a wind farm. Wind Energy Sci. 2021, 6, 949–959. [Google Scholar] [CrossRef]
- Yeter, B.; Garbatov, Y.; Soares, C.G. Risk-based maintenance planning of offshore wind turbine farms. Reliab. Eng. Syst. Saf. 2020, 202, 107062. [Google Scholar] [CrossRef]
- Ashwin, R. Understanding Risk-Aversion through Utility Theory. 2022. Available online: https://web.stanford.edu/class/cme241/lecture_slides/UtilityTheoryForRisk.pdf (accessed on 16 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).