Power to Hydrogen and Power to Water Using Wind Energy
Abstract
:1. Introduction
2. Materials and Methods
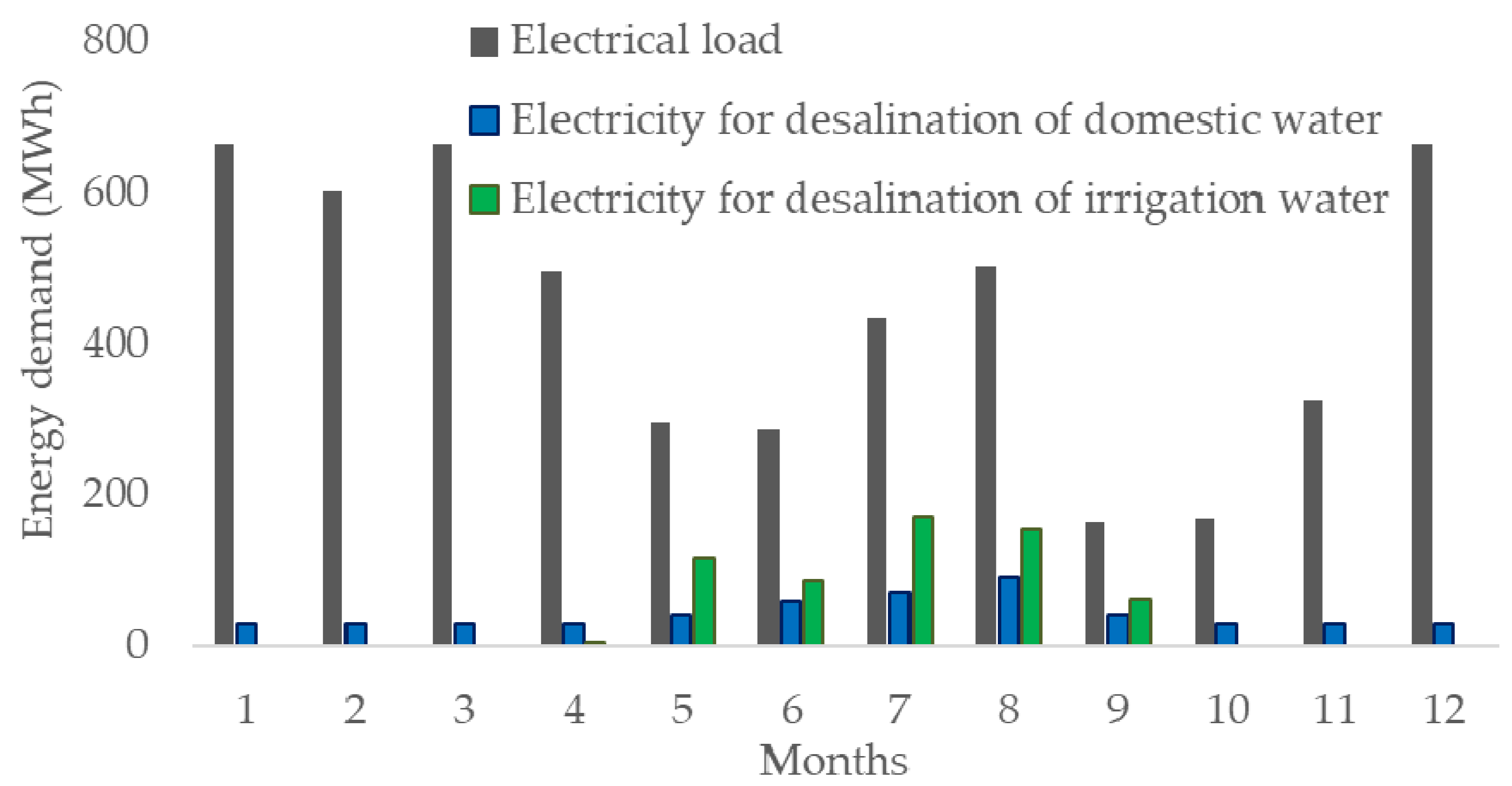
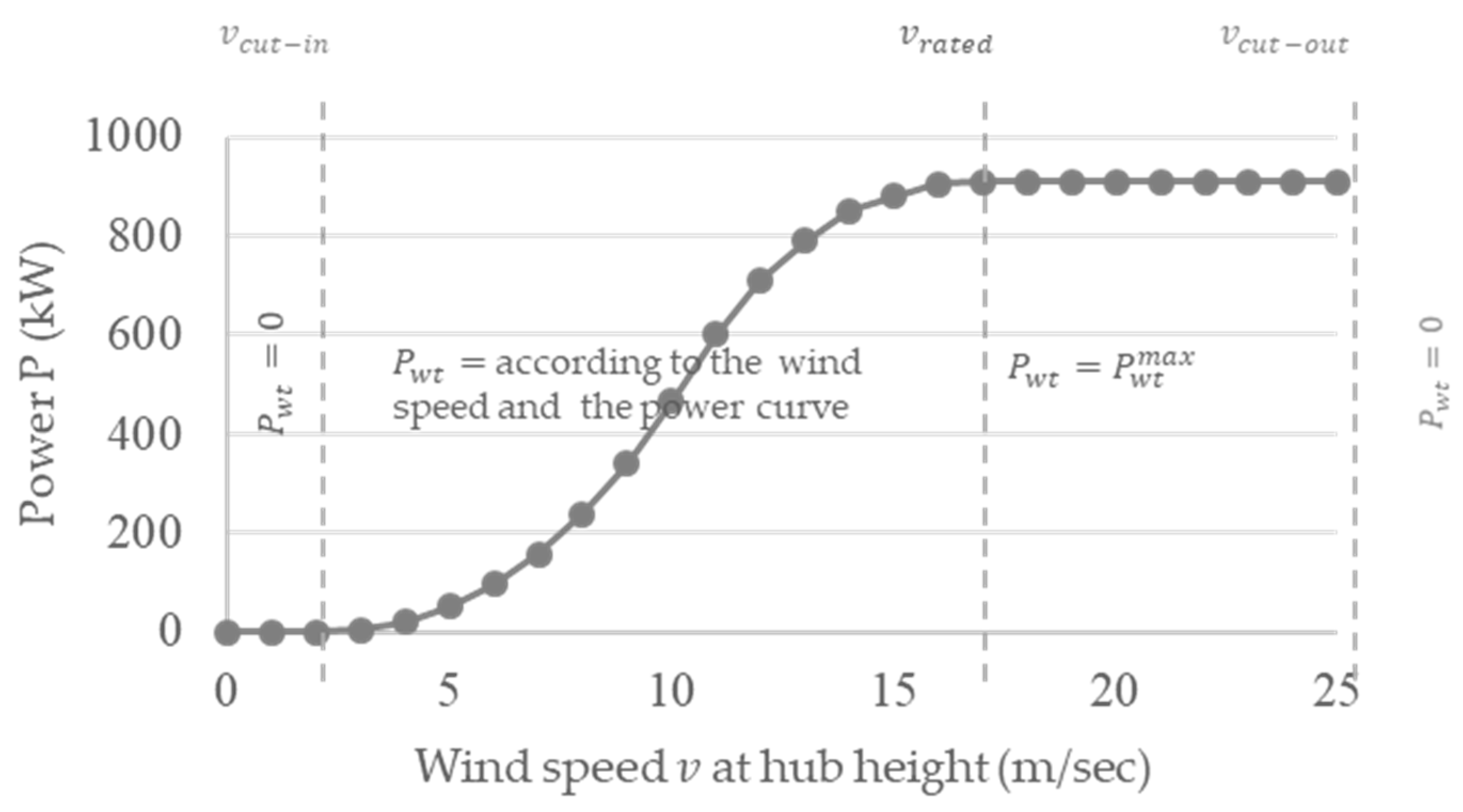
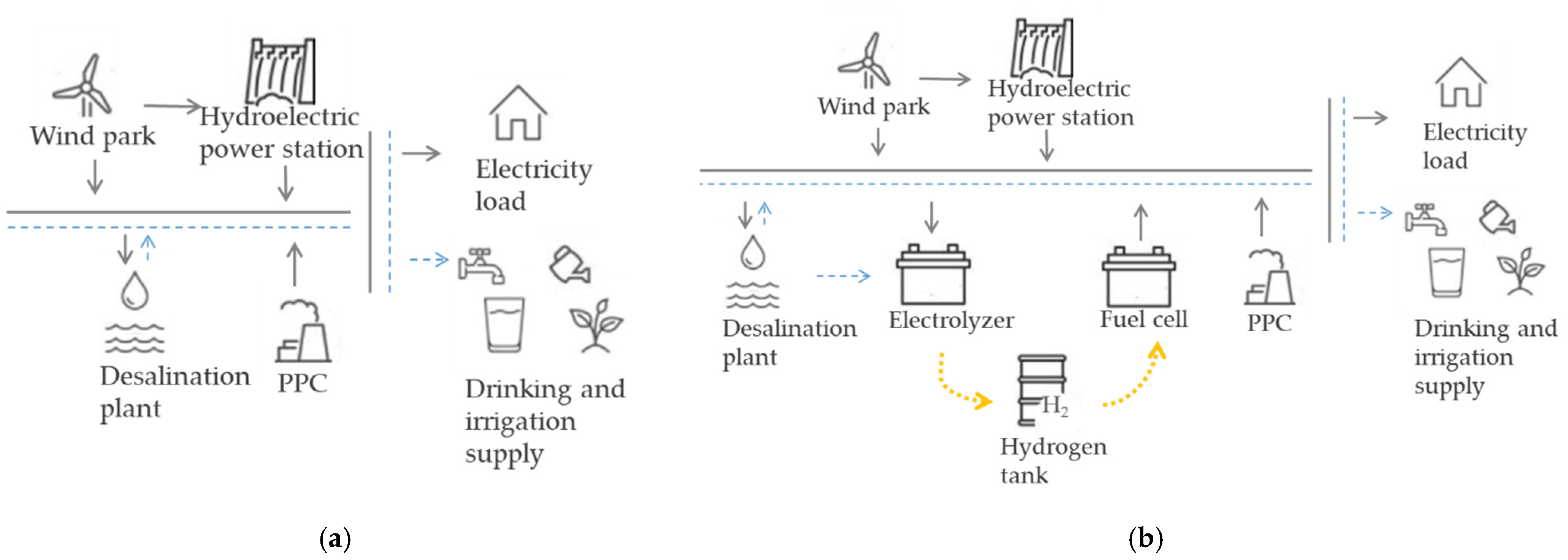
2.1. Case Study
2.2. Energy Management Strategies
2.3. Techno-Economic Analysis
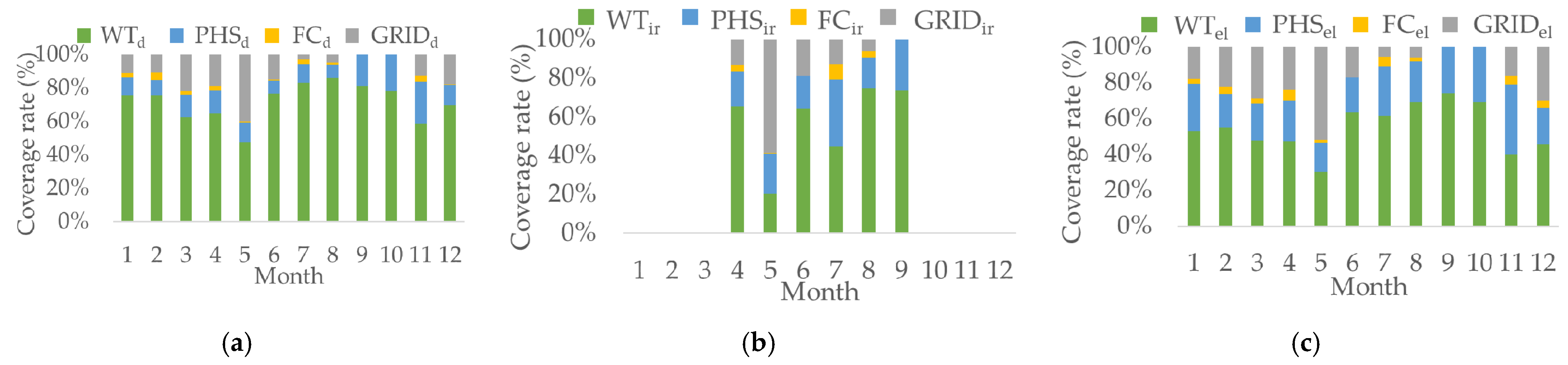
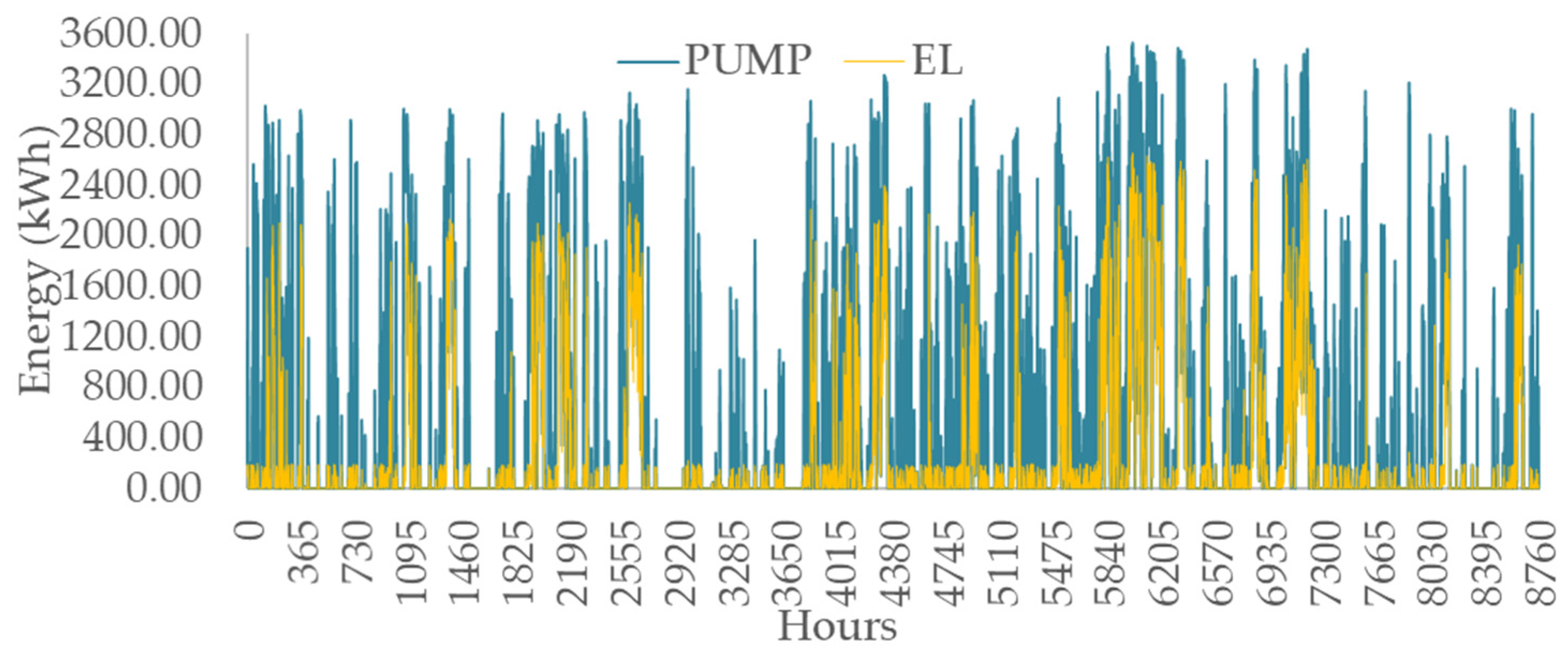
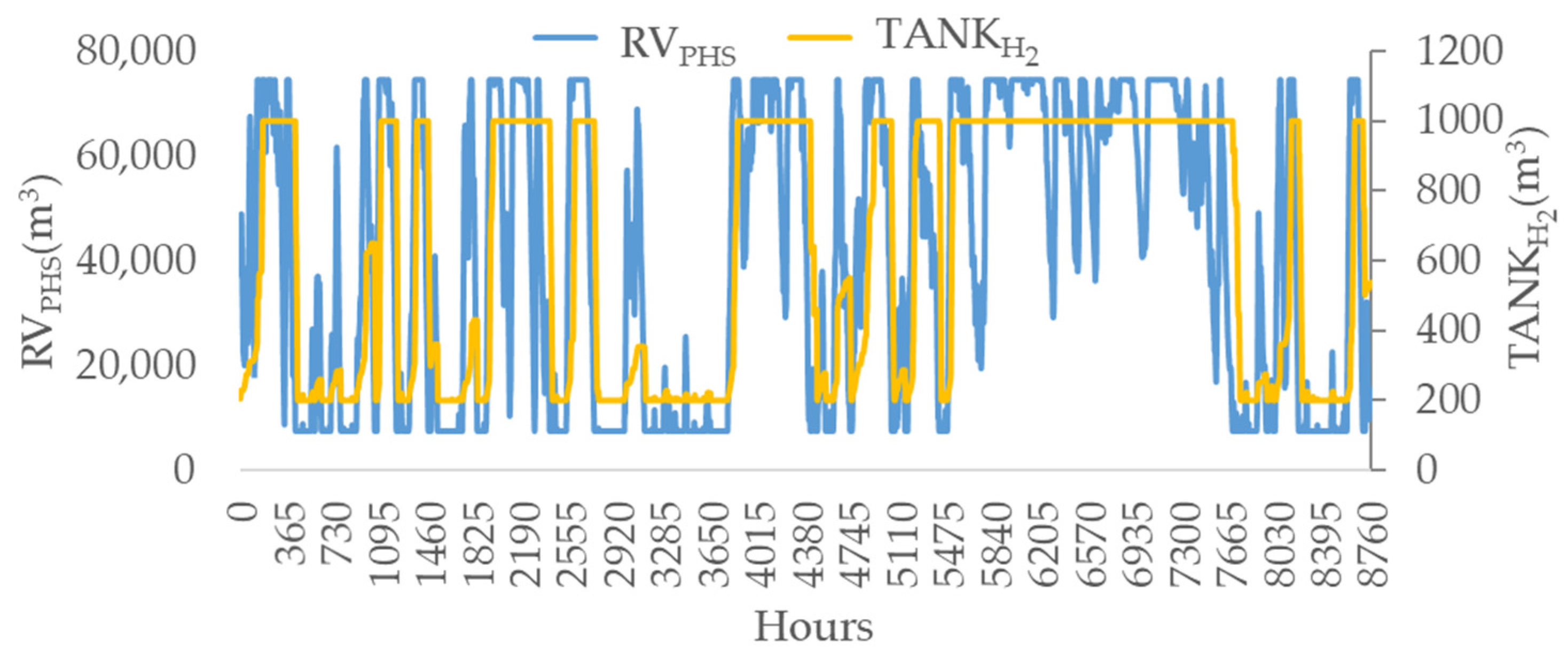
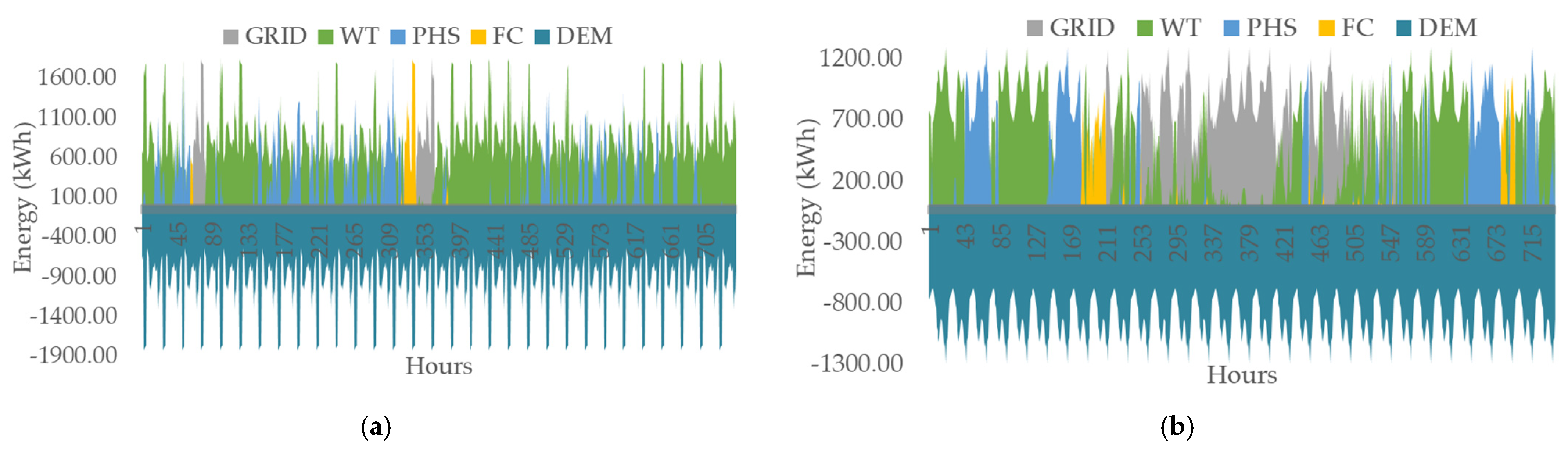
3. Results & Discussion
3.1. HRES Assessment
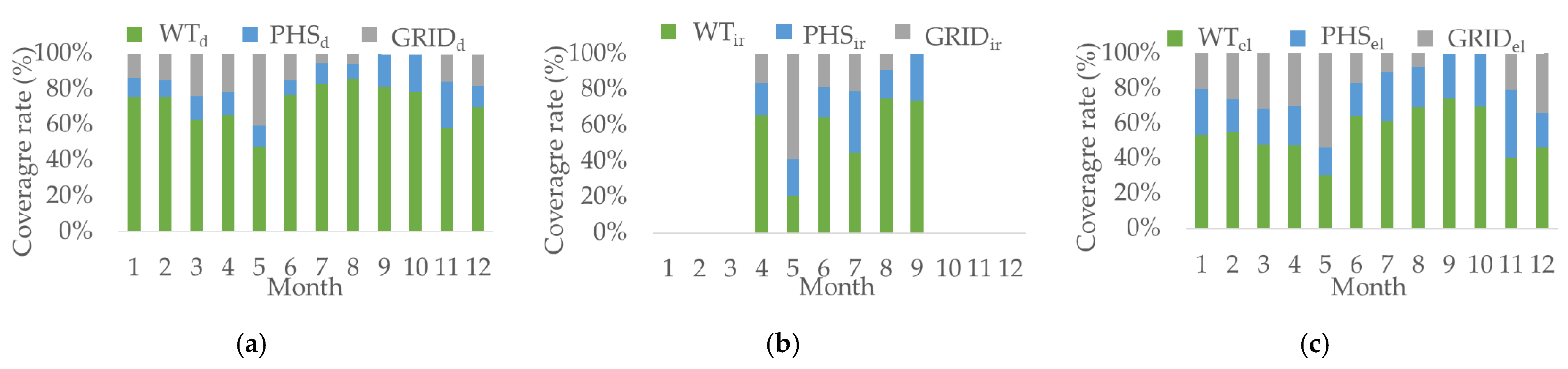
3.2. Storage System Operation
3.3. Energy Balance
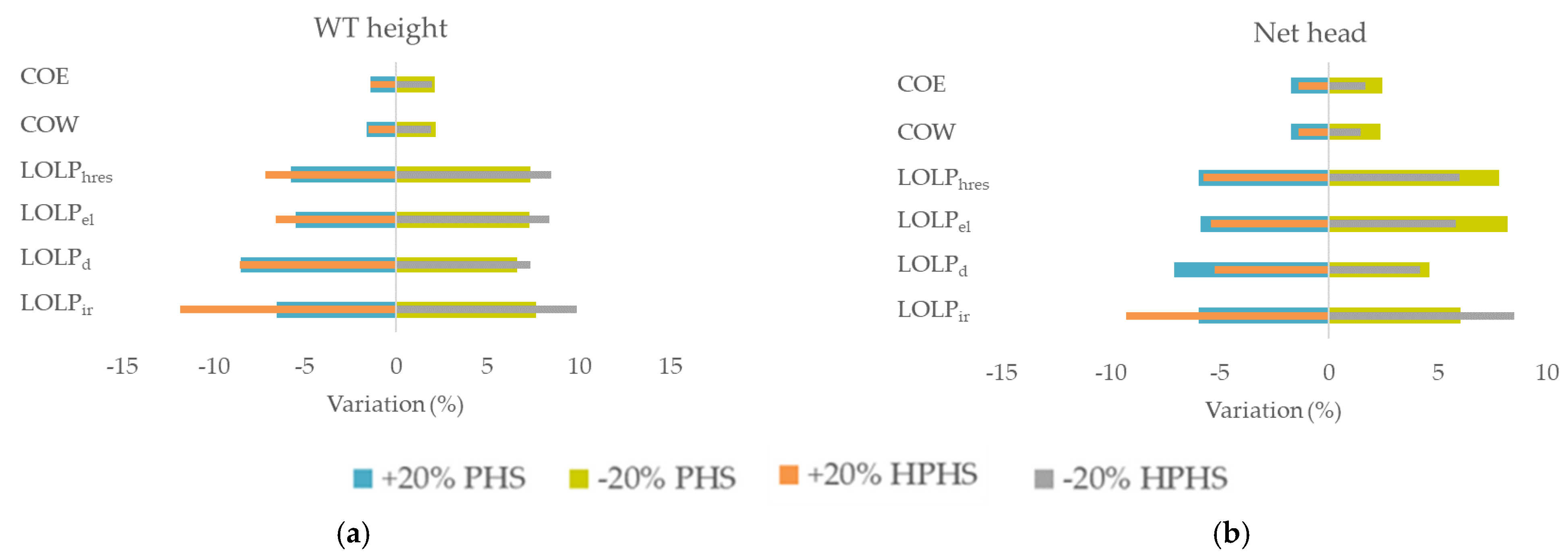
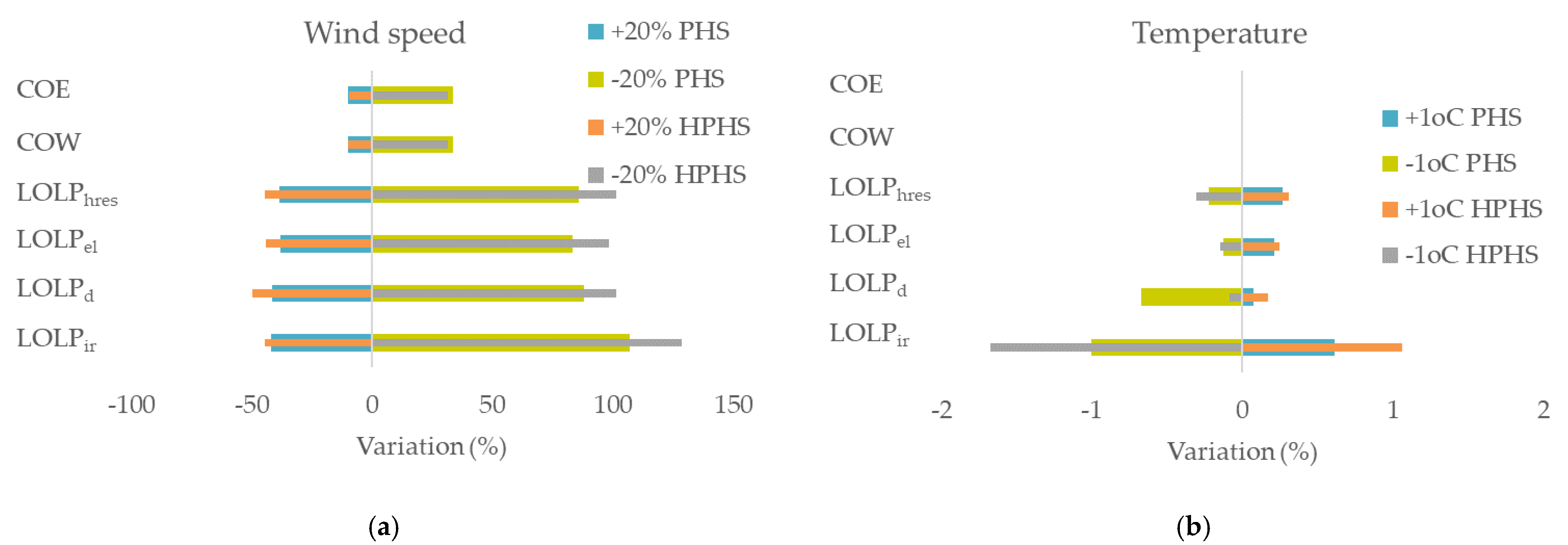
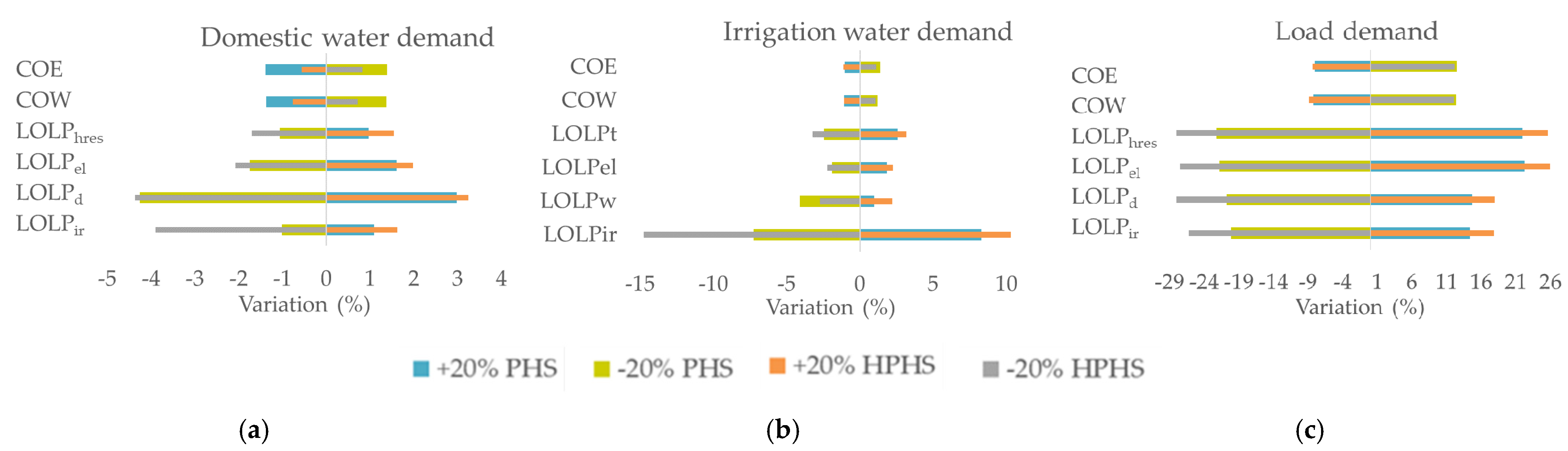
3.4. Sensitivity Analysis
4. Conclusions
- Evaluation of a hybrid pumped hydrogen storage system;
- Comparison between a single and a hybrid storage system, the PHS and the HPHS; in terms of six indices (COE, COW, LOLPhres, LOLPel, LOLPd, LOLPir);
- Reliability analysis for both storage technologies;
- Sensitivity analysis which presents how the results are affected for both storage technologies based on variations in installation height of the wind turbines and the upper reservoir, variations in the meteorological data (wind speed and temperature) and variations in demand data (load demand, domestic and irrigation water). Every parameter is examined in the context of an increase and a decrease of 20% in order to show the relationship between the change in the initial value and the six indices. Concerning the variation in temperature, an increase and a decrease of 1 °C are examined. Results give useful information about the impact of each parameter on the calculated indices. The simulation is conducted in an hourly step; meteorological data of wind speed, temperature and precipitation are selected, as well as data about electricity, domestic water and irrigation water demands.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CAPEX | initial investment cost of the whole HRES (EUR) |
| COE | cost of energy (EUR/kWh) |
| COW | cost of water (EUR/m3) |
| replacement cost (EUR) | |
| salvage cost (EUR) | |
| energy required for the desalination of seawater (kWh) | |
| energy produced from fuel cell (kWh) | |
| produced energy from the HRES (kWh) | |
| annual load demand (kWh) | |
| uncovered demand (kWh) | |
| energy surplus (kWh) | |
| hydroenergy (kWh) | |
| unexploited energy (kWh) | |
| gravity acceleration (m/s2) | |
| net head (m) | |
| produced hydrogen by the electrolyzer (kg) | |
| roughness length parameter (m) | |
| height of weather station (m) | |
| hub height of wind turbine (m) | |
| discount rate (%) | |
| lifetime of the HRES (years) | |
| lifetime of each component (years) | |
| LOLP | loss of load probability (%) |
| number of hours | |
| electrolyzer efficiency (%) | |
| fuel cell efficiency (%) | |
| pumping efficiency (%) | |
| hydro turbine efficiency (%) | |
| operation and maintenance cost (EUR) | |
| exploitable power of the wind turbine (kW) | |
| nominal power pf the wind turbine (kW) | |
| total capacity of the hydrogen tank (kg) | |
| maximum storage capacity of the hydrogen tank (kg) | |
| minimum storage capacity of the hydrogen tank (kg) | |
| total capacity of the upper reservoir (m3) | |
| maximum storage capacity of the upper reservoir (m3) | |
| minimum storage capacity of the upper reservoir (m3) | |
| volume of stored water (m3) | |
| wind speed (m/s) | |
| wind speed in the weather station (m/s) | |
| wind speed at hub height (m/s) |
Abbreviations
| HPHS | hybrid pumped hydrogen storage system |
| HRES | hybrid renewable energy system |
| NPV | net present value |
| PHS | pumped hydro storage system |
| PV | photovoltaic module |
| RES | renewable energy sources |
| WT | wind turbine |
| Greek letter | |
| ρ | water density (kg/m3) |
| Subscripts | |
| d | domestic water |
| el | electricity |
| hres | hybrid renewable energy system |
| ir | irrigation |
References
- Potashnikov, V.; Golub, A.; Brody, M.; Lugovoy, O. Decarbonizing Russia: Leapfrogging from Fossil Fuel to Hydrogen. Energies 2022, 15, 683. [Google Scholar] [CrossRef]
- Farh, H.M.; Al-Shamma’a, A.A.; Al-Shaalan, A.M.; Alkuhayli, A.; Noman, A.M.; Kandil, T. Technical and Economic Evaluation for Off-Grid Hybrid Renewable Energy System Using Novel Bonobo Optimizer. Sustainability 2022, 14, 1533. [Google Scholar] [CrossRef]
- Ioannidis, R.; Koutsoyiannis, D. A review of land use, visibility and public perception of renewable energy in the context of landscape impact. Appl. Energy 2020, 276, 115367. [Google Scholar] [CrossRef]
- Canbulat, S.; Balci, K.; Canbulat, O.; Bayram, I.S. Techno-economic analysis of on-site energy storage units to mitigate wind energy curtailment: A case study in Scotland. Energies 2021, 14, 1691. [Google Scholar] [CrossRef]
- Finnegan, W.; Jiang, Y.; Dumergue, N.; Davies, P.; Goggins, J. Investigation and validation of numerical models for composite wind turbine blades. J. Mar. Sci. Eng. 2021, 9, 525. [Google Scholar] [CrossRef]
- Subramanian, S.; Sankaralingam, C.; Elavarasan, R.M.; Vijayaraghavan, R.R.; Raju, K.; Mihet-Popa, L. An evaluation on wind energy potential using multi-objective optimization based non-dominated sorting genetic algorithm III. Sustainability 2021, 13, 410. [Google Scholar] [CrossRef]
- National Energy and Climate Plan. Available online: https://ec.europa.eu/energy/sites/ener/files/el_final_necp_main_en.pdf (accessed on 10 February 2022).
- Olabi, A.G.; Wilberforce, T.; Elsaid, K.; Salameh, T.; Sayed, E.T.; Husain, K.S.; Abdelkareem, M.A. Selection guidelines for wind energy technologies. Energies 2021, 14, 3244. [Google Scholar] [CrossRef]
- Baldinelli, A.; Barelli, L.; Bidini, G.; Cinti, G.; Di Michele, A.; Mondi, F. How to power the energy–water nexus: Coupling desalination and hydrogen energy storage in mini-grids with reversible solid oxide cells. Processes 2020, 8, 1494. [Google Scholar] [CrossRef]
- Das, P.; Das, B.K.; Mustafi, N.N.; Sakir, M.T. A review on pump-hydro storage for renewable and hybrid energy systems applications. Energy Storage 2021, 3, e223. [Google Scholar] [CrossRef]
- Alturki, F.A.; Awwad, E.M. Sizing and Cost Minimization of Standalone Hybrid WT/PV/Biomass/Pump-Hydro Storage-Based Energy Systems. Energies 2021, 14, 489. [Google Scholar] [CrossRef]
- Eisapour, A.H.; Jafarpur, K.; Farjah, E. Feasibility study of a smart hybrid renewable energy system to supply the electricity and heat demand of Eram Campus, Shiraz University; simulation, optimization, and sensitivity analysis. Energy Convers. Manag. 2021, 248, 114779. [Google Scholar] [CrossRef]
- Islam, M.S.; Das, B.K.; Das, P.; Rahaman, M.H. Techno-economic optimization of a zero emission energy system for a coastal community in Newfoundland, Canada. Energy 2021, 220, 119709. [Google Scholar] [CrossRef]
- Nassar, Y.F.; Abdunnabi, M.J.; Sbeta, M.N.; Hafez, A.A.; Amer, K.A.; Ahmed, A.Y.; Belgasim, B. Dynamic analysis and sizing optimization of a pumped hydroelectric storage-integrated hybrid PV/Wind system: A case study. Energy Convers. Manag. 2021, 229, 113744. [Google Scholar] [CrossRef]
- Yue, M.; Lambert, H.; Pahon, E.; Roche, R.; Jemei, S.; Hissel, D. Hydrogen energy systems: A critical review of technologies, applications, trends and challenges. Renew. Sust. Energ. Rev. 2021, 146, 111180. [Google Scholar] [CrossRef]
- Yu, M.; Wang, K.; Vredenburg, H. Insights into low-carbon hydrogen production methods: Green, blue and aqua hydrogen. Int. J. Hydrog. Energy 2021, 46, 21261–21273. [Google Scholar] [CrossRef]
- Kakoulaki, G.; Kougias, I.; Taylor, N.; Dolci, F.; Moya, J.; Jäger-Waldau, A. Green hydrogen in Europe–A regional assessment: Substituting existing production with electrolysis powered by renewables. Energy Convers. Manag. 2021, 228, 113649. [Google Scholar] [CrossRef]
- Elberry, A.M.; Thakur, J.; Santasalo-Aarnio, A.; Larmi, M. Large-scale compressed hydrogen storage as part of renewable electricity storage systems. Int. J. Hydrog. Energy 2021, 46, 15671–15690. [Google Scholar] [CrossRef]
- Hinokuma, T.; Farzaneh, H.; Shaqour, A. Techno-economic analysis of a fuzzy logic control based hybrid renewable energy system to power a university campus in Japan. Energies 2021, 14, 1960. [Google Scholar] [CrossRef]
- Ceran, B.; Mielcarek, A.; Hassan, Q.; Teneta, J.; Jaszczur, M. Aging effects on modelling and operation of a photovoltaic system with hydrogen storage. Appl. Energy 2021, 297, 117161. [Google Scholar] [CrossRef]
- Rezaei, M.; Naghdi-Khozani, N.; Jafari, N. Wind energy utilization for hydrogen production in an underdeveloped country: An economic investigation. Renew. Energy 2020, 147, 1044–1057. [Google Scholar] [CrossRef]
- Makhdoomi, S.; Askarzadeh, A. Impact of solar tracker and energy storage system on sizing of hybrid energy systems: A comparison between diesel/PV/PHS and diesel/PV/FC. Energy 2021, 231, 120920. [Google Scholar] [CrossRef]
- Ghenai, C.; Salameh, T.; Merabet, A. Technico-economic analysis of off grid solar PV/Fuel cell energy system for residential community in desert region. Int. J. Hydrog. Energy 2020, 45, 11460–11470. [Google Scholar] [CrossRef]
- Sultan, H.M.; Menesy, A.S.; Kamel, S.; Korashy, A.; Almohaimeed, S.A.; Abdel-Akher, M. An improved artificial ecosystem optimization algorithm for optimal configuration of a hybrid PV/WT/FC energy system. Alex. Eng. J. 2021, 60, 1001–1025. [Google Scholar] [CrossRef]
- Bertsiou, M.M.; Baltas, E. Management of energy and water resources by minimizing the rejected renewable energy. Sustain. Energy Technol. Assess. 2022, 52, 102002. [Google Scholar] [CrossRef]
- Dambone Sessa, S.; Tortella, A.; Andriollo, M.; Benato, R. Li-ion battery-flywheel hybrid storage system: Countering battery aging during a grid frequency regulation service. Appl. Sci. 2018, 8, 2330. [Google Scholar] [CrossRef] [Green Version]
- Javed, K.; Ashfaq, H.; Singh, R.; Hussain, S.M.; Ustun, T.S. Design and performance analysis of a stand-alone PV system with hybrid energy storage for rural India. Electronics 2019, 8, 952. [Google Scholar] [CrossRef] [Green Version]
- Marocco, P.; Ferrero, D.; Lanzini, A.; Santarelli, M. The role of hydrogen in the optimal design of off-grid hybrid renewable energy systems. J. Energy Storage 2022, 46, 103893. [Google Scholar] [CrossRef]
- Ferrario, A.M.; Bartolini, A.; Manzano, F.S.; Vivas, F.J.; Comodi, G.; McPhail, S.J.; Andujar, J.M. A model-based parametric and optimal sizing of a battery/hydrogen storage of a real hybrid microgrid supplying a residential load: Towards island operation. Adv. Appl. Energy 2021, 3, 100048. [Google Scholar] [CrossRef]
- Akter, H.; Howlader, H.O.R.; Nakadomari, A.; Islam, M.; Saber, A.Y.; Senjyu, T. A Short Assessment of Renewable Energy for Optimal Sizing of 100% Renewable Energy Based Microgrids in Remote Islands of Developing Countries: A Case Study in Bangladesh. Energies 2022, 15, 1084. [Google Scholar] [CrossRef]
- Kefif, N.; Melzi, B.; Hashemian, M.; Assad, M.E.H.; Hoseinzadeh, S. Feasibility and optimal operation of micro energy hybrid system (hydro/wind) in the rural valley region. Int. J. Low Carbon Technol. 2022, 17, 58–68. [Google Scholar] [CrossRef]
- Canales, F.A.; Jurasz, J.K.; Guezgouz, M.; Beluco, A. Cost-reliability analysis of hybrid pumped-battery storage for solar and wind energy integration in an island community. Sustain. Energy Technol. Assess. 2021, 44, 101062. [Google Scholar] [CrossRef]
- Lata-García, J.; Jurado, F.; Fernández-Ramírez, L.M.; Sánchez-Sainz, H. Optimal hydrokinetic turbine location and techno-economic analysis of a hybrid system based on photovoltaic/hydrokinetic/hydrogen/battery. Energy 2018, 159, 611–620. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.C. Control strategy of a hybrid renewable energy system based on reinforcement learning approach for an isolated microgrid. Appl. Sci. 2019, 9, 4001. [Google Scholar] [CrossRef] [Green Version]
- Dawood, F.; Shafiullah, G.M.; Anda, M. Stand-alone microgrid with 100% renewable energy: A case study with hybrid solar PV-battery-hydrogen. Sustainability 2020, 12, 2047. [Google Scholar] [CrossRef] [Green Version]
- Kaldellis, J.K.; Zafirakis, D. Prospects and challenges for clean energy in European Islands. The TILOS paradigm. Renew. Energy 2020, 145, 2489–2502. [Google Scholar] [CrossRef]
- Myronidis, D.; Nikolaos, T. Changes in climatic patterns and tourism and their concomitant effect on drinking water transfers into the region of South Aegean, Greece. Stoch. Environ. Res. Risk Assess. 2021, 35, 1725–1739. [Google Scholar] [CrossRef]
- Rezaei, M.; Mostafaeipour, A.; Jafari, N.; Naghdi-Khozani, N.; Moftakharzadeh, A. Wind and solar energy utilization for seawater desalination and hydrogen production in the coastal areas of southern Iran. J. Eng. Des. Technol. 2020, 18, 1951–1969. [Google Scholar] [CrossRef]
- Gude, V.G. Desalination and sustainability–an appraisal and current perspective. Water Res. 2016, 89, 87–106. [Google Scholar] [CrossRef]
- Alkaisi, A.; Mossad, R.; Sharifian-Barforoush, A. A review of the water desalination systems integrated with renewable energy. Energy Procedia 2017, 110, 268–274. [Google Scholar] [CrossRef]
- Fornarelli, R.; Shahnia, F.; Anda, M.; Bahri, P.A.; Ho, G. Selecting an economically suitable and sustainable solution for a renewable energy-powered water desalination system: A rural Australian case study. Desalination 2018, 435, 128–139. [Google Scholar] [CrossRef]
- Bertsiou, M.; Feloni, E.; Karpouzos, D.; Baltas, E. Water management and electricity output of a hybrid renewable energy system (HRES) in Fournoi island in Aegean Sea. Renew. Energ. 2018, 118, 790–798. [Google Scholar] [CrossRef]
- Stoyanov, L.; Bachev, I.; Zarkov, Z.; Lazarov, V.; Notton, G. Multivariate Analysis of a Wind–PV-Based Water Pumping Hybrid System for Irrigation Purposes. Energies 2021, 14, 3231. [Google Scholar] [CrossRef]
- Ajiwiguna, T.A.; Lee, G.R.; Lim, B.J.; Cho, S.H.; Park, C.D. Optimization of battery-less PV-RO system with seasonal water storage tank. Desalination 2021, 503, 114934. [Google Scholar] [CrossRef]
- Das, P.; Das, B.K.; Rahman, M.; Hassan, R. Evaluating the prospect of utilizing excess energy and creating employments from a hybrid energy system meeting electricity and freshwater demands using multi-objective evolutionary algorithms. Energy 2022, 238, 121860. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements (No. 1275); US Department of Agriculture: Washington, DC, USA, 1962.
- Lagouvardos, K.; Kotroni, V.; Bezes, A.; Koletsis, I.; Kopania, T.; Lykoudis, S.; Mazarakis, N.; Papagiannaki, K.; Vougioukas, S. The automatic weather stations NOANN network of the National Observatory of Athens: Operation and database. Geosci. Data J. 2017, 4, 4–16. [Google Scholar] [CrossRef]
- ENERCON Product Overview. Available online: https://www.enercon.de/fileadmin/Redakteur/Medien-Portal/broschueren/pdf/en/ENERCON_Produkt_en_06_2015.pdf (accessed on 3 May 2022).
- Bertsiou, M.M.; Theochari, A.P.; Baltas, E. Multi-criteria analysis and geographic information systems methods for wind turbine siting in a North Aegean island. Energy Sci. Eng. 2021, 9, 4–18. [Google Scholar] [CrossRef]
- Van Sark, W.G.; Van der Velde, H.C.; Coelingh, J.P.; Bierbooms, W.A. Do we really need rotor equivalent wind speed? Wind Energy 2019, 22, 745–763. [Google Scholar] [CrossRef] [Green Version]
- Simão, M.; Ramos, H.M. Hybrid pumped hydro storage energy solutions towards wind and PV integration: Improvement on flexibility, reliability and energy costs. Water 2020, 12, 2457. [Google Scholar] [CrossRef]
- Rievaj, V.; Gaňa, J.; Synák, F. Is hydrogen the fuel of the future? Transp. Res. Proc. 2019, 40, 469–474. [Google Scholar] [CrossRef]
- Hausmann, J.N.; Schlögl, R.; Menezes, P.W.; Driess, M. Is direct seawater splitting economically meaningful? Energy Environ. Sci. 2021, 14, 3679–3685. [Google Scholar] [CrossRef]
- Abdelshafy, A.M.; Hassan, H.; Jurasz, J. Optimal design of a grid-connected desalination plant powered by renewable energy resources using a hybrid PSO–GWO approach. Energy Convers. Manag. 2018, 173, 331–347. [Google Scholar] [CrossRef]
- Rajalakshmi, N.; Jafri, R.I.; Dhathathreyan, K.S. Electrocatalysts for Low Temperature Fuel Cells, Fundamentals and Recent Trends; Wiley-VCH Verlag GmbH & Co., KGaA: Weinheim, Germany, 2017; pp. 35–74. [Google Scholar]
- Robinius, M.; Raje, T.; Nykamp, S.; Rott, T.; Müller, M.; Grube, T.; Katzenbach, B.; Küppers, S.; Stolten, D. Power-to-Gas: Electrolyzers as an alternative to network expansion–An example from a distribution system operator. Appl. Energy 2018, 210, 182–197. [Google Scholar] [CrossRef]
- Bhandari, B.; Lee, K.T.; Lee, G.Y.; Cho, Y.M.; Ahn, S.H. Optimization of hybrid renewable energy power systems: A review. Int. J. Precis. Eng. Manuf. Green Technol. 2015, 2, 99–112. [Google Scholar] [CrossRef]
- Rezk, H.; Sayed, E.T.; Al-Dhaifallah, M.; Obaid, M.; Abou Hashema, M.; Abdelkareem, M.A.; Olabi, A.G. Fuel cell as an effective energy storage in reverse osmosis desalination plant powered by photovoltaic system. Energy 2019, 175, 423–433. [Google Scholar] [CrossRef] [Green Version]
- Ma, T.; Javed, M.S. Integrated sizing of hybrid PV-wind-battery system for remote island considering the saturation of each renewable energy resource. Energy Convers. Manag. 2019, 182, 178–190. [Google Scholar] [CrossRef]
- Baruah, A.; Basu, M.; Amuley, D. Modeling of an autonomous hybrid renewable energy system for electrification of a township: A case study for Sikkim, India. Renew. Sustain. Energy Rev. 2021, 135, 110158. [Google Scholar] [CrossRef]
- He, Y.; Guo, S.; Zhou, J.; Wu, F.; Huang, J.; Pei, H. The quantitative techno-economic comparisons and multi-objective capacity optimization of wind-photovoltaic hybrid power system considering different energy storage technologies. Energy Convers. Manag. 2021, 229, 113779. [Google Scholar] [CrossRef]



| Component | Parameter | Value (unit) |
|---|---|---|
| WT [60] | Initial cost (EUR/kW) | 906 |
| Operation and maintenance cost (EUR/kW) | 136 | |
| Lifetime (years) | 25 | |
| Reservoir [61] | Initial cost (EUR/m3) | 154 |
| Operation and maintenance cost (EUR/m3) | 3.1 | |
| Lifetime (years) | 35 | |
| Hydro turbine [61] | Initial cost (EUR/kW) | 910 |
| Operation and maintenance cost (EUR/kW) | 18 | |
| Replacement cost (EUR/kW) | 910 | |
| Lifetime (years) | 10 | |
| Pumping station [61] | Initial cost (EUR/kW) | 217 |
| Operation and maintenance cost (EUR/kW) | 4.35 | |
| Replacement cost (EUR/kW) | 217 | |
| Lifetime (years) | 20 | |
| Hydrogen tank [54] | Initial cost (EUR/kg) | 1182 |
| Operation and maintenance cost (EUR/kg) | 13.6 | |
| Replacement cost (EUR/kW) | 1092 | |
| Lifetime (years) | 20 | |
| Electrolyzer [54] | Initial cost (EUR/kW) | 606 |
| Operation and maintenance cost (EUR/kW) | 1.8 | |
| Replacement cost (EUR/kW) | 455 | |
| Lifetime (years) | 5 | |
| Fuell cell [54] | Initial cost (EUR/kW) | 910 |
| Operation and maintenance cost (EUR/kW) | 0.02 | |
| Lifetime (years) | 25 | |
| Desalination unit [54] | Initial cost (EUR/m3/day) | 484 |
| Operation and maintenance cost (EUR/m3/day) | 0.32 |
| Key Parameter | PHS | HPHS |
|---|---|---|
| COE | 0.287 | 0.360 |
| COW | 1.680 | 2.108 |
| LOLPhres | 22.65 | 19.47 |
| LOLPel | 23.57 | 20.23 |
| LOLPd | 13.41 | 11.69 |
| LOLPir | 22.84 | 19.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertsiou, M.M.; Baltas, E. Power to Hydrogen and Power to Water Using Wind Energy. Wind 2022, 2, 305-324. https://doi.org/10.3390/wind2020017
Bertsiou MM, Baltas E. Power to Hydrogen and Power to Water Using Wind Energy. Wind. 2022; 2(2):305-324. https://doi.org/10.3390/wind2020017
Chicago/Turabian StyleBertsiou, Maria Margarita, and Evangelos Baltas. 2022. "Power to Hydrogen and Power to Water Using Wind Energy" Wind 2, no. 2: 305-324. https://doi.org/10.3390/wind2020017
APA StyleBertsiou, M. M., & Baltas, E. (2022). Power to Hydrogen and Power to Water Using Wind Energy. Wind, 2(2), 305-324. https://doi.org/10.3390/wind2020017






