The Benefit of Horizontal Photovoltaic Panels in Reducing Wind Loads on a Membrane Roofing System on a Flat Roof
Abstract
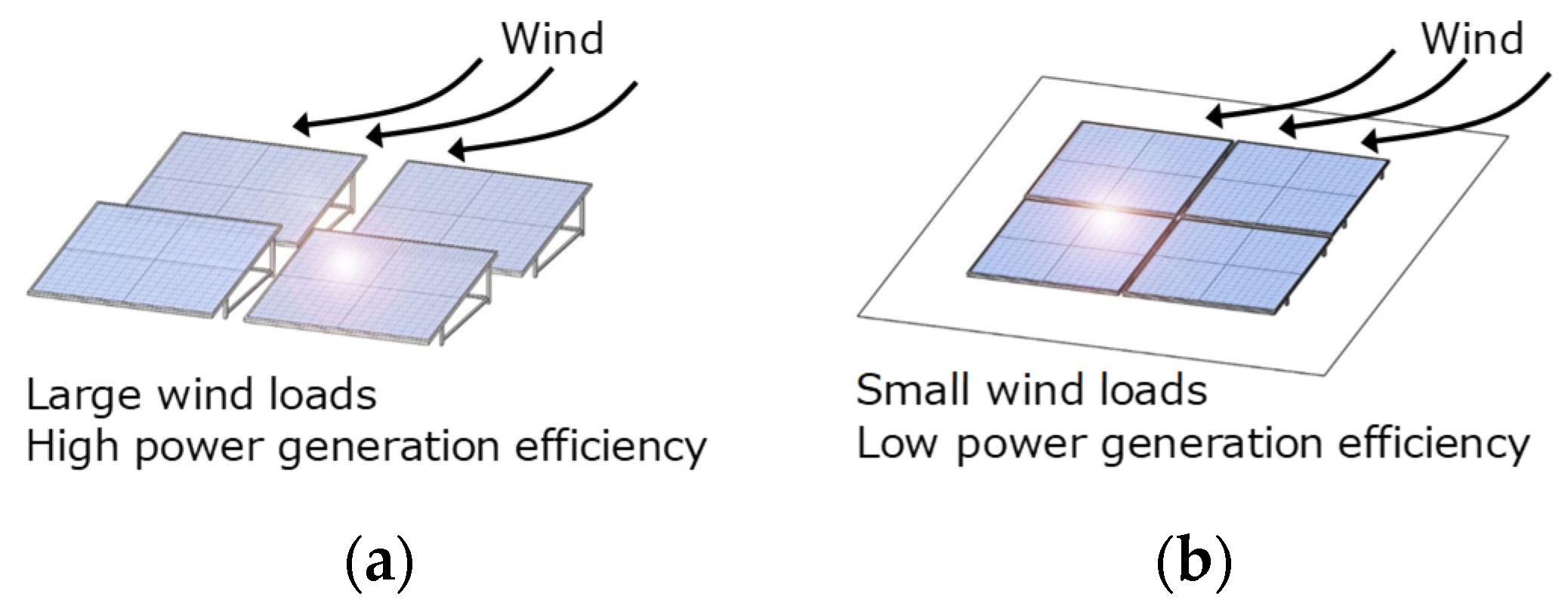
:1. Introduction
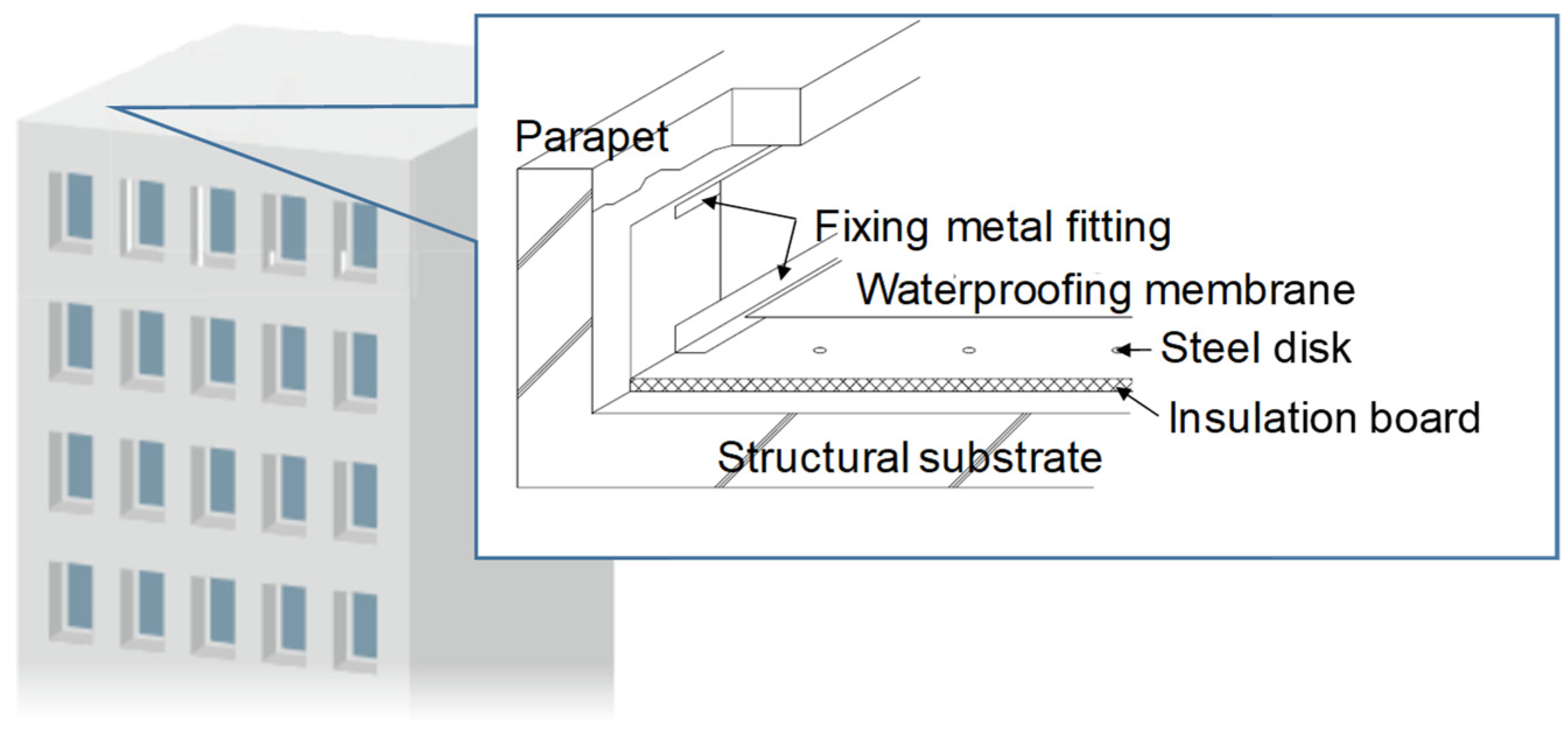
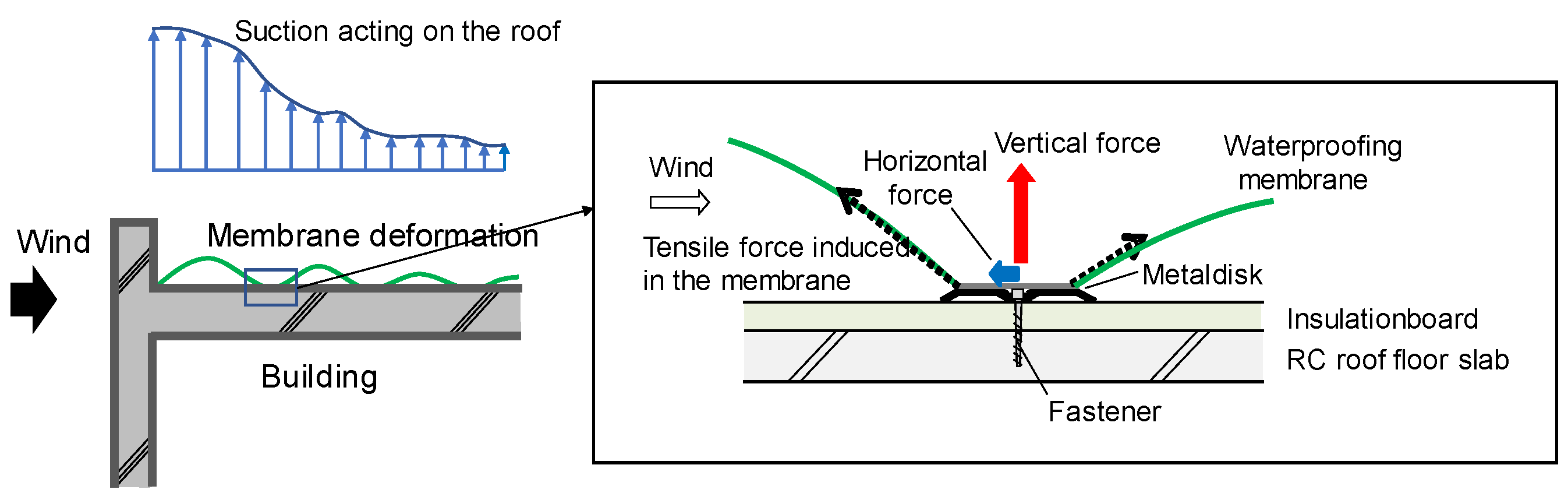
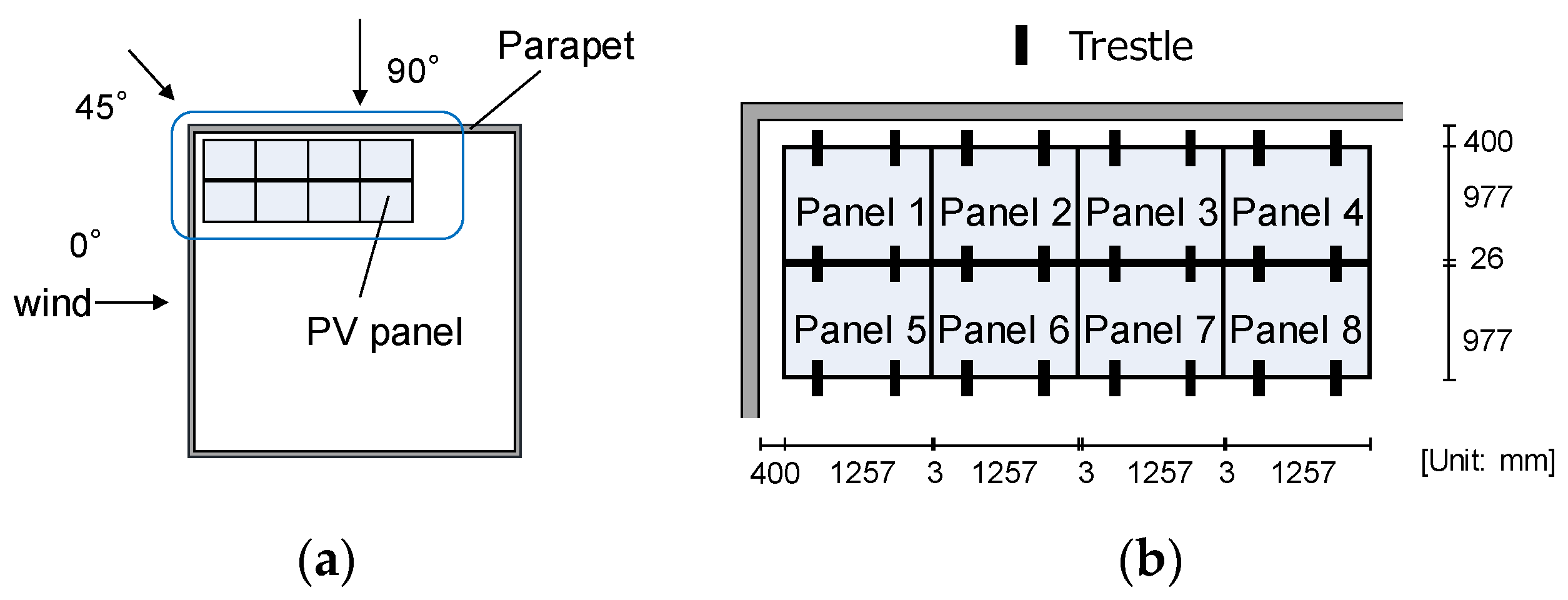
2. Investigated Building and Roofing System
3. Wind Tunnel Experiment of Wind Pressure Distributions
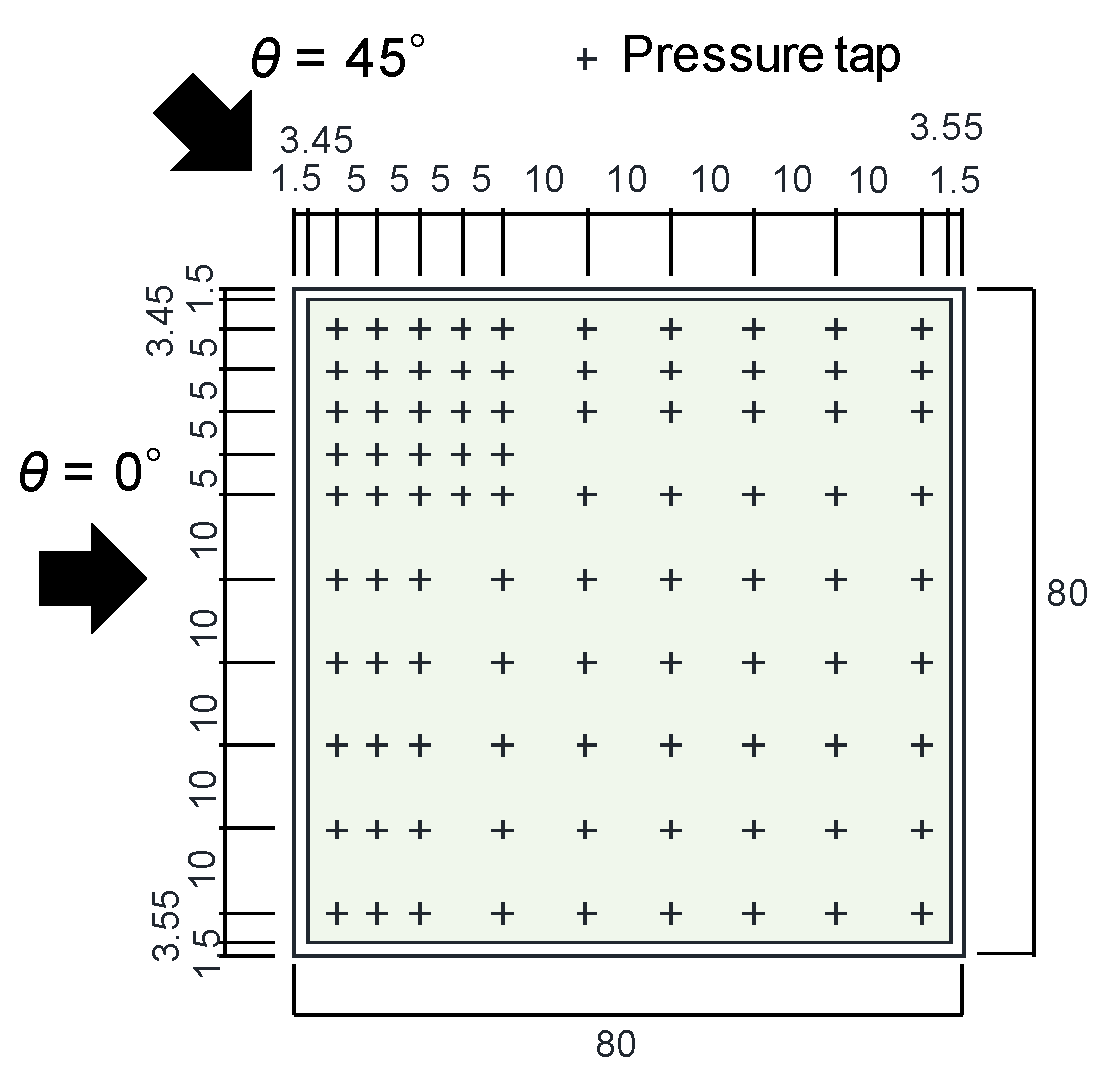
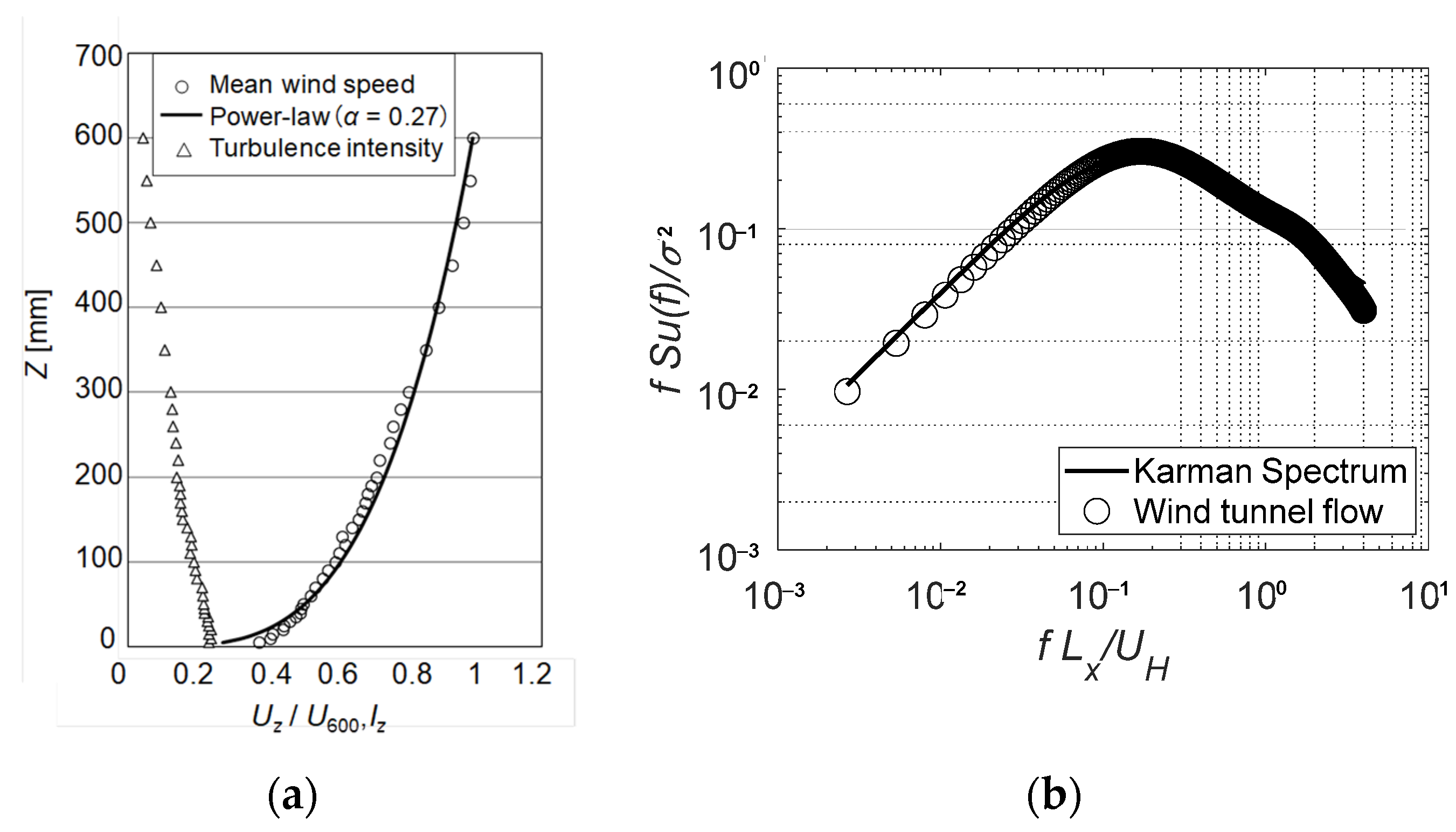
3.1. Experimental Method
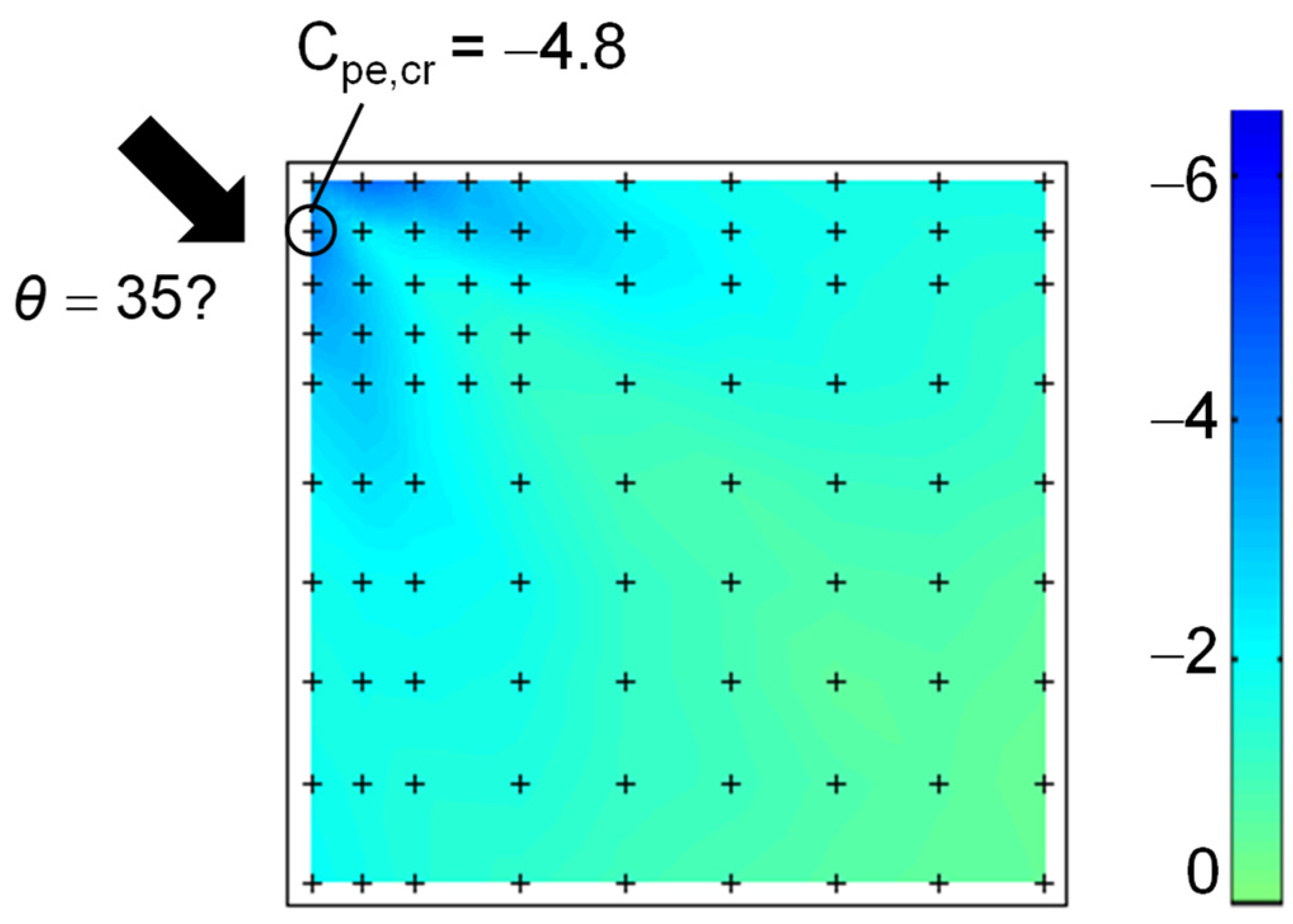
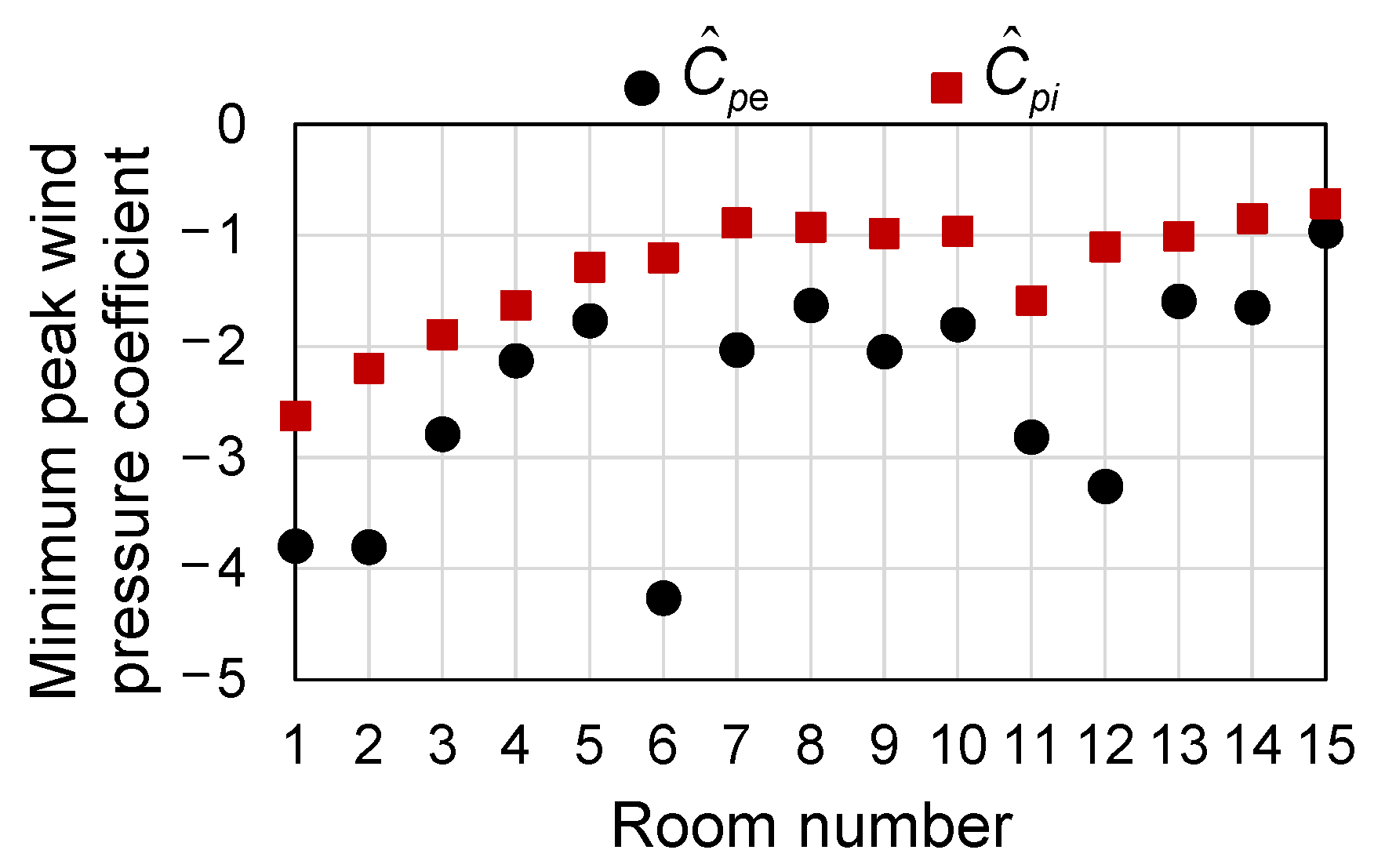
3.2. Experimental Results
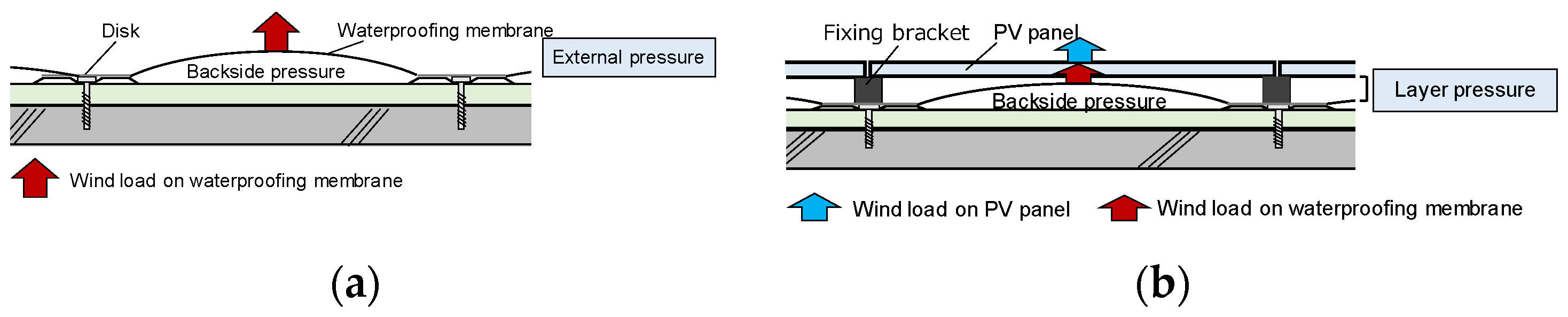
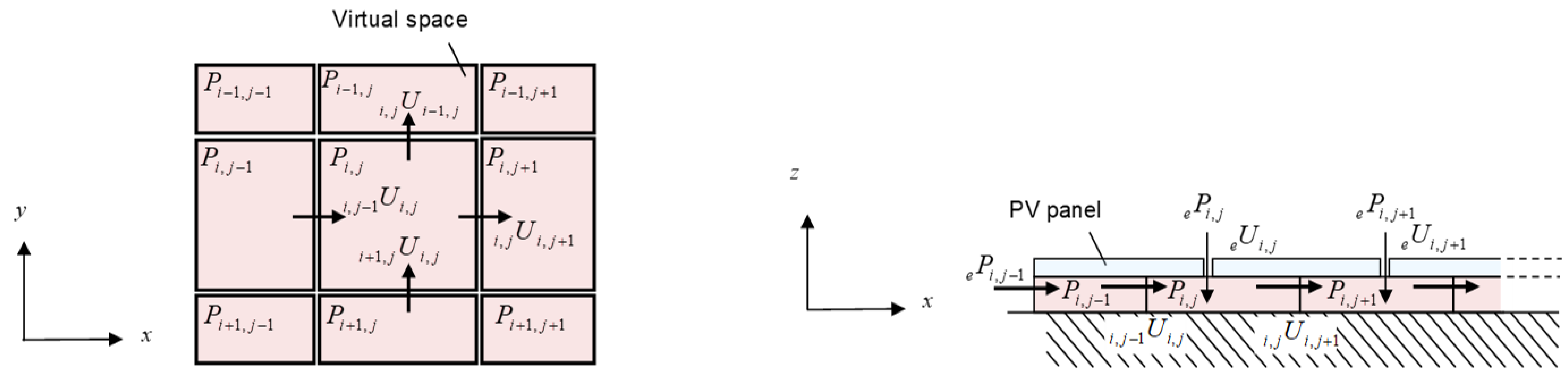
4. Simulation of Wind Pressures on PV Panels and Waterproofing Membrane
4.1. Method of Simulation
4.2. Results
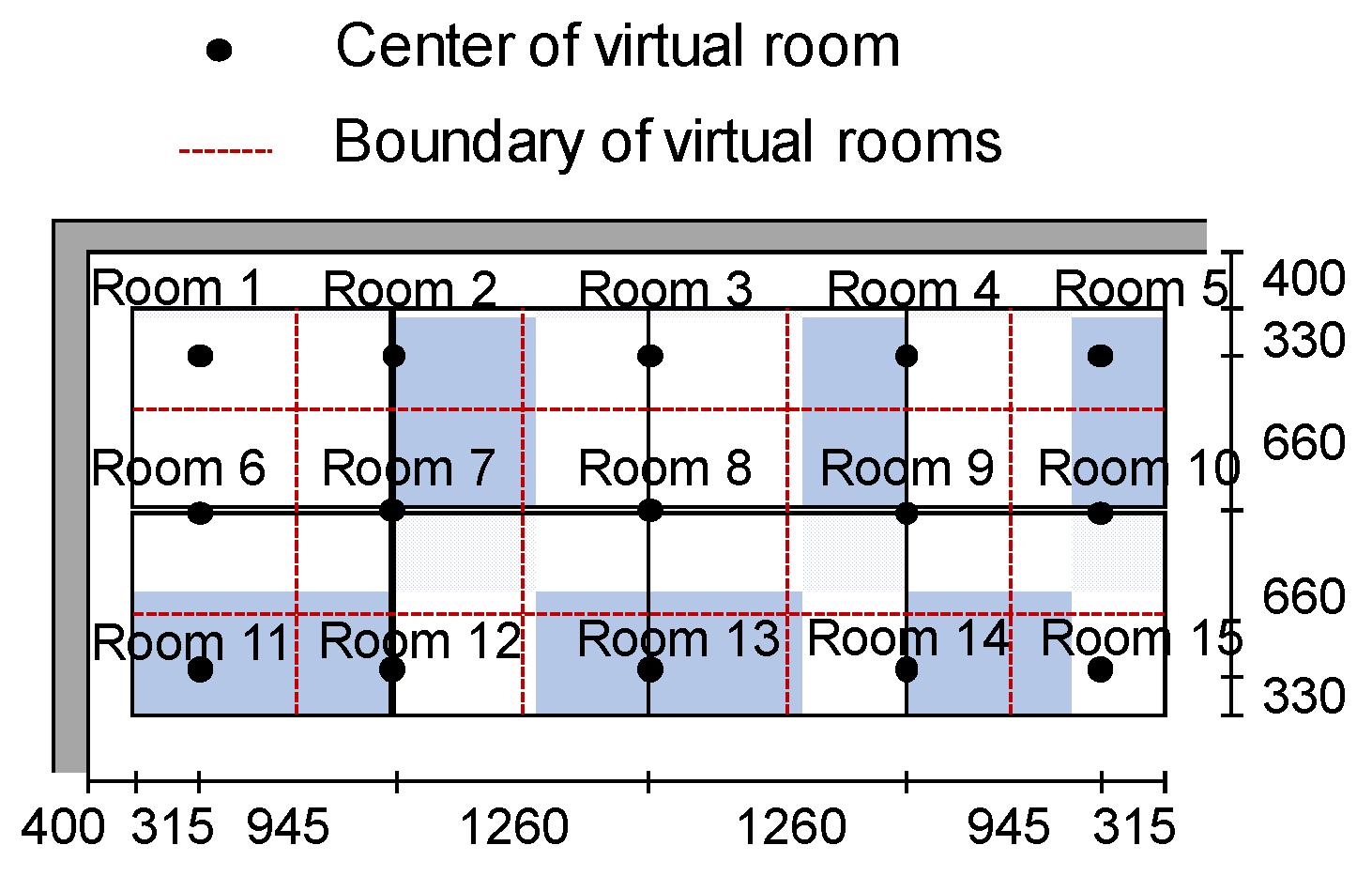
5. Finite Element Analysis of the Wind-Induced Behavior of the Roofing System
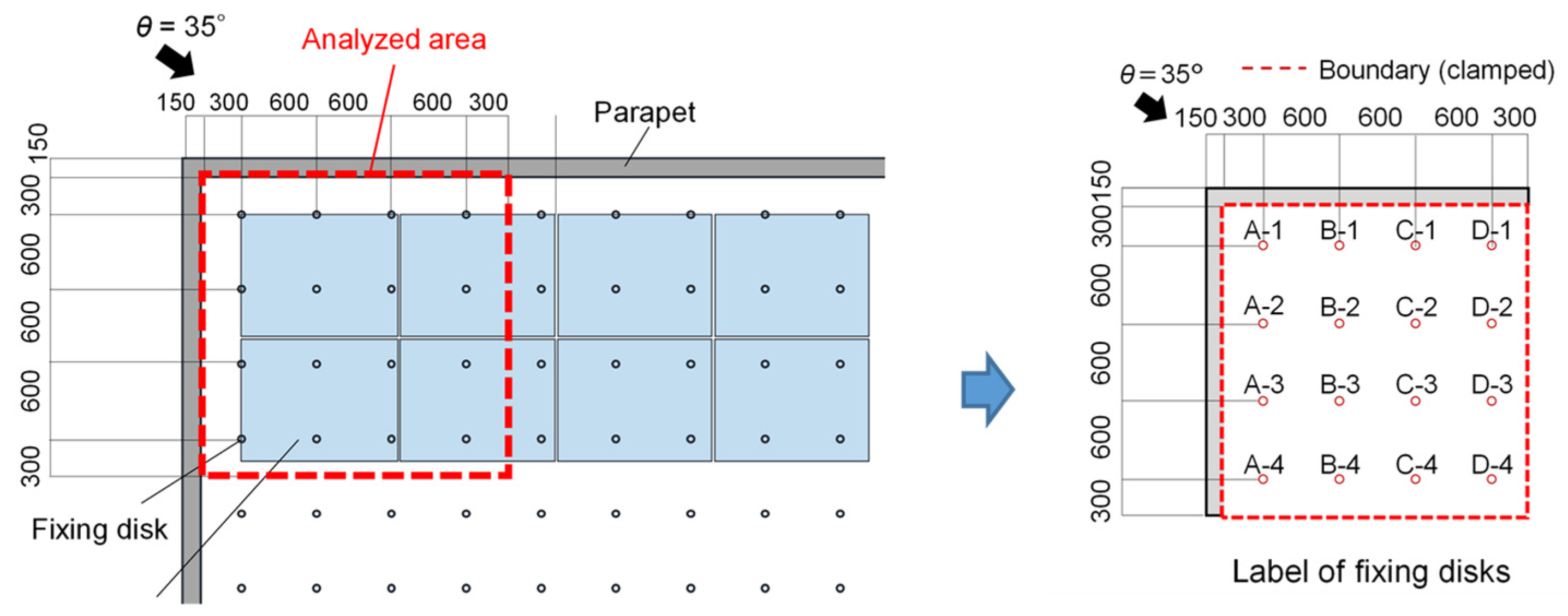
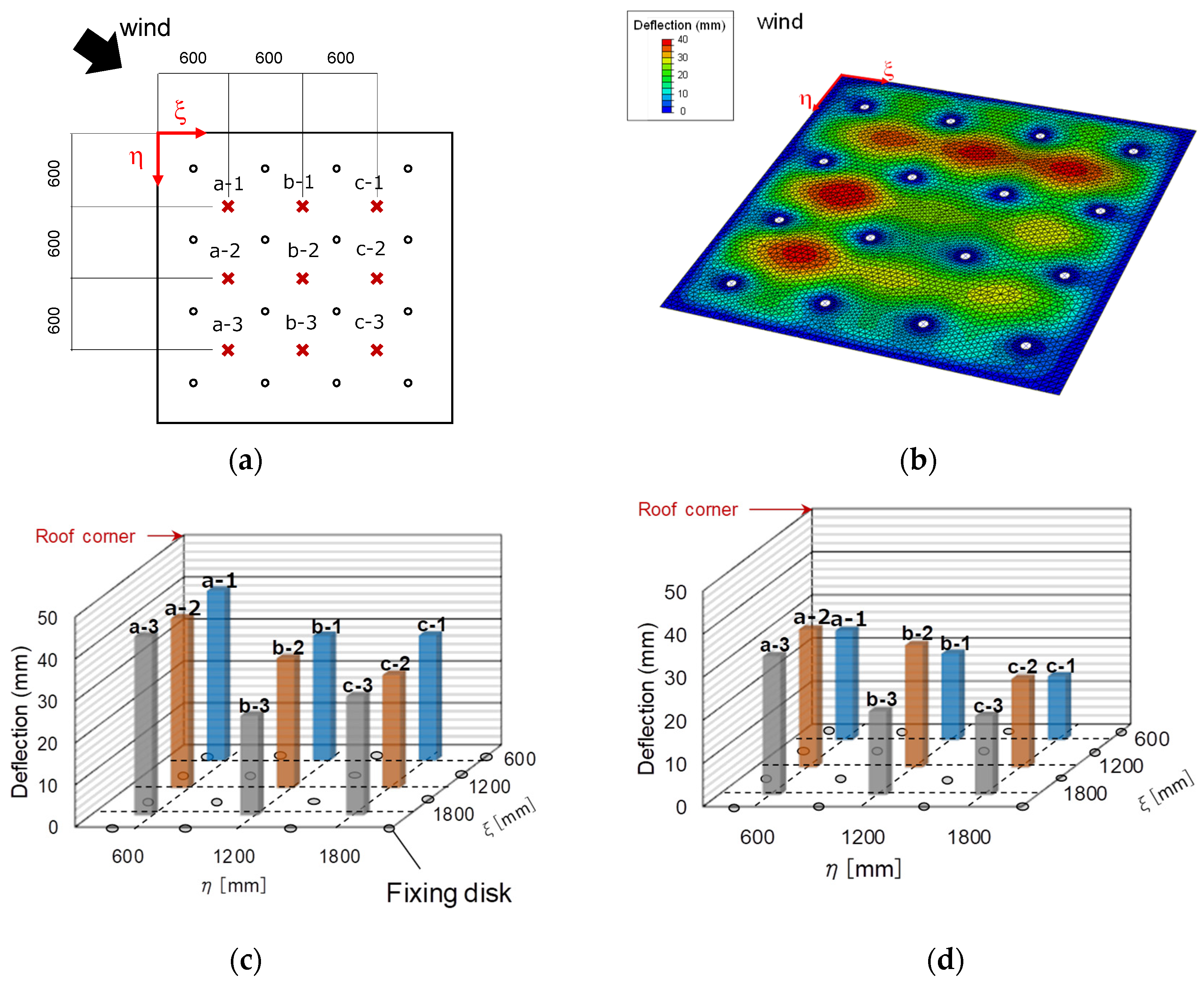
5.1. Analytical Model and Procedure
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baskaran, A.; Borujerdi, J. Application of numerical models to determine wind uplift ratings of roofs. Wind. Struct. Int. J. 2001, 4, 213–226. [Google Scholar] [CrossRef]
- Japan Association for Wind Engineering, Tokyo Polytechnic University. Manual of Wind Resistant Design for Photovoltaic System; Japan Association for Wind Engineering: Tokyo, Japan, 2017. (In Japanese) [Google Scholar]
- Architectural Institute of Japan. Wind Damage in 2004 and Lessons; Architectural Institute of Japan: Tokyo, Japan, 2006. (In Japanese) [Google Scholar]
- Cook, N. Dynamic response of single-ply membrane roofing systems. J. Wind. Eng. Ind. Aerodyn. 1992, 42, 1525–1536. [Google Scholar] [CrossRef]
- Gerhardt, H.; Kramer, C. Wind induced loading cycle and fatigue testing of lightweight roofing fixations. J. Wind. Eng. Ind. Aerodyn. 1986, 23, 237–247. [Google Scholar] [CrossRef]
- Gerhardt, H.J.; Kramer, C. Wind loading and fatigue behavior of fixings and bondings of roof coverings. J. Wind. Eng. Ind. Aerodyn. 1988, 29, 109–118. [Google Scholar] [CrossRef]
- Baskaran, A.; Chen, Y. Wind load cycle development for evaluating mechanically attached single-ply roofs. J. Wind. Eng. Ind. Aerodyn. 1998, 77–78, 83–96. [Google Scholar] [CrossRef]
- Baskaran, A.; Chen, Y.; Vilaipornsawai, U. A New Dynamic Wind Load Cycle to Evaluate Mechanically Attached Flexible Membrane Roofs. J. Test. Eval. 1999, 27, 249. [Google Scholar] [CrossRef]
- Miyauchi, H.; Katou, N.; Tanaka, K. Force transfer mechanism on fastener section of mechanically anchored waterproofing membrane roofs under wind pressure during typhoons. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 1174–1183. [Google Scholar] [CrossRef]
- Miyauchi, H.; Katou, N.; Tanaka, K. Behavior of a mechanically anchored waterproofing membrane system under wind suction and uniform pressure. Build. Environ. 2011, 46, 1047–1055. [Google Scholar] [CrossRef]
- Sugiyama, S.; Uematsu, Y.; Sato, K.; Usukura, T.; Ono, K. Development of a wind resistance performance test method for mechanically-attached waterproofing systems considering the time-space correlation of wind pressures. AIJ J. Technol. Des. 2019, 25, 585–589. (In Japanese) [Google Scholar] [CrossRef]
- Uematsu, Y.; Sugiyama, S.; Usukura, T. Wind-induced dynamic behavior of mechanically-attached single-ply membrane roofing systems installed on flat roofs. Eng. Sci. Technol. 2022, 3. (to be published). [Google Scholar]
- Kopp, G.A. Wind loads on low-profile, tilted, solar arrays placed on large, flat, low-rise building roofs. ASCE J. Struct. Eng. 2013, 140. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Q.; Tamura, Y. Effects of building parameters on wind loads on flat-roof-mounted solar arrays. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 210–224. [Google Scholar] [CrossRef]
- Alrawashdeh, H.; Stathopoulos, T. Wind loads on solar panels mounted on flat roofs: Effect of geometric scale. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104339. [Google Scholar] [CrossRef]
- Amano, T.; Fujii, K.; Tazaki, S. Wind loads on permeable roof-blocks in roof insulation systems. J. Wind. Eng. Ind. Aerodyn. 1988, 29, 39–48. [Google Scholar] [CrossRef]
- Oh, J.H.; Kopp, G.A.; Inculet, D.R. The UWO contribution to the NIST aerodynamic database for wind loads on low buildings: Part 3. Internal pressures. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 755–799. [Google Scholar] [CrossRef]
- Okada, H.; Ohkuma, T.; Katagiri, J. Study on estimation of wind pressure under roof tiles. J. Struct. Constr. Eng. Archit. Inst. Jpn. 2008, 73, 1943–1950. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Oh, J.-H.; Kopp, G.A. Modeling of spatially and temporary-varying cavity pressures in air-permeable, double-layer roof systems. Build. Environ. 2014, 82, 135–150. [Google Scholar] [CrossRef]
- Uematsu, Y.; Shimizu, Y.; Miyake, Y.; Kanegae, Y. Wind-induced scattering of permeable unit flooring decks loosely laid on rooftops and balconies of high-rise buildings. Tech. Trans. Civ. Eng. 2015, 2-B, 191–213. [Google Scholar]
- Yambe, T.; Uematsu, Y.; Sato, K.; Watanabe, T. Wind loads on photovoltaic systems installed parallel to the roof of flat-roofed building and its wind load reduction effect on the roofing system. AIJ J. Technol. Des. 2020, 26, 461–466. (In Japanese) [Google Scholar] [CrossRef]
- Yambe, T.; Uematsu, Y.; Sato, K. Wind Loads on Roofing System and Photovoltaic System Installed Parallel to Flat Roof. In STR-39, Proceedings of International Structural Engineering and Construction Holistic Overview of Structural Design and Construction, Limassol, Cyprus, 3–8 August 2020; Vacanas, Y., Danezis, C., Singh, A., Yazdani, S., Eds.; ISEC Press: Fargo, ND, USA, 2020. [Google Scholar]
- Lin, J.X.; Surry, D.; Tieleman, H.W. The distribution of pressure near roof corners of flat roof low buildings. J. Wind. Eng. Ind. Aerodyn. 1995, 56, 235–265. [Google Scholar] [CrossRef]
- Kawai, H.; Nishimura, G. Characteristics of fluctuating suction and conical vortices on a flat roof in oblique flow. J. Wind. Eng. Ind. Aerodyn. 1996, 60, 211–225. [Google Scholar] [CrossRef]
- Kawai, H. Structure of conical vortices related with suction fluctuation on a flat roof in oblique smooth and turbulent flows. J. Wind. Eng. Ind. Aerodyn. 1997, 69–71, 579–588. [Google Scholar] [CrossRef]
- Kawai, H. Local peak pressure and conical vortex on building. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 251–263. [Google Scholar] [CrossRef]
- Architectural Institute of Japan. Recommendations for Loads on Buildings; Architectural Institute of Japan: Tokyo, Japan, 2015. [Google Scholar]
- American Society of Civil Engineers. Wind Tunnel Testing for Buildings and Other Structures; ASCE/SEI 49-12; American Society of Civil Engineers: Reston, VA, USA, 2012. [Google Scholar]
- Lythe, G.; Surry, D. Wind loading of flat roofs with and without parapets. J. Wind. Eng. Ind. Aerodyn. 1983, 11, 75–94. [Google Scholar] [CrossRef]
- Baskaran, A.; Stathopoulos, T. Roof corner wind loads and parapet configurations. J. Wind. Eng. Ind. Aerodyn. 1988, 29, 79–88. [Google Scholar] [CrossRef]
- Furuichi, K.; Uematsu, Y.; Nakamura, S.; Sera, M. Evaluation of Dynamic Wind Loads for Mechanically-Attached Waterproofing Systems. In Proceedings of the 19th National Symposium on Wind Engineering, Tokyo, Japan, 29 November–1 December 2006. (In Japanese). [Google Scholar]
- Ueda, H.; Hibi, K.; Kikuchi, H. Simulation of wind induced internal pressures in low-rise buildings using the Poiseuille’s law for leak-flows. J. Struct. Constr. Eng. AIJ 2010, 75, 2115–2124. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Vickery, B.J. Gust-factors for internal pressures in low rise buildings. J. Wind. Eng. Ind. Aerodyn. 1986, 23, 259–271. [Google Scholar] [CrossRef]
- Gavanski, E.; Takahashi, N.; Uematsu, Y.; Morrison, M.J. Quantitative performance evaluation of time-varying wind pressure loading actuator. AIJ J. Technol. Des. 2015, 21, 1075–1080. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Oh, J.H.; Kopp, G.A. An experimental study of pressure equalization on double-layered roof system of low-rise buildings. In Proceedings of the 6th International Conference on Computational Wind Engineering, Hamburg, Germany, 8–12 June 2014. [Google Scholar]
- Watanabe, K.; Uematsu, Y. Evaluation of wind loads on ventilated exterior wall systems. J. Wind. Eng. 2014, 44, 23–32. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Yambe, T.; Yamamoto, A.; Uematsu, Y. Wind loads of photovoltaic panels mounted on a hip roof to the edge and their wind-load reduction effect on roof cladding. J. Struct. Constr. Eng. AIJ. to be published in December 2021 (In Japanese).
- Japanese Industrial Standard. Load Design Guide on Structures for Photovoltaic Array—JIS C 8955; Japanese Standard Association: Tokyo, Japan, 2017. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S.; Thomas, A.G.; Andrade, E.N.D.A. Large elastic deformations of isotropic materials VIII. Strain distribution around a hole in a sheet. Philosophical Transaction of the Royal Society of London, Series A. Math. Phys. Sci. 1951, 243, 289–298. [Google Scholar]

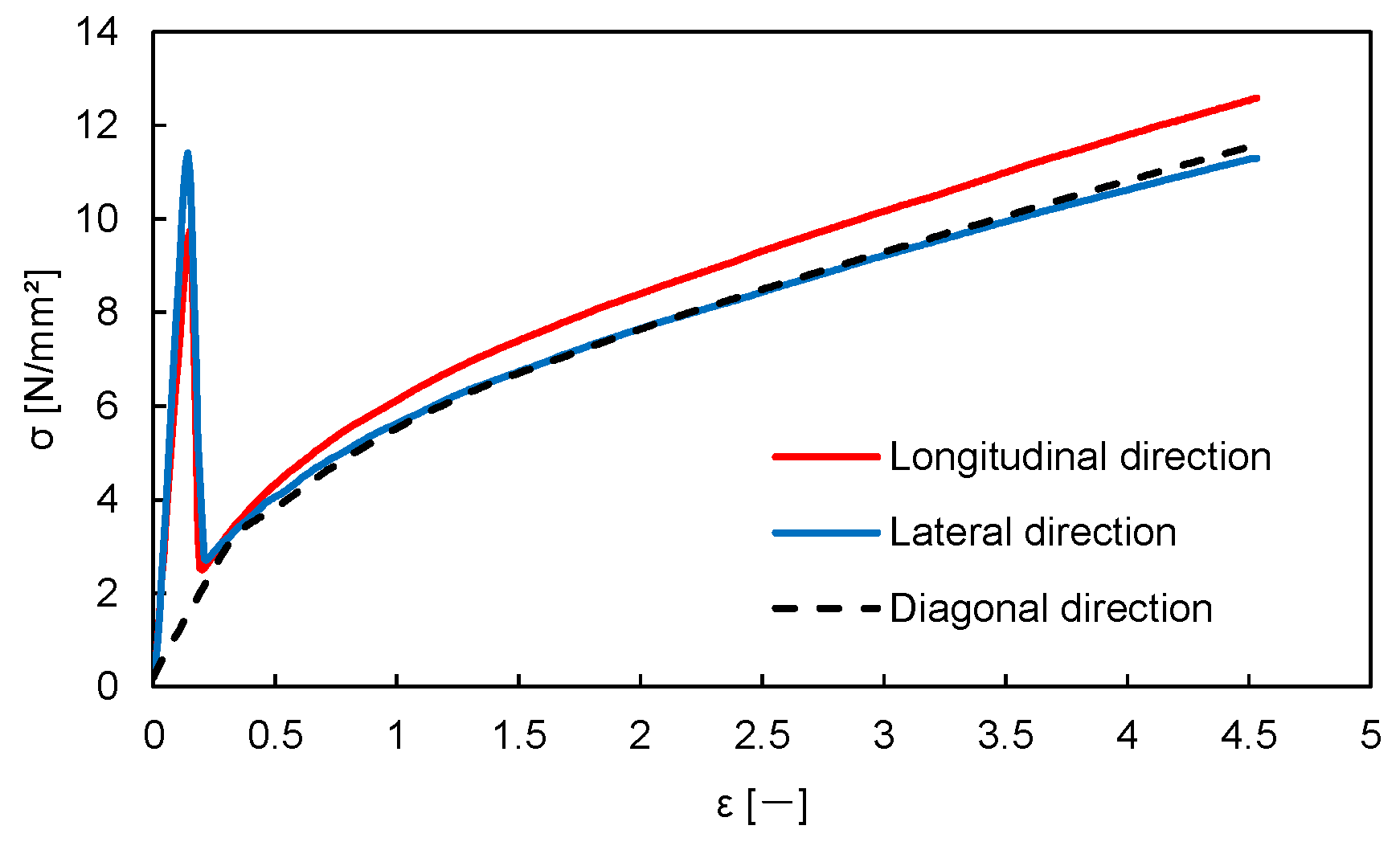





| Layer | t (mm) | E (N/mm2) | ν | G12 (N/mm2) | G23 (N/mm2) | G31 (N/mm2) | |
|---|---|---|---|---|---|---|---|
| Longitudinal | Lateral | ||||||
| PVC | 0.8 + 0.7 | 25.0 | 25.0 | 0.50 | 8.30 | 8.30 | 8.30 |
| Fiberglass | 0.01 | 65.0 | 70.3 | 0.24 | 0.001 | 28,000 | 28,000 |
| Fastener | Without PV Panels | With PV Panels | Reduction Rate (%) |
|---|---|---|---|
| A-1 | 770.2 | 599.9 | 22.1 |
| A-2 | 563.5 | 464.1 | 17.6 |
| A-3 | 576.9 | 478.5 | 17.1 |
| A-4 | 565.6 | 359.4 | 36.5 |
| B-1 | 618.5 | 385.2 | 37.7 |
| B-2 | 635.0 | 388.5 | 38.8 |
| B-3 | 605.1 | 450.8 | 25.5 |
| B-4 | 511.9 | 397.8 | 22.3 |
| C-1 | 726.5 | 509.0 | 29.9 |
| C-2 | 610.8 | 507.6 | 16.9 |
| C-3 | 399.4 | 287.4 | 28.0 |
| C-4 | 483.3 | 332.2 | 31.3 |
| D-1 | 599.7 | 419.2 | 30.1 |
| D-2 | 500.5 | 376.9 | 24.7 |
| D-3 | 386.1 | 270.9 | 29.8 |
| D-4 | 308.0 | 272.5 | 11.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uematsu, Y.; Yambe, T.; Watanabe, T.; Ikeda, H. The Benefit of Horizontal Photovoltaic Panels in Reducing Wind Loads on a Membrane Roofing System on a Flat Roof. Wind 2021, 1, 44-62. https://doi.org/10.3390/wind1010003
Uematsu Y, Yambe T, Watanabe T, Ikeda H. The Benefit of Horizontal Photovoltaic Panels in Reducing Wind Loads on a Membrane Roofing System on a Flat Roof. Wind. 2021; 1(1):44-62. https://doi.org/10.3390/wind1010003
Chicago/Turabian StyleUematsu, Yasushi, Tetsuo Yambe, Tomoyuki Watanabe, and Hirokazu Ikeda. 2021. "The Benefit of Horizontal Photovoltaic Panels in Reducing Wind Loads on a Membrane Roofing System on a Flat Roof" Wind 1, no. 1: 44-62. https://doi.org/10.3390/wind1010003
APA StyleUematsu, Y., Yambe, T., Watanabe, T., & Ikeda, H. (2021). The Benefit of Horizontal Photovoltaic Panels in Reducing Wind Loads on a Membrane Roofing System on a Flat Roof. Wind, 1(1), 44-62. https://doi.org/10.3390/wind1010003






