Abstract
Can we accurately model the spin state of a quantum particle? If so, we should be able to make identical copies of such a state and also obtain its mirror image. In quantum mechanics, many subatomic particles can form entangled pairs that are mirror images of each other, although the state of an individual particle cannot be duplicated or cloned as experimentally demonstrated by Aspect, Clauser and Zeilinger, the winners of the Nobel Prize in Physics 2022. We show that there is a higher-order symmetry associated with the SL(2,C) group that underlies the singlet state, which means that the singlet pairing preserves Lorentz transformations independently of the metric used. The Pauli exclusion principle can be derived from this symmetry.
1. Introduction
Entanglement is not an easy concept to grasp. At times, it is discussed in terms of the joint spin state of two particles with total spin angular momentum zero, but this is misleading in that it fails to grasp that the spin-singlet state is best conceived as a single entity and not as the outcome of summing two independent spin states. Indeed, therein lies the difficulty associated with the Einstein-Podolsky-Rosen paradox (EPR ). Considering such a state as composed of two statistically independent particles whose spin sums to zero (or a fixed constant) leads to a contradiction associated with Bell’s inequality, while in contrast, to consider an entangled state as constituting a new thing is not intuitively obvious. A singlet state is composed of a pair of particles that are mirror images of each other, yet they are not constructible by first specifying the details of one particle and then taking its image. The individual particles constitutive of the singlet state cannot be cloned [1,2,3]. As a pair, they constitute a rotationally invariant pure state (defined below). This characteristic of not being able to specify separately the properties of each particle composing the singlet is what we shall now explore, and in doing so try to elicit a top-down approach to quantum theory.
The existence of entanglement requires the addition of a new axiom to quantum mechanics connected with the nature of correlations. Singlet-state particles are correlated with each being a mirror image of the other in that, if an observation of a certain variable is performed on one, we instantaneously know the outcome on the second particle without having to perform another observation. Mathematically speaking, this means that we can write down two commuting operators for correlated particles regardless of their reference frame. In fact, the singlet state is unique in that it is an eigenstate with eigenvalue 1 for every element of the group SL(2,C) and consequently is Lorentz invariant [4]. It also means that from a mathematical perspective, the principle of micro-causality is violated in that commutative operators have at least one eigenvector in common. However, it does not mean that signals can be transmitted faster than the speed of light. There is no violation of the laws of physics. Commuting or partially commuting operators imply shared eigenvectors and shared eigenvectors imply two operators with similar characteristics, both classically and from a relativistic point of view. Singlet state particles conserve Lorentz invariance but as a higher order symmetry, meaning Lorentz invariance requires that a singlet state remains as a singlet state. We now investigate this in more detail and derive Fermi–Dirac statistics as a consequence of this invariance.
2. Mathematical Methods: Grasping the Difficulty, the Issue of Hidden Variables
What is the nature of entanglement? Briefly put, we can say that two or more particles are entangled if the wave function defined over a Hilbert Space is a pure state. In other words, it is not factorable. If the state is partially factorable, we can say that the state is a mixed state or partially entangled. Finally, if the state representing n particles can be written as a tensor product of n factors, then the state is not entangled. For example, in the case of three particles:
- (1)
- ,
- (2)
- with and entangled,
- (3)
- , as a product of factors, is not an entangled state.
Note that in the case of (1) and (2) there are other possibilities for defining pure and mixed states. It should also be noted that, while it is possible mathematically to have an infinite number of pure states, this does not necessarily mean they are realizable in physics. Our main interest in this article is related to rotationally invariant states. This means that for a quantum state in a Hilbert space R = , for R SO(2), where SO(2) represents the rotation group. For example, the two states and defined over a two-dimensional Hilbert space, where are orthogonal, are rotationally invariant in that
and
The rotational invariance also means that they are isotropically spin-correlated (ISC) states, in that, if a spin measurement is made in an arbitrary direction on one of the particles by a polarizer or a Stern-Gerlach device, the spin measurement in the same direction on the other particle is known with probability one. Indeed, in the case of the singlet state, it follows from the rotational invariance and the quantum-mechanical definition of probability over a Hilbert space that for sequential measurements made at an angle (Figure 1) with respect to the two different particles.
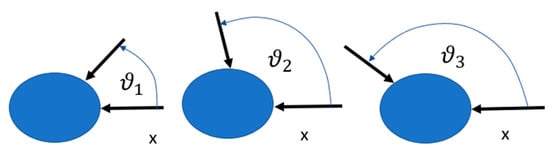
Figure 1.
Stern-Gerlach measurements in three directions on three ISC particles.
While in the case of the parallel state
Since, the theory works for all values of , without loss of generality we let . Note that for photons , while in the case of electrons = ½.
If by means of a wave function, it were possible to give a complete specification of a single particle then we should be able to replicate n identical copies of the same particle by repeating the specification process n times. Einstein believed that such a specification must necessarily involve “hidden variables [5]” and that the probability rules expressed by Equations (1) and (2) were not dependent upon the rotational invariance. Consequently, ISC states did not really exist and were merely a cloak for ignorance. The true state should be for parallel spin and for anti-parallel spin values. However, if the uncertainty principle is a real physical phenomenon, and would ontologically speaking represent the true state.
Either way, we expect the laws of probability to work. Consequently, from the Einsteinian perspective two or more independent particles can exist in principle and obey the same conditional probability rules (1) and (2). The difference will be in the underlying cause. From Einstein’s reductionist point of view, the set of properties associated with a single particle should determine the characteristics of each particle, whereas, from the strict quantum mechanical point of view, the relationship between the particles sublates their individual properties by adding something new that transcends any individual particle. Bell’s inequality or some variation thereof has become the standard methodological procedure for deciding between the two different epistemologies. A practical consequence of this, using red and green lights, can be found in reference [6].
2.1. A Coupling Principle
To distinguish the two approaches, we note that if the states are separable it should be possible in the case of three particles to construct a probability distribution , where for , = u (for “up”) or = d (for “down”) and is a random variable associated with the two orthogonal spin states and , both of which can be determined by a hidden variable. Without loss of generality, we can create (define) the two factorable states or but because of our initial ignorance, we express this as . Since any two particles in this latter state are pairwise ISC then all three particles are ISC by definition, and three independent observations can be made at angles , measured with respect to the x-axis (Figure 1). A total of eight observations are possible and are given by
S = {(u, u, u), (u, u, d), (u, d, u), (d, u, u), (u, d, d), (d, u, d), (d, d, u), (d, d, d)}.
Now consider the two subsets of observations given respectively by
A = {(u, u, d), (u, d, d)) and B = {(u, u, d), (u, d, d), (d, u, d), (u, d, u)}.
Clearly, A ⊂ B implies P(A) P(B). Moreover,
Therefore, by summing over the two different marginal probabilities in B and letting , we obtain from Equations (2)
which is a form of Bell’s inequality. Indeed, on taking and gives ¾ < ½, a contradiction [7]. This contradiction is a consequence of assuming that particle states are statistically independent and determined by “hidden parameters.” We conclude that statistically speaking they are not independent and that there are no intrinsic parameters in Einstein’s sense of the words. Moreover, this result was confirmed by the work of Aspect, Clauser and Zeilinger, winners of the Nobel Prize in Physics 2022 “for experiments with entangled photons, establishing the violation of Bell’s inequalities.”
P(A) = P(u, u, d) + P(u, d, d) = P(u,.,d)P[(.,u,.)|(u,., d)]+P(u,., d)P[(.,d,.)|(u,.,d)]
= P(u,.,d)[P[(.,u,.)|(u,.,d)]+P[(.,d,.)|(u,.,d)]
= P(u,.,d) having summed over the marginal distribution.
= P(u,.,d)[P[(.,u,.)|(u,.,d)]+P[(.,d,.)|(u,.,d)]
= P(u,.,d) having summed over the marginal distribution.
Another important result also follows. The contradiction has arisen by assuming that three (or more) ISC-observable states in the Einsteinian sense can coexist. The contradiction implies that three or more such states cannot exist. However, because the proof also prohibits hidden variables it follows that paired ISC particles must be of the form or and not or , otherwise, the individual states would be completely specifiable by a hidden variable, which is precisely what Bell’s inequality eliminates. We formulate this as a key methodological principle or law [7]: In multiple particle systems, isotropically spin correlated particles must occur in pairs.
2.2. An Intuitive Model
An intuitive example should help. Consider two adjoined walls forming an interior angle ϑ such that each wall is randomly painted red on one side and green on the other (Figure 2a,b). If we randomly choose a wall and look at one side, then the probability P(R) = P(G) = ½. If we now ask, what is the probability that two colors face each other it is possible to have two green walls facing each other and separated by an interior angle , which also means that the two reds are adjoined with respect to the exterior angle 2π − or vice versa. We can then define a probability model related to the interior (or exterior) angles by and .
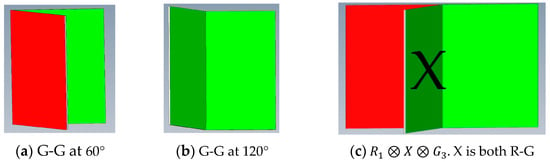
Figure 2.
Diagrams of adjoining walls. Each wall is red on one side and green on the other.
Now consider three walls with interior angles such that walls 1 and 2 have the same color facing each other and walls 2 and 3 have the same colors facing each other (Figure 2c). Translated into our color code this means that we have either the joint (superimposed) state and ( or the joint (superimposed) state and . However, although the problem is well-posed it becomes ill-posed if we try to write it as a triplet . We are in difficulty since seen from wall 1 is and seen from wall 3 is (Figure 2c). If we insist on imposing an absolute value on we arrive at an EPR paradox. The solution to avoiding the paradox is by introducing SO(2) relativity into paired states. Translated into the language of vectors it means replacing with and with which means the rotationally invariant state can be written as either . Moreover, the relativity effect also preserves the coupling. Only paired faces can have the same color. In the case of three walls, we either have the joint (superimposed) state and ( or the joint (superimposed) and ). This should serve as a more intuitive model for understanding entanglement.
Although useful, it still does not fully capture the quantum situation. In a classical sense, we not only know that the walls are facing each other but we can observe whether this pairing is or ) as in Figure 2c and avoid having to write a triplet In this sense, the characteristic of “facing each other” is merely an accident or what we call an epiphenomenon. Its real cause is a consequence of a random distribution of colors. One can then use the laws of conditional probability based on observations to avoid any contradiction. The only reason for writing the state of “facing each other” as a superimposed entangled state, is that we have not made an observation, although it is possible to do so. In this case, the superimposed state is merely a cloak for ignorance.
Quantum mechanics is something else. In principle, we cannot observe the way in which the walls are “facing each other.” Particles in the singlet are truly entangled and this is encapsulated by the action of the SO(2) group on the ISC states. It is intrinsically invariant in all frames of reference and therefore characterizes a true physical and geometrical property independent of any observer. The relativity effect associated with “facing each other” means that the ISC state is more than the sum of its individual parts. The rotational invariance is a property of the joint state but not of any individual particle. Indeed, the individual properties only emerge when an observer intervenes and breaks the symmetry.
In terms of quantum spin, we can pursue our analogy a bit further by replacing “red” and “green” with “up” and “down” and ask what is the difference between them if we are standing respectively at the north and the south poles? Usually, we indicate vectors as directed line segments with respect to an orthogonal coordinate system, in which case two vectors are equal when they point in the same direction and are (additive) inverses of each other when they point in the opposite directions. From the perspective of a Cartesian plane, what is “up” at the north pole is really “down” from the perspective of the south pole for a vector defined with respect to the axis of rotation and vice versa. Again, in this case, the problem of consistency will emerge for an outside observer for whom (u,d) only has a relative meaning with respect to an origin.
The quantum mechanical interpretation avoids the problem by not distinguishing between right and left, up or down, and interior or exterior angles in that for ISC states = and = They are invariant under SO(2). With only this information, spin states are indistinguishable. There is no difference between them from a probability point of view. When we in the laboratory frame make such a distinction, we do so by breaking the rotational invariance of the ISC coupling. Every observation is an act of symmetry breaking. Indeed, the principle of superposition for a single particle in the singlet allows for four possibilities:
- (1)
- (2)
- (3)
- (4)
which in the case of ISC states are the same for all four representations because of the rotational invariance. When it comes to these states, there is no preferred direction. It is only by way of observation that symmetry is broken and one direction prevails over another.
2.3. Method: What Is Happening Mathematically?
If Einstein’s viewpoint had been correct then for the event , re-indexed (to help readability) as we obtain having summed over the marginal probability densities in position (2). In other words, we would have implicitly assumed the validity of the Chapman–Kolmogorov (CK) equation that ∑, where the summation over k would correspond to the summation over ‘’ and ‘’ in the above equation. However, if we are to avoid a contradiction as above, this law cannot be considered valid for quantum spin theory. We might ask the reason why.
Mathematically, denoting an arbitrary rotation in the plane by , we then have on summing over k that ∑, which represents the product of two rotation matrices. Written in this form, it implies that the CK equation applies to rotations but not to the corresponding probability equations associated with these rotations. This means that when it comes to entanglement, we cannot sum over “well-defined” states because, in fact, they are not well-defined but are dependent upon the relative interior as well as the relative exterior angle of measurement analogous to the red and green walls above, already encapsulated in Equations (1) and (2). More specifically, since
it follows that Therefore the CK equations are not necessarily valid for quantum probabilities because they are derived from L² and not L¹ functions. The squaring process highlights the fact that values expressed by (u,u) and (d,d) cannot be distinguished and are analogous to having the colors (R,R) or (G,G) facing each other on adjoining walls. Briefly put, the Einstein model anticipates that the Markov property ∑applies whereas the quantum model anticipates that ∑. They are not compatible because of the squaring process.
3. Results
3.1. Relation between the Pauli Exclusion Principle and the Coupling Principle
One consequence of the mathematical contradiction involved with Bell’s inequality is the coupling principle, which states: isotropically spin-correlated particles must occur in pairs [7]. If confined to the plane, it allows for two possible (spinor conjugate) states: and . Both are invariant under rotations. If we require full symmetry under the action of SL(2,C) of which rotations form a subgroup then the coupling principle must necessarily imply the singlet state [8]. If extended to an n-particle system then we will find that the Fermi–Dirac statistic is the unique state that is invariant under the action of SL(n,C) [8]. Intuitively, it means that Fermi–Dirac states are composed of indistinguishable pairs. This version of the spin-statistics theorem is different from that of Pauli’s in that spin value is not the issue but rather the rotational invariance of the singlet state. Pauli’s derivation relied on the principle of micro-causality as applied to independent Klein–Gordan and Dirac fields, which translated into mathematical language meant that two observable operators must necessarily commute or anti-commute respectively beyond the light cone. However, because of the nature of entanglement, spin operators S(1) and S(2) associated with two different particles commute beyond the light cone when measured at the same angle and anti-commute only when orthogonal. Consequently, Pauli’s derivation is not applicable in this case. Indeed, Pauli notes “that for integral spin the quantization according to the exclusion principle is not possible. For this result it is essential that the use of the function in place of the function be, for general reasons, discarded” [9]. However, the “general reason” for discarding is the principle of micro-causality, which is not applicable to entangled operators.
3.2. Incorporating Entanglement into General Relativity
The first thing to note is that the singlet state is SL(2,C) invariant as is the metric of special relativity. Consequently, singlet states are Lorentz invariant. Secondly, when extended to general relativity by using the vierbien method the Lorentz invariance is maintained locally for all singlet states. However, since entanglement involves paired particles, it is important to realize that we are also dealing with a two-body problem considered as a single entity. Thirdly, it is important to realize that paired entanglement is a characteristic of all particles with spin regardless of the fields in which they are embedded. Specifically, if we have a linearized metric of the form 𝜉 = ds𝜉, where obey the Dirac algebra and ds is a differential eigenvalue of 𝜉, then for a singlet state we have (₁,)(ξ₁𝜉₂) = ds₁ds₂(ξ₁𝜉₂). Note that when the two components of the singlet state coalesce then = ds2. In the language of limits as then ds₁ds₂ ds2. Moreover, if both bodies have mass and we let m₁ and m₂, we obtain the representation of the singlet state in Minkowski space. A generalized Dirac equation may be obtained by taking the dual of the metric [10].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Park, J. The concept of transition in quantum mechanics. Foun. Phys. 1970, 1, 23–33. [Google Scholar] [CrossRef]
- Dieks, D. Communication by EPR devices. Phys. Lett. A 1982, 92, 271–272. [Google Scholar] [CrossRef]
- Wootters, W.; Zurek, W. A Single Quantum Cannot be Cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- O’Hara, P. The Einstein-Podolsky-Rosen paradox and SU(2) relativity. J. Phys. Conf. Ser. 2019, 1239, 012021. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen Paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Mermin, N.D. Quantum mysteries revisited. Am. J. Phys. 1990, 58, 731–734. [Google Scholar] [CrossRef]
- O’Hara, P. Rotational Invariance and the Spin Statistics Theorem. Foun. Phys. 2003, 33, 1349–1368. [Google Scholar] [CrossRef]
- O’Hara, P. A generalized spin statistics theorem. J. Phys. Conf. Ser. 2017, 845, 012030. [Google Scholar] [CrossRef]
- Pauli, W. The Connection Between Spin and Statistics. Phys. Rev. 1940, 58, 716–722. [Google Scholar] [CrossRef]
- O’Hara, P. Quantum Mechanics and the Metrics of General Relativity. Foun. Phys. 2005, 35, 1563–1584. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).