Nuclear Pasta in Cold Non-Accreting Neutron Stars: Symmetry Energy Effects †
Abstract
1. Introduction
2. Methods
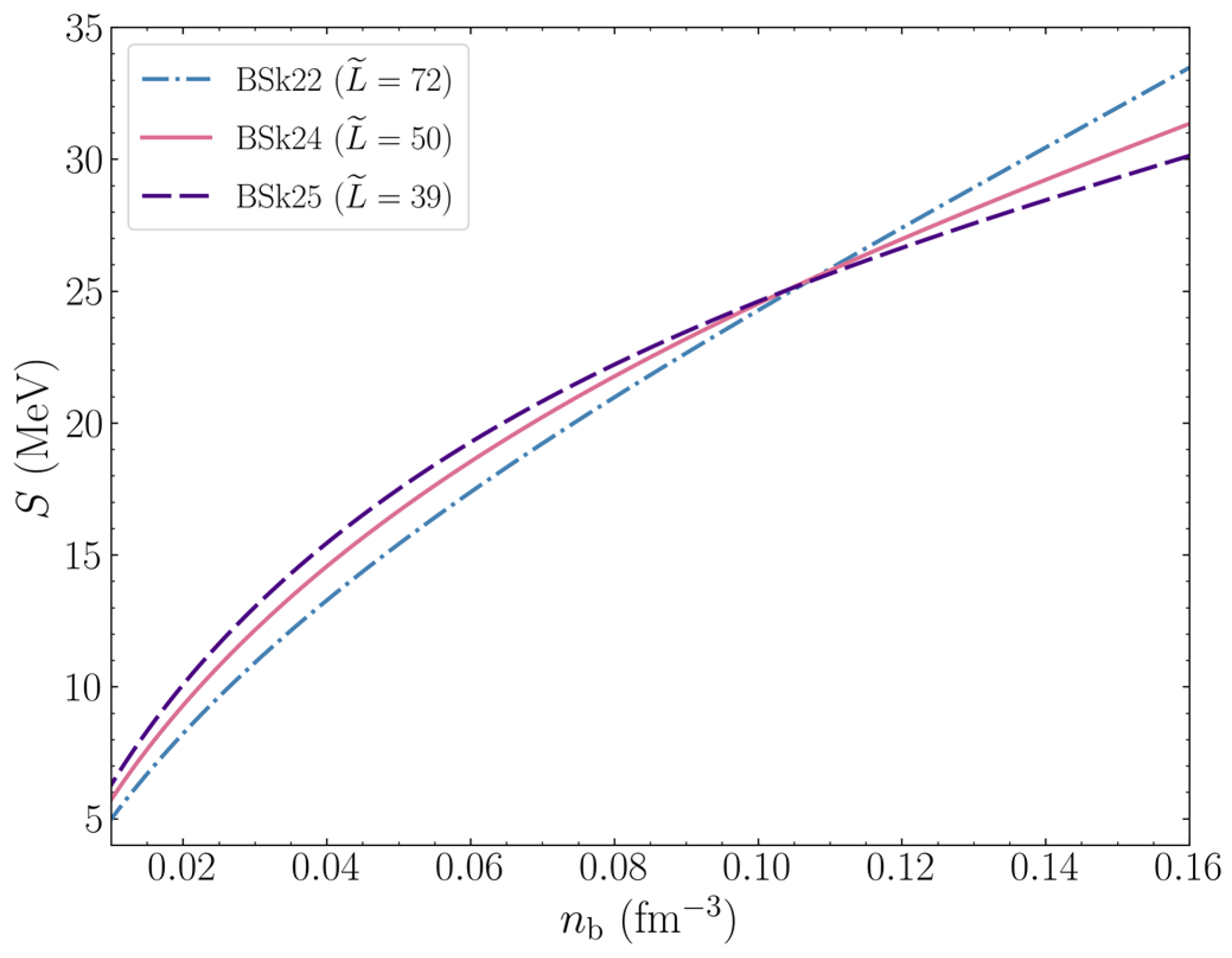
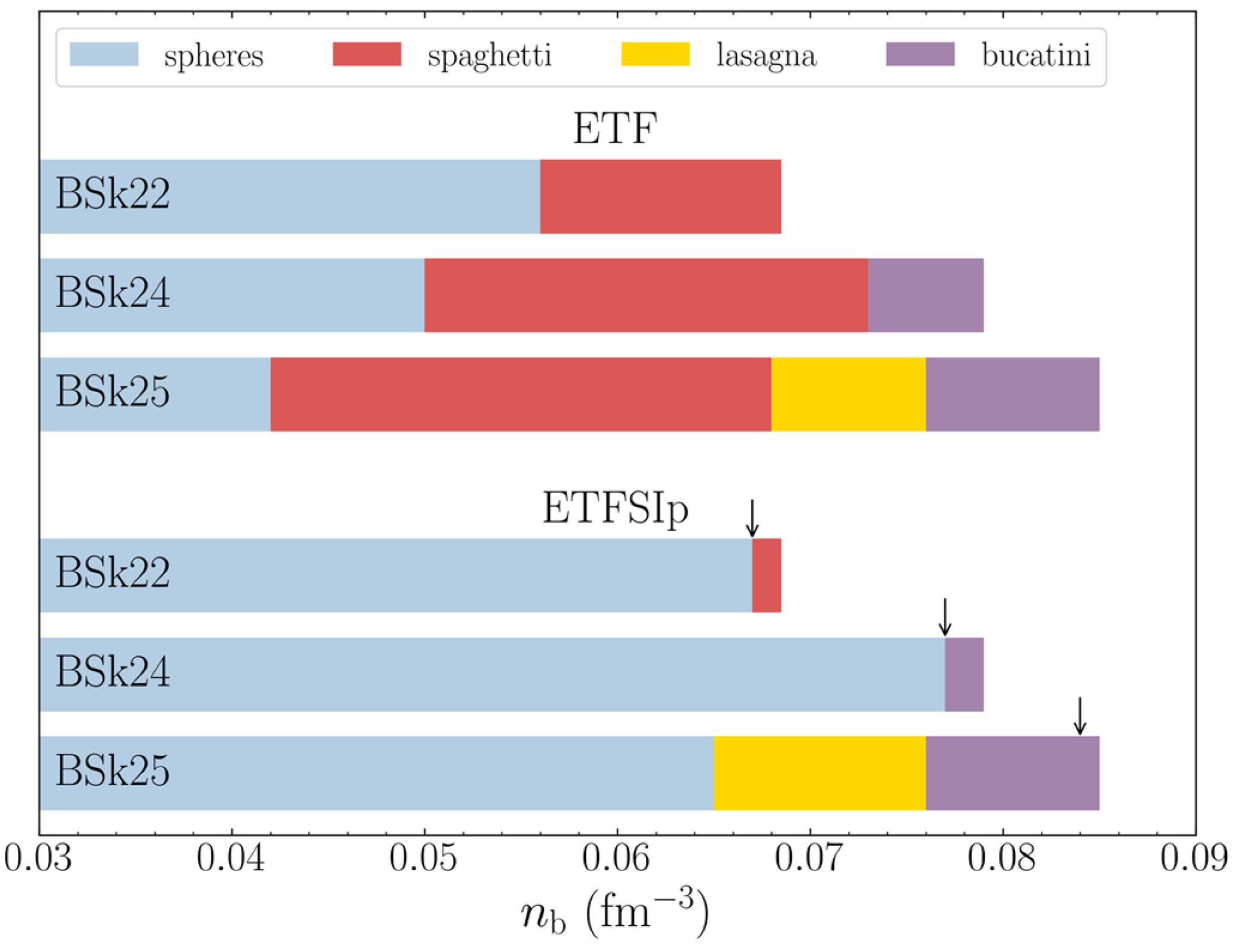
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ravenhall, D.G.; Pethick, C.J.; Wilson, J.R. Structure of Matter below Nuclear Saturation Density. Phys. Rev. Lett. 1983, 50, 2066–2069. [Google Scholar] [CrossRef]
- Hashimoto, M.; Seki, H.; Yamada, M. Shape of nuclei in the crust of a neutron star. Prog. Theor. Phys. 1984, 71, 320–326. [Google Scholar] [CrossRef]
- Dinh Thi, H.; Fantina, A.F.; Gulminelli, F. The effect of the energy functional on the pasta-phase properties of catalysed neutron stars. Eur. Phys. J. A 2021, 57, 296. [Google Scholar] [CrossRef]
- Newton, W.G.; Gearheart, M.; Li, B.A. A Survey of the Parameter Space of the Compressible Liquid Drop Model as Applied to the Neutron Star Inner Crust. Astrophys. J. Suppl. Ser. 2013, 204, 9. [Google Scholar] [CrossRef]
- Oyamatsu, K.; Iida, K. Symmetry energy at subnuclear densities and nuclei in neutron star crusts. Phys. Rev. C 2007, 75, 015801. [Google Scholar] [CrossRef]
- Grill, F.; Providência, C.; Avancini, S.S. Neutron star inner crust and symmetry energy. Phys. Rev. C 2012, 85, 055808. [Google Scholar] [CrossRef]
- Bao, S.S.; Shen, H. Impact of the symmetry energy on nuclear pasta phases and crust-core transition in neutron stars. Phys. Rev. C 2015, 91, 015807. [Google Scholar] [CrossRef]
- Shchechilin, N.N.; Zemlyakov, N.A.; Chugunov, A.I.; Gusakov, M.E. Pasta Phases in Neutron Star Mantle: Extended Thomas–Fermi vs. Compressible Liquid Drop Approaches. Universe 2022, 8, 582. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Schuetrumpf, B. Quantum nuclear pasta and nuclear symmetry energy. Phys. Rev. C 2017, 95, 055804. [Google Scholar] [CrossRef]
- Gögelein, P.; Müther, H. Nuclear matter in the crust of neutron stars. Phys. Rev. C 2007, 76, 024312. [Google Scholar] [CrossRef]
- Pethick, C.J.; Potekhin, A.Y. Liquid crystals in the mantles of neutron stars. Phys. Lett. B 1998, 427, 7–12. [Google Scholar] [CrossRef]
- Yakovlev, D.G. Electron transport through nuclear pasta in magnetized neutron stars. Mon. Not. R. Astron. Soc. 2015, 453, 581–590. [Google Scholar] [CrossRef]
- Caplan, M.E.; Horowitz, C.J. Colloquium: Astromaterial science and nuclear pasta. Rev. Mod. Phys. 2017, 89, 041002. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Berry, D.K.; Briggs, C.M.; Caplan, M.E.; Cumming, A.; Schneider, A.S. Disordered Nuclear Pasta, Magnetic Field Decay, and Crust Cooling in Neutron Stars. Phys. Rev. Lett. 2015, 114, 031102. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D.; Rea, N. A highly resistive layer within the crust of X-ray pulsars limits their spin periods. Nat. Phys. 2013, 9, 431–434. [Google Scholar] [CrossRef]
- Gearheart, M.; Newton, W.G.; Hooker, J.; Li, B.A. Upper limits on the observational effects of nuclear pasta in neutron stars. Mon. Not. R. Astron. Soc. 2011, 418, 2343–2349. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XIII. The 2012 atomic mass evaluation and the symmetry coefficient. Phys. Rev. C 2013, 88, 024308. [Google Scholar] [CrossRef]
- Audi, G.; Meng, W.; Wapstra, A.; Kondev, F.; MacCormick, M.; Xu, X.; Pfeiffer, B. The Ame2012 atomic mass evaluation. Chin. Phys. C 2012, 36, 1287. [Google Scholar] [CrossRef]
- Li, Z.H.; Schulze, H.J. Neutron star structure with modern nucleonic three-body forces. Phys. Rev. C 2008, 78, 028801. [Google Scholar] [CrossRef]
- Brack, M.; Guet, C.; Håkansson, H.B. Selfconsistent semiclassical description of average nuclear properties—A link between microscopic and macroscopic models. Phys. Rep. 1985, 123, 275–364. [Google Scholar] [CrossRef]
- Onsi, M.; Dutta, A.K.; Chatri, H.; Goriely, S.; Chamel, N.; Pearson, J.M. Semi-classical equation of state and specific-heat expressions with proton shell corrections for the inner crust of a neutron star. Phys. Rev. C 2008, 77, 065805. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Pastore, A.; Goriely, S. Role of proton pairing in a semimicroscopic treatment of the inner crust of neutron stars. Phys. Rev. C 2015, 91, 018801. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals—I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Chamel, N.; Goriely, S.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XI Stabilizing neutron stars against a ferromagnetic collapse. Phys. Rev. C 2009, 80, 065804. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. III. Inclusion of microscopic corrections to pasta phases. Phys. Rev. C 2022, 105, 015803. [Google Scholar] [CrossRef]
- Ducoin, C.; Margueron, J.; Providência, C. Nuclear symmetry energy and core-crust transition in neutron stars: A critical study. Europhys. Lett. 2010, 91, 32001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shchechilin, N.N.; Pearson, J.M.; Chamel, N. Nuclear Pasta in Cold Non-Accreting Neutron Stars: Symmetry Energy Effects. Phys. Sci. Forum 2023, 7, 10. https://doi.org/10.3390/ECU2023-14017
Shchechilin NN, Pearson JM, Chamel N. Nuclear Pasta in Cold Non-Accreting Neutron Stars: Symmetry Energy Effects. Physical Sciences Forum. 2023; 7(1):10. https://doi.org/10.3390/ECU2023-14017
Chicago/Turabian StyleShchechilin, Nikolai N., John M. Pearson, and Nicolas Chamel. 2023. "Nuclear Pasta in Cold Non-Accreting Neutron Stars: Symmetry Energy Effects" Physical Sciences Forum 7, no. 1: 10. https://doi.org/10.3390/ECU2023-14017
APA StyleShchechilin, N. N., Pearson, J. M., & Chamel, N. (2023). Nuclear Pasta in Cold Non-Accreting Neutron Stars: Symmetry Energy Effects. Physical Sciences Forum, 7(1), 10. https://doi.org/10.3390/ECU2023-14017






