f(R,T) Gravity and Constant Jerk Parameter in FLRW Spacetime †

Abstract

It is well known that the universe is undergoing accelerated expansion during recent times and that it underwent a decelerated expansion in early times. The deceleration parameter, essentially the second derivative of the scale factor, can be used to describe these eras, with a negative parameter for acceleration and a positive parameter for deceleration. Apart from the standard $\Lambda$CDM model in general relativity, there are many cosmological models in various other theories of gravity. In order to describe these models, especially the deviation from general relativity, the jerk parameter was introduced, which is basically the third derivative of the scale factor. In the $\Lambda$CDM model in general relativity, the jerk parameter j is constant, and $j=1$. The constant jerk parameter, $j=1$, leads to two different scale factor solutions, one power law and the other exponential. The power-law solution corresponds to a model in which our universe expands with deceleration, while the exponential solution corresponds to a model in which it expands by accelerating. In this study, the cosmological consequences of such a selection of the jerk parameter on the non-minimally coupled $f(R,T)$ theory of gravity (where R is the Ricci scalar, and T is the trace of the energy–momentum tensor) and the dynamic properties of these models are investigated on a flat Friedmann–Lemaitre–Robertson–Walker backgfround.

1. Introduction

It is known that while our universe was in a period of decelerated expansion in the past, it has been in a period of accelerated expansion during recent times. The accelerated expansion has been indicated by several astrophysical observations [1,2,3,4]. Einstein’s General Relativity (GR) cannot adequately explain this late-time acceleration. Therefore, various suggestions have been put forward to explain this acceleration. One of them is the concept of dark energy (DE), which connects accelerated expansion to an energy of unknown nature with negative pressure. Apart from the standard $\Lambda$ cold dark matter ($\Lambda$CDM) model in GR, in this framework, various DE terms are added to the energy–momentum tensor on the right-hand side of Einstein’s field equations [5,6,7,8,9,10,11,12,13]. Another attempt to explain this accelerated expansion is modified gravitation theories. Amongst these, $f(R,T)$ theory is important because it is a modified theory through a function that depends on both the curvature (R) and the matter source T [14]. In other words, the geometry–matter coupling is considered in $f(R,T)$ theory. In this theory, various universe models are studied by taking different forms of the $f(R,T)$ function. However, in general, it would not be wrong to say that non-minimally coupling forms are less considered [15,16,17,18].

In the present study, we consider $f(R,T)$ gravity on the background of the flat Friedman–Lemaitre–Robertson–Walker (FLRW) universe for a non-minimal coupling form, such as $f\left(R,T\right)=f_1\left(R\right)+f_2\left(R\right)f_3\left(T\right)$. To solve the field equations, we assume that the jerk parameter j is constant, and $j=1$. One of the two solutions to this assumption corresponds to the past period when the universe expanded by decelerating, and the other corresponds to the late period when it expanded by accelerating. In Section 2, the field equations of $f(R,T)$ gravity are given, the solutions of the field equations and their consequences are derived in Section 3, and the conclusion is formed in Section 4.

2. Field Equations of $\mathit{f}(\mathit{R},\mathit{T})$ Gravity

The $f(R,T)$ gravity field equations are based on the gravitational action [14]

$$S=\int \sqrt{-g}{d}^{4}x\left(\frac{1}{16\pi }f(R,T)+L_m\right),$$

(1)

where $f(R,T)$ is an arbitrary function of the Ricci scalar R and trace T of the energy–momentum tensor $T_{ij}$, g is the determinant of the metric tensor $g_{ij}$, and $L_m$ is the Lagrange density of the matter. The variation in the gravitational action S in Equation (1) with respect to the metric $g^{ij}$ gives the field equations of $f(R,T)$ gravity:

$$f_R(R,T)R_{ij}-\frac{1}{2}f(R,T)g_{ij}-({\nabla }_i{\nabla }_j-g_{ij}\square )f_R(R,T)=8\pi T_{ij}-f_T(R,T)(T_{ij}+{\Theta }_{ij}).$$

(2)

Here, ${\nabla }_i$ is the covariant derivative, $\square \equiv {\nabla }^i{\nabla }_i$ is the d’Alembertian operator, and $f_R(R,T)=\frac{\partial f(R,T)}{\partial R}$, $f_T(R,T)=\frac{\partial f(R,T)}{\partial T}$, and ${\Theta }_{ij}=g^{ab}\frac{\delta T_{ab}}{\delta g^{ij}}$ with

$$T_{ij}=-\frac{2}{\sqrt{-g}}\frac{\delta \left(\sqrt{-g}{L}_m\right)}{\delta g^{ij}}=L_m{g}_{ij}-2\frac{\delta L_m}{\delta g^{ij}}.$$

(3)

When calculating the variation, $L_m$ is taken to depend only on the metric tensor and not on its derivatives. If the matter assumed to fill the universe is considered to be a perfect fluid, then the energy–momentum tensor attached to it is

$$T_{ij}=(\rho +p)u_i{u}_j-p{g}_{ij}.$$

(4)

where $\rho$ and p is the energy density and pressure, respectively, and $u_i$ ($u^i{u}_i=1$) is the four-velocity vector of the fluid. When the matter’s Lagrangian $L_m=-p$ is taken, ${\Theta }_{ij}$ becomes

$${\Theta }_{ij}=-2T_{ij}-p{g}_{ij}.$$

(5)

Substituting this into Equation (2), the field equations take the form

$$f_R(R,T)R_{ij}-\frac{1}{2}f(R,T)g_{ij}-({\nabla }_i{\nabla }_j-g_{ij}\square )f_R(R,T)=8\pi T_{ij}+f_T(R,T)(T_{ij}+p{g}_{ij}).$$

(6)

Three different functional forms of the function $f(R,T)$ are considered in the study in Ref. [14]. In this study, we adopt the last of the forms (which is not usually chosen):

$$f(R,T)=f_1\left(R\right)+f_2\left(R\right)f_3\left(T\right),$$

(7)

where $f_i$ ($i=1,2,3.$) are arbitrary functions of their arguments. In this case, the field equations’ Equation (6) becomes:

$$\begin{array}{c}[f_1^{\prime }\left(R\right)+f_2^{\prime }\left(R\right)f_3\left(T\right)]R_{ij}-\frac{1}{2}{f}_1\left(R\right)g_{ij}+[g_{ij}\square -{\nabla }_i{\nabla }_j][f_1^{\prime }\left(R\right)+f_2^{\prime }\left(R\right)f_3\left(T\right)]\hfill \\ \hfill =[8\pi +f_2\left(R\right)f_3^{\prime }\left(T\right)]T_{ij}+f_2\left(R\right)[f_3^{\prime }\left(T\right)p+\frac{1}{2}{f}_3\left(T\right)]g_{ij}.\end{array}$$

(8)

Here, a prime (${}^{\prime }$) denotes a derivative with respect to the argument for any $f_i$ function. Now, we customize the functional form even more, taking it as

$$f_1\left(R\right)+f_2\left(R\right)f_3\left(T\right)=R+\lambda RT,$$

(9)

to obtain

$$\begin{array}{c}\hfill R_{ij}-\frac{1}{2}{g}_{ij}R=\frac{8\pi +\lambda R}{(1+\lambda T)}{T}_{ij}-\frac{\lambda }{(1+\lambda T)}[g_{ij}\square -{\nabla }_i{\nabla }_j]T+\frac{\lambda R}{(1+\lambda T)}p{g}_{ij},\end{array}$$

(10)

where $\lambda$ is a coupling constant. If $\lambda =0$ is put into Equation (10), it is clearly seen that the equations are reduced to the field equations of GR.

On the other hand, the usual conservation equation of GR is not valid in this theory, but it takes the following form for Equation (9) [18]:

$$(8\pi +\lambda R)\dot{\rho }+3H(p+\rho )=-\frac{\lambda R}{2}(\dot{\rho }-\dot{p})-\lambda \dot{R}(\rho +p)$$

(11)

where $H=\dot{a}/a$ is the Hubble parameter.

3. Modified Field Equations in the Flat FLRW Background

The homogeneous and isotropic flat FLRW metric is

$$d{s}^2=d{t}^2-a^2\left(t\right)(d{x}^2+d{y}^2+d{z}^2),$$

(12)

where $a\left(t\right)$ is the time-dependent scale factor. For the flat FLRW model, the modified field equations defined in Equation (10) lead to the following two independent equations

$$3H^2=8\pi \rho -3\lambda H(\dot{\rho }-3\dot{p})-3\lambda H^2(\rho -3p)-6\lambda (\dot{H}+2H^2)(\rho +p),$$

(13)

$$2\dot{H}+3H^2=-8\pi p-\lambda (2\dot{H}+3H^2)(\rho -3p)-\lambda (\ddot{T}-2H\dot{T}),$$

(14)

The trace of Equation (4) gives $T=\rho -3p$; hence, we have $\dot{T}=\dot{\rho }-3\dot{p}$ and $\ddot{T}=\ddot{\rho }-3\ddot{p}$. Substituting these expressions into Equation (14), we obtain

$$2\dot{H}+3H^2=-8\pi p^{tot}=-8\pi p-\lambda (2\dot{H}+3H^2)(\rho -3p)-\lambda [\ddot{\rho }-3\ddot{p}-3H(\dot{\rho }-3\dot{p})],$$

(15)

As can be seen, this last equation includes not only $\rho$ and p, but also their first and second derivatives with respect to time. To remove this mathematical difficulty, by adopting the barotropic EoS $p=\omega \rho$, we can rewrite Equation (11) as

$$\dot{\rho }=-\frac{3H(1+\omega )+\lambda \dot{R}}{8\pi +\frac{1}{2}\lambda R(3-\omega )}\rho ,$$

(16)

where $\omega$ is the EoS parameter. One more differentiation of the last equation with respect to time gives

$$\ddot{\rho }=\left\{-\frac{3\dot{H}(1+\omega )+\lambda \ddot{R}}{8\pi +\frac{1}{2}\lambda R(3-\omega )}+\frac{[3H(1+\omega )+\lambda \dot{R}(5-\omega )][3H(1+\omega )+\lambda \dot{R}]}{{[8\pi +\frac{1}{2}\lambda R(3-\omega )]}^2}\right\}\rho .$$

(17)

Here, $R=-6(\dot{H}+2H^2)$, $\dot{R}=-6(\ddot{H}+4H\dot{H})$ and $\ddot{R}=-6(\stackrel{⃛}{H}+4{\dot{H}}^2+4H\ddot{H})$, and the Hubble parameter H is defined as

$$H=\frac{\dot{a}}{a}.$$

(18)

Now, the field Equations (13) and (15) become

$$3H^2=8\pi \rho -3\lambda (1-3\omega )H[\dot{\rho }+H\rho ]-6\lambda (1+\omega )(\dot{H}+2H^2)\rho ,$$

(19)

$$2\dot{H}+3H^2=-8\pi \omega \rho -\lambda (1-3\omega )[(2\dot{H}+3H^2)\rho -2H\dot{\rho }+\ddot{\rho }],$$

(20)

Using these two equations, one obtains

$$\begin{array}{ccc}\hfill 2\dot{H}& =& -8\pi (1+\omega )\rho -\lambda (1-3\omega )[(2\dot{H}+3H^2)\rho -2H\dot{\rho }+\ddot{\rho }]\hfill \\ & & +3\lambda (1-3\omega )H[\dot{\rho }+H\rho ]-6\lambda (1+\omega )(\dot{H}+2H^2)\rho .\hfill \end{array}$$

(21)

The last equation is known as the generalized Raychaudhuri equation. One can solve $\rho$ from the generalized Raychaudhuri equation in terms of its first and second time derivatives as

$$\rho =\frac{1}{4}\left[\frac{2\dot{H}-5\lambda H(1-3w)\dot{\rho }+\lambda (1-3w)\ddot{\rho }}{-2\pi (1+w)+\lambda (1+3w)\dot{H}+3\lambda (1+w)H^2}\right],$$

(22)

Now, we need to know the expression of the Hubble parameter to obtain the explicit form of $\rho$. For this task, we limit ourselves to the assumption of a constant jerk parameter ($j=1$). The jerk parameter is basically the third derivative of the scale factor. Hence, our assumption is

$$j=\frac{\stackrel{⃛}{a}}{a{H}^3}=1,$$

(23)

Note that in the $\Lambda$CDM model of GR, the jerk parameter j is constant, and $j=1$. The integration of Equation (23) leads to two different scale factor solutions; one is power law, and the other one is exponential [19], as follows:

$$a={\left(\frac{3}{2}t+c\right)}^{\frac{2}{3}},$$

(24)

$$a=\alpha e^{\beta t},$$

(25)

where c, $\alpha$, and $\beta$ are the constants of integration. The power-law solution (24) is important for explaining the early universe, and the exponential solution (25) is important for the late universe. Now, regarding Equation (18) for the Hubble parameter and the definition of the deceleration parameter q, we obtain:

$$q=-1-\frac{\dot{H}}{H^2}.$$

(26)

In the remainder of our work, we consider these two solutions separately.

The power-law solution Equation (24) yields

$$H=\frac{2}{3t+2c},q=\frac{1}{2}.$$

(27)

The sign of the deceleration parameter is related to the shape of the expansion of the universe. A positive q indicates a decelerated expansion, and a negative q indicates an accelerated expansion. In this model, q equals 1/2, indicating that the power-law solution depicts a decelerated expanding universe model.

Using Equations (16) and (17), for the time derivatives of $\rho$, one can obtain the explicit expression of $\rho$. Nevertheless, the expression is very lengthy and complicated. Therefore, we consider Equation (16) with Equation (27)

$$\dot{\rho }=-\left(72\frac{\lambda }{{\left(3t+2c\right)}^3}+6\frac{1+\omega }{3t+2c}\right){\left(8\pi -6\frac{\lambda \left(3-\omega \right)}{{\left(3t+2c\right)}^2}\right)}^{-1}\rho ,$$

(28)

Upon integration, we obtain:

$$\rho ={\rho }_0{\left(3t+2c\right)}^{\frac{4}{3-\omega }}{[4\pi {\left(3t+2c\right)}^2+3\lambda \left(-3+w\right)]}^{\frac{-\omega \left(w-2\right)+3+16\pi }{8\pi \left(-3+\omega \right)}},$$

(29)

where ${\rho }_0$ is a constant of integration.

Equation (25), the exponential solution, yields:

$$H=\beta ,q=-1.$$

(30)

Since q is negative, the exponential solution leads to the accelerated expansion model. For this case, following the same procedure as in the previous model, Equation (16) becomes

$$\dot{\rho }=-\frac{3\beta \left(1+\omega \right)}{8\pi -6\lambda {\beta }^2\left(3-\omega \right)}\rho ,$$

(31)

and its integration yields

$$\rho ={\rho }_0{e}^{-\frac{3}{2}\frac{\beta \left(1+\omega \right)t}{3\lambda {\beta }^2\left(\omega -3\right)+4\pi }}.$$

(32)

Figure 1 shows the temporal changes of the energy density for the decelerating (left panel) model for the choice of the integrating constants $c=0$, $c_1=0$, and ${\rho }_0=1$; for the accelerating model (right panel) for the choice of the integrating constants $\beta =1$ and ${\rho }_0=1$; and for different values of the EoS parameter $\omega$. We can see that $\rho$ is a positive value for all t. These are necessary conditions for the physicality of the model.

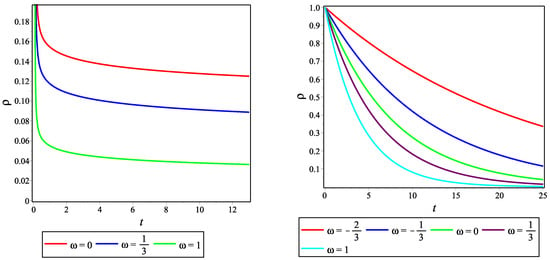
Figure 1. The energy density $\rho$ vs. the time t. The left panel shows the density of the decelerating model, and the right panel shows the density of the accelerating model.

4. Conclusions

We have studied dark energy with $j=1$ in $f(R,T)=f_1\left(R\right)+f_2\left(R\right)f_3\left(T\right)$ gravity. The simpler form $f_2\left(R\right)f_3\left(T\right)=\lambda T$ is usually studied in the literature. It is possible to obtain a viable model with a transition from deceleration to acceleration. We have not considered graphs of the geometrical parameters nor the pressure and equation of the state, or observational constraints. We will report on these aspects elsewhere.