Fluid Densities Defined from Probability Density Functions, and New Families of Conservation Laws †
Abstract
1. Introduction
2. The Velocivolumetric Eulerian Description
3. A Hierarchy of Densities
3.1. Probability Density Functions
- (a)
- A volumetric pdf [m−3];
- (b)
- A velocimetric pdf [(m s−1)−3];
- (c)
- A velocivolumetric (phase space) pdf [m−3 (m s−1)−3];
- (d)
- A conditional velocimetric pdf [(m s−1)−3]; and
- (e)
- A conditional volumetric pdf [m−3];
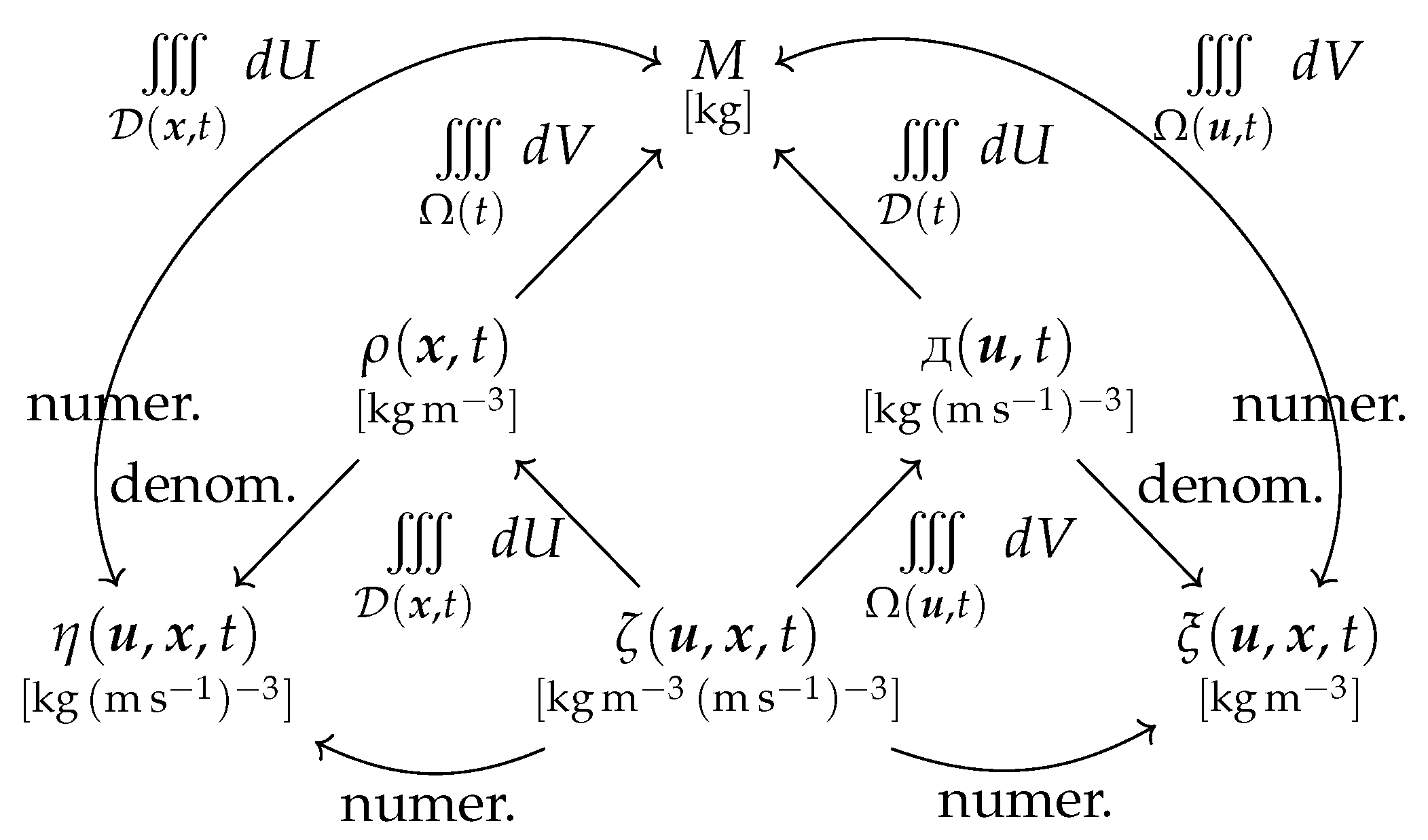
3.2. Fluid Densities
- (a)
- A volumetric fluid density , [kg m−3];
- (b)
- A velocimetric fluid density , [kg (m s−1)−3];
- (c)
- A velocivolumetric (phase space) fluid density , [kg m−3 (m s−1)−3];
- (d)
- A conditional velocimetric fluid density , [kg (m s−1)−3]; and
- (e)
- A conditional volumetric fluid density , [kg m−3];
3.3. Generalized Densities
- (a)
- Volumetric densities , [qty m−3];
- (b)
- Velocimetric densities , [qty (m s−1)−3];
- (c)
- Velocivolumetric (phase space) densities , [qty m−3 (m s−1)−3];
- (d)
- Conditional velocimetric densities , [qty (m s−1)−3]; and
- (e)
- Conditional volumetric densities , [qty m−3];
4. The Generalized Reynolds Transport Theorem and Example Systems
4.1. Volumetric-Temporal Formulation
4.2. Velocimetric-Temporal Formulation
4.3. Time-Independent Velocimetric-Spatial Formulation
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reynolds, O. Papers on Mechanical and Physical Subjects; Cambridge University Press: Cambridge, UK, 1903; Volume III. [Google Scholar]
- White, F.M. Fluid Mechanics, 2nd ed.; McGraw-Hill Higher Education: New York, NY, USA, 1986. [Google Scholar]
- Munson, B.R.; Young, D.F.; Okiishi, T.H.; Huebsch, W.W. Fundamentals of Fluid Mechanics, 6th ed.; John Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publicatiions: Mignola, NY, USA, 1984. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Durst, F. Fluid Mechanics; Springer: Berlin, Germany, 2008. [Google Scholar]
- Dvorkin, E.N.; Goldschmit, M.B. Nonlinear Continua; Springer: Berlin, Germany, 2006. [Google Scholar]
- Truesdell, C.; Toupin, R.A. The classical field theories. In Handbuch der Physik, Band III/1; Flügge, S., Ed.; Springer: Berlin, Germany, 1960; p. 347. [Google Scholar]
- Seguin, B.; Hinz, D.F.; Fried, E. Extending the transport theorem to rough domains of integration. Appl. Mech. Rev. 2014, 66, 050802. [Google Scholar] [CrossRef] [PubMed]
- Falach, L.; Segev, R. Reynolds transport theorem for smooth deformations of currents on manifolds. Math. Mech. Solids 2015, 20, 770–786. [Google Scholar] [CrossRef][Green Version]
- Gurtin, M.E.; Struthers, A.; Williams, W.O. A transport theorem for moving interfaces. Q. Appl. Math. 1989, 47, 773–777. [Google Scholar] [CrossRef]
- Ochoa-Tapia, J.A.; del Rio, J.A.; Whitaker, S. Bulk and surface diffusion in porous media: An application of the surface-averaging theorem. Chem. Eng. Sci. 1993, 48, 2061–2082. [Google Scholar] [CrossRef]
- Slattery, J.C.; Sagis, L.; Oh, E.-S. Interfacial Transport Phenomena, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Fosdick, R.; Tang, H. Surface transport in continuum mechanics. Math. Mech. Solids 2009, 14, 587–598. [Google Scholar] [CrossRef]
- Lidström, P. Moving regions in Euclidean space and Reynolds transport theorem. Math. Mech. Solids 2011, 16, 366–380. [Google Scholar] [CrossRef]
- Flanders, H. Differentiation under the integral sign. Am. Mon. 1973, 80, 615–627. [Google Scholar] [CrossRef]
- Frankel, T. The Geometry of Physics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Harrison, J. Operator calculus of differential chains and differential forms. J. Geom. Anal. 2015, 25, 357–420. [Google Scholar] [CrossRef][Green Version]
- Anderson, T.B.; Jackson, R. A fluid mechanical description of fluidized beds. Ind. Eng. Chem. Fund. 1967, 6, 527–539. [Google Scholar] [CrossRef]
- Whitaker, S. Diffusion and dispersion in porous media. AIChE J. 1967, 13, 420–427. [Google Scholar] [CrossRef]
- Slattery, J.C. Flow of viscoelastic fluids through porous media. AIChE J. 1967, 13, 1067–1071. [Google Scholar] [CrossRef]
- Marle, C.M. Écoulements monophasiques en milieu poreux. Rev. L’Inst. Franç. Pét. 1967, 22, 1471–1509. [Google Scholar]
- Niven, R.K.; Cordier, L.; Kaiser, E.; Schlegel, M.; Noack, B.R. Rethinking the Reynolds transport theorem, Liouville equation, and Perron-Frobenius and Koopman operators. arXiv 2020, arXiv:1810.06022. [Google Scholar]
- Niven, R.K.; Cordier, L.; Kaiser, E.; Schlegel, M.; Noack, B.R. New conservation laws based on generalized Reynolds transport theorems. In Proceedings of the 22nd Australasian Fluid Mechanics Conference AFMC2020, Brisbane, Australia, 7–10 December 2020; p. 110. [Google Scholar]
- Niven, R.K. A hierarchy of probability, fluid and generalized densities for the Eulerian velocivolumetric description of fluid flow, for new families of conservation laws. Entropy 2022, 24, 1493. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Bretthorst, G.L., Ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Matheron, G. Les variables régionalisées et leur estimation, une application de la théorie de fonctions aléatoires aux sciences de la nature; Masson et Cie: Paris, France, 1965. (In French) [Google Scholar]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics: Mechanics of Turbulence; Dover Publications: Mignola, NY, USA, 1971. [Google Scholar]
- Cushman, J.H. On unifying the concepts of scale, instrumentation, and stochastics in the development of multiphase transport theory. Water Resour. Res. 1984, 20, 1668–1676. [Google Scholar] [CrossRef]
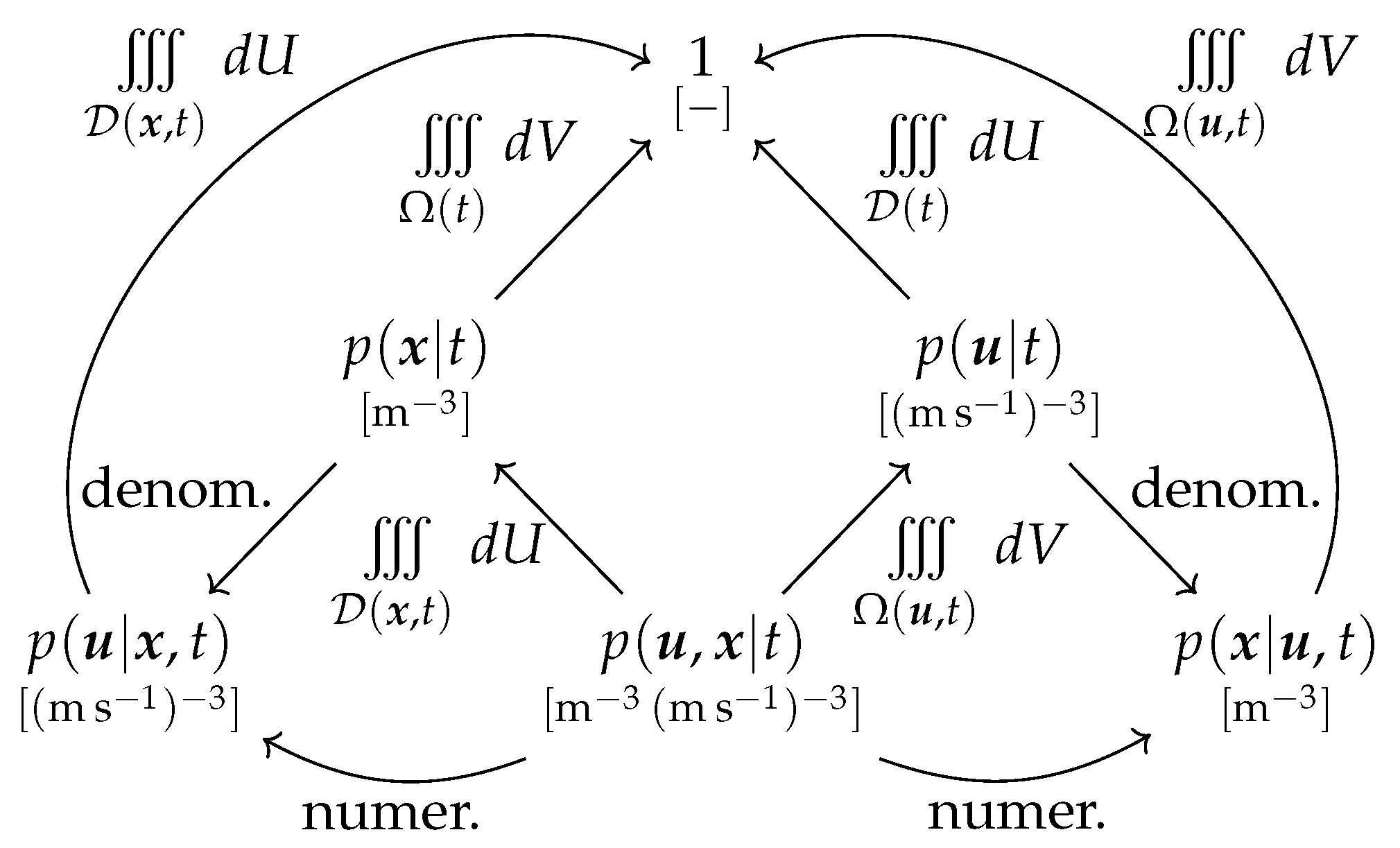
| Conserved Quantity | Density | Integral Equation | |
|---|---|---|---|
| Fluid mass | 0 | ||
| Species mass | |||
| Linear momentum | |||
| Angular momentum | |||
| Energy | |||
| Charge (in solution) | |||
| Entropy |
| Conserved Quantity | Density | Integral Equation | |
|---|---|---|---|
| Fluid mass | 0 | ||
| Species mass | |||
| Linear momentum | |||
| Angular momentum | |||
| Energy | |||
| Charge (in solution) | |||
| Entropy |
| Conserved Quantity | Density | Integral Equation | |
|---|---|---|---|
| Fluid mass | |||
| Species mass | |||
| Linear momentum | |||
| Angular momentum | |||
| Energy | |||
| Charge (in solution) | |||
| Entropy |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niven, R.K. Fluid Densities Defined from Probability Density Functions, and New Families of Conservation Laws. Phys. Sci. Forum 2022, 5, 14. https://doi.org/10.3390/psf2022005014
Niven RK. Fluid Densities Defined from Probability Density Functions, and New Families of Conservation Laws. Physical Sciences Forum. 2022; 5(1):14. https://doi.org/10.3390/psf2022005014
Chicago/Turabian StyleNiven, Robert K. 2022. "Fluid Densities Defined from Probability Density Functions, and New Families of Conservation Laws" Physical Sciences Forum 5, no. 1: 14. https://doi.org/10.3390/psf2022005014
APA StyleNiven, R. K. (2022). Fluid Densities Defined from Probability Density Functions, and New Families of Conservation Laws. Physical Sciences Forum, 5(1), 14. https://doi.org/10.3390/psf2022005014






