Reputation Communication from an Information Perspective ^†

Abstract

Communication, the exchange of information between intelligent agents, whether human or artificial, is susceptible to deception and misinformation. Reputation systems can help agents decide how much to trust an information source that is not necessarily reliable. Consequently, the reputation of the agents themselves determines the influence of their communication on the beliefs of others. This makes reputation a valuable resource, and thus a natural target for manipulation. To investigate the vulnerability of reputation systems, we simulate the dynamics of communicating agents seeking high reputation within their social group using an agent-based model. The simulated agents are equipped with a cognitive model that is limited in mental capacity but otherwise follows information-theoretic principles. Various malicious strategies of the agents are examined for their effects on group sociology, such as sycophancy, egocentrism, pathological lying, and aggressiveness. Phenomena resembling real social psychological effects are observed, such as echo chambers, self-deception, deceptive symbiosis, narcissistic supply, and freezing of group opinions. Here, the information-theoretical aspects of the reputation game simulation are discussed.

1. Introduction

1.1. Scope

In this paper, we discuss the information-theoretic perspective on the authors’ recent work on reputation game simulations [1,2]. For a thorough introduction to the conceptual and mathematical details of these socio-physical simulations, and for the related literature, we refer the reader to Enlin et al. [1]. For a discussion of the resulting sociological and psychological insights, more appropriate for sociological and psychological professionals, we refer the reader to Enlin et al. [2]. Here, the focus is on the abstract information-theoretic considerations underlying the reputation game.

It turns out that the simulation of the reputation game reproduces a number of well-known social psychological effects, such as echo chambers, self-deception, deceptive symbiosis, narcissistic supply, and the freezing of group opinions. Because the game builds on general information principles that are not necessarily tied to human actors, some of the emergent effects can be expected to occur in other contexts. These could be groups of animals, information-exchanging artificial intelligent systems, composite information-processing entities such as administrations, governments, or intelligence agencies, or—admittedly very speculatively—even non-human civilizations.

1.2. Rational

An agent that builds its knowledge solely from its own observations can only accumulate a limited amount of knowledge because the number of situations and perspectives it experiences is limited. Sharing knowledge via communication can eliminate the information bottleneck of owned senses, as now the collective perceptions of the social group with which an agent shares information can become the basis of its beliefs. This multiplies the amount of information an agent perceives by a large factor and is therefore an immense advantage. For example, the knowledge acquired can enable an agent to successfully navigate unfamiliar situations by relying on the experiences of others. In addition, there are a number of other positive effects that knowledge communication can have, such as synchronizing intentions, finding suitable partners, exchanging information for goods, and the like.

However, relying on communicated experience also has its drawbacks. Since the original perception that led to a communicated piece of information is usually not visible to a communicating actor, it is difficult to adequately account for it in the internal knowledge representation. Do two reports, each providing an indication of a particular possibility, count as two independent pieces of information? Or, are they just independent transmissions of the same original story? For proper reasoning, this makes a significant difference, because two reports that incorrectly report the same observation are counted as independent data, giving them too much weight and leading to overconfidence.

Worse, the unfiltered acceptance of information makes agents very vulnerable to manipulation. A malicious agent could communicate with fraudulent intent to trick the recipient of its messages into making decisions that are beneficial to the sender but not necessarily to the recipient. A trusted communicating network of agents is highly vulnerable to such deception, as it could even amplify deception messages that are cleverly designed for that purpose. Therefore, functional agents must be robust against deception. It would be best if deceptive messages were detected by the receiver and ignored in its information update on the subject of the message. However, the fact that (and how) lies were told should not be ignored, as this contains information about the sender’s intentions. These intentions need to be tracked by the receiver, as they are an important indicator of a sender’s overall reliability, and thus essential information for assessing the truthfulness of other messages from the same source.

Intelligent agents thus need to build beliefs about other agents’ intentions, their honesty, their level of information, and the like in order to protect themselves from deception. Such images within one mind about the properties of another mind are called “Theory of Mind”. The image of an agent in other agents’ Theories of Mind is its reputation. If it accurately reflects the agent’s character, reputation helps others judge how much its statements can be believed. Thus, an agent’s reputation largely determines how influential its communications are. As a result, a positive reputation itself becomes a desired resource for any agent. This also makes reputation a target for manipulation, especially for agents who rely on deception strategies and therefore need to hide their true character if they want to be successful with that.

Because building a Theory of Mind for other members of a social group requires gathering a great deal of information; the communicative exchange of reputational information between agents is not only beneficial but almost mandatory. An agent who does not participate in such exchanges risks missing warnings about malicious others. Such an agent also cannot be expected to have beliefs that are well-synchronized with the prevailing group opinion. This may cause the agent to develop positions that are too divergent from the group perspective, and thus risk being viewed as an unreliable source of information itself. Therefore, agents should be interested in sharing reputational information. In short, they need to gossip to learn about others’ reputations and to improve their own.

The reputation game simulation focuses on communication between intelligent agents where reputation is at stake. To simplify the setting, the agents in the game communicate only about the perceived honesty of another agent, their own, or that of their communication partner. The behavior of the agents is steered by fixed stochastic strategies for deciding to whom to talk, about whom, and whether to lie. This permits to evaluate the effectiveness of different strategies in controlled experiments. In future versions, the behavior might be derived from maximizing the expected return according to some objective functions, which then would allow to study how different strategies emerge. Other issues that may well occur in exchanges in real communication networks are ignored in the simulation, as the focus is solely on the emergence of social psychological phenomena within reputation communication.

These emergent phenomena turn out to be surprisingly rich, as the resulting dynamics are very complex due to the strong coupling between the reputations of the different agents. A visualization of a typical exchange between four agents is shown in Figure 1. There, first, agent red decides to exchange with agent black about agent cyan, black then talks to cyan about cyan, followed by cyan talking to red about black, and finally orange talking to red about orange. From this, the strong coupling of reputations should be apparent. What red says about cyan to black can influence what black says to cyan. This, in turn, can influence cyan’s opinion of black expressed to red, and either in terms of cyan’s belief in black’s honesty or its friendliness. Thus, what an agent says influences what it hears later on.

From this, it should be apparent that there are a number of different strategies that agents can use to enhance their own reputation. These range from being very honest to being very dishonest, from addressing agents with the highest or lowest reputation to making the interlocutor, themselves, or their own friends or enemies the subject of conversations and when and how they lie. Deception strategies can further exploit imperfections in the agents’ thinking. The simulated agents are intentionally not designed to be perfect Bayesian reasoning machines. They have a limited mental capacity that reflects some of the shortcomings of the human mind. In fact, any physical information processing system can have only have limited storage and processing capacity, so certain limitations are almost inevitable. In order to keep the complexity of the simulation low, but also to account for the fact that humans use a number of heuristics in their thinking, certain parameters of the agents’ Theory of Mind are determined by simple heuristics. These heuristics allow for manipulative attacks.

The simulation of the reputation game therefore makes it possible to examine different communication and counterstrategies, their inner workings, advantages, disadvantages, risks, and side effects.

2. Reputation Game

2.1. Game’s Setting

A brief overview of reputation game simulations should be in order. Details can be found in Enlin et al. [1]. The game is played by a set $\mathcal{A}=\{\mathrm{red},\mathrm{black},\mathrm{cyan},\dots \}$ of agents in rounds consisting of binary conversations, as shown in Figure 1. Each conversation is about the believed honesty of one of the agents. After each conversation, the agents involved update their beliefs about the topic of the conversation, the interlocutor, and themselves. In addition, they record some information about what the other person said, what they seem to believe, or what they want the receiver to believe. Finally, if the conversation was about themselves, they decide whether the other person should be considered a friend or an enemy.

Friends are other agents who help an agent maintain a high reputation, and thus in the reputation game, friendship is granted to those agents who speak more positively about one compared with the others. Enemies, on the other hand, are agents whose statements seem to harm one’s reputation. If an agent lies about a friend, they will influence the statement positively to benefit from a more respected supporter of themselves. If they lie about an enemy, agents will influence their statements negatively so that bad propaganda about them will be less well received by others. For the simulation of larger social groups, a continuous notion of friendship was developed as well [3], but this is not used in the small-group simulation runs discussed here.

Lying carries the risk for most agents of inadvertently signaling that they are lying. Such “blushing” happens to most agents in $10\%$ of lies and lets the recipient know with certainty that they have been lied to. Some special agents, such as aggressive and destructive ones, can lie without blushing. However, currently all agents assume that the frequency of blushing while lying is $10\%$ when trying to assess the reliability of a received statement.

The game is (usually) initialized with agents that do not have any specific knowledge about each other, as well as of themselves. The honesty of others, as well as their own, needs to be determined from observations, self-observations, and the clues delivered to them by the communications. The self-reputation, in the following called self-esteem, is an important property of agents. A high self-esteem allows agents to advertise themselves without lying. The game ends after a predetermined number of rounds, and the minds of the agents are analyzed in order to evaluate the effectiveness of the different strategies in reaching a high reputation.

2.2. Knowledge Representation

Since agents must deal with uncertainties, probabilistic reasoning is the basis of their thinking. The quantities of interest here are the honesty $x_a=P\left(a\mathrm{speaks}\mathrm{honestly}\right|x_a)\in [0,1]$ of each agent a, which form an honesty vector $x={\left(x_a\right)}_{a\in \mathcal{A}}$. The accumulated knowledge $I_a={\left(I_{ab}\right)}_{b\in \mathcal{A}}$ of an agent a about the honesty of all agents is represented by a probability distribution $\mathcal{P}\left(x\right|I_a)$. This is assumed to follow a certain parametric form,

$$\begin{array}{ccc}\hfill \mathcal{P}\left(x\right|I_a)& =& \prod _{b\in \mathcal{A}}\mathcal{P}\left(x_b\right|I_{ab}),\mathrm{with}{I}_{ab}=({\mu }_{ab},{\lambda }_{ab})\in {(-1,\infty ]}^2,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \mathcal{P}\left(x_b\right|I_{ab})& =& \mathrm{Beta}\left(x_b\right|{\mu }_{ab}+1,{\lambda }_{ab}+1)=\frac{x^{{\mu }_{ab}}{(1-x)}^{{\lambda }_{ab}}}{\mathcal{B}({\mu }_{ab}+1,{\lambda }_{ab}+1)},\mathrm{and}\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \mathcal{B}(\alpha ,\beta )& =& \frac{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\Gamma (\alpha +\beta )}.\hfill \end{array}$$

(3)

The reasoning behind this is as follows. First, to mimic limited cognitive capacity, agents store only probabilistic knowledge states that are products of knowledge about an individual agent. In this way, they do not store entanglement information, which prevents them from removing once-accepted messages from their belief system, even if they conclude that their source was deceptive. Second, the parametric form of the beta distribution is well-suited for storing knowledge about the frequency of events. If agents recognized lies and truths with certainty and stored only their numbers, those numbers would be ${\mu }_{ab}$ and ${\lambda }_{ab}$, respectively. If an agent learns that another person has reported from an absolutely trustworthy source that they have recently spread additional $\Delta {\mu }^{\prime }$ and $\Delta {\lambda }^{\prime }$ truths and lies, respectively, then the updated belief state is $I_{ab}^{\prime }=({\mu }_{ab}+\Delta {\mu }^{\prime },{\lambda }_{ab}+\Delta {\lambda }^{\prime })$.

The ability to store non-integer values for ${\mu }_{ab}$ and ${\lambda }_{ab}$ becomes important once uncertain message trustworthiness must be considered. Ideally, this would allow bimodal distributions, since the knowledge state after receiving a potentially deceptive message J should be a superposition of the state resulting from being updated by information from a trusted source $I_{ab}^{\prime }$ and the state after a detected lie; the latter being the original state $I_{ab}$ to block out the disinformation of the lie. This superposition is

$$\begin{array}{ccc}\hfill \mathcal{P}\left(x_b\right|J,I_a)& =& y_J\mathcal{P}\left(x_b\right|I_{ab}^{\prime })+(1-y_J)\mathcal{P}\left(x_b\right|I_{ab})\mathrm{with}\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill y_J& :=& P\left(J\mathrm{is}\mathrm{honest}\right|J,I_a)\mathrm{the}\mathrm{estimated}\mathrm{message}\mathrm{reliability}.\hfill \end{array}$$

(5)

However, the parametric form of the beta distribution used for knowledge storage prevents agents from storing such bimodal distributions. Instead, agents temporarily construct such bimodal posterior distributions, and then compress them into the parametric form of the beta distribution in Equation (1) for long-term storage. The principle of optimal belief approximation is used for this compression [4]. This states that the Kullback–Leibler (KL) divergence

$${\mathrm{KL}}_{x_b}((J,I_a),I_a^{\prime }):={\int }_0^{1}d{x}_b\mathcal{P}\left(x_b\right|J,I_a)ln\frac{\mathcal{P}\left(x_b\right|J,I_a)}{\mathcal{P}\left(x_b\right|I_{ab}^{\prime })}$$

(6)

between optimal and approximate belief states should be minimized with respect to the parameters $I_{ab}^{\prime }=({\mu }_{ab}^{\prime },{\lambda }_{ab}^{\prime })$ of the approximation. For the chosen parametric form of the beta distribution, this implies the conservation of the moments ${\langle ln{x}_b\rangle }_{\left(x_b\right|J,I_a)}$ and ${\langle ln(1-x_b)\rangle }_{\left(x_b\right|J,I_a)}$ in the [2] compression step. These are the surprises expected by agent a for the truth and lie of agent b. Many other details of the distribution, such as its bimodality and possible entanglements between the honesty of the subject and that of the speaker, are lost in the compression.

2.3. Honest Communication

Each agent $a\in \mathcal{A}$ randomly decides whether to communicate honestly in each communication, with its characteristic honesty frequency $x_a$. If the agent is honest, it simply communicates to the communicating partner b its belief state $I_{ac}$ about the topic c in the message $J=I_{ac}$. The act of communication from a to b about c is denoted by $a\stackrel{c}{\to }b$.

Honesty has the advantage that one does not run the risk of blushing. It also reduces the risk of being seen as a liar, provided that one’s own opinion and that of the recipient on the subject are sufficiently in agreement; otherwise, it actually increases this risk. The disadvantage of honesty for mostly honest agents is that it reduces their ability to manipulate those around them to their advantage. For mostly dishonest agents, the disadvantage of being honest is that they risk revealing their own dishonesty in a so-called confession (if their self-esteem is not inflated) or revealing their true opinion about others, which also risks reducing the effectiveness of their lies.

2.4. Deceptive Communication

Thus, there are a number of advantages to lying, and in the case that strategies for detecting deception are not present in the minds of agents, notorious and extreme lying would automatically be the most successful strategy. Therefore, for mental self-defense, every functioning agent must practice lie detection. For a lie to have even a chance of going unnoticed as such, its content must be adapted to the lie detection strategy of the recipient. Thus, lie detection determines how the optimal construction of lies works, and so we must first turn to lie detection.

Lie Detection: An agent b that receives a message in a communication $a\stackrel{c}{\to }b$ must determine a probability for its knowledge update that the message is honest (“$=\mathrm{h}$”). This is constructed as

$$\begin{array}{ccc}\hfill y_J& =& \mathcal{P}\left(\mathrm{h}\right|d,I_b)=\frac{\mathcal{P}\left(d\right|\mathrm{h},I_b)\mathcal{P}\left(\mathrm{h}\right|I_b)}{\mathcal{P}\left(d\right|I_b)},\mathrm{with}\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \mathcal{P}\left(d\right|I_b)& =& \mathcal{P}\left(d\right|\mathrm{h},I_b)\mathcal{P}\left(\mathrm{h}\right|I_b)+\mathcal{P}\left(d\right|\neg \mathrm{h},I_b)\mathcal{P}(\neg \mathrm{h}|I_b),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \mathcal{P}\left(d\right|\mathrm{h},I_b)& =& \prod _j\mathcal{P}\left(f_j\left(d\right)\right|\mathrm{h},I_b),\mathrm{and}\mathcal{P}\left(d\right|\neg \mathrm{h},I_b)=\prod _j\mathcal{P}\left(f_j\left(d\right)\right|\neg \mathrm{h},I_b).\hfill \end{array}$$

(9)

Here, d denotes the communication data (the setup $a\stackrel{c}{\to }b$, the statement J, and whether blushing was observed), $f_j\left(d\right)$ are various features that agent b extracts from these data, and $\mathcal{P}\left(\mathrm{h}\right|I_b)={\langle x_a\rangle }_{\left(x_a\right|I_{ba})}=:{\overline{x}}_{ba}$ is the reputation of a with b, i.e., agent b’s assumption about how frequently a is honest.

By using Equation (7) for message analysis, agents implicitly assume that the various data features used are statistically independent given the message’s honesty status ($\mathrm{h}$ or $\neg \mathrm{h}$). The features that ordinary agents use to detect lies are blushing (indicating lies), confessions (indicating truths), and the expected surprise $s_J:={\mathrm{KL}}_{x_c}(J,I_{bc})$ that the message would induce in them if they changed their belief about c to the assertion of the message.

The assumption that agents make about the surprise values of messages to them is that the lies underneath deviate more from their own beliefs than honest statements, and are thus more surprising. Although not necessarily true, this assumption protects their belief system from being easily altered by extreme claims made by other agents, since messages that have the potential to greatly change their minds are simply not believed. Where the line between predominantly trust or distrust is drawn depends on a number of factors. First, the reputation of the sender of the message ${\overline{x}}_{ba}$ has a major impact. Second, the receiver b of a message must compare the surprises of the message with a characteristic surprise scale ${\kappa }_b$ to judge whether or not the message deviates too much from one’s belief system. However, this scale ${\kappa }_b$ cannot be a fixed number, as it must adapt to evolving social situations, which may differ in terms of the size of lies typically used and the dispersion of honest opinions.

In the reputation game, a very simple heuristic is used for this setting (${\kappa }_b$ is the median of the surprise scores of the last ten messages received with positive surprises). Regardless of this specific choice, however, any socially communicating intelligent system will require a similar scale to assess the reliability of news in light of its own knowledge and to protect its belief system from distortions due to exaggerated claims. It is therefore to be expected that such a scale (or several of them) is present in any robust (in terms of deception and bias) social information processing system. The resulting social psychological phenomena should be relatively universal, and therefore found in a variety of societies, human and non-human.

Lie Construction: Given this strategy for detecting lies, it becomes clear how a successful lie must be composed. A lie cannot simply be an arbitrary statement, as this would be too easily detected. Nor can it simply be a distorted version of the sender’s belief, as this would statistically add surprise over honest statements to which the receiver pays attention (this was tried in an initial version of the simulation and failed grandiosely). Consequently, it should ideally be a distorted version of the receiver’s own belief to hide among the surprise values of the honest messages received. Additionally, the distortion should typically be smaller than the receiver’s reference surprise scale to go unnoticed.

To be successful, then, a liar must cultivate a picture of his victim’s beliefs, a rudimentary Theory of Mind. On this basis, the expected effect of the lie on the speaker can be estimated, and a lie with hopefully optimal effect can be constructed. Usually, this will not be too far from the recipient’s own belief to go unnoticed, but also not too close to still sufficiently move the victim’s mind in the desired direction. To determine the size of their lies, agents use their own perceived mean surprise scale $\kappa$, making the implicit (and not necessarily correct) assumption that all agents experience the same social atmosphere. This has very interesting consequences.

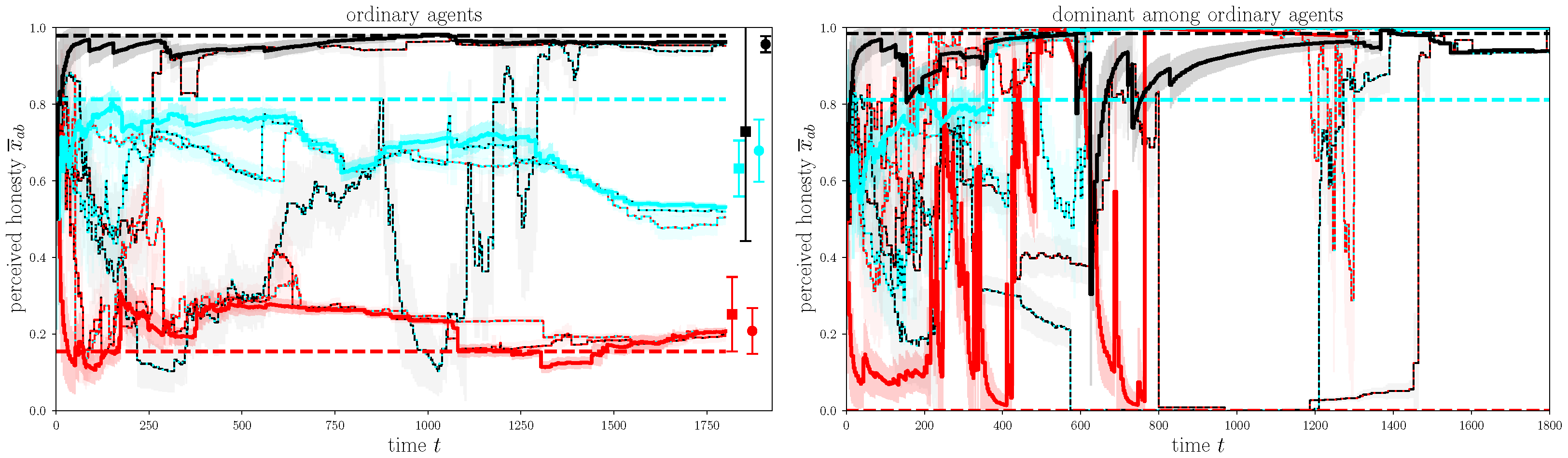
For any agent who is exposed to opinions significantly different from their own, whether they are lied to a lot or simply have a different belief system than their social group, the reference surprise scale will grow. Such an agent’s lies will have a larger size because the same surprise scale is used in detecting and constructing lies. Although these inflated lies may not be more convincing to the recipients, the recipients’ reference surprise scale will also increase. As a result, the other agents’ lies will also increase, which in turn will further increase the reference lie scale for everyone. In this way, a run away regime of inflating reference scales can develop, in which the social atmosphere becomes toxic, in the sense that the opinions expressed become extreme. This is clearly seen in several simulations of the reputation game, especially in the presence of agents using the dominant communication strategy, as discussed below.

It should be noted that, in addition, improved lie detection strategies adapted to the lie construction strategy described above are conceivable. In the reputation game simulations, so-called smart agents use their Theory of Mind to guess whether the message is more likely to be a truth (a message derived from the sender’s belief) or a lie (a message constructed from the sender’s belief about the receiver’s belief).

3. Reputation Dynamics

The reputation game exhibits complex and sometimes chaotic dynamics. In Figure 2 the time evolution of agents’ reputations and self-esteems ${\overline{x}}_{ba}$ (with $a,b\in \left\{\mathrm{black},\mathrm{cyan},\mathrm{red}\right\}$) is shown in two typical simulation runs. The left panel shows the interaction of three ordinary agents and the right panel shows a simulation in which agent red instead follows a dominant strategy. This means that red is a notorious liar ($x_{\mathrm{red}}=0$) and prefers to address the more well-reputed agents, mostly talking about itself, as well as being smart. Similar dominant self-promotion strategies are used, for example, by narcissistic personalities.

Both simulations were run with the same random number sequences, which means that the communication configurations (such as $a\stackrel{c}{\to }b$ and the expressions and relative sizes of the lies) have exactly the same sequences for agents black and cyan. The strong differences in the results are solely due to the differences in the communication strategy of red, as well as the amplification of resulting differences by the chaotic dynamics, the butterfly effect. The two simulations are typical of their individual set ups, in the sense that about half of the simulations are with such a set up but different random numbers, showing characteristic similarities. In the simulation with only ordinary agents, a reputation hierarchy often emerges that reflects the true honesties of the agents, as is the case in the left scenario of Figure 2. However, in simulations with dominant agents, those often manage to place themselves at the top of such hierarchies, as happens in the right scenario shown in Figure 2.

The dynamic that led to this is also interesting. In the simulation with dominant agent red, red quickly succeeds in convincing the most honest and initially also most respected agent black of red’s honesty, which then helps to convince cyan as well. Despite being established as the most reputable agent around time 250 (measured in communication events), red’s self-esteem is still low at that time due to the many lies red observes itself to make. Black and cyan, on the other hand, paint a much better picture of red in the many conversations they have with red about red. This means that red is exposed to a large number of opinions that differ greatly from its self-assessment. As a result, red’s reference surprise scale for lie detection and construction grows, making red’s statements more and more extreme, which ultimately makes others’ reference surprise scales and lies grow as well.

In the developing toxic atmosphere, even red has trouble distinguishing lies from truths. The reputation dynamic becomes very turbulent in the process, with the reputation of the most honest agent, black, being completely destroyed at times (between time 750 and 1250). This toxic and turbulent phase comes to an end when red’s self-esteem is raised to red’s reputation. Thereupon, red’s surprise reference scale can relax, eventually reducing the scope of their and others’ lies and allowing the reputation dynamics to freeze to a state in which red is still the most respected agent.

A number of well-known social psychological phenomena manifested themselves in this episode: The development of a toxic atmosphere triggered by the great cognitive dissonance red experienced between their low self-esteem and the echo of their self-promotion. The breakdown of red’s ability to reject unrealistic statements eventually leading to red’s successful self-deception about its honesty (although red experiences lying in every communication it makes). Black and cyan are manipulated into providing narcissistic supply for red’s self-esteem. Finally, the fact that black, as the most honest actor, temporarily suffers the lowest reputation can be seen as an incarnation of the Cassandra syndrome within the reputation game. All of these emerging phenomena, evidenced here with only a single simulation run, occur in a statistically robust manner. For more such phenomena, more runs, including ones under different configurations, their statistics, and a more detailed discussion and introduction to the reputation game, we refer the reader to Enlin et al. [1].

4. Conclusions

The reputation game simulation, despite its strong idealization, is able to replicate a number of well-known social psychological phenomena [1,2]. This paper is concerned with why many of these phenomena are a natural consequence of the imperfect information processing that inevitably occurs in social communication. Because there are usually strong incentives for social actors to deceive, participants in social interactions must expect and defy deception. This can be carried out by identifying untrustworthy members of their society and forming a picture of each individual’s trustworthiness, i.e., build a reputation system. Since it is ineffective (and dangerous) to rely solely on one’s own experiences to build a reputation system, sharing information about the reputations of others is beneficial and necessary. Since there are also advantages to having a good reputation, and thus being trustworthy (lower transaction costs in trade, access to more resources, more influence), fraudulent members of a society will inevitably seek to manipulate the reputation systems around them to their advantage. This can be carried out through a number of communication strategies. Here, we briefly discussed the dominant strategy, in which an actor uses self-propaganda to target highly regarded members of the social group. This turns out to be a high-risk high-gain strategy (in the simulation), as quite high reputations were actually achieved in about half of the simulation runs (with few agents) but rather low ones in the others. Similar dominant strategies can be observed in humans, especially in members of the dark triad of Machiavellian, sociopathic, and particularly narcissistic personalities.

An interesting consequence of this argument is that whenever social interactions allow deception, reputation communication should exist for the self-protection of the actors. However, reputation should also be a target of manipulation. For these, imperfections in the cognitive systems used are expected points of attack. In this context, the mental existence of a characteristic mental scale for news surprises was postulated, which tries to mark the demarcation line between honest statements and lies. This scale must be adaptable to different social standards, and this flexibility also allows its manipulation by propaganda and gaslighting [1]. Since this scale is probably also used in turn in the construction of lies, destructive build-up effects in communications within social groups are possible, leading to a toxic atmosphere.

In summary, several of the well-known social psychological phenomena and strategies related to adaptive social communication appear to be a direct consequence of information processing under cognitive impairment. Thus, they should not be unique to humans but should be more universal and expected in non-human societies, whether biological or artificial.