Experiments on Damage and Failure Behavior of Biaxially Loaded Specimens under Non-Proportional Load Paths †
Abstract
:1. Introduction
2. Continuum Damage Model
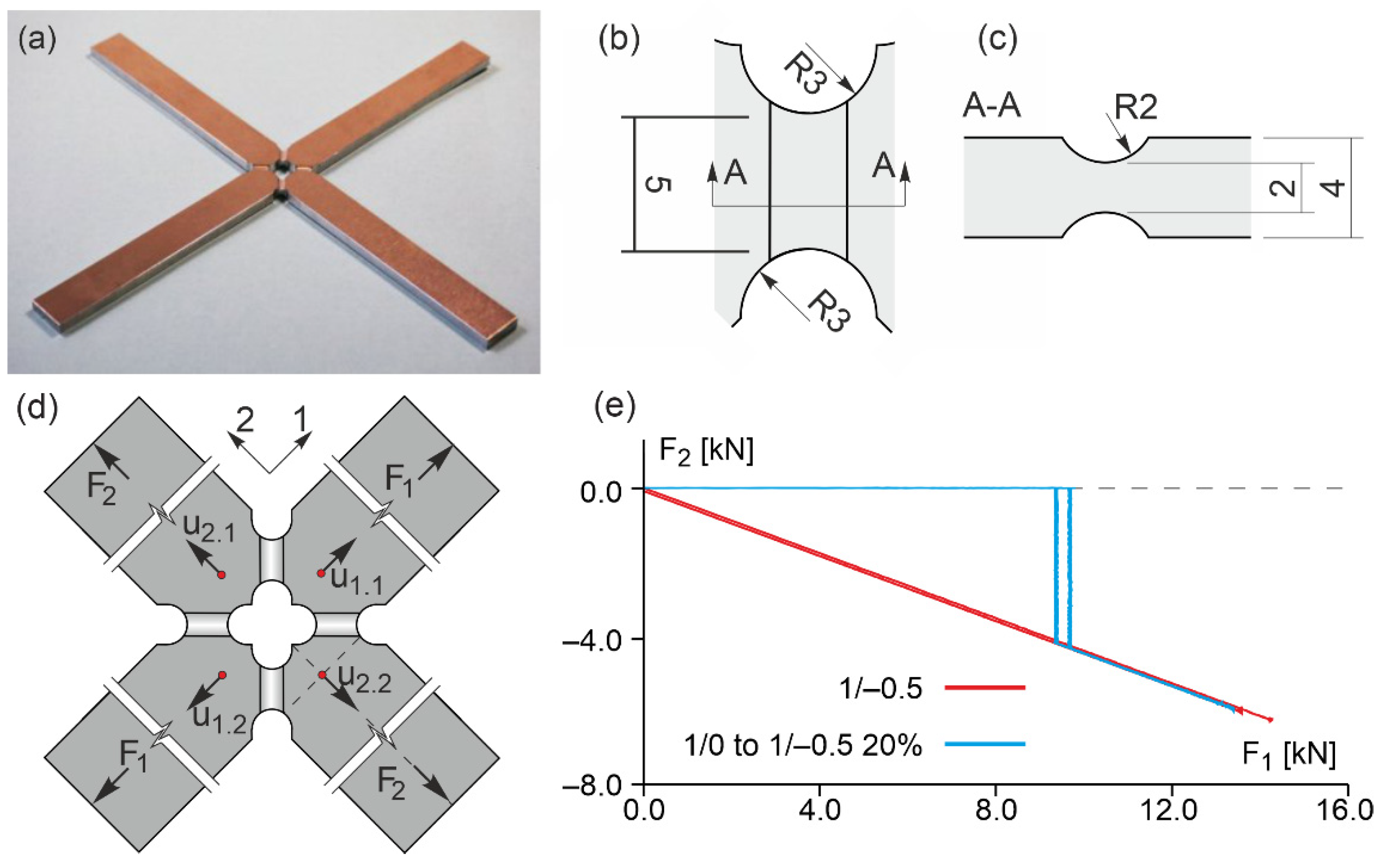
3. Experiments and Corresponding Numerical Simulations
3.1. Numerical Aspects
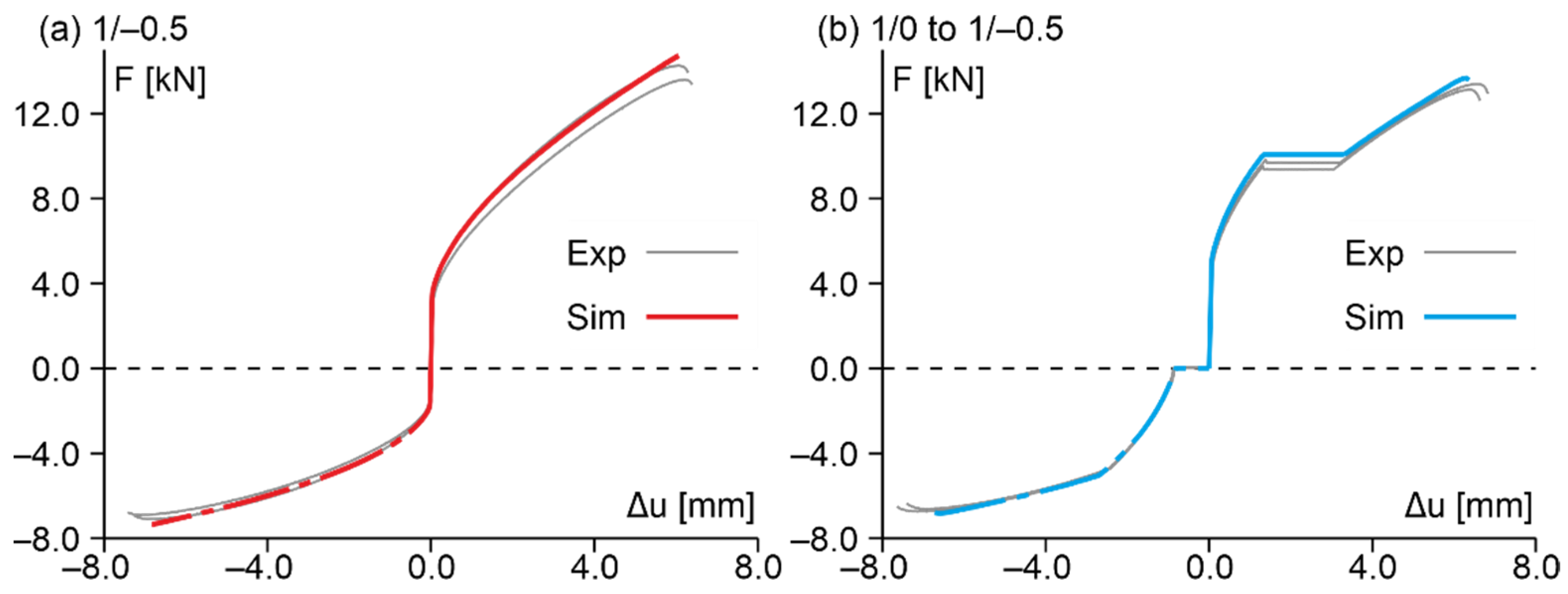
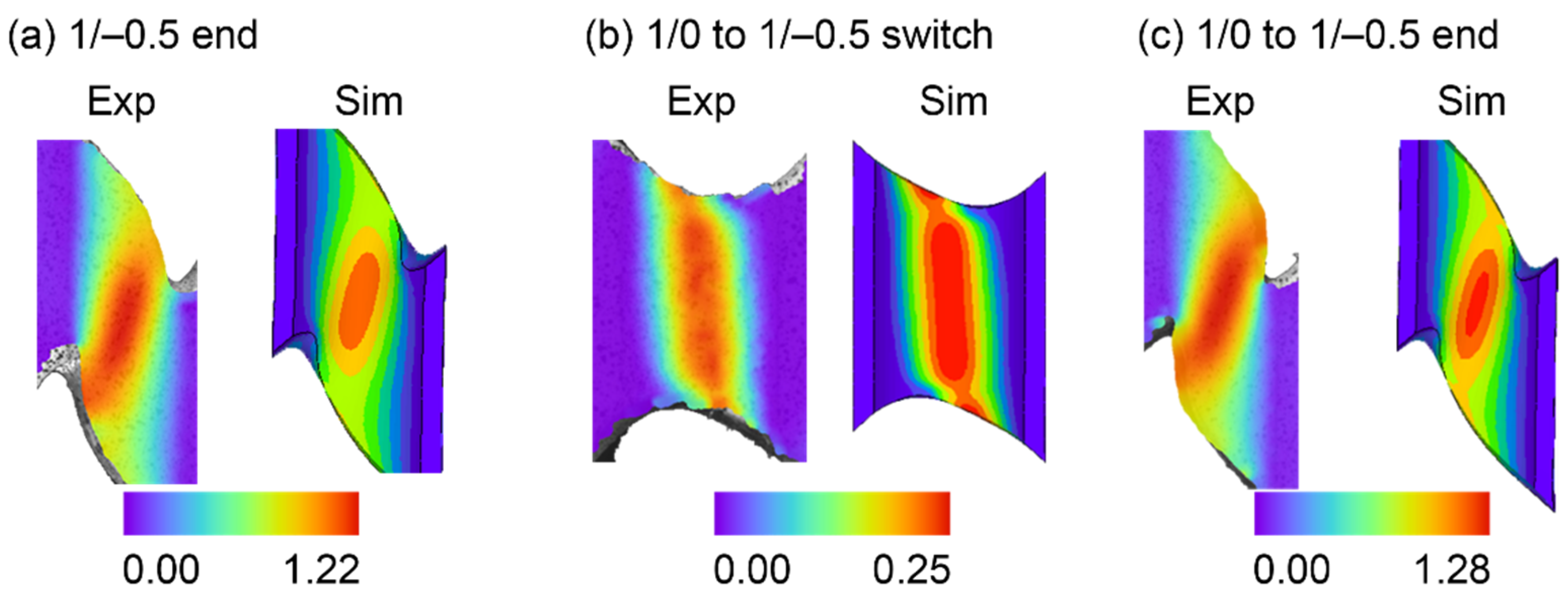
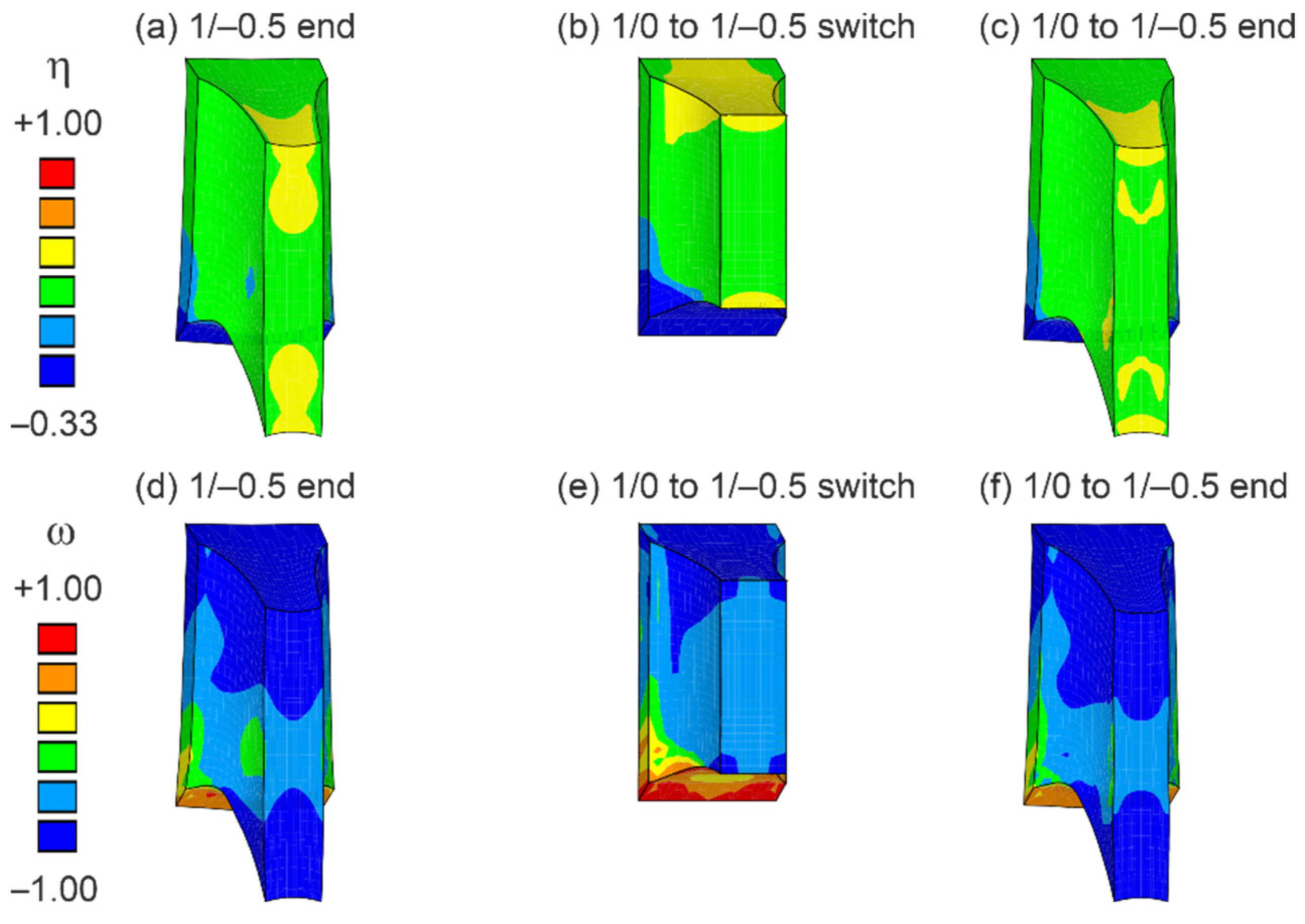
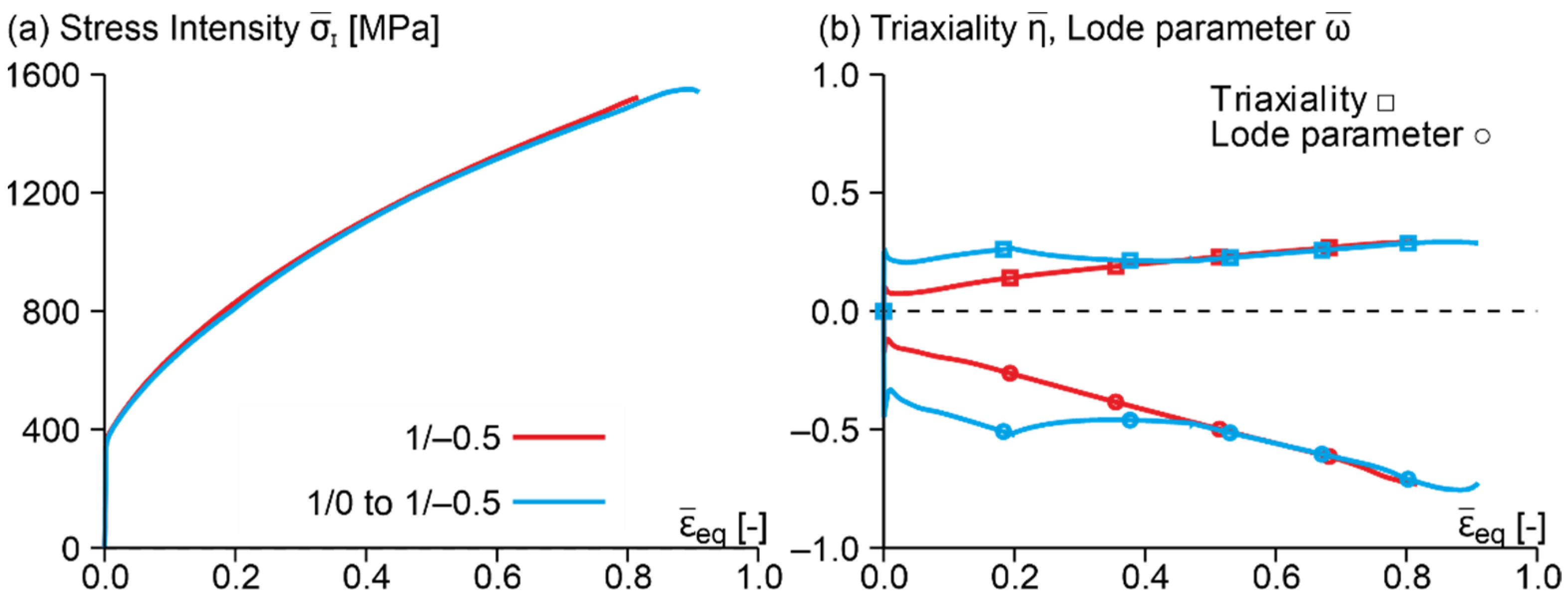
3.2. Results of Experiments and Numerical Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bao, Y.; Wierzbicki, T. On fracture locus in the equivalent strain and stress triaxiality space. Int. J. Mech. Sci. 2004, 46, 81–98. [Google Scholar] [CrossRef]
- Bonora, N.; Gentile, D.; Pirondi, A.; Newaz, G. Ductile damage evolution under triaxial state of stress: theory and experiments. Int. J. Plast. 2005, 21, 981–1007. [Google Scholar] [CrossRef]
- Driemeier, L.; Brünig, M.; Micheli, G.; Alves, M. Experiments on stress-triaxiality dependence of material behavior of aluminum alloys. Mech. Mater. 2010, 42, 207–217. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, G.; Roe, C. A Study on the effect of the stress state on ductile fracture. Int. J. Damage Mech. 2010, 19, 75–94. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Ductile fracture experiments with locally proportional loading histories. Int. J. Plast. 2016, 79, 328–354. [Google Scholar] [CrossRef]
- Chow, C.L.; Lu, T.J. An analytical and experimental study of mixed-mode ductile fracture under nonproportional loading. Int. J. Damage Mech. 1992, 1, 191–236. [Google Scholar] [CrossRef]
- Green, D.E.; Neale, K.W.; MacEwen, S.R.; Makinde, A.; Perrin, R. Experimental investigation of the biaxial behaviour of an aluminum sheet. Int. J. Plast. 2004, 20, 1677–1706. [Google Scholar] [CrossRef]
- Kulawinski, D.; Nagel, K.; Henkel, S.; Hübner, P.; Fischer, H.; Kuna, M.; Biermann, H. Characterization of stress–strain behavior of a cast TRIP steel under different biaxial planar load ratios. Eng. Fract. Mech. 2011, 78, 1684–1695. [Google Scholar] [CrossRef]
- Kuwabara, T. Advances in experiments on metal sheets and tubes in support of constitutive modeling and forming simulations. Int. J. Plast. 2007, 23, 385–419. [Google Scholar] [CrossRef]
- Brünig, M.; Zistl, M.; Gerke, S. Numerical analysis of experiments on damage and fracture behavior of differently preloaded aluminum alloy specimens. Metals 2021, 11, 381. [Google Scholar] [CrossRef]
- Dunand, M.; Mohr, D. Optimized butterfly specimen for the fracture testing of sheet materials under combined normal and shear loading. Eng. Fract. Mech. 2011, 78, 2919–2934. [Google Scholar] [CrossRef]
- Lian, J.; Liu, W.; Gastañares, X.; Juan, R.; Mendiguren, J. Plasticity evolution of an aluminum- magnesium alloy under abrupt strain path changes. Int. J. Mater. Form. 2022, 15, 40. [Google Scholar] [CrossRef]
- Kong, X.; Helfen, L.; Hurst, M.; Hänschke, D.; Missoum-Benziane, D.; Besson, J.; Baumbach, T.; Morgeneyer, T.F. 3D in situ study of damage during a ‘shear to tension’ load path change in an aluminium alloy. Acta Mater. 2022, 231, 117842. [Google Scholar] [CrossRef]
- Gerke, S.; Adulyasak, P.; Brünig, M. New biaxially loaded specimens for the analysis of damage and fracture in sheet metals. Int. J. Solids Struct. 2017, 110, 209–218. [Google Scholar] [CrossRef]
- Gerke, S.; Zistl, M.; Bhardwaj, A.; Brünig, M. Experiments with the X0-specimen on the effect of non-proportional loading paths on damage and fracture mechanisms in aluminum alloys. Int. J. Solids Struct. 2019, 163, 157–169. [Google Scholar] [CrossRef]
- Gerke, S.; Zistl, M.; Brünig, M. Experiments and numerical simulation of damage and fracture of the X0-specimen under non-proportional loading paths. Eng. Fract. Mech. 2020, 224, 106795. [Google Scholar] [CrossRef]
- Brünig, M. An anisotropic ductile damage model based on irreversible thermodynamics. Int. J. Plast. 2003, 19, 1679–1713. [Google Scholar] [CrossRef]
- Brünig, M. Numerical analysis of anisotropic ductile continuum damage. Comput. Methods Appl. Mech. Eng. 2003, 192, 2949–2976. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zistl, M.; Gerke, S.; Brünig, M. Experiments on Damage and Failure Behavior of Biaxially Loaded Specimens under Non-Proportional Load Paths. Phys. Sci. Forum 2022, 4, 23. https://doi.org/10.3390/psf2022004023
Zistl M, Gerke S, Brünig M. Experiments on Damage and Failure Behavior of Biaxially Loaded Specimens under Non-Proportional Load Paths. Physical Sciences Forum. 2022; 4(1):23. https://doi.org/10.3390/psf2022004023
Chicago/Turabian StyleZistl, Moritz, Steffen Gerke, and Michael Brünig. 2022. "Experiments on Damage and Failure Behavior of Biaxially Loaded Specimens under Non-Proportional Load Paths" Physical Sciences Forum 4, no. 1: 23. https://doi.org/10.3390/psf2022004023
APA StyleZistl, M., Gerke, S., & Brünig, M. (2022). Experiments on Damage and Failure Behavior of Biaxially Loaded Specimens under Non-Proportional Load Paths. Physical Sciences Forum, 4(1), 23. https://doi.org/10.3390/psf2022004023






