Direct and Inverse Characterization of the Asymmetric Hardening Behavior of Bulk Ti64 Alloy †
Abstract
1. Introduction
2. Materials and Methods
2.1. Material Model
2.2. Asymmetry Paramater Identification
3. Results and Discussion
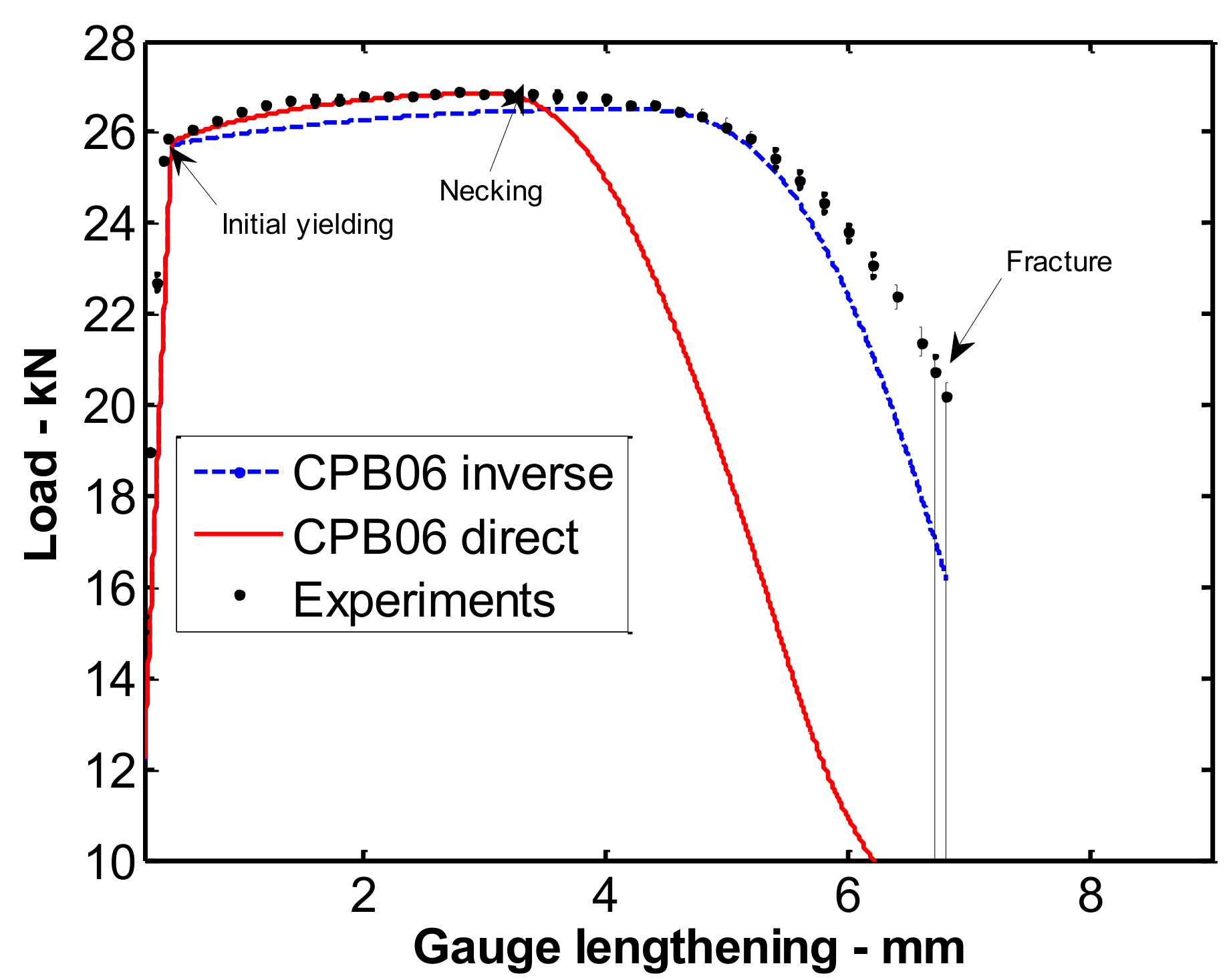
3.1. Tensile Loading Predictions
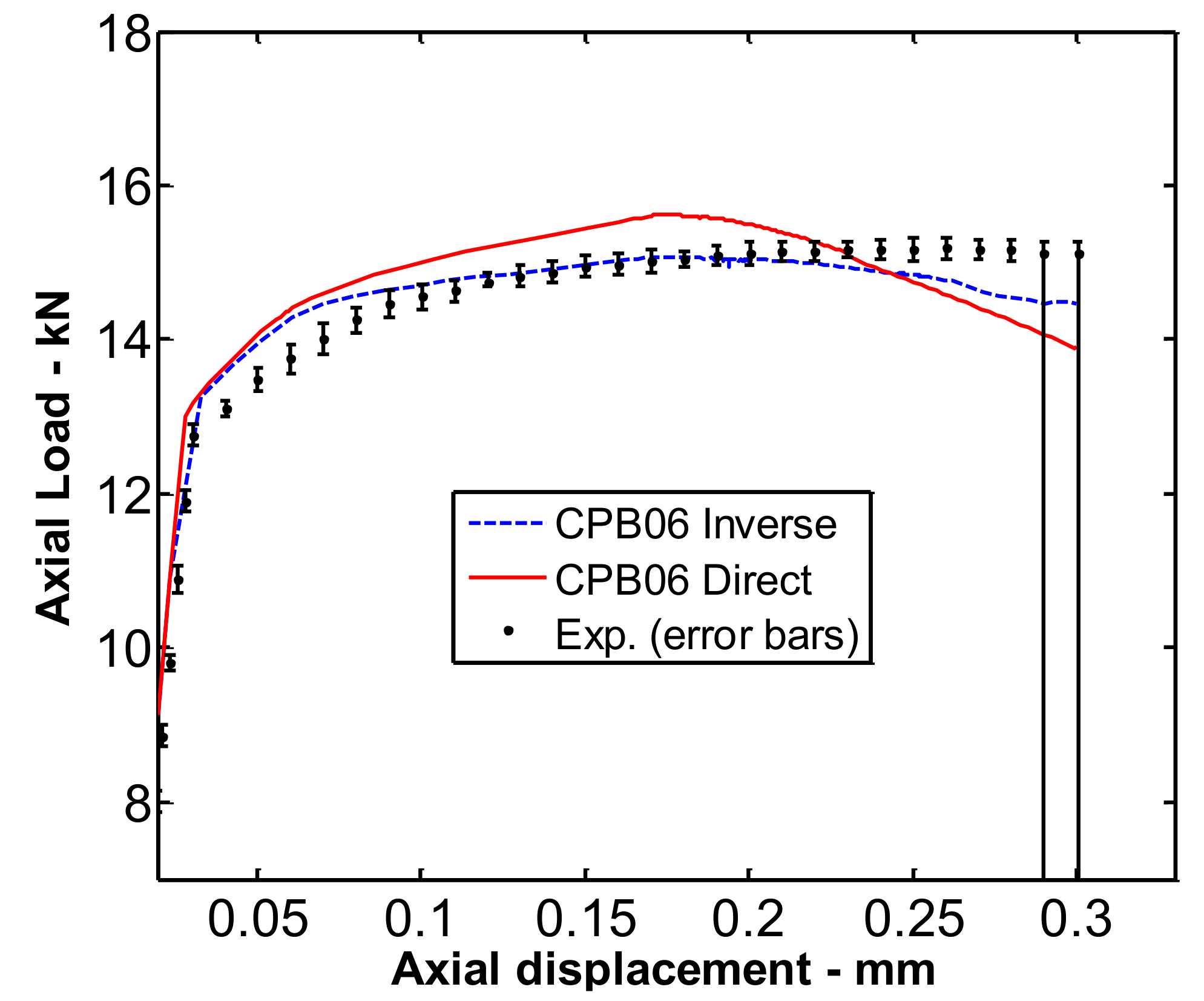
3.2. Compressive Loading Prediction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cazacu, O.; Revil-Baudard, B.; Chandola, N. Plasticity-Damage Couplings: From Single Crystal to Polycrystalline Materials; Springer: Berlin/Heidelberg, Germany, 2019; Volume 253. [Google Scholar]
- Rojas-Ulloa, C.; Valenzuela, M.; Tuninetti, V.; Habraken, A.-M. Identification and validation of an extended Stewart-Cazacu micromechanics damage model applied to Ti–6Al–4V specimens exhibiting positive stress triaxialities. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1248–1261. [Google Scholar] [CrossRef]
- Singh, A.; Basak, S.; Lin, L.P.; Roy, G.G.; Jha, M.N.; Mascarenhas, M.; Panda, S.K. Prediction of earing defect and deep drawing behavior of commercially pure titanium sheets using CPB06 anisotropy yield theory. J. Manuf. Process. 2018, 33, 256–267. [Google Scholar] [CrossRef]
- Jia, Y.; Bai, Y. Experimental study on the mechanical properties of AZ31B-H24 magnesium alloy sheets under various loading conditions. Int. J. Fract. 2016, 197, 25–48. [Google Scholar] [CrossRef]
- Zhang, K.; Badreddine, H.; Yue, Z.; Hfaiedh, N.; Saanouni, K.; Liu, J. Failure prediction of magnesium alloys based on improved CDM model. Int. J. Solids Struct. 2021, 217–218, 155–177. [Google Scholar] [CrossRef]
- Lee, H.; Jo, M.; Noh, G. Biomechanical effects of dental implant diameter, connection type, and bone density on microgap formation and fatigue failure: A finite element analysis. Comput. Methods Programs Biomed. 2021, 200, 105863. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.-H.; Song, N.-N.; Andrade Pires, F.M.; Santos, A.D. Prediction of Forming Limit Diagrams for Materials with HCP Structure. Acta Metall. Sin. 2015, 28, 1442–1451. [Google Scholar] [CrossRef][Green Version]
- Harbaoui, R.; Daghfas, O.; Znaidi, A.; Tuninetti, V. Mechanical behavior of materials with a compact hexagonal structure obtained by an advanced identification strategy of HCP material, AZ31B-H24. Frat. Integr. Strutt. 2020, 14, 295–305. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gilles, G.; Milis, O.; Pardoen, T.; Habraken, A.M. Anisotropy and tension–compression asymmetry modeling of the room temperature plastic response of Ti–6Al–4V. Int. J. Plast. 2015, 67, 53–68. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gilles, G.; Flores, P.; Pincheira, G.; Duchêne, L.; Habraken, A.-M. Impact of distortional hardening and the strength differential effect on the prediction of large deformation behavior of the Ti6Al4V alloy. Meccanica 2019, 54, 1823–1840. [Google Scholar] [CrossRef]
- Tuninetti, V.; Flores, P.; Valenzuela, M.; Pincheira, G.; Medina, C.; Duchêne, L.; Habraken, A.-M. Experimental characterization of the compressive mechanical behaviour of Ti6Al4V alloy at constant strain rates over the full elastoplastic range. Int. J. Mater. Form. 2020, 13, 709–724. [Google Scholar] [CrossRef]


| Strain Energy per Unit Volume (W/m3) | Anisotropic Constants of CPB06 | ||||||
|---|---|---|---|---|---|---|---|
| C11 | C12 | C13 | C22 | C23 | C33 | C44 = C55 = C66 | |
| 1.857 | 1 | −2.37 | −2.36 | −1.84 | 1.20 | −2.44 | −3.61 |
| 9.377 | 1 | −2.50 | −2.93 | −2.28 | 1.28 | −2.45 | 4.02 |
| 48.66 | 1 | −2.43 | −2.92 | 1.65 | −2.24 | 1.00 | −4.00 |
| 100.2 | 1 | −2.57 | −2.88 | 1.39 | −2.38 | 0.88 | −3.93 |
| 206.6 | 1 | −2.97 | −2.93 | 0.53 | −2.96 | 0.44 | −3.88 |
| Asymmetry Parameter k for Each Yield Surface | Strain Hardening Coefficients | |||||||
|---|---|---|---|---|---|---|---|---|
| 1.857 * | 9.377 * | 48.66 * | 100.2 * | 206.6 * | σy (MPa) | α | β | |
| Direct | −0.136 | −0.136 | −0.165 | −0.164 | −0.18 | 1081 | 0.14801 | −15.5 |
| Inverse | −0.136 | −0.136 | −0.125 | −0.114 | −0.11 | 1208 | 0.24007 | −5.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuninetti, V.; Gilles, G.; Sepúlveda, H.; Pincheira, G.; Flores, P.; Duchêne, L.; Habraken, A.M. Direct and Inverse Characterization of the Asymmetric Hardening Behavior of Bulk Ti64 Alloy. Phys. Sci. Forum 2022, 4, 2. https://doi.org/10.3390/psf2022004002
Tuninetti V, Gilles G, Sepúlveda H, Pincheira G, Flores P, Duchêne L, Habraken AM. Direct and Inverse Characterization of the Asymmetric Hardening Behavior of Bulk Ti64 Alloy. Physical Sciences Forum. 2022; 4(1):2. https://doi.org/10.3390/psf2022004002
Chicago/Turabian StyleTuninetti, Víctor, Gaëtan Gilles, Héctor Sepúlveda, Gonzalo Pincheira, Paulo Flores, Laurent Duchêne, and Anne Marie Habraken. 2022. "Direct and Inverse Characterization of the Asymmetric Hardening Behavior of Bulk Ti64 Alloy" Physical Sciences Forum 4, no. 1: 2. https://doi.org/10.3390/psf2022004002
APA StyleTuninetti, V., Gilles, G., Sepúlveda, H., Pincheira, G., Flores, P., Duchêne, L., & Habraken, A. M. (2022). Direct and Inverse Characterization of the Asymmetric Hardening Behavior of Bulk Ti64 Alloy. Physical Sciences Forum, 4(1), 2. https://doi.org/10.3390/psf2022004002






