On Two Measure-Theoretic Aspects of the Full Bayesian Significance Test for Precise Bayesian Hypothesis Testing †
Abstract
:1. Introduction
2. The Full Bayesian Significance Test
2.1. Notation
- (1)
- the prior model
- (2)
- the statistical model on , leading to , and
- (3)
- the posterior model
2.2. Theory behind the Full Bayesian Significance Test (FBST)
3. On Two Aspects of the FBST
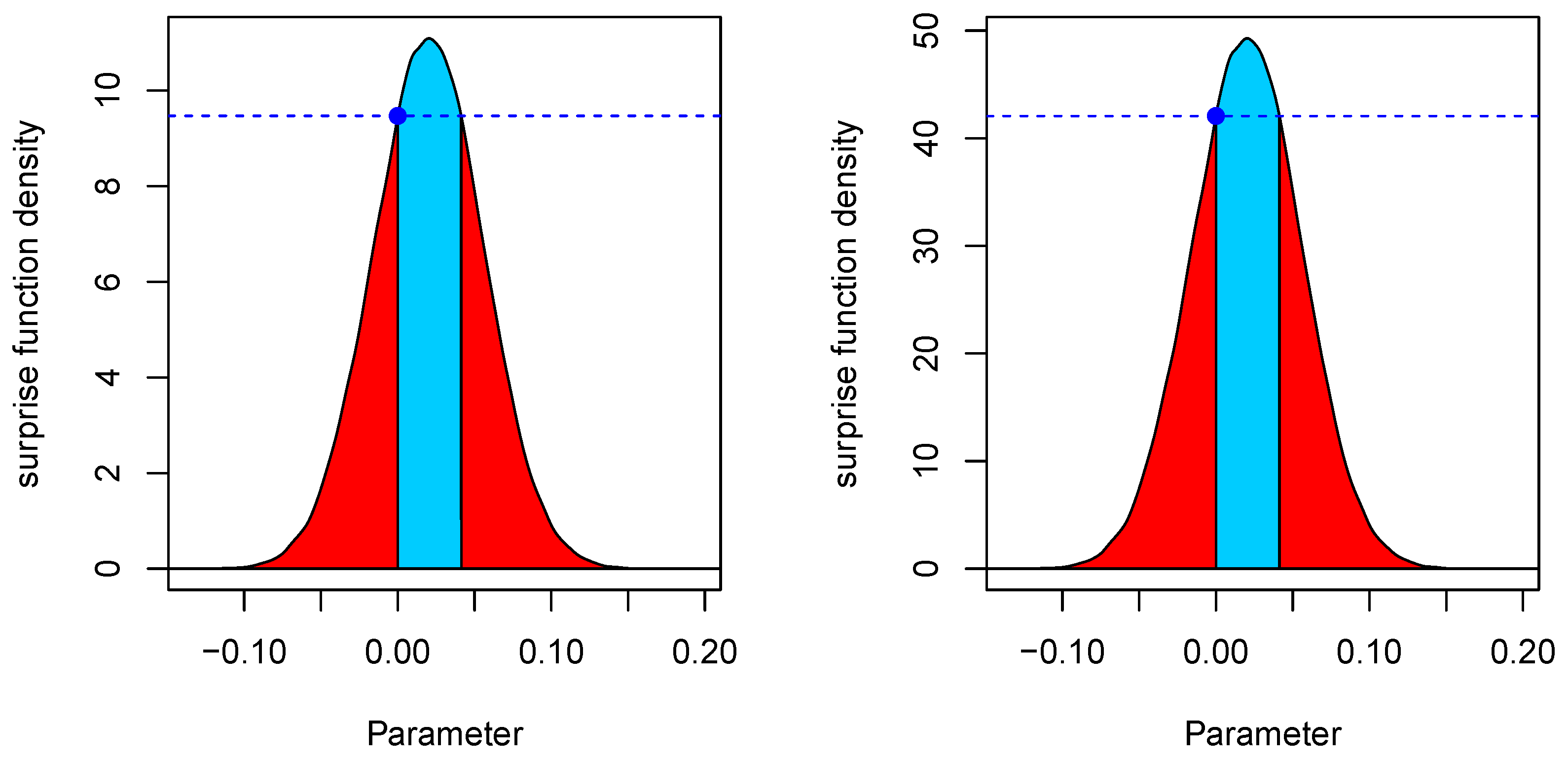
3.1. The Reference Criterion
3.2. Prior Probability of the e-Value
4. Solutions to the Two Aspects
4.1. The Reference Criterion
4.2. Prior Probability of the e-Value
5. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FBST | Full Bayesian Significance Test |
| NHST | Null Hypothesis Significance Testing |
Appendix A
References
- Gigerenzer, G. Mindless statistics. J.-Socio-Econ. 2004, 33, 587–606. [Google Scholar] [CrossRef]
- Pashler, H.; Harris, C.R. Is the Replicability Crisis Overblown? Three Arguments Examined. Perspect. Psychol. Sci. 2012, 7, 531–536. [Google Scholar] [CrossRef]
- Baker, M.; Penny, D. Is there a reproducibility crisis? Nature 2016, 533, 452–454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McElreath, R.; Smaldino, P.E. Replication, communication, and the population dynamics of scientific discovery. PLoS ONE 2015, 10, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ioannidis, J.P.A. What Have We (Not) Learnt from Millions of Scientific Papers with p-Values? Am. Stat. 2019, 73, 20–25. [Google Scholar] [CrossRef] [Green Version]
- Button, K.S.; Ioannidis, J.P.; Mokrysz, C.; Nosek, B.A.; Flint, J.; Robinson, E.S.; Munafò, M.R. Power failure: Why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 2013, 14, 365–376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kelter, R. Bayesian alternatives to null hypothesis significance testing in biomedical research: A non-technical introduction to Bayesian inference with JASP. BMC Med. Res. Methodol. 2020, 20, 1–12. [Google Scholar] [CrossRef]
- Kelter, R. Analysis of Bayesian posterior significance and effect size indices for the two-sample t-test to support reproducible medical research. BMC Med. Res. Methodol. 2020, 20, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Kelter, R. Bayesian survival analysis in STAN for improved measuring of uncertainty in parameter estimates. Meas. Interdiscip. Res. Perspect. 2020, 18, 101–119. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Morey, R.D.; Lee, M.D. Bayesian Benefits for the Pragmatic Researcher. Curr. Dir. Psychol. Sci. 2016, 25, 169–176. [Google Scholar] [CrossRef]
- Edwards, W.; Lindman, H.; Savage, L.J. Bayesian statistical inference for psychological research. Psychol. Rev. 1963, 70, 193–242. [Google Scholar] [CrossRef]
- Hendriksen, A.; de Heide, R.; Grünwald, P. Optional Stopping with Bayes Factors: A Categorization and Extension of Folklore Results, with an Application to Invariant Situations. Bayesian Anal. 2020, in press. [Google Scholar] [CrossRef]
- Berger, J.; Wolpert, R.L. The Likelihood Principle; Institute of Mathematical Statistics: Hayward, CA, USA, 1988. [Google Scholar]
- Pereira, C.A.d.B.; Stern, J.M. Evidence and credibility: Full Bayesian significance test for precise hypotheses. Entropy 1999, 1, 99–110. [Google Scholar] [CrossRef]
- Pereira, C.A.d.B.; Stern, J.M.; Wechsler, S. Can a Significance Test be genuinely Bayesian? Bayesian Anal. 2008, 3, 79–100. [Google Scholar] [CrossRef]
- Pereira, C.A.d.B.; Stern, J.M. The e-value: A fully Bayesian significance measure for precise statistical hypotheses and its research program. São Paulo J. Math. Sci. 2020, 1–19. [Google Scholar] [CrossRef]
- Kelter, R. Simulation data for the analysis of Bayesian posterior significance and effect size indices for the two-sample t-test to support reproducible medical research. BMC Res. Notes 2020, 13, 1–3. [Google Scholar] [CrossRef]
- Kelter, R. fbst: An R package for the Full Bayesian Significance Test for testing a sharp null hypothesis against its alternative via the e-value. Behav. Res. Methods 2021, in press. [Google Scholar] [CrossRef]
- Madruga, M.R.; Esteves, L.G.; Wechsler, S. On the Bayesianity of Pereira-Stern tests. Test 2001, 10, 291–299. [Google Scholar] [CrossRef]
- Diniz, M.; Pereira, C.A.B.; Polpo, A.; Stern, J.M.; Wechsler, S. Relationship between Bayesian and frequentist significance indices. Int. J. Uncertain. Quantif. 2012, 2, 161–172. [Google Scholar] [CrossRef]
- Ly, A.; Wagenmakers, E.J. A Critical Evaluation of the FBST ev for Bayesian Hypothesis Testing. Comput. Brain Behav. 2021, 1–8. [Google Scholar] [CrossRef]
- Kelter, R. On the Measure-Theoretic Premises of Bayes Factor and Full Bayesian Significance Tests: A Critical Reevaluation. Comput. Brain Behav. 2021, 1–11. [Google Scholar] [CrossRef]
- Kleijn, B. The Frequentist Theory of Bayesian Statistics; Springer: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Rosenman, R.H.; Brand, R.J.; Jenkins, D.; Friedman, M.; Straus, R.; Wurm, M. Coronary heart disease in Western Collaborative Group Study. Final follow-up experience of 8 1/2 years. JAMA 1975, 233, 872–877. [Google Scholar] [CrossRef]
- Rouder, J.N.; Speckman, P.L.; Sun, D.; Morey, R.D.; Iverson, G. Bayesian t tests for accepting and rejecting the null hypothesis. Psychon. Bull. Rev. 2009, 16, 225–237. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Schervish, M.J. Theory of Statistics; Springer Verlag: New York, NY, USA, 1995. [Google Scholar]
- Bauer, H. Measure and Integration Theory; De Gruyter: Berlin, Germany, 2001. [Google Scholar]
- Robert, C.P. The Bayesian Choice, 2nd ed.; Springer New York: Paris, France, 2007. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability, 1st ed.; The Clarendon Press: Oxford, UK, 1939. [Google Scholar]
- Haldane, J.B.S. A note on inverse probability. Math. Proc. Camb. Philos. Soc. 1932, 28, 55–61. [Google Scholar] [CrossRef]
- Popper, K. The Logic of Scientific Discovery; Routledge: London, UK; New York, NY, USA, 1959. [Google Scholar] [CrossRef]
- Berger, J. Statistical Decision Theory and Bayesian Analysis; Springer: New York, NY, USA, 1985. [Google Scholar]
- Rousseau, J. Approximating Interval hypothesis: P-values and Bayes factors. In Bayesian Statistics; Bernado, J., Berger, J., Dawid, A., Smith, A., Eds.; Oxford University Press: Valencia, Spain, 2007; Volume 8, pp. 417–452. [Google Scholar]
- Rao, C.R.; Lovric, M.M. Testing point null hypothesis of a normal mean and the truth: 21st Century perspective. J. Mod. Appl. Stat. Methods 2016, 15, 2–21. [Google Scholar] [CrossRef]
- Kelter, R. Bayesian and frequentist testing for differences between two groups with parametric and nonparametric two-sample tests. Wires Comput. Stat. 2020, 13, e1523. [Google Scholar] [CrossRef]
- Good, I. Surprise index. In Encyclopedia of Statistical Sciences; Kotz, S., Johnson, N., Reid, C., Eds.; John Wiley & Sons: New York, NY, USA, 1988; Volume 7. [Google Scholar]
- Good, I. C332. Surprise indexes and p-values. J. Stat. Comput. Simul. 1989, 32, 90–92. [Google Scholar] [CrossRef]
- Good, I.J. C420. The existence of sharp null hypotheses. J. Stat. Comput. Simul. 1994, 49, 241–242. [Google Scholar] [CrossRef]
- Stern, J.M. Significance tests, Belief Calculi, and Burden of Proof in legal and Scientific Discourse. Front. Artif. Intell. Its Appl. 2003, 101, 139–147. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelter, R. On Two Measure-Theoretic Aspects of the Full Bayesian Significance Test for Precise Bayesian Hypothesis Testing †. Phys. Sci. Forum 2021, 3, 10. https://doi.org/10.3390/psf2021003010
Kelter R. On Two Measure-Theoretic Aspects of the Full Bayesian Significance Test for Precise Bayesian Hypothesis Testing †. Physical Sciences Forum. 2021; 3(1):10. https://doi.org/10.3390/psf2021003010
Chicago/Turabian StyleKelter, Riko. 2021. "On Two Measure-Theoretic Aspects of the Full Bayesian Significance Test for Precise Bayesian Hypothesis Testing †" Physical Sciences Forum 3, no. 1: 10. https://doi.org/10.3390/psf2021003010
APA StyleKelter, R. (2021). On Two Measure-Theoretic Aspects of the Full Bayesian Significance Test for Precise Bayesian Hypothesis Testing †. Physical Sciences Forum, 3(1), 10. https://doi.org/10.3390/psf2021003010





