Abstract
We present an approach to enhance the performance and flexibility of the Bayesian inference of model parameters based on observations of the measured data. Going beyond the usual surrogate-enhanced Monte-Carlo or optimization methods that focus on a scalar loss, we place emphasis on a function-valued output of a formally infinite dimension. For this purpose, the surrogate models are built on a combination of linear dimensionality reduction in an adaptive basis of principal components and Gaussian process regression for the map between reduced feature spaces. Since the decoded surrogate provides the full model output rather than only the loss, it is re-usable for multiple calibration measurements as well as different loss metrics and, consequently, allows for flexible marginalization over such quantities and applications to Bayesian hierarchical models. We evaluate the method’s performance based on a case study of a toy model and a simple riverine diatom model for the Elbe river. As input data, this model uses six tunable scalar parameters as well as silica concentrations in the upper reach of the river together with the continuous time-series of temperature, radiation, and river discharge over a specific year. The output consists of continuous time-series data that are calibrated against corresponding measurements from the Geesthacht Weir station at the Elbe river. For this study, only two scalar inputs were considered together with a function-valued output and compared to an existing model calibration using direct simulation runs without a surrogate.
1. Introduction
Delayed acceptance [1,2] can accelerate Markov chain Monte Carlo (MCMC) sampling up to a factor of one over the acceptance rate. In order to do so, it requires a surrogate of the posterior that contains the cost function inside the likelihood in the case of model calibration. The simplest way to implement delayed acceptance relies on a surrogate with scalar output built for this cost function or for the likelihood. Here, we take an intermediate step and construct a surrogate for the functional output of a blackbox model to be calibrated against reference data. Typical examples are numerical simulations that output time-series or spatial data and depend on tunable input parameters.
There exist numerous related works treating blackbox models with functional outputs with surrogates. Campbell et al. [3] used an adaptive basis of principal component analysis (PCA) to perform global sensitivity analysis. Pratola et al. [4] and Ranjan et al. [5] used GP regression for sequential model calibration in a Bayesian framework. Lebel et al. [6] modeled the likelihood function in an MCMC model calibration via a Gaussian process. Perrin [7] compared the use of a multi-output GP surrogate with a Kronecker structure to an adaptive basis approach.
The present contribution relies on the adaptive basis approach in principal components (Karhunen–Loéve expansion or functional PCA) to reduce the dimensions of the functional output, while modeling the map from inputs to weights in this basis via GP regression. We demonstrate the application of this approach on two examples using usual and hierarchical Bayesian model calibration. In the latter case, a surrogate beyond the cost function is required if the likelihood depends on additional auxiliary parameters. As an example, we allow variations of the (fractional) order of the norm, thereby, marginalizing over different noise models, including Gaussian and Laplacian noise.
2. Gaussian Process Regression and Bayesian Global Optimization
Gaussian process regression [8,9,10] is a commonly used tool to construct flexible non-parameteric surrogates. Based on the observed outputs at training points and a covariance function , the GP regressor predicts a Gaussian posterior distribution at any point . For a single prediction , the expected value and variance of this distribution are given by
where is the mean model, the covariance matrix K contains entries based on the training set, are entries of a row vector, and is a scalar. The unit matrix I is added with the noise covariance , which regularizes the problem and is usually estimated in an optimization loop together with other kernel hyperparameters.
Such a surrogate with uncertainty information can be used for Bayesian global optimization [11,12,13] of the log-posterior as a cost function. Here, we apply this method to reach the vicinity of the posterior’s mode before sampling. As an acquisition function, we use the expected improvement (see, e.g., [12]) at a newly observed location given existing training data ,
where is the optimum value for observed thus far. Due to the non-linear transformation from the functional blackbox output to the value of the cost function, it is more convenient to realize Bayesian optimization with a direct GP surrogate of the cost function that is constructed in addition to the surrogate for the functional output for the KL expansion coefficients described below.
3. Delayed Acceptance MCMC
Delayed acceptance MCMC builds on a fast surrogate for the posterior to reject unlikely proposals early [1,2]. Following the usual Metropolis–Hastings algorithm, the probability to accept a new proposal in this first stage in the n-the step of the Markov chain is, as usual,
where g is a transition probability that has been suitably tuned during warmup. The true posterior is only evaluated if the proposal “survives” this first stage and enters the final acceptance probability
Actual computation is typically performed in the logarithmic space with a cost function
If this function is fixed, it is most convenient to directly build a surrogate for the log-posterior including the corresponding prior.
4. Bayesian Hierarchical Models and Fractional Norms
One application of modeling the full functional output instead of only the cost function is the existence of additional distribution parameters in the likelihood in addition to the original model inputs . Such dependencies appear within Bayesian hierarchical models [14], where are again subject to a certain (prior) distribution with possibly further levels of hyperparameters. There are essentially two ways to construct a surrogate with support for additional parameters : Building a surrogate for the cost function that adds as independent variables or constructing a surrogate with functional output for and keeping the dependencies on exact. Here, we focus on the latter, and apply this surrogate within delayed acceptance MCMC with both, and as tunable parameters.
As an example, we use a more general noise model than the usual Gaussian likelihood that builds on arbitrary norms [15,16,17] with real-valued not fixed while traversing the Markov chain. We allow members of the exponential family for observational noise and specify only its scale, but keep as a free parameter. Namely, we model the likelihood for observing in the output as
with the normalized norm to the power of ,
as the loss function between observed data and blackbox model . Choosing the usual norm leads to a Gaussian likelihood for the noise model, whereas using the norm means Laplacian noise. To maintain the relative scale when varying , it is important to add the term from (7) to the negative log-likelihood. In the following use cases, we are going to compare the cases of fixed and variable .
5. Linear Dimension Reduction via Principal Components
Formally, the blackbox output for given input can be a function in an infinite-dimensional Hilbert space (though sampled at a finite number of points in practice). Linear dimension reduction in such a space means finding the optimum set of basis functions that spans the output space for any input given to the blackbox. The reduced model of order r is then given by
This approach is known as the Karhunen–Loéve (KL) expansion [18] in case are interpreted as realizations of a random process, or as the functional principal component analysis (FPCA) [19]. For our application, this distinction does not matter. The KL expansion boils down to solving a regression problem in the non-orthogonal basis of N observed realizations to represent new observations. Then, an eigenvalue problem is solved to invert the collocation matrix with entries
Here, the inner product in Hilbert spaces and its approximation for a finite set of support points is given by
If (many support points, few samples), solving the eigenvalue problem of the collocation matrix M is more efficient than the dual one of the covariance matrix C with in the usual PCA (see [9] for their equivalence via the singular value decomposition of ). The question of at which r to truncate the eigenspectrum in (9) depends on the desired accuracy in the output, which is briefly analyzed in the following paragraph.
Error Estimate
Here, we justify why we can assume an truncation error of the order of the ratio between the smallest eigenvalue considered in the approximation and the largest one. The truncated SVD can be shown to be the best linear approximation of lower rank r to an matrix M in terms of the Frobenius norm (see, e.g., [20]). Its value is simply computed from the norm of singular values,
where in the case of real eigenvalues of a positive semi-definite matrix as for the covariance or collocation matrix. The truncation error is given by
The error estimate for the KL expansion uses this convenient property together with the fact that the Frobenius norm is compatible with the usual norm of vectors , i.e.,
Representing via the first r eigenvalues of the collocation matrix yields a relative squared reconstruction error of
The last estimate is relatively crude if , and the spectrum decays fast with the index variable k. If one assumes a decay rate with
one obtains
where is the Riemann zeta function. This function diverges for a spectral decay of order and reaches its asymptotic value relatively quickly for (e.g., ). The spectral decay rate can be fitted in a log–log plot of over index k and takes values between and 5 in our use case. The underlying assumptions are violated if the spectrum stagnates at a large number of constant eigenvalues for higher indices k.
6. Implementation and Results
The idea behind the realization of MCMC with a function-valued surrogate is quite simple. Instead of directly using the surrogate for the cost ℓ with fixed , we take a step in-between. Multiple surrogates are built, where each maps the input to one weight in the KL expansion. A surrogate for the model output is then given by replacing by in (9). The according surrogate for the cost function uses instead of in (8). Dependencies on are kept exact in this approach. The main algorithm proceeds in the following steps:
- Construct a GP surrogate for the cost function on a space-filling sample sequence over the whole prior range.
- Refine the sampling points near the posterior’s mode through Bayesian global optimization with the cost surrogate.
- Train a multi-output GP surrogate for the functional output on the refined sampling points.
- Use the function-valued surrogate for delayed acceptance in the MCMC run.
For all GP surrogates, we use a Matern 5/2 kernel for together with a linear mean model for , as realized in the Python package GPy [21]. For step 4, we use Gibbs sampling and the surrogate for , yielding the full output rather than only the distance to a certain reference dataset. The idea to refine the surrogate iteratively during MCMC had to be abandoned early. The problem is that detailed balance is violated as soon as the surrogate proposal probabilities change when modifying the GP regressor with a new point. In the following application cases, we compare a usual MCMC evaluation using the full model to MCMC with delayed acceptance using the GP surrogate together with the KL expansion/functional PCA (GP+KL) in the output function space.
6.1. Toy Model
First, we test the quality of the algorithm on a toy model given by
We choose reference values to test the calibration of against the according output and add Gaussian noise of amplitude . A flat prior is used for . For the hierarchical model case (7), we choose a starting guess of for the norm’s order and a Gaussian prior with around this value together with a positivity constraint. The initial sampling domain in the square . The comparison between MCMC and delayed acceptance MCMC is made once for fixed (Gaussian likelihood) and then for a hierarchical model with a random walk also in . The respective Markov chain with 10,000 steps has a correlation length of steps (Figure 1) and yields a posterior parameter distribution for depicted in Figure 2.
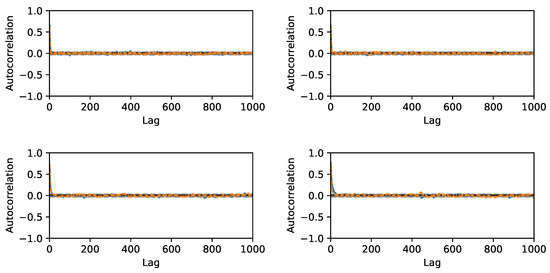
Figure 1.
Autocorrelation over lag in MCMC steps for inputs (solid) and (dashed) in the toy model. Top: Gaussian likelihood, and bottom: hierarchical model. Left: full MCMC, and right: delayed acceptance MCMC with GP+KL surrogate.

Figure 2.
Posterior distribution of the calibrated parameters in (18). Top: Gaussian likelihood, bottom: hierarchical model. Left: full MCMC, right: delayed acceptance MCMC with GP+KL surrogate.
The results in Figure 2 show good agreement in the posterior distributions of full MCMC and delayed acceptance MCMC. Compared to the case with fixed , the additional freedom in in the hierarchical model leads to further exploration of the parameter space. The posterior of according to the Markov chain is given in Figure 3. The similarity to the prior distribution shows that the data does not yield new information on how to choose .

Figure 3.
Posterior distribution of the fractional order in the loss function with norm. Left: full MCMC, right: delayed acceptance MCMC with GP+KL surrogate.
6.2. Riverine Diatom Model
The final application of the described method is on a riverine diatom model [22,23]. This model predicts the chlorophyll a concentration at an observation point at the Elbe river as a time series and depends on several input parameters. For simplicity, and to limit computational resources, we select only two of the six scalar inputs and use fixed values for the remaining four. Namely, the chosen parameters and appear in the growth rate inside the diatom model. The latter is given by the “Smith formula” [24] for photosynthesis,
where D is the water depth, and is the radiation intensity prescribed at the water surface. Light attenuation is modeled to be proportional to the chlorophyll a concentration . Equations are solved within a Lagrangian setup, following water parcels that travel down the Elbe river. Data points of the local chlorophyll time series simulated at Geesthacht Weir are made up by chlorophyll a values at the Lagrangian trajectory end points. These values are the functional model output for which the model is calibrated with respect to measurements . As the parameters are positive and limited by reasonable maximum values from domain knowledge, we use a half-sided Cauchy (Lorentz) prior
Here, we choose a scale value for which of the probability volume is contained within. Considering the cumulative distribution, we have to set
to realize this condition.
As in the case of the toy model, we use 10,000 steps in the Markov chain. The results for autocorrelation and posterior samples using the full model versus delayed acceptance are shown in Figure 4 and Figure 5. The correlation time of ≈500 steps is much larger than in the toy model, and the decay of the autocorrelation over the lag roughly matches between the two approaches. Delayed acceptance sampling produces similar posterior samples in Figure 5 at about one third of the overall computation time. There, one also sees the issue of high correlation between and in the posterior of the calibration, making Gibbs sampling inefficient in that particular case.

Figure 4.
Autocorrelation over lag in MCMC steps for inputs (solid) and (dashed) in the riverine diatom model. Top: Gaussian likelihood, bottom: hierarchical model. Left: full MCMC, right: delayed acceptance MCMC with GP + KL surrogate.
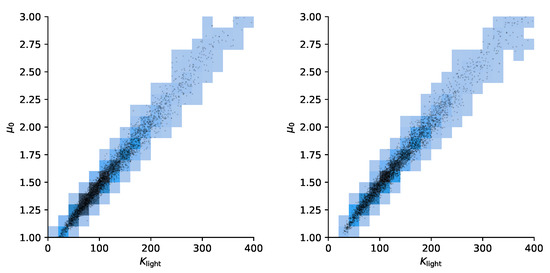
Figure 5.
Posterior distribution of calibrated parameters for the riverine diatom model. Left: full MCMC, right: delayed acceptance MCMC with GP + KL surrogate.
7. Conclusions and Outlook
We illustrated the application of function-valued surrogates to delayed acceptance MCMC for parameter calibration in simple as well as hierarchical Bayesian models. Using a surrogate for the functional output rather than a cost function or likelihood is useful for several reasons. Conceptually, it allows introducing additional distribution parameters in Bayesian hierarchical models. Our results demonstrate that it is possible and efficient to perform MCMC with delayed acceptance on such models while keeping the dependencies in these additional parameters exact. In particular, the fractional order of the norm appearing in the cost function was left free, which is useful for robust model calibration.
The method was applied to a toy model and an application case of a riverine diatom model. In both cases, using delayed acceptance with a surrogate for the functional output produced results comparable to using the full model at only about one third of the actual model evaluations. Compared to direct surrogate modeling of the cost function, we could also observe an increase in the quality of the predicted cost. This is likely connected to the higher flexibility of modeling weights to multiple principal components with Gaussian processes with individual hyperparameters.
The described approach is not immune to the curse of dimensionality. On the one hand, the number of required GP regressors grows linearly with the effective dimensions of the output function space. Since evaluation is fast and parallelizable, this is a minor issue in practice. On the other hand, increasing the dimension of the input space soon prohibits the construction of a reliable surrogate due to the required number training points to fill the parameter space. In such cases, the preprocessing overhead is expected to outweigh the speedup of delayed acceptance MCMC for either functional or scalar surrogates. More detailed investigations will be required to give quantitative estimates on this trade off.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available in a publicly accessible repository. The data presented in this study are openly available in Zenodo at https://doi.org/10.5281/zenodo.5773865, reference number [25].
Acknowledgments
This study is a contribution to the Reduced Complexity Models grant number ZT-I-0010 funded by the Helmholtz Association of German Research Centers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Christen, J.A.; Fox, C. Markov Chain Monte Carlo Using an Approximation. J. Comput. Graph. Stat. 2005, 14, 795–810. [Google Scholar] [CrossRef]
- Wiqvist, S.; Picchini, U.; Forman, J.L.; Lindorff-Larsen, K.; Boomsma, W. Accelerating Delayed-Acceptance Markov Chain Monte Carlo Algorithms. arXiv 2019, arXiv:1806.05982. [Google Scholar]
- Campbell, K.; McKay, M.D.; Williams, B.J. Sensitivity Analysis When Model Outputs Are Functions. Reliab. Eng. Syst. Saf. 2006, 91, 1468–1472. [Google Scholar] [CrossRef]
- Pratola, M.T.; Sain, S.R.; Bingham, D.; Wiltberger, M.; Rigler, E.J. Fast Sequential Computer Model Calibration of Large Nonstationary Spatial-Temporal Processes. Technometrics 2013, 55, 232–242. [Google Scholar] [CrossRef]
- Ranjan, P.; Thomas, M.; Teismann, H.; Mukhoti, S. Inverse Problem for a Time-Series Valued Computer Simulator via Scalarization. Open J. Stat. 2016, 6, 528–544. [Google Scholar] [CrossRef] [Green Version]
- Lebel, D.; Soize, C.; Fünfschilling, C.; Perrin, G. Statistical Inverse Identification for Nonlinear Train Dynamics Using a Surrogate Model in a Bayesian Framework. J. Sound Vib. 2019, 458, 158–176. [Google Scholar] [CrossRef] [Green Version]
- Perrin, G. Adaptive Calibration of a Computer Code with Time-Series Output. Reliab. Eng. Syst. Saf. 2020, 196, 106728. [Google Scholar] [CrossRef] [Green Version]
- O’Hagan, A. Curve Fitting and Optimal Design for Prediction. J. R. Stat. Soc. Ser. B 1978, 40, 1–24. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef] [Green Version]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- Osborne, M.A.; Garnett, R.; Roberts, S.J. Gaussian Processes for Global Optimization; Learning and 3rd International Conference on Learning and Intelligent Optimization, LION 3; Springer: Trento, Italy, 2009. [Google Scholar]
- Preuss, R.; von Toussaint, U. Global Optimization Employing Gaussian Process-Based Bayesian Surrogates. Entropy 2018, 20, 201. [Google Scholar] [CrossRef] [PubMed]
- Allenby, G.M.; Rossi, P.E.; McCulloch, R.E. Hierarchical Bayes Models: A Practitioners Guide; SSRN Scholarly Paper ID 655541; Social Science Research Network: Rochester, NY, USA, 2005. [Google Scholar] [CrossRef] [Green Version]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the Surprising Behavior of Distance Metrics in High Dimensional Space; Database Theory—ICDT 2001; Lecture Notes in Computer Science; Van den Bussche, J., Vianu, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 420–434. [Google Scholar] [CrossRef] [Green Version]
- Dose, V. Bayesian Estimate of the Newtonian Constant of Gravitation. Meas. Sci. Technol. 2006, 18, 176–182. [Google Scholar] [CrossRef]
- Flexer, A.; Schnitzer, D. Choosing Lp Norms in High-Dimensional Spaces Based on Hub Analysis. Neurocomputing 2015, 169, 281–287. [Google Scholar] [CrossRef] [Green Version]
- Newman, A.J. Model Reduction via the Karhunen-Loeve Expansion Part I: An Exposition; Institute for Systems Research Technical Reports; Univ. Maryland: College Park, MD, USA, 1996. [Google Scholar]
- Shang, H.L. A Survey of Functional Principal Component Analysis. AStA Adv. Stat. Anal. 2014, 98, 121–142. [Google Scholar] [CrossRef] [Green Version]
- Cadzow, J.A. Spectral Analysis. In Handbook of Digital Signal Processing; Elsevier: Amsterdam, The Netherlands, 1987; pp. 701–740. [Google Scholar]
- GPy. GPy: A Gaussian Process Framework in Python; Software Publication, Univ. Sheffield: Sheffield, UK, 2012. [Google Scholar]
- Callies, U.; Scharfe, M.; Ratto, M. Calibration and Uncertainty Analysis of a Simple Model of Silica-Limited Diatom Growth in the Elbe River. Ecol. Model. 2008, 213, 229–244. [Google Scholar] [CrossRef]
- Scharfe, M.; Callies, U.; Blöcker, G.; Petersen, W.; Schroeder, F. A Simple Lagrangian Model to Simulate Temporal Variability of Algae in the Elbe River. Ecol. Model. 2009, 220, 2173–2186. [Google Scholar] [CrossRef]
- Smith, E.L. Photosynthesis in Relation to Light and Carbon Dioxide. Proc. Natl. Acad. Sci. USA 1936, 22, 504–511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albert, C.G.; von Toussaint, U.; Callies, U. Dataset for article “Surrogate-Enhanced Parameter Inference for Function-Valued Models”, v1.0. Zenodo, 2021.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).