Abstract
We consider and prove the existence of stable, spherical, and thin fluid shells in the context of a Schwarzschild–Rindler-anti-de Sitter (SRAdS) background. We identify the metric parameter regions that allow the existence and stability of these shells for three cases of fluid equations of state. The case of the vacuum shell is especially interesting since it remains consistent with past studies by two of the authors of this manuscript, which showed the existence of stable spherical domain walls in the context of the same metric. This type of structure could be an alternative to the idea of the gravastar star formations.
Keywords:
stability; fluid equation of state; gravastar; Rindler; anti-de Sitter; domain wall; spherical shell 1. Introduction
The concept of thin spherical shells in General Relativity holds great significance as a theoretical construct because, as was first shown in [1], one can use it to model the interactions between matter and gravity and find analytical solutions to the Einstein equations governing them.
The gravastar [2,3,4,5,6] is a theoretical, spherical and stable thin shell configuration that can be used to accurately describe an alternative to black holes as the last step of stellar evolution. The concept of gravastars portrays star structures that alternate between a Schwarzschild metric for their exterior and a de Sitter metric for their interior space, with the inner region considered traditionally as a gravitational Bose–Einstein condensate with zero entropy.
As shown in [7], a stable spherical thin shell solution similar to that of the gravastar can be found when considering a non-trivial background geometry of Schwarzschild-anti-deSitter curved spacetime [7,8] with a Rindler acceleration term, coupled with spherically symmetric scalar field dynamical equations. This metric is a Schwarzschild–Rindler-anti-deSitter (SRAdS) metric [9],
where is the well known cosmological constant, and b is the parameter attributed to the Rindler acceleration.
This SRAdS metric (1) has been subject to constraints appended by solar system observations [10,11]; it can produce flat rotation curves [12] and it has been shown to partially explain [13,14] the Pioneer anomaly [15,16].
A new analysis [17] was instigated by the fact that this type of metric has a demonstrated ability to support metastable structures such as spherical domain walls. Specifically, the question that was raised was whether this metric could foster thin shell solutions adhering to the three most general forms of equations of state, corresponding to a vacuum shell, a stiff matter shell and a dust shell.
In what follows, we will show how we made use of the Israel junction conditions formalism to explore the aforementioned question by breaking it down to four simpler points of interest:
- Is it possible to construct stable, thin, fluid shells within an SRAdS metric?
- If so, which are the specific, general conditions that have to be met in order to achieve stability?
- What are the numerical metric parameter ranges that enable stability, considering the conditions induced by the different equations of state?
- How does the radius R of the stable shell change as a function of the metric parameters within the allowed numerical space?
As mentioned above, we have made use of the Israel junction condition formalism in order to interpolate between the two metric parts of the shell, in each case of the equations of state. The value of the shell mass m has been considered to be discontinuous radially across the shell, inside and outside, in contrast to the values of the b and parameters that are considered to have continuous fixed values when crossing the shell.
The manuscript is structured as follows: In the first section, we show the general theory that has been developed entailing the derivation of stability conditions for a static and spherical shell with a general equation of state on an SRAdS metric background geometry. In Section 3, we show how these results can be applied to three specific cases of fluid equations of state, as well as how we can derive the conditions for stability in each case. Finally, in the last Section 4 of the manuscript, we discuss the opportunities for extending the analysis presented here.
The following assumptions have been made in the entirety of the manuscript: We set , as well as . For the parameter values considered here, an event horizon exists but no cosmological horizon, and the shell radius is always outside the event horizon of the black hole.
2. Existence and Stability of Thin Shell Solutions
We begin by defining a spherical thin shell with a radius R, which alternates between an interior () and an exterior () SRAds metric of the form [2,3,18],
where
and
Considering the case of a shell in the context of the SRAdS metric (1), one can derive the Israel junction conditions in the form of [3]
where () denotes the derivative of the mass with respect to r, and the dot corresponds to the derivative with respect to the proper time, defined as
From these equations, one can derive the equation for the energy conservation of the shell
Therefore, the necessary general conditions for the existence and stability of a static fluid shell take the form,
where we have made the assumption that Equation (9) is exactly the same as that of a particle moving in a straight line with zero energy. For the SRAdS metric, the general form of the potential of the shell has the form
In what follows, we show the derivation of the system of equations that constrain the ranges of of , which permit the existence of stable, spherical fluid shells. Specifically, we concern ourselves with three distinct types of fluid shells—the vacuum, the stiff matter, and the dust fluid shell. We also derive the numerical ranges of the metric parameters that allow for stability.
3. Specific Cases of Shell Stability
3.1. Shell with Vacuum Fluid Equation of State
Firstly, we concern ourselves with the case of the vacuum shell with an equation of state,
Therefore, the surface density takes the form,
In this case, the system of Equation (11), necessary for the existence and stability of a shell solution, becomes
Whereas its solution is written as
where corresponds to perturbations of the surface density .
The fact that the parameters R and display lower limits, as seen in Equations (20) and (21), allows us to derive boundaries on the values of that permit the existence and stability of the stable shell solutions. These lower and upper boundaries are of the form,
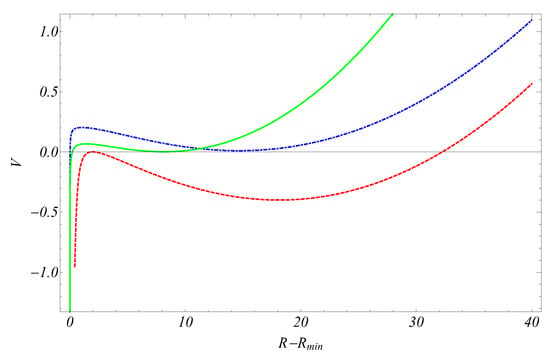
In Figure 1 [17], we can see the aforementioned boundaries as well as the parameter space that allows for stability considering the values of . The minimum value of the parameter b is increased as is increased (see Equation (22)). For the three sets of , displayed as color coded dots in the the right panel of Figure 1, we show their corresponding potentials in Figure 2 [17], noticing that only those potentials that correspond to the parameter sets that exist inside the stability region display a minimum that indicates stability.
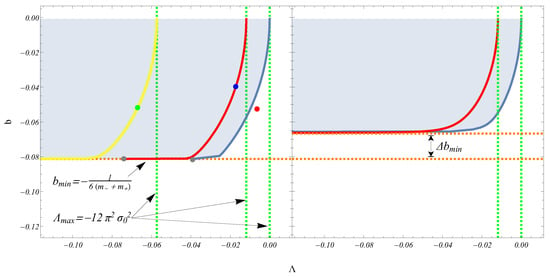
Figure 1.
We see how the stability regions (light blue region) vary for two cases of exterior masses of the shell. Each of the different colored curves correspond to different values of the surface density . The left panel corresponds to and the right to .
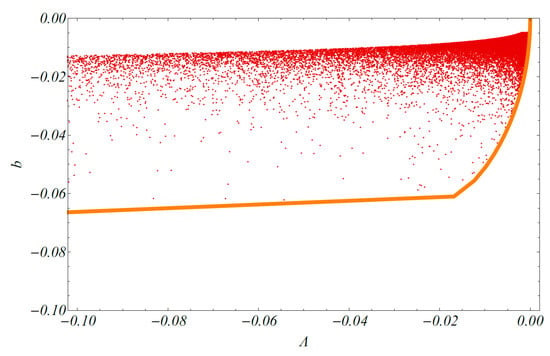
In order to validate our analytical results, we have performed a random Monte Carlo process, selecting a set of points in the parameter space for which there exist stable, spherical shell solutions, as seen in Figure 3 [17]. We have obtained these points by fixing , , and repeating a process of considering random values of within the limits set by the stability constraint (20) such that (see Equation (21)). For each point in the set of values, we derive the stability metric parameters .
3.2. Stiff Matter and Pressurless Dust Fluid Shells
Regarding the stiff matter shell the equation of state takes the form
with a surface density of
whereas for the case of the dust fluid shell, the equation of state is
with a surface density,
The potentials (12) are,
and
for each case, respectively. Solving the system (11) for these potentials produces and b of the form,
for the stiff matter case, and
for the dust fluid shell.
We expect that the range of the metric parameters that allow for the stability of the stiff matter shell solutions will be narrower than that of the vacuum shell. This is because the potential of Equation (29) contains an extra repulsive term proportional to , and therefore has the side effect of diminishing the attraction produced by the anti-deSitter term (), which is very important for the stability of the shell.
The potential (30) that corresponds to the dust fluid shell does not contain any high order terms of R, for example, ; this benefits the stability at a larger R by not constraining the effect of the anti-deSitter term (). This means that the stability range for the case of the dust fluid shell is much wider than the case of the stiff matter equation of state.
4. Conclusions
We have constructed thin, spherical, fluid shell structures in the SRAdS metric and we have proved their stability. These shells are very similar to the gravastar structures [2,3,19,20,21], but instead of having an interior described by a de Sitter metric, they are described by the SRAdS metric throughout.
Our analysis could present the opportunity for interesting extensions, including the investigation of the existence and stability of spherical fluid shells in the context of various metrics. Perhaps one could consider a non continuous metric broken up into two pieces, half containing a Schwarzschild term and half containing a Rindler term.
Arguably, the most important extension of our study would be the investigation of the observational effects produced by these types of shell structures. We can study the lensing patterns produced by the light-like geodesics along the lines of References [22,23]. Such observational signatures can be directly compared with those of gravastars [24]. Lastly, it would be interesting to investigate non-spherical fluid shells in the context of rotating spacetimes coupled with the cosmological constant.
Funding
This research is co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning 2014–2020” in the context of the project “Scalar fields in Curved Spacetimes: Soliton Solutions, Observational Results and Gravitational Waves” (MIS 5047648).
References
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Nuovo Cim. B 1966, 44S10, 1. [Google Scholar] [CrossRef]
- Mazur, P.O.; Mottola, E. Gravitational vacuum condensate stars. Proc. Natl. Acad. Sci. USA 2004, 101, 9545–9550. [Google Scholar] [CrossRef] [PubMed]
- Visser, M.; Wiltshire, D.L. Stable gravastars: An Alternative to black holes? Class. Quantum Gravity 2004, 21, 1135–1152. [Google Scholar] [CrossRef]
- Lobo, F.S. Stable dark energy stars. Class. Quantum Gravity 2006, 23, 1525–1541. [Google Scholar] [CrossRef]
- DeBenedictis, A.; Horvat, D.; Ilijic, S.; Kloster, S.; Viswanathan, K. Gravastar solutions with continuous pressures and equation of state. Class. Quantum Gravity 2006, 23, 2303–2316. [Google Scholar] [CrossRef]
- Ansoldi, S. Spherical black holes with regular center: A Review of existing models including a recent realization with Gaussian sources. In Proceedings of the Conference on Black Holes and Naked Singularities, Milan, Italy, 10–12 May 2008. [Google Scholar]
- Alestas, G.; Perivolaropoulos, L. Evading Derrick’s theorem in curved space: Static metastable spherical domain wall. Phys. Rev. D 2019, 99, 064026. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. Gravitational Interactions of Finite Thickness Global Topological Defects with Black Holes. Phys. Rev. 2018, 97, 124035. [Google Scholar] [CrossRef]
- Grumiller, D. Model for gravity at large distances. Phys. Rev. Lett. 2010, 105, 211303. [Google Scholar] [CrossRef]
- Carloni, S.; Grumiller, D.; Preis, F. Solar system constraints on Rindler acceleration. Phys. Rev. D 2011, 83, 124024. [Google Scholar] [CrossRef]
- Iorio, L. Solar system constraints on a Rindler-type extra-acceleration from modified gravity at large distances. JCAP 2011, 05, 019. [Google Scholar] [CrossRef]
- Mannheim, P.D.; Kazanas, D. Exact Vacuum Solution to Conformal Weyl Gravity and Galactic Rotation Curves. Astrophys. J. 1989, 342, 635–638. [Google Scholar] [CrossRef]
- Grumiller, D.; Preis, F. Rindler force at large distances. Int. J. Mod. Phys. D 2011, 20, 2761–2766. [Google Scholar] [CrossRef]
- Iorio, L. Impact of a Pioneer/Rindler-type acceleration on the Oort cloud. Mon. Not. R. Astron. Soc. 2012, 419, 2226–2232. [Google Scholar] [CrossRef]
- Anderson, J.D.; Laing, P.A.; Lau, E.L.; Liu, A.S.; Nieto, M.M.; Turyshev, S.G. Indication, from Pioneer 10/11, Galileo, and Ulysses data, of an apparent anomalous, weak, long range acceleration. Phys. Rev. Lett. 1998, 81, 2858–2861. [Google Scholar] [CrossRef]
- Lammerzahl, C.; Preuss, O.; Dittus, H. Is the physics within the Solar system really understood? Astrophys. Space Sci. Libr. 2008, 349, 75–101. [Google Scholar] [CrossRef]
- Alestas, G.; Kraniotis, G.; Perivolaropoulos, L. Existence and stability of static spherical fluid shells in a Schwarzschild-Rindler–anti–de Sitter metric. Phys. Rev. D 2020, 102, 104015. [Google Scholar] [CrossRef]
- Frauendiener, J.; Hoenselaers, C.; Konrad, W. A shell around a black hole. Class. Quantum Gravity 1990, 7, 585–587. [Google Scholar] [CrossRef][Green Version]
- Martin Moruno, P.; Montelongo Garcia, N.; Lobo, F.S.; Visser, M. Generic thin-shell gravastars. JCAP 2012, 03, 034. [Google Scholar] [CrossRef]
- Uchikata, N.; Yoshida, S. Slowly rotating thin shell gravastars. Class. Quantum Gravity 2016, 33, 025005. [Google Scholar] [CrossRef]
- Broderick, A.E.; Narayan, R. Where are all the gravastars? Limits upon the gravastar model from accreting black holes. Class. Quantum Gravity 2007, 24, 659–666. [Google Scholar] [CrossRef]
- Lim, Y.K.; Wang, Q.H. Exact gravitational lensing in conformal gravity and Schwarzschild–de Sitter spacetime. Phys. Rev. D 2017, 95, 024004. [Google Scholar] [CrossRef]
- Cutajar, D.; Adami, K.Z. Strong lensing as a test for Conformal Weyl Gravity. Mon. Not. Roy. Astron. Soc. 2014, 441, 1291–1296. [Google Scholar] [CrossRef]
- Sakai, N.; Saida, H.; Tamaki, T. Gravastar Shadows. Phys. Rev. 2014, D90, 104013. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).