Hydrodynamic Effects of Mastigonemes in the Cryptophyte Chilomonas paramecium
Abstract
1. Introduction
2. Methods
2.1. Choice and Cultivation of the Cryptophyte Species
2.2. Acquisition of the Flagellar Waveforms from Phase-Contrast Microscopy and High-Speed Imaging
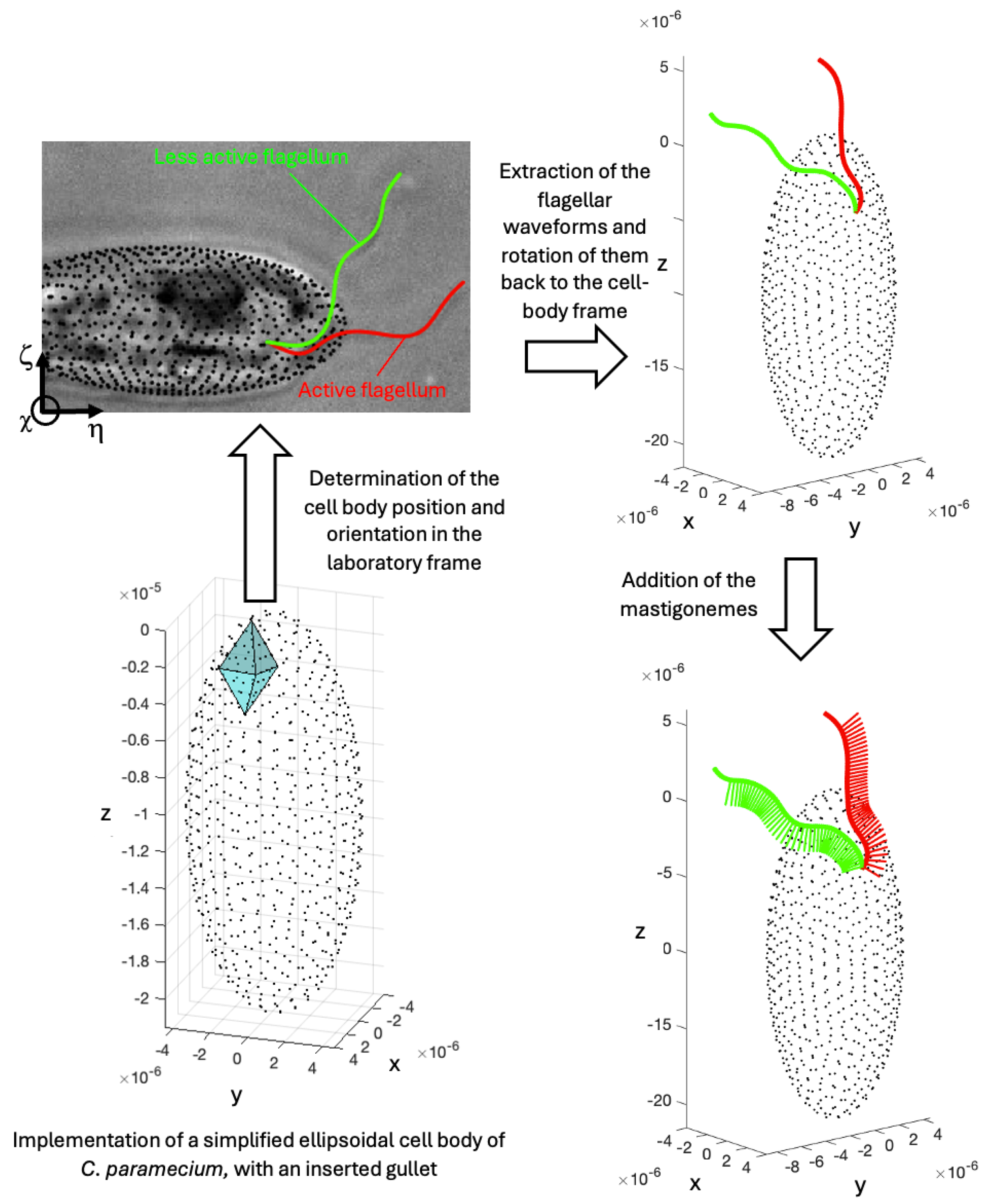
2.3. Tracking the Cell Body Position and Orientation
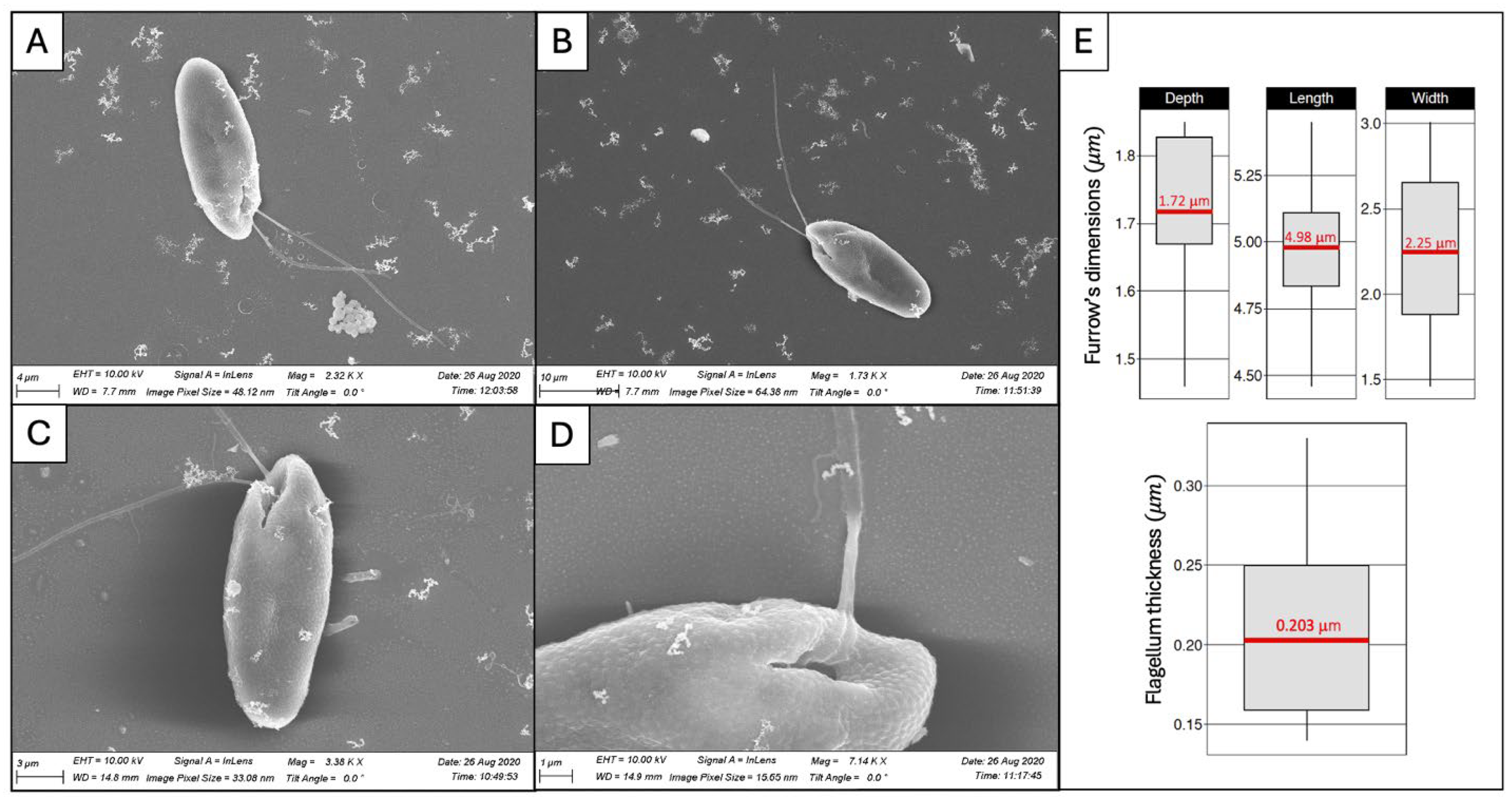
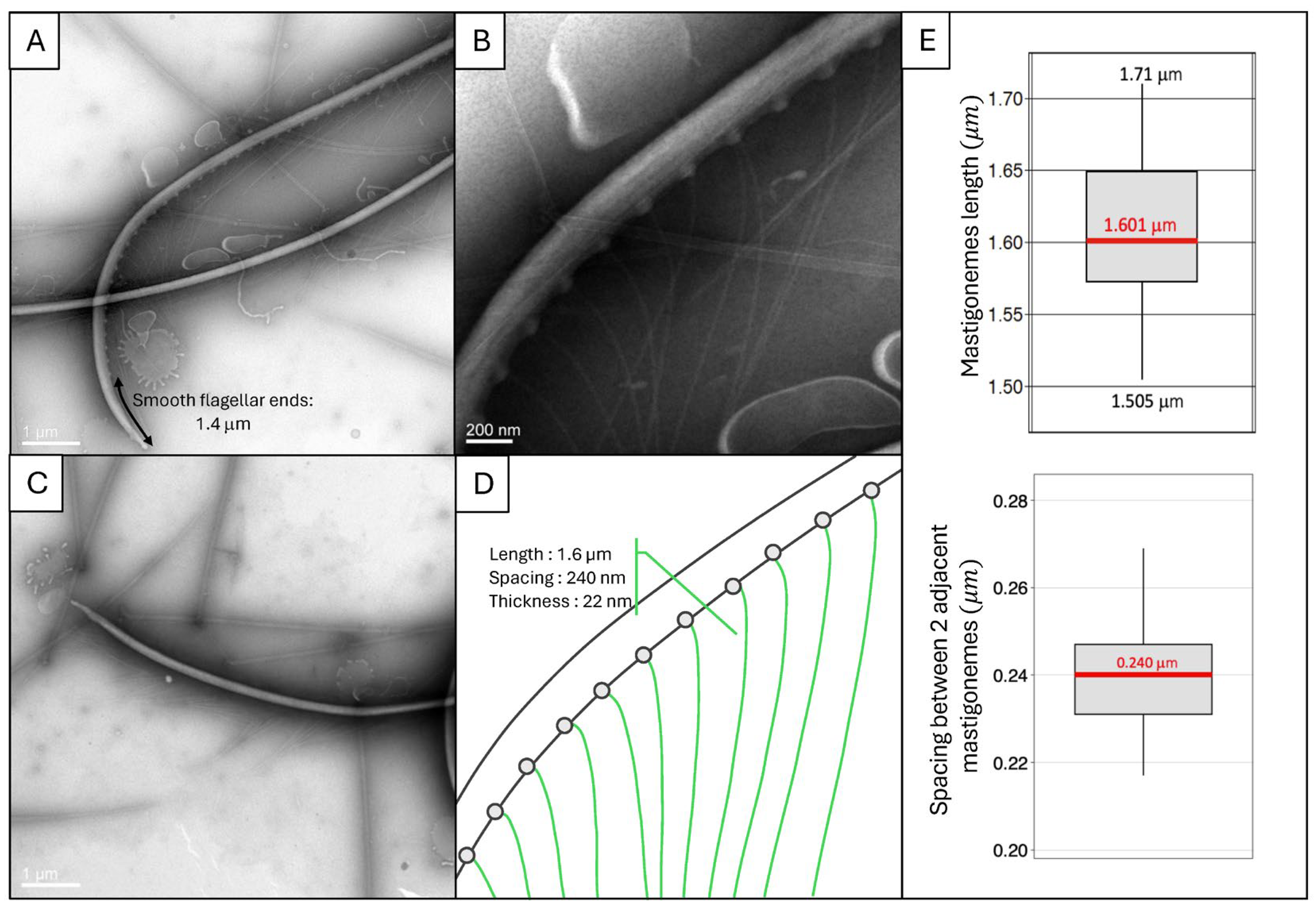
2.4. Acquisition of the Cell Body and Flagellar Ultrastructures Geometry from Observations Using Electron Microscopy
2.5. Prediction of Swimming from Flagellar Motions Using the Method of Regularized Stokeslets
3. Results
3.1. Experimental Observations
3.1.1. Experimental Observations of C. paramecium Geometry
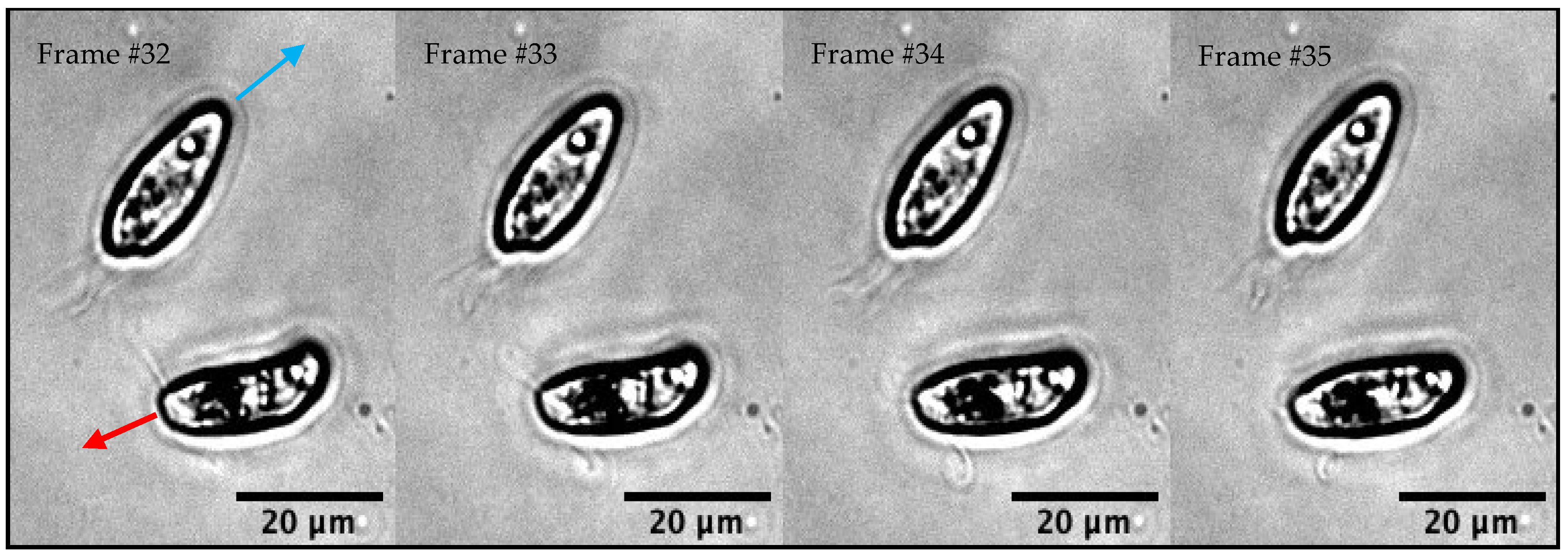
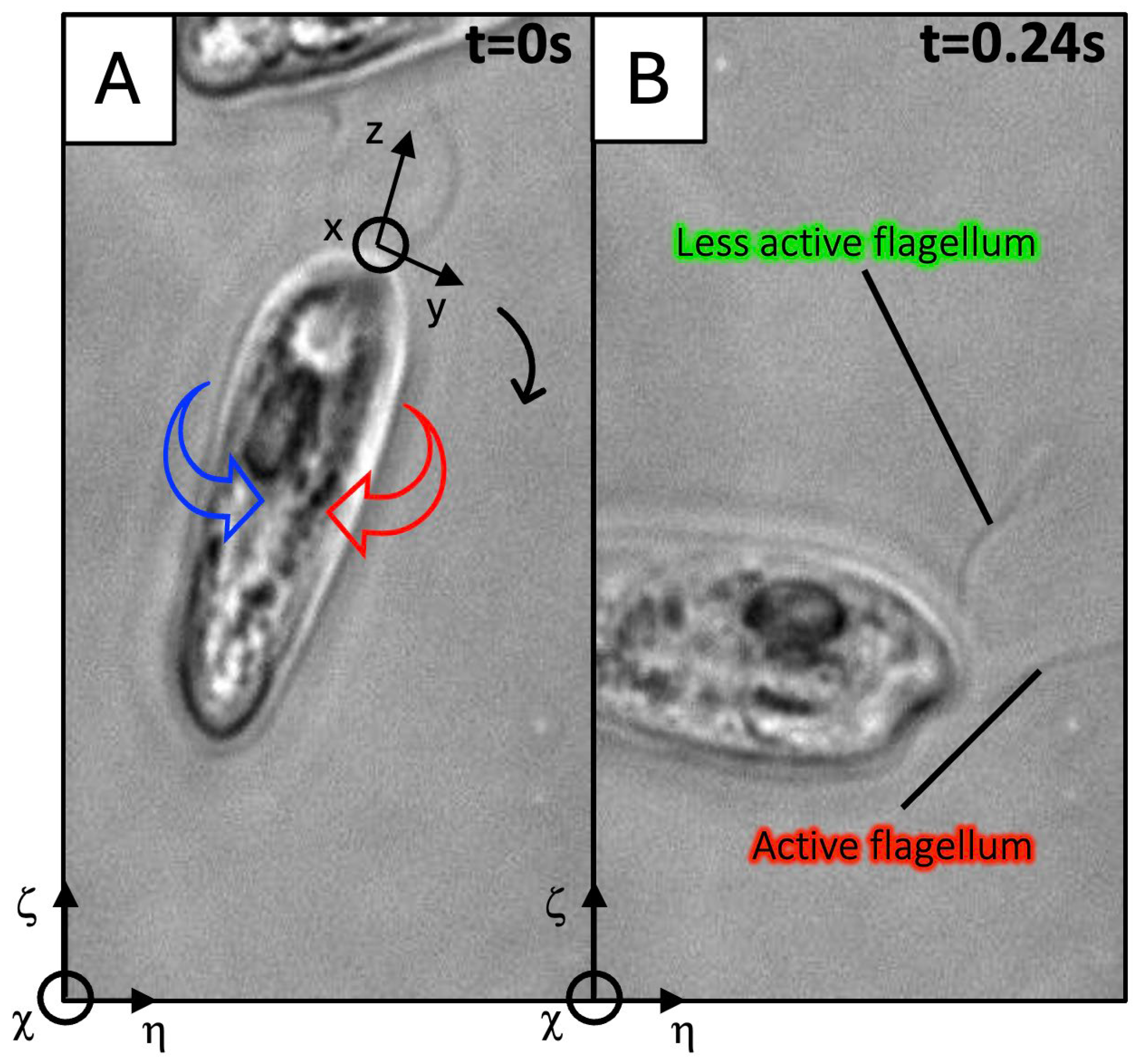
3.1.2. Experimental Observations of C. paramecium Motility and Flagellar Waveforms
3.2. Flagellar Waveform Extraction, Kinematic Analysis, and Simulation Inputs
3.2.1. Description of the Video of Interest
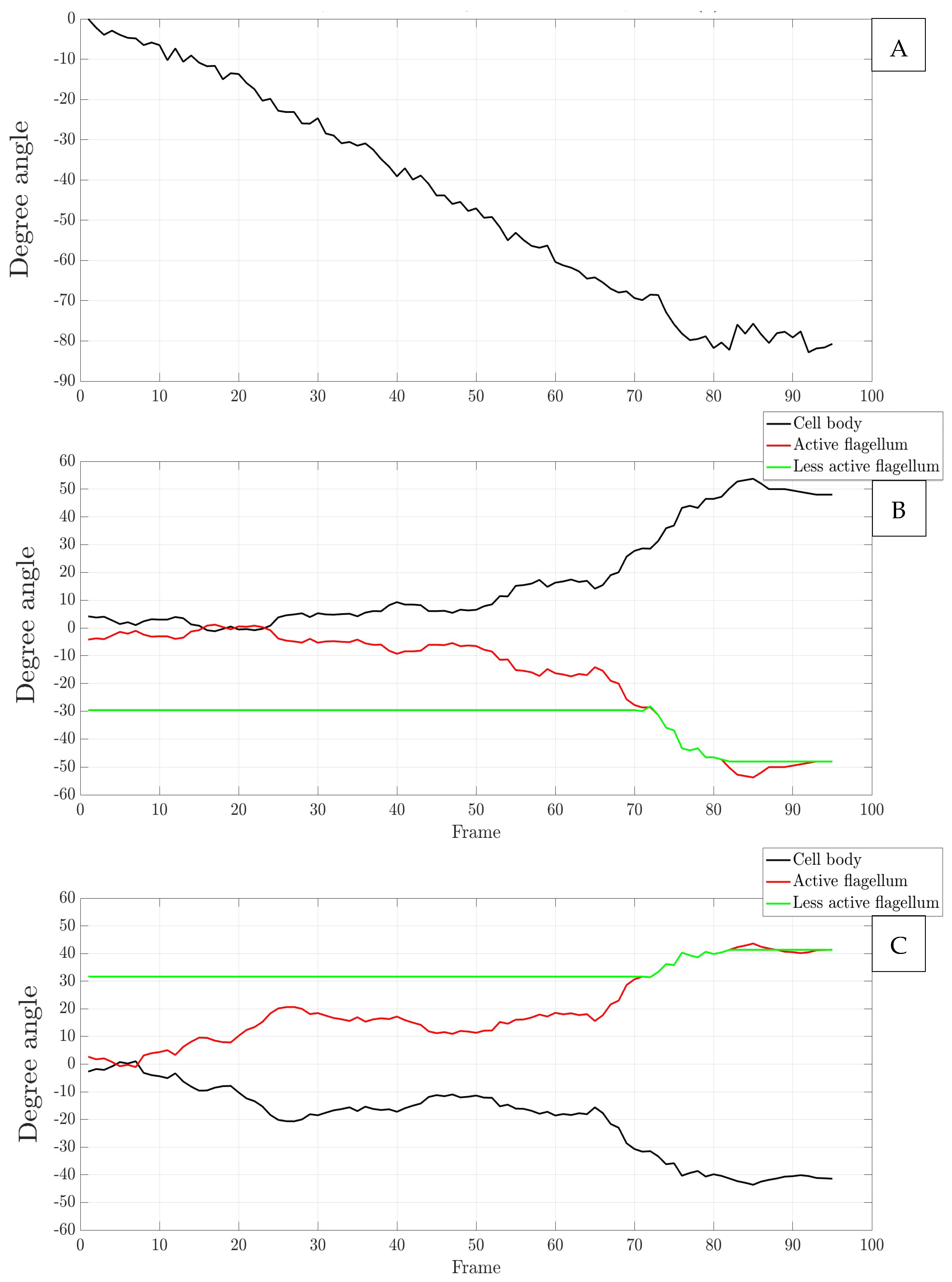
3.2.2. Analysis of Flagellar Waveform Variation
3.3. Numerical Study of the Hydrodynamic Effects of Rigid Mastigonemes in C. paramecium
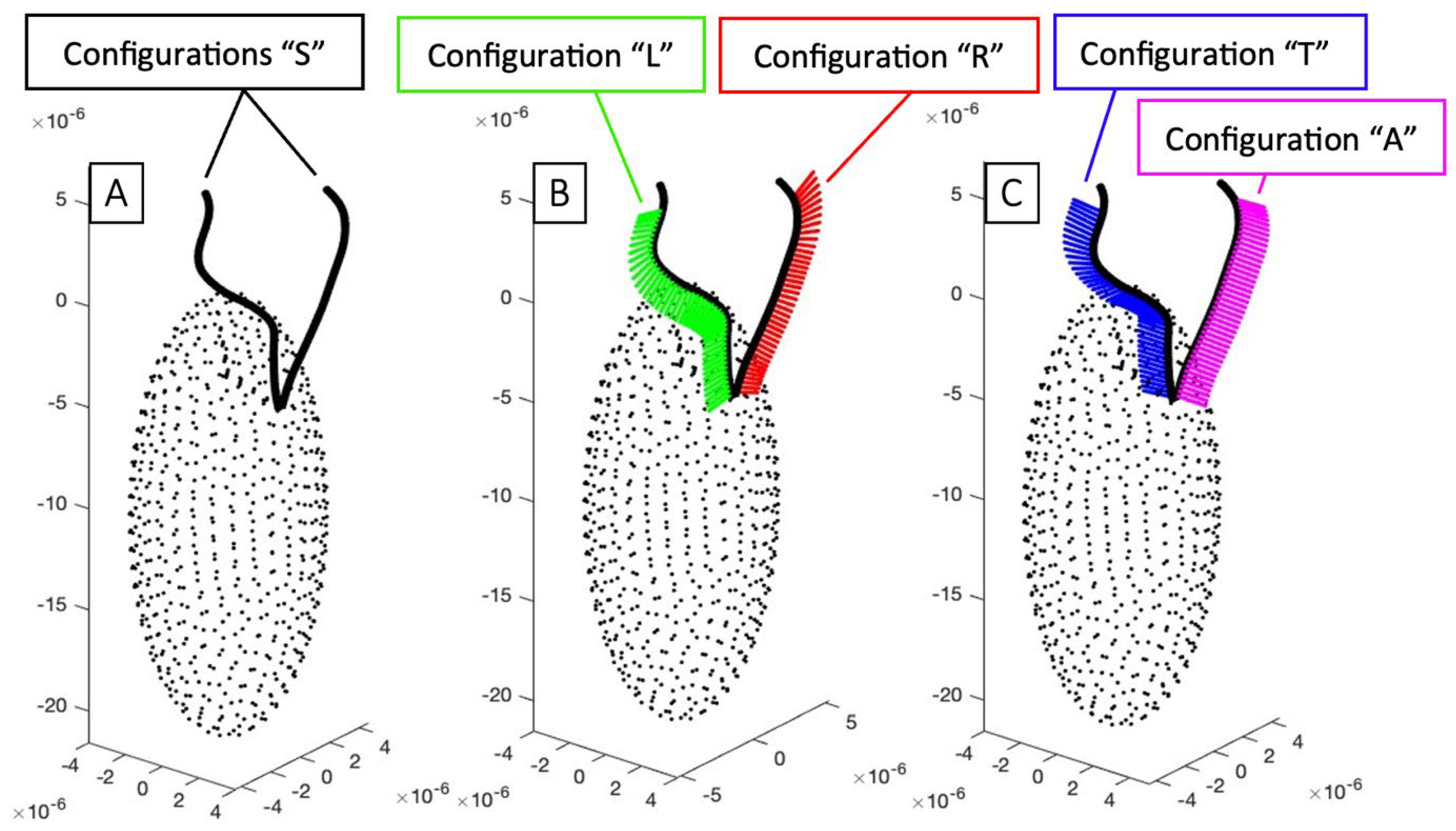
3.3.1. Mastigoneme Configurations
- Mastigonemes oriented toward the right in the beating plane, labeled as “R”.
- Mastigonemes oriented toward the left in the beating plane, labeled as “L”.
- Mastigonemes oriented toward the cell body in the plane perpendicular to the beating plane, labeled as “T”.
- Mastigonemes oriented away from the cell body in the plane perpendicular to the beating plane, labeled as “A”.
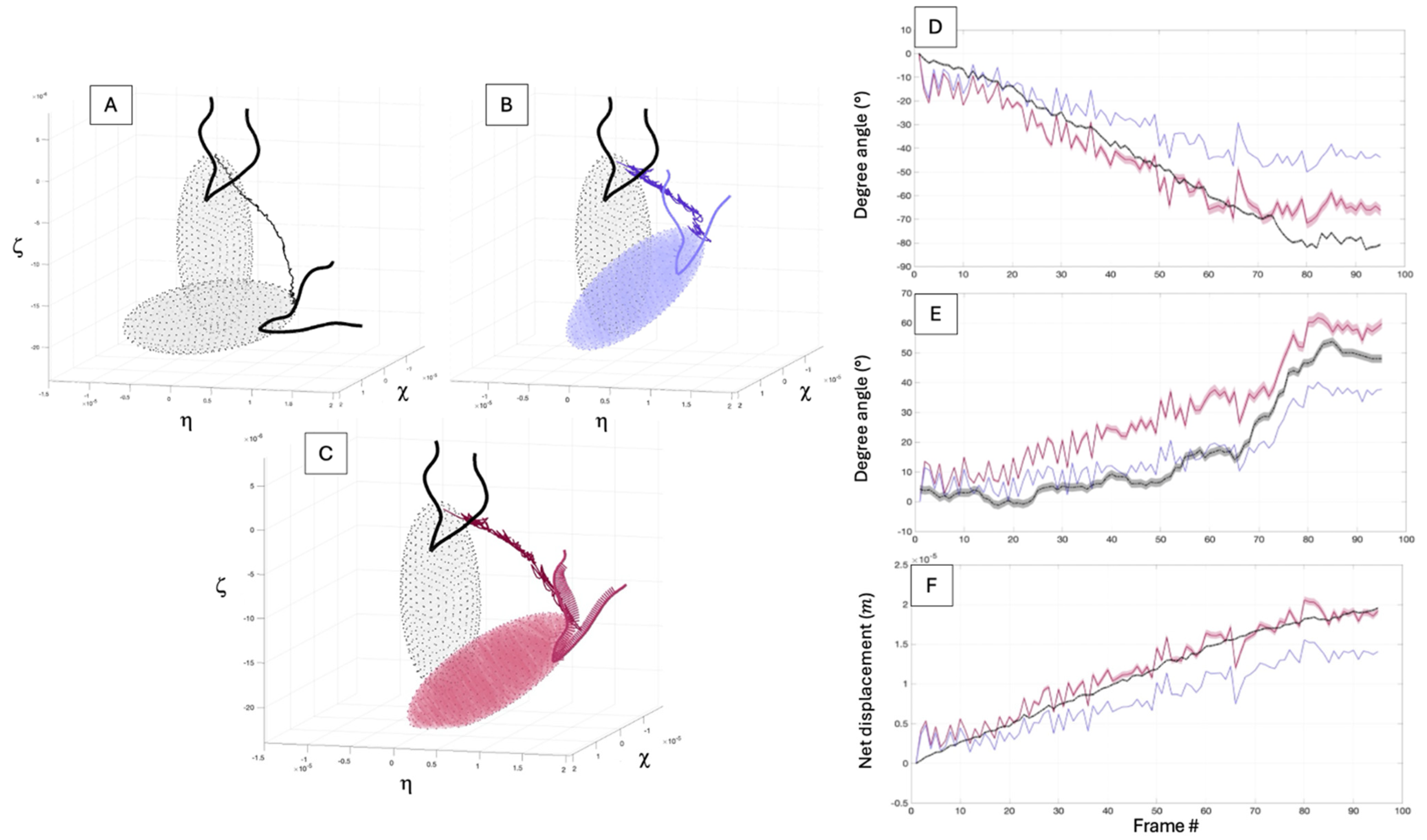
3.3.2. Simulation Overview
3.3.3. Numerical Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
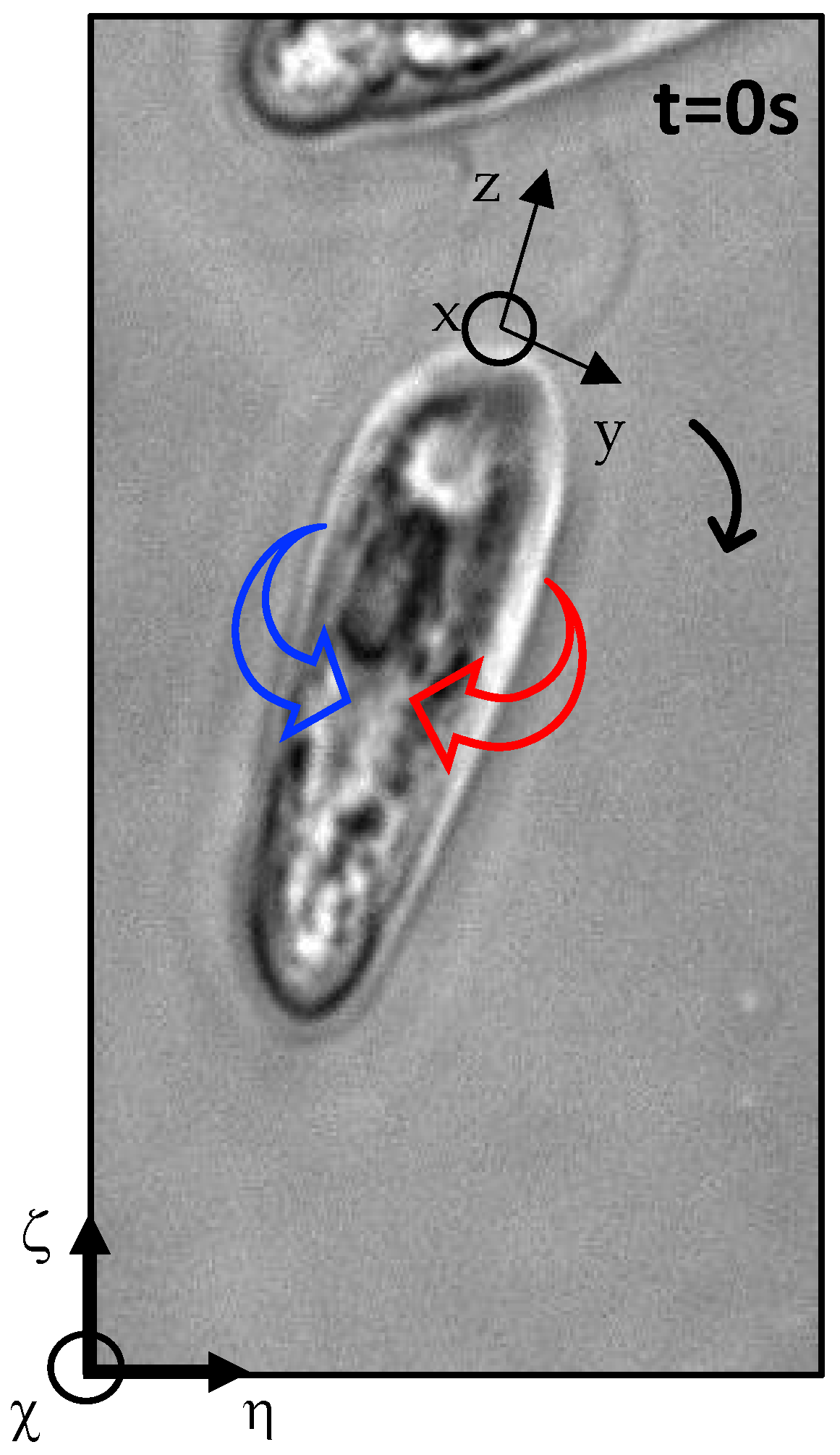
Appendix A. Figures Depicting Longitudinal Rotation Angles
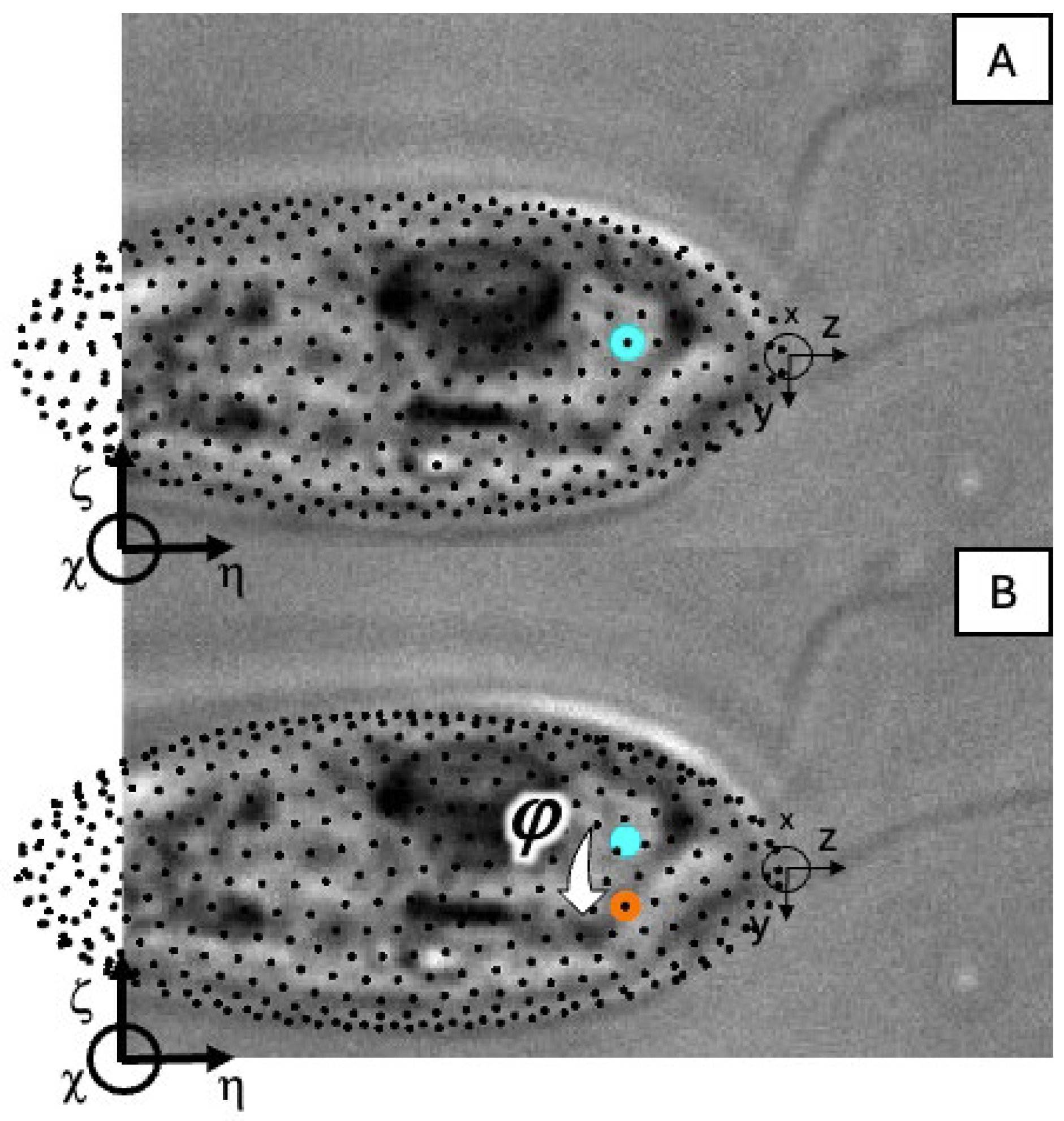

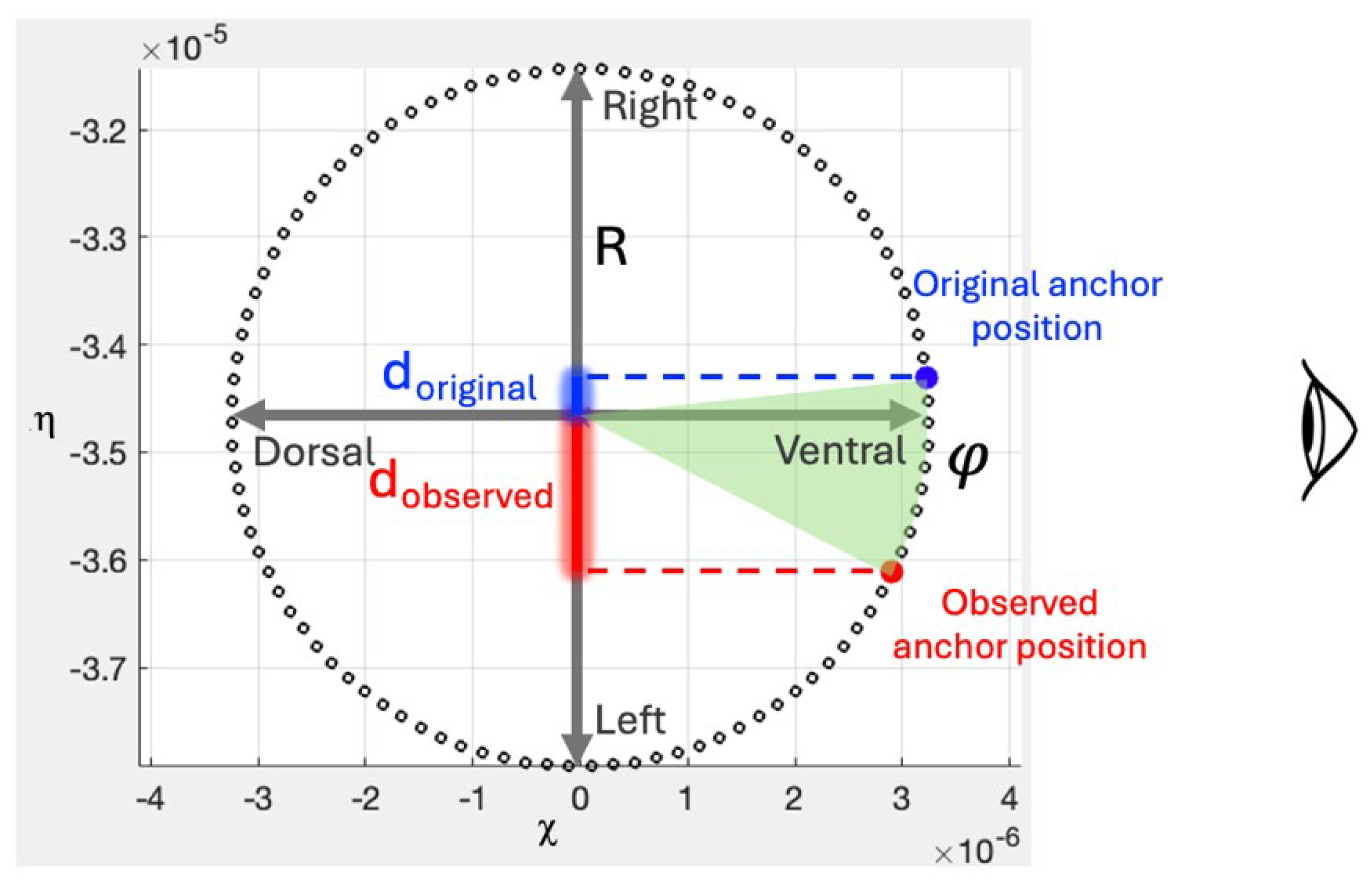
Appendix B. Error Propagation for Uncertainties in Longitudinal Rotation Angles
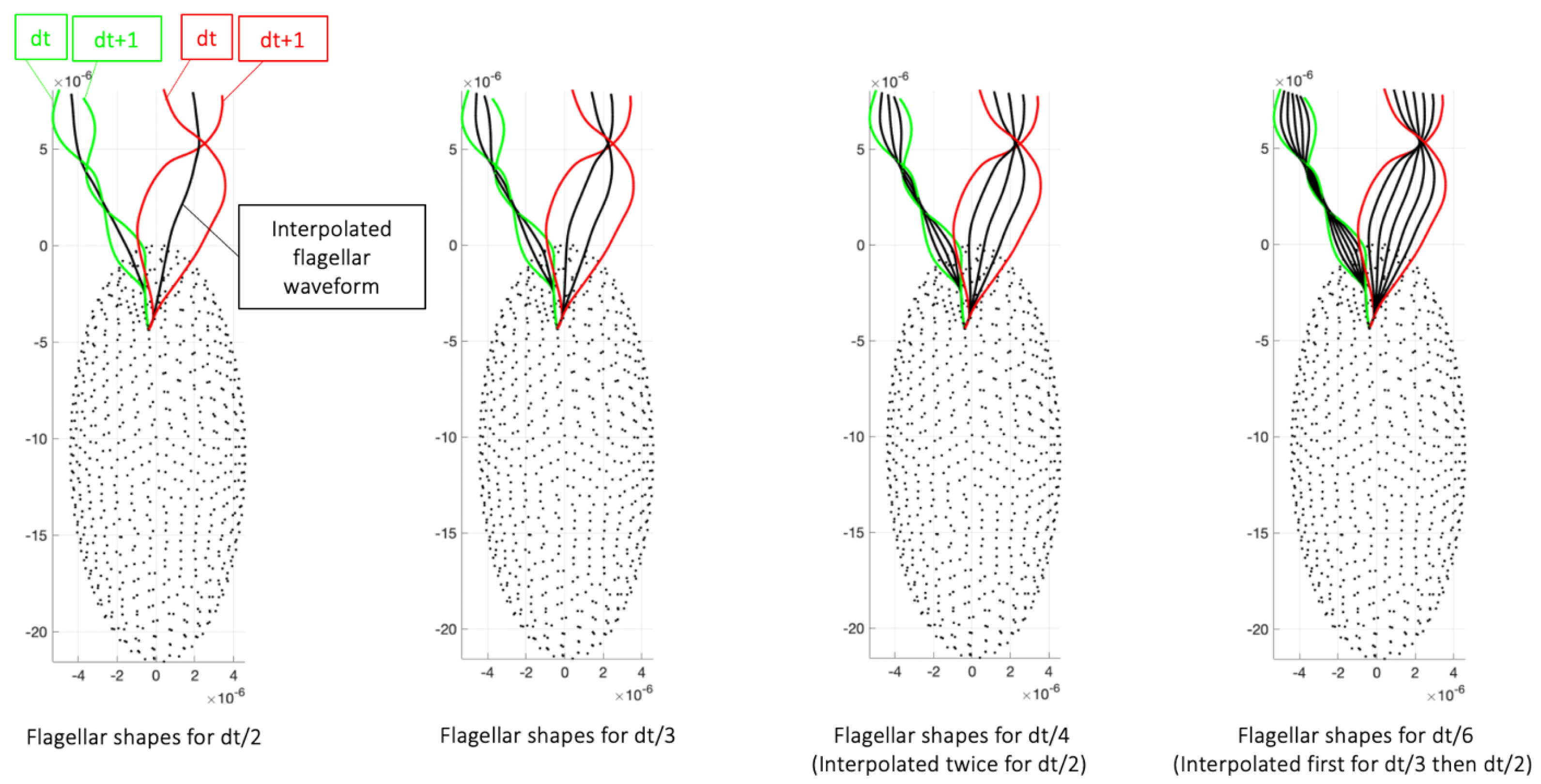
Appendix C. Convergence Study with Respect to Timestep Used in Simulation

References
- Lisicki, M.; Velho Rodrigues, M.F.; Goldstein, R.E.; Lauga, E. Swimming eukaryotic microorganisms exhibit a universal speed distribution. eLife 2019, 8, e44907. [Google Scholar] [CrossRef] [PubMed]
- Javornický, P.; Hindák, F. Cryptomonas frigoris spec. nova (Cryptophyceae), the new cyst-forming flagellate from the snow of the High Tatras. Biologia 1970, 25, 241–250. [Google Scholar] [PubMed]
- Klaveness, D. Ecology of the Cryptomonadida: A first review. In Growth and Reproductive Strategies of Freshwater Phytoplankton; Cambridge University Press: Cambridge, UK, 1988; pp. 105–133. [Google Scholar]
- Hill, D.R.A. A revised circumscription of Cryptomonas (Cryptophyceae) based on examination of Australian strains. Phycologia 1991, 30, 170–188. [Google Scholar] [CrossRef]
- Alcocer, J.; Lugo, A.; Sánchez, M.d.R.; Escobar, E. Isabela Crater-Lake: A Mexican insular saline lake. Hydrobiologia 1998, 381, 1–7. [Google Scholar] [CrossRef]
- Garibotti, I.; Vernet, M.; Ferrario, M.; Smith, R.; Ross, R.; Quetin, L. Phytoplankton Spatial Distribution Patterns along the Western Antarctic Peninsula (Southern Ocean). Mar. Ecol. Prog. Ser. 2003, 261, 21–39. [Google Scholar] [CrossRef]
- Hoef-Emden, K. Revision of the genus Cryptomonas (Cryptophyceae) II: Incongruences between the classical morphospecies concept and molecular phylogeny in smaller pyrenoid-less cells. Phycologia 2007, 46, 402–428. [Google Scholar] [CrossRef]
- Phlips, E.J.; Havens, K.E.; Lopes, M.R.M. Seasonal dynamics of phytoplankton in two Amazon flood plain lakes of varying hydrologic connectivity to the main river channel. Fundam. Appl. Limnol. 2008, 172, 99–109. [Google Scholar] [CrossRef]
- Hoef-Emden, K.; Archibald, J.M. Cryptophyta (Cryptomonads). In Handbook of the Protists; Archibald, J.M., Simpson, A.G.B., Slamovits, C.H., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 851–891. [Google Scholar] [CrossRef]
- Spaulding, S.A.; MCKnight, D.M.; Smith, R.L.; Dufford, R. Phytoplankton population dynamics in perennially ice-covered Lake Fryxell, Antarctica. J. Plankton Res. 1994, 16, 527–541. [Google Scholar] [CrossRef]
- Doust, A.B.; Wilk, K.E.; Curmi, P.M.G.; Scholes, G.D. The photophysics of cryptophyte light-harvesting. J. Photochem. Photobiol. Chem. 2006, 184, 1–17. [Google Scholar] [CrossRef]
- Spear-Bernstein, L.; Miller, K.R. Unique Location of the Phycobiliprotein Light-Harvesting Pigment in the Cryptophyceae. J. Phycol. 1989, 25, 412–419. [Google Scholar] [CrossRef]
- Moal, J.; Martin-Jezequel, V.; Harris, R.; Samain, J.-F.; Poulet, S. Interspecific and intraspecific variability of the chemical-composition of marine-phytoplankton. Oceanol. Acta 1987, 10, 339–346. [Google Scholar]
- Pedrós-Alió, C.; Massana, R.; Latasa, M.; Garcí-Cantizano, J.; Gasol, J.M. Predation by ciliates on a metalimnetic Cryptomonas population: Feeding rates, impact and effects of vertical migration. J. Plankton Res. 1995, 17, 2131–2154. [Google Scholar] [CrossRef]
- Weisse, T.; Kirchhoff, B. Feeding of the heterotrophic freshwater dinoflagellate Peridiniopsis berolinense on cryptophytes: Analysis by flow cytometry and electronic particle counting. Aquat. Microb. Ecol. 1997, 12, 153–164. [Google Scholar] [CrossRef]
- Roberts, E.C.; Laybourn-Parry, J. Mixotrophic cryptophytes and their predators in the Dry Valley lakes of Antarctica. Freshw. Biol. 1999, 41, 737–746. [Google Scholar] [CrossRef]
- Tirok, K.; Gaedke, U. Regulation of planktonic ciliate dynamics and functional composition during spring in Lake Constance. Aquat. Microb. Ecol. 2007, 49, 87–100. [Google Scholar] [CrossRef]
- Buma, A.G.J.; Treguer, P.; Kraay, G.W.; Morvan, J. Algal pigment patterns in different watermasses of the Atlantic sector of the Southern Ocean during fall 1987. Polar Biol. 1990, 11, 55–62. [Google Scholar] [CrossRef]
- Moline, M.A.; Claustre, H.; Frazer, T.K.; Schofield, O.; Vernet, M. Alteration of the food web along the Antarctic Peninsula in response to a regional warming trend. Glob. Change Biol. 2004, 10, 1973–1980. [Google Scholar] [CrossRef]
- Jeong, H.J.; Yoo, Y.D.; Lee, K.H.; Kim, T.H.; Seong, K.A.; Kang, N.S.; Lee, S.Y.; Kim, J.S.; Kim, S.; Yih, W.H. Red tides in Masan Bay, Korea in 2004–2005: I. Daily variations in the abundance of red-tide organisms and environmental factors. Harmful Algae 2013, 30, S75–S88. [Google Scholar] [CrossRef]
- Johnson, M.D.; Stoecker, D.K.; Marshall, H.G. Seasonal dynamics of Mesodinium rubrum in Chesapeake Bay. J. Plankton Res. 2013, 35, 877–893. [Google Scholar] [CrossRef]
- Piwosz, K.; Wiktor, J.M.; Niemi, A.; Tatarek, A.; Michel, C. Mesoscale distribution and functional diversity of picoeukaryotes in the first-year sea ice of the Canadian Arctic. ISME J. 2013, 7, 1461–1471. [Google Scholar] [CrossRef]
- Šupraha, L.; Bosak, S.; Ljubešić, Z.; Mihanović, H.; Olujić, G.; Mikac, I.; Viličić, D. Cryptophyte bloom in a Mediterranean estuary: High abundance of Plagioselmis cf. prolonga in the Krka River estuary (eastern Adriatic Sea). Sci. Mar. 2014, 78, 329–338. [Google Scholar] [CrossRef]
- Unrein, F.; Gasol, J.M.; Not, F.; Forn, I.; Massana, R. Mixotrophic haptophytes are key bacterial grazers in oligotrophic coastal waters. ISME J. 2014, 8, 164–176. [Google Scholar] [CrossRef] [PubMed]
- Yoo, Y.D.; Seong, K.A.; Jeong, H.J.; Yih, W.; Rho, J.-R.; Nam, S.W.; Kim, H.S. Mixotrophy in the marine red-tide cryptophyte Teleaulax amphioxeia and ingestion and grazing impact of cryptophytes on natural populations of bacteria in Korean coastal waters. Harmful Algae 2017, 68, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Moran, J.; McKean, P.G.; Ginger, M.L. Eukaryotic Flagella: Variations in Form, Function, and Composition during Evolution. BioScience 2014, 64, 1103–1114. [Google Scholar] [CrossRef]
- Rossez, Y.; Wolfson, E.B.; Holmes, A.; Gally, D.L.; Holden, N.J. Bacterial Flagella: Twist and Stick, or Dodge across the Kingdoms. PLOS Pathog. 2015, 11, e1004483. [Google Scholar] [CrossRef] [PubMed]
- Namdeo, S.; Khaderi, S.N.; den Toonder, J.M.J.; Onck, P.R. Swimming direction reversal of flagella through ciliary motion of mastigonemes. Biomicrofluidics 2011, 5, 034108. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Lou, X.; Wingfield, J.L.; Lin, J.; Nicastro, D.; Lechtreck, K. Chlamydomonas PKD2 organizes mastigonemes, hair-like glycoprotein polymers on cilia. J. Cell Biol. 2020, 219, e202001122. [Google Scholar] [CrossRef] [PubMed]
- Novarino, G. A companion to the identification of cryptomonad flagellates (Cryptophyceae = Cryptomonadea). Hydrobiologia 2003, 502, 225–270. [Google Scholar] [CrossRef]
- Kugrens, P.; Lee, R.E.; Andersen, R.A. Ultrastructural Variations in Cryptomonad Flagella. J. Phycol. 1987, 23, 511–518. [Google Scholar] [CrossRef]
- Morrall, S.; Greenwood, A.D. A comparison of the periodic substructure of the trichocysts of the Cryptophyceae and Prasinophyceae. Biosystems 1980, 12, 71–83. [Google Scholar] [CrossRef]
- Kugrens, P.; Clay, B.L. 21-CRYPTOMONADS. In Freshwater Algae of North America; Wehr, J.D., Sheath, R.G., Eds.; Aquatic Ecology; Academic Press: Cambridge, MA, USA, 2003; pp. 715–755. [Google Scholar] [CrossRef]
- Kugrens, P.; Lee, R.E. Ultrastructural Evidence for Bacterial Incorporation and Myxotrophy in the Photosynthetic Cryptomonad Chroomonas pochmanni Huber-Pestalozzi (Chyptomonadida). J. Protozool. 1990, 37, 263–267. [Google Scholar] [CrossRef]
- Brennen, C. Locomotion of Flagellates with Mastigonemes. J. Mechanochem. Cell Motil. 1976, 3, 207–217. [Google Scholar] [PubMed]
- Cahill, D.M.; Cope, M.; Hardham, A.R. Thrust reversal by tubular mastigonemes: Immunological evidence for a role of mastigonemes in forward motion of zoospores of Phytophthora cinnamomi. Protoplasma 1996, 194, 18–28. [Google Scholar] [CrossRef]
- Holwill, M.E.; Sleigh, M.A. Propulsion by hispid flagella. J. Exp. Biol. 1967, 10, 267–276. [Google Scholar] [CrossRef] [PubMed]
- Amador, G.J.; Wei, D.; Tam, D.; Aubin-Tam, M.-E. Fibrous Flagellar Hairs of Chlamydomonas reinhardtii Do Not Enhance Swimming. Biophys. J. 2020, 118, 2914–2925. [Google Scholar] [CrossRef] [PubMed]
- Kent, W.S. A Manual of the Infusoria: Including a Description of All Known Flagellate, Ciliate, and Tentaculiferous Protozoa, British and Foreign, and an Account of the Organization and the Affinities of the Sponges; David Bogue: Boca Raton, FL, USA, 1880; Volume 1. [Google Scholar]
- Pratt, D.M. The Phytoplankton of Narragansett Bay. Limnol. Oceanogr. 1959, 4, 425–440. [Google Scholar] [CrossRef]
- Jones, E.E. The Protozoa of Mobile Bay, Alabama; University of South Alabama: Mobile, AL, USA, 1974; pp. 1–113. [Google Scholar]
- Kevan, L. Hadrien Mary Kappa, GitHub Repository 2013. Available online: https://github.com/fiji/Kappa (accessed on 16 February 2024).
- Merk, A.; Bartesaghi, A.; Banerjee, S.; Falconieri, V.; Rao, P.; Davis, M.I.; Pragani, R.; Boxer, M.B.; Earl, L.A.; Milne, J.L.S.; et al. Breaking Cryo-EM Resolution Barriers to Facilitate Drug Discovery. Cell 2016, 165, 1698–1707. [Google Scholar] [CrossRef] [PubMed]
- Cortez, R. The Method of Regularized Stokeslets. SIAM J. Sci. Comput. 2001, 23, 1204–1225. [Google Scholar] [CrossRef]
- Cortez, R.; Fauci, L.; Medovikov, A. The method of regularized Stokeslets in three dimensions: Analysis, validation, and application to helical swimming. Phys. Fluids 2005, 17, 031504. [Google Scholar] [CrossRef]
- Flores, H.; Lobaton, E.; Méndez-Diez, S.; Tlupova, S.; Cortez, R. A study of bacterial flagellar bundling. Bull. Math. Biol. 2005, 67, 137–168. [Google Scholar] [CrossRef]
- Goto, T.; Masuda, S.; Terada, K.; Takano, Y. Comparison between Observation and Boundary Element Analysis of Bacterium Swimming Motion. JSME Int. J. Ser. C 2001, 44, 958–963. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Tran-Cong, T.; Ramia, M. A boundary-element analysis of flagellar propulsion. J. Fluid Mech. 1987, 184, 533–549. [Google Scholar] [CrossRef]
- Ramia, M.; Tullock, D.L.; Phan-Thien, N. The role of hydrodynamic interaction in the locomotion of microorganisms. Biophys. J. 1993, 65, 755–778. [Google Scholar] [CrossRef] [PubMed]
- Shum, H.; Gaffney, E.; Smith, D. Modelling bacterial behaviour close to a no-slip plane boundary: The influence of bacterial geometry. R. Soc. Lond. Proc. Ser. A 2010, 466, 1725–1748. [Google Scholar] [CrossRef]
- Smith, D.J.; Gaffney, E.A.; Gadêlha, H.; Kapur, N.; Kirkman-Brown, J.C. Bend propagation in the flagella of migrating human sperm, and its modulation by viscosity. Cell Motil. Cytoskelet. 2009, 66, 220–236. [Google Scholar] [CrossRef] [PubMed]
- Martindale, J.D.; Jabbarzadeh, M.; Fu, H.C. Choice of computational method for swimming and pumping with nonslender helical filaments at low Reynolds number. Phys. Fluids 2016, 28, 021901. [Google Scholar] [CrossRef]
- Christensen, T. Algae: A Taxonomic Survey; AiO Tryk A/S: Odense, Denmark, 1980. [Google Scholar]
- Votta, J.J.; Jahn, T.L.; Griffith, D.L.; Fonseca, J.R. Nature of the Flagellar Beat in Trachelomonas volvocina, Rhabdomonas spiralis, Menoidium cultellus, and Chilomonas paramecium. Trans. Am. Microsc. Soc. 1971, 90, 404. [Google Scholar] [CrossRef] [PubMed]
- Manwell, R.D. Introduction to Protozoology; Dover Publications: New York, NY, USA, 1968. [Google Scholar]
- Bouck, G.B. The Structure, Origin, Isolation, and Composition of the Tubular Mastigonemes of the Ochromonas Flagellum. J. Cell Biol. 1971, 50, 362–384. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Mekonnen, B.; Alkhofash, R.; Ingle, A.V.; Workman, E.B.; Feather, A.; Zhang, G.; Chasen, N.; Liu, P.; Lechtreck, K.F. The Small Interactor of PKD2 protein promotes the assembly and ciliary entry of the Chlamydomonas PKD2–mastigoneme complexes. J. Cell Sci. 2024, 137, jcs261497. [Google Scholar] [CrossRef]
- Dai, J.; Ma, M.; Niu, Q.; Eisert, R.J.; Wang, X.; Das, P.; Lechtreck, K.F.; Dutcher, S.K.; Zhang, R.; Brown, A. Mastigoneme structure reveals insights into the O-linked glycosylation code of native hydroxyproline-rich helices. Cell 2024, 187, 1907–1921.e16. [Google Scholar] [CrossRef]
- Kage, A.; Omori, T.; Kikuchi, K.; Ishikawa, T. The shape effect of flagella is more important than bottom-heaviness on passive gravitactic orientation in Chlamydomonas reinhardtii. J. Exp. Biol. 2020, 223, jeb205989. [Google Scholar] [CrossRef]
- Jabbarzadeh, M.; Fu, H. A numerical method for inextensible elastic filaments in viscous fluids. J. Comput. Phys. 2020, 418, 109643. [Google Scholar] [CrossRef]
- Asadzadeh, S.S.; Walther, J.H.; Andersen, A.; Kiørboe, T. Hydrodynamic interactions are key in thrust-generation of hairy flagella. Phys. Rev. Fluids 2022, 7, 073101. [Google Scholar] [CrossRef]
- Asadzadeh, S.S.; Walther, J.H.; Kiørboe, T. Conflicting Roles of Flagella in Planktonic Protists: Propulsion, Resource Acquisition, and Stealth. PRX Life 2023, 1, 013002. [Google Scholar] [CrossRef]

| 100 | |
| 200 nm | |
| active flagellum | 113 nm |
| less-active flagellum | 128 nm |
| on active flagellum | 41 |
| on less-active flagellum | 48 |
| for 1.6 μm mastigonemes | 139 |
| 11.5 nm | |
| 825 nm | |
| 21.4 nm | |
| 21.4 nm | |
| 11.5 nm | |
| 275.2 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez Arias, L.; Webb, B.; Samsami, K.; Nikolova, L.; Silva, M.; Fu, H.C. Hydrodynamic Effects of Mastigonemes in the Cryptophyte Chilomonas paramecium. Hydrobiology 2024, 3, 159-182. https://doi.org/10.3390/hydrobiology3030012
Sanchez Arias L, Webb B, Samsami K, Nikolova L, Silva M, Fu HC. Hydrodynamic Effects of Mastigonemes in the Cryptophyte Chilomonas paramecium. Hydrobiology. 2024; 3(3):159-182. https://doi.org/10.3390/hydrobiology3030012
Chicago/Turabian StyleSanchez Arias, Ludivine, Branden Webb, Kiarash Samsami, Linda Nikolova, Malan Silva, and Henry C. Fu. 2024. "Hydrodynamic Effects of Mastigonemes in the Cryptophyte Chilomonas paramecium" Hydrobiology 3, no. 3: 159-182. https://doi.org/10.3390/hydrobiology3030012
APA StyleSanchez Arias, L., Webb, B., Samsami, K., Nikolova, L., Silva, M., & Fu, H. C. (2024). Hydrodynamic Effects of Mastigonemes in the Cryptophyte Chilomonas paramecium. Hydrobiology, 3(3), 159-182. https://doi.org/10.3390/hydrobiology3030012





