Stochastic Analysis of a System of Two Interconnected Inventories
Abstract
1. Introduction
2. Literature Review
3. Notations and Description of the Model
3.1. Notations
3.2. Description of the Model
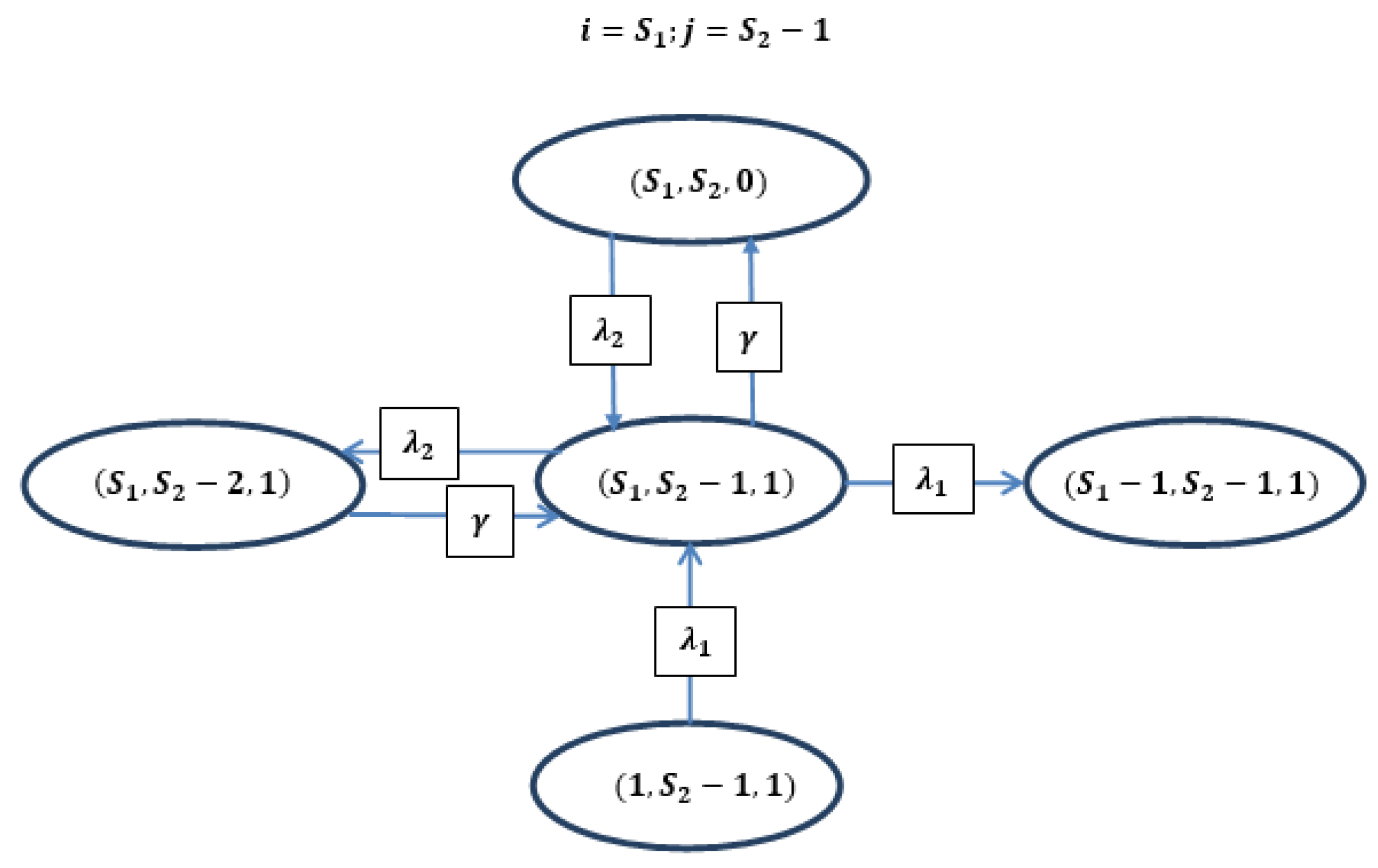
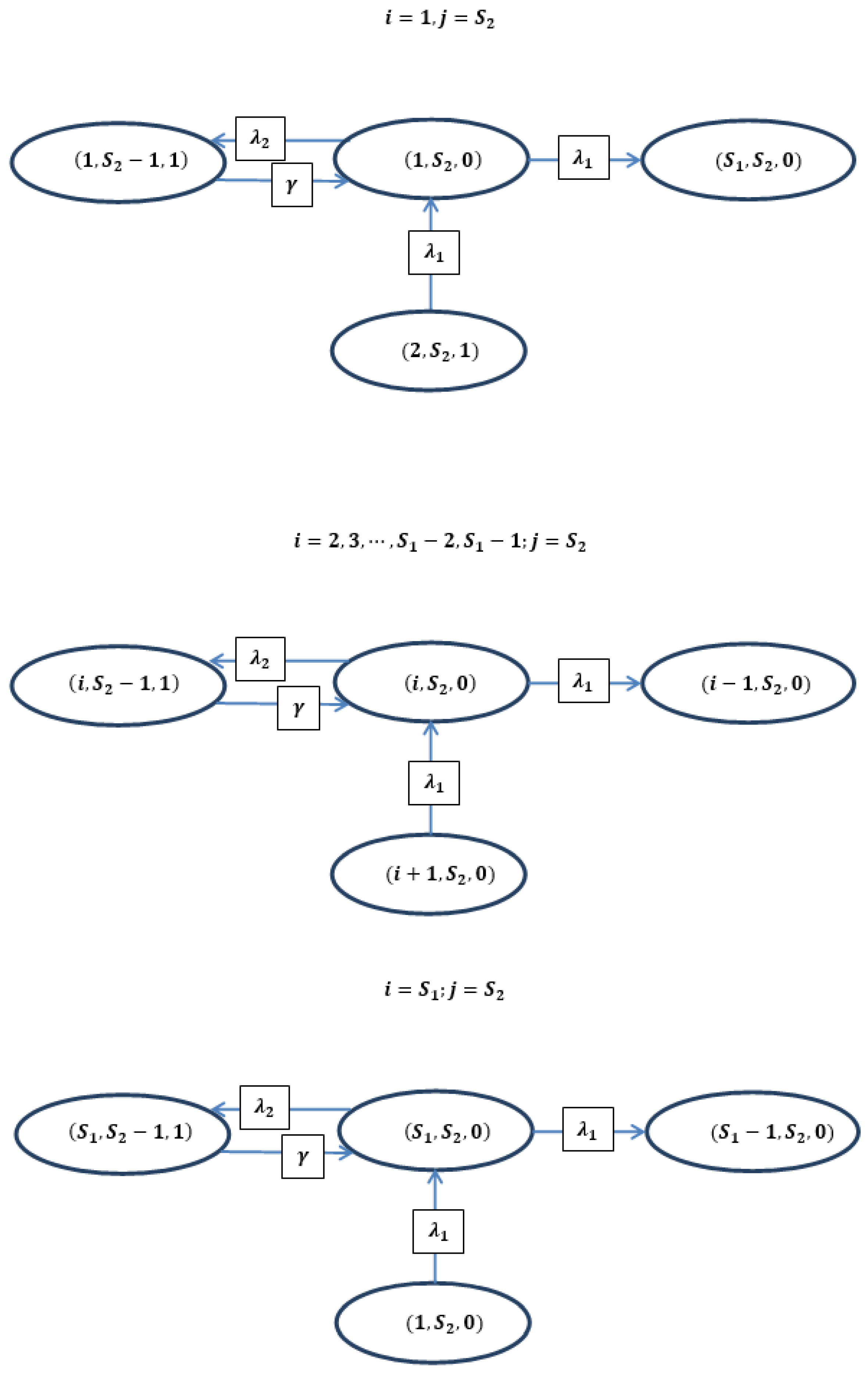
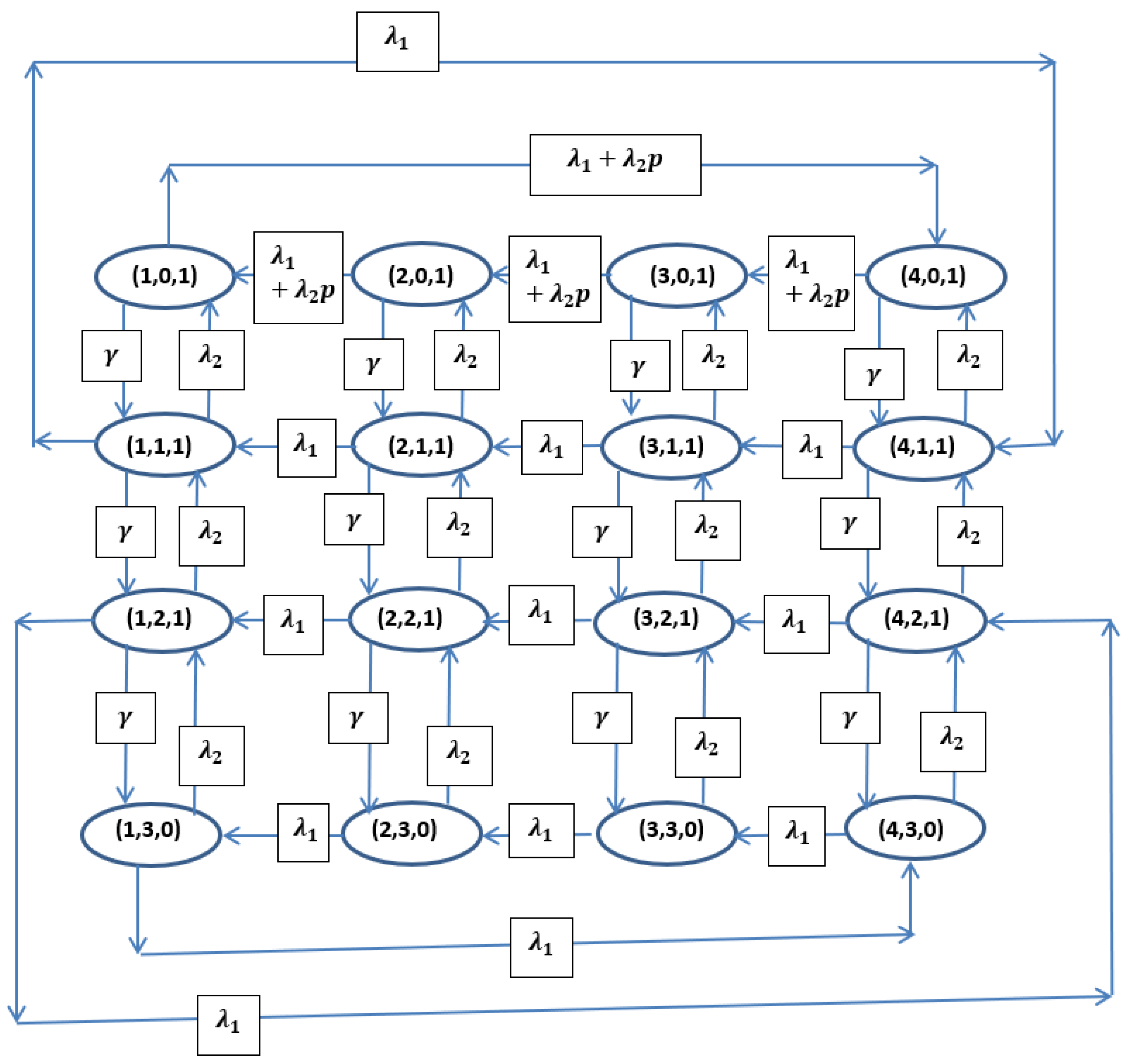
4. Governing Equations
5. Steady-State Probabilities
6. Measures of Performance
6.1. Probability That Both Inventories Are Full at Time t
6.2. Probability That the Production Machine Is Idle
6.3. Mean Number of Times the Production Machine Is Switched On
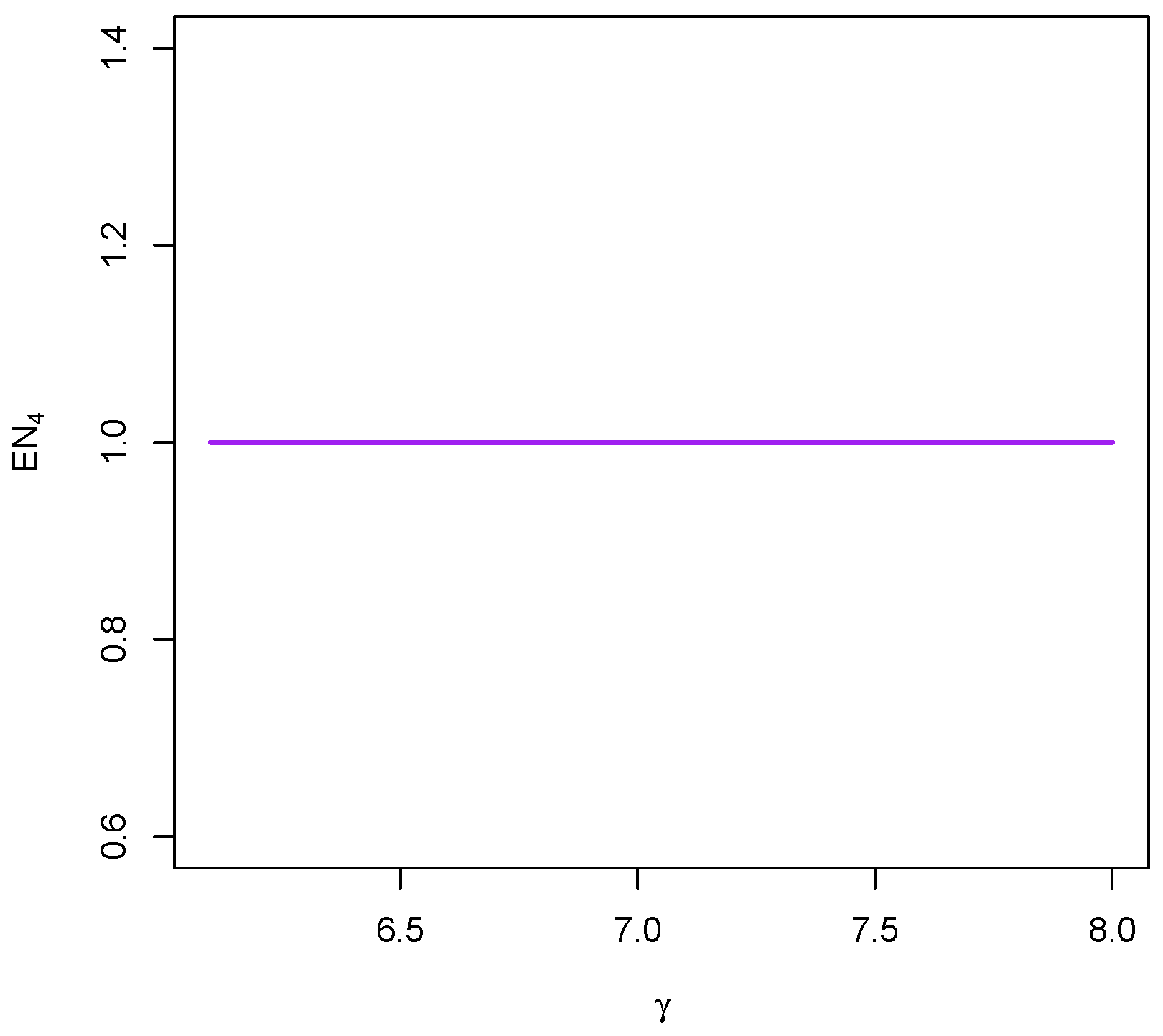
6.4. Mean Number of Times the Production Machine Is Switched Off
6.5. Mean Number of Times Substitution Takes Place
6.6. Mean Number of Times Replenishment of Type 1 Product Is Made
6.7. Mean Number of Times Type 2 Product Inventory Enters into Empty State
7. Numerical Illustration
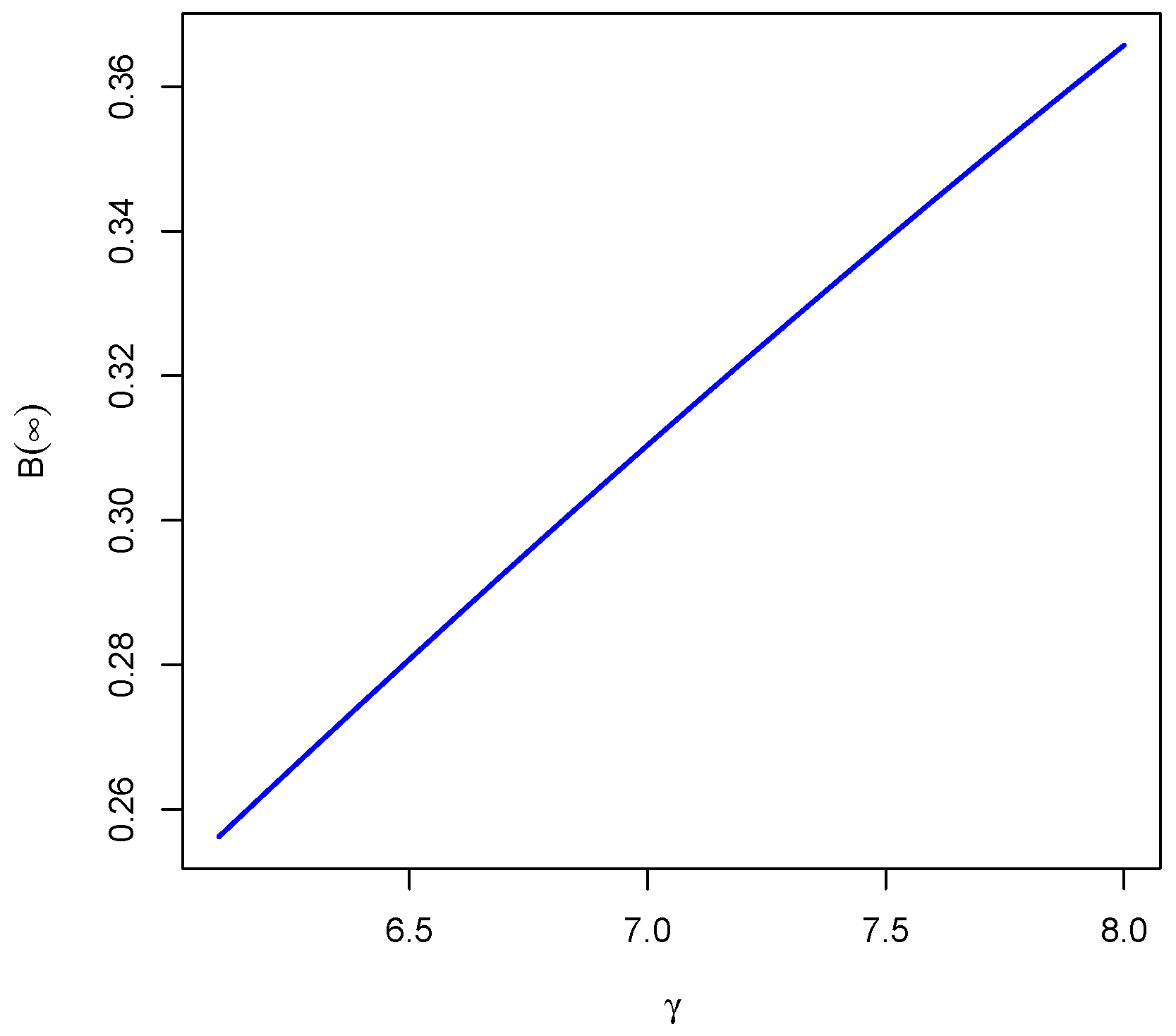
7.1. Stationary Probability That Both Inventories Are Full
7.2. Stationary Probability That the Production Machine Is Idle
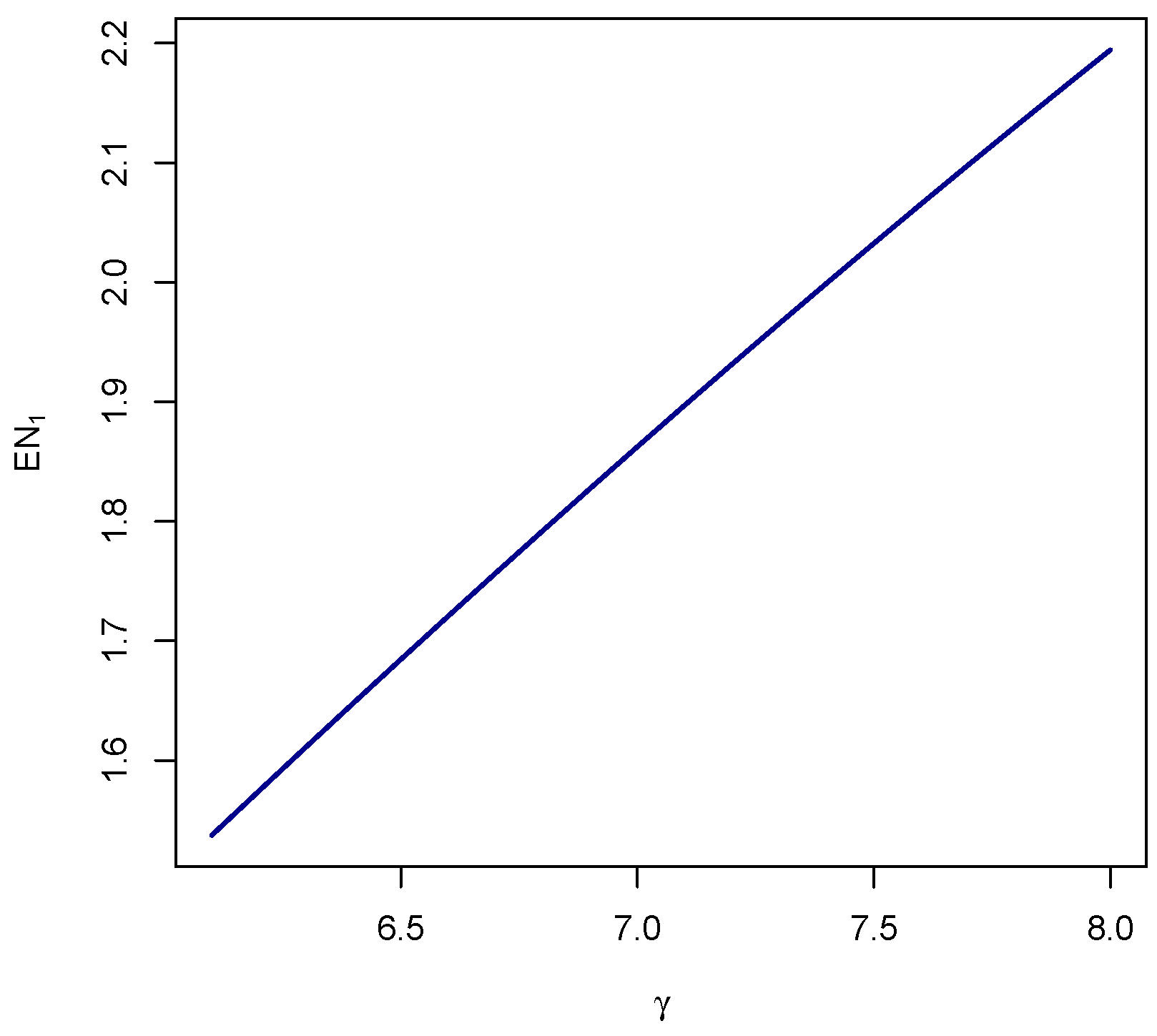
7.3. Mean Stationary Rate of Occurrence of Switching-On Events
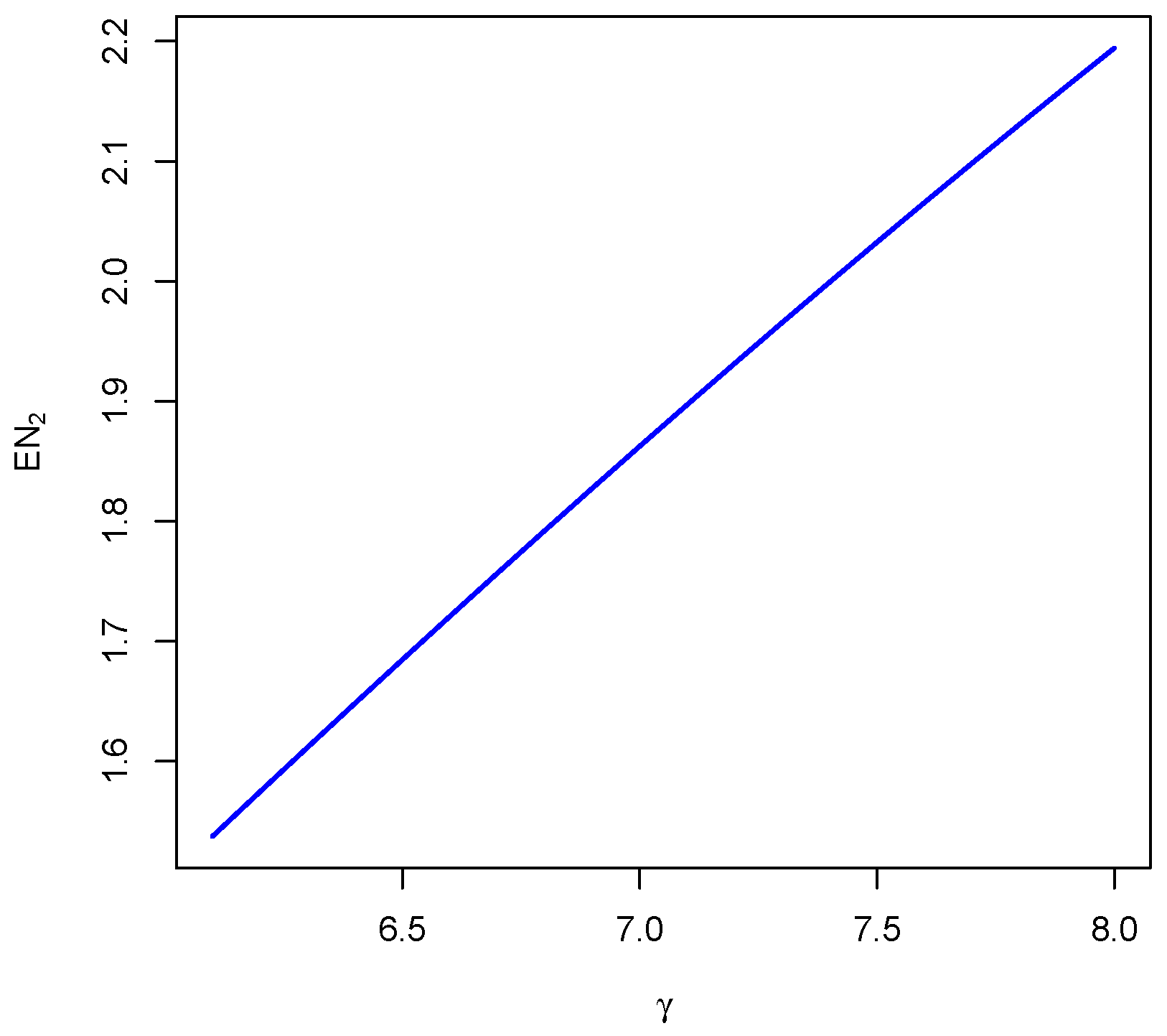
7.4. Mean Stationary Rate of Occurrence of Switching-Off Events
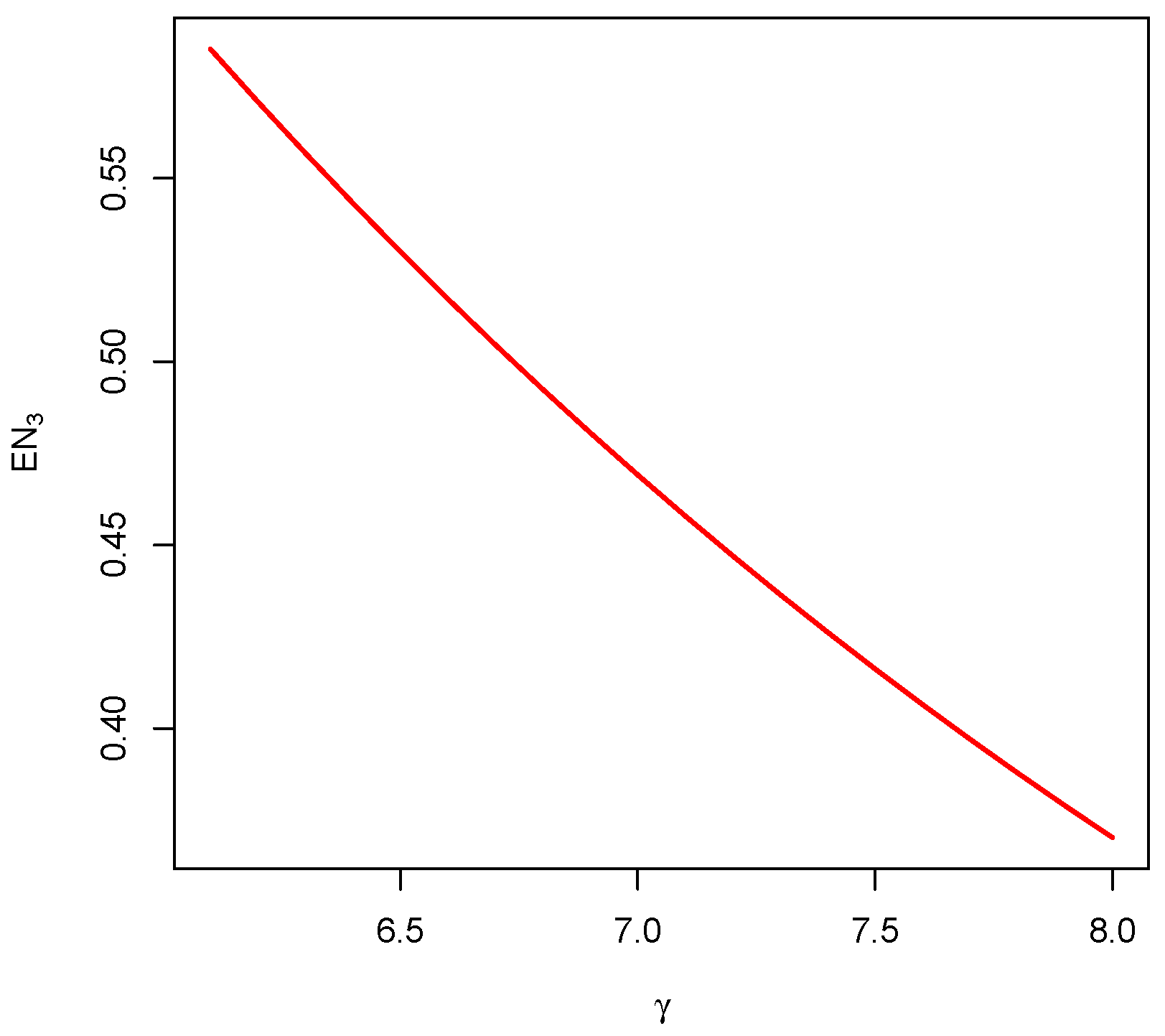
7.5. Stationary Mean Rate of Occurrences of Substitutions
7.6. Mean Stationary Rate of Occurrence of Events of Replenishment of Type-A Product
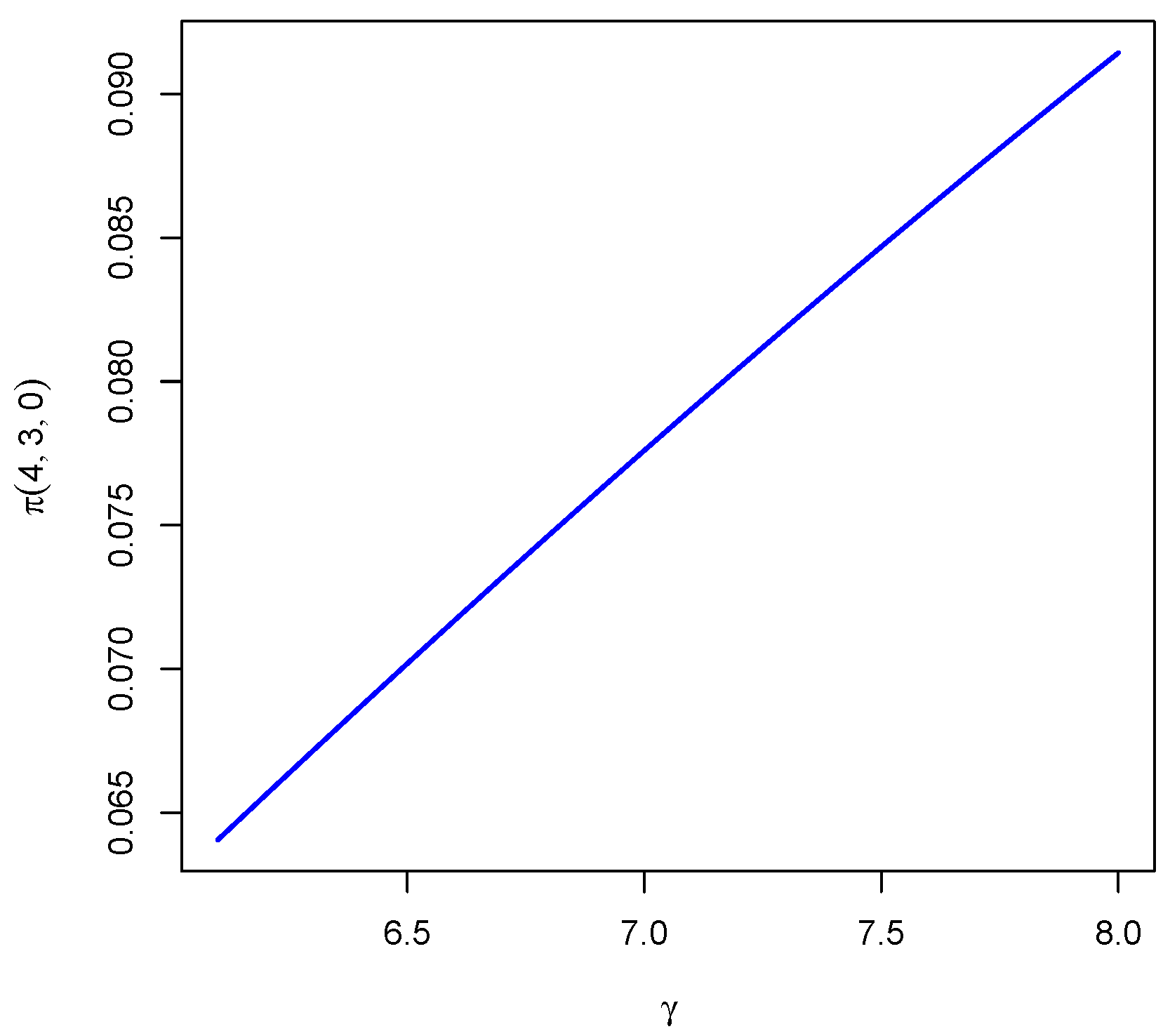
7.7. Mean Stationary Rate of Occurrence of Level of Inventory 2 Entering into 0 State
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harris, F.W. How many parts to make at once. Mag. Manag. 1913, 10, 135–136. [Google Scholar] [CrossRef]
- Kalpakam, S.; Sapna, K.P. Continuous review (s, S) inventory system with random lifetimes and positive leadtimes. Oper. Res. Lett. 1994, 16, 115–119. [Google Scholar] [CrossRef]
- Ravichandran, N. Stochastic analysis of a continuous review perishable inventory system with positive lead time and Poisson demand. Eur. J. Oper. Res. 1995, 84, 444–457. [Google Scholar] [CrossRef]
- Liu, L.; Cheung, K.L. Service constrained inventory models with random lifetimes and lead times. J. Oper. Res. Soc. 1997, 48, 1022–1028. [Google Scholar] [CrossRef]
- Lian, Z.; Liu, L. Continuous review perishable inventory systems: Models and heuristics. IIE Trans. 2001, 33, 809–822. [Google Scholar] [CrossRef]
- Yadavalli, V.S.S.; Van Schoor, C.D.W. A perishable product inventory system operating in a random environment. S. Afr. J. Ind. Eng. 2004, 15, 107–131. [Google Scholar] [CrossRef]
- Lian, Z.; Liu, X.; Zhao, N. A perishable inventory model with Markovian renewal demands. Int. J. Prod. Econ. 2009, 121, 176–182. [Google Scholar] [CrossRef]
- Alizadeh, M.; Eskandari, H.; Sajadifar, S.M. A modified (S − 1, S) inventory system for deteriorating items with Poisson demand and non-zero lead time. Appl. Math. Model. 2014, 38, 699–711. [Google Scholar] [CrossRef]
- Tao, Y.; Lee, L.H.; Chew, E.P.; Sun, G.; Charles, V. Inventory control policy for a periodic review system with expediting. Appl. Math. Model. 2017, 49, 375–393. [Google Scholar] [CrossRef]
- Cao, P.; Yao, D. Dual sourcing policy for a continuous-review stochastic inventory system. IEEE Trans. Autom. Control 2018, 64, 2921–2928. [Google Scholar] [CrossRef]
- Cao, P.; Yao, D. Optimal pricing and inventory control strategy for a continuous-review system with product return. Oper. Res. Lett. 2022, 50, 295–302. [Google Scholar] [CrossRef]
- Siriruk, P.; Kotekangpoo, A. Order Quantity Optimization Model for Perishable Products Under Continuous Review (Q, r) Inventory Policy with Stochastic Demand and Positive Lead Time. Omega 2025, 138, 103392. [Google Scholar] [CrossRef]
- Chen, X.; Feng, Y.; Keblis, M.F.; Xu, J. Optimal inventory policy for two substitutable products with customer service objectives. Eur. J. Oper. Res. 2015, 246, 76–85. [Google Scholar] [CrossRef]
- Hadley, G.; Whitin, T.M. Analysis of Inventory Systems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Silver, E.A. A control system for coordinated inventory replenishment. Int. J. Prod. Res. 1974, 12, 647–671. [Google Scholar] [CrossRef]
- Mcgillivray, R.; Silver, E. Some Concepts For Inventory Control Under Substitutable Demand. Inf. Syst. Oper. Res. 1978, 16, 47–63. [Google Scholar] [CrossRef]
- Ramaswami, V. Algorithms for a continuous-review (s, S) inventory system. J. Appl. Probab. 1981, 18, 461–472. [Google Scholar] [CrossRef]
- Federgruen, A.; Groenevelt, H.; Tijms, H.C. Coordinated replenishments in a multi-item inventory system with compound Poisson demands. Manag. Sci. 1984, 30, 344–357. [Google Scholar] [CrossRef]
- Ignall, E. Optimal continuous review policies for two product inventory systems with joint setup costs. Manag. Sci. 1969, 15, 278–283. [Google Scholar] [CrossRef]
- Parlar, M.; Goyal, S.K. Optimal ordering decisions for two substitutable products with stochastic demands. Opsearch 1984, 21, 1–15. [Google Scholar]
- Krishnamoorthy, A.; Varghese, T.V. A two commodity inventory problem. Int. J. Inf. Manag. Sci. 1994, 3, 55–70. [Google Scholar]
- Smith, S.A.; Agrawal, N. Management of Multi-Item Retail Inventory Systems with Demand Substitution. Oper. Res. 2000, 48, 50–64. [Google Scholar] [CrossRef]
- Anbazhagan, N.; Arivarignan, G. Two-commodity inventory system with individual and joint ordering policies. Int. J. Manag. Syst. 2003, 19, 129–144. [Google Scholar]
- Yadavalli, V.S.S.; Anbazhagan, N.; Arivarignan, G. A two-commodity continuous review inventory system with lost sales. Stoch. Anal. Appl. 2004, 22, 479–497. [Google Scholar] [CrossRef]
- Yadavalli, V.S.S.; Van Schoor, C.D.W.; Udayabaskaran, S. A substitutable two-product inventory system with joint-ordering policy and common demand. Appl. Math. Comput. 2006, 172, 1257–1271. [Google Scholar] [CrossRef]
- Sivakumar, B. Two-commodity inventory system with retrial demand. Eur. J. Oper. Res. 2008, 187, 70–83. [Google Scholar] [CrossRef]
- Marisamy, K.; Krishnan, K. Analysis of substitutable inventory system in supply chain with direct demand and partial backlogging. Int. J. Stat. Appl. Math. 2018, 3, 331–335. [Google Scholar]
- Poormoaied, S.; Atan, Z. A continuous review policy for two complementary products with interrelated demand. Comput. Ind. Eng. 2020, 150, 106980. [Google Scholar] [CrossRef]
- Kumaresan, P.; Sivakumar, B.; Arivarignan, G. Continuous-review (s,S) inventory system with lost sales and variable lead times. RAIRO Oper. Res. 2025, 59, 1959–1980. [Google Scholar] [CrossRef]
- Bitran, G.R.; Dasu, S. Ordering policies in an environment of stochastic yields and substitutable demands. Oper. Res. 1992, 40, 999–1017. [Google Scholar] [CrossRef]
- Xia, Y. Competitive strategies and market segmentation for suppliers with substitutable products. Eur. J. Oper. Res. 2011, 210, 194–203. [Google Scholar] [CrossRef]
- Maddah, B.; Kharbeche, M.; Pokharel, S.; Ghoniem, A. Joint replenishment model for multiple products with substitution. Appl. Math. Model. 2016, 40, 7678–7688. [Google Scholar] [CrossRef]
- Farahani, M.; Shavandi, H.; Rahmani, D. A location-inventory model considering a strategy to mitigate disruption risk in supply chain by substitutable products. Comput. Ind. Eng. 2017, 108, 213–224. [Google Scholar] [CrossRef]
- Pan, Q.H.; He, X.; Skouri, K.; Chen, S.C.; Teng, J.T. An inventory replenishment system with two inventory-based substitutable products. Int. J. Prod. Econ. 2018, 204, 135–147. [Google Scholar] [CrossRef]
- Perlman, Y. Inventory Levels of Two Stockout-based Substitutable Products under Centralized and Competitive Settings. IFAC-PapersOnLine 2019, 52, 1450–1454. [Google Scholar] [CrossRef]
- Beranek, M.; Buscher, U. Optimal price and quality decisions of a supply chain game considering imperfect quality items and market segmentation. Appl. Math. Model. 2021, 91, 1227–1244. [Google Scholar] [CrossRef]
- Cho, G.; Zanoni, S.; Kim, T. Effects of demand substitution on a multi-product and multi-stage ramp-up production system. Appl. Math. Model. 2025, 116412. [Google Scholar] [CrossRef]
- Gavish, B.; Graves, S.C. A One-Product Production/Inventory Problem under Continuous Review Policy. Oper. Res. 1980, 28, 1228–1236. [Google Scholar] [CrossRef]
- Arreola-Risa, A. Integrated multi-item production-inventory systems. Eur. J. Oper. Res. 1996, 89, 326–340. [Google Scholar] [CrossRef]
- Kulkarni, V.; Yan, K. Production-inventory systems in stochastic environment and stochastic lead times. Queueing Syst. 2012, 70, 207–231. [Google Scholar] [CrossRef]
- Karim, R.; Nakade, K. A stochastic model of a production-inventory system with consideration of production disruption. Int. J. Adv. Oper. Manag. 2019, 11, 287–316. [Google Scholar] [CrossRef][Green Version]
- Jose, K.P.; Reshmi, P.S. A production inventory model with deteriorating items and retrial demands. Opsearch 2020, 58, 71–82. [Google Scholar] [CrossRef]
- Mattam, B.J.; Jose, K.P. Stochastic Analysis of a Production Inventory System with Deteriorating Items, Unreliable Server and Retrial of Customers. In Information Technologies and Mathematical Modelling. Queueing Theory and Applications; Dudin, A., Nazarov, A., Moiseev, A., Eds.; Communications in Computer and Information Science; Springer: Cham, Switzerland, 2024; Volume 2163. [Google Scholar]
- Bai, B.; Li, B.; Jia, X. The impacts of stockout cost on a stochastic production-inventory system in minimizing total cost conditional value-at-risk. Flex. Serv. Manuf. J. 2025, 37, 943–978. [Google Scholar] [CrossRef]
- Al-Zahrani, S.M.; Elsmih, F.E.I.; Al-Zahrani, K.S.; Saber, S. A Fractional Order SITR Model for Forecasting of Transmission of COVID-19: Sensitivity Statistical Analysis. Malays. J. Math. Sci. 2022, 16, 517–536. [Google Scholar] [CrossRef]
- Saber, S.; Solouma, E.; Althubyani, M.; Messaoudi, M. Statistical Insights into Zoonotic Disease Dynamics: Simulation and Control Strategy Evaluation. Symmetry 2025, 17, 733. [Google Scholar] [CrossRef]
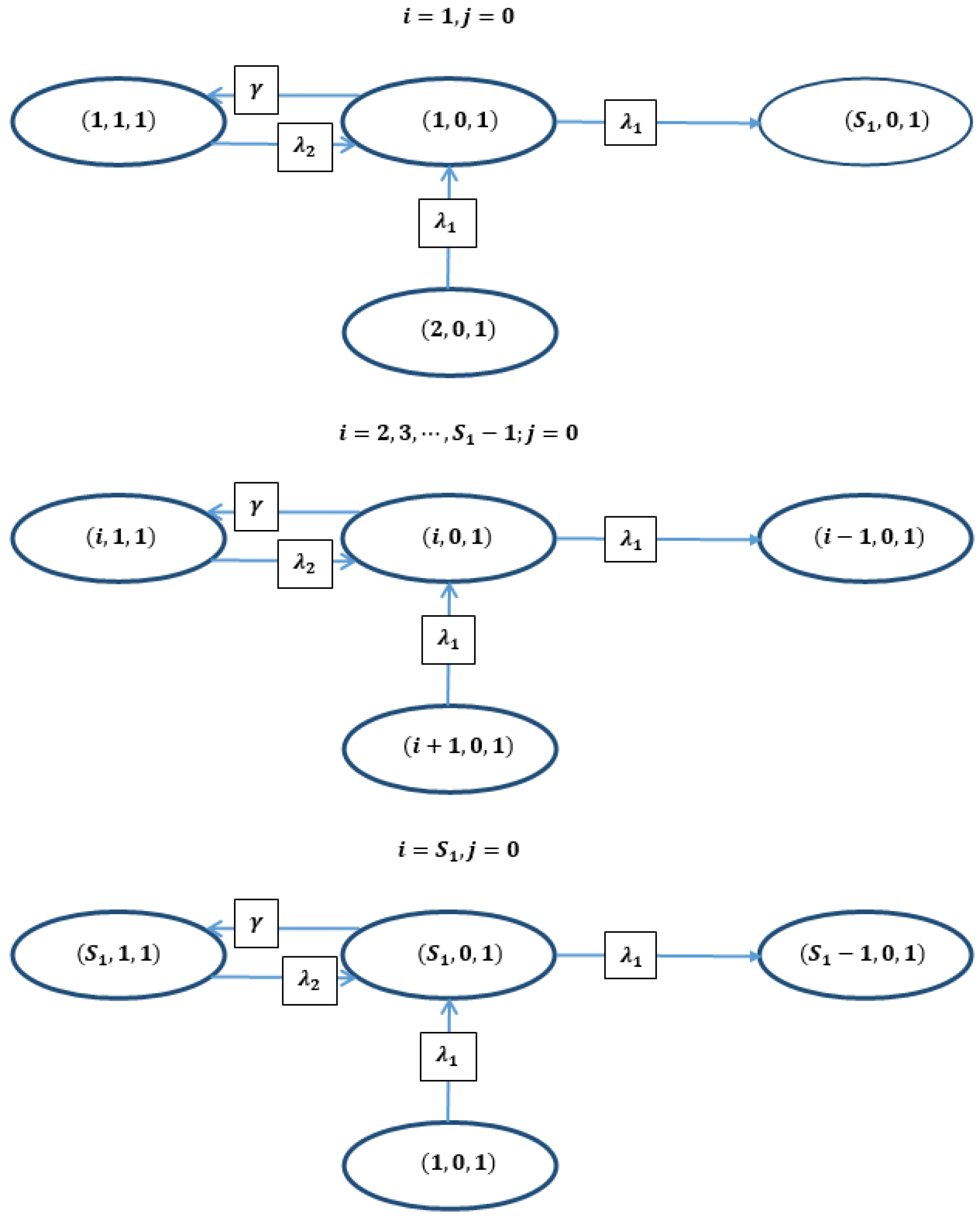
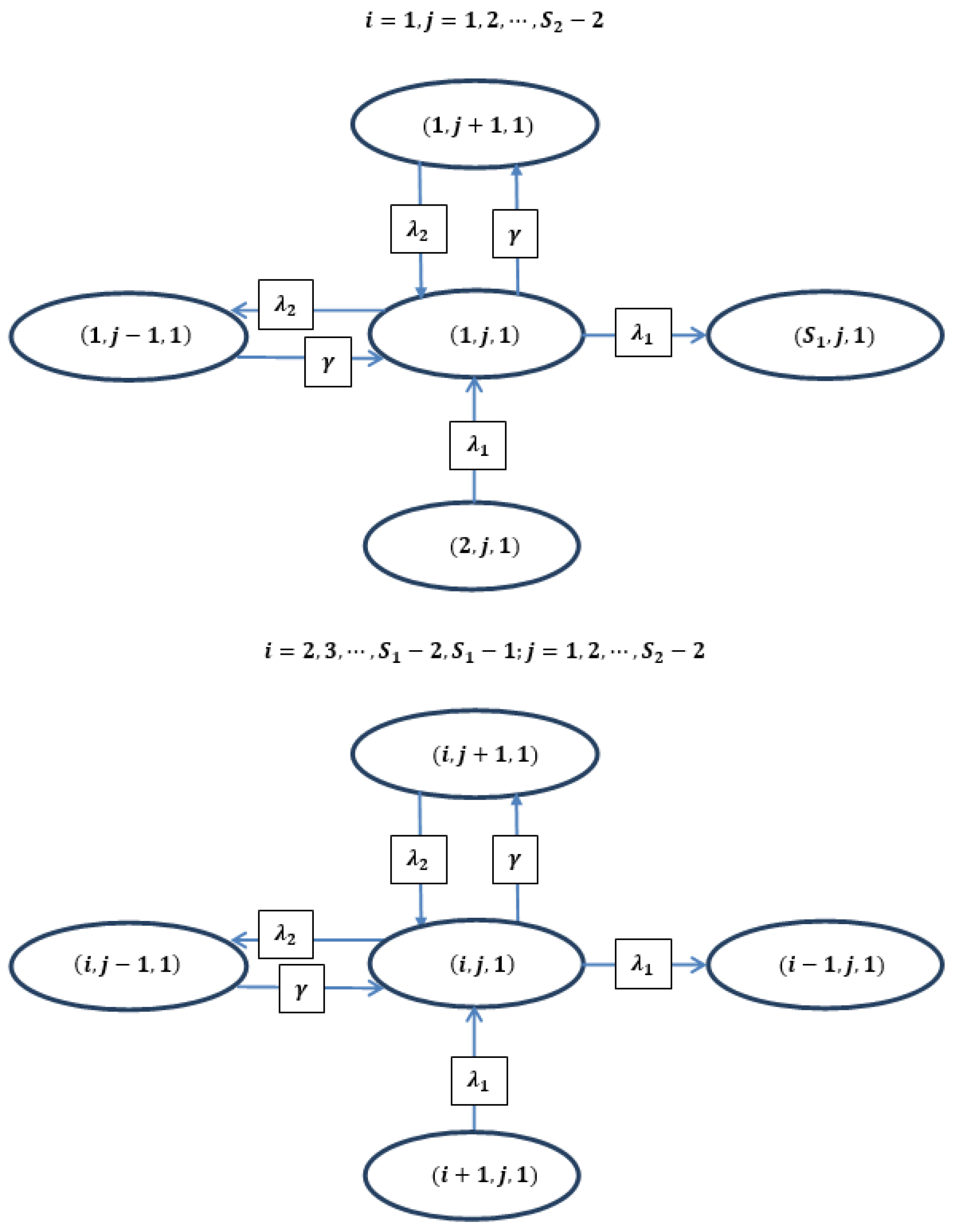
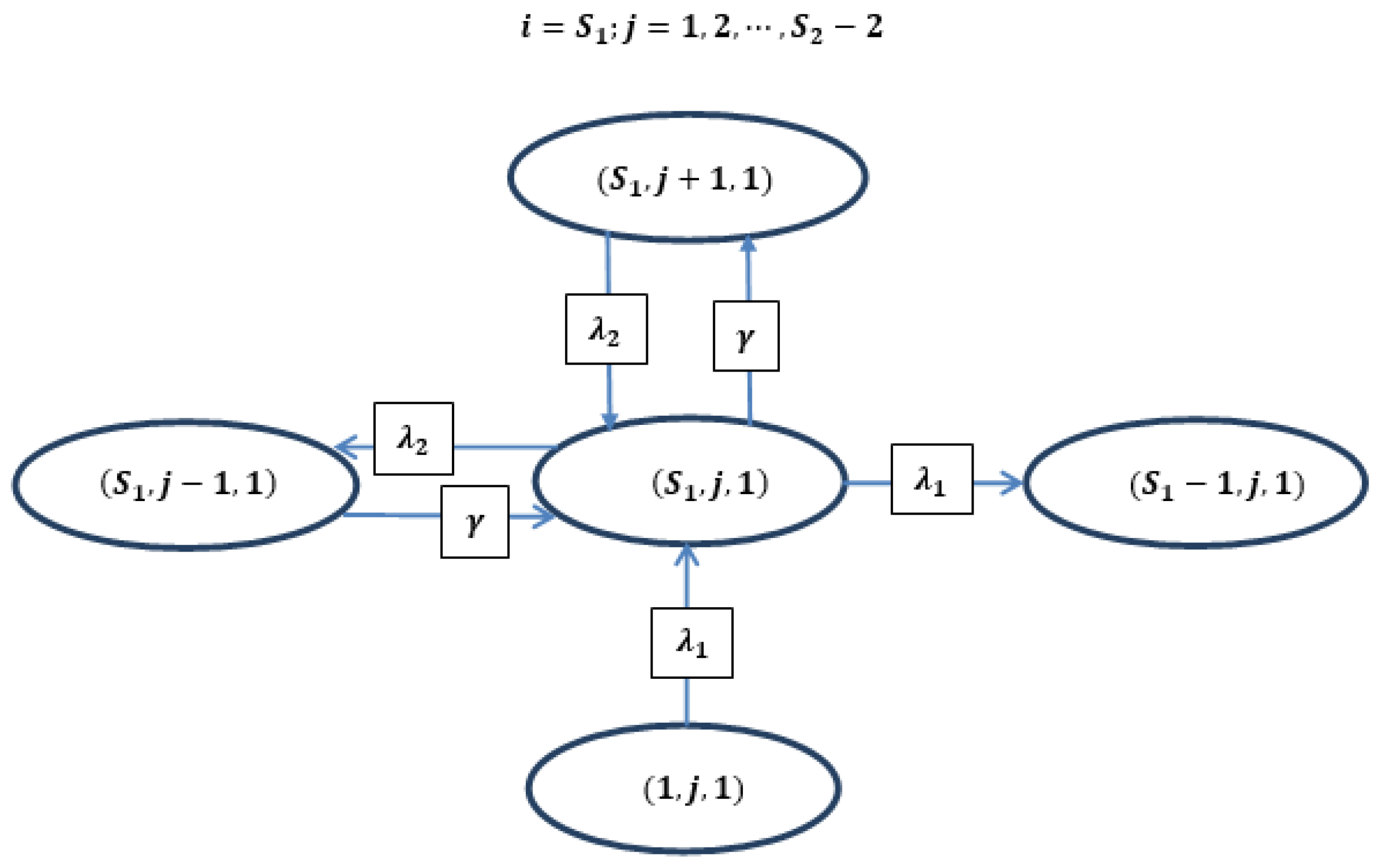
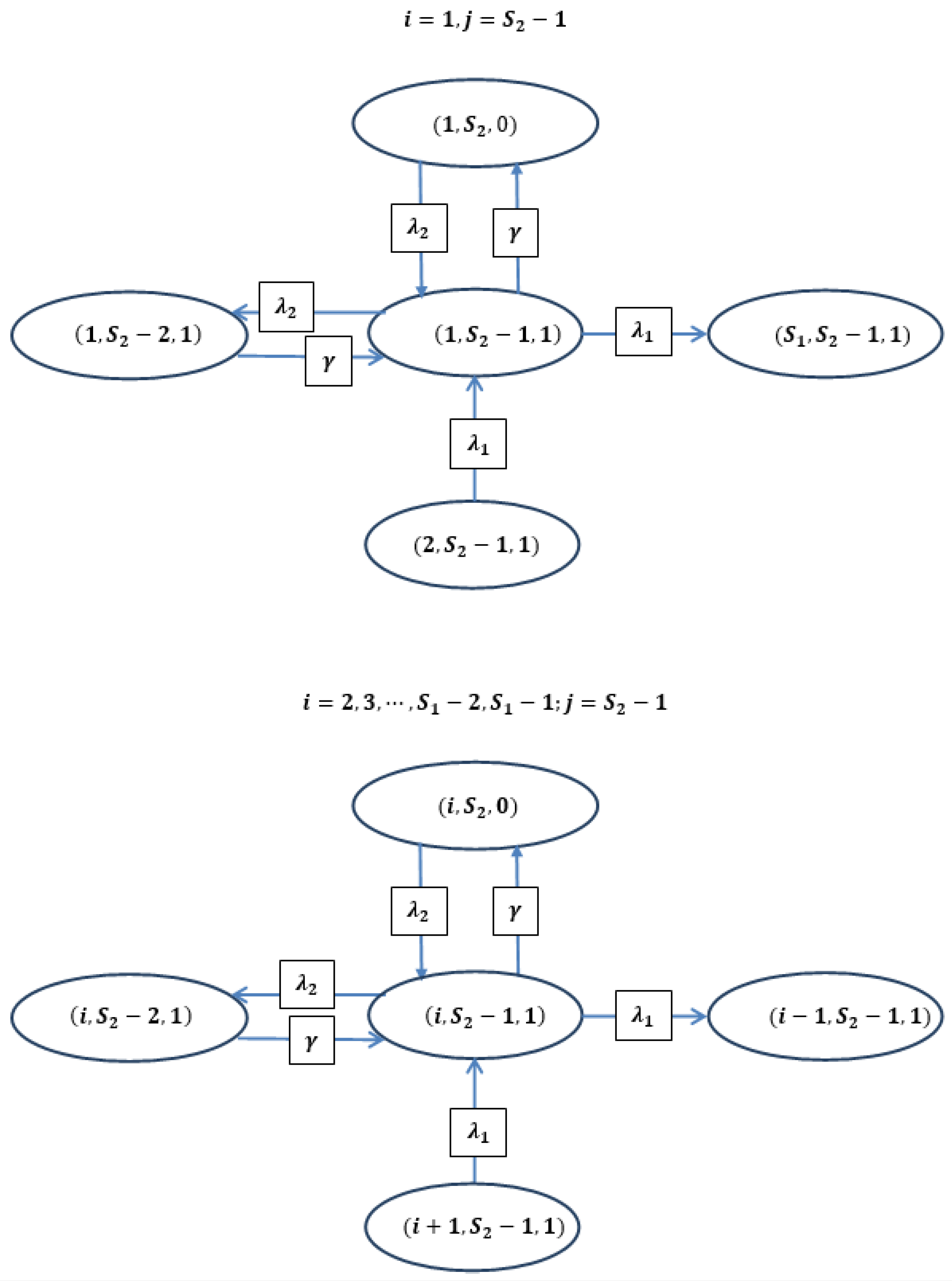
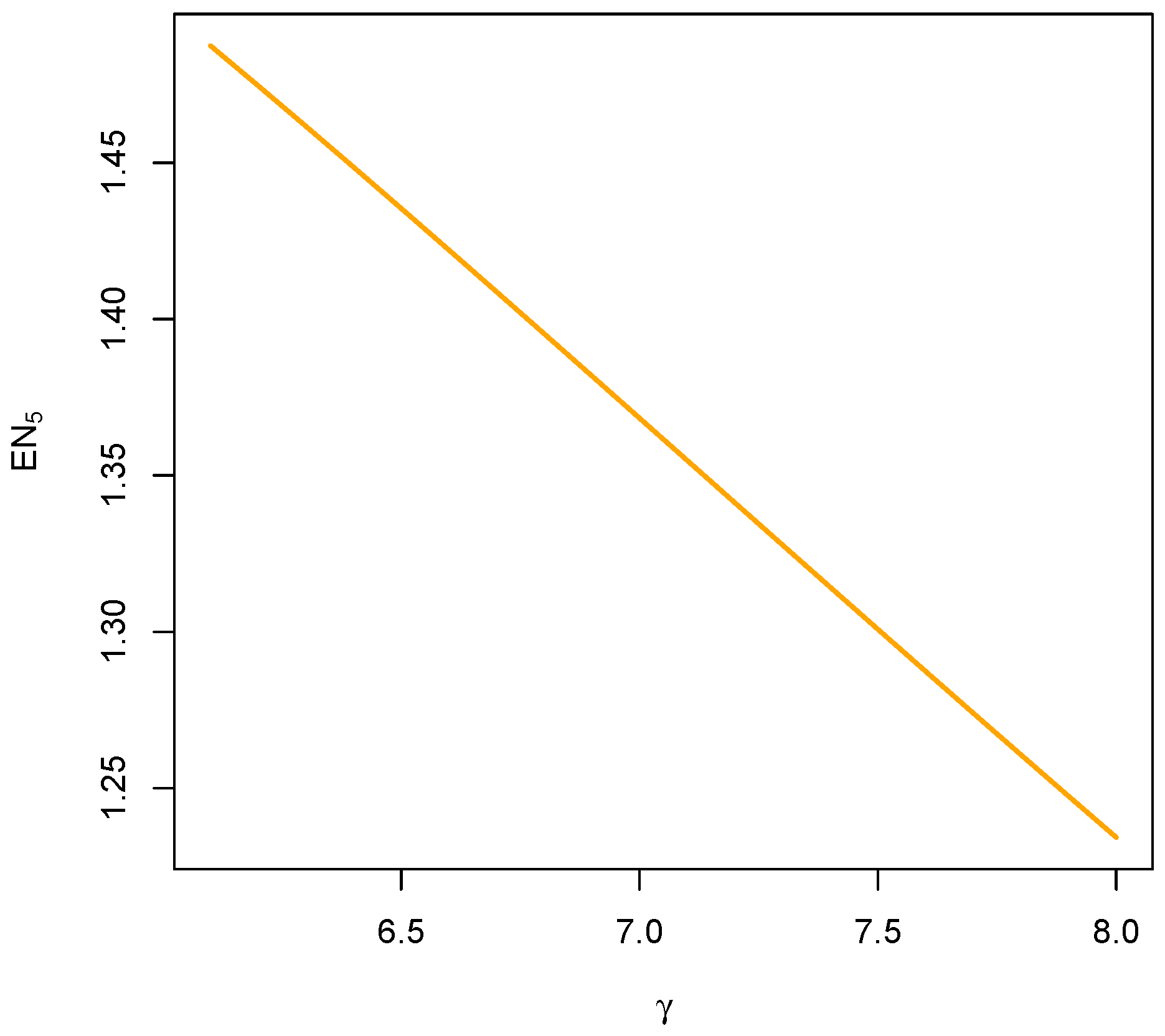
| Symbol | Description |
|---|---|
| State probabilities | |
| Maximum capacity of inventory i, | |
| Rate of demand for product i, | |
| Rate of production | |
| Number of items available in Inventory j, at time t | |
| State of the production machine at time t: 0 if idle, 1 otherwise | |
| System state vector: | |
| State space set: | |
| State space set: | |
| Convolution of and : | |
| Laplace transform of : |
| Values | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 6.1 | 6.2 | 6.3 | 6.4 | 6.5 | 6.6 | 6.7 | 6.8 | 6.9 | 7.0 | |
| 0.0609590 | 0.0594604 | 0.0580030 | 0.0565857 | 0.0552077 | 0.0538677 | 0.0525648 | 0.0512980 | 0.0500663 | 0.0488688 | |
| 0.0619750 | 0.0614424 | 0.0609031 | 0.0603581 | 0.0598083 | 0.0592545 | 0.0586974 | 0.0581378 | 0.0575763 | 0.0570136 | |
| 0.0630079 | 0.0634905 | 0.0639483 | 0.0643820 | 0.0647923 | 0.0651799 | 0.0655454 | 0.0658895 | 0.0662127 | 0.0665158 | |
| 0.0640581 | 0.0656068 | 0.0671457 | 0.0686741 | 0.0701917 | 0.0716979 | 0.0731924 | 0.0746747 | 0.0761446 | 0.0776018 | |
| 0.0609590 | 0.0594604 | 0.0580030 | 0.0565857 | 0.0552077 | 0.0538677 | 0.0525648 | 0.0512980 | 0.0500663 | 0.0488688 | |
| 0.0619750 | 0.0614424 | 0.0609031 | 0.0603581 | 0.0598083 | 0.0592545 | 0.0586974 | 0.0581378 | 0.0575763 | 0.0570136 | |
| 0.0630079 | 0.0634905 | 0.0639483 | 0.0643820 | 0.0647923 | 0.0651799 | 0.0655454 | 0.0658895 | 0.0662127 | 0.0665158 | |
| 0.0640581 | 0.0656068 | 0.0671457 | 0.0686741 | 0.0701917 | 0.0716979 | 0.0731924 | 0.0746747 | 0.0761446 | 0.0776018 | |
| 0.0609590 | 0.0594604 | 0.0580030 | 0.0565857 | 0.0552077 | 0.0538677 | 0.0525648 | 0.0512980 | 0.0500663 | 0.0488688 | |
| 0.0619750 | 0.0614424 | 0.0609031 | 0.0603581 | 0.0598083 | 0.0592545 | 0.0586974 | 0.0581378 | 0.0575763 | 0.0570136 | |
| 0.0630079 | 0.0634905 | 0.0639483 | 0.0643820 | 0.0647923 | 0.0651799 | 0.0655454 | 0.0658895 | 0.0662127 | 0.0665158 | |
| 0.0640581 | 0.0656068 | 0.0671457 | 0.0686741 | 0.0701917 | 0.0716979 | 0.0731924 | 0.0746747 | 0.0761446 | 0.0776018 | |
| 0.0609590 | 0.0594604 | 0.0580030 | 0.0565857 | 0.0552077 | 0.0538677 | 0.0525648 | 0.0512980 | 0.0500663 | 0.0488688 | |
| 0.0619750 | 0.0614424 | 0.0609031 | 0.0603581 | 0.0598083 | 0.0592545 | 0.0586974 | 0.0581378 | 0.0575763 | 0.0570136 | |
| 0.0630079 | 0.0634905 | 0.0639483 | 0.0643820 | 0.0647923 | 0.0651799 | 0.0655454 | 0.0658895 | 0.0662127 | 0.0665158 | |
| 0.0640581 | 0.0656068 | 0.0671457 | 0.0686741 | 0.0701917 | 0.0716979 | 0.0731924 | 0.0746747 | 0.0761446 | 0.0776018 | |
| 0.0477044 | 0.0465723 | 0.0454715 | 0.0444012 | 0.0433604 | 0.0423484 | 0.0413643 | 0.0404073 | 0.0394766 | 0.0385714 | |
| 0.0564502 | 0.0558867 | 0.0553237 | 0.0547615 | 0.0542005 | 0.0536413 | 0.0530842 | 0.0525295 | 0.0519775 | 0.0514286 | |
| 0.0667994 | 0.0670641 | 0.0673105 | 0.0675391 | 0.0677507 | 0.0679457 | 0.0681247 | 0.0682883 | 0.0684371 | 0.0685714 | |
| 0.0790460 | 0.0804769 | 0.0818944 | 0.0832983 | 0.0846883 | 0.0860645 | 0.0874267 | 0.0887749 | 0.0901088 | 0.0914286 | |
| 0.0477044 | 0.0465723 | 0.0454715 | 0.0444012 | 0.0433604 | 0.0423484 | 0.0413643 | 0.0404073 | 0.0394766 | 0.0385714 | |
| 0.0564502 | 0.0558867 | 0.0553237 | 0.0547615 | 0.0542005 | 0.0536413 | 0.0530842 | 0.0525295 | 0.0519775 | 0.0514286 | |
| 0.0667994 | 0.0670641 | 0.0673105 | 0.0675391 | 0.0677507 | 0.0679457 | 0.0681247 | 0.0682883 | 0.0684371 | 0.0685714 | |
| 0.0790460 | 0.0804769 | 0.0818944 | 0.0832983 | 0.0846883 | 0.0860645 | 0.0874267 | 0.0887749 | 0.0901088 | 0.0914286 | |
| 0.0477044 | 0.0465723 | 0.0454715 | 0.0444012 | 0.0433604 | 0.0423484 | 0.0413643 | 0.0404073 | 0.0394766 | 0.0385714 | |
| 0.0564502 | 0.0558867 | 0.0553237 | 0.0547615 | 0.0542005 | 0.0536413 | 0.0530842 | 0.0525295 | 0.0519775 | 0.0514286 | |
| 0.0667994 | 0.0670641 | 0.0673105 | 0.0675391 | 0.0677507 | 0.0679457 | 0.0681247 | 0.0682883 | 0.0684371 | 0.0685714 | |
| 0.0790460 | 0.0804769 | 0.0818944 | 0.0832983 | 0.0846883 | 0.0860645 | 0.0874267 | 0.0887749 | 0.0901088 | 0.0914286 | |
| 0.0477044 | 0.0465723 | 0.0454715 | 0.0444012 | 0.0433604 | 0.0423484 | 0.0413643 | 0.0404073 | 0.0394766 | 0.0385714 | |
| 0.0564502 | 0.0558867 | 0.0553237 | 0.0547615 | 0.0542005 | 0.0536413 | 0.0530842 | 0.0525295 | 0.0519775 | 0.0514286 | |
| 0.0667994 | 0.0670641 | 0.0673105 | 0.0675391 | 0.0677507 | 0.0679457 | 0.0681247 | 0.0682883 | 0.0684371 | 0.0685714 | |
| 0.0790460 | 0.0804769 | 0.0818944 | 0.0832983 | 0.0846883 | 0.0860645 | 0.0874267 | 0.0887749 | 0.0901088 | 0.0914286 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadavalli, V.S.S.; Tshinangi, K.; Adetunji, O. Stochastic Analysis of a System of Two Interconnected Inventories. AppliedMath 2025, 5, 174. https://doi.org/10.3390/appliedmath5040174
Yadavalli VSS, Tshinangi K, Adetunji O. Stochastic Analysis of a System of Two Interconnected Inventories. AppliedMath. 2025; 5(4):174. https://doi.org/10.3390/appliedmath5040174
Chicago/Turabian StyleYadavalli, Venkata S. S., Kapya Tshinangi, and Olufemi Adetunji. 2025. "Stochastic Analysis of a System of Two Interconnected Inventories" AppliedMath 5, no. 4: 174. https://doi.org/10.3390/appliedmath5040174
APA StyleYadavalli, V. S. S., Tshinangi, K., & Adetunji, O. (2025). Stochastic Analysis of a System of Two Interconnected Inventories. AppliedMath, 5(4), 174. https://doi.org/10.3390/appliedmath5040174






