Regularization of Nonlinear Volterra Integral Equations of the First Kind with Smooth Data
Abstract
1. Introduction
2. Analytical Results
- (a)
- , ,, ;
- (b)
- —a nonincreasing function of ;
- (c)
- —a nonincreasing function of ;
- (d)
- .
- (e)
3. Numerical Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allaei, S.; Yang, Z.; Brunner, H. Existence, uniqueness and regularity of solutions to a class of third-kind Volterra integral equations. J. Integral Equ. Appl. 2015, 27, 325–342. [Google Scholar] [CrossRef]
- Nemati, S.; Lima, P.M.; Torres, D.F.M. Numerical solution of a class of third-kind Volterra integral equations using Jacobi wavelets. Numer. Algorithms 2021, 86, 675–691. [Google Scholar] [CrossRef]
- Usta, F. Bernstein approximation technique for numerical solution of Volterra integral equations of the third kind. Comp. Appl. Math. 2021, 40, 161. [Google Scholar] [CrossRef]
- Ma, X.; Huang, C. Recovery of high order accuracy in spectral collocation method for linear Volterra integral equations of the third-kind with non-smooth solutions. J. Comput. Appl. Math. 2021, 392, 113458. [Google Scholar] [CrossRef]
- Hashemizadeh, E.; Jami, P. A Method for Numerical Solution of Third-Kind Volterra Integral Equations Using Krall-Laguerre Polynomials. arXiv 2021, arXiv:2102.05603. [Google Scholar] [CrossRef]
- Bedelova, N.; Asanov, A.; Orozmamatova, Z.; Abdullaeva, Z. Regularization and choice of the parameter for the third kind nonlinear Volterra-Stieltjes integral equation solutions. Int. J. Mod. Nonlinear Theory Appl. 2021, 10, 81–90. [Google Scholar] [CrossRef]
- Lamm, P.K. A survey of regularization methods for first-kind Volterra equations. In Surveys on Solution Methods for Inverse Problems; Colton, D., Engl, H.W., Louis, A.K., McLaughlin, J.R., Rundell, W., Eds.; Springer: Vienna, Austria, 2000; pp. 53–82. [Google Scholar] [CrossRef]
- Delves, L.M.; Mohamed, J.L. Computational Methods for Integral Equations; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Esuabana, I.M.; Abasiekwere, U.A.; Moffat, I.U. Solution methods for integral equations—A survey. J. Math. Comput. Sci. 2020, 10, 3109–3142. [Google Scholar]
- Song, H.; Yang, Z.; Brunner, H. Analysis of collocation methods for nonlinear Volterra integral equations of the third kind. Calcolo 2019, 56, 7. [Google Scholar] [CrossRef]
- Allaei, S.S.; Yang, Z.; Brunner, H. Collocation methods for third-kind VIEs. IMA J. Numer. Anal. 2017, 37, 1104–1124. [Google Scholar] [CrossRef]
- Volterra, V. Theory of Functionals, Integral and Integro-Differential Equations; Nauka: Moscow, Russia, 1982. [Google Scholar]
- Brunner, H.; van der Houwen, P.J. The Numerical Solution of Volterra Equations, CWI Monographs 3; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Brunner, H. Collocation Methods for Volterra Integral and Related Functional Equations; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Linz, P. Analytical and Numerical Methods for Volterra Equations; SIAM: Philadelphia, PA, USA, 1985. [Google Scholar]
- Sergeev, V.O. Regularization of Volterra equations of the first kind. Dokl. Akad. Nauk SSSR 1971, 197, 531–534. [Google Scholar]
- Magnitsky, N.A. On the approximate solution of some Volterra integral equations of the first kind. Bull. Mosc. State Univ. 1978, 1, 91–96. [Google Scholar]
- Denisov, A.M. On the approximate solution of the Volterra equation of the first kind. Comput. Math. Math. Phys. 1975, 15, 1053–1056. [Google Scholar] [CrossRef]
- Imanaliyev, M.I.; Asanov, A. Regularization, Uniqueness and Existence of Solutions for Volterra Integral Equations of the First Kind; Research on Integro—Differential Equations; Ilim: Frunze, Kyrgyzstan, 1988; pp. 3–38. [Google Scholar]
- Karakeev, T.T. Regularization of Systems of Volterra Linear Integral Equations of the Third Kind. Lobachevskii J. Math. 2020, 41, 1823–1828. [Google Scholar] [CrossRef]
- Karakeev, T.T.; Imanaliyev, T.M. Regularization of Volterra linear integral equations of the first kind with the smooth data. Lobachevsky J. Math. 2020, 41, 39–45. [Google Scholar] [CrossRef]
- Hale, J.K. Ordinary Differential Equations, 2nd ed.; Krieger: Malabar, FL, USA, 1980; p. 361. [Google Scholar]
- Kamen, G.; Smirnov, G.N. Course of Differential Equations; Fizmatlit: Moscow, Russia, 1958; p. 456. [Google Scholar]
- Omurov, T.D.; Karakeev, T.T. Regularization and Numerical Methods for Solving Inverse and Nonlocal Boundary Value Problems; Ilim: Bishkek, Kyrgyzstan, 2006; p. 164. [Google Scholar]
- Demidovich, B.P. Lectures on the Mathematical Theory of Stability; Nauka: Moscow, Russia, 1967; p. 472. [Google Scholar]
- Asanov, A.; Obodoeva, G. Regularization and Uniqueness of Solutions of Linear Integral Volterra Equations of the Third Kind; Research on Integro-Differential Equations; Ilim: Frunze, Kyrgyzstan, 1994; pp. 65–74. [Google Scholar]

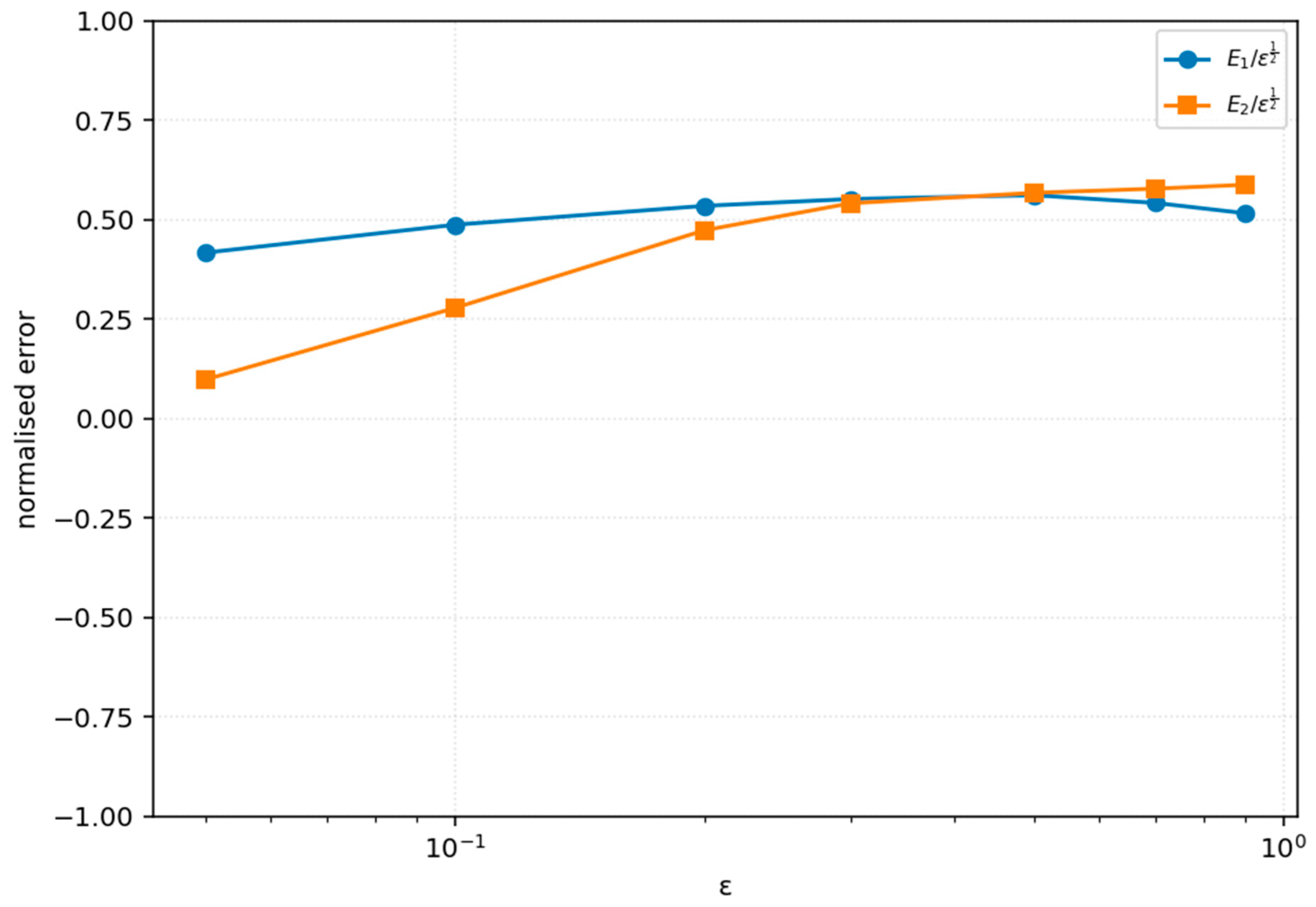
| 0.9 | 4.889 × 10−1 | 5.569 × 10−1 | 5.569 × 10−1 |
| 0.7 | 4.530 × 10−1 | 4.829 × 10−1 | 4.829 × 10−1 |
| 0.5 | 3.966 × 10−1 | 4.008 × 10−1 | 4.008 × 10−1 |
| 0.3 | 3.019 × 10−1 | 2.960 × 10−1 | 3.019 × 10−1 |
| 0.2 | 2.388 × 10−1 | 2.113 × 10−1 | 2.388 × 10−1 |
| 0.1 | 1.538 × 10−1 | 8.771 × 10−2 | 1.538 × 10−1 |
| 0.05 | 9.310 × 10−2 | 2.178 × 10−2 | 9.310 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karakeev, T.; Mustafayeva, N. Regularization of Nonlinear Volterra Integral Equations of the First Kind with Smooth Data. AppliedMath 2025, 5, 146. https://doi.org/10.3390/appliedmath5040146
Karakeev T, Mustafayeva N. Regularization of Nonlinear Volterra Integral Equations of the First Kind with Smooth Data. AppliedMath. 2025; 5(4):146. https://doi.org/10.3390/appliedmath5040146
Chicago/Turabian StyleKarakeev, Taalaibek, and Nagima Mustafayeva. 2025. "Regularization of Nonlinear Volterra Integral Equations of the First Kind with Smooth Data" AppliedMath 5, no. 4: 146. https://doi.org/10.3390/appliedmath5040146
APA StyleKarakeev, T., & Mustafayeva, N. (2025). Regularization of Nonlinear Volterra Integral Equations of the First Kind with Smooth Data. AppliedMath, 5(4), 146. https://doi.org/10.3390/appliedmath5040146







