Regularization of Nonlinear Volterra Integral Equations of the First Kind with Smooth Data

Abstract

The paper investigates the regularization of solutions to nonlinear Volterra integral equations of the first kind, under the assumption that a solution exists and belongs to the space of continuous functions. The kernel of the equation is a differentiable function and vanishes on the diagonal at an interior point of the integration interval. By applying an appropriate differential operator (with respect to x), the Volterra integral equation of the first kind is reduced to a Volterra integral equation of the third kind, equivalent with respect to solvability. The subdomain method is employed by partitioning the integration interval into two subintervals. Within the imposed constraints, a compatibility condition for the solutions is satisfied at the junction point of the partial subintervals. A Lavrentiev-type regularizing operator is constructed that preserves the Volterra structure of the equation. The uniform convergence of the regularized solution to the exact solution is proved, and conditions ensuring the uniqueness of the solution in Hölder space are established.

1. Introduction

Volterra integral equations of the third kind are widely used in mathematical modeling problems involving memory, where the current state of a system depends on its past states. Such equations arise in various applied fields, from problems in rheology and heat conduction to the dynamics of biological populations and plasma electrodynamics [1,2,3].

A distinctive feature of third-kind integral equations is the degeneracy of the kernel on the diagonal, where the coefficient vanishes at one or several points of the integration interval, resulting in the loss of stability for standard numerical methods such as collocation schemes and direct decomposition techniques [4,5,6]. As a result, classical a priori error estimates for the solution become inapplicable.

To address this problem, the $\epsilon$-regularization method is commonly employed, which consists in adding a small positive parameter to the degenerate coefficient [7,8]. The first systematic studies of this approach were carried out in the context of linear equations with a simple coefficient zero [9]. Subsequent studies have shown that the accuracy and convergence rate of the regularized solution depend significantly on the multiplicity of the zero of the function, as well as on the chosen regularization technique and numerical method [8,9,10]. Recent studies actively focus on the development of efficient numerical algorithms employing various orthogonal polynomials, spectral methods, and collocation techniques [11].

In addition to their theoretical significance, first-kind Volterra integral equations arise in many practical contexts, such as inverse heat conduction, viscoelastic materials, control systems with memory, plasma dynamics, and population biology. While regularization of boundary degeneracies has been widely studied, the case of an interior zero of the kernel has attracted less attention. The novelty of this paper lies in the construction of a Lavrentiev-type operator that preserves the Volterra structure while ensuring uniform convergence and uniqueness of the solution in Hölder spaces. This approach complements and extends recent studies on regularization techniques and numerical algorithms for Volterra equations [9,10,11]. Compared to existing results, our method improves stability conditions and demonstrates accuracy in the presence of an internal degeneracy.

2. Analytical Results

The theory of Volterra integral equations of the first kind has been extensively developed in cases where the kernel K(x,t) does not vanish on the diagonal t = x at any point of the given interval, or when the kernel vanishes identically on the diagonal along with its derivatives on $x$ up to order $n-1$ on the diagonal, while the $n$th derivative does not vanish at any point on the interval [12,13,14,15]. Difficulties arise when the kernel vanishes on the diagonal at points within the given interval. Under such conditions, regularization methods are among the most effective tools for analysis [16,17,18,19,20,21].

Consider the nonlinear Volterra integral equation of the first kind

$${\int }_0^{x}K\left(x,t,u\left(t\right)\right)dt=g\left(x\right),$$

(1)

where the $K\left(x,t,u\right)=K\left(x,t\right)u\left(t\right)+N_0\left(x,t,u\left(t\right)\right).$ The given functions satisfy the conditions:

(a)

$K\left(x,t\right)\in C^{\mathrm{1,0}}\left(D\right)$, $D=\left\{\left(x,t\right)|0\le t\le x\le b\right\},k\left(x\right)=K(x,x)$,

$g\left(x\right),k\left(x\right)\in C^1 [0,b]$, $g^{\left(i\right)}\left(0\right)=0, { k}^{\left(i\right)}\left(b_1\right)=0\left(\mathrm{i}=\mathrm{0,1}\right),0<k\left(x\right) \forall x\in \left[0,b_1\right)\cup \left(b_1,b\right],$ $b_1\in \left(0,b\right)$;

(b)

$k\left(x\right)$—a nonincreasing function of $x\in [0,b_1]$;

(c)

$k\left(x\right)$—a nonincreasing function of $x\in [b_1,b]$;

(d)

$N_0\left(x,t,u\right)\in C^{\mathrm{1,0},0}\left(D\times R^1\right), N_{0x}^{\left(i\right)}\left(x,x,u\right)=0, i=\mathrm{0,1}$.

$C^{\mathrm{1,0},0}\left(D\times R^1\right)$ is the space of continuous functions of $\left(x,t,u\right)$, that have continuous derivatives with respect to the first argument $x$. Here, $N_0\left(x,t,u\right)$ belongs to this space, which guarantees the smoothness of the kernel with respect to the variable $x$.

By applying the operator $C_{1}I+D$, where I is the identity operator, and ${0<C}_1=const,D=d/dx$—the differentiation operator, Equation (1) is transformed into a Volterra integral equation of the third kind

$$k\left(x\right)u\left(x\right)+{\int }_0^{x}L\left(x,t\right)u\left(t\right)dt={\int }_0^{x}N\left(x,t,u\left(t\right)\right)dt+f\left(x\right),$$

(2)

where $L\left(x,t\right)=C_{1}K\left(x,t\right)+K_x\left(x,t\right),N\left(x,t,u\right)=-C_1{N}_0\left(x,t,u\right)-{\displaystyle \frac{\partial }{\partial x}}{N}_0\left(x,t,u\right)$, $f\left(x\right)=C_{1}g\left(x\right)+g^{\prime }\left(x\right).$

Let

(e)

$\left|N\left(x,t,u\right)-N\left(x,t,u_0\right)-\right. \left.N\left(\nu ,t,u\right)+N\left(\nu ,t,u_0\right)\right|\le L_N\left(x-\nu \right)\left|u-u_0\right|,$

$0\le t\le \nu \le x\le b, 0<L_N=const.$

For $x\in \left[0,b_1\right],$ Equation (2) reduces to the following equation

$$k\left(x\right)v\left(x\right)+{\int }_0^{x}L\left(x,t\right)v\left(t\right)dt={\int }_0^{x}N\left(x,t,v\left(t\right)\right)dt+f\left(x\right), x\in \left[0,b_1\right].$$

(3)

Let us rewrite Equation (3) in the form

$$k\left(x\right)v\left(x\right)+{\int }_0^{x}L\left(t,t\right)v\left(t\right)dt={\int }_0^x[L\left(t,t\right)-L\left(x,t\right)]v\left(t\right)dt+{\int }_0^{x}N\left(x,t,v\left(t\right)\right)dt+f\left(x\right),$$

(4)

and consider an equation with a small parameter $\epsilon$from the interval (0,1)

$$\begin{gathered} \left(\epsilon +k\left(x\right)\right)v_{\epsilon }\left(x\right)+\underset{0}{\overset{x}{\int }}L\left(t,t\right)v_{\epsilon }\left(t\right)dt=\underset{0}{\overset{x}{\int }}\left[L\left(t,t\right)-L\left(x,t\right)\right]v_{\epsilon }\left(t\right)dt \\ +{\int }_0^{x}N\left(x,t,v_{\epsilon }\left(t\right)\right)dt+\mathsf{\epsilon }v\left(0\right)+f\left(x\right), x\in \left[0,b_1\right]. \end{gathered}$$

(5)

Theorem 1.

Assume that conditions (a), (b), (d), and (e) hold, and that $L\left(x,x\right)\ge d_1>0$ for all $x\in [a,b]$ , and suppose that Equation (1) has a solution  $u\left(x\right) \in C^{\gamma }[0,b], 0<\gamma \le 1$ . Then, as $\epsilon \to 0,$ solution of Equation (5) converges uniformly to the solution of Equation (3). Moreover, the following estimate

$${‖v_{\epsilon }\left(x\right)-v\left(x\right)‖}_{C[0,b_1]}\le exp\left(b_1{M}_2{M}_1\right)(d_2\epsilon +d_3{\epsilon }^{\gamma }){‖u‖}_{\gamma *},$$

$$M_2=2{\theta }_1^{-2}{d}_1^{-1}+b_1{k}^{-1}\left(0\right), 0<{\theta }_1<1, {M_1=L_1+C_1{L}_2+L_N,‖\bullet ‖}_{C[0,b_1]}=\underset{[0,b_1]}{\mathit{max}}\left|\bullet \right|,$$

$L_1=\underset{D}{\mathit{max}}\left|K_x(x,t)\right|, {0<L}_2-$ Lipschitz coefficient of a function  $K_x\left(x,t\right)$ with respect to x,  ${‖u‖}_{\gamma *}=\underset{\begin{array}{c}(x,s)\in [0,b]\\ x\ne s\end{array}}{sup}\{\left|v\left(x\right)-v\left(s\right)\right|/{\left|x-s\right|}^{\gamma }\}$ ,

$$d_2=(1+d_4)b^{\gamma }/k\left(0\right), d_4=\underset{[0,b_1]}{max}\left|k^{\prime }\left(x\right)\right|, d_3=(2+d_4){\gamma }_0^{-(1+\gamma )}{d}_1^{-\gamma },$$

${\gamma }_0=\mathit{min}({\theta }_1,1-\gamma )$ .

Proof of Theorem 1.

Using substitution

$${\eta }_{\epsilon }\left(x\right)=v_{\epsilon }\left(x\right)-v\left(x\right)$$

(6)

from (5) and (4) we obtain

$$\begin{gathered} \left(\epsilon +k\left(x\right)\right){\eta }_{\epsilon }\left(x\right)+\underset{0}{\overset{x}{\int }}L\left(t,t\right){\eta }_{\epsilon }\left(t\right)dt=\underset{0}{\overset{x}{\int }}\left[L\left(t,t\right)-L\left(x,t\right)\right]{\eta }_{\epsilon }\left(t\right)dt \\ +\underset{0}{\overset{x}{\int }}\left[N\left(x,t,v_{\epsilon }\left(t\right)\right)-N\left(x,t,v\left(t\right)\right)\right]dt+\mathsf{\epsilon }\left[v\left(0\right)-v\left(x\right)\right], x\in \left[0,b_1\right]. \end{gathered}$$

The given equation, using a resolvent

$$R\left(x,t;\epsilon \right)=-{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(x\right)}}\mathit{exp}\left(-\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right)$$

of the kernels $\left(-{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(x\right)}}\right),$is obtained by the standard resolvent method, according to the theorem on the integrating factor of a linear ODE ([22] (p. 6) or [23] (p. 34))

$$exp\left[\underset{0}{\overset{x}{\int }}{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(t\right)}}dt\right],$$

and it is transformed to the following form

$$\begin{gathered} {\eta }_{\epsilon }\left(x\right)=-{\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{0}{\overset{x}{\int }}{\displaystyle \frac{exp\left[-{\int }_t^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}ds\right]L\left(t,t\right)}{\epsilon +k\left(t\right)}}\{\underset{0}{\overset{t}{\int }}[L\left(s,s\right)-L\left(t,s\right)]{\eta }_{\epsilon }\left(s\right)ds \\ +\underset{0}{\overset{t}{\int }}\left[N\left(t,s,v_{\epsilon }\left(s\right)\right)-N\left(t,s,v\left(s\right)\right)\right]ds+\mathsf{\epsilon }\left[v\left(0\right)-v\left(t\right)\right]\}dt \\ +{\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\left\{\underset{0}{\overset{x}{\int }}\left[L\left(t,t\right)-L\left(x,t\right)\right]{\eta }_{\epsilon }\left(t\right)dt+\underset{0}{\overset{x}{\int }}\left[N\left(x,t,v_{\epsilon }\left(t\right)\right)-N\left(x,t,v\left(t\right)\right)\right]dt+\mathsf{\epsilon }\left[v\left(0\right)-v\left(x\right)\right]\right\},x\in \left[0,b_1\right], \end{gathered}$$

We are making an equivalent change below. Here ${\int }_t^x{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds$ plays the role of an integrating factor generated by the resolvent method. It accumulates the effect of the kernel regularization along the trajectory from $t$ to $x,$ ensuring that the exponential factor stablizes the solution and makes the convergence analysis tractable.

$$\begin{gathered} {\eta }_{\epsilon }\left(x\right)=-{\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{0}{\overset{x}{\int }}exp\left[-\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left\{\underset{0}{\overset{t}{\int }}[L\left( x,s\right)-\right.L\left(t,s\right)]{\eta }_{\epsilon }{\displaystyle \left(s\right)ds} \\ +\left.\underset{t}{\overset{x}{\int }}\left[L\left(x,s\right)-L\left(s,s\right)\right]{\eta }_{\epsilon }\left(s\right)ds+\underset{0}{\overset{t}{\int }}\left[N\left(t,s,v_{\epsilon }\left(s\right)\right)-N\left(t,s,v\left(s\right)\right)\right]ds \\ -\underset{0}{\overset{x}{\int }}\left[N\left(x,s,v_{\epsilon }\left(s\right)\right)-N\left(x,s,v\left(s\right)\right)\right]ds+\epsilon \left[v\left(t\right)-v\left(x\right)\right]\right\}dt \\ +{\displaystyle \frac{exp\left[-{\int }_0^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}ds\right]}{\epsilon +k\left(x\right)}}\left\{{\int }_0^x[L\left(t,t\right)-L\left(x,t\right)]{\eta }_{\epsilon }\left(t\right)dt+{\int }_0^x\left[N\left(x,t,v_{\epsilon }\left(t\right)\right)-N\left(x,t,v\left(t\right)\right)\right]dt-\epsilon \left[v\left(x\right)-v\left(0\right)\right]\right\}, \end{gathered}$$

(7)

$x\in \left[0,b_1\right].$.

Let us use the notation

$$G_{\epsilon }\left(x\right)={\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{0}{\overset{x}{\int }}exp\left[-\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left(x-t\right)dt, x\in \left[0,b_1\right].$$

Since $k\left(x\right)$ is non-increasing on  $x\in \left[0,b_1\right]$, then for $s\le x$

$$\epsilon +k\left(x\right)\le \epsilon +k\left(s\right)$$

and under conditions that (a), (b) follow ([24], (p. 22))

$$L\left(x,x\right){\theta }_2+k^{\prime }\left(x\right)\ge 0, {\theta }_1+{\theta }_2=1, 0<{\theta }_1<1.$$

(8)

Then using the inequality data and the formula

$${\displaystyle \frac{\epsilon +k\left(t\right)}{\epsilon +k\left(x\right)}}exp\left[-{\int }_t^x{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]=exp\left[-{\int }_t^x{\displaystyle \frac{L\left(s,s\right)+k^{\prime }\left(s\right)}{\epsilon +k\left(s\right)}}ds\right],$$

(9)

to $L\left(x,x\right)\ge d_1>0$ we get

$$\begin{gathered} \left|G_{\epsilon }\left(x\right)\right|\le d_1^{-1}\underset{0}{\overset{x}{\int }}exp\left[-{\int }_t^x{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(t\right)}}{\displaystyle \frac{\epsilon +k\left(t\right)}{\epsilon +k\left(x\right)}}\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)ds}{\epsilon +k\left(s\right)}}dt \\ =d_1^{-1}\underset{0}{\overset{x}{\int }}exp\left[-{\theta }_1\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(t\right)}}\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)ds}{\epsilon +k\left(s\right)}}dt\le d_1^{-1}{\theta }_1^{-2}. \end{gathered}$$

Based on this assessment, taking into account (e) and inequality

$$\left|L\left(x,s\right)-L\left(t,\mathrm{s}\right)\right|\le \left(L_1+C_1{L}_2\right)\left(x-t\right), t\le x,$$

we have

$$\begin{gathered} \left|-{\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{0}{\overset{x}{\int }}{\displaystyle \frac{\mathit{exp}\left[-{\int }_t^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}\mathit{ds}\right]L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left\{\underset{0}{\overset{t}{\int }}[L\left( x,s\right)-\right.L\left(t,s\right)]{\eta }_{\epsilon }{\displaystyle \left(s\right)ds}\right. \\ +\underset{t}{\overset{x}{\int }}\left[L\left(x,s\right)-L\left(s,s\right)\right]{\eta }_{\epsilon }\left(s\right)ds+\underset{0}{\overset{t}{\int }}\left[N\left(t,s,v_{\epsilon }\left(s\right)\right)-N\left(t,s,v\left(s\right)\right)\right]ds \\ \left.-\underset{0}{\overset{x}{\int }}\left[N\left(x,s,v_{\epsilon }\left(s\right)\right)-N\left(x,s,v\left(s\right)\right)\right]ds\right|\le 2M_1\left|G_{\epsilon }\left(x\right)\right|\underset{0}{\overset{x}{\int }}\left|{\eta }_{\epsilon }\left(t\right)\right|dt \\ \le 2d_1^{-1}{\theta }_1^{-2}{M}_1\underset{0}{\overset{x}{\int }}\left|{\eta }_{\epsilon }\left(t\right)\right|dt. \end{gathered}$$

For the second term of (7), we use inequality (8) and formula (9). Then

$$\begin{gathered} \left|{\displaystyle \frac{exp\left[-{\int }_0^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}ds\right]}{\epsilon +k\left(x\right)}}\underset{0}{\overset{x}{\int }}\left[L\left(t,t\right)-L\left(x,t\right)\right]{\eta }_{\epsilon }\left(t\right)dt\right. \\ \left.+\underset{0}{\overset{x}{\int }}\left[N\left(x,t,v_{\epsilon }\left(t\right)\right)-N\left(x,t,v\left(t\right)\right)\right]dt\right|\le M_1{\displaystyle \frac{b_1}{\epsilon +k\left(0\right)}} \\ \times \mathit{exp}\left(-\underset{0}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)+k^{\prime }\left(s\right)}{\epsilon +k\left(s\right)}}ds\right)\underset{0}{\overset{x}{\int }}\left|{\eta }_{\epsilon }\left(t\right)\right|dt\le b_1{k}^{-1}{\displaystyle \left(0\right)}{M}_1\underset{0}{\overset{x}{\int }}\left|{\eta }_{\epsilon }\left(t\right)\right|dt. \end{gathered}$$

By virtue of these estimates from (7), we obtain

$$\left|{\eta }_{\epsilon }\left(x\right)\right|\le M_2{M}_1{\int }_0^x\left|{\eta }_{\epsilon }\left(t\right)\right|dt+\left|\left(H_{\epsilon }v\right)\left(x\right)\right|,$$

(10)

where $\left(H_{\epsilon }u\right)\left(x\right)\equiv {\displaystyle \frac{\epsilon }{\epsilon +k\left(x\right)}}{\int }_0^x{\displaystyle \frac{\mathit{exp}\left[-{\int }_t^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}\mathit{ds}\right]L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left[v\left(x\right)-v\left(t\right)\right]dt-0$

$$-{\displaystyle \frac{\epsilon }{\epsilon +k\left(x\right)}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\int }_0^x{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]\left[v\left(x\right)-v\left(0\right)\right], x\in \left[0,b_1\right].$$

(11)

Let us apply the Gronwall–Bellman inequality [25] (p. 38) and proceed to the norm. Hence, from (10) we get the following estimate

$$\begin{gathered} \left(H_{\epsilon }u\right)\left(x\right)\equiv {\displaystyle \frac{\epsilon }{\epsilon +k\left(x\right)}}\underset{0}{\overset{x}{\int }}{\displaystyle \frac{\mathit{exp}\left(-{\int }_t^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}\mathit{ds}\right)L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left[v\left(x\right)-v\left(t\right)\right]dt \\ -{\displaystyle \frac{\epsilon }{\epsilon +k\left(x\right)}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\underset{0}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right)\left[v\left(x\right)-v\left(0\right)\right], x\in \left[0,b_1\right] \end{gathered}$$

When conditions (a)–(b) hold, a $v\left(x\right)\in C^{\mathsf{\gamma }}\left[0,b_1\right], 0<\gamma \le 1\left(H_{\epsilon }u\right)\left(x\right)$ evaluation takes place for all functions for the operator [26] (p. 65).

When conditions (a)–(b) hold, for every function $u\left(x\right)\in C^{\mathsf{\gamma }}\left[0,b_1\right]$ with $0<\gamma \le 1$, the following estimate holds for $\left(H_{\epsilon }u\right)\left(x\right)$ for all $x\in \left[0,b_1\right]$ (see [26] (p. 65))

$${‖\left(H_{\epsilon }u\right)\left(x\right)‖}_{C[0,b_1]}\le \left(d_2\epsilon +d_3{\epsilon }^{\gamma }\right){‖u‖}_{\gamma *}.$$

Therefore, taking (6) into account, as $\epsilon \to 0,$ the function $u_{\epsilon }\left(x\right)\to u\left(x\right)$ uniformly.

Let $x\in [b_1,b]$. Then from (2) we get

$$k\left(x\right)w\left(x\right)+{\int }_{b_1}^{x}L\left(x,t\right)w\left(t\right)dt={\int }_{b_1}^{x}N\left(x,t,w\left(t\right)\right)dt+F\left(x\right), x\in \left[b_1,b\right]$$

(12)

where $F\left(x\right)=f\left(x\right)-{\int }_0^{b_1}L\left(x,t\right)v\left(t\right)dt+{\int }_0^{b_1}N\left(x,t,v\left(t\right)\right)dt, x\in \left[b_1,b\right],$ with $F\left(b_1\right)=0.$

The equation with a small parameter $\epsilon$ from the interval $\left(\mathrm{0,1}\right)$ corresponding to Equation (12) has the form

$$\begin{gathered} \left(\epsilon +k\left(x\right)\right)w_{\epsilon }\left(x\right)+\underset{b_1}{\overset{x}{\int }}L\left(t,t\right)w_{\epsilon }\left(t\right)dt=\underset{b_1}{\overset{x}{\int }}\left[L\left(t,t\right)-L\left(x,t\right)\right]w_{\epsilon }\left(t\right)dt \\ +{\int }_{b_1}^{x}N\left(x,t,w_{\epsilon }\left(t\right)\right)dt+\mathsf{\epsilon }w\left(b_1\right)+F\left(x\right), x\in \left[b_1,b\right], \end{gathered}$$

(13)

$w\left(b_1\right)=v_{\epsilon }\left(b_1\right).$ □

Theorem 2.

Assume that conditions (a) and (b)–(e) hold, and  $L\left(x,x\right)\ge d_1>0$. Then, as  $\epsilon \to 0,$ the solution of Equation (13) uniformly converges to solution of Equation (12); moreover, the estimate holds

$${‖w_{\epsilon }\left(x\right)-w\left(x\right)‖}_{C[b_1,b]}\le M_0{\epsilon }^{\gamma } ,$$

where  $M_0=d_1^{-\gamma }\left(d_5+d_6\right)M_3{‖u‖}_{{\gamma }^{*}}, d_5={\int }_{b_1}^{\infty }{\tau }^{\gamma }{e}^{-\tau }d\tau , d_6=\underset{\tau \ge 0}{sup}\left({\tau }^{\gamma }{e}^{-\tau }\right)$,

$$M_3=\mathit{exp}\left(M_1(b-b_1)d_1^{-1}\left[1+e^{-1}\right]\right)$$

Proof of Theorem 2.

Using substitution

$${\mu }_{\epsilon }\left(x\right)=w_{\epsilon }\left(x\right)-w\left(x\right), x\in [b_1,b]$$

from (12) and (13) we obtain

$$\begin{gathered} \left(\epsilon +k\left(x\right)\right){\mu }_{\epsilon }\left(x\right)+\underset{b_1}{\overset{x}{\int }}L\left(t,t\right){\mu }_{\epsilon }\left(t\right)dt=\underset{b_1}{\overset{x}{\int }}\left[L\left(t,t\right)-L\left(x,t\right)\right]{\mu }_{\epsilon }\left(t\right)dt \\ +\underset{b_1}{\overset{x}{\int }}\left[N\left(x,t,w_{\epsilon }\left(t\right)\right)-N\left(x,t,w\left(t\right)\right)\right]dt+\mathsf{\epsilon }\left[w\left(b_1\right)-w\left(x\right)\right],x\in [b_1,b]. \end{gathered}$$

Since $k\left(x\right)$ is non-decreasing on $x\in [b_1,b]$, then at $s\le x$

$${\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\le {\displaystyle \frac{1}{\epsilon +k\left(s\right)}}.$$

Then using the condition $L\left(x,x\right)\ge d_1>0,$ for the function

$$G_{\epsilon 1}\left(x\right)={\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{b_1}{\overset{x}{\int }}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left(x-t\right)dt$$

we get

$$\left|G_{\epsilon 1}\left(x\right)\right|\le d_1^{-1}\underset{b_1}{\overset{x}{\int }}{\displaystyle \frac{exp\left[-{\int }_t^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}ds\right]L\left(t,t\right)}{\epsilon +k\left(t\right)}}\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)ds}{\epsilon +k\left(s\right)}}dt\le d_1^{-1}.$$

Based on this estimate from the equation

$$\begin{gathered} {\mu }_{\epsilon }{\displaystyle \left(x\right)}=-{\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{b_1}{\overset{x}{\int }}exp\left[-\underset{t}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right]{\displaystyle \frac{L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left\{\underset{b_1}{\overset{t}{\int }}[L\left( x,s\right)-\right.L\left(t,s\right)] \\ \times {\mu }_{\epsilon }\left(s\right)ds+\underset{t}{\overset{x}{\int }}\left[L\left(x,s\right)-L\left(s,s\right)\right]{\mu }_{\epsilon }\left(s\right)ds+\epsilon \left[w\left(t\right)-w\left(x\right)\right] \\ +\underset{b_1}{\overset{t}{\int }}\left[N\left(t,\mathrm{s},w_{\epsilon }\left(s\right)\right)-N\left(t,\mathrm{s},w\left(s\right)\right)\right]ds-\left.\underset{b_1}{\overset{x}{\int }}\left[N\left(x,s,w_{\epsilon }\left(s\right)\right)-N\left(x,s,w\left(s\right)\right)\right]ds\right\}dt \\ +{\displaystyle \frac{exp\left[-{\int }_{b_1}^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}ds\right]}{\epsilon +k\left(x\right)}} \\ \times \left\{{\int }_{b_1}^x\left[L\left(t,t\right)-L\left(x,t\right)\right]{\eta }_{\epsilon }\left(t\right)dt+{\int }_{b_1}^x\left[N\left(x,t,w_{\epsilon }\left(t\right)\right)-N\left(x,t,w\left(t\right)\right)\right]dt+\mathsf{\epsilon }\left[w\left(b_1\right)-w\left(x\right)\right]\right\}, \end{gathered}$$

(14)

we have

$$\begin{gathered} \left|-{\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{b_1}{\overset{x}{\int }}{\displaystyle \frac{\mathit{exp}\left[-\underset{t}{\overset{x}{\int }}\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}\mathit{ds}\right]L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left\{\underset{b_1}{\overset{t}{\int }}[L\left( x,s\right)-\right.L\left(t,s\right)]{\mu }_{\epsilon }{\displaystyle \left(s\right)}ds\right. \\ +\underset{t}{\overset{x}{\int }}\left[L\left(x,s\right)-L\left(s,s\right)\right]{\mu }_{\epsilon }\left(s\right)ds+\underset{b_1}{\overset{t}{\int }}\left[N\left(t,\mathrm{s},w_{\epsilon }\left(s\right)\right)-N\left(t,\mathrm{s},w\left(s\right)\right)\right]ds \\ -\underset{b_1}{\overset{x}{\int }}[N\left(x,s,w_{\epsilon }\left(s\right)\right)-N\left(x,s,w\left(s\right)\right)]ds\left\}dt\right| \\ \le 2M_1\left|G_{\epsilon 1}\left(x\right)\right|\underset{b_1}{\overset{x}{\int }}\left|{\mu }_{\epsilon }\left(t\right)\right|dt\le {2d}_1^{-1}{M}_4\underset{b_1}{\overset{x}{\int }}\left|{\mu }_{\epsilon }\left(t\right)\right|dt. \end{gathered}$$

Using inequality $\underset{v\ge 0}{\mathit{sup}}\left[v{e}^{-v}\right]\le e^{-1},$where $v={\displaystyle \frac{1}{\epsilon +k\left(x\right)}}{\int }_{b_1}^{x}L\left(s,s\right)ds,$ and condition (c), we have

$$\begin{gathered} \left|\frac{\mathit{exp}[-{\int }_{b_1}^x{\displaystyle \frac{L(s,s)}{\epsilon +k\left(s\right)}}ds]}{\epsilon +k\left(x\right)}\right\{\underset{b_1}{\overset{x}{\int }}[L(t,t)-L(x,t)]{\mu }_{\epsilon }(t)dt \\ +\underset{b_1}{\overset{x}{\int }}{\displaystyle \left[N\right(x,t,w_{\epsilon }\left(t\right))-N(x,t,w\left(t\right)\left)\right]}dt\left\}\right|\le M_1\frac{d_1^{-1}}{\epsilon \mathrm{+}k\left(x\right)} \\ \times \mathit{exp}\left(-{\displaystyle \frac{1}{\epsilon +k\left(x\right)}}\underset{b_1}{\overset{x}{\int }}L\left(s,s\right)ds\right)\underset{b_1}{\overset{x}{\int }}L\left(s,s\right)ds\underset{b_1}{\overset{x}{\int }}\left|{\mu }_{\epsilon }\left(t\right)\right|dt \\ \le \underset{v\ge 0}{\mathit{sup}}\left[v{e}^{-v}\right]d_1^{-1}{M}_1\underset{b_1}{\overset{x}{\int }}\left|{\mu }_{\epsilon }\left(t\right)\right|dt\le {\left(e{d}_1\right)}^{-1}{M}_1\underset{b_1}{\overset{x}{\int }}\left|{\mu }_{\epsilon }\left(t\right)\right|dt. \end{gathered}$$

By virtue of these estimates from (14), we obtain

$$\left|{\mu }_{\epsilon }\left(x\right)\right|\le d_1^{-1}\left(1+e^{-1}\right)M_1{\int }_{b_1}^x\left|{\mu }_{\epsilon }\left(t\right)\right|dt+\left|\left(H_{\epsilon }w\right)\left(x\right)\right|,$$

(15)

where

$$\begin{gathered} \left(H_{\epsilon }u\right)\left(x\right)\equiv {\displaystyle \frac{\epsilon }{\epsilon +k\left(x\right)}}\underset{b_1}{\overset{x}{\int }}{\displaystyle \frac{\mathit{exp}\left(-{\int }_t^x\frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}\mathit{ds}\right)L\left(t,t\right)}{\epsilon +k\left(t\right)}}\left[w\left(x\right)-w\left(t\right)\right]dt \\ -{\displaystyle \frac{\epsilon }{\epsilon +k\left(x\right)}}exp\left(-\underset{b_1}{\overset{x}{\int }}{\displaystyle \frac{L\left(s,s\right)}{\epsilon +k\left(s\right)}}ds\right)\left[w\left(x\right)-w\left(b_1\right)\right] \end{gathered}$$

The application of the Gronwall–Bellman inequality for (15) and the transition to the norm leads to the estimation

$${‖{\mu }_{\epsilon }\left(x\right)‖}_{C[b_1,b]}\le M_3{‖\left(H_{\epsilon }w\right)\left(x\right)‖}_{C[b_1,b]}.$$

When conditions (a) and (b) hold, the $w\left(x\right)\in C^{\mathsf{\gamma }}[b_1,b], 0<\gamma \le 1$ evaluation takes place for the functions [15]

$${‖\left(H_{\epsilon }w\right)\left(x\right)‖}_{C[b_1,b]}\le d_1^{-\gamma }\left(d_5+d_6\right){‖u‖}_{\gamma *}{\epsilon }^{\gamma },$$

Theorem 2 has been proved.

The solution of $u\left(x\right)$ Equation (1) is determined by the rule:

$$u\left(x\right)=\left\{\begin{array}{c}v\left(x\right), x\in \left[0,b_1\right], \\ w\left(x\right), x\in [\left.b_1, b\right], w\left(b_1\right)=v\left(b_1\right), \end{array}\right.$$

where $v\left(x\right)$ is the solution of Equation (3), $w\left(x\right)$ is the solution of Equation (12). In this case, the regularized solution is $u_{\epsilon }\left(x\right)$ based on the rule

$$u_{\epsilon }\left(x\right)=\left\{\begin{array}{c}{v}_{\epsilon }\left(x\right), x\in \left[0,b_1\right], \\ w_{\epsilon }\left(x\right), x\in [\left.b_1, b\right], w_{\epsilon }\left(b_1\right)=v_{\epsilon }\left(b_1\right),\end{array} \right.$$

where $v_{\epsilon }\left(x\right)$—solution of Equation (5), and $w_{\epsilon }\left(x\right)$—solution of Equation (13).

It follows from Theorems 1 and 2 that when the conditions of these theorems hold, the regularized solution $u_{\epsilon }\left(x\right)$ uniformly converges to the solution of Equation (2). □

Lemma 1.

Under assumptions  $\left(a\right)–\left(e\right)$, the solution of Equation (1) is unique in  $C^{\gamma }[0,b]$.

Proof of Lemma 1.

Suppose ${\mathrm{u}}_1\left(\mathrm{x}\right)$ and ${\mathrm{u}}_2\left(\mathrm{x}\right)$ are two solutions. Then their difference

$$\mathrm{z}\left(\mathrm{x}\right)={\mathrm{u}}_1\left(\mathrm{x}\right)-{\mathrm{u}}_2\left(\mathrm{x}\right)$$

Satisfies an equation of the same type with homogeneous right-hand side. Applying the Lipschitz condition $\left(\mathrm{e}\right)$ together with Gronwall’s inequality, we obtain

$$\left|\left|\mathrm{z}\right|\right|=0$$

Hence ${\mathrm{u}}_1={\mathrm{u}}_2$, which proves uniqueness (see also [26]). □

3. Numerical Experiments

An example is provided to demonstrate the accuracy of the estimates established in Theorems 1 and 2 in the presence of an interior zero $k\left(x\right)$.

Let the domain of definition be $0\le t\le x\le 1$ (thus, $b_1={\displaystyle \frac{1}{2}}$).

We will take the exact solution for verification as follows:

$$u\left(x\right)=e^x$$

The regularizing function is $k\left(x\right)$ defined as:

$$k\left(x\right)={\left(x-{\displaystyle \frac{1}{2}}\right)}^2$$

This function belongs to ${\mathrm{C}}^1\left[\mathrm{0,1}\right]$, which is non-negative throughout the domain, and equals to zero only at an interior point $b_1={\displaystyle \frac{1}{2}}$.

The kernel decomposition into its linear and nonlinear components is given by the following representation:

$$K\left(x,t\right)={\left(x-{\displaystyle \frac{1}{2}}\right)}^2+\left(x-t\right)$$

Therefore, $K\left(x,x\right)=k\left(x\right)$ and

$$N_0\left(x,t,u\right)=\lambda {\left(x-t\right)}^2{u}^2, \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} \lambda =0.05.$$

Then the full kernel takes the form

$$K\left(x,t,u\right)=K\left(x,t\right)u{+N}_0\left(x,t,u\right).$$

The right-hand side is $g\left(x\right)$ obtained by substituting $u\left(x\right)=e^x$ into the definition of the integral

$$g\left(x\right)={\left(x-{\displaystyle \frac{1}{2}}\right)}^2\left(eˣ-1\right)+eˣ-x-1+\lambda \left[-{\displaystyle \frac{1}{2}} x^2-{\displaystyle \frac{1}{2}} x-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{e^{2x}}{4}}\right].$$

It is straightforward to verify that conditions (a)–(d) are satisfied in this example.

Here is a description of the numerical scheme for solving the regularized problem (5) and (13). The equations are discretized using the trapezoid method on a uniform grid $M=400$. The resulting system remains upper triangular; at each node, a single scalar equation is solved, which, due to property (d), turns out to be linear. The Picard iteration converges in three steps for $\epsilon \ge 0.05$; and for $\epsilon <0.05$ one additional local Newton step is applied. The numerical values in

Table 1. Maximum errors for different values of $\epsilon$.

$\mathit{\epsilon }$	${\mathit{E}}_1={‖\mathit{v}\left(\mathit{x}\right)-{\mathit{v}}_{\mathit{\epsilon }}\left(\mathit{x}\right)‖}_{\mathit{C}[0,{\mathit{b}}_1]}$	${\mathit{E}}_2={‖\mathit{w}\left(\mathit{x}\right)-{\mathit{w}}_{\mathit{\epsilon }}\left(\mathit{x}\right)‖}_{\mathit{C}[{\mathit{b}}_1,\mathit{b}]}$	${‖\mathit{u}\left(\mathit{x}\right)-{\mathit{u}}_{\mathit{\epsilon }}\left(\mathit{x}\right)‖}_{\mathit{C}[0,\mathit{b}]}$
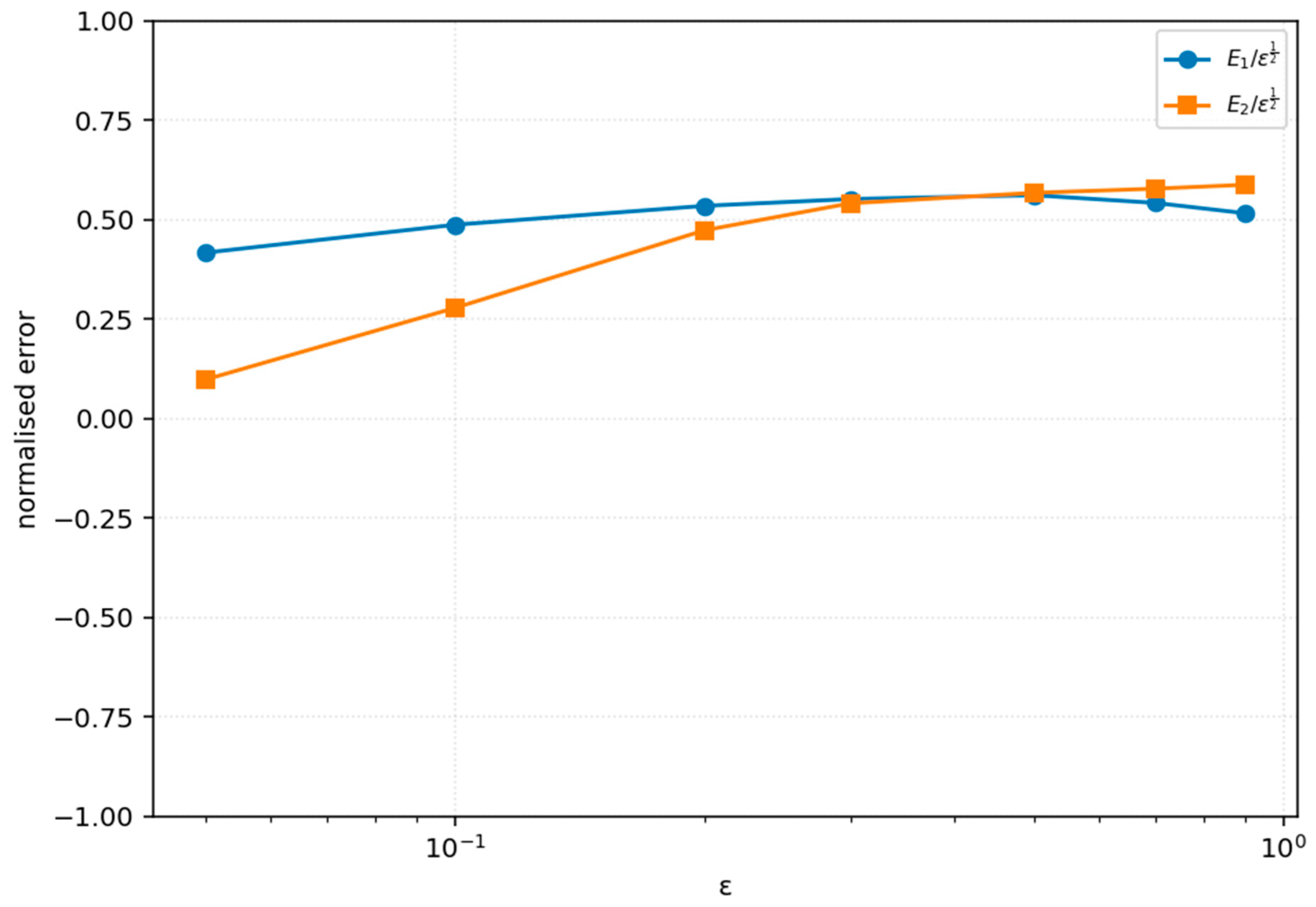
0.9	4.889 × 10−1	5.569 × 10−1	5.569 × 10−1
0.7	4.530 × 10−1	4.829 × 10−1	4.829 × 10−1
0.5	3.966 × 10−1	4.008 × 10−1	4.008 × 10−1
0.3	3.019 × 10−1	2.960 × 10−1	3.019 × 10−1
0.2	2.388 × 10−1	2.113 × 10−1	2.388 × 10−1
0.1	1.538 × 10−1	8.771 × 10−2	1.538 × 10−1
0.05	9.310 × 10−2	2.178 × 10−2	9.310 × 10−2

are consistent with Figure 1: the global error always equals the larger of the two local errors, and as $\epsilon \le 0.1{, E}_1$ associated with the degenerate region becomes dominant.

For the Picard iterations, the initial guess was chosen as $u^0\left(x\right)=0$. The stopping criterion was

$$‖u^{(k+1)}-u^{\left(k\right)}‖<{10}^{-6}.$$

In practice, convergence was reached within three iterations for $\epsilon \ge 0.05$. For smaller $\epsilon$, an additional single Newton correction was applied after the third Picard step. This strategy ensured both efficiency and robustness of the numerical algorithm.

The numerical data are consistent with the estimate. On $\left[0,b_1\right]$, the error fits $A_1\epsilon +B_1{\epsilon }^{{\displaystyle \frac{1}{2}}}$; for small $\epsilon \to 0$ the ${\epsilon }^{{\displaystyle \frac{1}{2}}}$ contribution prevails (see the ${\epsilon }^{{\displaystyle \frac{1}{2}}}$-scaled plot in Figure 2).

As shown in Figure 1, the error over the interval is well approximated by the expression $A_1\epsilon +B_1{\epsilon }^{{\displaystyle \frac{1}{2}}}$.

On the segment $\left[b_1,b\right]$, a pure power-law behavior in ${\epsilon }^{{\displaystyle \frac{1}{2}}}$ is observed, consistent with the theoretical estimate from Theorem 2. Normalization of errors to ${\epsilon }^{{\displaystyle \frac{1}{2}}}$ (Figure 2) brings both curves to a plateau $B_1{,B}_2\approx 0.51$, which is consistent with the estimates given in Theorems 1 and 2.

4. Discussion

This work examined a nonlinear Volterra integral equation of the first kind whose kernel is differentiable and vanishes on the diagonal at an interior point of the integration interval. Applying a differential operator in $\mathit{x}$ yields an equivalent Volterra equation of the third kind while preserving the Volterra structure. The interval is split at the degeneracy point, and a compatibility condition is imposed at the interface. Within this framework, a Lavrentiev-type regularizing operator is constructed, and uniform convergence of the regularized solution is proved together with uniqueness in a Hölder space.

The numerical results are consistent with the theory. On $[0, b_1]$ the error is well approximated by $A_1\epsilon +B_1{\epsilon }^{{\displaystyle \frac{1}{2}}}$, whereas on $[b_1,b]$ a pure ${\epsilon }^{{\displaystyle \frac{1}{2}}}$ rate is observed. After normalization by ${\epsilon }^{{\displaystyle \frac{1}{2}}}$, both curves flatten to constants ≈ 0.51, in agreement with the theoretical estimates.

These findings demonstrate that the proposed regularization framework is consistent and stable across different parameter values. The method maintains the causal structure of Volterra equations, which makes it well-suited for iterative schemes. Limitations of the present study include the focus on a single interior degeneracy and smooth data. Future research will address more general kernels, multiple degeneracies, and noisy data.

5. Conclusions

This paper develops a regularization method for nonlinear first-kind Volterra integral equations with an interior kernel degeneracy. The main contributions are:

1. the construction of a Lavrentiev-type operator that preserves the causal (upper-triangular) Volterra structure;

2. proofs of uniform convergence of the regularized solutions and uniqueness in Hölder spaces;

3. numerical experiments that are consistent with the theoretical error bounds.

Solvability of the first-kind problem is interpreted via an equivalent third-kind formulation on two subintervals separated by the degeneracy point; for this formulation we establish uniform convergence and Hölder-space uniqueness. The approach is straightforward to implement and maintains the natural causality of Volterra schemes.

Limitations of the present study include the focus on a single interior degeneracy and smooth data; extensions to multiple or higher-order degeneracies and less regular kernels/data are not addressed here. Further work will target adaptive refinement near the degeneracy, incorporation of stochastic right-hand sides, and analysis of the influence of noise on the regularization error.