Integrating Machine Learning and Fractional-Order Dynamics for Enhanced Psoriasis Prediction and Clinical Decision Support
Abstract
1. Introduction
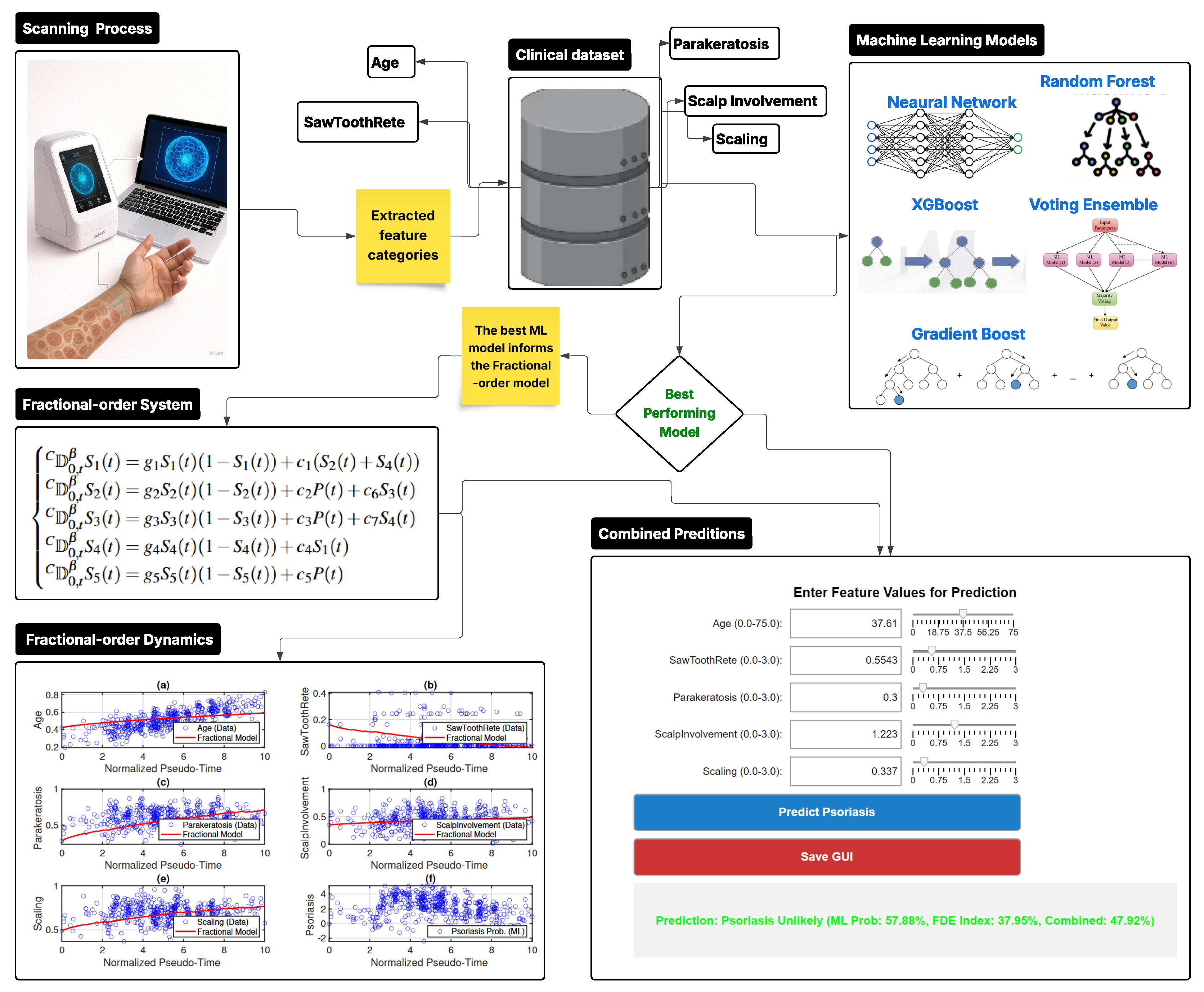
2. Methodology
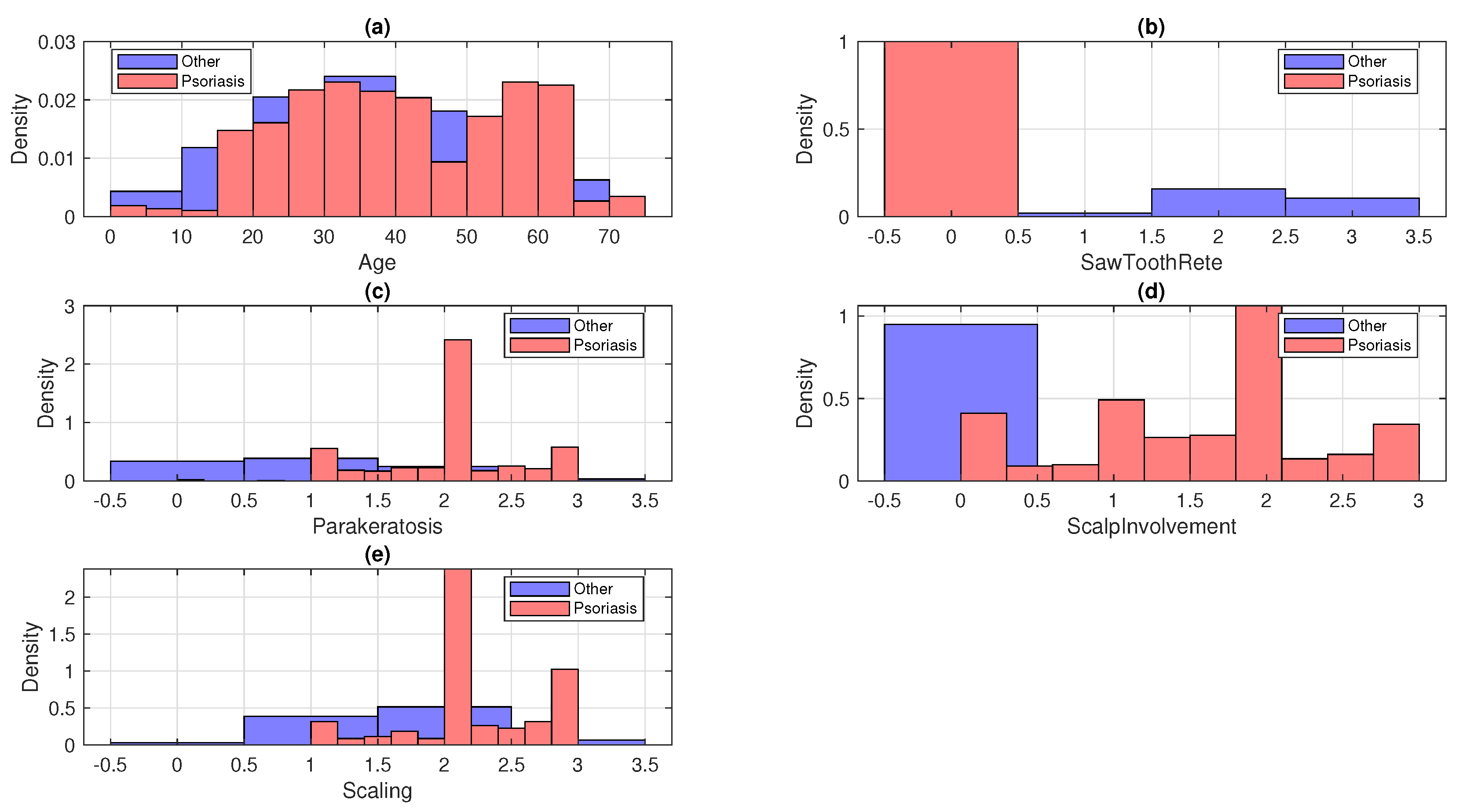
3. Data Summary
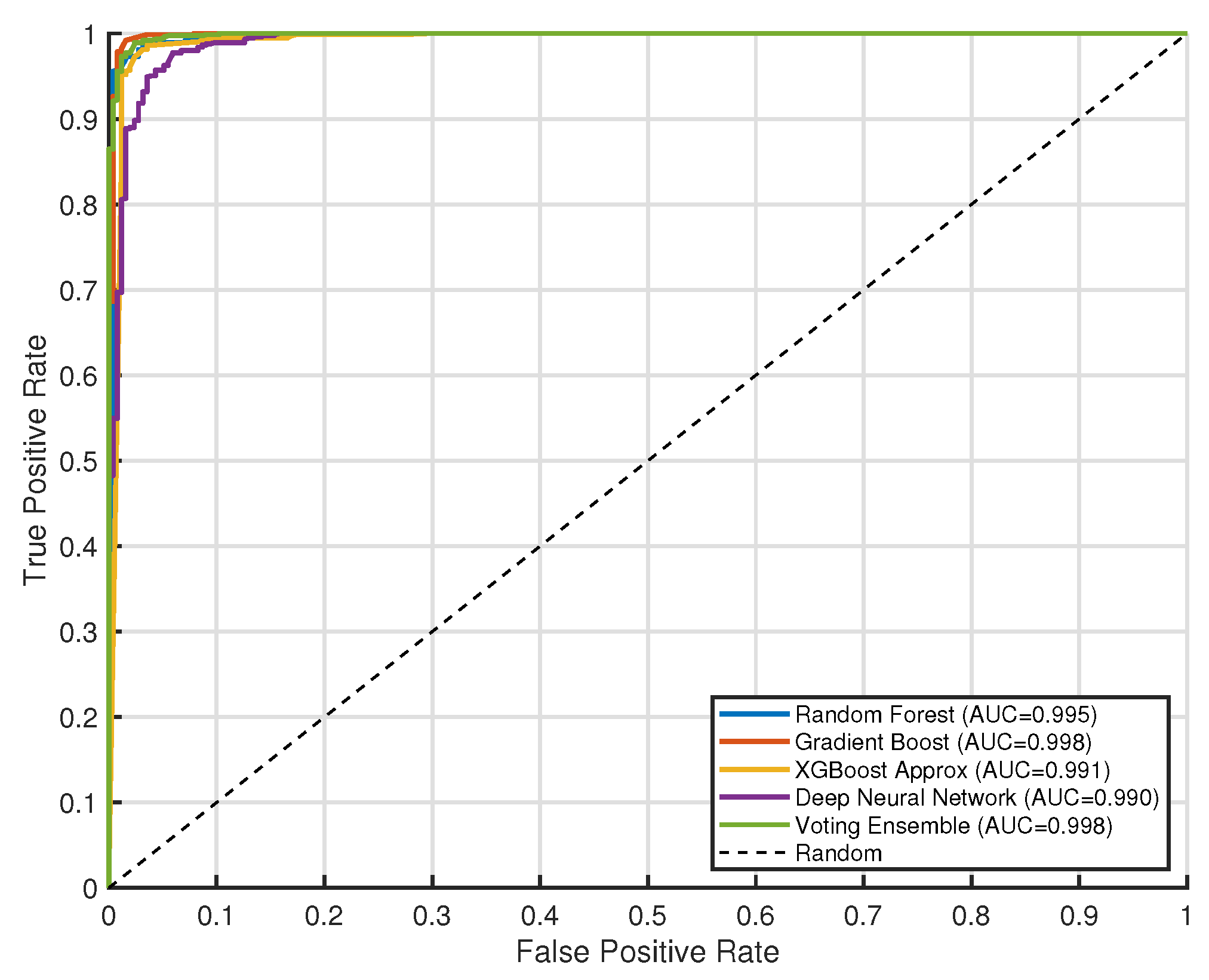
4. Machine Learning Models
4.1. Random Forest
4.2. Gradient Boost
4.3. XGBoost Approx
4.4. Deep Neural Network
4.5. Voting Ensemble
5. Fractional-Order Modeling
6. Numerical Method for the Fractional-Order Model
6.1. Predictor-Corrector Method
6.1.1. Predictor Step
6.1.2. Corrector Step
6.2. Numerical Stability and Constraints
6.2.1. Normalization of Features
- Uniform Scale: Normalization enables features with different units and ranges (Age in years, Scaling as a severity score) to be modeled on a common scale, ensuring that the coefficients and in the FDE model operate on comparable magnitudes.
- Numerical Stability: By constraining to , the nonlinear terms remain bounded, reducing the risk of numerical overflow or instability in the predictor-corrector method implemented via fde12.
- Physical Relevance: The normalized features represent relative severity or presence within their observed ranges, making the model outputs interpretable as proportions of maximum observed values.
6.2.2. Estimated Values and Ranges
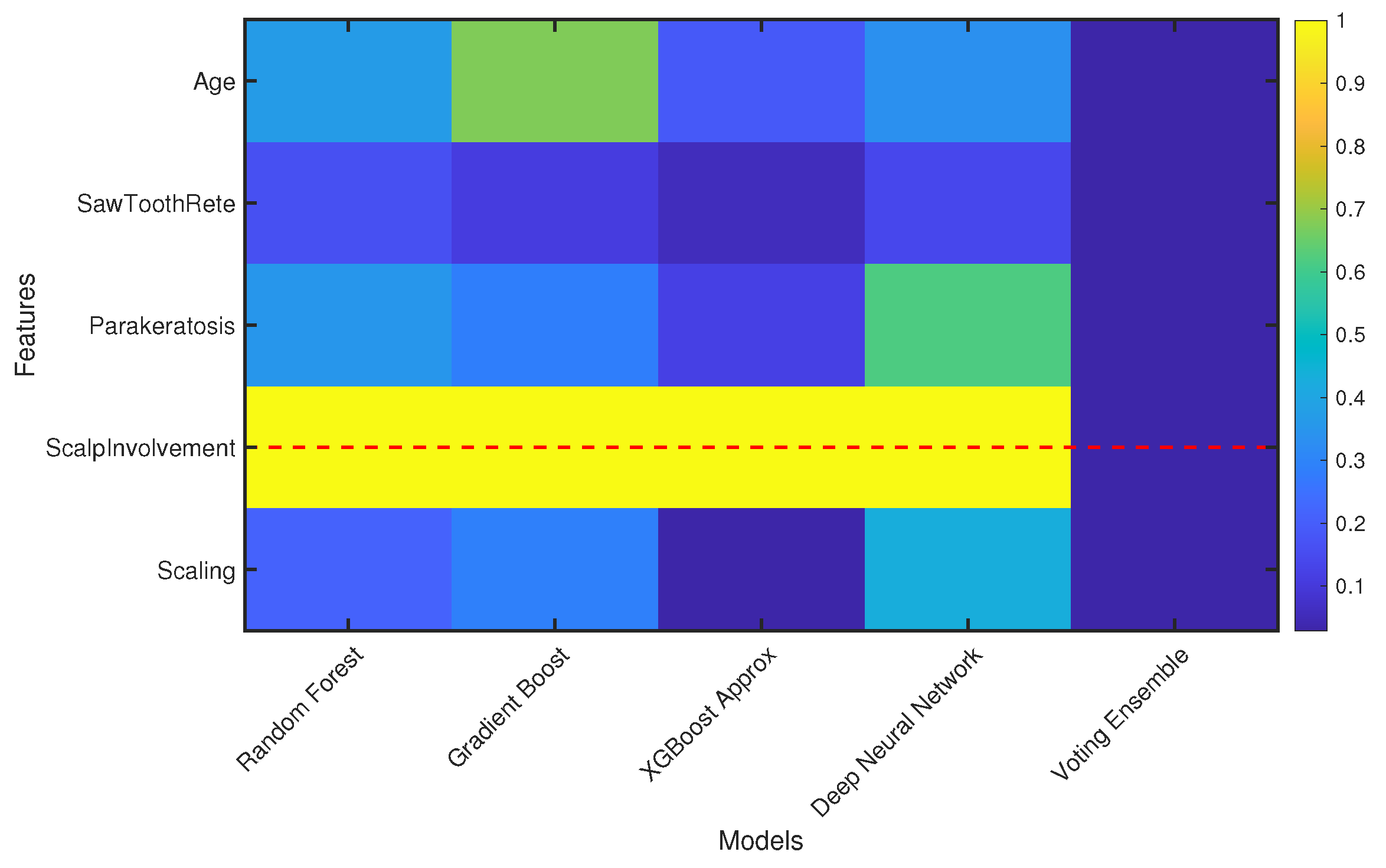
- Feature Selection: Features are selected dynamically using MRMR, prioritizing relevance to psoriasis classification. The table lists the variables as placeholders, as actual features depend on the dataset and MRMR scores.
- Raw Ranges: Ranges are derived from the dataset after preprocessing. Age typically spans 0 to 100 years, while most clinical features (Scaling, Erythema, Parakeratosis, Scalp Involvement) are scored from 0 to 3 based on clinical grading in the UCI Dermatology Dataset.
- Normalization: Each feature is normalized using the min-max formula. For example, an Age of 50 years maps to if the range is . A Scaling score of 1.5 maps to if the range is .
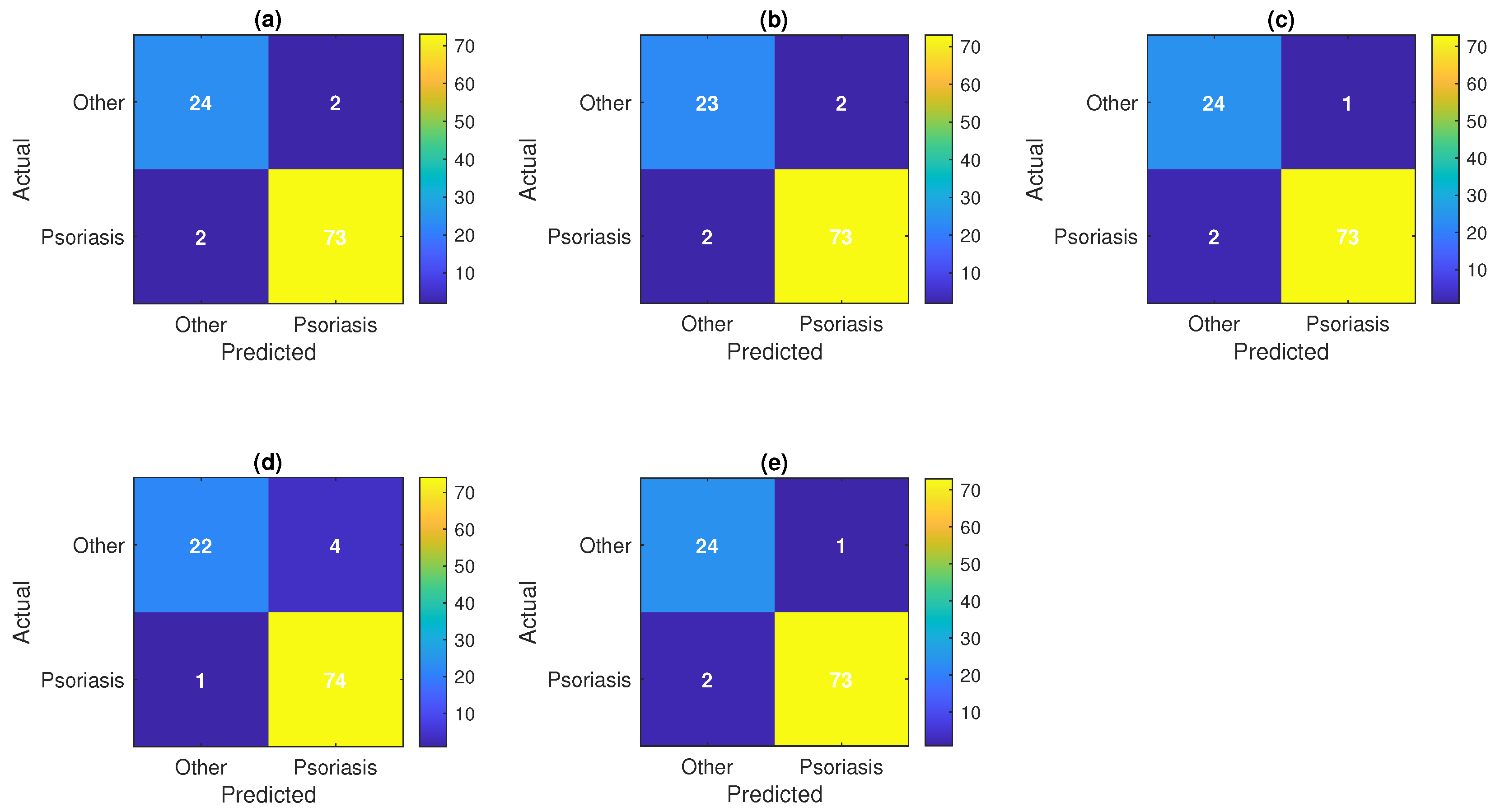
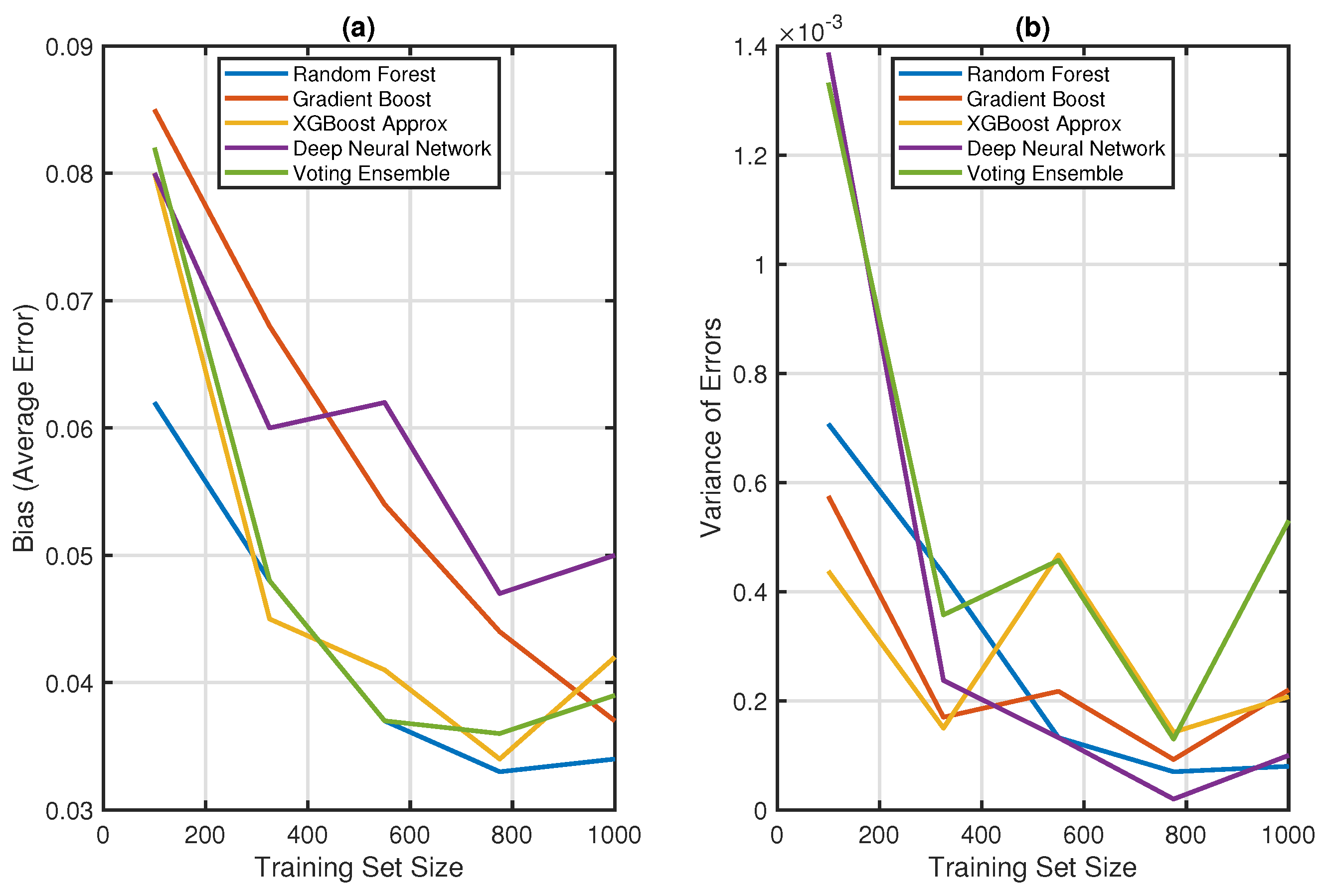
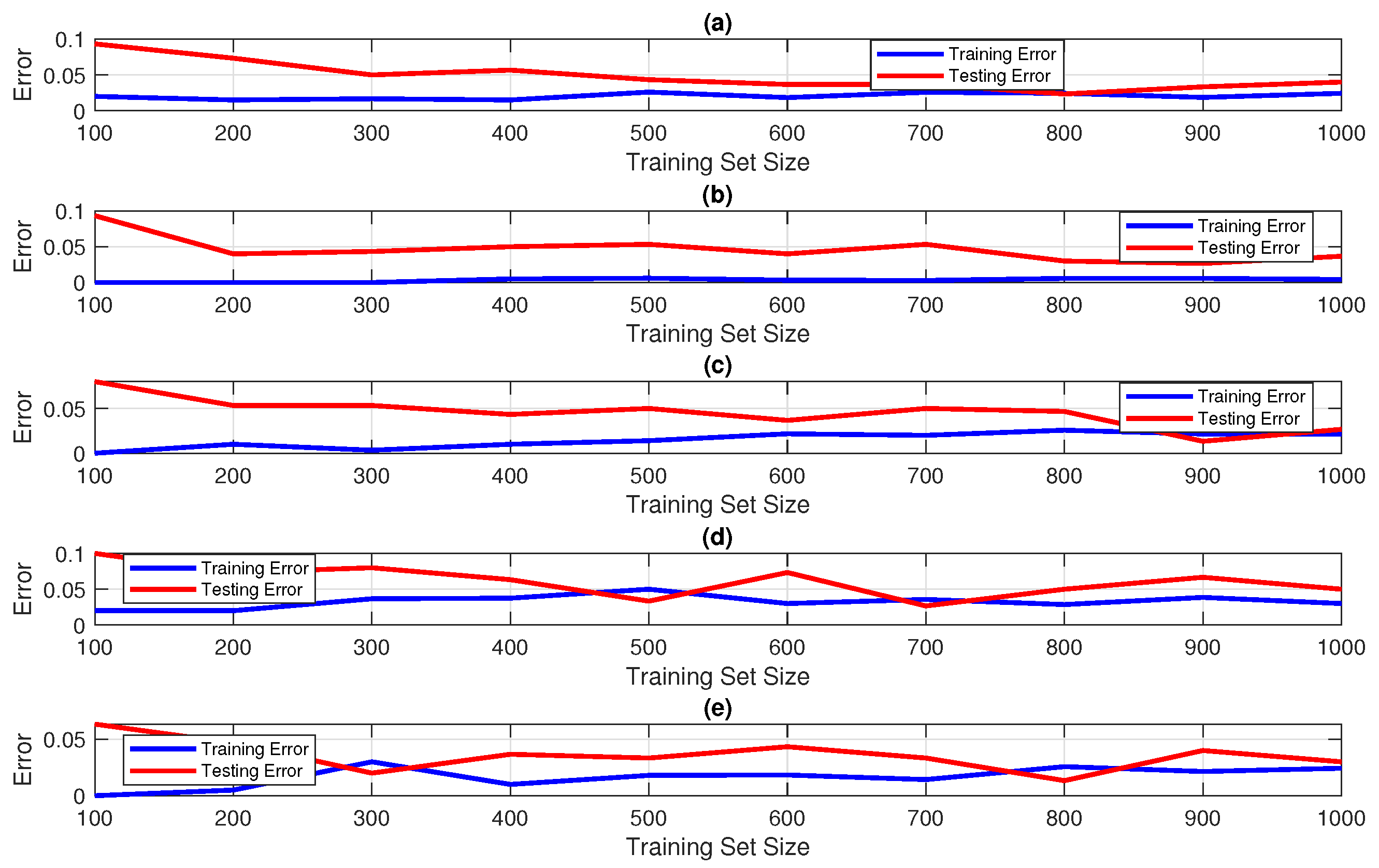
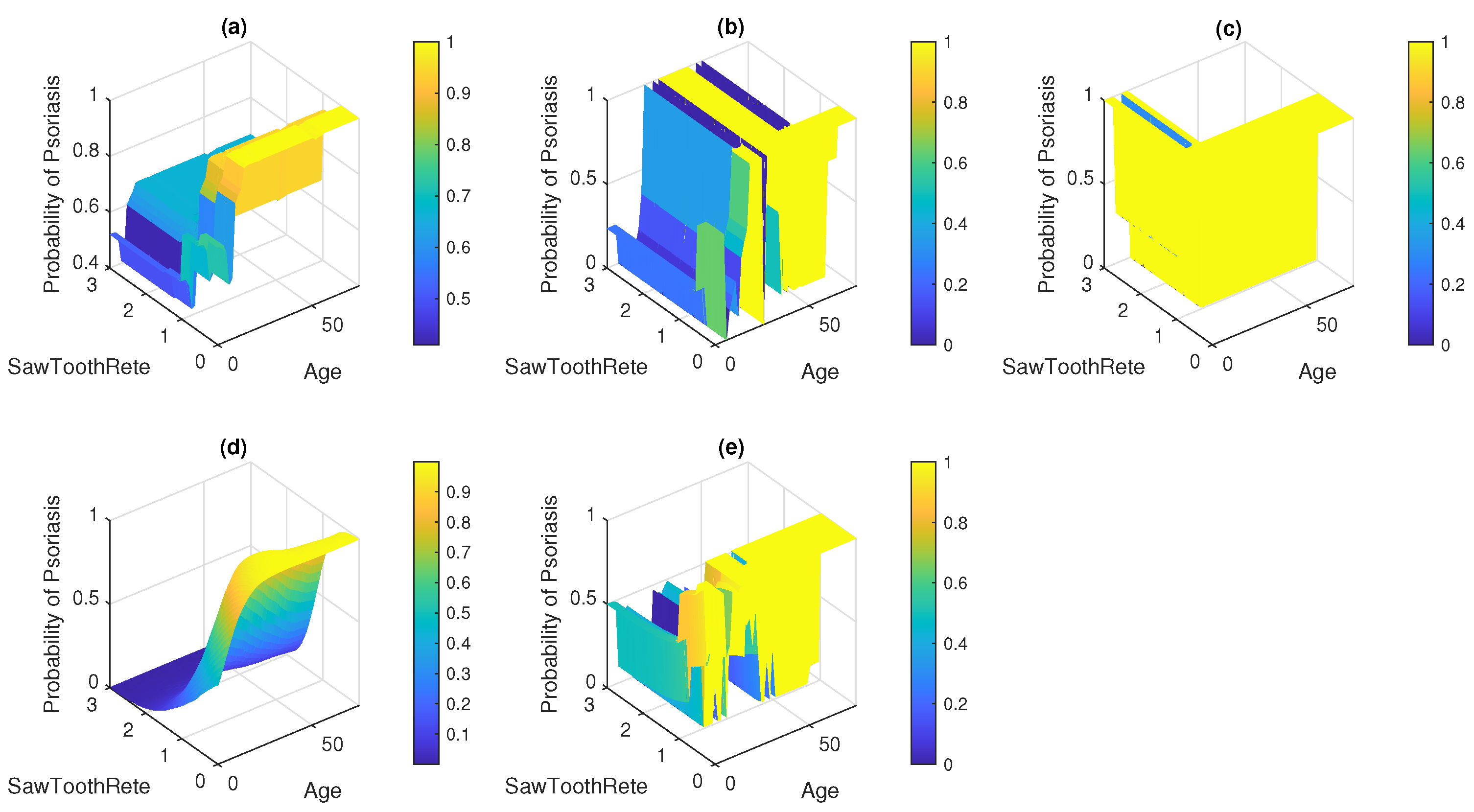
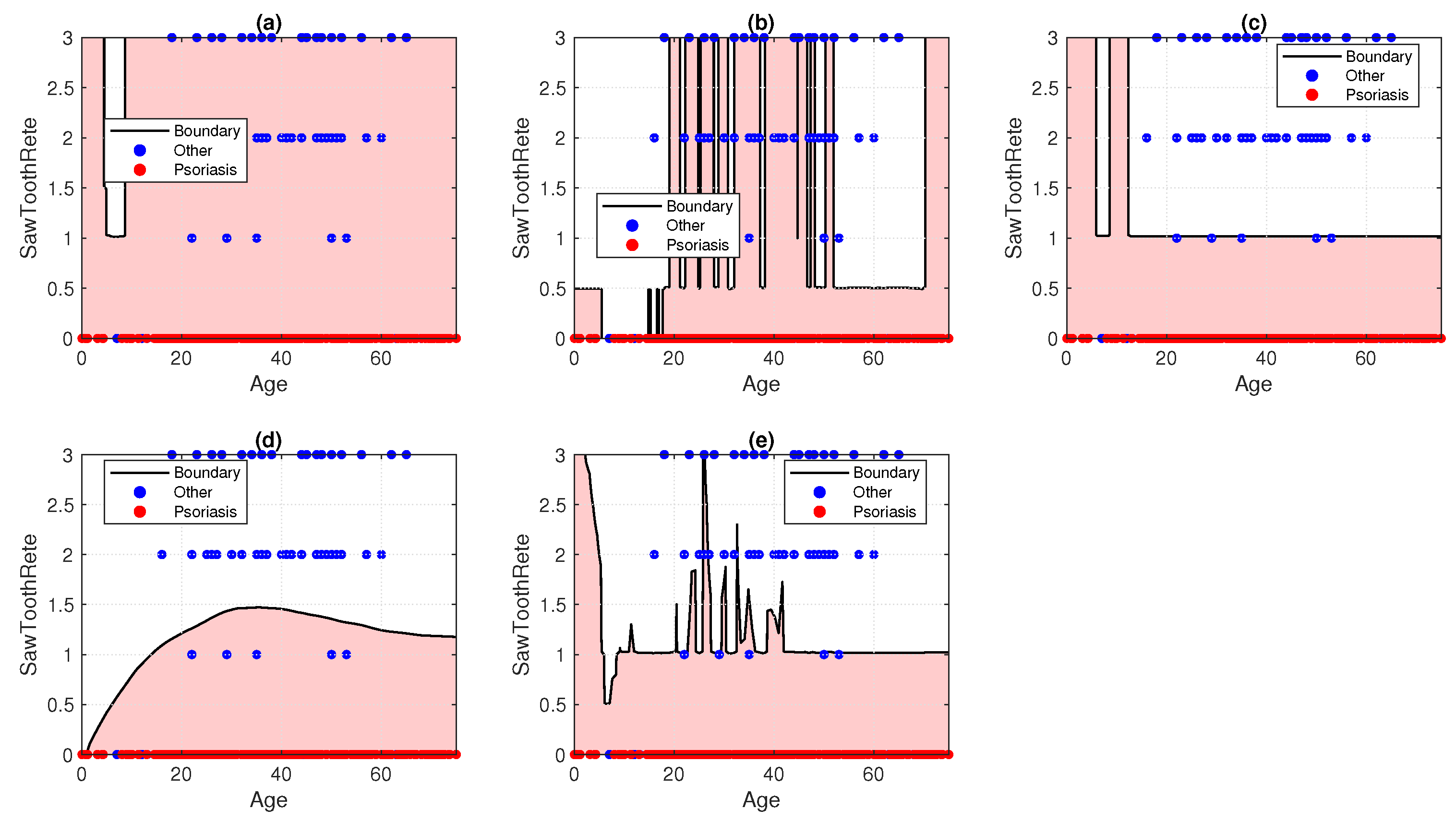
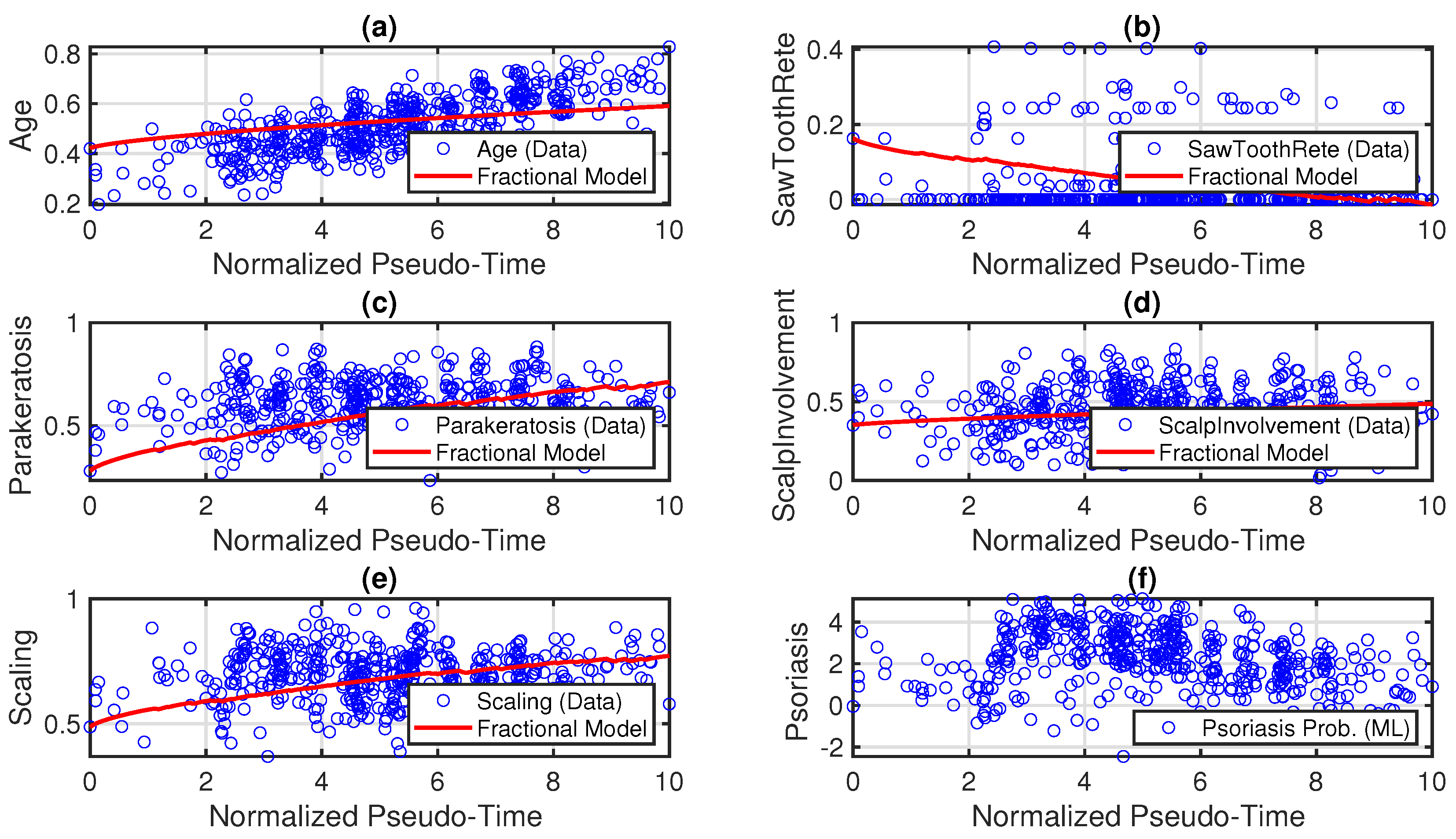
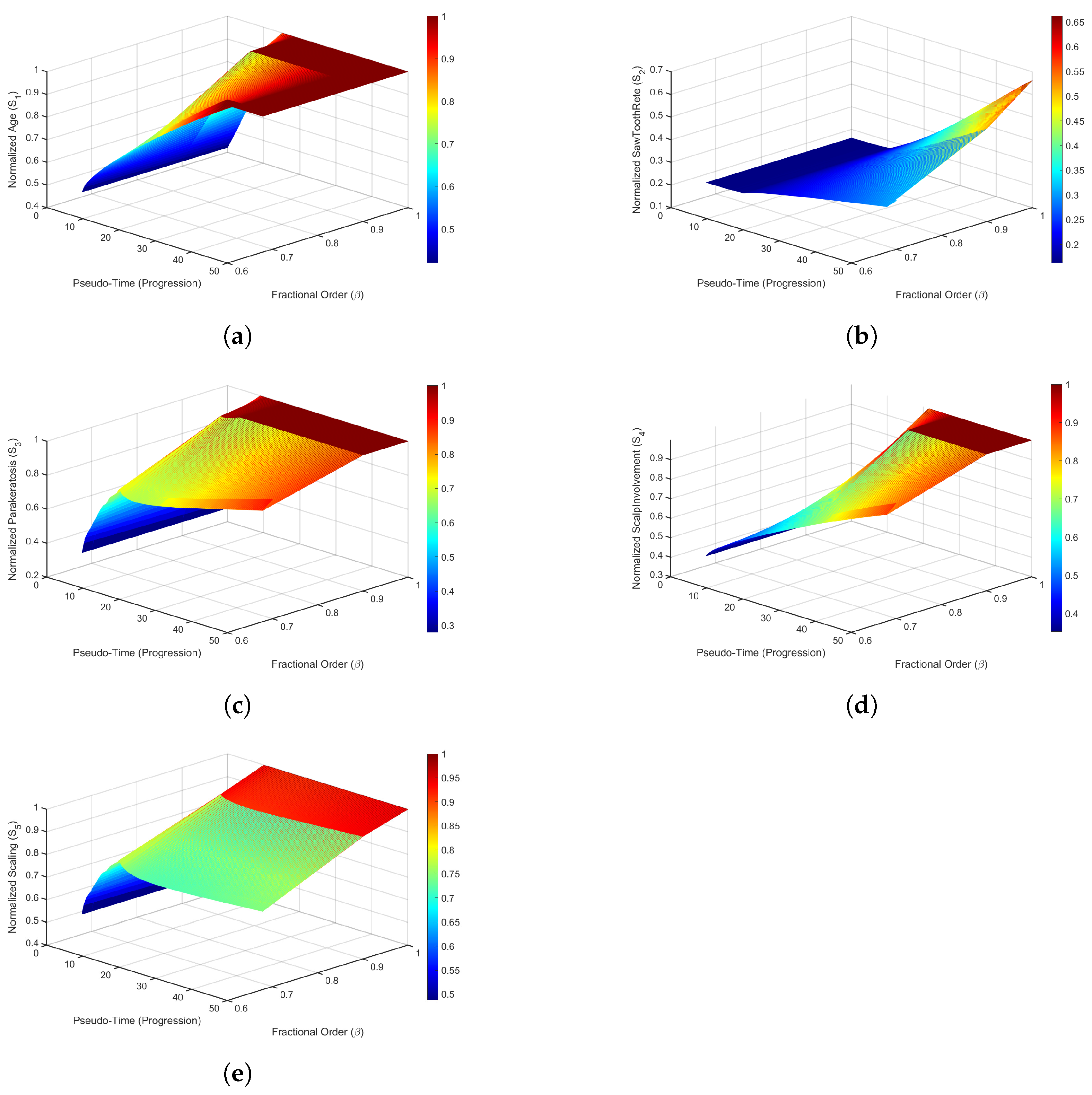
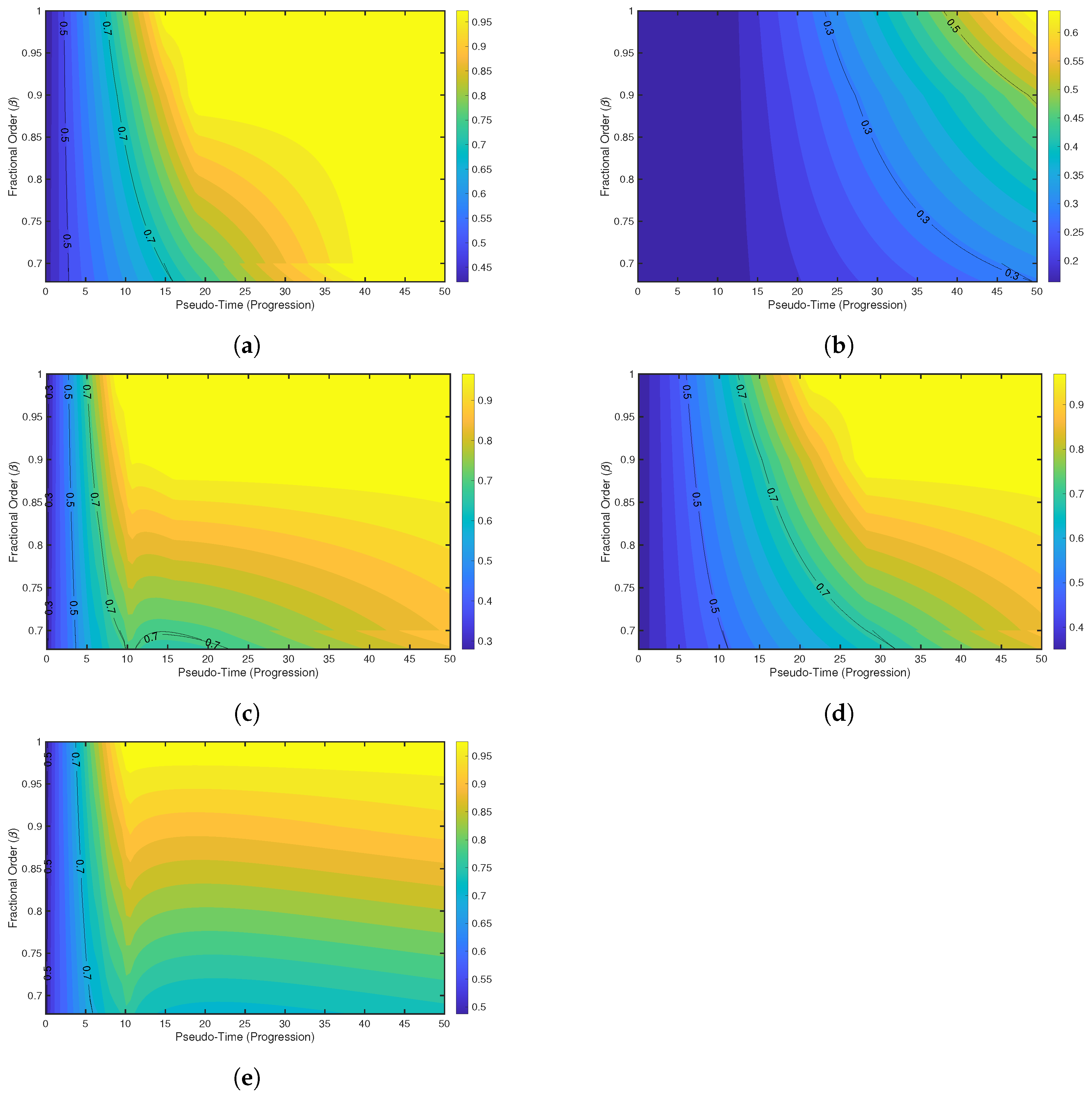
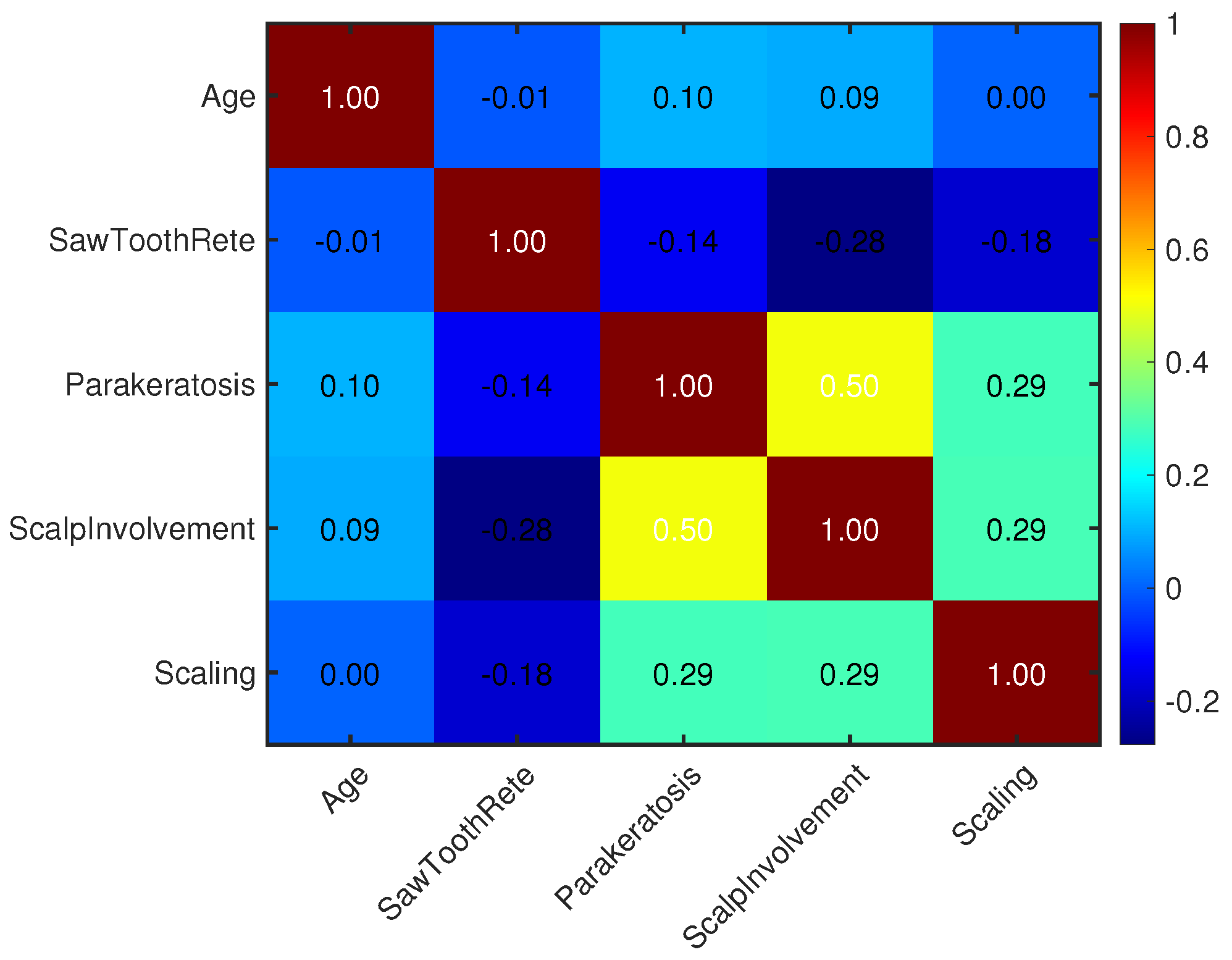
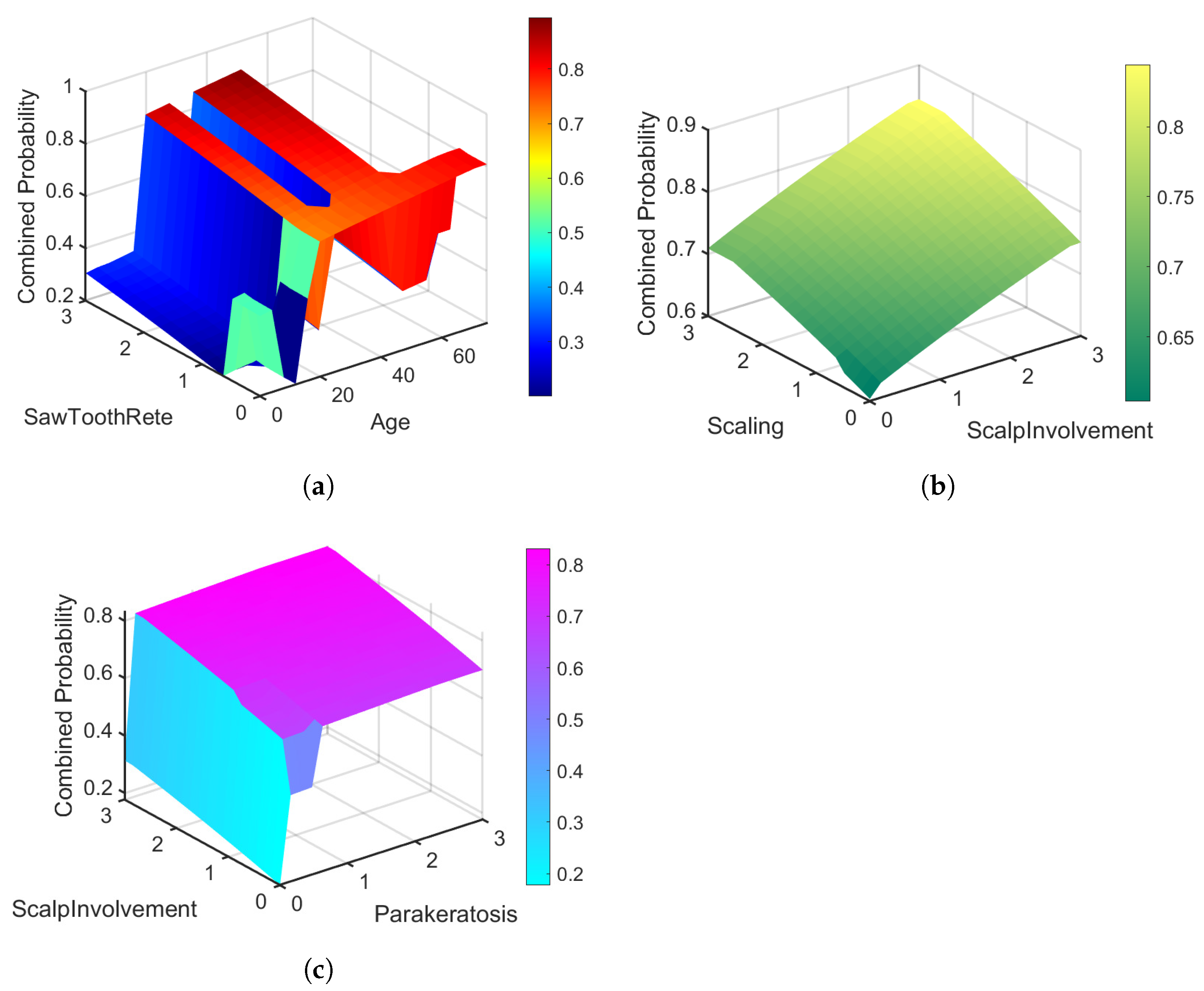
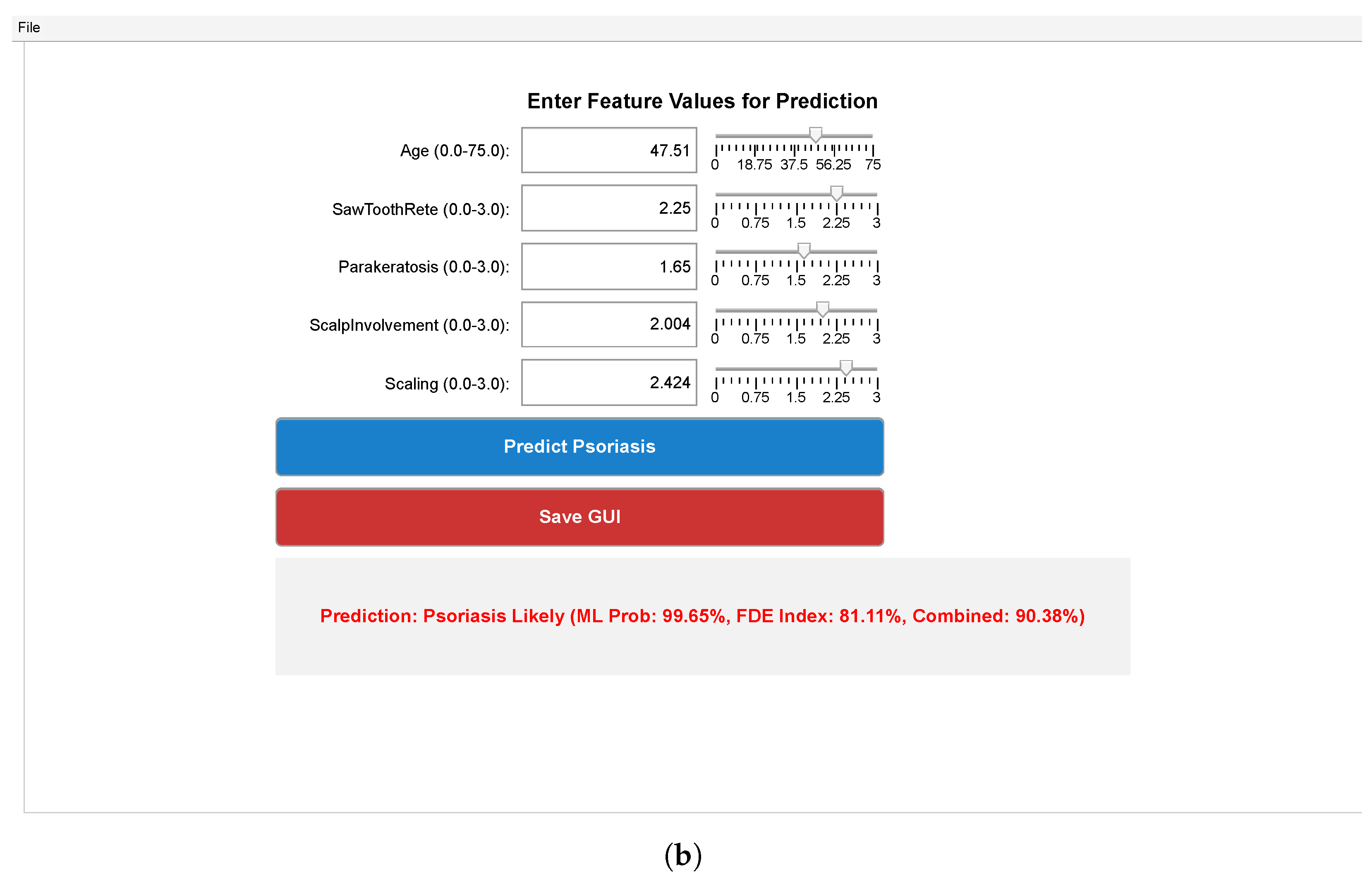
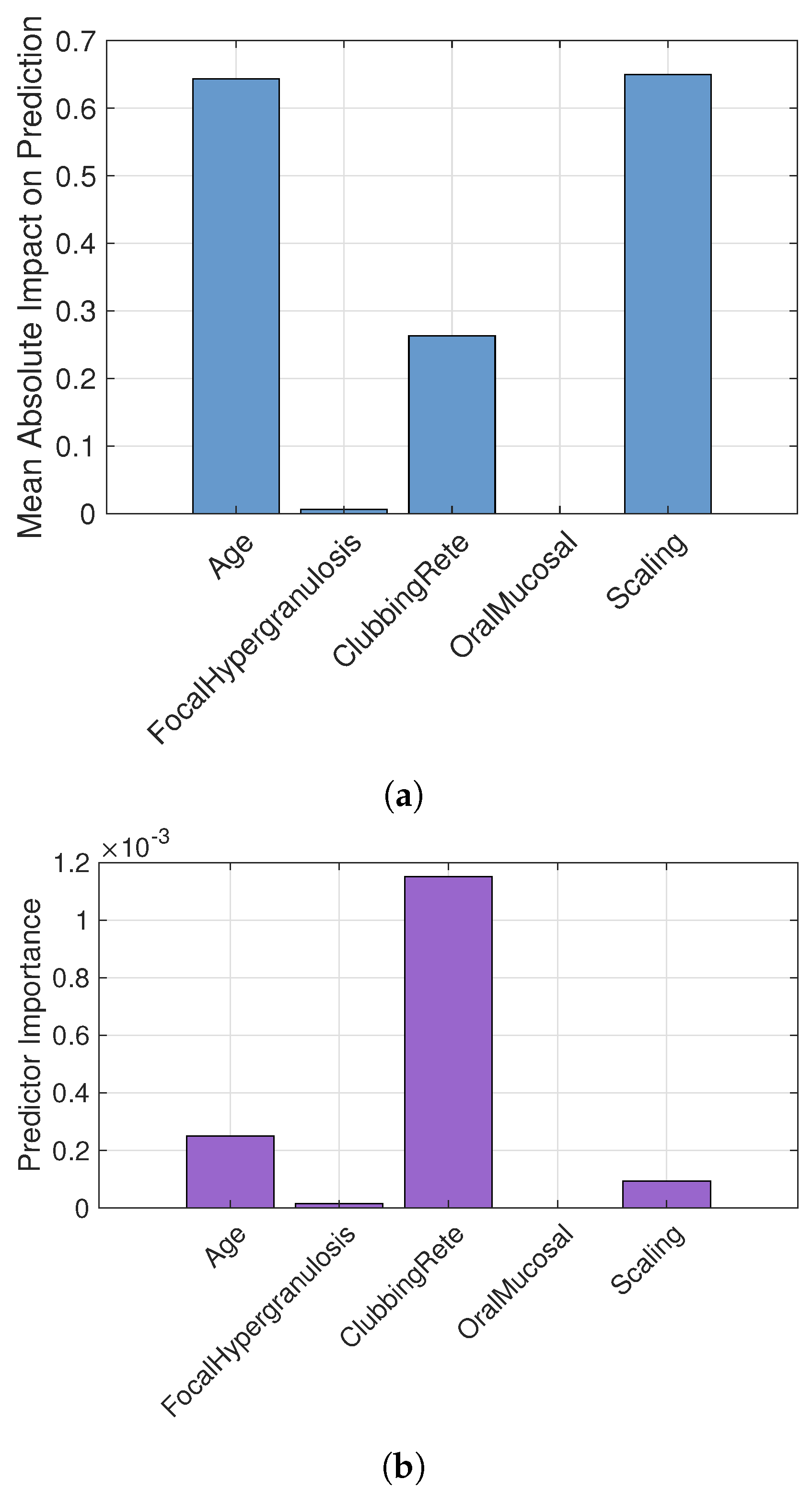
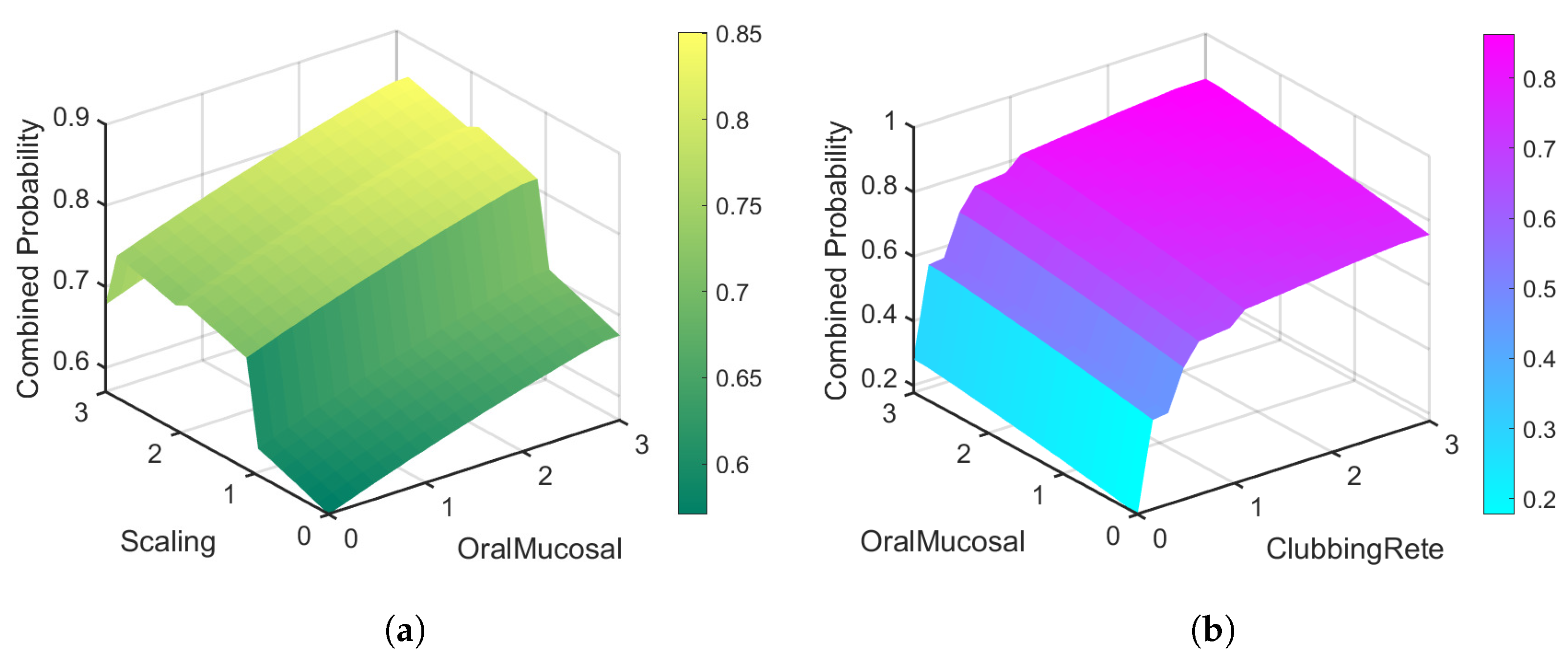
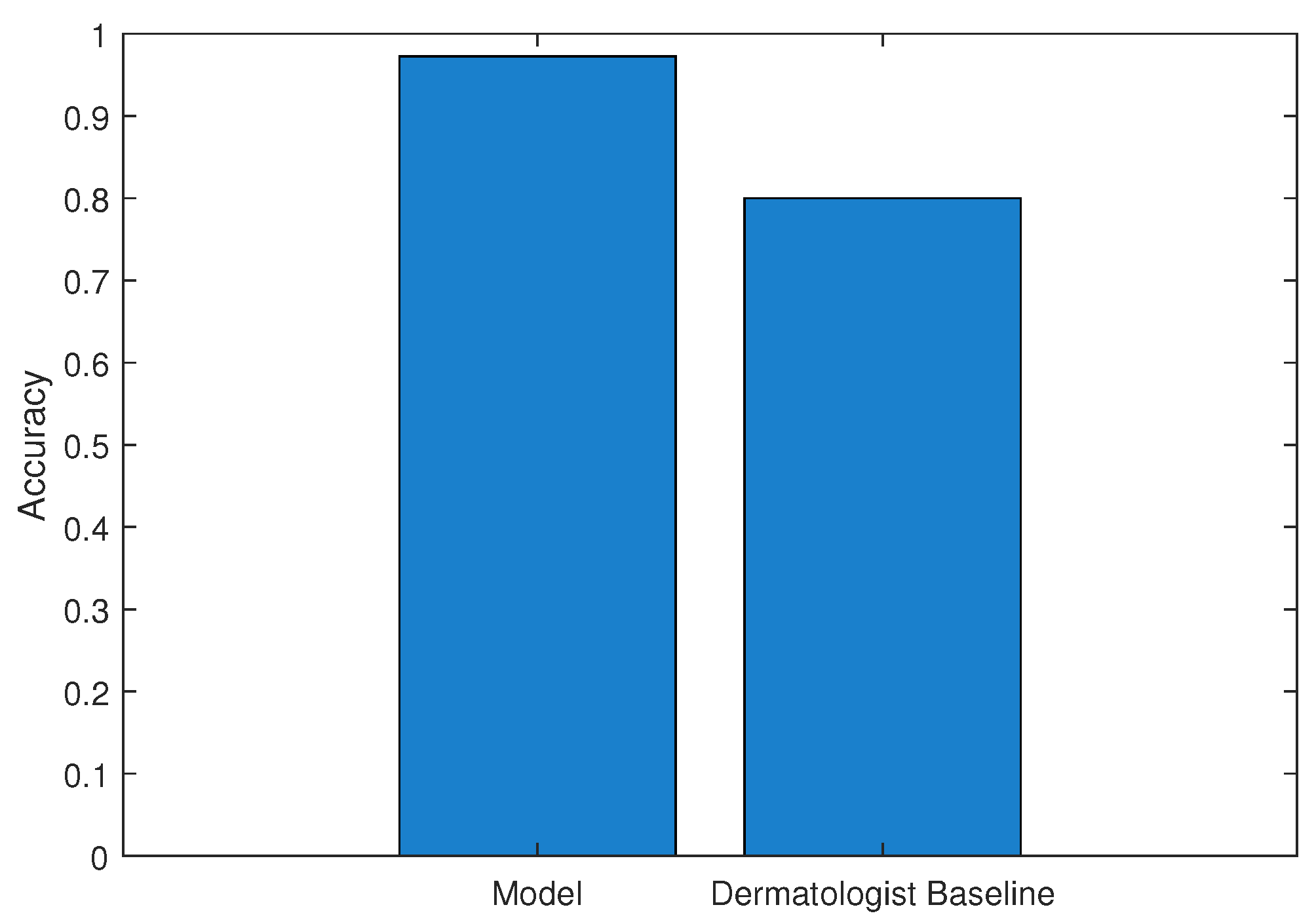
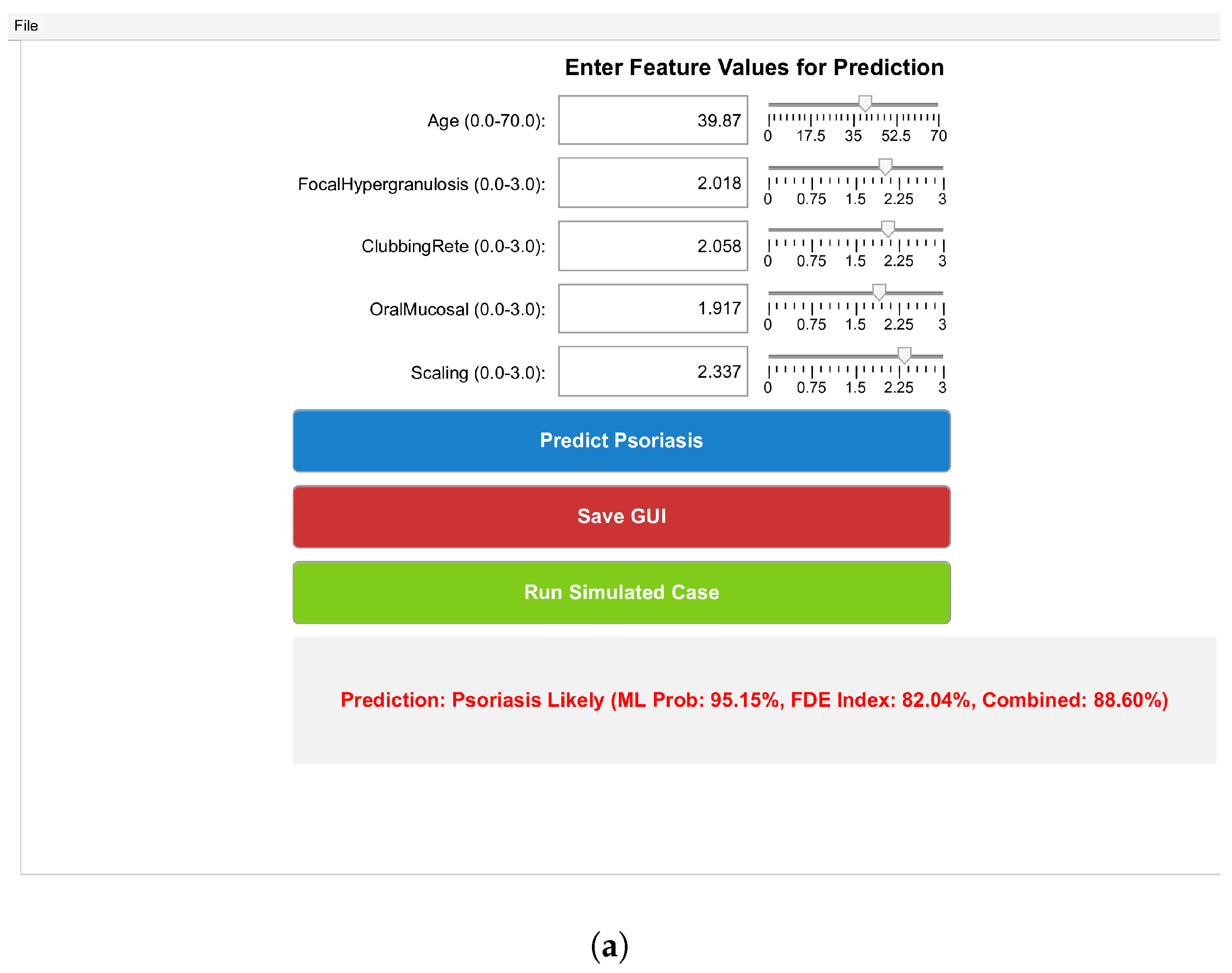
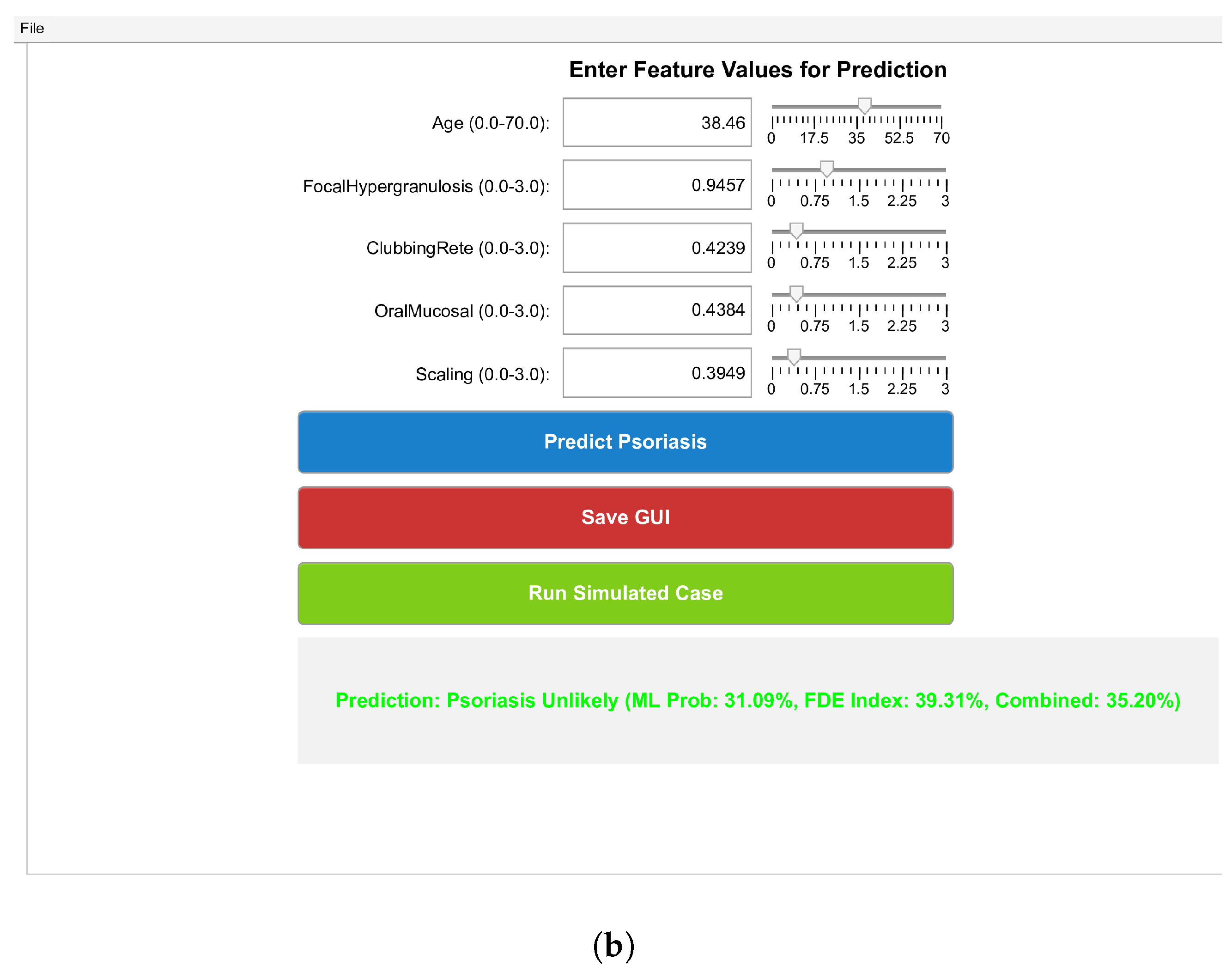
7. Result and Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Alsararatee, H.H. Diagnostic tools and methods for dermatological assessment. Br. J. Nurs. 2025, 34, 502–512. [Google Scholar] [CrossRef] [PubMed]
- Patra, P.; Harrison, T.; Khoury, M. Challenges in diagnosis and treatment of pediatric psoriasis and atopic dermatitis. Arch. Dermatol. Res. 2025, 317, 393. [Google Scholar] [CrossRef]
- Lakum, M. The Hidden Struggle: Understanding the Psychosocial Impact of Dermatological Diseases. Indian J. Postgrad. Dermatol. 2024, 2, 74–79. [Google Scholar] [CrossRef]
- Parisi, R.; Iskandar, I.Y.; Kontopantelis, E.; Augustin, M.; Griffiths, C.E.; Ashcroft, D.M. National, regional, and worldwide epidemiology of psoriasis: Systematic analysis and modelling study. BMJ 2020, 369, m1590. [Google Scholar] [CrossRef]
- Dairov, A.; Issabekova, A.; Sekenova, A.; Shakhatbayev, M.; Ogay, V. Prevalence, incidence, gender and age distribution, and economic burden of psoriasis worldwide and in Kazakhstan. J. Clin. Med. Kazakhstan 2024, 21, 18–30. [Google Scholar] [CrossRef]
- Amiri, F.; Safiri, S.; Aletaha, R.; Mousavi, S.E.; Sullman, M.J.; Houshyar, Y.; Kolahi, A.-A.; Arshi, S. The Burden of Viral Skin Diseases in the Middle East and North Africa Region, 1990–2021. J. Infect. Public Health 2025, 18, 102784. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Figueras, M.T.; Puig, L. Histopathological diagnosis of psoriasis and psoriasiform dermatitides. Diagn. Histopathol. 2025, 31, 87–97. [Google Scholar] [CrossRef]
- Shehzadi, N.; Rehman, A.; Naz, S.; Rehman, S.; Khalifa, F. Machine learning and deep learning based psoriasis recognition system: Evaluation, management, prognosis—Where we are and the way to the future. Artif. Intell. Rev. 2025, 58, 263. [Google Scholar] [CrossRef]
- Khokhar, M.; Yadav, D.; Sharma, P. Transforming healthcare in the age of artificial intelligence: A new era of diagnostic excellence in laboratory medicine. Indian J. Clin. Biochem. 2025, 40, 163–164. [Google Scholar] [CrossRef] [PubMed]
- Sarker, M. Revolutionizing healthcare: The role of machine learning in the health sector. J. Artif. Intell. Gen. Sci. (JAIGS) 2024, 2, 36–61. [Google Scholar] [CrossRef]
- Hanna, M.G.; Pantanowitz, L.; Dash, R.; Harrison, J.H.; Deebajah, M.; Pantanowitz, J.; Rashidi, H.H. Future of artificial intelligence (AI)-machine learning (ML) trends in pathology and medicine. Mod. Pathol. 2025, 38, 100705. [Google Scholar] [CrossRef]
- AlSuwaidan, L. Deep learning based classification of dermatological disorders. Biomed. Eng. Comput. Biol. 2023, 14, 11795972221138470. [Google Scholar] [CrossRef]
- Virgens, G.S.; Teodoro, J.A.; Iarussi, E.; Rodrigues, T.; Amaral, D.T. Enhancing and advancements in deep learning for melanoma detection: A comprehensive review. Comput. Biol. Med. 2025, 194, 110533. [Google Scholar] [CrossRef]
- Sugiman, S.; Salman, S.; Catur, A.D.; Asmara, Y.P. Modelling the flexural properties of filled epoxy: Effects of volume fraction. E3s Web Conf. 2023, 465, 01028. [Google Scholar] [CrossRef]
- Dewi, D.A.; Thinakan, R.; Batumalay, M.; Kurniawan, T.B. A model for pervasive computing and wearable devices for sustainable healthcare applications. Int. J. Adv. Comput. Sci. Appl. 2023, 14, 527–530. [Google Scholar] [CrossRef]
- Acay, B.; Inc, M.; Khan, A.; Yusuf, A. Fractional methicillin-resistant Staphylococcus aureus infection model under Caputo operator. J. Appl. Math. Comput. 2021, 67, 755–783. [Google Scholar] [CrossRef]
- Karaca, Y. Computational complexity-based fractional-order neural network models for the diagnostic treatments and predictive transdifferentiability of heterogeneous cancer cell propensity. Chaos Theory Appl. 2023, 5, 34–51. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Sher, M.; Shah, K.; Sarwar, M.; Amacha, I.; Alqudah, M.; Al-Jaser, A. Analysis of a class of fractal hybrid fractional differential equation with application to a biological model. Sci. Rep. 2024, 14, 18937. [Google Scholar] [CrossRef] [PubMed]
- Swain, S.; Swain, S.; Panda, B.; Tripathy, M.C. Modeling and optimal analysis of lung cancer cell growth and apoptosis with fractional-order dynamics. Comput. Biol. Med. 2025, 188, 109837. [Google Scholar] [CrossRef] [PubMed]
- Nagpurkar, M.B.; Kachhia, K.B. A novel numerical method for solving fractal-fractional differential equations with exponential memories. J. Appl. Math. Comput. 2025, 71, 1453–1475. [Google Scholar] [CrossRef]
- Saadeh, R.; Abdoon, M.A.; Qazza, A.; Berir, M.; Guma, F.E.; Al-Kuleab, N.; Degoot, A.M. Mathematical modeling and stability analysis of the novel fractional model in the Caputo derivative operator: A case study. Heliyon 2024, 10, e26611. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, R.; Biswas, R.K. Mathematical Model of the Disease Psoriasis: An Optimal Control-Based Approach. In Control and Measurement Applications for Smart Grid: Select Proceedings of SGESC 2021; Springer Nature: Singapore, 2022; pp. 167–178. [Google Scholar] [CrossRef]
- Cao, X.; Datta, A.; Al Basir, F.; Roy, P.K. Fractional-order model of the disease psoriasis: A control based mathematical approach. J. Syst. Sci. Complex. 2016, 29, 1565–1584. [Google Scholar] [CrossRef]
- Roy, P.K.; Datta, A. Mathematical Models for Therapeutic Approaches to Control Psoriasis; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Singh, A.; Chavada, A.; Pathak, N. Fractional Calculus Approach to Pancreatic Cancer Therapy: Modeling Tumor and Immune Interactions with siRNA Treatment. Int. J. Appl. Comput. Math. 2025, 11, 61. [Google Scholar] [CrossRef]
- Ahmed, S.; Ullah, S.; Riaz, M.; Ahmed, W.; Sheikh, M. Numerical Analysis of Fractional Logistic Growth Models Using Computational Methods with MATLAB Codes. Int. J. Appl. Comput. Math. 2025, 11, 198. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, X.; Cui, Z. Primary resonance analysis of a novel fractional-order coronary artery model. Aims Math. 2025, 10, 14996–15011. [Google Scholar] [CrossRef]
- Amilo, D.; Sadri, K.; Hincal, E.; Farman, M.; Nisar, K.S. Dual approach artificial neural networks-fractional order operator to enhancing in vitro fertilization predictions and success measure. Model. Earth Syst. Environ. 2025, 11, 281. [Google Scholar] [CrossRef]
- Amilo, D.; Sadri, K.; Hincal, E. A hybrid approach to heart disease prediction using a fractional-order mathematical model and machine learning algorithm. Comput. Methods Biomech. Biomed. Eng. 2025, 1–30. [Google Scholar] [CrossRef]
- Amilo, D.; Sadri, K.; Hincal, E.; Farman, M.; Nisar, K.S.; Hafez, M. An integrated machine learning and fractional calculus approach to predicting diabetes risk in women. Healthc. Anal. 2025, 8, 100402. [Google Scholar] [CrossRef]
- Debelee, T.G. Skin lesion classification and detection using machine learning techniques: A systematic review. Diagnostics 2023, 13, 3147. [Google Scholar] [CrossRef]
- Raman, R.; Kumar, V.; Saini, D.; Rabadiya, D.; Patre, S.; Meenakshi, R. Machine Learning-Driven Approaches for Dermatological Disease Diagnosis. In Proceedings of the 2024 International Conference on Data Science and Network Security (ICDSNS), Tiptur, India, 26–27 July 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Amini, M.; Vatankhah, R. The Effect of Disease Stage on Melanoma Treatment Efficacy: Insights from Mathematical Modeling and In vivo Clinical Data. Bull. Math. Biol. 2025, 87, 90. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, G.; Silva, J.; Santurio, D.S.; Mancera, P.F.A. A mathematical model to describe the melanoma dynamics under effects of macrophage inhibition and car t-cell therapy. Trends Comput. Appl. Math. 2024, 25, e01734. [Google Scholar] [CrossRef]
- Ilter, N.; Guvenir, H. Dermatology [Dataset]; UCI Machine Learning Repository: 1998. Available online: https://archive.ics.uci.edu/dataset/33/dermatology (accessed on 10 October 2025).
- Abu-Shady, M.; Kaabar, M.K. A generalized definition of the fractional derivative with applications. Math. Probl. Eng. 2021, 2021, 9444803. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Number of Instances | 366 |
| Number of Attributes | 34 |
| Number of Classes | 6 |
| Class Distribution (Psoriasis) | 30.60% |
| Oversampled Instances | 1000 |
| Top Selected Features | 5 |
| Feature Names | Age, SawToothRete, Parakeratosis, Scalp Involvement, Scaling |
| Missing Values | Handled by median imputation |
| Dataset Source | UCI Dermatology Dataset [35] |
| Feature | State | Typical Raw Range | Normalized Range |
|---|---|---|---|
| Age | |||
| Scaling | |||
| Erythema | |||
| Parakeratosis | |||
| Scalp Involvement |
| Model | Accuracy | Precision | Recall | F1 Score | AUC |
|---|---|---|---|---|---|
| XGBoost Approx | 0.972 ± 0.010 | 0.984 ± 0.008 | 0.979 ± 0.009 | 0.981 ± 0.007 | 0.984 ± 0.006 |
| Voting Ensemble | 0.969 ± 0.012 | 0.986 ± 0.007 | 0.972 ± 0.011 | 0.979 ± 0.008 | 0.992 ± 0.005 |
| Random Forest | 0.968 ± 0.011 | 0.977 ± 0.009 | 0.980 ± 0.008 | 0.979 ± 0.007 | 0.986 ± 0.006 |
| Gradient Boost | 0.957 ± 0.013 | 0.969 ± 0.010 | 0.973 ± 0.009 | 0.971 ± 0.008 | 0.974 ± 0.007 |
| Deep Neural Network | 0.955 ± 0.015 | 0.952 ± 0.012 | 0.989 ± 0.006 | 0.970 ± 0.009 | 0.975 ± 0.008 |
| Symbol | Description |
|---|---|
| Normalized Age feature | |
| Normalized SawToothRete feature | |
| Normalized Parakeratosis feature | |
| Normalized Scalp Involvement feature | |
| Normalized Scaling feature | |
| Machine learning-predicted psoriasis probability at pseudo-time t | |
| Growth rates for each state variable (dimensionless) | |
| Coupling coefficient from to (dimensionless) | |
| Coupling coefficient from to (dimensionless) | |
| Coupling coefficient from to (dimensionless) | |
| Coupling coefficient from to (dimensionless) | |
| Coupling coefficient from to (dimensionless) | |
| Coupling coefficient from to (dimensionless) | |
| Coupling coefficient from to (dimensionless) | |
| Fractional order of the derivative (between 0 and 1) |
| Property | Value |
|---|---|
| Dataset Size (Original) | 366 samples, 34 features |
| Class Distribution | 30.60% psoriasis cases |
| Dataset Size (After Oversampling) | 1000 instances |
| Selected Features | Age, SawToothRete, Parakeratosis, Scalp Involvement, Scaling |
| Iterations | 54 |
| Function Evaluations | 774 |
| Function Evaluations | 774 |
| Final Objective Value (Fval) | |
| Feasibility | |
| Final Step Length | |
| Final Norm of Step | |
| Final First-order Optimality | |
| Stopping Criteria | Step size tolerance satisfied, constraints met |
| Optimized Parameter g | [0.0500, 0.0500, 0.0500, 0.0500, 0.0500] |
| Optimized Parameter c | [0.0413, –0.0423, 0.0684, 0.0252, 0.0509, 0.0012, 0.0280] |
| Optimized Parameter | 0.6781 |
| Minimum Cost (Weighted MSE) | 0.0031 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amilo, D.; Sadri, K.; Hincal, E.; Hafez, M. Integrating Machine Learning and Fractional-Order Dynamics for Enhanced Psoriasis Prediction and Clinical Decision Support. AppliedMath 2025, 5, 143. https://doi.org/10.3390/appliedmath5040143
Amilo D, Sadri K, Hincal E, Hafez M. Integrating Machine Learning and Fractional-Order Dynamics for Enhanced Psoriasis Prediction and Clinical Decision Support. AppliedMath. 2025; 5(4):143. https://doi.org/10.3390/appliedmath5040143
Chicago/Turabian StyleAmilo, David, Khadijeh Sadri, Evren Hincal, and Mohamed Hafez. 2025. "Integrating Machine Learning and Fractional-Order Dynamics for Enhanced Psoriasis Prediction and Clinical Decision Support" AppliedMath 5, no. 4: 143. https://doi.org/10.3390/appliedmath5040143
APA StyleAmilo, D., Sadri, K., Hincal, E., & Hafez, M. (2025). Integrating Machine Learning and Fractional-Order Dynamics for Enhanced Psoriasis Prediction and Clinical Decision Support. AppliedMath, 5(4), 143. https://doi.org/10.3390/appliedmath5040143







