Abstract
The proposed study explores the consistency of the geometrical character of surfaces under scaling, rotation and translation. In addition to its mathematical significance, it also exhibits advantages over image processing and economic applications. In this paper, the authors used partition-based principal component analysis similar to two-dimensional Sub-Image Principal Component Analysis (SIMPCA), along with a suitably modified atypical wavelet transform in the classification of 2D images. The proposed framework is further extended to three-dimensional objects using machine learning classifiers. To strengthen fairness, we benchmarked against both Random Forest (RF) and Support Vector Machine (SVM) classifiers using nested cross-validation, showing consistent gains when TIFV is included. In addition, we carried out a robustness analysis by introducing Gaussian noise to the intensity channel, confirming that TIFV degrades much more gracefully compared to traditional descriptors. Experimental results demonstrate that the method achieves improved performance compared to traditional hand-crafted descriptors such as measured values and histogram of oriented gradients. In addition, it is found to be useful that this proposed algorithm is capable of establishing consistency locally, which is never possible without partition. However, a reasonable amount of computational complexity is reduced. We note that comparisons with deep learning baselines are beyond the scope of this study, and our contribution is positioned within the domain of interpretable, affine-invariant descriptors that enhance classical machine learning pipelines.
1. Introduction
The consistency of the geometry of various space curves and surfaces under some affine transformations is mathematically intriguing despite the simplicity in nature of such surfaces. In continuation of earlier attempts with respect to the aforementioned characters over the transformation—namely, scaling, rotation and translation [1,2,3]—recent developments in Principal Component Analysis (PCA) [4,5,6,7,8] convinced the authors to conduct this study using recent techniques of PCA. We briefly present a literature review on the invariance property of curves and surfaces, along with recent PCA results, for the sake of the readers. Freudenstein, McGarva, Sun, Wu, Yue and Uesaka [9,10,11,12,13,14,15] have studied the geometrical consistency of curves in discussed harmonic terms related to the four-bar linkage mechanism. Due to certain limitations [16,17] in using Fourier coefficients on open curves, Liu et al. [1,18] introduced wavelet coefficient descriptors for such non periodic curves. However, independent studies on curves that are not associated with a four-bar linkage mechanism have been conducted by Hung et al. and Teing et al. [19,20]. In this sequence of attempts, Vignesh and Palanisamy derived invariant features of plane and space curves [2,3] using atypical wavelet coefficients. It is significant to state that such studies on the geometrical consistency of curves are found to be employed in problems of image classification, economics and shape interrogation. In recent years, deep learning methods, particularly Convolutional Neural Networks (CNNs), have become the dominant paradigm for image classification due to their ability to automatically learn hierarchical features from raw images [21,22,23]. Notable architectures such as AlexNet [21], ResNet [22] and Inception-v3 [23] have demonstrated remarkable performance across various domains, including medical imaging, remote sensing and general object recognition [21,22,23]. However, these methods often require large labeled datasets and significant computational resources [22,23]. In contrast, handcrafted feature extraction remains relevant, especially in scenarios with limited data or the need for model interpretability [24]. Studies have shown that handcrafted features can outperform CNNs in small-sample settings and offer increased interpretability [24]. Our work explores this alternative approach, focusing on novel, hand-crafted invariant features that capture geometric and structural properties of shapes, providing complementary insights and potentially interpretable features that are robust under affine transformations.
Numerous studies have also been conducted on the geometrical consistency of surfaces, as reported by Figueroa et al., Montaldo, Onnis and Aydin [25,26,27,28,29,30,31]. Below, we present significant studies on the invariance of surfaces. Figueroa et al. [27] investigated the classification problem as it relates to mean curvature surfaces that are invariant with respect to one-dimensional closed subgroups using a left-invariant metric (g) in the Heisenberg group. Montaldo and Onnis [28] studied invariance properties of surfaces under the composition of translations along R and rotations and, hence, classified helicoidal and translational constant mean curvature surfaces. The profile curves of invariant surfaces over the action of a one-parameter subgroup of isometries were classified by Onnis [29]. The invariance property of surfaces over the action of a one-parameter subgroup constituted by a three-dimensional manifold of constant Gaussian curvature was determined by Montaldo and Onnis using reduction procedure [30]. Translated surfaces with constant curvature produced in the isotropic three-space using 2D and 3D curves were classified successfully by Aydin [31].
The development of research on PCA has motivated the authors to attempt, SIMPCA, which succeeded in an earlier attempt to establish geometrical consistency. Yang et al. [4] proposed a new PCA strategy known as 2DPCA, which is directly based on 2D images rather than converting them with 1D vectors. Kumar and Negi [8] designed a new algorithm for PCA that partitions each image into sub-images, after which the 2DPCA technique is employed—known as two-dimensional SIMPCA. It works based on local image variation and is found to be an efficient technique for classification problems. These novel algorithms led to Extended Sub Image PCA (ESIMPCA) and Extended Flexible PCA (EFLPCA), as proposed by Tapan Kumar et al. [32]. A vital problem associated with having lesser fewer coefficients under 2DPCA was resolved by Zhang and Zhou using two-directional 2DPCA [6]. Despite various other attempts in this direction by numerous researchers, in our work, we use an algorithm similar to two-dimensional SIMPCA. However, the aim of this article is to establish the consistency of the geometrical characteristics of surfaces using suitably modified atypical wavelet coefficients [2,3] of the two-dimensional SIMPCA obtained from the sample points of the considered surfaces. A parameter from said wavelet coefficients is derived for this purpose, and it is interesting to observe that this parameter plays a crucial role in reasonably reducing the computational complexity of the previous techniques. The rest of the paper is structured as follows. The proposed work is discussed in Section 2. Illustrated examples of the proposed work are presented in Section 3. The classification problem is studied in Section 4. The paper concludes with Section 5.
2. Proposed Work
We intend to explore the consistency of geometrical character under scaling, rotation and translation of surfaces in three-dimensional space. The significance of the proposed work lies in the combination of the principal components of the sample points and the wavelet transform of the resulting principal components. This becomes possible due to the property of PCA that nullifies the effect of rotation, whereas the wavelet transform negates the translation effect. However, we consider the ratio of detailed wavelet coefficients to cancel out the effect of scaling and partition PCA to reduce the computational complexity. For this purpose, we consider as a surface. Let be the collection of sample points of the above surfaces, where i and j are natural numbers, and . Let be a block-wise partition, where , and . Therefore, the size of every partitions is . This results in every partition () being a vector, each of whose components is three-dimensional. Now, for every partition (), we compute the mean vector () for all j and k; then, we define , which is known as the partition covariance matrix. If we denote as the sum of the covariance matrices of all partitions, then . Using diagonalization, we then perform eigenvalue decomposition of , where , and Q = are principal directions. Each partition () is then represented in the principal direction as . The above representation is similar to SIMPCA [6,8,32]. Then, the atypical wavelet transform [2,3] of each partition is denoted by , where W is a wavelet transform matrix of order . Instead of applying a wavelet transform to the entire vector-valued function, we apply wavelet transform to each of the three components independently, after which the components are collected in order.
Let , where S, and M represent the scaling, rotation and translation matrices, respectively [3]. Let be the partition of the transformed surface. Now, we obtain the atypical wavelet transform for the principal component of the above partitions—say, . In fact, the above wavelet transformation can be computed using the wavelet matrix (W) as . In each partition of both the actual and transformed surfaces, the rows leaving the first row correspond to the detailed vector of the wavelet transform. For these rows, we compute the component-wise ratios of all the detailed wavelet vectors relative to those of the last level, detailed vector. Interestingly, these ratios remains the same across the corresponding partitions of both the original and transformed surfaces. This invariance follows from Theorems A1–A3 given in Appendix A, since the resulting principal components of transformed surfaces differ only by scaling and translation. However, the wavelet transform nullifies the translation impact, whereas the ratio of the detailed wavelet coefficients will nullify the scaling effect. Thus, these ratios packed as a vector can be called the Transformation Invariant Feature Vector (TIFV) of any surface.
It is significant to highlight the advantage of establishing the consistency of geometrical characters through the proposed algorithm using partition. The proposed algorithm reasonably reduces the amount of computation relative to computation without partition. Additionally, it is helpful that the proposed algorithm is capable of establishing consistency locally, which is never possible without partition. It is to be noted that the invariance property can be established irrespective of the value of L using the proposed method. However, for larger L values, the performance will not be impacted much in classification problems, even if certain data are misread or unavailable due to this property of local consistency. This advantage of the proposed method is in addition to the complexity reduction. The details of the reduction in computational complexity are discussed in the following theorem.
Theorem 1.
The computational complexity of obtaining the wavelet transform of sample points from a three-dimensional surface using the direct method is , while using the partition-based algorithm reduces the complexity to , where is the partition parameter.
Proof.
Consider a surface parameterized as
Let
be the sample points of the surface, where i and j are natural numbers and the dimensions are given by . By concatenating the columns of A, we obtain a matrix (B) of size . Then, the wavelet transform of B is , where W is a wavelet matrix of order . The number of operations required to compute the wavelet transform in this case is
Ignoring constants and lower order terms, the complexity is
Instead of processing the full matrix at once, we partition it. Let represent a partition, where , and . Therefore, the size of every partition is . This results in every partition () corresponding to a vector, each of whose components is three-dimensional. The wavelet transform of every is , where W is a wavelet matrix of order . Now, the number of operations required to compute the wavelet transform of the entire surface with partitioning is
which simplifies asymptotically to
The proof of the theorem is evident from the above results. □
3. Illustrated Examples
The proposed method based on partition is used to capture the consistency of geometrical characters considering the sample points of the actual surface and their transformations. Figure 1 depicts the actual, scaled, rotated and translated versions of the considered surface. In fact, we newly construct a matrix representation of size of 1024 equally spaced sample points on the surface (, , ). The computations are carried out using Python 3.11 programming. The above generated points are partitioned as discussed in Section 2. Therefore, the size of each partition of the considered grid is , where . A common principal direction is obtained for every partition of each L. Thus, the principal components of the abovementioned grids are computed. All the levels of wavelet transform are computed for the points obtained by PCA of each partition. The transformation of the sample points using in our study is carried out as detailed below. Scaling, rotation and translation are performed using scaling, rotation and translations in both the row and column as and . The partition and the principal components are computed for the transformed points as for actual points. Then, we calculate the proposed atypical detailed wavelet coefficients [2,3] of the principal components for the partitions on both sets of points. For this purpose, we use various orthogonal wavelets to perform an atypical wavelet transform. Despite the actual size of grid points, we provide only sample grid points for the sake of convenient presentation. Table 1 and Table 2 present the abovementioned sample grid of detailed wavelet coefficients of the points obtained by PCA of both the original and transformed images shown in Figure 2 by the Daubechies family of wavelets ().
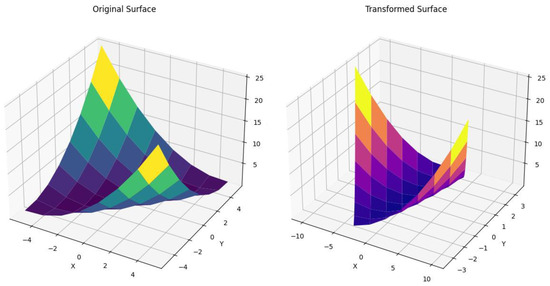
Figure 1.
, , .

Table 1.
Wavelet detail coefficients of original image. th vector of ith level wavelet detail coefficients.

Table 2.
Wavelet detail coefficients of transformed image. th vector of ith level wavelet detail coefficients.
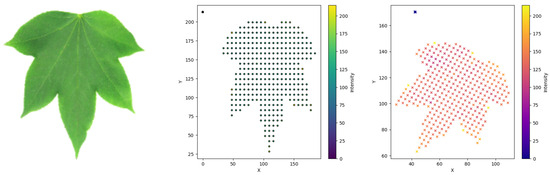
Figure 2.
Original image, surface points and transformed points.
However, the geometrical consistency between the two sets of partitions is evidenced neither by the sample points nor by their wavelet coefficients. It is interesting to note the consistency of geometrical characters as the ratios of all the detailed wavelet coefficients to those of the last-level detailed wavelet coefficient [1,2,3]. They are calculated for both sets of actual and transformed wavelet coefficients of each partition, showing that the vectors are the same; this TIFV is presented in Table 3.

Table 3.
TIFV of the image.
It is evident from Theorem 1 that the number of operations required to compute the wavelet transform of a surface with a grid size of considered in the illustrated example without partition is 6048, and the number of operations with partitioning is 1440 for , 672 for and 288 for . Therefore, the proposed method reasonably reduces computational complexity. It is also to be noted that the TIFV established using this method is not affected, even when certain data are misread or unavailable. This is shown in Table 3 for large L values.
4. Leaf Image Classification Using Partition
In this section, we study the influence of partition-based feature vectors in the classification of leaf shapes of the Flavia dataset (http://sourceforge.net/projects/flavia/files/Leaf%20Image%20Dataset/, accessed on 15 September 2025) [33,34] shown in Figure 3. A dataset of 25 images of each of the 32 types of the Flavia leaf dataset is investigated for the purpose of classification. We use machine learning techniques based on the RF method and SVM [35,36,37,38] for the study of classification. The proposed model consists of the five steps shown in Figure 4. The images of the leaves are resized so as to be uniform. The surface points of the resized leaf images are considered to proceed with the proposed algorithm. For this purpose, we generated sample points of three components from every leaf that are comparable with the points of the surface, described as follows. These points, in fact, are obtained as the location of the image in two dimensions and the intensity value of the image at that location as the third component. Suppose that the intensity value of the image at a location is denoted as ; then, the generated points will be of the form , that is, comparable with the points on the surface. The above such points are generated by grid sampling combined with point-in-contour filtering for the actual image and its transformations. We note, however, that the choice of intensity () as the third coordinate, while mathematically valid, does not represent a fundamental geometric property of the leaf and may be influenced by lighting or scanning; a binary mask representation would provide a purer geometric alternative. For our study, we normalize the size of each leaf image to 32 by 32 pixels. The feature parameter described in Section 2 of our study is extracted using Python programming for the abovementioned images. In the next step, the conventional Measured Values (MVs) [3,39] and Histogram of Oriented Gradient (HOG) [40], along with the proposed feature vector using leaf images, are computed. We used Google Colab for machine learning algorithms. It primarily offers CPU computing, GPU support and substantial memory. It also offers cloud-based storage for our datasets, code and experiment results, ensuring accessibility and reproducibility. Google Colab supports Python, making it compatible with popular machine learning libraries like Scikit-learn and Tensor Flow. In fact, the proposed work uses features of MVs and HOGs of the two dimensional images, along with the feature vector of the partitioned surface points of the leaf images. The MVs include the length of the contour line; area; major axis of the approximate ellipse, which is the length of the leaf; minor axis of the approximate ellipse, which is width of the leaf; and ratio of length over width [3,39]. HOG features are then computed using 9 orientation bins, pixels per cell and cells per block. In fact, the HOG descriptor is formed by computing gradient orientation histograms in small cells, grouping those into blocks for normalization and concatenating all block-level histograms to form a single feature vector [40]. Ellipse approximation of the leaf and normalized leaf, as well as HOG descriptor visualization, is shown in Figure 5. The proposed method of achieving consistency of the geometrical characters of the surfaces discussed in Section 2 is used in the classification study of the Flavia dataset. It is significant to note that the inclusion of the proposed feature vector, along with the rest of the features, enhances the classification efficiency.

Figure 3.
Leaf images of 32 shapes in the Flavia dataset.
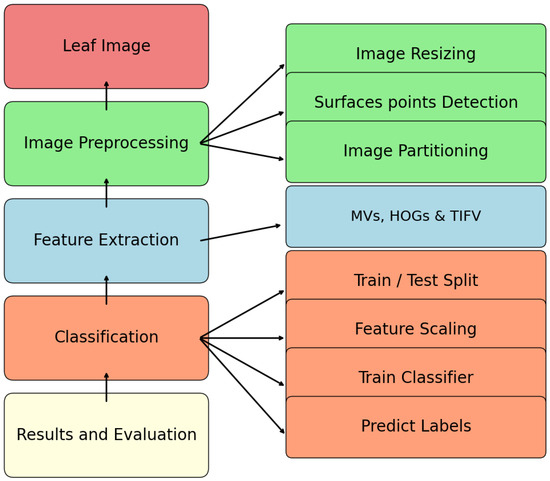
Figure 4.
Steps of leaf classification process.

Figure 5.
Approximate ellipse, Normalized leaf and HOG descriptor.
4.1. Classification by Random Forest Method
We use the sklearn module for the training our RF model—specifically, the RF Classifier function [37]. Hyperparameter tuning and cross-validation strategies are expected to significantly impact model performance [37]. We used 100 binary decision trees in this study. The random forest approach considers the 496 pairs from the Flavia dataset for the study reported in [39]. For each image pair, we generate the subsets from the complete dataset for the two images that are considered for comparison. Features and labels are combined for the two images to form the training set. We carry out six classification studies of leaf images—the first experiment uses MVs only; the second experiment uses MVs and HOGs; the third study uses TIFVs, along with MVs; the fourth study uses HOGs only; the fifth study uses TIFVs, along with HOGs; and the sixth study uses only TIFVs. The classification performance was measured using the weighted recall ratio. Recall ratios equal to or greater than 0.8, 0.7 and 0.65 and less than 0.65 were classified as great, good, fair and requiring re-work, respectively. The first study, which uses MVs only revealed that 254 out of the 496 pairs achieved a recall ratio of ≥0.65, which is 51.21% accuracy; the second study using MVs and HOGs shows 462 out of the 496 pairs achieved a recall ratio of ≥0.65, which is 93.15% accuracy; the third study using MVs and TIFVs shows that all 496 pairs achieved a recall ratio of ≥0.65, which is 100% accuracy; the fourth study using HOGs only shows 461 out of the 496 pairs achieved a recall ratio of ≥0.65, which is 92.94% accuracy; the fifth study using HOGs and TIFVs shows that all 496 pairs achieved a recall ratio of ≥0.65, which is 100% accuracy; and the sixth study using TIFVs only shows that all 496 pairs achieved a recall ratio of ≥0.65, which is 100% accuracy. The comparison of these six studies revealed that the feature vector proposed in this article improves the classification performance of the random forest method. This analysis is presented using a bar chart in Figure 6 for visualization, and the corresponding results are presented in Table 4. We also used a cross-validation (CV) technique to ensure the performance of the classification considering the combination of MVs, HOGs and TIFVs.
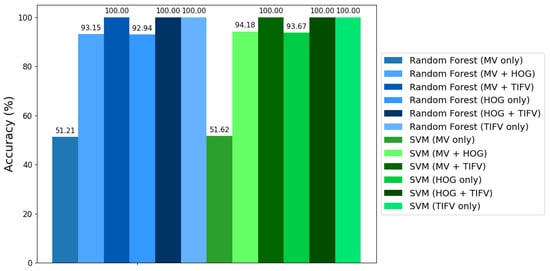
Figure 6.
Comparative analysis.

Table 4.
Analysis of feature-set combinations.
4.2. Classification by Support Vector Machine
We use the sklearn module for the training of our SVM—specifically, the Support Vector Classifier (SVC) function. The SVC is employed as the base classifier within the binary relevance transformation. The linear kernel parameter associated with the SVC is used in our study [36]. Feature scaling is used in our study to help the SVM algorithm converge faster and ensure that the decision boundary is not biased towards features with larger numeric ranges. We also use the multi-label binarizer, which simplifies multi-label classification tasks by converting them into multiple binary classification subtasks, making it easier for SVM to learn and make predictions. In fact, we use tensor flow, which provides GPU acceleration for certain operations and significantly speeds up computations. To ensure the reproducibility of data splitting, the random state parameter is set to 42 when splitting the data into training and testing sets [36]. We then proceeded with the algorithm by considering MVs in one case, MVs and HOGs in a second case, MVs and TIFVs in a third case, HOGs only in the fourth case, HOGs and TIFVs in the fifth case and TIFVs only in the sixth case. In all the cases, labeled datasets were provided as input. In our study, we used a linear kernel for classification. In fact, 80% of 800 images are used as the training set and 20% are taken for the test set. The SVM algorithm finds an optimal hyperplane that separates the classes using the training set and classifies the data of the test set [36]. The results of the SVM algorithm show that the classification model including TIFVs performs much better, with 100% accuracy, compared to the model with only MVs, which achieves 51.62% accuracy, whereas the combination of MVs along with HOGs achieves 94.18% and HOGs only achieves 93.67% accuracy. Of course, studies are also carried out using the polynomial kernel and the RBF kernel, which results in the same classification accuracy level. This analysis is presented using a bar chart in Figure 6 for visualization, and the corresponding results are presented in Table 4. Thus, this classification study clearly shows that the inclusion of TIFVs, as proposed in Section 2, improves the classification performance.
Furthermore, we employed both RF and SVM classifiers for evaluation of the effectiveness of different feature combinations comprising MVs, HOGs and TIFVs. To ensure the robustness of performance estimation and to avoid optimistic bias in model selection, nested cross-validation was applied for both classifiers. Specifically, a 5 × 3 nested CV scheme was used. Table 5 and Table 6 present the classification accuracies for RF and SVM, respectively, comparing simple three-fold CV against nested CV. The results clearly show that while MVs alone achieve only around 50% accuracy, the inclusion of TIFVs significantly improves performance for both classifiers. In particular, SVM with TIFVs achieves up to 99.2% nested CV accuracy, while RF with TIFVs attains 98.9% accuracy, demonstrating the strong discriminative power of the proposed TIFV descriptor.

Table 5.
Random Forest: comparison of classification accuracy (%) using simple CV and nested CV.

Table 6.
Support Vector Machine: Comparison of classification accuracy (%) using simple CV and nested CV.
To further validate these results, a confusion matrix was constructed for the best performing case of SVM with TIFVs. As shown in Figure 7, the predictions form an almost perfect diagonal matrix, confirming the high class separability.
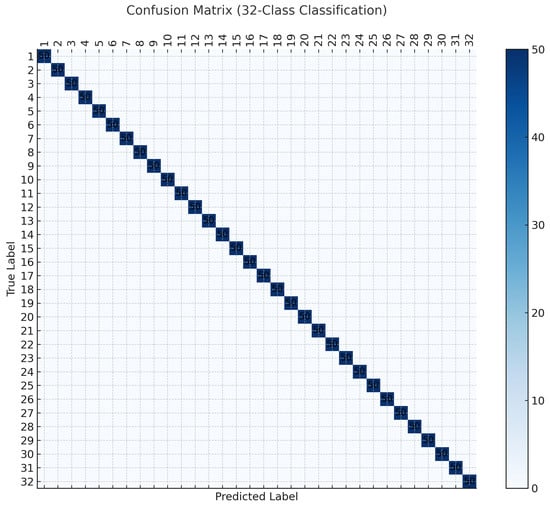
Figure 7.
Confusion matrix for the 32-class classification task on the Flavia dataset using nested cross-validation.
4.3. Robustness to Additive Noise
To assess robustness, we inject Gaussian perturbations into the intensity channel () of our normalized images as
with (values are clipped to the valid 8-bit range).
At each noise level, we evaluate two complementary settings:
Train–clean/Test–noisy: Models are trained on clean augmented images and tested on noisy versions.
Train–noisy/Test–noisy (matched): The training and test sets are corrupted at the same noise level. The evaluation uses the same nested cross-validation protocol as in the main experiments. The inner loop tunes the partition depth (L), wavelet family and kernel hyperparameters (for SVM), while the outer loop estimates generalization performance. We report the mean ± std of accuracy, macro F1 and macro recall across outer folds.
To further stabilize the wavelet-based TIFV descriptors under perturbations, we employ -regularized ratios, i.e.,
and also consider log-ratio features, i.e.,
as an ablation. These stabilizations are motivated by the sensitivity of direct ratios to small denominators in the presence of noise.
4.4. Noise Robustness Results
Figure 8 shows the accuracy vs. noise level for MVs, HOGs and TIFVs. TIFVs degrade gracefully as increases and outperform MVs and HOGs at all noise levels. Table 7 summarizes numerical results at representative noise levels. The relative accuracy drop of TIFVs from to is modest compared with HOGs and MVs. Using -regularized (and log) ratios further improves stability under higher noise levels. Similar trends are observed for macro F1 and macro recall. In the train–noisy/test–noisy (matched) setting, performance is uniformly higher than train–clean/test–noisy, indicating that the classifier can adapt to corrupted inputs. While Table 6 summarizes the baseline classification performance under clean conditions, it does not account for distortions that often arise in practical scenarios. To address this, Table 7 reports the nested CV performance when Gaussian noise of varying strength () is added to the intensity channel. The results highlight that although MVs degrade rapidly with noise, HOGs remain moderately stable and TIFVs exhibit strong robustness, retaining high accuracy and balanced macro F1/recall even at . This confirms that TIFVs not only achieve the best clean-image performance but also maintain reliability under noisy conditions. We restrict Table 7 to individual feature families; the combined variants follow the same robustness trends and are omitted for brevity. Note that Table 7 reports results for the train–clean/test–noisy setting only, whereas Figure 8 illustrates both train–clean/test–noisy and train–noisy/test–noisy (matched) scenarios to highlight the impact of training on noisy data.
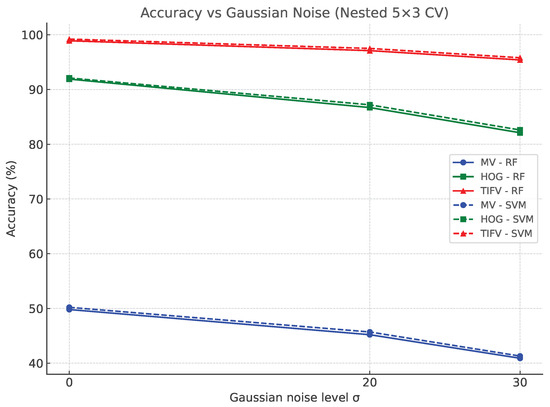
Figure 8.
Accuracy versus Gaussian noise level (; added only to ) under nested cross-validation. Curves compare MV, HOG, and TIFV features. Solid lines: train–clean/test–noisy; dashed: train–noisy/test–noisy (matched). TIFVs maintain the highest accuracy and show the slowest degradation as increases.

Table 7.
Nested CV performance under Gaussian noise added to (mean ± std across outer folds). corresponds to clean images. Results are reported for both RF and SVM.
5. Conclusions
The consistency of the geometrical character of surfaces under scaling, rotation and translation is studied in this article. For this purpose, the authors used the principal components by partitioning the considered surface. This investigation employed a suitably modified atypical wavelet transform of principal components. We used various orthogonal wavelets to perform an atypical wavelet transform. The results were found to be independent of the wavelets used. We captured the consistency of geometrical character using a specific ratio of detailed wavelet coefficients. It is significant to observe that the above ratio is useful in improving the performance of classification studies. The results show that the proposed TIFV significantly improves the classification performance. It is also interesting to note that the computation of wavelet transformation based on partition is much less complex, and it turns out to be beneficial that the proposed algorithm is capable of establishing consistency locally, which is never possible without partition. To strengthen fairness, we benchmarked the proposed TIFV descriptor against both Random Forest and SVM classifiers using nested cross-validation, showing consistent gains when the TIFV is included. In addition, robustness analysis under Gaussian noise perturbations further confirmed the superiority of the TIFV; both RF and SVM maintained high accuracies compared to conventional descriptors, even at higher noise levels. These improvements are demonstrated against traditional hand-crafted descriptors such as MVs and HOGs. Furthermore, we performed a robustness analysis under Gaussian noise perturbations, and the results confirm that the TIFV maintains high accuracy and degrades significantly less than competing descriptors. It is also be noted that comparisons against modern deep learning baselines are beyond the present scope and remain an important avenue for future work.
Author Contributions
Conceptualization, V.D., T.P. and K.S.; methodology, V.D., T.P. and K.S.; software, V.D.; validation, V.D., T.P. and K.S.; formal analysis, V.D., T.P. and K.S.; investigation, V.D., T.P. and K.S.; resources, V.D., T.P. and K.S.; writing—original draft preparation, V.D., T.P. and K.S.; writing—review and editing, V.D., T.P. and K.S.; supervision, T.P. and K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors thank the Department of Mathematics, Amrita School of Physical Sciences, Coimbatore, Amrita Vishwa Vidyapeetham, Tamil Nadu, for providing all the necessary facilities and a highly encouraging work environment, which was a key factor in the completion of our research work. The authors wish to acknowledge the valuable comments and suggestions of the anonymous reviewers that improved the quality of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest that are relevant to the content of this article. The authors have no relevant financial or non-financial interests to disclose. The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| PCA | Principal Component Analysis |
| TIFV | Transformation Invariant Feature Vector |
| SVM | Support Vector Machine |
| SVC | Support Vector Classifier |
| MV | Measured Values |
| HOG | Histogram of Oriented Gradient |
Appendix A
Theorem A1.
For any set of data matrices ( and any orthogonal rotation matrix (R) the principal components obtained from the covariance matrix of rotated data matrices remain invariant.
Proof.
Let be k matrices, each of size , representing n samples with m features. Also, let be the covariance matrix of for . We define the total covariance matrix as . If we apply a rotation transformation to the data matrix ( using an orthogonal rotation matrix (R), the transformed data matrix is . Then, the corresponding covariance matrix after rotation is, say, . We denote the sum of all transformed matrices as = . Let v be an eigenvector of C with an eigenvalue of , satisfying . Now, after rotation, the equation becomes , since . Then, . Thus, it is proven that the eigenvalues remain unchanged under rotation, but eigenvectors are rotated by for any covariance matrix. Therefore, the principal components of the original data are expressed as , and rotated data matrices are expressed as . Thus, PCA is invariant under rotation. □
Theorem A2.
For any set of data matrices () and any translation matrix (M), the principal components obtained from the covariance matrix of translated data matrices are translated.
Proof.
Let be k matrices, each of size , representing n samples with m features. Also, let be the covariance matrix of for . We define the total covariance matrix as . If we shift each column of by a constant translation vector (), . Then, the new covariance matrix remains unchanged, that is, , due to the properties of covariance. Therefore, it is evident that principal directions are invariant under translation. Then, the principal components of translated data are expressed as . □
Theorem A3.
For any set of data matrices () and any scaling matrix (S) that is diagonal, the principal components obtained from the covariance matrix of scaled data matrices are scaled.
Proof.
Let be k matrices, each of size , representing n samples with m features. Also, let be the covariance matrix of for . We define the total covariance matrix as . If we apply the scaling matrix (S), which is diagonal, the scaled data become . Then, the corresponding covariance matrices after scaling are expressed as . We denote the sum of all data matrices as = . Let v be an eigenvector of C with an eigenvalue of , satisfying after scaling (); since S is diagonal, the eigenvectors remain the same, and the new eigenvalues are . Thus, we have proven that the eigenvalues of the covariance matrix corresponding to scaling are scaled by , but the eigenvectors remain the same. Then, the principal components of scaled data are expressed as . Thus, principal components of scaled data matrices are just scaled. □
References
- Liu, W.; Sun, J.; Zhang, B.; Chu, J. Wavelet feature parameters representations of open planar curves. Appl. Math. Model. 2018, 57, 614–624. [Google Scholar] [CrossRef]
- Vignesh, D.; Palanisamy, T. Invariance Of Geometry Of Planar Curves Using Atypical Wavelet Coefficients. J. Appl. Sci. Eng. 2022, 26, 731–737. [Google Scholar] [CrossRef]
- Vignesh, D.; Palanisamy, T. Transformation invariant features of space curves and its application in classification problems. J. Appl. Sci. Eng. 2024, 27, 2825–2832. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, D.; Frangi, A.F.; Yang, J.y. Two-dimensional PCA: A new approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Zhu, Y. Subpattern-based principle component analysis. Pattern Recognit. 2004, 37, 1081–1083. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, Z.H. (2D) 2PCA: Two-directional two-dimensional PCA for efficient face representation and recognition. Neurocomputing 2005, 69, 224–231. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, Z.H.; Chen, S. Diagonal principal component analysis for face recognition. Pattern Recognit. 2006, 39, 140–142. [Google Scholar] [CrossRef]
- Kumar, K.V.; Negi, A. Novel approaches to principal component analysis of image data based on feature partitioning framework. Pattern Recognit. Lett. 2008, 29, 254–264. [Google Scholar] [CrossRef]
- Freudenstein, F. Harmonic analysis of crank-and-rocker mechanisms with application. J. Appl. Mech. 1959, 26, 673–675. [Google Scholar] [CrossRef]
- McGarva, J.; Mullineux, G. A new methodology for rapid synthesis of function generators. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1992, 206, 391–398. [Google Scholar] [CrossRef]
- McGarva, J.; Mullineux, G. Harmonic representation of closed curves. Appl. Math. Model. 1993, 17, 213–218. [Google Scholar] [CrossRef]
- Jianwei, S.; Jinkui, C.; Baoyu, S. A unified model of harmonic characteristic parameter method for dimensional synthesis of linkage mechanism. Appl. Math. Model. 2012, 36, 6001–6010. [Google Scholar] [CrossRef]
- Wu, J.; Ge, Q.; Gao, F. An efficient method for synthesizing crank-rocker mechanisms for generating low harmonic curves. In Proceedings of the ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; Volume 49040, pp. 531–538. [Google Scholar] [CrossRef]
- Yue, C.; Su, H.J.; Ge, Q.J. A hybrid computer-aided linkage design system for tracing open and closed planar curves. Comput.-Aided Des. 2012, 44, 1141–1150. [Google Scholar] [CrossRef]
- Uesaka, Y. A new Fourier descriptor applicable to open curves. Electron. Commun. Jpn. (Part I Commun.) 1984, 67, 1–10. [Google Scholar] [CrossRef]
- Anusha, S.; Sriram, A.; Palanisamy, T. A Comparative Study on Decomposition of Test Signals Using Variational Mode Decomposition and Wavelets. Int. J. Electr. Eng. Inform. 2016, 8, 886. [Google Scholar] [CrossRef]
- Anand, R.; Veni, S.; Aravinth, J. Robust classification technique for hyperspectral images based on 3D-discrete wavelet transform. Remote Sens. 2021, 13, 1255. [Google Scholar] [CrossRef]
- Sun, J.; Liu, W.; Chu, J. Synthesis of spherical four-bar linkage for open path generation using wavelet feature parameters. Mech. Mach. Theory 2018, 128, 33–46. [Google Scholar] [CrossRef]
- Hung, K.C.; Truong, T.K.; Jeng, J.H.; Yao, J.T. Uniqueness wavelet descriptor for plane closed curves. In Proceedings of the 1997 IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, BC, Canada, 20–22 August 1997; Volume 1, pp. 294–297. [Google Scholar] [CrossRef]
- Tieng, Q.M.; Boles, W.W.; Deriche, M. Space curve recognition based on the wavelet transform and string-matching techniques. In Proceedings of the IEEE International Conference on Image Processing, Washington, DC, USA, 23–26 October 1995; Volume 2, pp. 643–646. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv 2016. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- Lin, W.; Hasenstab, K.; Moura Cunha, G.; Schwartzman, A. Comparison of handcrafted features and convolutional neural networks for liver MR image adequacy assessment. Sci. Rep. 2020, 10, 20336. [Google Scholar] [CrossRef]
- Olver, P.J. Equivalence, Invariants and Symmetry; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Olver, P.J. Differential invariants of surfaces. Differ. Geom. Its Appl. 2009, 27, 230–239. [Google Scholar] [CrossRef]
- Figueroa, C.B.; Mercuri, F.; Pedrosa, R.H. Invariant surfaces of the Heisenberg groups. Ann. Mat. Pura Appl. 1999, 177, 173–194. [Google Scholar] [CrossRef]
- Montaldo, S.; Onnis, I.I. INVARIANT CMC SURFACES IN H 2× R. Glasg. Math. J. 2004, 46. [Google Scholar] [CrossRef]
- Onnis, I.I. Invariant surfaces with constant mean curvature in. Ann. Mat. Pura Appl. 2008, 187, 667–682. [Google Scholar] [CrossRef]
- Montaldo, S.; Onnis, I.I. Invariant surfaces of a three-dimensional manifold with constant Gauss curvature. J. Geom. Phys. 2005, 55, 440–449. [Google Scholar] [CrossRef]
- Aydin, M.E. Classification results on surfaces in the isotropic 3-space. arXiv 2016, arXiv:1601.03190. [Google Scholar] [CrossRef]
- Sahoo, T.K.; Banka, H.; Negi, A. Novel approaches to one-directional two-dimensional principal component analysis in hybrid pattern framework. Neural Comput. Appl. 2020, 32, 4897–4918. [Google Scholar] [CrossRef]
- Xu, G.; Li, C. Plant leaf classification and retrieval using multi-scale shape descriptor. J. Eng. 2021, 2021, 467–475. [Google Scholar] [CrossRef]
- Wagle, S.A.; Harikrishnan, R.; Ali, S.H.M.; Faseehuddin, M. Classification of plant leaves using new compact convolutional neural network models. Plants 2021, 11, 24. [Google Scholar] [CrossRef] [PubMed]
- Azlah, M.A.F.; Chua, L.S.; Rahmad, F.R.; Abdullah, F.I.; Wan Alwi, S.R. Review on techniques for plant leaf classification and recognition. Computers 2019, 8, 77. [Google Scholar] [CrossRef]
- Bist, U.S.; Singh, N. Analysis of recent advancements in support vector machine. Concurr. Comput. Pract. Exp. 2022, 34, e7270. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Oo, L.M.; Aung, N.Z. A simple and efficient method for automatic strawberry shape and size estimation and classification. Biosyst. Eng. 2018, 170, 96–107. [Google Scholar] [CrossRef]
- Ishikawa, T.; Hayashi, A.; Nagamatsu, S.; Kyutoku, Y.; Dan, I.; Wada, T.; Oku, K.; Saeki, Y.; Uto, T.; Tanabata, T.; et al. Classification of strawberry fruit shape by machine learning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 463–470. [Google Scholar] [CrossRef]
- Baghdadi, S.; Aboutabit, N. View-independent vehicle category classification system. Int. J. Adv. Comput. Sci. Appl. 2021, 12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).