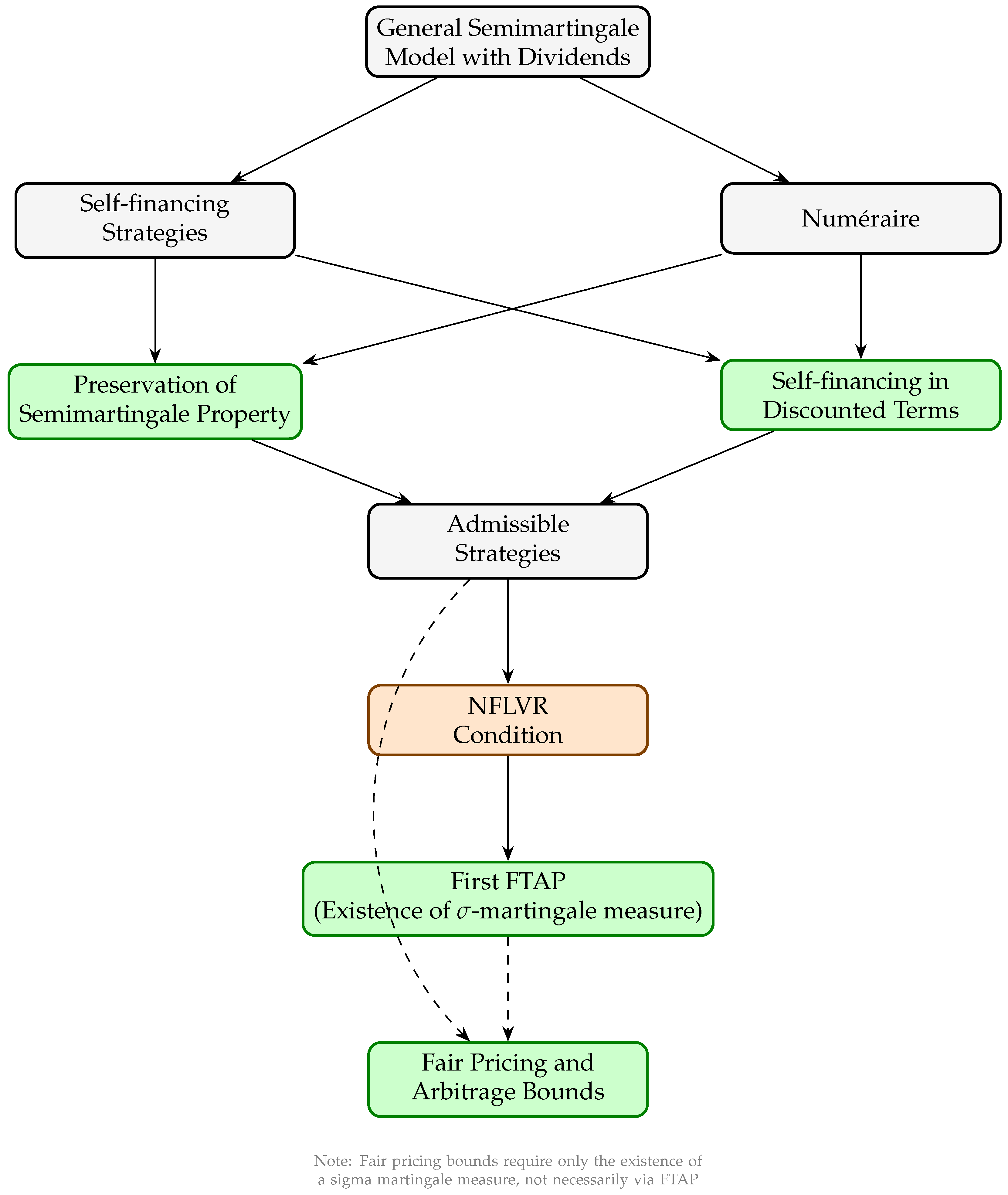
The General Semimartingale Market Model
Abstract
1. Introduction
- The model in [24] is formulated in a discounted framework (also referred to as a normalized setting). However, most models used in practice are expressed in non-discounted terms, as this facilitates the verification of model assumptions against real-world data. The question of how, and under which conditions, a non-discounted semimartingale model can be transformed into a discounted one has not been addressed in generality, but only for specific model classes, as noted by Platen and Heath [29].
- The framework presented in [24] does not account for dividends or other intermediate cash flows. As a result, it excludes important applications, such as models for the pricing and hedging of futures contracts. While dividend-paying assets can still be modeled as semimartingales, the precise conditions under which the semimartingale property is preserved under various transformations need clarification, as discussed in Korn [30] and Rogers and Williams [31]. In many cases, models with dividends can be converted into equivalent models without dividends (see, for instance, [32] (Section 2.3)). Consequently, a generalization of the basic semimartingale model to incorporate dividends is both natural and desirable. The importance of dividend modeling has been demonstrated empirically by Whaley [33], who showed significant pricing errors when dividends are not properly accounted for in American option valuation.
- Several foundational properties of semimartingale market models are often taken for granted without rigorous validation in this highly general setting. This includes concepts such as admissible strategies, discounted asset processes, and the choice of numéraire.
2. The General Semimartingale Model with Dividends
- The semimartingale property of price processes is preserved under small proportional transaction costs.
- The existence of equivalent sigma martingale measures extends to models with small transaction costs, though the measures must be interpreted in a bid–ask spread context.
- Self-financing strategies can be generalized to account for transaction costs by modifying the wealth equation to include cost terms.
- Fair pricing bounds widen to reflect the bid–ask spread, but the fundamental arbitrage relationships remain intact.
- is a filtered probability space with probability measure .
- The processes and are semimartingales for all .
- The filtration satisfies the usual conditions and the -algebra is trivial: implies or .
- Capital calls in private equity or venture capital investments;
- Margin requirements in leveraged positions;
- Storage costs for commodity investments;
- Management fees in fund structures;
- Tax liabilities passed through to investors.
2.1. Self-Financing Trading Strategies
- (a)
- A -dimensional process is called a trading strategy.
- (b)
- The wealth process of the investor is defined aswhere represents the number of the i-th security that an investor holds in his portfolio at t.
2.2. Numéraire
- (a)
- is called an equivalent martingale measure if is a -martingale for all .
- (b)
- is called an equivalent local martingale measure if is a local -martingale for all .
- (c)
- is called an equivalent sigma martingale measure if is a sigma martingale under for all .
- Martingales represent fair games where expected future value equals current value. This is the strongest condition and ensures that all trading strategies have bounded expected returns.
- Local martingales allow for the possibility of asset price bubbles, where prices can temporarily deviate from fundamental values. They are martingales when stopped at appropriate times but may exhibit explosive behavior.
- Sigma martingales are the weakest condition still sufficient for no-arbitrage. They allow for both bubbles and certain types of market incompleteness while maintaining the essential no-arbitrage property. In mathematical terms, a strict local martingale is a process that essentially has no trend but cannot, not even locally, be integrated (see [52] for more details).
2.3. Admissible Strategies
2.3.1. Overview of Admissibility Definitions
- (a)
- (b)
- (c)
- is square integrable [45];
- (d)
- (e)
- (f)
- (g)
2.3.2. Economic and Mathematical Analysis of Admissibility Conditions
- (i)
- X is a local martingale.
- (ii)
- There exist a local martingale M and a càdlàg finite variation process A such that .
- (iii)
- There exist a local martingale M and a càdlàg process A (with locally integrable) for which .
- (iv)
- There exist a local martingale M and a càdlàg finite variation process A such that .
- (v)
- There exist a local martingale M and a càdlàg process A (with locally integrable) satisfying .
- where ;
- for some and all n;
- .
- (i)
- The market satisfies the No Free Lunch with Vanishing Risk (NFLVR) condition.
- (ii)
- There exists a probability measure such that S is a sigma martingale under .
- Suppose a corporation pays a continuous-time dividend at rate per share, where . So . Under a martingale measure , then, the discounted price process is no longer a martingale but the process .
- With a tracker certificate on a share, the dividend distributions of the share are automatically invested in new shares of the same company. If the certificate starts with one share (or the value ), then in the above example, the replicating portfolio at time t consists of shares whose discounted value isThis can be seen from the fact that solves the differential equation with and the dividend payment can finance the purchase of shares. Alternatively, one shows that the strategy satisfies the self-financing condition from (2). Indeed, with the bank account as the numéraire, the following holds for this strategy with Integration by Parts:Thus, (9) is satisfied, and it follows by Theorem 2 that is self-financing. Since integrals of locally bounded integrands are again local martingales according to Theorem A3, is a local martingale if is one, and since conversely from (11)is also a local martingale if is one. Thus, it holds that for a measure , the process is a -local martingale if and only if the process is a -local martingale.
- In the Black–Scholes model, if there is a continuous dividend payoff of the above kind, thenThe change of measure in the Black–Scholes model is thus given byand the process is a standard Brownian motion under . Putting this into the price process yieldsSo, after the change in measure, the dividend payment leads to a reduction in the drift of the share.
- Storage limitations mean excess supply cannot be easily absorbed.
- Renewable energy sources (wind, solar) may continue producing even when demand is low.
- Nuclear and coal plants face high costs for reducing output, making negative prices preferable to shutdown.
- Grid stability requirements may necessitate continued generation despite oversupply.
- Oil markets famously saw negative prices in April 2020 when storage capacity was exhausted.
- Natural gas prices at specific hubs can turn negative due to pipeline constraints.
- Agricultural products with high storage or disposal costs may trade at negative prices.
- Central bank policies have pushed rates below zero in Europe and Japan.
- Government bonds trade at negative yields, implying negative forward rates.
- Interest rate derivatives must be priced in environments where the underlying can be negative.
3. Fair Prices
- (a)
- A claim with expiration date T is a non-negative random variable .
- (b)
- An admissible trading strategy is called a hedge for a claim X if
- (c)
- A claim is called attainable if there exists an admissible trading strategy such thatThis corresponding trading strategy is called a perfect hedge.
- (d)
- A financial market model is called complete if for every claim there exists a perfect hedge.
- (a)
- A perfect hedge ϕ is called a martingale hedge if is a -martingale.
- (b)
- Let Φ denote the set of all admissible strategies.
- (i)
- The superhedging price or seller’s arbitrage price of a claim X is given by
- (ii)
- The buyer’s arbitrage price is defined as
- (c)
- For a specific equivalent sigma martingale measure , we callthe risk-neutral price with respect to measure of X.
- (a)
- It always holds that
- (b)
- If a martingale hedge ϕ exists, then
- (a)
- Since according to Theorem 3 is a -supermartingale for all admissible and is the trivial -algebra, it holds for with thatThus, .For the second inequality, we proceed analogously and obtain for with :Taking the supremum, we get .
- (b)
- Now let be a martingale hedge and therefore is a -martingale. It follows thatTogether with (a), this now leads to (13).
4. Application to Dividend-Paying Equity Markets
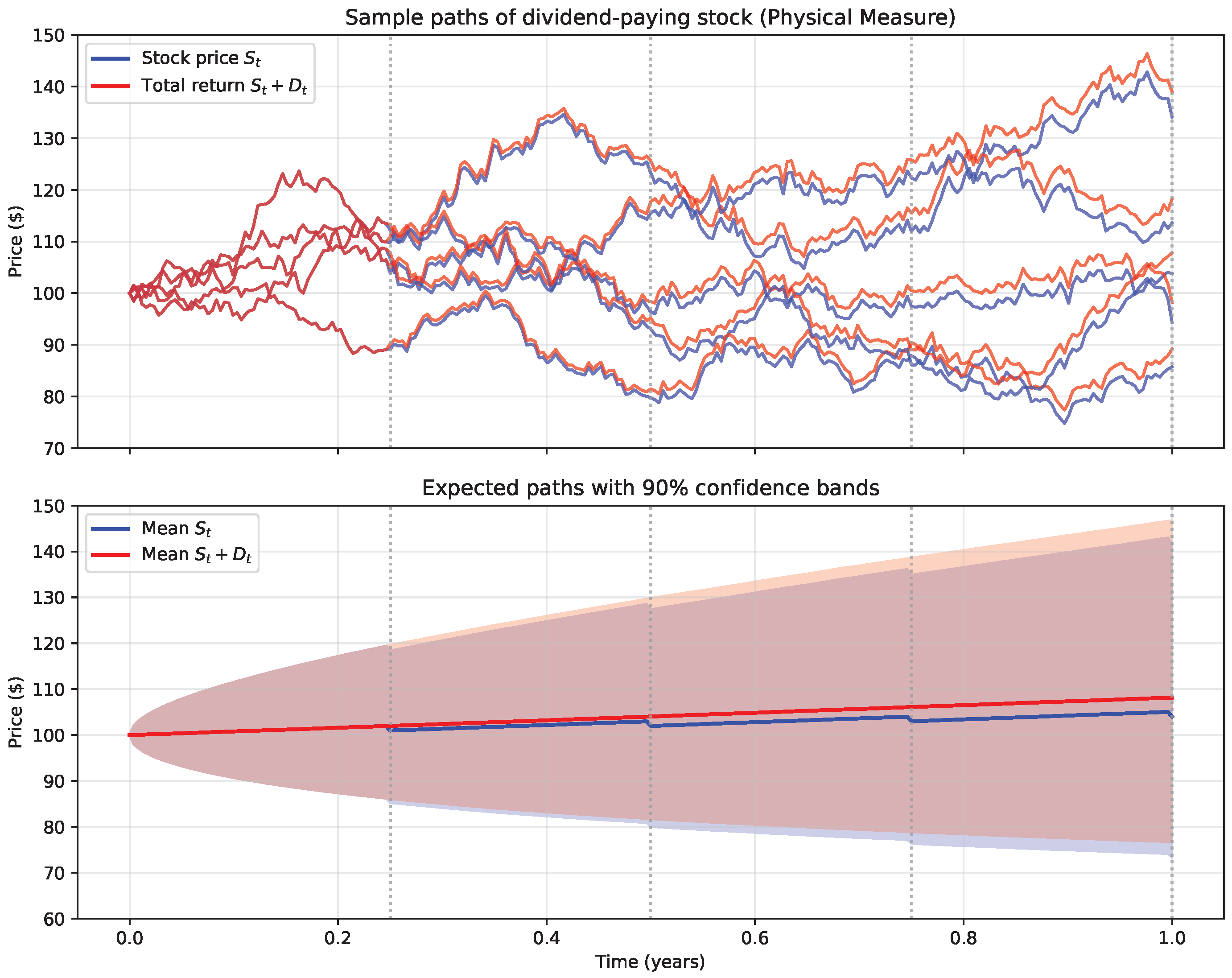
4.1. The Model
- Both S and D are càdlàg semimartingales: S has continuous and jump parts, while D is purely discontinuous.
- For the money market numéraire , we have since N is continuous while D is purely discontinuous.
- The discounted total return process is a local martingale under an equivalent risk-neutral measure .
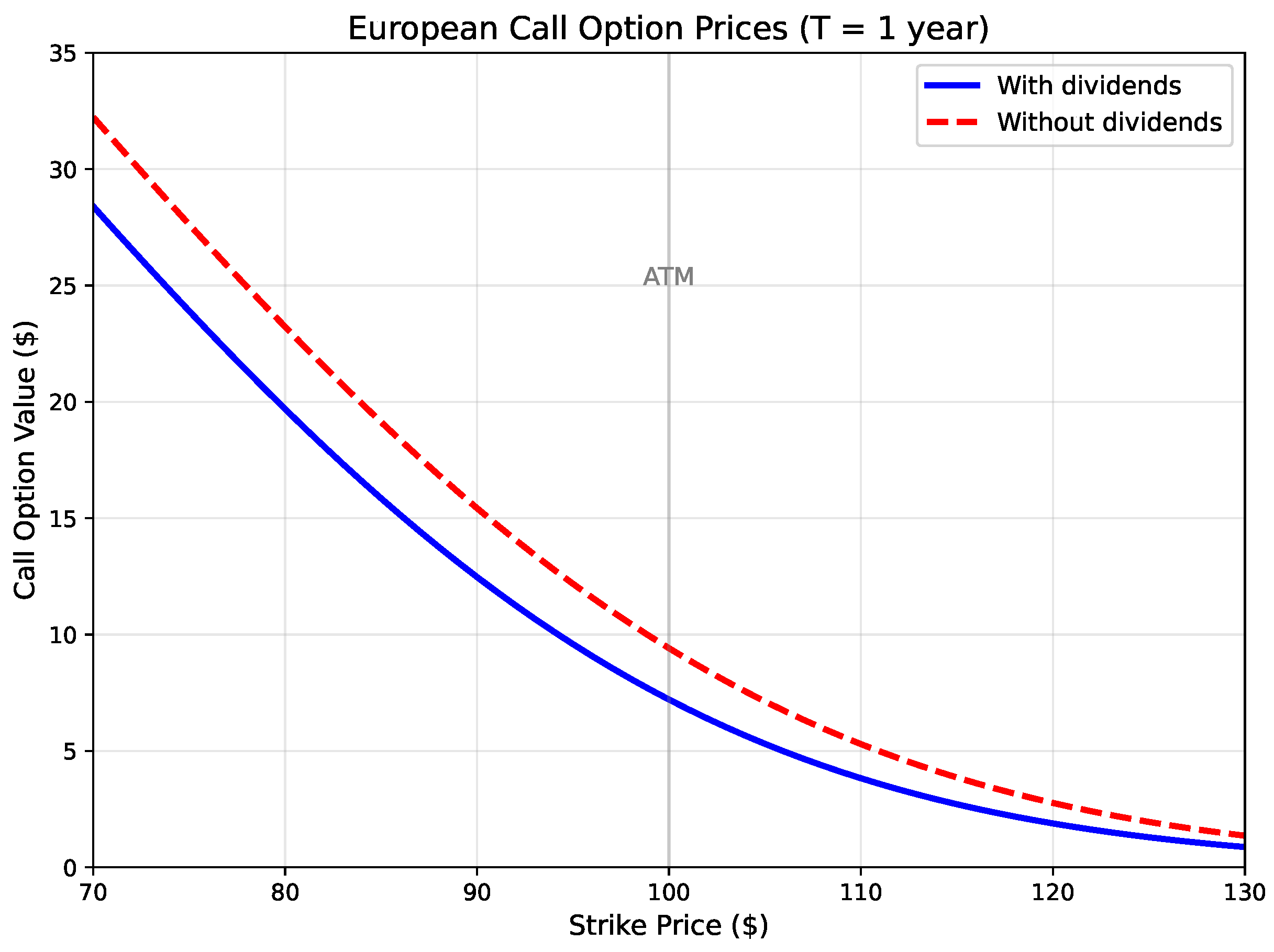
4.2. Numerical Implementation
- At-the-money call value decreases from $9.41 (no dividends) to $7.21 (with dividends), a 23% reduction.
- Total return including dividends shows approximately 8.2% expected annual return under .
- Mean stock price at maturity is $104.03 (excluding dividends), with 90% confidence interval [$73.36, $141.72].
5. Conclusions
- Theoretical unification: We provided rigorous conditions under which the semimartingale property is preserved when moving between nominal and discounted frameworks, filling a gap in the literature.
- Dividend treatment: We extended the classical framework to incorporate general dividend processes, with precise conditions () ensuring the self-financing property transfers correctly.
- Admissibility concepts: We clarified various notions of admissible strategies and justified our choice of the economically meaningful bounded-below condition.
- Practical application: We demonstrated the framework’s relevance through a comprehensive application to dividend-paying equity markets with discrete payments.
- Transaction cost robustness: We showed that our theoretical results remain valid under small transaction costs, providing a foundation for more realistic market models.
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Referenced Results
- (a)
- For and ,Hence,
- (b)
- (c)
- almost surely, for all .
- (d)
- (e)
- if and only if .
- (f)
- If X is an FV semimartingale, then
- (g)
- If , the notion of integrability does not change, and agrees -a.s. with the same process defined under .
- (a)
- and .
- (b)
- For any stopping time T, we have
- (c)
- The quadratic variation is a positive, increasing process.
- (d)
- If X is an FV process, then
- (a)
- A d-dimensional process X is a topological semimartingale if and only if each of its d components is a topological semimartingale in the one-dimensional sense.
- (b)
- A process that is locally a topological semimartingale or prelocally a topological semimartingale is automatically a topological semimartingale (i.e., the property is preserved under localization).
- (c)
- If , then any topological semimartingale under remains a topological semimartingale under .
- (a)
- ;
- (b)
- ;
- (c)
- , for any .
References
- Bachelier, L. Théorie de la spéculation. In Proceedings of the Annales Scientifiques de l’École Normale Supérieure; Société Mathématique de France: Paris, France, 1900; Volume 17, pp. 21–86. [Google Scholar]
- Itô, K. Stochastic integral. Proc. Imp. Acad. 1944, 20, 519–524. [Google Scholar] [CrossRef]
- Itô, K. On a stochastic integral equation. Proc. Jpn. Acad. 1946, 22, 32–35. [Google Scholar] [CrossRef]
- Itô, K. Stochastic differential equations in a differentiable manifold. Nagoya Math. J. 1950, 1, 35–47. [Google Scholar] [CrossRef]
- Itô, K. Multiple Wiener integral. J. Math. Soc. Jpn. 1951, 3, 157–169. [Google Scholar] [CrossRef]
- Itô, K. On a formula concerning stochastic differentials. Nagoya Math. J. 1951, 3, 55–65. [Google Scholar] [CrossRef]
- Itô, K. On Stochastic Differential Equations; Memoirs of the American Mathematical Society; American Mathematical Society: Providence, RI, USA, 1951; Volume 4. [Google Scholar]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Doob, J. Stochastic Processes; Wiley Classics Library; John Wiley & Sons: New York, NY, USA, 1953; Volume 7. [Google Scholar]
- Meyer, P.A. A decomposition theorem for supermartingales. Ill. J. Math. 1962, 6, 193–205. [Google Scholar] [CrossRef]
- Meyer, P.A. Decomposition of supermartingales: The uniqueness theorem. Ill. J. Math. 1963, 7, 1–17. [Google Scholar] [CrossRef]
- Kunita, H.; Watanabe, S. On square integrable martingales. Nagoya Math. J. 1967, 30, 209–245. [Google Scholar] [CrossRef]
- Meyer, P.A. Intégrales stochastiques I. Semin. Probab. Strasbg. 1967, 39, 72–94. [Google Scholar]
- Meyer, P.A. Intégrales stochastiques II. Semin. Probab. Strasbg. 1967, 1, 95–117. [Google Scholar]
- Meyer, P.A. Intégrales stochastiques III. Semin. Probab. Strasbg. 1967, 1, 118–141. [Google Scholar]
- Meyer, P.A. Intégrales stochastiques IV. Semin. Probab. Strasbg. 1967, 1, 142–162. [Google Scholar]
- Doléans-Dade, C.; Meyer, P.A. Intégrales stochastiques par rapport aux martingales locales. In Séminaire de Probabilités IV, Université de Strasbourg; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1970; Volume 124, pp. 77–107. [Google Scholar]
- Meyer, P. Un Cours sur les Intégrales Stochastiques. In Séminaire de Probabilités 1967–1980; Lecture Notes in Mathematics; Émery, M., Yor, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 1771, pp. 174–329. [Google Scholar] [CrossRef]
- Jacod, J. Calcul Stochastique et Problèmes de Martingales; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1979; Volume 714, p. x+280. [Google Scholar]
- Chou, C.S.; Meyer, P.A.; Stricker, C. Sur les intégrales stochastiques de processus prévisibles non bornés. In Séminaire de Probabilités XIV, 1978/79; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1980; Volume 784, pp. 128–139. [Google Scholar] [CrossRef]
- Jacod, J. Intégrales stochastiques par rapport à une semimartingale vectorielle et changements de filtration. In Séminaire de Probabilités XIV, 1978/79; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1980; Volume 784, pp. 161–172. [Google Scholar]
- Harrison, J.M.; Pliska, S.R. Martingales and stochastic integrals in the theory of continuous trading. Stoch. Process. Their Appl. 1981, 11, 215–260. [Google Scholar] [CrossRef]
- Delbaen, F.; Schachermayer, W. A general version of the fundamental theorem of asset pricing. Math. Ann. 1994, 300, 463–520. [Google Scholar] [CrossRef]
- Delbaen, F.; Schachermayer, W. The Fundamental Theorem of Asset Pricing for Unbounded Stochastic Processes. Math. Ann. 1998, 312, 215–250. [Google Scholar] [CrossRef]
- Jarrow, R. The arbitrage theory of capital asset pricing and the martingale property of asset prices. Econ. Theory 1999, 13, 253–264. [Google Scholar]
- Bichteler, K. Stochastic Integration and Lp-Theory of Semimartingales. Ann. Probab. 1981, 9, 49–89. [Google Scholar] [CrossRef]
- Kabanov, Y.; Safarian, M. Markets with Transaction Costs: Mathematical Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Fontana, C. Weak and strong no-arbitrage conditions for continuous financial markets. Int. J. Theor. Appl. Financ. 2015, 18, 1550005. [Google Scholar] [CrossRef]
- Platen, E.; Heath, D. A Benchmark Approach to Quantitative Finance; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Korn, R. Optimal portfolios with a positive lower bound on final wealth. Quant. Financ. 2005, 5, 315–321. [Google Scholar] [CrossRef]
- Rogers, L.C.G.; Williams, D. Diffusions, Markov Processes and Martingales: Volume 2, Itô Calculus; Cambridge Mathematical Library, Cambridge University Press: Cambridge, UK, 2000; p. xvi+480. [Google Scholar]
- Jarrow, R. Continuous-Time Asset Pricing Theory: A Martingale-Based Approach, 2nd ed.; Springer Finance, Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Whaley, R.E. Valuation of American call options on dividend-paying stocks: Empirical tests. J. Financ. Econ. 1982, 10, 29–58. [Google Scholar] [CrossRef]
- Harvey, C.R.; Whaley, R.E. Dividends and S&P 100 index option valuation. J. Futur. Mark. 1992, 12, 123–137. [Google Scholar] [CrossRef]
- Wilkens, S.; Wimschulte, J. The pricing of dividend futures in the European market: A first empirical analysis. J. Deriv. Hedge Funds 2009, 16, 136–143. [Google Scholar] [CrossRef]
- Sohns, M. The General Semimartingale Model with Dividends. In Proceedings of the Results of Social Science Research with Economic and Financial Effects (10th Annual Conference), Prague, Czech Republic, 15 November 2023. [Google Scholar] [CrossRef]
- Cohen, S.; Elliott, R. Stochastic Calculus and Applications; Probability and Its Applications; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Sohns, M. General Stochastic Vector Integration—Three Approaches. Preprints 2025. [Google Scholar] [CrossRef]
- Guasoni, P. No arbitrage under transaction costs, with fractional Brownian motion and beyond. Math. Financ. 2006, 16, 569–582. [Google Scholar] [CrossRef]
- Kabanov, Y.M.; Stricker, C. Hedging and liquidation under transaction costs in currency markets. Financ. Stochastics 2001, 5, 237–248. [Google Scholar] [CrossRef]
- Mixon, S. Option markets and implied volatility: Past versus present. J. Financ. Econ. 2009, 94, 171–191. [Google Scholar] [CrossRef]
- Ansel, J.P.; Stricker, C. Lois de martingale, densités et décomposition de Föllmer Schweizer. Ann. Henri Poincaré Inst. (B) Probab. Stat. 1992, 28, 375–392. [Google Scholar]
- Kardaras, C.; Platen, E. On the semimartingale property of discounted asset-price processes. Stoch. Process. Their Appl. 2011, 121, 2678–2691. [Google Scholar] [CrossRef]
- Bingham, N.; Kiesel, R. Risk-Neutral Valuation: Pricing and Hedging of Financial Derivatives, 2nd ed.; Springer Finance, Springer: London, UK, 2013. [Google Scholar] [CrossRef]
- Elliott, R.; Kopp, P. Mathematics of Financial Markets, 2nd ed.; Springer Finance, Springer: New York, NY, USA, 2005; p. xii+352. [Google Scholar]
- Pascucci, A. PDE and Martingale Methods in Option Pricing; Bocconi & Springer Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Geman, H.; Karoui, N.; Rochet, J. Changes of Numéraire, Changes of Probability Measure and Option Pricing. J. Appl. Probab. 1995, 32, 443–458. [Google Scholar] [CrossRef]
- Ebenfeld, S. Grundlagen der Finanzmathematik: Mathematische Methoden, Modellierung von Finanzmärkten und Finanzprodukten; Schäffer-Poeschel: Stuttgart, Germany, 2007. [Google Scholar]
- Klein, I.; Schmidt, T.; Teichmann, J. No Arbitrage Theory for Bond Markets. In Advanced Modelling in Mathematical Finance; Springer: Berlin/Heidelberg, Germany, 2016; pp. 381–421. [Google Scholar] [CrossRef]
- Qin, L.; Linetsky, V. Long-Term Risk: A Martingale Approach. Econometrica 2017, 85, 299–312. [Google Scholar] [CrossRef]
- Herdegen, M.; Schweizer, M. Strong bubbles and strict local martingales. Int. J. Theor. Appl. Financ. 2016, 19, 1650022. [Google Scholar] [CrossRef]
- Sohns, M. σ-Martingales: Foundations, Properties, and a New Proof of the Ansel–Stricker Lemma. Mathematics 2025, 13, 682. [Google Scholar] [CrossRef]
- Shiryaev, A.N. Essentials of Stochastic Finance; Advanced Series on Statistical Science & Applied Probability; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 1999; Volume 3, p. xvi+834. [Google Scholar] [CrossRef]
- Shiryaev, A.N.; Cherny, A. Vector stochastic integrals and the fundamental theorems of asset pricing. Proc. Steklov Inst. Math. Interperiodica Transl. 2002, 237, 6–49. [Google Scholar]
- Filipovic, D. Term-Structure Models. A Graduate Course; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Biagini, F. Second Fundamental Theorem of Asset Pricing. Encycl. Quant. Financ. 2010, 4, 1623–1628. [Google Scholar] [CrossRef]
- Musiela, M.; Rutkowski, M. Martingale Methods in Financial Modelling, 2nd ed.; Stochastic Modelling and Applied Probability; Springer: Berlin/Heidelberg, Germany, 2005; Volume 36, p. xx+638. [Google Scholar]
- Klebaner, F.C. Introduction to Stochastic Calculus with Applications, 2nd ed.; Imperial College Press: London, UK, 2005; p. xvi+412. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations: An Introduction with Applications, 6th ed.; Universitext; Springer: Berlin/Heidelberg, Germany, 2010; p. 404. [Google Scholar] [CrossRef]
- Kuo, H.H. Introduction to Stochastic Integration, 1st ed.; Universitext; Springer: New York, NY, USA, 2006; p. x+278. [Google Scholar] [CrossRef]
- Yan, J.A. Introduction to Stochastic Finance, 1st ed.; Universitext; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Harrison, J.M.; Pliska, S.R. A stochastic calculus model of continuous trading: Complete markets. Stoch. Process. Their Appl. 1983, 15, 313–316. [Google Scholar] [CrossRef]
- Cox, A.; Hobson, D. Local martingales, bubbles and option prices. Financ. Stoch. 2005, 9, 477–492. [Google Scholar] [CrossRef]
- Jarrow, R.A.; Protter, P.; Shimbo, K. Asset Price Bubbles in Complete Markets. In Advances in Mathematical Finance; Fu, M.C., Jarrow, R.A., Yen, J.Y.J., Elliott, R.J., Eds.; Applied and Numerical Harmonic Analysis; Birkhäuser Boston: Boston, MA, USA, 2007; pp. 97–121. [Google Scholar] [CrossRef]
- Jarrow, R.; Protter, P.; Shimbo, K. Asset Price Bubbles in Incomplete Markets. Math. Financ. 2010, 20, 145–185. [Google Scholar] [CrossRef]
- Merton, R. Option Pricing when Underlying Stock Returns are Discontinuous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar] [CrossRef]
- Wilmott, P. Derivatives: The Theory and Practice of Financial Engineering; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sohns, M. The General Semimartingale Market Model. AppliedMath 2025, 5, 97. https://doi.org/10.3390/appliedmath5030097
Sohns M. The General Semimartingale Market Model. AppliedMath. 2025; 5(3):97. https://doi.org/10.3390/appliedmath5030097
Chicago/Turabian StyleSohns, Moritz. 2025. "The General Semimartingale Market Model" AppliedMath 5, no. 3: 97. https://doi.org/10.3390/appliedmath5030097
APA StyleSohns, M. (2025). The General Semimartingale Market Model. AppliedMath, 5(3), 97. https://doi.org/10.3390/appliedmath5030097




