The Double Laplace–Adomian Method for Solving Certain Nonlinear Problems in Applied Mathematics

Abstract

The objective of this investigation is to obtain numerical solutions for a variety of mathematical models in a wide range of disciplines, such as chemical kinetics, neurosciences, nonlinear optics, metallurgical separation/alloying processes, and asset dynamics in mathematical finance. This research features numerical simulations conducted with a remarkably low error measure, providing a visual representation of the examined models in these areas. The proposed method is the double Laplace–Adomian decomposition method, which facilitates the numerical acquisition and analysis of solutions. This paper presents the first report of numerical simulations employing this innovative methodology to address these problems. The findings are expected to benefit the natural sciences, mathematical modeling, and their practical applications, representing the innovative aspect of this article. Additionally, this method can analyze many classes of partial differential equations, whether linear or nonlinear, without the need for linearization or discretization.

1. Introduction

Nonlinear ordinary differential equations (NLODEs) or nonlinear partial differential equations (NLPDEs) can be used to model a vast majority of nonlinear phenomena in applied mathematics. In the fields of engineering, applied mathematics, and natural sciences, there are a few of these equations that are absolutely necessary, and they can be solved by employing various approaches, whether they are analytical or numerical in nature. Researchers have conducted an enormous number of analytical and numerical studies to find solutions consistent with these problems in general. However, while computational tools make it relatively easy to analyze linear problems, precisely solving nonlinear problems remains a significant challenge. Despite the ongoing advancement of analytical methodologies, multiple disadvantages and limits persist. Nevertheless, certain analytical techniques yield approximate solutions to nonlinear problems, such as perturbation methods [1,2,3,4], homotopy perturbation [5,6,7,8,9,10], Adomian decomposition methods (ADMs) [11,12,13,14,15,16], collocation methods [17,18,19,20], and Laplace–Adomian decomposition methods (LADMs) [21,22,23,24], which are effective for addressing NLODEs and NLPDEs. These methods, while useful, often require careful application and a profound understanding of the underlying mathematics to ensure their effectiveness. Researchers continue to explore and refine these techniques, aiming to enhance their accuracy and expand their applicability across various fields of science and engineering. As advancements in computational power and data analysis techniques emerge, the potential for these methods to revolutionize problem-solving grows even more promising. This ongoing evolution not only offers fresh opportunities for research but also fosters interdisciplinary collaboration, bridging gaps between theoretical and practical applications.

The Thomas equation for chemical kinetics, a version of the nonlinear Schrödinger equation, a generalized Boussinesq equation, the Allen–Cahn equation used in materials science, and a nonlinear adaptation of the Black–Scholes equation are examined in this paper. The double Laplace–Adomian decomposition method (DLADM) will be used for the first time to estimate numerical solutions for the mathematical models describing the equations. The suggested technique is a systematic and efficient strategy for solving these nonlinear systems. Its primary benefit is that it enables the numerical computation of solutions without linearization, discretization, perturbation, or any other constraints that may compromise accuracy. This approach not only preserves the integrity of the original equations but also enhances the quality of numerical solutions obtained. As a result, it opens up new avenues for exploring complex phenomena in various areas of mathematical applications, where precision is crucial.

The main novelty of this study is the introduction of a new method called the double Laplace–Adomian decomposition method, which helps solve various mathematical models in several disciplinary fields. The results fuel advances in natural sciences and mathematical modeling, with potential for broad practical and theoretical impact.

The double Laplace–Adomian decomposition method has recently been successfully employed to solve fractional-order NLPDEs in [25,26,27] and for the calculation of electron-acoustic waves for a Korteweg–De Vries equation in [28]. Also in [29], the authors achieved a generalization of the method and applied it to the solution of coupled Sine–Gordon-type equations. These advancements highlight the versatility and effectiveness of the double Laplace–Adomian decomposition method in addressing complex mathematical problems.

We have structured the remainder of this paper as follows. In Section 2, we briefly show the technical requirements related to the double Laplace transform and its properties to address the rest of this manuscript. In Section 3, we present the methodology and the algorithm used in the rest of this article derived from the combination of the ADM with the double Laplace transform. In Section 4, we illustrate the effectiveness, accuracy, and efficiency of the proposed methodology by providing numerical solutions to examples derived from various scientific fields. In the final Section 5 of this article, we discuss the conclusions drawn from the entire study.

2. Technical Prerequisites

This section reviews the fundamental definitions and basic properties of the Laplace transform and the double Laplace transform. The double Laplace transform extends the concept of the standard Laplace transform, allowing for the analysis of functions of two variables. This powerful tool is particularly useful in solving partial differential equations (PDEs), providing a way to handle complex time-dependent behaviors. Furthermore, we will briefly review the key steps of the widely recognized Adomian decomposition method, which will be essential in establishing the methodology of our research.

2.1. Laplace Transform: Brief Review

The Laplace transform is a potent mathematical tool that is named after Pierre-Simon, Marquis de Laplace (1749–1827), a French philosopher, mathematician, and astronomer. Although he did not “invent” it in its present form, he made significant contributions to its application, particularly in his research on probability theory [30]. His work laid the groundwork for many modern mathematical techniques, and the Laplace transform itself has become essential in engineering, physics, and control theory, allowing for the simplification of complex differential equations. Today, it is widely used to analyze linear time-invariant systems and solve problems across various scientific disciplines.

Definition 1.

For all real numbers $t\ge 0$, the Laplace transform of a function $f\left(t\right)$ is the function $F\left(s\right)$, which is defined by

$$F\left(s\right)=\mathcal{L}\left\{f\left(t\right)\right\}={\int }_0^{\infty }{e}^{-st}f\left(t\right)dt,$$

(1)

whenever the improper integral exists. In general s is a complex number.

Definition 2.

If the Laplace transform of $f\left(t\right)$ is $F\left(s\right)=\mathcal{L}\left\{f\right(t\left)\right\}$, then the inverse Laplace transform of $F\left(s\right)$ is $f\left(t\right)$. Conversely, it is defined by

$${\mathcal{L}}^{-1}\left\{F\left(s\right)\right\}=f\left(t\right).$$

(2)

The main properties of the Laplace transform are be listed below.

• Linearity property: For all real numbers $c_1$ and $c_2$, we have

  $$\mathcal{L}\{c_{1}f\left(t\right)+c_{2}g\left(t\right)\}=c_1\mathcal{L}\left\{f\left(t\right)\right\}+c_2\mathcal{L}\left\{g\left(t\right)\right\},$$

  (3)

  $${\mathcal{L}}^{-1}\{c_{1}F\left(s\right)+c_{2}G\left(s\right)\}=c_1{\mathcal{L}}^{-1}\left\{F\left(s\right)\right\}+c_2{\mathcal{L}}^{-1}\left\{G\left(s\right)\right\}.$$

  (4)
• Shifting property: For all real numbers $\omega$

  $$\mathcal{L}\left\{e^{\omega t}f\left(t\right)\right\}=F(s-\omega ),$$

  (5)

  $${\mathcal{L}}^{-1}\left\{F(s-\omega )\right\}=e^{\omega t}f\left(t\right).$$

  (6)
• Laplace transform of derivatives: Suppose that the functions $f^{\prime },f^{″},\dots ,f^{\left(n\right)}$ are continuous for $t\ge 0$ and of exponential order. Then $\mathcal{L}\left\{f^{\left(n\right)}\left(t\right)\right\}$ exists, and

  (a)

  $$\mathcal{L}\left\{f^{\left(n\right)}\left(t\right)\right\}=s^{n}F\left(s\right)-s^{n-1}f\left(0\right)-s^{n-2}{f}^{\prime }\left(0\right)-\cdots -s{f}^{n-2}\left(0\right)-f^{n-1}\left(0\right),$$

  (7)

  (b)

  $$\mathcal{L}\left\{t^{n}f\left(t\right)\right\}={(-1)}^n{F}^{\left(n\right)}\left(s\right).$$

  (8)

Definition 3.

The convolution of functions f and g is defined as

$$f\left(t\right)\ast g\left(t\right)={\int }_0^{t}f\left(x\right)g(t-x)dx.$$

(9)

It is known that the convolution is commutative and that it is satisfied:

$${\mathcal{L}}^{-1}\left\{F\left(s\right)G\left(s\right)\right\}=f\left(t\right)\ast g\left(t\right).$$

(10)

2.2. Double Laplace Transform and Basic Properties

In the middle of the 20th century, the double Laplace transform arose as a natural extension of the single Laplace transform to solve partial differential equations and gained prominence as a powerful tool in applied mathematics, physics, and engineering [31,32].

Definition 4.

Consider a function $u(x,y)$ for $x,t>0$; the double Laplace transform is defined as

$$U(p,s)={\mathcal{L}}_{xt}\left\{u(x,t)\right\}={\int }_0^{\infty }{e}^{-px}{\int }_0^{\infty }{e}^{-st}u(x,t)dtdx,$$

(11)

whenever the improper double integral exists. In general p and s are complex numbers.

Definition 5.

If the double Laplace transform of $u(x,t)$ is $U(p,s)$, then the inverse double Laplace transform of $U(p,s)$ is $u(x,t)$. It is represented by a complex double integral formula

$${\mathcal{L}}_{xt}^{-1}\left\{U(p,s)\right\}={\displaystyle \frac{1}{2\pi i}}{\int }_{c-i\infty }^{c+i\infty }{e}^{pt}{\int }_{d-i\infty }^{d+i\infty }{e}^{sx}U(p,s)dpds.$$

(12)

It must be fulfilled that $U(p,s)$ is an analytic function for all p and s in a region of the complex plane such that $Re\left(p\right)\ge c$ and $Re\left(s\right)\ge d$. That is, the integrals are evaluated along vertical lines in the complex plane, positioned at c and d, respectively, to avoid the poles of the function U and to ensure the analyticity and convergence of the integrals. These vertical paths are known as Bromwich contours [33].

The operator ${\mathcal{L}}_{xt}^{-1}$ is also linear, and its main properties with regard to the partial derivatives are described below.

(i)

The double Laplace transform of first partial derivatives is given by

$${\mathcal{L}}_{xt}\left\{{\displaystyle \frac{\partial u(x,t)}{\partial x}}\right\}=pU(p,s)-U(0,s),$$

(13)

$${\mathcal{L}}_{xt}\left\{{\displaystyle \frac{\partial u(x,t)}{\partial t}}\right\}=sU(p,s)-U(p,0).$$

(14)

(ii)

The double Laplace transform of n-th partial derivatives is given by

$${\mathcal{L}}_{xt}\left\{{\displaystyle \frac{{\partial }^{n}u(x,t)}{\partial x^n}}\right\}=p^{n}U(p,s)-\sum _{i=0}^{n-1}{p}^{n-1-i}{\displaystyle \frac{{\partial }^{i}U(0,s)}{\partial x^i}},$$

(15)

$${\mathcal{L}}_{xt}\left\{{\displaystyle \frac{{\partial }^{n}u(x,t)}{\partial t^n}}\right\}=s^{n}U(p,s)-\sum _{j=0}^{n-1}{s}^{n-1-j}{\displaystyle \frac{{\partial }^{j}U(p,0)}{\partial t^j}}.$$

(16)

(iii)

The double Laplace transform of the mixed partial derivative is given by

$${\mathcal{L}}_{xt}\left\{{\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x\partial t}}\right\}=psU(p,s)-pU(p,0)-sU(0,s)+u(0,0).$$

(17)

(iv)

The double Laplace transform of a product of functions of one independent variable is expressed by

$${\mathcal{L}}_{xt}\left\{u\left(x\right)v\left(t\right)\right\}=\mathcal{L}\left\{u\left(x\right)\right\}\mathcal{L}\left\{v\left(t\right)\right\}.$$

(18)

The double Laplace transform can be useful for solving wave, Laplace, heat, and non-homogeneous partial differential equations, which appear in many areas of physics, applied mathematics, and engineering. It is a highly effective instrument for reducing calculations in various engineering and mathematics disciplines. Additionally, it offers a potent approach to linear system analysis. This method is frequently employed to resolve differential and integral equations [34]. In [35,36,37,38,39,40,41], the authors implemented the double Laplace transform when solving a variety of NLPDE-modeled problems, including those with standard and fractional derivatives. In [34,42], researchers analyzed the transform to uncover new properties that have many applications. These properties enhance the versatility of the double Laplace transform, making it a valuable tool in both theoretical and practical contexts.

3. Methodology

In this section, we will provide an overview of the double Laplace–Adomian method (DLADM), a methodology that has not received much attention in mathematical applications. This approach integrates the ADM and the double Laplace transform. To decompose the nonlinear term in the PDE, we will use the Adomian polynomials. The components are determined recursively, and the solution is constructed as an infinite series. The effectiveness of the DLADM lies in its ability to simplify complex problems by transforming them into a more manageable form.

The following are the steps inherent in the double Laplace–Adomian method.

As an illustration of a general problem, let us examine the following NLPDE presented in its operational form:

$$(D_t^n+L+N)u(x,t)=f(x,y).$$

(19)

where $D_t^n$ is the differential operator that denotes the nth time derivative, L is the linear component of the equation, N is the nonlinear component, and f is any function that has a double Laplace transform. Furthermore, suppose that NLPDE (19) has as initial conditions $u(x,0)$, $D_{t}u(x,0)$,…, $D_t^{n-1}(x,0)$.

The following result is obtained by using the double Laplace transform on both sides of Equation (19):

$${\mathcal{L}}_{xt}\left\{D_t^{n}u(x,t)\right\}+L{\mathcal{L}}_{xt}\left\{u(x,t)\right\}+N{\mathcal{L}}_{xt}\left\{u(x,t)\right\}={\mathcal{L}}_{xt}\left\{f(x,t)\right\}.$$

(20)

Applying the definitions shown in Section 2 of the double Laplace transform to the nth derivative, we derive

$${\mathcal{L}}_{xt}\left\{u(x,t)\right\}=H(p,s)-{\displaystyle \frac{1}{s^n}}L{\mathcal{L}}_{xt}\left\{u(x,t)\right\}-{\displaystyle \frac{1}{s^n}}N{\mathcal{L}}_{xt}\left\{u(x,t)\right\},$$

(21)

where we have considered

$$H(p,s)={\displaystyle \frac{1}{s^n}}\left[{\mathcal{L}}_{xt}\left\{f(x,t)\right\}+\sum _{j=0}^{n-1}{s}^{n-1-j}{\displaystyle \frac{{\partial }^{j}U(p,0)}{\partial t^j}}\right].$$

(22)

The two main principles of the ADM are as follows [43,44]:

• Decomposition of the solution: The central idea of the ADM is to decompose the NLPDE solution u into a series whose terms are generated recursively; that is,

  $$u(x,t)=\sum _{n=0}^{\infty }{u}_n(x,t)=u_0(x,t)+u_1(x,t)+u_2(x,t)+\dots$$

  (23)
  Then, every $u_n$ is calculated iteratively.
• Decomposition of nonlinear terms: This is a crucial part of the ADM. The nonlinear term $N\left(u\right)$ is decomposed into an infinite series of Adomian polynomials, denoted as $P_n$:

  $$N\left(u\right)=\sum _{n=0}^{\infty }{P}_n(u_0,u_1,\dots ,u_n).$$

  (24)
  These Adomian polynomials are generated in a manner that implies they are solely dependent on the components $u_0$, $u_1$,…, $u_n$.
  Kataria and Vellaisamy in [45] introduced a recursive technique for computing Adomian polynomials, eliminating the need for laborious computations of the nth derivative. With this method, each $P_n$ is computed as

  $$P_0\left(u_0\right)=N\left(u_0\right),$$

  (25)

  $$P_n(u_0,u_1,\dots ,u_n)={\displaystyle \frac{1}{2\pi }}{\int }_{-\pi }^{\pi }N\left(\sum _{k=0}^n{u}_k{e}^{ik\omega }\right)e^{-in\omega }d\omega ,n\ge 1.$$

  (26)

The subsequent step requires applying an inverse double Laplace transform to both sides of Equation (21) to obtain

$$u(x,t)={\mathcal{L}}_{xt}^{-1}\left\{H(p,s)\right\}-{\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^n}}L{\mathcal{L}}_{xt}\left\{u(x,t)\right\}\right\}-{\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^n}}N{\mathcal{L}}_{xt}\left\{u(x,t)\right\}\right\}.$$

(27)

We may now implement the two basic ideas of the ADM on both sides of Equation (27), producing

$$\sum _{n=0}^{\infty }{u}_n(x,t)={\mathcal{L}}_{xt}^{-1}\left\{H(p,s)\right\}-{\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^n}}{\mathcal{L}}_{xt}\{L\sum _{n=0}^{\infty }{u}_n(x,t)+\sum _{n=0}^{\infty }{P}_n\}\right\}.$$

(28)

By equating the terms on both sides, we derive

$$\begin{array}{cc}\hfill u_0(x,t)=& {\mathcal{L}}_{xt}^{-1}\left\{H(p,s)\right\},\hfill \\ \hfill u_1(x,t)=& -{\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^n}}{\mathcal{L}}_{xt}\{L{u}_0(x,t)+P_0\left(u_0\right)\}\right\},\hfill \\ \hfill u_2(x,t)=& -{\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^n}}{\mathcal{L}}_{xt}\{L{u}_1(x,t)+P_1(u_0,u_1)\}\right\},\hfill \\ \hfill u_3(x,t)=& -{\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^n}}{\mathcal{L}}_{xt}\{L{u}_2(x,t)+P_2(u_0,u_1,u_2)\}\right\},\hfill \\ \hfill ⋮\end{array}$$

(29)

In general, the nth component $u_n$ is obtained as

$$u_n(x,t)=-{\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^n}}{\mathcal{L}}_{xt}\{L{u}_{n-1}(x,t)+P_{n-1}(u_0,u_1,\dots ,u_{n-1})\}\right\}.$$

(30)

The exact solution can be obtained as

$$u(x,t)=\sum _{n=0}^{\infty }{u}_n(x,t).$$

(31)

The K-th term approximation of the solution is finally presented as

$$u_K(x,t)=\sum _{n=0}^{K-1}{u}_n(x,t),K\ge 1.$$

(32)

In the same way, the algorithm described above can be rewritten if the differential operator in Equation (19) is $D_x^n$, $D_{xt}^n$, etc.

We will now apply the technique described by the DLADM to address a few problems modeled by an NLPDE that have significant mathematical applications.

4. Illustrative Examples of Application

This section will employ the algorithm provided by the DLADM for solving several problems modeled by NPDEs, which hold significant relevance for the application of mathematics across different fields of natural science and engineering. These problems often arise in contexts such as fluid dynamics, heat transfer, and material science, where nonlinear behaviors are prevalent. By leveraging the DLADM algorithm, we aim to provide efficient and accurate solutions that enhance our understanding of these complex systems. To the best of our knowledge, none of these problems has been examined using the mathematical method provided in this paper. All numerical calculations are conducted with Mathematica-Wolfram version 14.2.1 software.

4.1. Model 1: Solitons in Biomembranes

The dynamic behavior of solitons in biomembranes is described by the generalized Boussinesq equation (BE), expressed as follows [46]:

$$\left\{\begin{array}{c}{u}_{tt}-k^2{u}_{xx}+a_{1}u{u}_x+a_2{u}^2{u}_{xx}+b_1{\left(u_x\right)}^2+b_{2}u{\left(u_x\right)}^2+c{u}_{xxxx}=0,\hfill \\ u(x,0)=u_0\left(x\right),u_t(x,0)=u_1\left(x\right).\hfill \end{array}\right.$$

(33)

The change in membrane area density as a function of x and t is represented by $u(x,t)$ in Equation (33). The nerve axon is represented as a one-dimensional cylinder with lateral density excitations that propagate along the coordinate x and time t. These excitations are critical for the transmission of nerve impulses, allowing for the rapid communication of signals within the nervous system. Learning about the behavior of $u(x,t)$ offers explanations for the dynamics of action potentials and their influence on neuronal function. In addition, the parameters $a_1$ and $a_2$ represent the nonlinear elastic behavior of the biomembrane, as a real nerve is not isolated but is viscously coupled to the surrounding fluids. In addition, $b_1$ and $b_2$ are experimentally determined parameters that determine the density dependence of sound velocity. Lastly, the parameters $k^2$ and c are used to quantify the dispersion and friction of the nerve axon, respectively [47].

For the problem of the existence and uniqueness of solutions for equations of the same type as Equation (33), the reader may refer to [48].

The model’s initial conditions are determined by the coefficients of Equation (33) and are given as follows [49]:

$$u(x,0)={\displaystyle \frac{A}{cosh\left(Bx\right)+C}},u_t(x,0)={\displaystyle \frac{ABvsinh\left(Bx\right)}{{(cosh\left(Bx\right)+C)}^2}},$$

(34)

where v is the velocity of the soliton and the parameters A, B, and C are given by

$$A={\displaystyle \frac{12({\nu }^2-k^2)}{\sqrt{{(a_1+b_1)}^2-6(2a_2+b_2)({\nu }^2-k^2)}}},$$

(35)

$$B=\sqrt{{\displaystyle \frac{k^2-{\nu }^2}{c}}},$$

(36)

$$C={\displaystyle \frac{-(a_1+b_1)}{\sqrt{{(a_1+b_1)}^2-6(2a_2+b_2)({\nu }^2-k^2)}}}.$$

(37)

The algorithm that the DLADM generates to solve Equation (33) is as follows:

$$\left\{\begin{array}{c}{u}_0(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^2}}(sU(p,0)-U_t(p,0))\right\},\hfill \\ u_n(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s^2}}{\mathcal{L}}_{xt}\{L{u}_{n-1}(x,t)+P_{n-1}(u_0,u_1,\dots ,u_{n-1})\}\right\},n\ge 1.\hfill \end{array}\right.$$

(38)

The linear operator L acting on $u_{n-1}$ is given by

$$L{u}_{n-1}(x,t)=k^2{\displaystyle \frac{{\partial }^2{u}_{n-1}(x,t)}{\partial x^2}}-c{\displaystyle \frac{{\partial }^4{u}_{n-1}(x,t)}{\partial x^4}}.$$

The initial set of Adomian polynomials that correspond to the decomposition of the nonlinear operator $Nu=-a_{1}u{u}_x-a_2{u}^2{u}_{xx}-b_1{\left(u_x\right)}^2-b_{2}u{\left(u_x\right)}^2$ is as follows:

$$\begin{array}{cc}\hfill P_0& =a_1{u}_0{u}_{0x}+a_2{u}_0^2{u}_{0xx}+b_1{u}_{0x}^2+b_2{u}_{0x}^2{u}_0,\hfill \\ \hfill P_1& =a_1\left(u_{0x}{u}_1+u_0{u}_{1x}\right)+a_2\left(u_0^2{u}_{1xx}+2u_0{u}_1{u}_{0xx}\right)+2b_1{u}_{0x}{u}_{1x}+b_2\left(u_{0x}^2{u}_1+2u_{0x}{u}_{1x}{u}_0\right),\hfill \\ \hfill P_2& =a_1\left(u_{0x}{u}_2+u_{1x}{u}_1+u_0{u}_{2x}\right)+a_2\left(u_1^2{u}_{0xx}+2u_0{u}_2{u}_{0xx}+2u_0{u}_1{u}_{1xx}+u_0^2{u}_{2xx}\right)\hfill \\ \hfill & +b_1\left(2u_{0x}{u}_{2x}+u_{1x}^2\right)+b_2\left(u_{1x}^2{u}_0+2u_{0x}{u}_{2x}{u}_0+2u_{0x}{u}_{1x}{u}_1+u_{0x}^2{u}_2\right),\hfill \\ \hfill P_3& =a_1\left(u_{0x}{u}_3+u_{1x}{u}_2+u_{2x}{u}_1+u_{3x}{u}_0\right)+b_1\left(2u_{0x}{u}_{3x}+2u_{1x}{u}_{2x}\right)\hfill \\ \hfill & +a_2\left(u_1^2{u}_{1xx}+2u_1{u}_2{u}_{0xx}+2u_0{u}_3{u}_{0xx}+2u_0{u}_2{u}_{1xx}+2u_0{u}_1{u}_{2xx}+u_0^2{u}_{3xx}\right)\hfill \\ \hfill & +b_2\left(u_{1x}^2{u}_1+2u_{1x}{u}_{2x}{u}_0+2u_{0x}{u}_{3x}{u}_0+2u_{0x}{u}_{2x}{u}_1+2u_{0x}{u}_{1x}{u}_2+u_{0x}^2{u}_3\right),\hfill \\ \hfill P_4& =a_1\left(u_{0x}{u}_4+u_0{u}_{4x}+u_{1x}{u}_3+u_1{u}_{3x}+u_2{u}_{2x}\right)+b_1\left(2u_{0x}{u}_{4x}+2u_{1x}{u}_{3x}+u_{2x}^2\right)\hfill \\ \hfill & +a_2(u_1^2{u}_{2xx}+2u_1{u}_2{u}_{1xx}+u_2^2{u}_{0xx}+2u_1{u}_3{u}_{0xx}+2u_0{u}_4{u}_{0xx}\hfill \\ \hfill & +2u_0{u}_3{u}_{1xx}+2u_0{u}_2{u}_{2xx}+2u_0{u}_1{u}_{3xx}+u_0^2{u}_{4xx})\hfill \\ \hfill & +b_2(u_{1x}^2{u}_2+2u_{1x}{u}_{2x}{u}_1+u_{2x}^2{u}_0+2u_{1x}{u}_{3x}{u}_0+2u_{0x}{u}_{4x}{u}_0+2u_{0x}{u}_{3x}{u}_1\hfill \\ \hfill & +2u_{0x}{u}_{2x}{u}_2+2u_{0x}{u}_{1x}{u}_3+u_{0x}^2{u}_4).\hfill \end{array}$$

(39)

The following Adomian polynomials for this example are calculated in a similar way.

We simulate the behavior of the achieved solitons on biomembranes using the algorithm described in Equation (38). This includes a test of the hypothetical parameters suggested in Table 1. The results obtained are shown in Figure 1 and Figure 2.

Table 1. Coefficients of Equation (33) used to simulate solitons in biomembranes.

Cases	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{b}}_1$	${\mathit{b}}_2$	c	${\mathit{k}}^2$	A	B	C	$\mathit{\nu }$	K	$\left|\mathbf{Max}\mathbf{Error}\right|$
1	$1.5$	$0.1$	$3.2$	$0.5$	$-1.5$	$4.0$	$1.46$	$6.05$	$1.05$	$7.67$	14	$1.5\times {10}^{-8}$
2	$-1.0$	$2.2$	$5.2$	$-3.3$	$0.03$	$1.0$	$2.05$	$5.34$	$1.55$	$1.04$	14	$2.0\times {10}^{-8}$

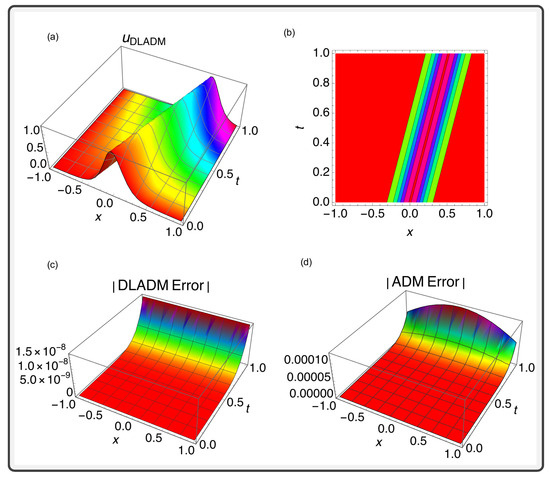
Figure 1. (a) A 3D bright soliton generated using the DLADM with 14 steps for the parameters specified in Case 1 of Table 1. (b) A 2D contour plot illustrating the soliton solution of Equation (33). (c) A graph representing the error associated with DLADM. (d) A graph showing the error associated with the ADM.

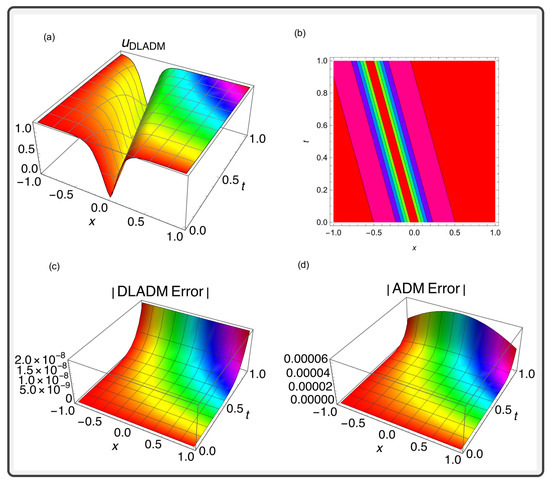
Figure 2. (a) A 3D bright soliton generated using the DLADM with 14 steps for the parameters specified in Case 2 of Table 1. (b) A 2D contour plot illustrating the soliton solution of Equation (33). (c) A graph representing the error associated with the DLADM. (d) A graph showing the error associated with the ADM.

Remark 1.

Figure 1 shows that the solutions of Equation (33) have a limited maximum height and a lowest speed of movement that matches the pulse speed in myelinated neurones [50]. Furthermore, the black soliton shown in Figure 2 shows a lot of decoherence and could harm the solitons that help with nerve transmission by causing destructive interference, which lowers the stability of neurones [51]. The errors associated with the DLADM and traditional AMD can be distinguished in both figures.

4.2. Model 2: Ion Exchange Processes

The Thomas equation [52] will be the main topic of this application problem. It is presented in its dimensional form as

$$\left\{\begin{array}{c}{u}_{xt}+{\alpha }_1{u}_t+{\alpha }_2{u}_x+{\alpha }_3{u}_x{u}_t=0,\hfill \\ u(x,0)=f\left(x\right),u_t(0,t)=g\left(t\right).\hfill \end{array}\right.$$

(40)

In this context, ${\alpha }_1$, ${\alpha }_2$, and ${\alpha }_3$ are constants that help analyze the dynamics of the system. The velocity of a flux is represented by ${\alpha }_1$, depending on the characteristics of the physical phenomenon. The flow rate variations in space at a specific time are denoted by ${\alpha }_2$. In addition, the effectiveness of the nonlinearity of the system’s behavior is also determined by the constant ${\alpha }_3$, which governs the transport of energy and velocity in space and time. Critical parameters, including the ion exchange rate and the maximal capacity of the ion exchanger, are determined using the Thomas model to predict the effectiveness of an ion exchange column.

For the problem of the existence and uniqueness of solutions for equations of the same type as Equation (40), the reader may refer to [53].

The initial conditions of the model are determined by the coefficients of Equation (40) and are specified as follows [54]:

$$u(x,0)=Ax+ln[cosh\left(Ax\right)]+C,u_t(0,t)=A\lambda t+ln[cosh\left(A\lambda t\right)]+C,$$

(41)

where A and C are constants, and the parameter $\lambda$ is defined as

$$\lambda ={\displaystyle \frac{{\alpha }_1{\alpha }_3}{2A-{\alpha }_2}},{\alpha }_2\ne 2A.$$

(42)

The algorithm that the DLADM generates to solve Equation (40) is as follows:

$$\left\{\begin{array}{c}{u}_0(x,t)={\mathcal{L}}_{xt}^{-1}\{{\displaystyle \frac{1}{s}}U(p,0)+{\displaystyle \frac{1}{p}}U(0,s)-{\displaystyle \frac{C}{ps}}\},\hfill \\ u_n(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{ps}}{\mathcal{L}}_{xt}\{L{u}_{n-1}(x,t)+P_{n-1}(u_0,u_1,\dots ,u_{n-1})\}\right\},n\ge 1.\hfill \end{array}\right.$$

(43)

The linear operator L acting on $u_{n-1}$ is given by

$$L{u}_{n-1}(x,t)={\alpha }_1{\displaystyle \frac{\partial u_{n-1}(x,t)}{\partial t}}+{\alpha }_2{\displaystyle \frac{\partial u_{n-1}(x,t)}{\partial x}}.$$

The following is a list of the first set of Adomian polynomials corresponding to the decomposition of the nonlinear operator $Nu={\alpha }_3{u}_x{u}_t$:

$$\begin{array}{cc}\hfill P_0& ={\alpha }_3{u}_{0x}{u}_{0t},\hfill \\ \hfill P_1& ={\alpha }_3(u_{0x}{u}_{1t}+u_{0t}{u}_{1x}),\hfill \\ \hfill P_2& ={\alpha }_3(u_{0x}{u}_{2t}+u_{1x}{u}_{1t}+u_{2x}{u}_{0t}),\hfill \\ \hfill P_3& ={\alpha }_3(u_{0x}{u}_{3t}+u_{1x}{u}_{2t}+u_{2x}{u}_{1t}+u_{3x}{u}_{0t}),\hfill \\ \hfill P_4& ={\alpha }_3(u_{0x}{u}_{4t}+u_{1x}{u}_{3t}+u_{2x}{u}_{2t}+u_{3x}{u}_t+u_{4x}{u}_{0t}),\hfill \\ \hfill P_5& ={\alpha }_3(u_{0x}{u}_{5t}+u_{1x}{u}_{4t}+u_{2x}{u}_{3t}+u_{3x}{u}_{2t}+u_{4x}{u}_{1t}+u_{5x}{u}_{0t}),\hfill \\ \hfill P_6& ={\alpha }_3(u_{0x}{u}_{6t}+u_{1x}{u}_{5t}+u_{2x}{u}_{4t}+u_{3x}{u}_{3t}+u_{4x}{u}_{2t}+u_{5x}{u}_{1t})+u_{6x}{u}_{0t}).\hfill \end{array}$$

(44)

The solution $u(x,t)$ of Equation (40) increases our comprehension of the temporal distribution of ions in the chemical process, probably related to water potabilization treatment. We simulate the behavior of $u(x,t)$ using the algorithm described in Equation (40). This includes a test of the hypothetical parameters suggested in Table 2. The simulation’s graphical representations are displayed in Figure 3.

Table 2. Coefficients of the Thomas Equation (40) to simulate $u(x,t)$.

Case	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\alpha }}_3$	K-Steps	DLADM $\left|\mathbf{Max}\mathbf{Error}\right|$	ADM $\left|\mathbf{Max}\mathbf{Error}\right|$
1	$4.0$	$2.2$	$1.5$	14	$4.0\times {10}^{-7}$	$8.1\times {10}^{-4}$

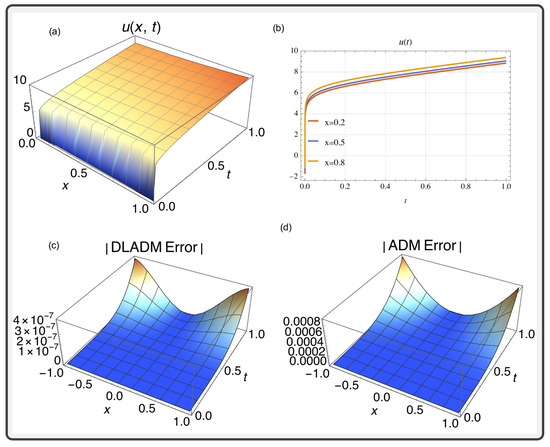
Figure 3. (a) A 3D plot solution using the DLADM and 14 steps for the parameters given in Case 1 of Table 2. (b) The breakthrough curves of the Thomas equation for adsorption varying with time for $t\in [0,1]$ in a fixed-bed adsorption column at $x=0.2$, $x=0.5$, and $x=0.8$. (c) DLADM error graph. (d) ADM error graph. Consider $A=3$ and $C=8$.

Remark 2.

Figure 3 shows that the breakthrough curve starts with a low dimensionless concentration, meaning the adsorbent is effectively removing the adsorbate. As time advances, the adsorbent reaches saturation, and the dimensionless concentration rises, ultimately nearing an upper limit value, signifying that the effluent concentration approximates the initial intake concentration, indicating column exhaustion. This graph representation is a crucial illustration in chemical engineering for comprehending and planning adsorption processes. Understanding the dynamics of this groundbreaking curve is essential for optimizing the design and operation of adsorption systems. By analyzing the curve, engineers can determine the optimal conditions for maximum efficiency and longevity in the adsorbent material. Additionally, the same figure displays the errors committed by both the DLADM and the classic ADM technique.

4.3. Model 3: Schrödinger Equation with Defocusing Strength Nonlinearities

The nonlinear Schrödinger equation (NLSE) is a crucial equation in numerous fields of physics and mathematics, characterizing the evolution of wave packets in nonlinear mediums. The current study will examine the one-dimensional NLSE expressed as follows:

$$i{u}_t=-u_{xx}+g\left(x\right){\left|u\right|}^{2}u,t\ge 0.$$

(45)

The amplitude of the field is denoted by $u(x,t)$ in Equation (45), and the strength of the nonlinearity that varies along the x spatial direction is denoted by $g\left(x\right)$. The dynamics of matter waves in a Bose–Einstein condensate (BEC) can be described using Equation (45). In BEC systems, nonlinearity that varies spatially can occur due to Feshbach resonance influenced by changing external fields [55].

For the problem of the existence and uniqueness of solutions for equations of the same type as Equation (45), the reader may refer to [56].

The initial condition for the model described by Equation (45), with regard to bright solitons, can be determined as follows [57]:

$$u(x,0)=e^{-{\displaystyle \frac{x^2}{4}}}.$$

(46)

The algorithm that the DLADM generates to solve Equation (45) is as follows:

$$\left\{\begin{array}{c}{u}_0(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s}}U(p,0)\right\},\hfill \\ u_n(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s}}{\mathcal{L}}_{xt}\{-L{u}_{n-1}(x,t)+P_{n-1}(u_0,u_1,\dots ,u_{n-1})\}\right\},n\ge 1.\hfill \end{array}\right.$$

(47)

The linear operator L acting on $u_{n-1}$ is given by

$$L{u}_{n-1}=i{\displaystyle \frac{{\partial }^2{u}_{n-1}(x,t)}{\partial x^2}}.$$

The following is a list of the first set of Adomian polynomials corresponding to the decomposition of the nonlinear operator $Nu=-ig\left(x\right)u^2{u}^{*}$:

$$\begin{array}{cc}\hfill P_0& =-ig\left(x\right)\left(u_0^2{u}_0^{*}\right),\hfill \\ \hfill P_1& =-ig\left(x\right)(2u_0{u}_1{u}_0^{*}+u_0^2{u}_1^{*}),\hfill \\ \hfill P_2& =-ig\left(x\right)(2u_0{u}_2{u}_0^{*}+u_1^2{u}_0^{*}+2u_0{u}_1{u}_1^{*}+u_0^2{u}_2^{*}),\hfill \\ \hfill P_3& =-ig\left(x\right)(2u_0{u}_3{u}_0^{*}+2u_1{u}_2{u}_0^{*}+2u_0{u}_2{u}_1^{*}+u_1^2{u}_1^{*}+2u_0{u}_1{u}_2^{*}+u_0^2{u}_3^{*}),\hfill \\ \hfill P_4& =-ig\left(x\right)(u_0^{*}{u}_2^2+2u_0{u}_0^{*}{u}_4+2u_0^{*}{u}_1{u}_3+2u_0{u}_1^{*}{u}_3+2u_1{u}_1^{*}{u}_2+2u_0{u}_2^{*}{u}_2+u_1^2{u}_2^{*}+2u_0{u}_1^{*}{u}_3+u_0^2{u}_4^{*}).\hfill \end{array}$$

(48)

Feshbach resonances are a crucial tool for controlling interactions between atoms in ultracold quantum gases. They have led to numerous experimental applications, paving the way for significant breakthroughs. Consequently, identifying soliton-type solutions for Equation (45) would greatly enhance our understanding of this physical phenomenon.

In the following, using the recurrence relations given by Equation (47) already found for the problem (45), we evaluate the effectiveness of the DLADM in solving the NLSE with ${g\left(x\right)\left|u\right|}^{2}u$ as the nonlinear potential where $g\left(x\right)$ is a nonconstant function.

We perform a simulation using the DLADM considering $g\left(x\right)=(1+x^2)e^{{\displaystyle \frac{x^2}{2}}}$ and the initial condition $u(x,0)=e^{-{\displaystyle \frac{x^2}{4}}}$ with the number of steps $K=14$. The graphical results are shown in Figure 4. Moreover, the errors committed for different values of t and at different values of x are shown in Table 3.

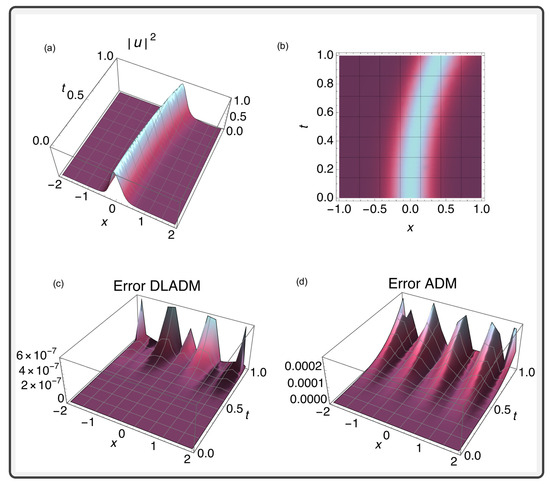
Figure 4. (a) A 3D bright soliton simulation for the NLSE using the DLADM with $K=14$ steps. (b) A 2D density plot illustrating the soliton solution of Equation (45). (c) DLADM error graph. (d) ADM error graph.

Table 3. The absolute error when $t=0.25$, $t=0.50$, and $t=0.75$ for bright soliton simulation.

x	Absolute Error at $\mathit{t}=0.25$	Absolute Error at $\mathit{t}=0.50$	Absolute Error at $\mathit{t}=0.75$
$-0.75$	$5.12\times {10}^{-8}$	$4.91\times {10}^{-7}$	$9.16\times {10}^{-6}$
$-0.50$	$4.05\times {10}^{-8}$	$7.23\times {10}^{-7}$	$8.32\times {10}^{-6}$
$-0.25$	$2.80\times {10}^{-9}$	$5.66\times {10}^{-8}$	$7.55\times {10}^{-7}$
$0.25$	$3.05\times {10}^{-9}$	$5.48\times {10}^{-8}$	$7.37\times {10}^{-7}$
$0.50$	$4.27\times {10}^{-8}$	$6.79\times {10}^{-7}$	$8.15\times {10}^{-6}$
$0.75$	$4.96\times {10}^{-8}$	$5.13\times {10}^{-7}$	$8.96\times {10}^{-6}$

In Appendix A, we can explicitly see the values that the simulation using Mathematica software version 14.2.1 yields for both the first Adomian polynomials $P_i$ and the successive approximations $u_i$ to the solution u.

Remark 3.

The complex laws revealed through wave packet analysis highlight the profound impact of coefficients’ arrangements on the behavior of wave packets, as shown in the graphs in Figure 4. These images show how specific arrangements of nonlinear terms and position-dependent coefficients can create localized structures, leading to solitons that behave differently from regular waves. Furthermore, numerical simulations provide an interesting perspective on the time evolution of these solutions, showcasing their susceptibility to complex phenomena such as wave breaking and dispersion. Understanding these effects is crucial for optimizing performance in advanced fiber-optic communication systems. Additionally, the same figure displays the errors committed by both the DLADM and the classic ADM technique.

4.4. Model 4: Allen–Cahn Equation

The Allen–Cahn equation is an important one in mathematical physics that explains how different parts of multi-component alloy systems separate, including changes from order to disorder. Disorder can lead to various microstructural changes that significantly influence the material properties. By understanding the processes described by the Allen–Cahn equation, researchers can anticipate and manage the changes in multi-component alloy systems. This understanding enhances the performance of these systems in real-world applications. The equation is named after John W. Cahn and Sam Allen, who developed it in the 1970s [58].

The Allen–Cahn equation that is the subject of this example is as described as follows:

$$u_t=u_{xx}+g\left(t\right)(u^3-u),t\ge 0.$$

(49)

In Equation (49), $u(x,t)$ denotes the variation between the concentrations of two components in a mixture, reflecting the material’s condition at location x and time t, while $g\left(t\right)$ is a positive periodic function [59]. The Allen–Cahn equation is an effective tool for the simulation and comprehension of delicate phenomena that involve phase transformations and interfaces.

In Appendix C, the reader will find a proof that demonstrates the existence and uniqueness of weak solutions for the Allen–Cahn equation using a variational formulation, given a specific type of initial condition.

The initial condition for the model given by Equation (49), assuming periodic solutions, may be established as follows [59]:

$$u(x,0)=sin\left(\pi x\right).$$

(50)

The algorithm that the DLADM generates to solve Equation (49) is as follows:

$$\left\{\begin{array}{c}{u}_0(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s}}U(p,0)\right\},\hfill \\ u_n(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s}}{\mathcal{L}}_{xt}\{L{u}_{n-1}(x,t)+P_{n-1}(u_0,u_1,\dots ,u_{n-1})\}\right\},n\ge 1.\hfill \end{array}\right.$$

(51)

The linear operator L acting on $u_{n-1}$ is given by

$$L{u}_{n-1}={\displaystyle \frac{{\partial }^2{u}_{n-1}(x,t)}{\partial x^2}}+g\left(t\right)u_{n-1}.$$

The following is a list of the first set of Adomian polynomials corresponding to the decomposition of the nonlinear operator $Nu=g\left(t\right)u^3$:

$$\begin{array}{cc}\hfill P_0& =g\left(t\right)\left(u_0^3\right),\hfill \\ \hfill P_1& =g\left(t\right)\left(3u_0^2{u}_1\right),\hfill \\ \hfill P_2& =g\left(t\right)(3u_0^2{u}_2+3u_0{u}_1^2),\hfill \\ \hfill P_3& =g\left(t\right)(3u_0^2{u}_3+6u_0{u}_1{u}_2+u_1^3),\hfill \\ \hfill P_4& =g\left(t\right)(3u_0^2{u}_4+6u_0{u}_1{u}_3+3u_0{u}_2^2+3u_1^2{u}_2),\hfill \\ \hfill P_5& =g\left(t\right)(3u_0^2{u}_5+6u_0{u}_1{u}_4+6u_0{u}_2{u}_3+3u_1^2{u}_3+3u_1{u}_2^2).\hfill \end{array}$$

(52)

We perform a simulation using the DLADM considering $g\left(t\right)=10cos\left(t\right)+11$ and the initial condition $u(x,0)=sin\left(\pi x\right)$ with the number of steps $K=15$. The graphical results are shown in Figure 5. Moreover, the errors committed for different values of t and at different values of x by the DLADM and ADM are shown in Table 4 and Table 5, respectively.

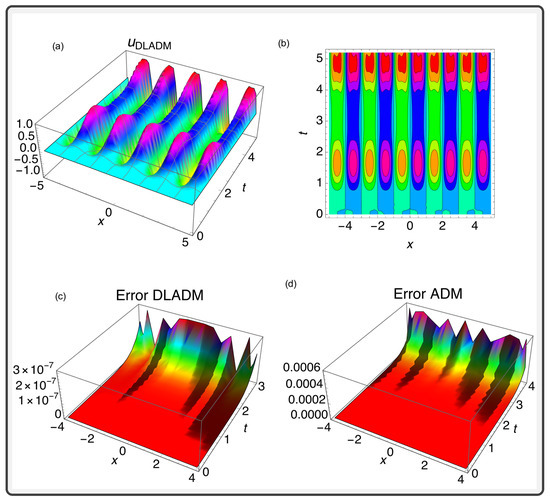
Figure 5. (a) A 3D plot of the simulation of the periodic solution for the Allen–Cahn equation using the DLADM with $K=15$ steps. (b) A 2D contour plot illustrating the soliton solution of Equation (49). (c) DLADM error graph. (d) ADM error graph.

Table 4. The absolute error by the DLADM when $t=1.0$, $t=2.0$, and $t=3.0$ for the periodic solution for the Allen–Cahn equation.

x	Absolute Error at $\mathit{t}=1.0$	Absolute Error at $\mathit{t}=2.0$	Absolute Error at $\mathit{t}=3.0$
$-4.0$	$3.52\times {10}^{-7}$	$8.91\times {10}^{-6}$	$9.76\times {10}^{-5}$
$-3.0$	$3.02\times {10}^{-7}$	$6.53\times {10}^{-7}$	$7.35\times {10}^{-6}$
$-2.0$	$2.90\times {10}^{-8}$	$5.96\times {10}^{-7}$	$4.15\times {10}^{-6}$
$-1.0$	$1.05\times {10}^{-8}$	$4.38\times {10}^{-8}$	$2.57\times {10}^{-7}$
$1.0$	$1.22\times {10}^{-8}$	$4.45\times {10}^{-8}$	$2.15\times {10}^{-7}$
$2.0$	$2.96\times {10}^{-8}$	$5.66\times {10}^{-7}$	$4.56\times {10}^{-6}$
$3.0$	$3.05\times {10}^{-7}$	$7.01\times {10}^{-7}$	$7.90\times {10}^{-6}$
$4.0$	$3.47\times {10}^{-7}$	$8.85\times {10}^{-7}$	$9.84\times {10}^{-5}$

Table 5. The absolute error by the ADM when $t=1.0$, $t=2.0$, and $t=3.0$ for the periodic solution for the Allen–Cahn equation.

x	Absolute Error at $\mathit{t}=1.0$	Absolute Error at $\mathit{t}=2.0$	Absolute Error at $\mathit{t}=3.0$
$-4.0$	$5.22\times {10}^{-5}$	$9.33\times {10}^{-4}$	$8.34\times {10}^{-3}$
$-3.0$	$4.55\times {10}^{-5}$	$8.43\times {10}^{-4}$	$7.03\times {10}^{-3}$
$-2.0$	$2.46\times {10}^{-5}$	$6.60\times {10}^{-4}$	$6.10\times {10}^{-3}$
$-1.0$	$1.34\times {10}^{-5}$	$4.95\times {10}^{-4}$	$5.76\times {10}^{-3}$
$1.0$	$1.44\times {10}^{-5}$	$5.56\times {10}^{-4}$	$6.66\times {10}^{-3}$
$2.0$	$2.45\times {10}^{-5}$	$5.98\times {10}^{-4}$	$4.56\times {10}^{-3}$
$3.0$	$3.95\times {10}^{-5}$	$8.78\times {10}^{-4}$	$7.70\times {10}^{-3}$
$4.0$	$5.88\times {10}^{-5}$	$9.45\times {10}^{-4}$	$8.78\times {10}^{-3}$

In Appendix B, we can explicitly see the values that the simulation using Mathematica software version 14.2.1 yields for both the first Adomian polynomials $P_i$ and the successive approximations $u_i$ to the solution u.

Remark 4.

Figure 5 shows a solution of the Allen–Cahn equation for phase separation on a rectangular domain with periodic initial conditions. Phase separation occurs in mixtures of two substances with different properties, such as metals in certain alloys. Understanding the dynamics of phase separation through mathematical models like the Allen–Cahn equation is key to maximizing material design and performance. Additionally, the same figure displays the errors committed by both the DLADM and the classic ADM technique.

4.5. Model 5: Nonlinear Black–Scholes Equation with Variable Volatility

In financial mathematics, the Black–Scholes–Merton equation is a fundamental PDE. The development of this equation in 1973 by Fischer Black and Myron Scholes, along with subsequent contributions from Robert Merton, transformed the field of option pricing and laid a crucial foundation for modern finance theory [60,61].

In the past thirty years, there has been increased interest in nonlinear Black–Scholes equations due to their ability to provide more accurate valuations by incorporating real-world factors. These factors include transaction costs, risks associated with an unprotected portfolio, the preferences of large investors, and the conditions of illiquid markets. Such elements can influence stock prices, volatility, drift, and option pricing.

The present problem treats the nonlinear Black–Scholes equation, in which the nonlinearities are influenced by illiquid markets and the behavior of large traders, expressed as follows [62]:

$$\left\{\begin{array}{c}{u}_t+{\displaystyle \frac{1}{2}}{\sigma }^2{x}^2{u}_{xx}(1+2\rho x{u}_{xx})+rx{u}_x-ru=0,\hfill \\ u(x,0)=f\left(x\right),x\in [0,\infty ).\hfill \end{array}\right.$$

(53)

where u represents the option price as a function of the underlying price x and time t. Furthermore, we assume that the interest rate r and volatility $\sigma$ are non-negative constants, whereas $\rho$ is a constant that describes the price of risk.

For the problem of the existence and uniqueness of solutions for equations of the same type as Equation (53), the reader may refer to [63].

The algorithm that the DLADM generates to solve Equation (53) is as follows:

$$\left\{\begin{array}{c}{u}_0(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s}}U(p,0)\right\},\hfill \\ u_{n+1}(x,t)={\mathcal{L}}_{xt}^{-1}\left\{{\displaystyle \frac{1}{s}}{\mathcal{L}}_{xt}\{-L{u}_n(x,t)-P_n(u_0,u_1,\dots ,u_n)\}\right\},n\ge 0.\hfill \end{array}\right.$$

(54)

In this problem, the linear operator L acting on $u_n$ is given by

$$L{u}_n={\displaystyle \frac{1}{2}}{\sigma }^2{x}^2{\displaystyle \frac{{\partial }^2{u}_n(x,t)}{\partial x^2}}+rx{\displaystyle \frac{\partial u_n(x,t)}{\partial x}}-r{u}_n.$$

The following is a list of the first set of Adomian polynomials corresponding to the decomposition of the nonlinear operator $Nu=\rho {\sigma }^2{x}^3{u}_{xx}^2$:

$$\begin{array}{cc}\hfill P_0& =\rho {\sigma }^2{x}^3\left(u_{0,xx}^2\right),\hfill \\ \hfill P_1& =\rho {\sigma }^2{x}^3\left(2u_{0,xx}{u}_{1,xx}\right),\hfill \\ \hfill P_2& =\rho {\sigma }^2{x}^3(2u_{0,xx}{u}_{2,xx}+u_{1,xx}^2),\hfill \\ \hfill P_3& =\rho {\sigma }^2{x}^3(2u_{0,xx}{u}_{3,xx}+2u_{1,xx}{u}_{2,xx}),\hfill \\ \hfill P_4& =\rho {\sigma }^2{x}^3(2u_{0,xx}{u}_{4,xx}+2u_{1,xx}{u}_{3,xx}+u_{2,xx}^2),\hfill \\ \hfill P_5& =\rho {\sigma }^2{x}^3(2u_{0,xx}{u}_{5,xx}+2u_{1,xx}{u}_{4,xx}+2u_{2,xx}{u}_{3,xx}).\hfill \end{array}$$

(55)

We perform a simulation using the DLADM with the number of steps $N=14$ and considering the initial condition $u(x,0)=x+10(x^2+2)$. In addition, let us consider the model data $\sigma =0.5$, $\rho =0.1$, and $r=1.2$. The graphical results are shown in Figure 6.

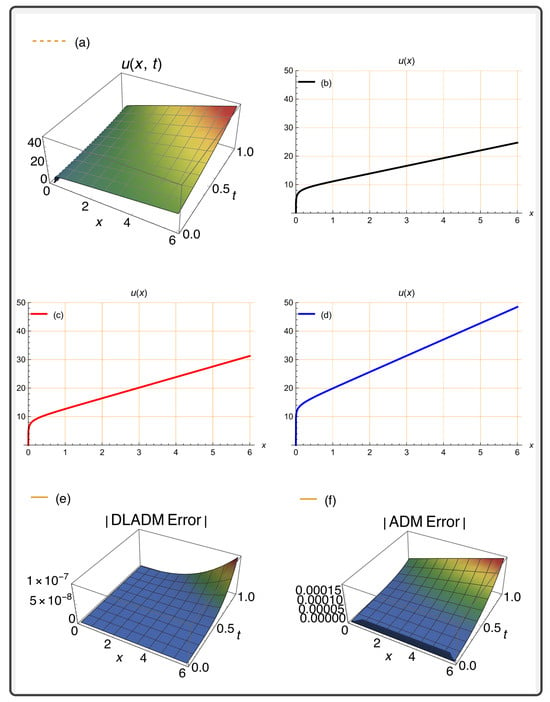
Figure 6. (a) A 3D simulation for the option price using the DLADM with $K=14$ steps. (b) Option price at time $t=0.25$ years. (c) Option price at time $t=0.5$ years. (d) Option price at time $t=1.0$ years. (e) DLADM error graph. (f) ADM error graph.

Remark 5.

Figure 6 shows that the option always exceeds the price of the underlying asset as a result of variable volatility. The Black–Scholes model remains a fundamental element of quantitative finance and an essential instrument for comprehending and valuing derivatives. Numerous extensions and changes have been created to mitigate its limits and adapt it to more complex financial instruments. The errors made by both the DLADM and the traditional ADM approach are shown in the same figure.

5. Conclusions

This article introduces a novel approach, the DLADM, for resolving nonlinear problems associated with applied mathematics. Several fields, including neuroscience, chemical kinetics, nonlinear optics, metallurgical separation processes, and finance, implement numerical simulations in their mathematical models. The DLADM facilitates the searching of numerical solutions with significantly less error, eliminating the need for linearization or discretization, hence enhancing result accuracy. The findings are pertinent to natural science and mathematical modeling, presenting new opportunities for investigating intricate processes. This study represents the first report of numerical simulations using this technology, emphasizing its potential for practical applications.