1. Introduction
The max-cut problem is a well-known NP-hard problem in graph theory. It has several applications in different domains, including computer science, engineering, and physics [
1]. Over the years, numerous exact algorithmic approaches have been proposed to solve the max-cut problem, with notable solvers such as BiqBin and BiqMac gaining recognition [
2,
3]. Despite advancements, solving the max-cut problem optimally remains a computational challenge, even for moderately sized instances [
1,
4]. As a result, approximation and heuristic algorithms are often employed to find near-optimal solutions efficiently [
5].
Commander [
6] suggested a heuristic solution for the max-cut problem, utilizing a continuous greedy randomized adaptive search technique to enhance the modeling capabilities. Building on this, Muñoz-Arias et al. [
7] explored the performance of the Goemans and Williamson approximation algorithm on various graph families, including K-regular and weighted complete graphs. Similarly, Wang et al. [
8] introduced the concept of a relation tree to represent graph cuts and compared multiple solving algorithms across graph classes to evaluate their relative effectiveness. Dolezal et al. [
9] contributed a comparative analysis of several approximation strategies, highlighting the conditions under which each performs optimally.
In recent decades, a shift has occurred toward more refined relaxation techniques, particularly those rooted in semidefinite programming (SDP) and Lagrangian duality [
10]. Charfreitag et al. [
11] proposed an improved integer programming formulation for max-cut, employing odd-cycle inequalities within branch-and-cut frameworks to strengthen the linear relaxation and reduce the solving time for dense graphs. Hrga and Povh [
12] investigated augmented Lagrangian methods for solving the SDP relaxation of the max-cut problem. Their use of L-BFGS-B optimization demonstrated high-quality upper bounds for instances.
Lu et al. [
13] developed a branch-and-bound (B&B) algorithm based on SDP relaxations, incorporating a novel hierarchical decomposition strategy. Their approach achieved considerable computational gains over methods such as BiqCrunch and bundle. A critical contribution in this domain is by Gruber and Rendl [
14], who introduced the bundle method to efficiently solve Lagrangian relaxations of combinatorial optimization problems. By maintaining a compact cutting plane model, they demonstrated scalability and solution accuracy, laying the groundwork for further hybrid methods.
Expanding on this, Rendl et al. [
15] combined SDP and polyhedral relaxations into a B&B strategy, using the bundle method for upper bound calculations. Their algorithm proved highly effective for dense graphs with up to 100 nodes. More recently, Gu and Yang [
16] applied pointer networks and reinforcement learning to approximate max-cut solutions in large graphs, reflecting a growing synergy between combinatorial optimization and deep learning techniques. Avinash [
17] analyzed the exactness of SDP relaxations, identifying graph structures where these relaxations are tight and establishing conditions for solution uniqueness.
Many researchers have proposed algorithms to solve the max-cut problem, relying on various approximation methods such as the interior point method and the penalty method [
18,
19,
20]. However, these approaches are generally inefficient for solving optimization problems with a large number of constraints. In contrast, the bundle method is more efficient than previous methods in solving optimization problems with a large number of constraints, particularly for large-scale graphs. This efficiency stems from the bundle method’s ability to approximate the non-smooth objective function using multiple subgradients gathered across iterations, rather than relying solely on local information like gradient-based methods. Furthermore, instead of incorporating all the constraints explicitly in each iteration, the bundle approach leverages Lagrangian relaxation and constructs moderately sized subproblems, which dramatically reduces the computational burden. As Gruber and Rendl [
14] demonstrate, this allows for rapid and scalable optimization, making the bundle method particularly well suited for large-scale combinatorial problems.
Building on this advantage, this study proposes a bundle-method-based algorithm specifically designed to efficiently solve the max-cut problem on large-scale graphs. The proposed approach achieved high-quality SDP bounds with fewer computations and a shorter processing time compared to existing methods.
This article is organized as follows.
Section 2 introduces the key concepts necessary for this study, including semidefinite programming, combinatorial optimization, and general bundle methods. It also describes the new SDP relaxation applied to the max-cut problem, and outlines our proposed method for computing SDP bounds, including a convergence analysis.
Section 3 presents the numerical results, which are analyzed in detail in
Section 4. Finally,
Section 5 concludes the paper with a summary of the findings.
2. Materials and Methods
2.1. Semidefinite Programming
Semidefinite programming (SDP) is a significant category of convex optimization problems that aim to optimize a linear objective function [
20]. To mathematically formulate SDP problems, let
represent the collection of all real symmetric matrices of dimension
. The notation
signifies that
is a positive semidefinite matrix. Moreover, define
as the collection of all positive semidefinite matrices. The primal problem of SDP is given by the following:
where
and
constitute the given problem data [
21].
And the dual problem of SDP is formulated as follows:
2.2. Problem Formulation
The central problem under consideration is the max-cut problem, which holds a significant position within the class of combinatorial optimization problems. Due to its broad applicability across various fields, semidefinite programming (SDP) serves as a powerful tool for tackling it. Goemans and Williamson presented a fundamental approach using SDP, attaining a 0.878-approximation for max-cut in polynomial time [
22,
23]. The max-cut problem aims to divide the set of
vertices in an undirected graph
into two subsets,
and
, where
, to maximize the number of edges connecting
and
[
24]. To mathematically define max-cut, let
represent an assignment of vertices to clusters. Associate weights
with each edge
, where
if
and
are not connected by an edge. The max-cut problem can be defined by the following [
25]:
2.3. Semidefinite Relaxation of the Max-Cut Problem
This subsection presents a concise overview of the standard SDP relaxation and its dual formulation for the max-cut problem. For further technical details, the reader is referred to source [
25]. The focus here, however, is on the proposed SDP relaxation.
The basic SDP relaxation of the max-cut is given by the following:
where
is a symmetric positive semidefinite matrix,
is the Laplace matrix of the graph, and
is the all-ones vector. Its dual formulation is expressed as follows:
where
is the dual variable vector associated with the diagonal constraint on
.
Our approach to semidefinite relaxation formulates the SDP without considering the complete graph. Instead, we index the matrix variable solely with pairs of nodes that correspond to non-zero weighted edges—specifically, those included in the edge set
. Let
,
; it is defined as follows:
This construction represents the structure of a cut using a binary vector
, where each entry indicates the partition assignment of a node. The scalar component
erves as a normalization term, while each entry
reflects the relative position of nodes
and
with respect to the cut, based on the product
for edges
. Accordingly, the vector
takes the following form:
A product of this vector yields the matrix
, whose block matrix form is denoted by the following:
To guarantee that is consistent with an underlying cut, certain equality constraints must be satisfied. These include the following:
Four-cycle symmetry constraint:
Additional 4-cycle condition:
Equation (9a,b) have already been trivially proven to hold for matrices derived from a valid cut vector . Equation (9c) can be justified by the following:
If
, then the corresponding triangle constraints must be satisfied:
Since no constraints exist for this edge, the following condition can be added:
To define the cost structure of the relaxation, a matrix
is constructed using the graph Laplacian
. Its entries are defined as follows:
Thus,
takes the following structured form:
is associated with a cut
, then the entries satisfy the following condition:
This behavior implies that the inner product computes the weight of the cut .
Based on this derivation, the following SDP relaxation is obtained:
Here, represents a set of equality constraints—including triangle relations and, when applicable, 4-cycle conditions—that ensure the structural integrity of the cut within the graph.
2.4. The Bundle Method
The bundle method enhances the convergence rate and numerical stability of the cutting plane method by integrating a regularization strategy [
26]. Unlike the cutting plane method, which relies solely on the lower approximation function, the bundle method refines its iterates by solving a regularized master problem, effectively taking a proximal step towards the lower approximation model
:
where
represents the current reference point, while
serves as a penalty for deviations from
. The bundle method updates the iterate
only when the decrease in the objective function
meets or exceeds a specified fraction of the reduction predicted by the approximated model
. Specifically,
; this ensures controlled and effective progress in optimization.
Otherwise, if sufficient progress is not achieved, we retain the previous iterate with
(null step). In either case, the subgradient
at the new point
is used to refine the lower approximation
. Specifically, this can be updated using the following:
In particular, the bundle method ensures convergence, provided that the lower approximation model satisfies the following three key properties for all :
Minorant: The function
serves as a lower bound for
, ensuring that
Subgradient lower bound: The function
is bounded below by the linearization defined by a subgradient
. Specifically, it satisfies the following:
Model subgradient lower bound: The function
is lower-bounded by the linearization of the previous model
, given by the following:
where
certifies the optimality of
for Problem (15).
With these foundations in place, the general algorithm for the bundle method is now presented in Algorithm 1 [
2,
10]:
| Algorithm 1. Bundle Method |
| Input: , , , , . |
| for do |
| Repeat: solve (15) to obtain a candidate iterate . |
| if (16) satisfied then |
| set . |
| else . |
| end if |
| Update approximation model without violating (18a)–(18c). |
| if stopping criterion then |
| Quit |
| end if |
| end for |
2.5. Proposed Method
The semidefinite relaxation of the max-cut problem is given in Equation (14) and is addressed through the proposed solution framework. The method can be derived as follows:
Let
, where the constraint
ensures positive semidefiniteness and
enforces unit values on the diagonal to approximate the binary structure. Thus, Equation (14) is equivalent to the SDP relaxation.
To derive its dual, the Lagrangian is introduced as follows:
This formulation incorporates the constraint into the objective via the dual variable
. The corresponding dual function is as follows:
The expression reflects the interaction between the original objective function and the constraint structure within the dual formulation.
Whenever
, the subgradient
provides the constraint residual, which is essential for bundle-based subgradient updates.
The Lagrangian dual problem is then as follows:
Under standard convexity conditions, the equality between the primal and dual optima holds due to strong duality. To approximate the dual function computationally, a bundle of matrices
is employed, and the following approximation is defined:
The feasible set is now restricted to a polyhedral subset, reducing computational complexity. Each can be expressed as a convex combination where .
At each iteration, a regularized minimization is performed to stabilize updates:
where
and the proximal term
stabilizes convergence by penalizing large deviations from the current center
. This formulation ensures smoothness and convergence through proximal regularization.
Introducing notation: define
,
, and
. Then,
is as follows:
This linear reformulation in enables an efficient evaluation of the approximate dual function at each iteration.
In the following, a detailed outline of the algorithm developed to solve the semidefinite relaxation of the max-cut problem, as formulated in Equation (14), is presented.
2.6. Convergence of the Method
Problem (25) to be solved can be defined by the following:
Also, in Equation (26), the inner product is a convex quadratic unconstrained problem in
; then, by sitting
, the minimizer is obtained:
By substituting Equation (28) into Equation (27), the following result can be derived:
This convex quadratic problem over Λ can be solved more efficiently using an interior point approach. Consequently, the convergence of Algorithm 2 is supported by Robinson’s analysis within the convergence theory for the bundle approach [
27].
| Algorithm 2. Our proposed technique for Solving |
| Input: Define , and b, |
| with initial point (optimal), |
| and parameters t, α and ε. |
| Start: , done = false. |
| Evaluate at . |
| Solve max s.t. givining , |
| , |
| Subgradient . |
| Repeat: solve (25), which is minimized (26) and obtain. |
| . |
| . |
| if and |
| Evaluate at . |
| Solve max s.t. givining , |
| , |
| Subgradient . |
| if |
| Serious step: |
| Increase |
| else |
| Null step: decrease . |
| Append to , to and to . |
| . |
| else |
| done |
Algorithm 2 is more efficient for solving graphs containing a star because it leverages the relaxation method . This method possesses a significant property: the bound it provides is at least as strong as the bound obtained from solving ). This is formally demonstrated in the following theorem.
Theorem 1. Suppose there exists a vertex such that . Then, the upper bound obtained from is at least as strong as the bound from ).
Proof of Theorem 1. Let Y be the optimal solution to the relaxation problem (
) and
with
. Define the matrix
is given by the following:
For all That is, is the principal submatrix of formed by selecting the rows and columns indexed by . Since is a solution of (), we have ; it follows that .
Furthermore, because is the principal submatrix of , and is a positive semidefinite matrix, this implies that is also positive semidefinite. Furthermore, we obtain . Hence, is a feasible solution for , and consequently, the optimal value of is at least . □
2.7. BiqMac and BiqBin Solvers
The BiqMac and BiqBin solvers are widely recognized as two of the most potent techniques for tackling binary quadratic problems. The foundation of BiqMac is the enhanced SDP relaxation. By solely dialyzing the triangle inequality requirements with dual variable
, the authors derived the partial dual function:
Assessing the dual function and calculating a subgradient necessitates resolving a semidefinite program of the model
, which can be efficiently handled by utilizing an interior-point approach specifically designed for the problem. To approximate the minimizer of the dual problem,
The bundle approach is employed. BiqBin further strengthens this by dialyzing both pentagonal and heptagonal inequalities. Consequently, the bundle approach is employed to optimize the partial dual function of , providing an even more refined approach to solving binary quadratic problems.
3. Results
In this test, the proposed method was compared with two semidefinite exact solvers: BiqBin and BiqMac. A wide variety of test problems (or graphs) were collected from the BiqMac library. The instances of those problems were taken from sources [
24,
25]. Here, the numerical results of the proposed approach, along with those of BiqMac and BiqBin, are presented for the aforementioned graphs. Throughout this section, the dimension, the number of edges, and the density of the graph are denoted by
,
, and
, respectively.
3.1. Experimental Setup
All the computational experiments were conducted on a personal workstation equipped with an Intel Core i7-12700H processor (14 cores, 20 threads), 32 GB of RAM, and the 64-bit version of Windows 11. The proposed algorithm, along with the baseline solvers BiqMac and BiqBin, was implemented in Python 3.10 using standard numerical libraries, including NumPy and CVXPY.
To ensure statistical reliability, each problem instance was executed five times under identical hardware and software conditions. The reported CPU time reflects the mean value, accompanied by the standard deviation. As all the algorithms considered in this study are deterministic, the variation across runs was negligible. Nonetheless, pairwise comparisons using the Wilcoxon signed-rank test were performed on selected performance metrics to further ensure robustness and fairness in the evaluation.
Additionally, three key metrics were used to evaluate the performance: (1) the CPU time, which measures the elapsed wall-clock time and reflects the computational efficiency under consistent system conditions; (2) the number of function calls, indicating the algorithmic cost in evaluating the objective function or its gradient; and (3) the number of iterations, highlighting the convergence behavior and algorithmic stability. Collectively, these metrics provide a comprehensive assessment of the computational and optimization performance, enabling a robust and balanced comparison across methods.
3.2. Numerical Results of Instances Introduced by Glover, Kockenberger, and Alidaee
In
Table 1,
Table 2 and
Table 3, the set of instances introduced by Glover, Kockenberger, and Alidaee (denoted by gka) were applied as shown. The properties of the applied problems of the numerical results are outlined in the following points:
The collection of instances represented by gka_i_c is characterized by ∈ [40, 100] and ∈ [0.1, 0.8]. Also, the diagonal and off-diagonal coefficients are located in the intervals [−100, 100] and [−50, 50], respectively.
The collection of instances represented by gka_i_d is characterized by = 100 and ∈ [0.1, 0.8]. Also, the diagonal and off-diagonal coefficients are located in the intervals [−100, 100] and [−50, 50], respectively.
The collection of instances represented by gka_i_e is characterized by = 200 and ∈ [0.1, 0.5]. Moreover, their diagonal and off-diagonal coefficients are located in the intervals [−100, 100] and [−50, 50], respectively.
Table 1,
Table 2 and
Table 3 present the raw performance metrics obtained from solving instances of the gka benchmark sets using our proposed method and the BiqMac and BiqBin solvers. These metrics include the number of iterations, the number of function calls, and the CPU time required to reach convergence across a range of instance sizes and densities.
To statistically validate the performance differences, the Wilcoxon signed-rank test was applied to the CPU time results between our proposed method and each baseline (BiqMac and BiqBin) across all problem sets. This non-parametric test was selected due to its robustness and suitability for paired comparisons of performance measures without assuming normality. The test results, which are summarized in
Table 4, indicate that the observed improvements were statistically significant in cases (
p < 0.05), particularly favoring the bundle method in terms of the computational efficiency.
These findings reinforce the consistency and robustness of the proposed algorithm, supporting its advantage over existing methods when solving gka instances of varying complexity.
3.2.1. Interpretation of Statistical Test Results for gka Instances
The outcomes of the Wilcoxon signed-rank test, summarized in
Table 4, provide strong statistical evidence in favor of the proposed method. For all problem sets examined (
gka_i_c,
gka_i_d, and
gka_i_e), the
p-values were consistently below the 0.05 significance threshold, indicating that the observed reductions in the CPU time were unlikely due to random variation. Particularly notable are the cases where the W-statistic equaled 0.0 or 1.0, reflecting a consistent dominance of the proposed method across nearly all instance comparisons. These findings highlight the method’s robustness and computational efficiency, reinforcing its suitability as a competitive alternative to existing solvers.
3.2.2. Numerical Results of Graph gka3d
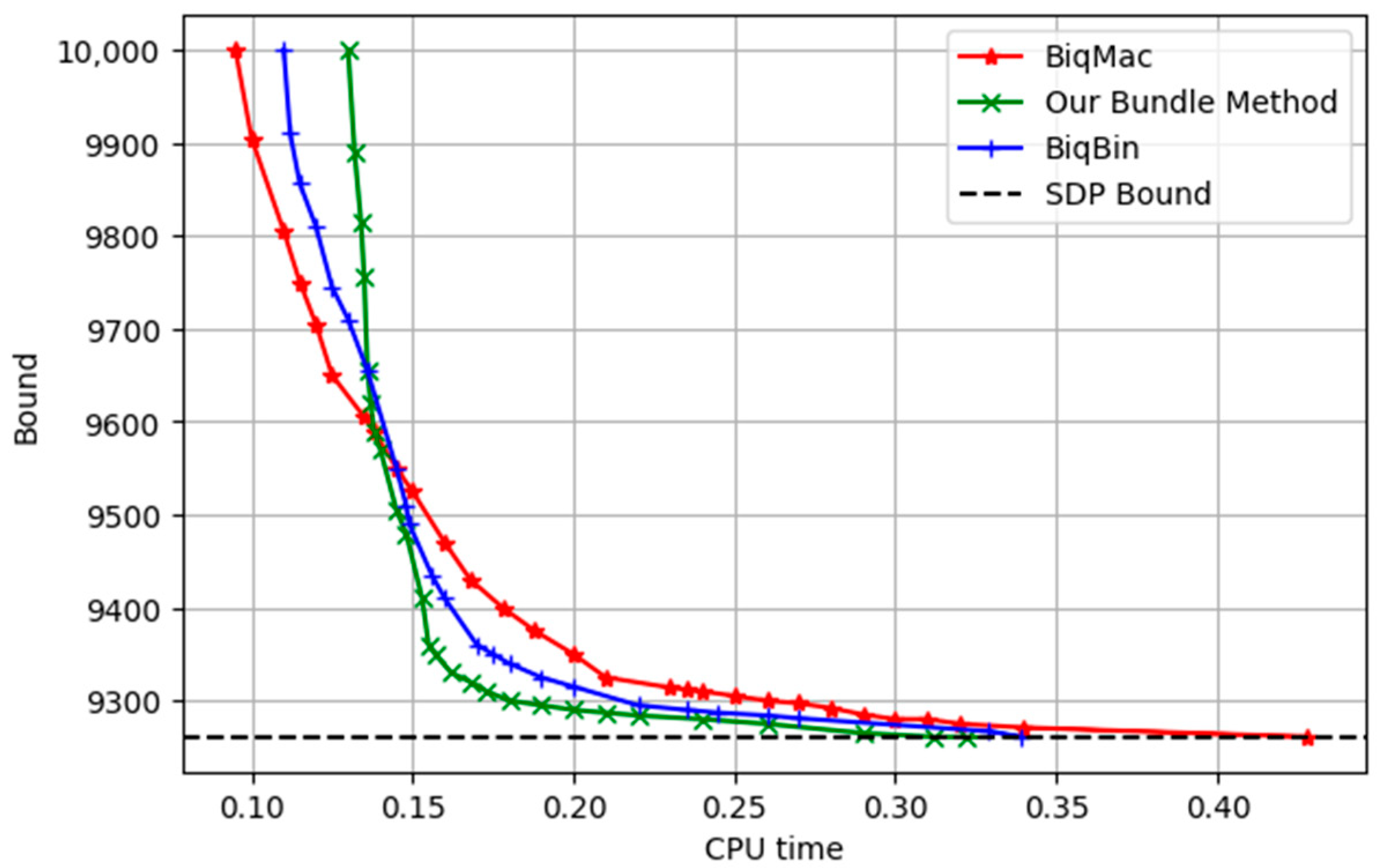
The graph named gka3d represents an instance of Glover, Kockenberger, and Alidaee, characterized by , , and an SDP bound of approximately 9261.
In
Figure 1, we illustrate the relationship between the CPU time and the bounds to compare the convergence and performance of the proposed method, as well as the BiqMac and BiqBin solvers. Our observations revealed that, at bounds of more than 9590, the BiqMac approach exhibited a faster convergence than the other two methods. However, as the solution neared the SDP bound, our bundle method achieved the fastest convergence. Moreover, the BiqMac approach converged after 0.4279 s and the BiqBin approach converged after 0.3391 s, while only 0.3218 s were required for the convergence by our bundle approach.
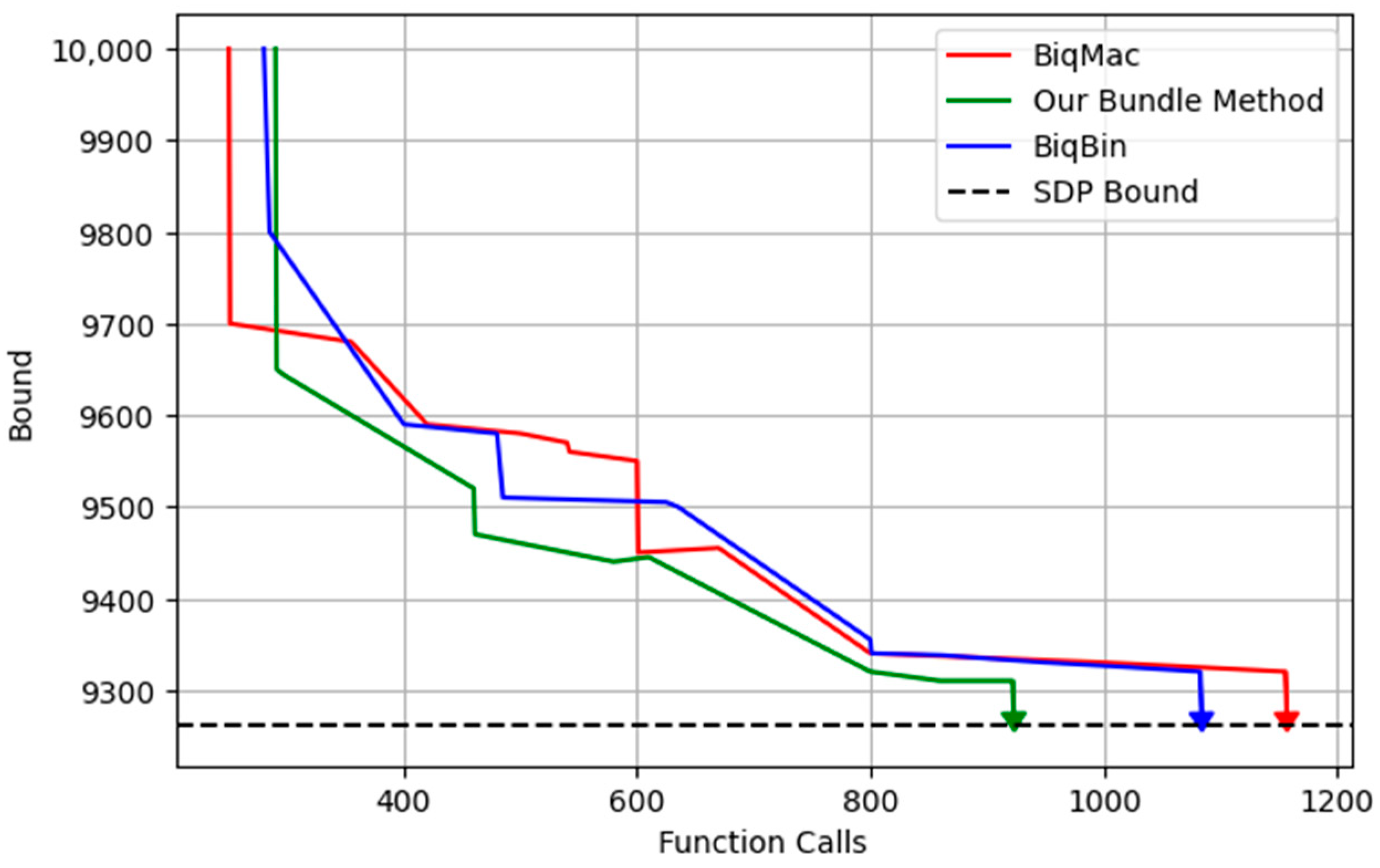
Furthermore,
Figure 2 illustrates the relationship between the number of function calls and the bounds of the above graph. While the function calls remain unaffected by any other software running concurrently with our solver on the same computer, the CPU time may vary between runs due to the presence of other active software on the system. From the results, we observed that BiqMac initially converged faster than the other two approaches, aligning with the bundle method at a bound of 9693. Beyond this threshold, the proposed bundle method outperformed the others, requiring 922 function calls for convergence, 1083 function calls for BiqBin, and 1156 function calls for BiqMac.
This analysis underscores the efficiency of the proposed bundle approach in handling convergence near SDP bounds.
3.3. Numerical Results of Instances Introduced by Beasley
Experiments were conducted in this test using the Beasley dataset (bqp) from the BiqMac library, specifically the instances denoted as bqp100, bqp250, and bqp500, corresponding to graphs with 100, 250, and 500 nodes, respectively. Each instance has a density of
. The results presented in
Table 5,
Table 6 and
Table 7 provide a comparative analysis of the CPU time, the number of function calls and iterations required to solve the given graph using the proposed method, and the BiqMac and BiqBin solvers.
As shown in
Table 8, the results reveal that the proposed method achieved statistically significant improvements in cases (
p < 0.05), particularly demonstrating its advantage in computational efficiency across increasing problem sizes.
These outcomes emphasize the reliability and consistency of the proposed algorithm when applied to the bqp benchmark set, further validating its potential as a scalable and effective alternative to existing solvers.
3.3.1. Interpretation of Statistical Test Results for bqp Instances
The results of the Wilcoxon signed-rank test, summarized in
Table 8, offer compelling statistical support for the superiority of the proposed method. For all instance categories evaluated (bqp100_i, bqp250_i, and bqp500_i), the
p-values fell below the standard 0.05 threshold, indicating that the improvements in the CPU time were unlikely to be due to chance. Especially noteworthy are the comparisons where the W-statistic equaled 0.0 or 1.0, which reflect a consistent performance gain of the proposed method over the baselines across nearly all individual instances.
Together, these findings highlight the method’s robustness and scalability, reinforcing its effectiveness in tackling binary quadratic programming problems of an increasing size and complexity.
3.3.2. Numerical Results of Graph bqp500-1
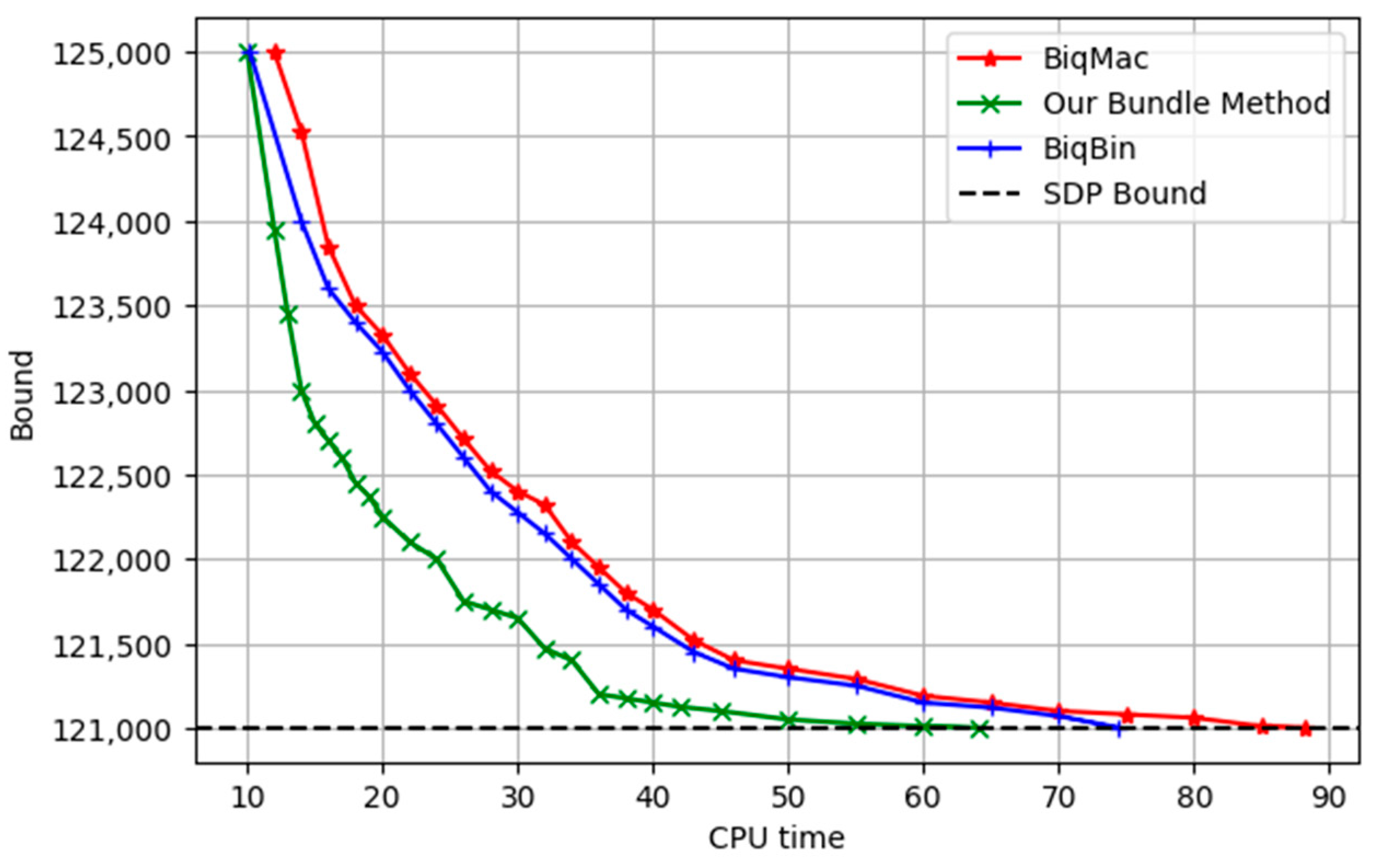
To illustrate the effectiveness of our approach, we examined the instance bqp500-1, which contains 500 nodes.
Figure 3 presents a plot of the CPU time against the bound, with the semidefinite programming (SDP) bound at 121,001.
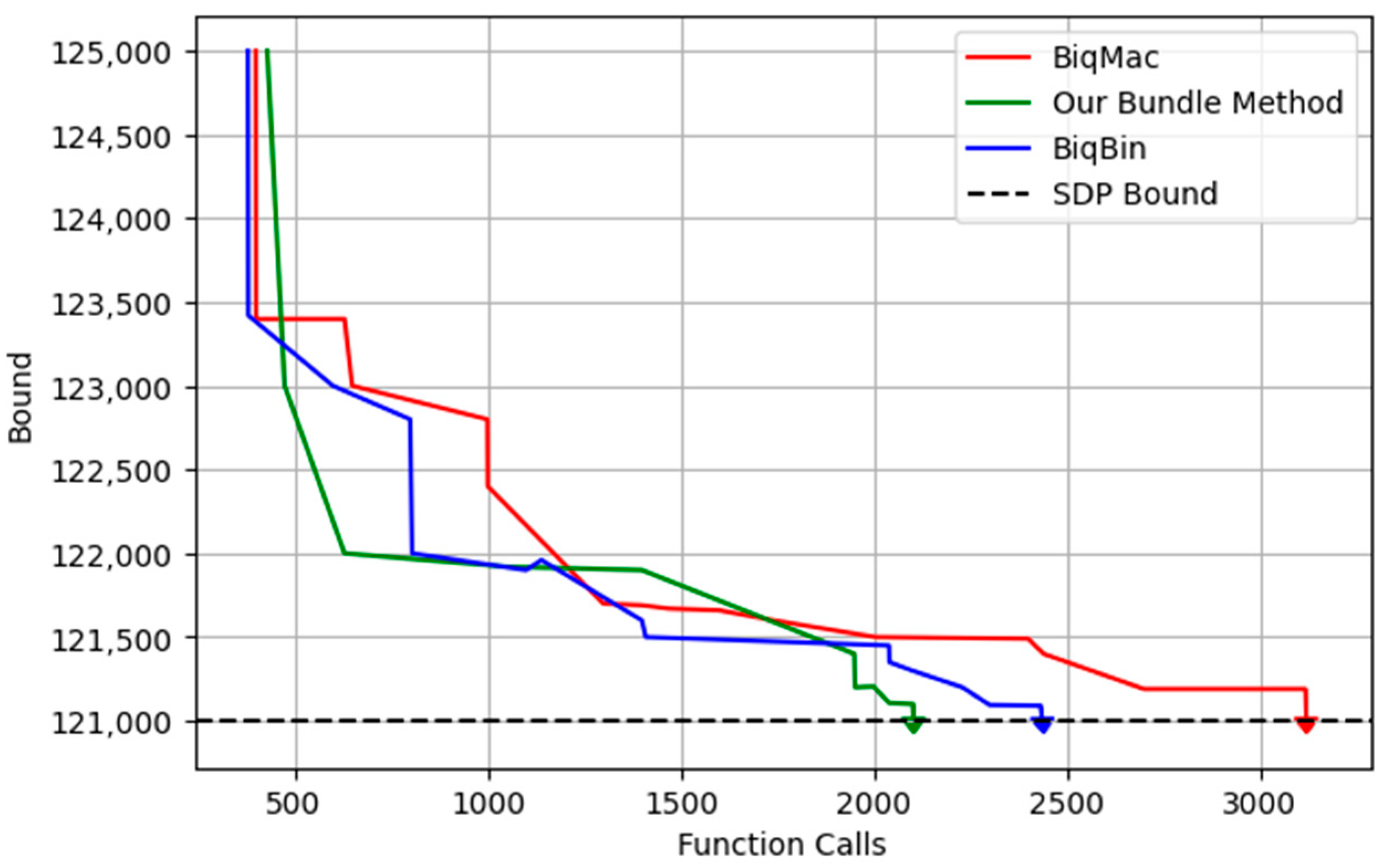
Figure 4 presents a plot of the number of function calls against the bound. From
Figure 1 and
Figure 2, we observed that the proposed bundle method required 64.0592 s of CPU time to achieve the SDP bound, whereas BiqBin and BiqMac required 74.4438 s and 88.2436 s, respectively. Additionally, our method demonstrated a superior efficiency, requiring only 2102 function calls to reach the SDP bound, while BiqBin and BiqMac required 2435 and 3119 function calls, respectively.
3.4. Numerical Results for the Graph Identified as w0.1_100.
A performance evaluation of the three methods was carried out using a collection of graphs labeled w0.1_100.i from the BiqMac library, consisting of 10 distinct instances. Each instance is characterized by a graph of dimension
and edge density
. The integer edge weights were randomly selected from the interval [−10, 10].
Table 9 presents a comparative analysis of the CPU time, the number of function calls, and the number of iterations required to solve the given graph instances using the proposed approach, alongside the BiqMac and BiqBin solvers.
To statistically substantiate the observed performance differences, the Wilcoxon signed-rank test was employed to compare the CPU time between the proposed method and each of the baseline solvers across the 10 problem instances.
Table 10 presents the results of this analysis. As observed, the
p-values fell well below the 0.05 significance threshold in both comparisons, indicating that the improvements in the CPU time achieved by the proposed method were statistically significant. These results further affirm the computational efficiency and reliability of the proposed approach, particularly when applied to sparse graphs with randomly weighted edges.
Interpretation of Statistical Test Results for w0.1_100.i Instances
The Wilcoxon signed-rank test results summarized in
Table 10 provide strong statistical evidence for the performance advantage of the proposed method on the w0.1_100.i instance set. Both comparisons—against BiqBin and BiqMac—yielded
p-values below the standard significance level (0.0221 and 0.0347, respectively), reinforcing the conclusion that the CPU time improvements are not attributable to random variation. Remarkably, the W-statistic values of 1.0 and 0.0 reflect near-universal performance superiority across all the evaluated instances.
Collectively, these findings corroborate the method’s robustness, even when applied to uniformly structured, yet randomly weighted, graph models, underscoring its effectiveness as a general-purpose solver for binary quadratic problems.
4. Discussion
To assess the efficacy and scalability of the proposed method, extensive numerical comparisons were conducted on several benchmark families, including the Glover–Kockenberger–Alidaee (gka), Beasley (bqp), and w0.1_100.i instances. These benchmarks comprise diverse graph structures across varying sizes and densities, offering a comprehensive platform for a performance evaluation.
Firstly, a further evaluation of the proposed method performance was conducted on the gka benchmark instances, as presented in
Table 1,
Table 2 and
Table 3. These include problem sets of varying sizes and densities, offering a comprehensive benchmark for an algorithmic comparison.
As shown in
Table 1 (gka_i_c with
]), the proposed method achieved the shortest CPU times in five out of seven instances. The average runtime was 0.2596 s, compared to 0.3595 s for BiqMac and 0.3587 s for BiqBin. It also required an average of 34.1 iterations and 38.3 function calls, significantly outperforming BiqBin (54.9/48.1) and BiqMac (42.3/39.4) in terms of the computational effort. This demonstrates the method’s efficiency for graphs with small to moderate dimensions and varying densities.
As detailed in
Table 2 (gka_i_d with fixed
), the proposed method maintained its advantage, achieving the shortest CPU time in eight out of ten instances. The average runtime was 0.4572 s, while BiqMac and BiqBin recorded 0.5614 and 0.6294 s, respectively. Moreover, the method averaged 52.9 iterations and 1153.5 function calls, once again surpassing BiqMac (66.2/1293.9) and BiqBin (83.0/1403.6). These trends suggest that the proposed approach becomes increasingly efficient as the edge density increases—a critical advantage for real-world graph applications.
In
Table 3 (gka_i_e,
), the proposed method continued to perform strongly, attaining the best CPU time in four out of five instances. Its average runtime was 1.3927 s, compared to 1.8585 for BiqMac and 1.6869 for BiqBin. It also maintained a reasonable iteration count (110.0) and function calls (1171.2), outperforming BiqMac (121.0/1334.2) and BiqBin (149.2/1542.2). The ability to maintain a low computational overhead even at larger problem scales further confirms the scalability of the proposed method.
These findings collectively underscore the robustness, adaptability, and scalability of our bundle method. Whether the graph is sparse or dense, small or large, the method consistently delivers lower runtimes and fewer evaluations, making it a strong candidate for solving semidefinite relaxations of the max-cut problem under practical constraints.
The performance of the proposed method is now evaluated on the Beasley (bqp) benchmark instances, as shown in
Table 5,
Table 6 and
Table 7. These datasets—bqp100, bqp250, and bqp500—represent graphs of increasing size with a fixed edge density of
, providing a valuable test of scalability and computational resilience.
As shown in
Table 5 (bqp100 with
), the proposed method achieved the shortest CPU time in seven out of ten cases. The average CPU time was 0.4874 s, outperforming BiqMac (0.5544 s) and BiqBin (0.5970 s). Moreover, the proposed approach required the fewest average number of iterations (56.3) and function calls (1118.3) compared to BiqMac (65.2/1295.2) and BiqBin (72.9/1469.6). These results confirm the method’s efficiency for moderately sized graphs.
In
Table 6 (bqp250 with
), the proposed method continued to demonstrate a competitive performance. It recorded the shortest CPU time in six out of ten cases, with an average of 2.8098 s, while BiqMac and BiqBin recorded 3.4297 s and 4.1662 s, respectively. The bundle method also required fewer resources in terms of iterations (75.5) and function calls (2445.7) on average, in contrast to BiqMac (77.1/2491.0) and BiqBin (80.0/2936.3). These findings highlight the method’s balanced performance and scalability for larger graphs.
In
Table 7 (bqp500 with
), the proposed method achieved the shortest CPU time in seven out of ten instances. The average runtime was 45.56 s, significantly lower than BiqMac (56.56 s) and BiqBin (70.30 s). The method also required the lowest average number of iterations (76.9) and function calls (3420.4), outperforming BiqMac (91.3/3512.1) and BiqBin (85.9/3955.7). These results indicate the method’s robustness and sustained efficiency, even at a substantially increased problem scale.
Altogether, these findings reinforce the capability of the proposed bundle method to solve semidefinite relaxations of max-cut efficiently across varying instance sizes. The method consistently achieved reduced runtimes and computational workload compared to established solvers, demonstrating strong practical relevance and scalability.
Finally, the performance of the proposed method was assessed on the w0.1_100.i instances from the BiqMac library. As shown in
Table 9, our bundle method consistently outperformed both BiqBin and BiqMac across the ten problem instances. Specifically, the proposed approach achieved the shortest CPU times, with an average time of 0.8717 s compared to 1.1595 s for BiqMac and 1.2295 s for BiqBin. In addition, our method required the fewest function calls and iterations in the majority of instances, demonstrating an improved computational efficiency without compromising the accuracy. These results further underscore the effectiveness of the proposed method for solving graphs with moderate dimensions (
,
), where the proposed approach reliably converges to the SDP bound with a lower computational overhead. The performance on these structurally randomized problems highlights the robustness of the bundle method in handling varied input characteristics.
In summary, the proposed bundle method consistently demonstrated a superior performance across all the tested benchmarks, achieving the lowest runtimes and requiring fewer iterations and function evaluations, even as the problem complexity increased. These results establish the method as a robust and scalable solution for semidefinite relaxations of the max-cut problem. Overall, these results confirm that our method is highly effective for solving large-scale graphs with a substantial number of nodes.
5. Conclusions
This study proposed a novel bundle-based approximation algorithm for solving the max-cut problem via a newly formulated semidefinite relaxation. The method demonstrated strong theoretical convergence and consistently outperformed the solvers BiqMac and BiqBin across a wide range of benchmark instances from the BiqMac library. It achieved lower CPU times, fewer iterations, and reduced function evaluations, particularly for large-scale and dense graphs, thereby confirming its robustness and scalability.
The algorithm’s efficiency stems from its low per-iteration complexity, relying primarily on solving a sparse linear system and projecting onto the nonnegative orthant and the semidefinite cone. These computational advantages make it a promising tool for addressing NP-hard combinatorial optimization problems in practice.
However, this study is not without limitations. The current implementation was tested only on graphs with up to 500 nodes, leaving its performance on significantly larger or real-time instances unverified. Additionally, the method assumes fixed edge densities and does not yet incorporate adaptive mechanisms for varying graph topologies or dynamic data streams.
Future research will focus on extending the algorithm’s applicability to larger-scale and dynamic graphs, integrating parallelization strategies, and exploring hybrid approaches that combine bundle methods with machine learning to guide search directions or predict promising cuts. Investigating tighter relaxations and incorporating additional cutting planes may also further enhance the solution quality.
In conclusion, the proposed method offers a scalable, efficient, and theoretically grounded approach for solving semidefinite relaxations of the max-cut problem. Its consistent performance across diverse benchmarks highlights its potential for broader applications in combinatorial optimization and related fields.