Two-Way Conversion Between Fifth-Order Stokes Wave Theories

Abstract

Stokes wave is a classical problem in physics. Various Stokes wave theories in different forms have been developed to help us better understand their characteristics and for engineering applications. Exploring whether these Stokes wave theories can be converted into each other is a mathematical issue. We select three Stokes wave theories with different expansion parameters, all expressed in terms of water depth measured from the mean water level (MWL). Using series reversion to convert between the different expansions, we successfully transform the expressions for the velocity potential, wave profile, and dynamic properties between two of the Stokes wave theories. Through this conversion, we identify an incorrect expression for the water level in one Stokes wave theory.

1. Introduction

Stokes waves are steady periodic motions with a free surface that occur in an inviscid fluid layer of constant mean depth, typically in deep or intermediate water, under gravity and without surface tension [1]. Stokes waves are used to determine wave kinematics in the design of coastal and offshore structures [2].

A second-order Stokes wave theory for intermediate water and a third-order solution for infinite depth were first derived by Stokes [3]. Stokes [4] further extended the fourth-order solutions for the free surface profile and the velocity potential function in infinite depth and derived the third-order solutions for intermediate depth in implicit forms. Later, different forms of the third-order Stokes wave theory using different expansion parameters and methods for intermediate water were proposed [5,6,7,8]. Since 1955, several fifth-order solutions in different forms have been proposed and applied in engineering [9,10,11,12,13,14,15,16,17]. A review of Stokes wave theories can be found in Zhao and Liu [16].

Zhao et al. [15] summarise three reasons for the diversity of existing Stokes solutions. The first reason is the use of different definitions for the expansion or perturbation parameter. A common parameter is ε = kH/2, where k is the wave number and H is the wave height [11,14]. Another expansion parameter, ā ≈ kH/2, differs from ε and must be determined when H is given [10,15,16]. The second reason is the water depth used in the solution, either below the still water level (SWL) or the mean water level (MWL). The difference between SWL and MWL due to wave motion is called the DWL (difference in water level). For example, some solutions are based on mean water depth [10,14], while others use still water depth [12,15]. The third reason is the definition of wave celerity. Stokes [3] introduced two types of celerity: one with zero velocity and another with zero volume flux. Fenton [14] provided a method to satisfy both definitions.

Stokes wave solutions derived using the perturbation method include large coefficients and many terms at higher orders, thus increasing the risk of typographical errors in published formulas. For instance, a sign error in the fourth-order wave speed in [10] was noted by [10,18], and an incorrect denominator in the fifth-order potential in [14] was corrected by [19]. After correcting such errors and applying binomial approximations, Zhao and Liu [16] found that three fifth-order Stokes wave theories differ in their expressions for the potential function, wave profile, and wave celerity. This observation inspired us to explore whether these different forms can be mathematically converted into one another.

Pure Stokes waves are irrotational flows because they are only affected by gravity. A wind-generated current in a continental shelf and shallow sea, or tidal flows due to the ebb and flood, can be well described by constant vorticity [20]. Dyachenko and Hur [21] developed a numerical algorithm to solve the modified Babenko equation for waves with a constant vorticity in a finite depth. An electrohydrodynamic model serves as a model for waves with a linearly sheared current in electric field manipulation. In this case, the flow becomes rotational, and its solution is more complicated. Conformal mapping coordinates and pseudo-spectral numerical methods are required to obtain a special result for this flow field, namely, three stagnation points on the free surface [22,23]. Based on the framework [16], fifth-order Stokes wave solutions in a linear shear current were derived [24].

Capillary–gravity waves, generated at the air-water interface in the presence of surface tension, have wide applications. The role of surface tension on free and forced gravity waves was reviewed by Perlin and Schultz [25]. The blocking dynamics of barotropic (surface) and baroclinic (internal) gravity–capillary wave modes were theoretically analysed by Boral et al. [26]. Hsu et al. [27] obtained a third-order perturbation series approximation for two-dimensional periodic gravity–capillary waves propagating steadily in finite depth on a linear shear current. These latest papers provide references to recent research methods and earlier literature.

In this study, we focus on three specific pure Stokes wave theories: those of Skjelbreia and Hendrickson (SH60) [10], Fenton(F85) [14], and Zhao and Liu (ZL22) [16]. SH60 and ZL22 provide solutions for the potential function, wave profile, and wave celerity in a fixed coordinate system, all in terms of mean water depth. F85 is based on a steady-state stream function in a moving frame and is also expressed in terms of mean water depth after transformation.

These three theories use different expansion parameters and different forms involving hyperbolic functions of kh, making it difficult to directly compare higher-order coefficients. To resolve this, we first unify the notations and apply the series reversion method to convert the solutions. We begin by comparing F85 and ZL22, the details of which are provided in the Methods and Results sections. During the conversion process, we found that the water level difference (WLD) in ZL22 does not satisfy known formulas for wave dynamic properties [28,29]. This discrepancy is discussed in the Discussion section. The conversion between SH60 and F85 is also examined. In addition to theoretical explanations of the conversion of the three solutions, different wave profiles are compared graphically to illustrate the differences among these solutions.

2. Materials and Methods

2.1. Unified Coordinates and Symbols

To compare the theories effectively, we begin by unifying the coordinate systems and notations used in F85 and ZL22. ZL22 defines the velocity potential in a fixed coordinate system based on the MWL, while F85 employs a moving frame with the origin at the bottom. We reframe the F85 solution in coordinates consistent with MWL, enabling a meaningful comparison.

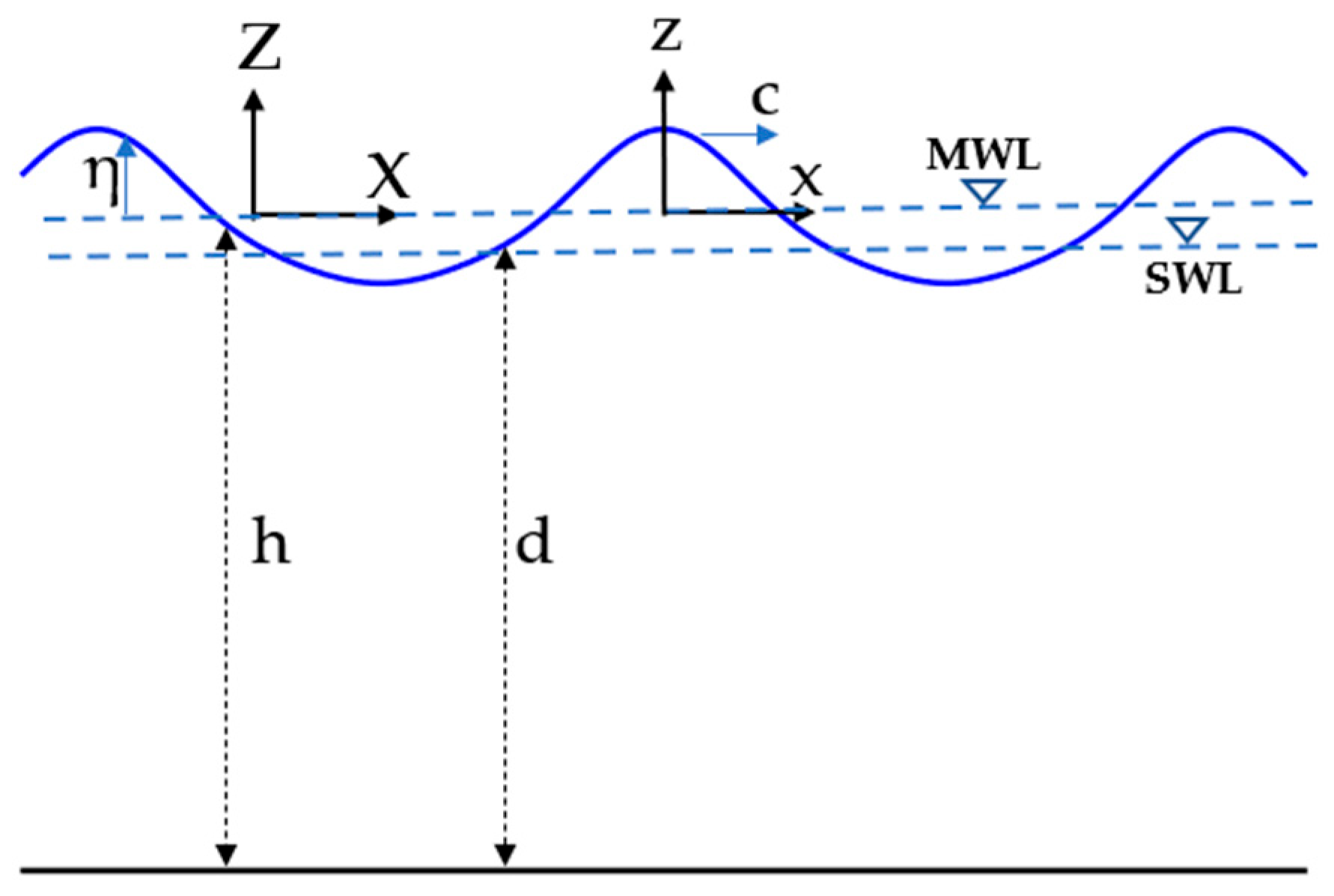
In this unified system, (X, Z) represents the fixed coordinate system, and (x, z) represents the moving coordinate system. These are related by x = X − ct, and z = Z, where c is the wave celerity. Both solutions are expressed as functions of mean water depth, h. Figure 1 illustrates the different coordinate systems and water level definitions. MWL is a little higher than SWL. Alternative definition of still water depth is denoted by d.

To clearly indicate the physical meaning of the different symbols used in the three solutions,

Table 1. Specific designations of important physical qualities for the SH60, F85, and ZL22.

Physical quantity	SH60	F85	ZL22
Velocity potential	${\varphi }_{SH}$	${\varphi }_F$	${\varphi }_Z$
Wave profile	${\eta }_{SH}$	${\eta }_F$	${\eta }_Z$
Expansion parameter	$\widehat{a}\approx kH/2$	$\epsilon =kH/2$	$\overline{a } \approx kH/2$
Wave frequency	${\omega }_{SH}$	${\omega }_F$	$\omega$
Wave celerity	$c_{SH}$	$c_F$	$c$
Coefficient of potential	$A_{ij}^{SH}$	$A_{ij}^F$	$A_{ij}$
Coefficient of Wave profile	$B_{ij}^{SH}$	$B_{ij}^F$	$B_{ij}$
Bernoulli′s constant	$R_{SH}$	$R_F$	$–$

provides a list of specific designations.

2.2. The Governing Equation and Solution of ZL22

The ZL22 formulation solves the Laplace equation for the velocity potential, $\varphi$(X, Z, t), subject to a no-flux boundary condition at the bottom and kinematic and dynamic boundary conditions at the free surface.

The velocity potential satisfying the Laplace equation is

$${\displaystyle \frac{{\partial }^2\varphi }{\partial X^2}}+{\displaystyle \frac{{\partial }^2\varphi }{\partial Z^2}}=0,-\infty <X<\infty ,-h\le Z\le \eta \left(X, t\right).$$

(1)

The no-flux boundary condition must be satisfied at the bottom:

$${\displaystyle \frac{\partial \varphi }{\partial Z}}=0, Z=-h.$$

(2)

The kinematic and dynamic free surface boundary conditions can be expressed, respectively, as

$${\displaystyle \frac{\partial \varphi }{\partial Z}}={\displaystyle \frac{\partial \eta }{\partial t}}+{\displaystyle \frac{\partial \varphi }{\partial X}}{\displaystyle \frac{\partial \eta }{\partial X}}, Z=\eta \left(X, t\right),$$

(3)

and

$${\displaystyle \frac{\partial \varphi }{\partial t}}+{\displaystyle \frac{1}{2}}\left[{\left({\displaystyle \frac{\partial \varphi }{\partial X}}\right)}^2+{\left({\displaystyle \frac{\partial \varphi }{\partial Z}}\right)}^2\right]+g\eta =0, Z=\eta \left(X, t\right),$$

(4)

where g is the gravitational acceleration and $\eta (X, t)$ is the wave profile.

ZL22 applied the perturbation technique with an expansion parameter or perturbation parameter, $\overline{a}=ka, \mathrm{w}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{h} \mathrm{i}\mathrm{s} \mathrm{c}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{e} \mathrm{t}\mathrm{o} \mathrm{h}\mathrm{a}\mathrm{l}\mathrm{f} H$, to the combined kinematic and dynamic free surface boundary condition to obtain the free surface profile and velocity potential.

The fifth-order ZL22 solution for the velocity potential and free surface profile in terms of $\overline{a }$ was expressed by

$$\begin{array}{c}{\displaystyle \frac{{\varphi }_{Z}k}{c_0}}=A_{11}\overline{a }{\displaystyle \frac{\cosh \mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh kh}}\mathrm{s}\mathrm{i}\mathrm{n}\theta +\left(A_{22}{\overline{a}}^2+A_{42}{\overline{a}}^4\right){\displaystyle \frac{\cosh 2\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 2kh}}\mathrm{s}\mathrm{i}\mathrm{n}2\theta \\ +\left(A_{33}{\overline{a}}^3+A_{53}{\overline{a}}^5\right){\displaystyle \frac{\cosh 3\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 3kh}}\mathrm{s}\mathrm{i}\mathrm{n}3\theta +A_{44}{\overline{a}}^4{\displaystyle \frac{\cosh 4\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 4kh}}\mathrm{s}\mathrm{i}\mathrm{n}4\theta \\ +A_{55}{\overline{a}}^5{\displaystyle \frac{\cosh 5\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 5kh}}\mathrm{s}\mathrm{i}\mathrm{n}5\theta +\left(C_2{\overline{a}}^2+C_4{\overline{a}}^4\right){\omega }_{0}t,\end{array}$$

(5)

and

$$\begin{array}{c}k{\eta }_Z=\left(\overline{a}+B_{31}{\overline{a}}^3+B_{51}{\overline{a}}^5\right)\mathrm{c}\mathrm{o}\mathrm{s}\theta +\left(B_{22}{\overline{a}}^2+B_{42}{\overline{a}}^4\right)\mathrm{c}\mathrm{o}\mathrm{s}2\theta \\ +\left(B_{33}{\overline{a}}^3+B_{53}{\overline{a}}^5\right)\mathrm{c}\mathrm{o}\mathrm{s}3\theta +B_{44}{\overline{a}}^4\mathrm{c}\mathrm{o}\mathrm{s}4\theta +B_{55}{\overline{a}}^5\mathrm{c}\mathrm{o}\mathrm{s}5\theta ,\end{array}$$

(6)

$${\displaystyle \frac{c}{c_0}}={\displaystyle \frac{\omega }{{\omega }_0}}=1+{\omega }_2{\overline{a }}^2+{\omega }_4{\overline{a }}^4,$$

(7)

where $\theta =kX-\omega t$ is the phase function, $\omega =2\mathrm{\pi }/T$ is the wave frequency, and T is the wave period. ${\omega }_0$ = $\sqrt{gk\tanh kh}$ is the wave frequency of the first-order solution, which indicates that the dispersion relation and $c_0$ = ${\omega }_0/\mathrm{k}$ is the corresponding wave celerity. The form of the dimensionless velocity potential is different from that of ZL22. The original $\cosh \mathrm{i}k\left(z+h\right), i=1, 2, \cdots ,5 ,$ form of ZL22 is divided by $\cosh \mathrm{i}\mathrm{k}\mathrm{h}$ in Equation (5) to facilitate simplification in deep water limits. The first and second subscripts of the coefficients, ${\mathrm{A}}_{ij} \mathrm{a}\mathrm{n}\mathrm{d} B_{ij} (i,j=1, 2,\cdots , 5)$ indicate the i-th order and j-th harmonic. The original $A_{ij}$ derived from ZL22 must be multiplied by $\cosh \mathrm{i}kh$. The subscript Z mainly indicates the result of ZL22.

Equation (5) shows that the velocity potential includes five periodic harmonic terms of various orders and one term that increases linearly with time. The first harmonic only contains the first-order solution. The fifth-order free surface solutions contribute to the first and third harmonics, while the fourth-order solution contributes to the second harmonic. The wave frequency includes high-order contributions, which are ${\omega }_2 \mathrm{a}\mathrm{n}\mathrm{d} {\omega }_4$. The expressions of $A_{ij} \mathrm{a}\mathrm{n}\mathrm{d} B_{ij}$, and $\omega$ are listed in

Table 2. Formulas for the coefficients of $A_{ij}, B_{ij},\mathrm{a}\mathrm{n}\mathrm{d} {\omega }_i$ in the ZL22 solution.

$A_{11}$ = $1/\sigma$

$A_{22}$ = $(3-3{\sigma }^4)/\left(8{\sigma }^4\right)$

$A_{33}$ = $(9+5{\sigma }^2-53{\sigma }^4+39{\sigma }^6)/\left(64{\sigma }^7\right)$

$A_{42}$ = $(1+{\sigma }^2)(-81-54{\sigma }^2+864{\sigma }^4-682{\sigma }^6+145{\sigma }^8)/\left(768{\sigma }^{10}\right)$

$\begin{array}{cc}{A}_{44}=\hfill & -\left(\right((-1+{\sigma }^2)(1+6{\sigma }^2+7{\sigma }^4)(405-1269{\sigma }^2+747{\sigma }^4+197{\sigma }^6))\hfill \\ \hfill & /\left(1536{\sigma }^{10}\right(5+{\sigma }^2\left)\right))\hfill \end{array}$

$\begin{array}{cc}{A}_{53}=\hfill & -\left(\right(1215+648{\sigma }^2-20313{\sigma }^4+30408{\sigma }^6-13155{\sigma }^8-144{\sigma }^{10}+829{\sigma }^{12})\hfill \\ \hfill & (1+3{\sigma }^2))/(4096{\sigma }^{13}(5+{\sigma }^2))\hfill \end{array}$

$\begin{array}{cc}{A}_{55}=\hfill & \left(\right(-2025+9855{\sigma }^2-10242{\sigma }^4-3962{\sigma }^6+5483{\sigma }^8+1083{\sigma }^{10})\hfill \\ \hfill & (-1+{\sigma }^2)\left(1+10{\sigma }^2+5{\sigma }^4\right))/(4096{\sigma }^{13}(5+{\sigma }^2)(5+3{\sigma }^2)) \hfill \end{array}$

$B_{22}=3-{\sigma }^2)/(4{\sigma }^3)$

$B_{31}$ = $(3+8{\sigma }^2-9{\sigma }^4)/(16{\sigma }^4)$

$B_{33}$ = $(27-9{\sigma }^2+9{\sigma }^4-3{\sigma }^6)/\left(64{\sigma }^6\right)$

$B_{42}$ = $-(81+54{\sigma }^2-1152{\sigma }^4+826{\sigma }^6-129{\sigma }^8)/\left(384{\sigma }^9\right)$

$B_{44}$ = $(405+81{\sigma }^2+522{\sigma }^4-262{\sigma }^6+{\sigma }^8+21{\sigma }^{10})/\left(384{\sigma }^9\right(5+{\sigma }^2\left)\right)$

$B_{51}$ = $(81+891{\sigma }^2-540{\sigma }^4+6016{\sigma }^6-7437{\sigma }^8+2925{\sigma }^{10})//\left(3072{\sigma }^{10}\right)$

$\begin{array}{cc}{B}_{53}=\hfill & \left(9\left(-405-891{\sigma }^2+7371{\sigma }^4-2611{\sigma }^6+793{\sigma }^8-665{\sigma }^{10}+17{\sigma }^{12}+39{\sigma }^{14}\right)\right)\hfill \\ \hfill & /\left(4096{\sigma }^{12}\right(5+{\sigma }^2\left)\right)\hfill \end{array}$

$\begin{array}{cc}{B}_{55}=\hfill & \left(5\right(6075+8910{\sigma }^2+25866{\sigma }^4-498{\sigma }^6-3896{\sigma }^8+2618{\sigma }^{10}-570{\sigma }^{12}\hfill \\ \hfill & -150{\sigma }^{14}+45{\sigma }^{16}\left)\right)/\left(12288{\sigma }^{12}\right(25+20{\sigma }^2+3{\sigma }^4\left)\right)\hfill \end{array}$

${\omega }_2$ = $(9-10{\sigma }^2+9{\sigma }^4)/$($16{\sigma }^4)$

${\omega }_4$ = $(81-603{\sigma }^2+3618{\sigma }^4-3662{\sigma }^6+1869{\sigma }^8-663{\sigma }^{10})/\left(1024{\sigma }^{10}\right)$

$C_2$ = $-$(${1-\sigma }^2)/(4{\sigma }^2)$

$C_4$ = $-$($9{(1-{\sigma }^2)}^4)/(64{\sigma }^8)$

. Some high-order coefficients were originally expressed in terms of both $\sigma =\tanh kh$ and ${\alpha }_1$, but for the convenience of subsequent comparison, the coefficients in Table 2 are expressed by $\sigma$.

2.3. The Governing Equation and Solution of F85

F85 uses a stream function formulation in a moving frame, which is later converted to a velocity potential form. The equations are solved with boundary conditions imposed on streamlines. The expansion parameter differs from that of ZL22, and stream function values are adjusted to account for the change in reference level from the bottom to the MWL. The resulting fifth-order solutions for wave profile and potential function are given, with coefficients provided in

Table 3. Formulas for the coefficients of $A_{ij}^F, B_{ij}^F, {\omega }_i^F, D_i^F,$and $E_i^F$in the F85 solution.

$A_{11}^F$ = $A_{11}$

$A_{22}^F$ = $A_{22}$

$A_{31}^F$ = $-(27+3{\sigma }^2+41{\sigma }^4-39{\sigma }^6)/\left(64{\sigma }^7\right)$

$A_{33}^F$ = $A_{33}$

$A_{42}^F$ = $-(1+{\sigma }^2)(162-81{\sigma }^2-261{\sigma }^4-19{\sigma }^6+103{\sigma }^8)/(384{\sigma }^{10})$

$A_{44}^F=A_{44}$

$\begin{array}{cc}{A}_{51}^F=\hfill & (62775+89370{\sigma }^2-199602{\sigma }^4-91438{\sigma }^6-131460{\sigma }^8-75986{\sigma }^{10}\hfill \\ \hfill & +30114{\sigma }^{12}+12262{\sigma }^{14}+861{\sigma }^{16})/\left(4096{\sigma }^{13}\right(5+{\sigma }^2\left)\right(5+3{\sigma }^2\left)\right)\hfill \end{array}$

$\begin{array}{cc}{A}_{53}^F=\hfill & \left(\right(-1215+1782{\sigma }^2+3051{\sigma }^4-3540{\sigma }^6-1017{\sigma }^8+894{\sigma }^{10}+173{\sigma }^{12})\hfill \\ \hfill & (1+3{\sigma }^2))/(1024{\sigma }^{13}(5+{\sigma }^2))\hfill \end{array}$

$A_{55}^F=A_{55}$

$B_{22}^F=B_{22}$ $C_{\epsilon \widehat{a}5}$is different from $C_{\epsilon \overline{a}5}$

$B_{31}^F$ = $(-27+9{\sigma }^2-9{\sigma }^4+3{\sigma }^6)/\left(64{\sigma }^6\right)$

$B_{33}^F=$ − $B_{31}^F$ = $B_{33}$

$B_{42}^F=$($-81+198{\sigma }^4-88{\sigma }^6+3{\sigma }^8)/(96{\sigma }^9)$

$B_{44}^F$ = $B_{44}$

$\begin{array}{cc}{B}_{53}^F=\hfill & -\left(\right(9(405+216{\sigma }^2-1305{\sigma }^4+148{\sigma }^6-25{\sigma }^8+28{\sigma }^{10}+5{\sigma }^{12}))\hfill \\ \hfill & /\left(1024{\sigma }^{12}\right(5+{\sigma }^2\left)\right)\hfill \end{array}$

$B_{55}^F$ = $B_{55}$

${\omega }_2^F$ = ${\omega }_2$

${\omega }_4^F$ = $(-405-117{\sigma }^2+2454{\sigma }^4-2194{\sigma }^6+351{\sigma }^8+39{\sigma }^{10})/\left(1024{\sigma }^{10}\right)$

$D_2$ = $-$1$/\left(2{\sigma }^{1/2}\right)$

$D_4$ = ($9+3{\sigma }^2+7{\sigma }^4-3{\sigma }^6)/(64{\sigma }^{13/2})$

$E_2^F$ = ($9-6{\sigma }^2+5{\sigma }^4)/(16{\sigma }^4)$

$E_4^F$ = $(-405-27{\sigma }^2+1710{\sigma }^4-1110{\sigma }^6+55{\sigma }^8+33{\sigma }^{10})/\left(1024{\sigma }^{10}\right)$

.

For the derivation of the F85 solution, a velocity potential, $\psi$(x, z) also satisfies the Laplace equation

$${\displaystyle \frac{{\partial }^2\psi }{\partial x^2}}+{\displaystyle \frac{{\partial }^2\psi }{\partial z^2}}=0,-\infty <x<\infty ,-h\le z\le \eta \left(x\right).$$

(8)

The bottom condition and the kinematic boundary condition on the free surface are constant values of stream functions, which are as follows

$$\psi \left(x,-h\right)=ch,$$

(9)

and

$$\psi \left(x,\eta \left(x\right)\right)=-Q_F,$$

(10)

where $-Q_F$ is the stream function value denoting the total volume rate of flow underneath the stationary wave per unit length normal to the (x, z) plane. The original stream function value of F85 at the bottom is set to zero. Because the coordinates are moved up by h compared to F85, the stream function values of all streamlines are added with ch. This increase in the stream function value does not affect the velocity performance of the flow field. By specifying the stream function values in Equations (9) and (10), the relationship between the stream function value on the surface and F85 is $-Q_F=-Q+ch$ where $-Q$ is the stream function value on the surface of F85.

The dynamic free surface boundary condition is

$${\displaystyle \frac{1}{2}}\left[{\left({\displaystyle \frac{\partial \psi }{\partial x}}\right)}^2+{\left({\displaystyle \frac{\partial \psi }{\partial z}}\right)}^2\right]+g\eta =R_F, Z=\eta \left(X\right),$$

(11)

where $R_F$ is the positive Bernoulli’s constant.

The expansion parameter, $\epsilon =kH/2,$ is used to obtain the steam function, free surface profile, wave celerity, and two constants, $Q_F$ and $R_F$. To facilitate the comparison with the velocity potential of ZL22, the relationship between velocity potential and stream function can be used, which is $\partial \varphi /\partial x=\partial \psi /\partial y$ and $\partial \varphi /\partial z=-\partial \psi /\partial x$. F85 converts the stream function solution into the velocity potential solution and the free surface in terms of $\epsilon .$

$$\begin{array}{c}{\displaystyle \frac{{\varphi }_{F}k}{c_0}}=-{\displaystyle \frac{c^{F}kx}{c_0}}+(A_{11}^F\epsilon +A_{31}^F{\epsilon }^3+A_{51}^F{\epsilon }^5){\displaystyle \frac{\cosh \mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh kh}}\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\theta }\\ +\left({A_{22}^F\epsilon }^2+A_{42}^F{\epsilon }^4\right){\displaystyle \frac{\cosh 2\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 2kh}}\mathrm{s}\mathrm{i}\mathrm{n}2\mathsf{\theta }+\left(A_{33}^F{\epsilon }^3+A_{53}^F{\epsilon }^5\right){\displaystyle \frac{\cosh 2\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 2kh}}\mathrm{s}\mathrm{i}\mathrm{n}3\mathsf{\theta }\\ +A_{44}^F{\epsilon }^4{\displaystyle \frac{\cosh 4\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 4kh}}\mathrm{s}\mathrm{i}\mathrm{n}4\mathsf{\theta }+A_{55}^F{\epsilon }^5{\displaystyle \frac{\cosh 5\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 5kh}}\mathrm{s}\mathrm{i}\mathrm{n}5\mathsf{\theta },\end{array}$$

(12)

and

$$\begin{array}{c}k{\eta }_F=(\epsilon +B_{31}^F{\epsilon }^3-(B_{53}^F{+B_{55}^F)\epsilon }^5)\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\theta }+\left(B_{22}^F{\epsilon }^2+B_{42}^F{\epsilon }^4\right)\mathrm{c}\mathrm{o}\mathrm{s}2\mathsf{\theta }\\ +\left({-B_{31}^F\epsilon }^3+B_{53}^F{\epsilon }^5\right)\mathrm{c}\mathrm{o}\mathrm{s}3\mathsf{\theta }+B_{44}^F{\epsilon }^4\mathrm{c}\mathrm{o}\mathrm{s}4\mathsf{\theta }+B_{55}^F{\epsilon }^5\mathrm{c}\mathrm{o}\mathrm{s}5\mathsf{\theta },\end{array}$$

(13)

$${\displaystyle \frac{c_F}{c_0}}={\displaystyle \frac{{\omega }_F}{{\omega }_0}}=1+{\omega }_2^F{\epsilon }^2+{\omega }_4^F{\epsilon }^4,$$

(14)

$$Q_F{({\displaystyle \frac{k^3}{g}})}^{1/2}=D_2{\epsilon }^2+D_4{\epsilon }^4,$$

(15)

$${\displaystyle \frac{R_{F}k}{g}}=\mathsf{\sigma }({\displaystyle \frac{1}{2}}+E_2^F{\epsilon }^2+E_4^F{\epsilon }^4),$$

(16)

where $\theta =kx$ is the phase function. The leading term of Equation (12) indicates a current opposite the positive x-axis due to the use of the moving coordinates. The reason for the modification of Equation (12) is the same as that of Equation (5). For some low-order coefficients that are the same as those of ZL22, these coefficients are represented by the corresponding coefficient symbols of ZL22. Because the coordinates are raised from the original bottom of F85 to MWL, the kh term in the original $Q_F$ and $R_F$ expression needs to be deleted. The coefficients obtained by F85 are expressed as a function of $S=\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}2kh$. For comparison with ZL22, the original coefficients have been converted in terms of only $\mathsf{\sigma }$. This must be noted.

Table 3 shows that $A_{ii}^F$and $B_{ii}^F$ are the same as $A_{ii}$ and $B_{ii}$, respectively, while $A_{ij}^F$and $B_{ij}^F$ are different from${ A}_{ij}$ and $B_{ij}$ for $\mathrm{i}\ne \mathrm{j}$. Both the solutions for $A_{ii}^F$and $B_{ii}^F$ are obtained from a homogeneous equation without a forcing term and are homogeneous without a particular solution. However, the solutions for $A_{ij}^F$and $B_{ij}^F$ for $\mathrm{i}\ne \mathrm{j}$ are obtained from a non-homogeneous equation with a forcing term from the wave interaction of different harmonics. $A_{ij}^F$and $B_{ij}^F$ is a particular solution depending on the components of the wave interaction of different harmonics.

2.4. Series Reversion

The corresponding low-order coefficients in Table 2 and Table 3 are the same, but the high-order ones are different. This difference is understandable because different expansion parameters are used. Therefore, to convert the solutions of ZL22 and F85, it is necessary to establish the relationship between the two parameters.

ZL22 considered an application for specifying the wave amplitude of the first harmonic, $\tilde{a}$, in the final solution instead of $\overline{a}$.

$$\tilde{a}=\overline{a}+B_{31}{\overline{a}}^3+B_{51}{\overline{a}}^5.$$

(17)

For F85, the expansion parameter in this case changes to

$$\tilde{\epsilon }=\epsilon +B_{31}^F{\epsilon }^3-(B_{53}^F{+B_{53}^F)\epsilon }^5.$$

(18)

When $\tilde{a}$ or $\tilde{\epsilon }$, ω, and h are prescribed for ZL22 and F85, respectively, the dispersion relation, Equation (7) or (14), must be solved together with the equation above to determine the corresponding a or $\epsilon$ and k. ZL22 employed the binomial approximation to find the inversion of Equations (17) and (18). The resulting conversions are written as

$$\overline{a}=\tilde{a}-B_{31}{\tilde{a}}^3-B_{51}{\tilde{a}}^5.$$

(19)

and

$$\epsilon =\tilde{\epsilon }-B_{31}^F{\tilde{\epsilon }}^3+(B_{53}^F{+B_{53}^F)\tilde{\epsilon }}^5.$$

(20)

When $\tilde{a}$ or $\tilde{\epsilon }$ is prescribed, substituting the approximation above, Equations (19) and (20), to the coefficients of ZL22 and F85 and neglecting the terms higher than the fifth-order terms, give alternative expressions for the velocity potential, wave profile, and some dynamic properties in terms of $\tilde{a}$ or $\tilde{\epsilon }$. ZL22 shows that both resulting free surface profile was examined to be identical, but the wave celerity is slightly different, and some coefficients of the velocity potential are also different. Under the same wave amplitude of the first harmonic, the coefficients after conversion may not be the same.

Three various cases are considered in F85. The simplest case is that H, k, and h are prescribed. F85 can be directly applied. However, the a value of ZL22 must be obtained from the wave height condition before calculating other physical quantities.

The wave height condition is, that is H = η(θ = 0) − η(θ = π),

$$\epsilon =\overline{a}+(B_{31}{+B_{33})\overline{a}}^3+\left(B_{51}+B_{53}+B_{55}\right){\overline{a}}^5.$$

(21)

Equation (21) provides a direct conversion of the parameters from F85 to ZL22, that is, the $\epsilon$ in the F85 solution is replaced by the right-hand side of Equation (21). All coefficients of F85 can be transformed and written in terms of $\overline{a}$ instead of $\epsilon$.

Equation (21) is a series in terms of $\overline{a}$. To convert the coefficients of ZL22 to the results of F85, $\overline{a}$ must be represented by $\epsilon$. This conversion must be able to obtain a series of $\epsilon$ to represent $\overline{a}$. In this paper we take the technique of series reversion [30] instead of the binomial approximation used by ZL22. Series reversion is the computation of the coefficients of the inverse function given those of the forward function. For a function expressed in a series with no constant term as

$$y=a_1{x+{a_{2}x}^2+a_{3}x}^3+\cdots .$$

(22)

The series expansion of the inverse series is given by

$$x=b_1{y+{b_{2}y}^2+b_{3}y}^3+\cdots .$$

(23)

Substituting Equation (22) into Equation (21) yields

$$y=a_1{{b_{1}y+({a_2{b}_1^2+a_1{b}_2^2)y}^2+(a}_3{b}_1^2+{2a}_1{b}_1{b}_2+a_1{b}_3)y}^3+\cdots$$

(24)

Equating the coefficients of the order quantities of y on the left and right sides of Equation (23), up to the fifth-order, then gives

$$\begin{array}{c}\begin{array}{c}{b}_1=a_1^{-1},\\ b_2=-a_1^{-3}{a}_2,\\ b_3=a_1^{-5}\left({2a}_2^2-a_1{a}_3\right),\end{array}\\ b_4=a_1^{-7}\left({5a_1{a}_2{a}_3-a}_1^2{a}_4-{5a}_2^3\right),\\ b_5=a_1^{-9}\left({6a}_1^2{a}_2{a}_4+3a_1^2{a}_3^2+{14a}_2^4-a_1^3{a}_5-21a_1{a_2^{2}a}_3\right).\end{array}$$

(25)

The second-order and fourth-order coefficients of Equation (21) are zero. According to Equation (25), the reverse series of Equation (21) is

$$\overline{a}=\epsilon -(B_{31}{+B_{33})\epsilon }^3+3(B_{31}+B_{33}{)}^2-\left(B_{51}+B_{53}+B_{55}\right){\epsilon }^5.$$

(26)

If we compare Equations (17) and (26), we can see that the binomial approximation is less than the series reverse in the fifth order by $3(B_{31}+B_{33}{)}^2$. We replace the parameters, $\overline{a}$, of ZL22 using Equation (26) into $\epsilon$ and provide the F85 solution.

2.5. Relation Between Dynamic Properties

Equations (21) and (26) can be used for two-way conversion of the velocity potential, wave profile, and wave celerity. However, the dynamic properties of F85, $R_F$, and Q are not available in ZL22, so these two dynamic properties must be transformed through other methods. The horizontal component of particle velocity in the fixed coordinates is $U=\partial \varphi /\partial X$, and in the moving coordinates, it is $u=-c+\partial \varphi /\partial x.$The vertical component of a particle in both coordinates is the same. Substituting Equation (5) into Equation (4) yields

$$\left(-\omega {\displaystyle \frac{\partial \varphi }{\partial X}}{\displaystyle \frac{\partial X}{\partial \theta }}+\left(C_2\overline{a }+C_4{\overline{a}}^3\right){\omega }_0\right)+{\displaystyle \frac{1}{2}}\left[U^2+V^2\right]+g\eta =0.$$

(27)

Through $U=u+c$ and $V=v$, Equation (27) can be written as

$${\displaystyle \frac{1}{2}}\left(u^2+v^2\right)+g\eta ={\displaystyle \frac{c^2}{2}}-\left({\mathrm{C}}_2{\overline{a}}^2+{\mathrm{C}}_4{\overline{a}}^4\right){\omega }_0=R_F.$$

(28)

Equation (28) shows that the Bernoulli constant, R, is equal to half the square of the wave celerity minus the time linear rate of change of the velocity potential.

Cokelet [28] set the value of the streamline at the free surface and bottom to be zero and${ Q}_c$ and derived the relationship between $Q_c$ and the SWL depth, d:

$$Q_c=cd.$$

(29)

F85 specified the stream function value on the bottom to be zero and $-Q$ on the surface. By the definition of the function at two streamlines, it is known that $Q_c=Q$. Through Equation (9) of F85 for $Q_F$, Equation (29) can be written as

$$Q_F=-c\left(h-d\right).$$

(30)

The $h-d$ value represents WLD. Equation (30) shows the equality of $Q_F$ and $c\left(h-d\right)$.

The $h-d$ obtained by ZL22 is

$$k(h-d)={\mathsf{\sigma }(\mathrm{C}}_2{\overline{a}}^2+{\mathrm{C}}_4{\overline{a}}^4).$$

(31)

3. Results

3.1. Conversion in the Deep Water Limits

When h approaches infinity for the condition of deep water, $\cosh \mathrm{i}\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)/\cosh ikh$turns to $\exp \mathrm{i}kz$ and $\mathsf{\sigma }$ becomes 1. Therefore, the value of ${\mathrm{A}}_{ij} \mathrm{a}\mathrm{n}\mathrm{d} B_{ij}$ is the sum of the coefficients of all powers of $\mathsf{\sigma }$. Both Stokes wave solutions are simplified and easily compared as listed in

Table 4. The velocity potential function, wave profile, and dynamic properties of F85 and ZL22 in deep water.

Properties	Solution	Expression
${\displaystyle \frac{\varphi k}{c_0}}$	ZL22	$\overline{a }{e}^{kz}\mathrm{s}\mathrm{i}\mathrm{n}\theta +{\displaystyle \frac{1}{2}}{{\overline{a}}^{4}e}^{2kz}\mathrm{s}\mathrm{i}\mathrm{n}2\theta +{\displaystyle \frac{1}{12}}{{\overline{a}}^{5}e}^{3kz}\mathrm{s}\mathrm{i}\mathrm{n}3\theta$
	F85	$-{\displaystyle \frac{c^{F}kx}{c_0}}+\left(\epsilon -{\displaystyle \frac{1}{2}}{\epsilon }^3-{\displaystyle \frac{37}{24}}{\epsilon }^5\right) e^{kz}\mathrm{s}\mathrm{i}\mathrm{n}\theta +{\displaystyle \frac{1}{2}}{{\epsilon }^4 e}^{2kz}\mathrm{s}\mathrm{i}\mathrm{n}2\theta$ $+{\displaystyle \frac{1}{12}}{{\epsilon }^{5}e}^{3kz}\mathrm{s}\mathrm{i}\mathrm{n}3\theta$
$k\eta$	ZL22	$(\overline{a}+{\displaystyle \frac{1}{8}}{\overline{a}}^3+{\displaystyle \frac{121}{192}}{\overline{a}}^5)\mathrm{c}\mathrm{o}\mathrm{s}\theta +({\displaystyle \frac{1}{2}}{\overline{a}}^2+{\displaystyle \frac{5}{6}}{\overline{a}}^4)\mathrm{c}\mathrm{o}\mathrm{s}2\theta$ $+({\displaystyle \frac{3}{8}}{\overline{a}}^3+{\displaystyle \frac{171}{128}}{\overline{a}}^5)\mathrm{c}\mathrm{o}\mathrm{s}3\theta$
	F85	$(\epsilon -{\displaystyle \frac{3}{8}}{\epsilon }^3-{\displaystyle \frac{211}{192}}{\epsilon }^5)\mathrm{c}\mathrm{o}\mathrm{s}\theta +({\displaystyle \frac{1}{2}}{\epsilon }^2+{\displaystyle \frac{1}{3}}{\epsilon }^4)\mathrm{c}\mathrm{o}\mathrm{s}2\theta$ $+({\displaystyle \frac{3}{8}}{\epsilon }^3+{\displaystyle \frac{99}{128}}{\epsilon }^5)\mathrm{c}\mathrm{o}\mathrm{s}3\theta +{\displaystyle \frac{1}{3}}{\epsilon }^4\mathrm{c}\mathrm{o}\mathrm{s}4\theta +{\displaystyle \frac{125}{384}}{\epsilon }^5\mathrm{c}\mathrm{o}\mathrm{s}5\theta$
${\displaystyle \frac{c}{c_0}}$	ZL22	$1+{\displaystyle \frac{1}{2}}{\overline{a}}^2+{\displaystyle \frac{5}{8}}{\overline{a}}^4$
	F85	$1+{\displaystyle \frac{1}{2}}{\overline{\epsilon }}^2+{\displaystyle \frac{1}{8}}{\overline{\epsilon }}^4$
$\overline{a } \mathrm{v}\mathrm{s}. \epsilon$	ZL22	$\overline{a}=\epsilon -{\displaystyle \frac{1}{2}}{\epsilon }^3-{\displaystyle \frac{37}{24}}{\epsilon }^5$
	F85	$\epsilon =\overline{a}+{\displaystyle \frac{1}{2}}{\overline{a}}^3+{\displaystyle \frac{55}{24}}{\overline{a}}^5$
$R_F$	F85	${\displaystyle \frac{1}{2}}{\epsilon }^2+{\displaystyle \frac{1}{4}}{\epsilon }^4$
$Q_F$	F85	$-{\displaystyle \frac{1}{2}}{\epsilon }^2+{\displaystyle \frac{1}{4}}{\epsilon }^4$
k(h − d)	ZL22	0

. Based on Equations (21) and (24), the conversion of $\overline{a } \mathrm{v}\mathrm{s}. \epsilon$for deep water can be obtained. The results are also listed in Table 4.

Through the conversion from $\epsilon$ to $\overline{a}$ in Table 4, the leading harmonic coefficient, $\overline{a}$, of the velocity potential of ZL22 can be converted to that of F85. The coefficients of the second and third harmonic terms after conversion are the same if the coefficients above fifth-order ones are ignored.

For the conversion of the wave profile, substituting $\overline{a}=\epsilon -{\displaystyle \frac{1}{2}}{\epsilon }^3-{\displaystyle \frac{37}{24}}{\epsilon }^5$ for the coefficient of each harmonic of ZL22, through algebraic manipulation and ignoring higher-order terms, we obtain the converted coefficient of each harmonic of F85, which is the same as that in Table 4. We use the conversion of $\epsilon =\overline{a}+{\displaystyle \frac{1}{2}}{\overline{a}}^3+{\displaystyle \frac{55}{24}}{\overline{a}}^5$, the velocity potential and wave profile of F85 can also be completely converted to that of ZL22.

The fourth-order coefficient of wave celerity in ZL22 and F85 solution is different. However, the fourth-order coefficient, ${\displaystyle \frac{5}{8}}{\overline{a}}^4,$of wave celerity in ZL22 after the conversion of $\overline{a}=\epsilon -{\displaystyle \frac{1}{2}}{\epsilon }^3-{\displaystyle \frac{37}{24}}{\epsilon }^5$ can be converted to ${\displaystyle \frac{1}{8}}{\overline{\epsilon }}^4$, which is the same as that of F85 in Table 4.

Due to zero ${\mathrm{C}}_2$ and ${\mathrm{C}}_4$ in deep water, Equation (26) turns out to be $R_F={\displaystyle \frac{c^2}{2}}$. If we first square the wave celerity of ZL22, $1+{\displaystyle \frac{1}{2}}{\overline{a}}^2+{\displaystyle \frac{5}{8}}{\overline{a}}^4,$ then substitute $\overline{a}=\epsilon -{\displaystyle \frac{1}{2}}{\epsilon }^3-{\displaystyle \frac{37}{24}}{\epsilon }^5$ into it, and ignore terms of higher order than the fifth order, we obtain the form of $R_F$in Table 4.

Equation (30) shows that $Q_F$ is proportional to WLD. The WLD obtained by ZL22 in deep water is zero; however, the $Q_F$ of F85 is $-{\displaystyle \frac{1}{2}}{\epsilon }^2+{\displaystyle \frac{1}{4}}{\epsilon }^4$, which is non-zero and depends on wave steepness.

Through the conversion process between F85 and ZL22 in deep water, we found that the wave level difference (WLD) in ZL22 does not satisfy the established formulas for wave dynamic properties [28,29]. We further verified that the formula for WLD provided by Zhao and Liu [16] can be converted into $Q_F$ of F85. This confirms that the WLD in F85 is mathematically consistent with the fundamental dynamic property equations, while the expression in ZL22 deviates from this consistency. The detailed result will be presented in the Discussion section.

3.2. Transformation from F85 to ZL22

To convert F85 to ZL22, we must substitute Equation (21) into the solution of F85. Substituting the coefficients, $B_{31}, B_{33}, B_{51}, B_{53}, B_{55},$ in Table 2 into Equation (21) yields

$$\begin{array}{c}\epsilon =\overline{a}+{\overline{a}}^3\left(\right(27+3{\sigma }^2+41{\sigma }^4-39{\sigma }^6)/(64{\sigma }^6\left)\right)+{\overline{a}}^5(-2025-8370{\sigma }^2+95652{\sigma }^4\\ +21694{\sigma }^6+37098{\sigma }^8-23446{\sigma }^{10}-23724{\sigma }^{12}+12554{\sigma }^{14}+3207{\sigma }^{16})\\ /\left(1024{\sigma }^{12}\right(5+{\sigma }^2\left)\right(5+3{\sigma }^2\left)\right)=\overline{a}+C_{\epsilon \overline{a}3}{\overline{a}}^3+C_{\epsilon \overline{a}5}{\overline{a}}^5.\end{array}$$

(32)

We take the coefficient, $A_{11}^F\epsilon +A_{31}^F{\epsilon }^3+A_{51}^F{\epsilon }^5,$of the first harmonic velocity potential of F85 as an example explanation. We first substitute Equation (32) into $\epsilon , { \epsilon }^3,$and ${\epsilon }^5$ and multiply the corresponding coefficients, $A_{11}^F, A_{31}^F, A_{51}^F$ in Table 3. After algebraic operations, during which terms above the fifth order, O(${\overline{a}}^6$), are ignored, the result is $\overline{a} /\mathsf{\sigma }$, which is the same as in Table 2. For the conversions of other harmonic terms, we have verified that we can completely convert F85 to ZL22 after executing the above conversion steps.

For wave profile, the coefficient of the first harmonic of F85 is $\epsilon +B_{31}^F{\epsilon }^3-(B_{53}^F + {B_{55}^F)\epsilon }^5.$ Following the above conversion steps with the coefficient, $B_{31}^F$ $B_{53}^F, \mathrm{a}\mathrm{n}\mathrm{d} B_{55}^F$ yields $\overline{a}+{\mathrm{B}}_{31}{\overline{a}}^3+{\mathrm{B}}_{51}{\overline{a}}^5$, which is identical to the coefficient of the first harmonic of the wave profile of ZL22. The other harmonic terms of the wave profile of F85 can be completely converted into the form of ZL22.

3.3. Transformaton from ZL22 to F85

Substituting the coefficients, $B_{31}, B_{33}, B_{51}, B_{53}, B_{55},$ in Table 2 into Equation (26) to convert ZL22 to F85 yields

$$\begin{array}{c}\overline{a}=\epsilon -{\epsilon }^3 \left(\right(27+3{\sigma }^2+41{\sigma }^4-39{\sigma }^6)/(64{\sigma }^6\left)\right)+{\epsilon }^5(62775+89370{\sigma }^2-199602{\sigma }^4\\ -91438{\sigma }^6-131460{\sigma }^8-75986{\sigma }^{10}+30114{\sigma }^{12}+12262{\sigma }^{14}+861{\sigma }^{16})\\ /\left(4096{\sigma }^{12}\right(5+{\sigma }^2\left)\right(5+3{\sigma }^2\left)\right)=\epsilon -C_{\overline{a}\epsilon 3}{\epsilon }^3+C_{\overline{a}\epsilon 5}{\epsilon }^5,\end{array}$$

(33)

where $C_{\overline{a}\epsilon 3}=C_{\epsilon \overline{a}3}$.

The first harmonic velocity potential of ZL22 is taken as an example explanation. Its coefficient is very simple to be $\overline{a} /\mathsf{\sigma }$. After the algebraic operation of $\epsilon /\mathsf{\sigma }+A_{31}^F{ \epsilon }^3+A_{51}^F{\epsilon }^5$, its coefficient of $\epsilon ,{ \epsilon }^3$, and ${\epsilon }^5$is the same as that of the first harmonic of Equation (12). The conversion of other harmonic terms is also verified to be identical.

For the wave profile, the coefficient of the first harmonic of ZL22 is $\overline{a}+{\mathrm{B}}_{31}{\overline{a}}^3+{\mathrm{B}}_{51}{\overline{a}}^5.$ The coefficient ${\mathrm{B}}_{31}$and ${\mathrm{B}}_{51}$ in Table 2 multiplied by the cubic and quintic powers of Equation (33) and ignoring terms above the fifth order, O(${\epsilon }^6$) after algebraic operation, we have the result $\epsilon +B_{31}^F{\epsilon }^3-(B_{53}^F{+B_{55}^F)\epsilon }^5$. The other harmonic terms of the wave profile of ZL22 can also be completely converted into the form of F85. The descriptions in these two sections prove that the periodic part of the velocity potential and wave profile between F85 and ZL22 can be converted into each other.

3.4. Transformaton of Dynamic Properties

A common dynamic property of both ZL22 and F85 is the wave celerity. The coefficient of ${\omega }_4^F$ is different from ${\omega }_4$, while ${\omega }_2^F$ = ${\omega }_2$. Therefore, ZL22 stated that the wave celerity of both solutions is slightly different. However, the coefficient of the fourth order wave celerity is different; in addition, there is another difference in the expansion parameters. If the term of ${\omega }_2^F{\epsilon }^2$ is replaced by Equation (32) for ${\epsilon }^2$, ${\omega }_2^F{(\overline{a}+C_{\epsilon \overline{a}3}{\overline{a}}^3)}^2$ produces a fourth-order term, ${\omega }_2^F\left(2C_{\epsilon \overline{a}3}\right){\overline{a}}^4$. After algebraic operation the coefficient of this term is ${\omega }_4$. On the contrary, if we substitute Equation (33) into the term of ${\omega }_2{\overline{a}}^2$, ${\omega }_2{(\epsilon +C_{\overline{a}\epsilon 3}{\epsilon }^3)}^2$ produces a fourth-order term, ${\omega }_2\left(2C_{\overline{a}\epsilon 3}\right){\epsilon }^4$. After algebraic operation the coefficient of this term is ${\omega }_4^F$. Therefore, we have confirmed that the wave velocities of both solutions can be identically converted to each other.

Equation (28) indicates that $R_F$ of F85 equals to ${\displaystyle \frac{c^2}{2}}-\left({\mathrm{C}}_2{\overline{a}}^2+{\mathrm{C}}_4{\overline{a}}^4\right){\omega }_0,$ where $c=c_0(1+{\omega }_2{\overline{a }}^2+{\omega }_4{\overline{a }}^4)$. Inserting Equation (33) into above formula and taking the coefficient of each order up to the fifth order, we can, after algebraic operation, find the final coefficient of the second and fourth orders for R the same as that in Table 4.

Equation (30) cannot be satisfied between the value of surface streamline and WLD in deep water discussed above. In immediate water depth, Equation (30) cannot be satisfied either. What should the WLD be? This will be discussed in the next section.

3.5. Two-Way Conversion Between F85 and SH60

The above results have shown that the solutions of F85 and ZL22 can be converted into each other, and possible errors can be found. But whether this method can also convert other solutions needs to be further verified. We chose the solution of SH60 because SH60 used $\cosh kd$ and $\sinh kd$ as the basic functions for all coefficients, and the wave profile form is different from ZL22. The key to the conversion of expansion parameters depends on the wave profile rather than the velocity potential. In order to avoid repeating the method and simplify the text, only the key steps and results are briefly described here.

The expression for the velocity potential and wave profile of SH60 is written as

$$\begin{array}{c}{\displaystyle \frac{{\varphi }_{SH}k}{c_0}}={\displaystyle \frac{c_{SH} }{c_0}}\left[\right(A_{11}^{SH}\widehat{a}+A_{31}^{SH}{\widehat{a}}^3+A_{51}^{SH}{\widehat{a}}^5){\displaystyle \frac{\cosh \mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh kh}}\mathrm{s}\mathrm{i}\mathrm{n}\theta \\ +\left({A_{22}^{SH}\widehat{a}}^2+A_{42}^{SH}{\widehat{a}}^4\right){\displaystyle \frac{\cosh 2\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 2kh}}\mathrm{s}\mathrm{i}\mathrm{n}2\theta +\left(A_{33}^{SH}{\widehat{a}}^3+A_{53}^{SH}{\widehat{a}}^5\right){\displaystyle \frac{\cosh 2\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 2kh}}\mathrm{s}\mathrm{i}\mathrm{n}3\theta \\ +A_{44}^{SH}{\widehat{a}}^4{\displaystyle \frac{\cosh 4\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 4kh}}\mathrm{s}\mathrm{i}\mathrm{n}4\theta +A_{55}^{SH}{\widehat{a}}^5{\displaystyle \frac{\cosh 5\mathrm{k}\left(\mathrm{z}+\mathrm{h}\right)}{\cosh 5kh}}\mathrm{s}\mathrm{i}\mathrm{n}5\theta ],\end{array}$$

(34)

and

$$\begin{array}{c}k{\eta }_{SH}=\widehat{a} \mathrm{c}\mathrm{o}\mathrm{s}\theta +\left(B_{22}^{SH}{\widehat{a}}^2+B_{42}^{SH}{\epsilon }^4\right)\mathrm{c}\mathrm{o}\mathrm{s}2\theta +\left({B_{33}^{SH}\widehat{a}}^3+B_{53}^{SH}{ \widehat{a}}^5\right)\mathrm{c}\mathrm{o}\mathrm{s}3\theta \\ +B_{44}^{SH}{\widehat{a}}^4\mathrm{c}\mathrm{o}\mathrm{s}4\theta +B_{55}^{SH}{\widehat{a}}^5\mathrm{c}\mathrm{o}\mathrm{s}5\theta .\end{array}$$

(35)

where $\widehat{a}$ is the expansion parameter of SH60. The coefficients $B_{ij}^{SH}(\mathrm{i}\ne \mathrm{j})$ and ${\omega }_4^{SH}$, are listed in

Table 5. Formulas for the coefficients of $A_{ij}^{SH}, B_{ij}^{SH}$, and ${\omega }_i^{SH}$in the SH60 solution.

$A_{31}^{SH}$ = $(-6+{\sigma }^2)/8{\sigma }^5$

$A_{42}^{SH}$ = $-(1+{\sigma }^2)(162-81{\sigma }^2-261{\sigma }^4-19{\sigma }^6+103{\sigma }^8)/(384{\sigma }^{10})$

$A_{51}^{SH}$ = $(-162+1593{\sigma }^2-4617{\sigma }^4+1825{\sigma }^6+159{\sigma }^8+18{\sigma }^{10})/\left(1536{\sigma }^{11}\right)$

$\begin{array}{cc}{A}_{53}^{SH}=\hfill & \left(\right(-1215-3888{\sigma }^2+25065{\sigma }^4-24608{\sigma }^6+2539{\sigma }^8+2512{\sigma }^{10}+107{\sigma }^{12})\hfill \\ \hfill & (1+3{\sigma }^2))/(4096{\sigma }^{13}(5+{\sigma }^2))\hfill \end{array}$

$B_{42}^{SH}=-(81+162{\sigma }^2-900{\sigma }^4+406{\sigma }^6-21{\sigma }^8)/\left(384{\sigma }^9\right)$

$\begin{array}{cc}{B}_{53}^{SH}=\hfill & \left(9\left(-405-1431{\sigma }^2+6003{\sigma }^4-943{\sigma }^6+217{\sigma }^8-157{\sigma }^{10}-23{\sigma }^{12}+3{\sigma }^{14}\right)\right)\hfill \\ \hfill & /\left(4096{\sigma }^{12}\right(5+{\sigma }^2\left)\right)\hfill \end{array}$

${\omega }_4^{SH}$ = $\left(81-819{\sigma }^2+3282{\sigma }^4-2590{\sigma }^6+573{\sigma }^8-15{\sigma }^{10}\right)/\left(1024{\sigma }^{10}\right)$

$E_2^{SH}=(-1+{\sigma }^2)/\left(4{\sigma }^2\right)$

$E_4^{SH}=(-1+{\sigma }^2)(9-33{\sigma }^2+11{\sigma }^4+9{\sigma }^6)/\left(64{\sigma }^8\right)$

. Since${ B}_{ii}^{SH}$ is the same as $B_{ii}$ and ${ A}_{ii}^{SH}$ is the same as $A_{ii},$neither ${ B}_{ii}^{SH}$nor ${ A}_{ii}^{SH}$ is included in Table 5.

The wave speed of SH60 is

$${\displaystyle \frac{c_{SH}}{c_0}}={\displaystyle \frac{{\omega }_{SH}}{{\omega }_0}}=1+{\omega }_2{\widehat{a}}^2+{\omega }_4^{SH}{\widehat{a}}^4,$$

(36)

where the second order quantity is the same as ZL22, but the fourth order quantity is different. The Bernoulli constant of SH60 is

$${\displaystyle \frac{R_{SH}k}{g}}={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{c_{SH}}{c_0}}\right)}^2-\left(E_2^{SH}{\widehat{a}}^2+E_4^{SH}{\widehat{a}}^4\right).$$

(37)

Comparing Equations (16) and (37), we can see a key difference: the first term on the right side of SH60 is the square of the dimensionless wave celerity, while the first term of F85 is the square of the linear wave celerity. This fundamental distinction means the correction terms for the Bernoulli constant are different between SH60 and F85.

Following the procedure of the conversion between F85 and ZL22, two-way conversion of expansion parameters between F85 and SH60 is written as

$$\begin{array}{c}\epsilon =\widehat{a}+{\widehat{a}}^3 \left(\right(27-9{\sigma }^2+9{\sigma }^4-3{\sigma }^6)/(64{\sigma }^6\left)\right)+{ \widehat{a}}^5(-6075-45360{\sigma }^2\\ +205956{\sigma }^4+89112{\sigma }^6-16642{\sigma }^8+2368{\sigma }^{10}-4668{\sigma }^{12}+-552{\sigma }^{14}+117{\sigma }^{16})\\ /\left(3072{\sigma }^{12}\right(5+{\sigma }^2\left)\right(5+3{\sigma }^2\left)\right)=\widehat{a}+C_{\epsilon \widehat{a}3}{\widehat{a}}^3+C_{\epsilon \widehat{a}5}{\widehat{a}}^5,\end{array}$$

(38)

and

$$\begin{array}{c}\widehat{a}=\epsilon -C_{\epsilon \widehat{a}3}{\epsilon }^3+{\epsilon }^5(188325+203310{\sigma }^2-764046{\sigma }^4-340410{\sigma }^6+53932{\sigma }^8\\ -6070{\sigma }^{10}+14622{\sigma }^{12}+2370{\sigma }^{14}-225{\sigma }^{16}\left)\right)/\left(12288{\sigma }^{12}\right(5+{\sigma }^2\left)\right(5+3{\sigma }^2\left)\right)\\ =\epsilon -C_{\epsilon \widehat{a}3}{\epsilon }^3+C_{\widehat{a}\epsilon 5}{\epsilon }^5,\end{array}$$

(39)

where $C_{\epsilon \widehat{a}3}$ is different from $C_{\epsilon \overline{a}3}$ and$C_{\epsilon \widehat{a}5}$ is also different from $C_{\epsilon \overline{a}5}$. The third-order parameter conversion between F85 and SH60 is the same as that between F85 and ZL22. When H is specified, $\widehat{a}$ is different from $\overline{a}$ and $\epsilon$.

Based on Equation (38) we can prove that the coefficient of the second and third harmonic of the F85 wave profile can be converted into that of SH60. On the contrary, substituting Equation (39) for the second and third harmonic of the SH60 wave profile, we can have the same form of F85.

Taking the first harmonic term of velocity potential as an example, the process of converting SH60 to F85 is explained. The coefficient, $A_{11}^{SH}\widehat{a}+A_{31}^{SH}{\widehat{a}}^3+A_{51}^{SH}{\widehat{a}}^5,$ must first be multiplied by the wave velocity of Equation (36). Then, the parameter conversion of Equation (39) is used to convert the series of $\widehat{a}$ to the series of $\epsilon$. We arrange the odd-order coefficients and compare them with the coefficients of the first harmonic term in Table 3 to confirm that the coefficients of these orders are exactly the same. Following the above steps, we can also successfully convert the coefficients of the second and third harmonic terms. Since $A_{44}^{SH}$ is the same as $A_{44}^F$ and $A_{55}^{SH}$ is the same as $A_{55}^F$, the fourth and fifth harmonic terms of SH60 and F85 are the same. Therefore, it is confirmed that the fifth-order velocity potential of SH60 can be converted into that of F85. As for the reverse conversion, the coefficient of F85 needs to be converted into the series of a using Equation (38), and then divided by $c_{SH}/c_0$ to obtain the velocity potential coefficient in Table 5.

The first harmonic coefficient of the SH60’s wave profile contains only $\widehat{a}$. If the parameter conversion of Equation (39) is substituted, the third-order quantity can be easily obtained, which is $-B_{31}^F$ in Table 3. Using $B_{53}^F$ and $B_{55}^F$ in Table 3 to calculate $-\left(B_{53}^F+B_{55}^F\right)$, we can obtain the first fifth-order quantity of the F85’s wave profile, which is exactly equal to the fifth-order quantity, $C_{\widehat{a}\epsilon 5}$, in Equation (39). The other four harmonics were also confirmed to be convertible.

The form of ${\omega }_4^{SH}$ is different from ${\omega }_4^F.$ This results in the expansion parameter $\widehat{a}$ and $\epsilon$ in spite of the same ${\omega }_2$ of the second order. Taking the square of Equation (39) and collecting the coefficient of the fourth order, $2C_{\epsilon \widehat{a}3}$, and then multiplying ${\omega }_4^{SH}$, we can obtain the coefficient of ${\epsilon }^4$, ${\omega }_4^F$. Substituting Equation (36) into Equation (37) and utilizing the relevant coefficients from Table 5, the results are organized and confirmed to be the Bernoulli constant of F85. Finally, we can prove the two-way convertibility between F85 and SH60.

3.6. Difference Analysis

The physical validity of F85 and ZL22 was examined using experimental data on particle velocity and wave profile [14,31]. Zhao et al. [15] showed the discrepancy in key specified physical quantities among these three theories. These theories have been proven to be suitable for engineering applications, and there is no need to verify their physical validity again. To show that the conversion of the theories is correct up to the fifth order (i.e., the difference is above the sixth order), we also chose two wave conditions for comparison, as shown in

Table 6. Parameters for two cases at a constant wave length, L = 100m.

Case	H (m)	h (m)	H/L	h/L	Ur
I	4.475	25	0.0895	0.5	0.716
II	3.0	10	0.060	0.2	25

.

We use the guideline for selecting appropriate analytical periodic water wave solutions, based on two physical parameters: the frequency dispersion parameter (h/L) and the nonlinearity parameter (H/L) [31]. When the Ursell number, Ur = (H/L)(h/L)³, is larger than 26, Stokes wave theories are not recommended [31].

Case I is for deep water, and its H/L is very close to the deep-water limit, 0.0896 [31]. Case II is in the intermediate-depth regime.

The numerical comparison of wave parameters for Case I and Case II is presented in

Table 7. List of Wave Parameters Calculated from Three Wave Theories for Two Cases. The percentage difference is defined as the ratio of the difference between ZL22 and F85, or SH60 and F85.

Case	Author	a (m)	Dif (a)	c (m/s)	Dif (c)	ηc (m)	Dif (ηc)	ηt (m)	Dif (ηt)
I	SH60	2.160	−3.46%	$9.1764$	$0.19\%$	$2.3398$	$-0.32\%$	$-2.1352$	$-0.32\%$
	F85	2.2375	0 *	$9.1593$	0 *	$2.3472$	0 *	$-2.1278$	0 *
	ZL22	2.13526	−4.57%	$9.1822$	$0.25\%$	$2.3374$	$-0.42\%$	$-2.1376$	$-0.42\%$
II	SH60	$1.4782$	$-1.45\%$	8.9916	0.19%	1.5299	$-0.32\%$	−1.4701	$-0.32\%$
	F85	1.5	0 *	8.9877	0 *	1.5306	0 *	−1.4694	0 *
	ZL22	$1.4709$	$-1.94\%$	8.9928	0.25%	1.5296	$-0.42\%$	−1.4704	$-0.42\%$

* The percentage difference for F85 is zero because its value serves as the baseline for the comparison.

. For Case I, the expansion parameter of SH60 and ZL22 is smaller than that of F85, with percentage differences of −3.46% and −4.57%, respectively. This occurs because Equations (33) and (38) are fifth-order polynomials of expansion parameters. When the high-order value on the right side of the equation is positive, the expansion parameter must be lower than the value on the left side. F85 has the smallest wave celerity. The corresponding percentage differences for SH60 and ZL22 are 0.19% and 0.25%, respectively. The wave crest of F85 is higher than that of SH60 and ZL22, which means the wave trough of SH60 and ZL22 is lower than that of F85. The corresponding percentage differences for SH60 and ZL22 are −0.32% and −0.42%, respectively.

For Case II, the physical quantities are lower than those of Case I, but their order of magnitude remains the same. Except for the expansion parameters, the difference percentage results are consistent with those of Case I.

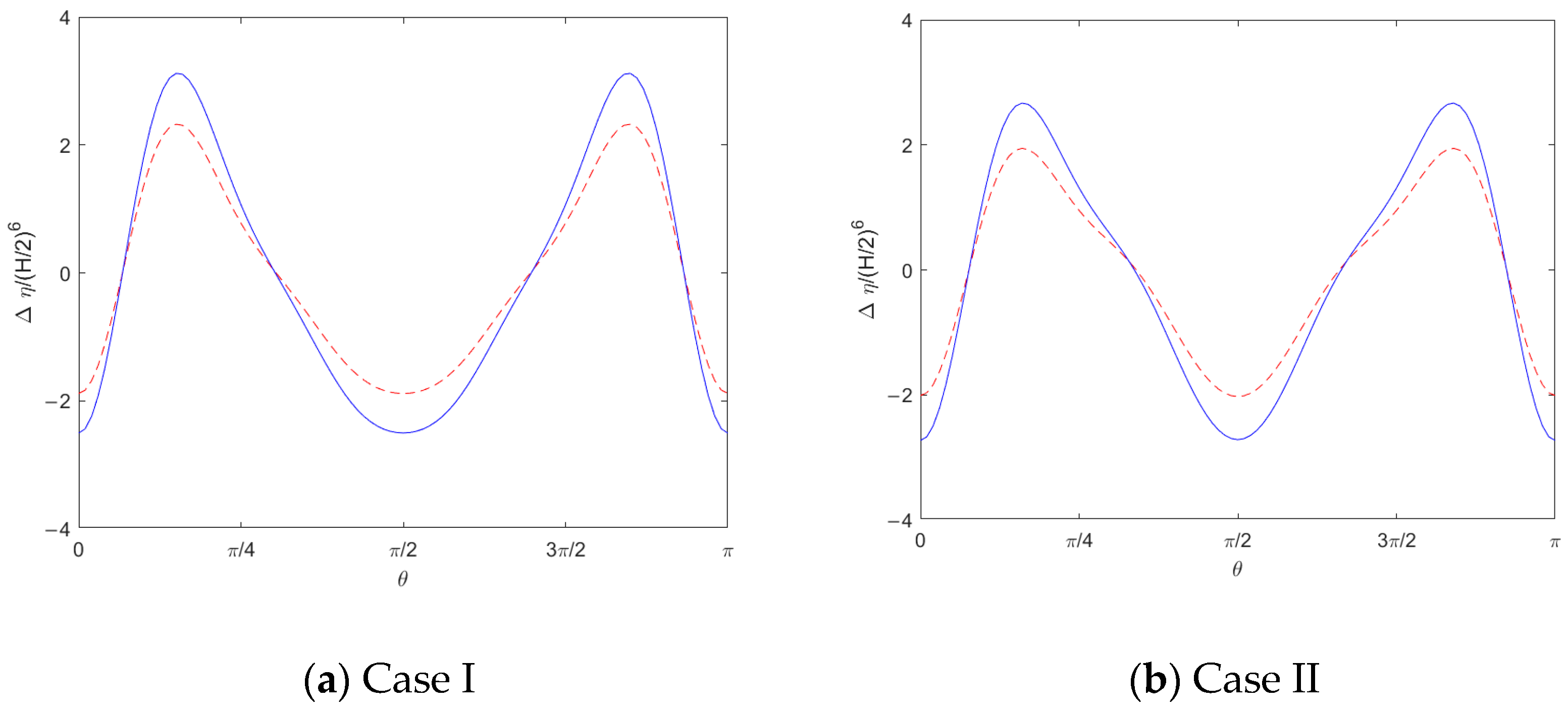
The values of the key physical quantities obtained from the three Stokes wave theories are very similar. To further illustrate that these theories are accurate up to the fifth order, we will now examine the wave profile calculations. The results, shown in Figure 2, display the relative difference with respect to the sixth power of the specified amplitude. If this relative difference is less than 10, it indicates that the wave profiles of ZL22 and F85 are identical up to the fifth order, with discrepancies appearing only from the sixth order onward.

Comparing Figure 2a and Figure 2b, we can see that the relative difference between SH60 and ZL22 exhibits a similar variation across both cases. However, the extreme values for SH60 are consistently lower than those for ZL22. Specifically, for Case I, SH60 shows maximum and minimum values of 2.32 and −1.89, respectively. For Case II, these values are 1.94 and −2.02. In contrast, ZL22 has maximum and minimum values of 3.12 and −2.50 for Case I, and 2.67 and −2.73 for Case II.

These results in Figure 2 further confirm that all three Stokes wave theories are accurate up to the fifth order.

4. Discussion

The figure 12 in Cokolet [28] indicated that the WLD increases with the wave amplitude, even in deep water. Therefore, the result of ZL22 stating that WLD is zero in deep water indicates that its expression is incorrect. If ${\mathrm{W}\mathrm{L}\mathrm{D}}_c$ = –Q/c is obtained from Equation (30) after algebraic operation, it can be written as

$$k{\mathrm{W}\mathrm{L}\mathrm{D}}_c=-\left(-{\displaystyle \frac{{ϵ}^2}{2\sigma }}+{\displaystyle \frac{\left(9+21{\sigma }^2-13{\sigma }^4+15{\sigma }^6\right){ϵ}^4}{64{\sigma }^7}}\right)={\displaystyle \frac{{\overline{a}}^2}{2\sigma }}-{\displaystyle \frac{9\left(-1+{\sigma }^2-3{\sigma }^4+3{\sigma }^6\right){\overline{a}}^4}{32{\sigma }^7}}.$$

(40)

Zhao et al. [15] showed that the derived ${\mathrm{W}\mathrm{L}\mathrm{D}}_Z$ in Equation (38) of their paper is

$$k{\mathrm{W}\mathrm{L}\mathrm{D}}_Z={\displaystyle \frac{c_1}{s_1}}[{\displaystyle \frac{{ϵ}^2}{2}}+{ϵ}^4(-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{9}{8s_1^2}}+{\displaystyle \frac{75}{64s_1^4}}+{\displaystyle \frac{9}{32s_1^6}}\left)\right],$$

(41)

where $c_1=\cosh kd$ and $s_1=\sinh kd$.

For deep water, $d\to \infty$ so that $c_1/s_1\to 0, s_1\to \infty .$ Equation (41) shows the WLD in deep water is ${ϵ}^2/2-{ϵ}^4/2$. Based on Equation (40) the WLD for deep water can also be obtained as ${ϵ}^2/2-{ϵ}^4/2$ or ${\overline{a}}^2/2$. Using the formula of $\overline{a}=\epsilon -{\displaystyle \frac{1}{2}}{\epsilon }^3-{\displaystyle \frac{37}{24}}{\epsilon }^5$ for deep water in the Section 3.1, ${\overline{a}}^2/2$ can be converted to be ${ϵ}^2/2-{ϵ}^4/2$.

Equation (41) is expressed in terms of $\cosh kd$ and $\sinh kd$ and Equation (40) is in terms of $\sigma =\tanh kh$. Therefore, the fourth-order coefficient of WLD is obviously different. If we convert Equation (41) to (40), we need to expand the series of $\cosh kh$ and $\sinh kh$ instead of $\cosh kd$ and $\sinh kd$. Since WLD is a series $ϵ$ and implicitly includes a function of $\cosh kd$ and $\sinh kd$, the series expansion results in a cumbersome derivation.

This confirms that the WLD in F85 is mathematically consistent with the fundamental dynamic property equations, while the expression in ZL22 deviates from this consistency. Our findings emphasize the importance of correctly defining all reference levels—especially MWL and SWL—when comparing or converting between different Stokes wave theories. Even small differences in these definitions can lead to significant discrepancies in derived physical properties. Therefore, caution must be taken when interpreting or applying published high-order Stokes wave solutions, particularly those involving dynamic quantities dependent on nonlinear terms. For the selection of wave conditions for each-order Stokes wave theory, please refer to the applicable range shown in a new diagram [24].

5. Conclusions

Stokes waves represent a classical topic in physical mechanics, which is characterized by steady, periodic motion. Various formulations of Stokes wave theory have been developed to analyze wave kinematics and support the design of coastal and offshore structures. With the aid of MATLAB( R2025a (25.1))’s Symbolic Toolbox, Zhao and Liu [16] derived an alternative formulation and compared several fifth-order Stokes wave theories. They pointed out discrepancies in the high-order coefficients of velocity potential and wave celerity among these theories. This observation prompted us to investigate whether different formulations of Stokes wave theory can be converted into each other from a mathematical perspective.

We selected three fifth-order Stokes wave theories—SH60, F85, and ZL22—which employ distinct expansion parameters and differ in their expressions for velocity potential, wave profile, and wave celerity. However, all are based on the same mean water level (MWL) depth. The coefficients in these theories are expressed using hyperbolic functions of kh, resulting in significant differences in form and appearance. To facilitate comparison, we converted the original expressions for the velocity potential, wave profile, and wave celerity into a unified form using the common parameter $\mathsf{\sigma }=\tanh kh$, as shown in Table 1 and Table 2.

Instead of the binomial approximation adopted by ZL22, we employed the series reversion method to convert between different expansion parameters. Although the expressions for velocity potential and wave profile in ZL22 can be successfully converted into those of F85, the set-down (WLD) of ZL22 does not match the physically consistent value obtained from F85. During the conversion process between F85 and ZL22, we discovered that the set-down (or water level displacement) in ZL22 does not conform to established dynamic property formulas. This highlights a fundamental inconsistency in the ZL22 formulation regarding dynamic wave properties. The results confirm that this method allows for accurate two-way conversion between the selected Stokes wave theories.

Due to the cumbersome derivation and the large number of coefficients associated with the perturbation method, no research on Stokes wave theory above the sixth order has been published to date. This makes it impossible to confirm whether this method can be applied to the two-way conversion of higher-order Stokes wave theory. However, because the Stokes wave theory for deep water conditions is significantly simpler than that for finite water depth, it might be feasible to attempt higher-order conversions of two Stokes wave theories in deep water in the future.