New Insight on Damped Oscillating Regular Structures from “Effective” Proton Electromagnetic Form Factor Data
Abstract
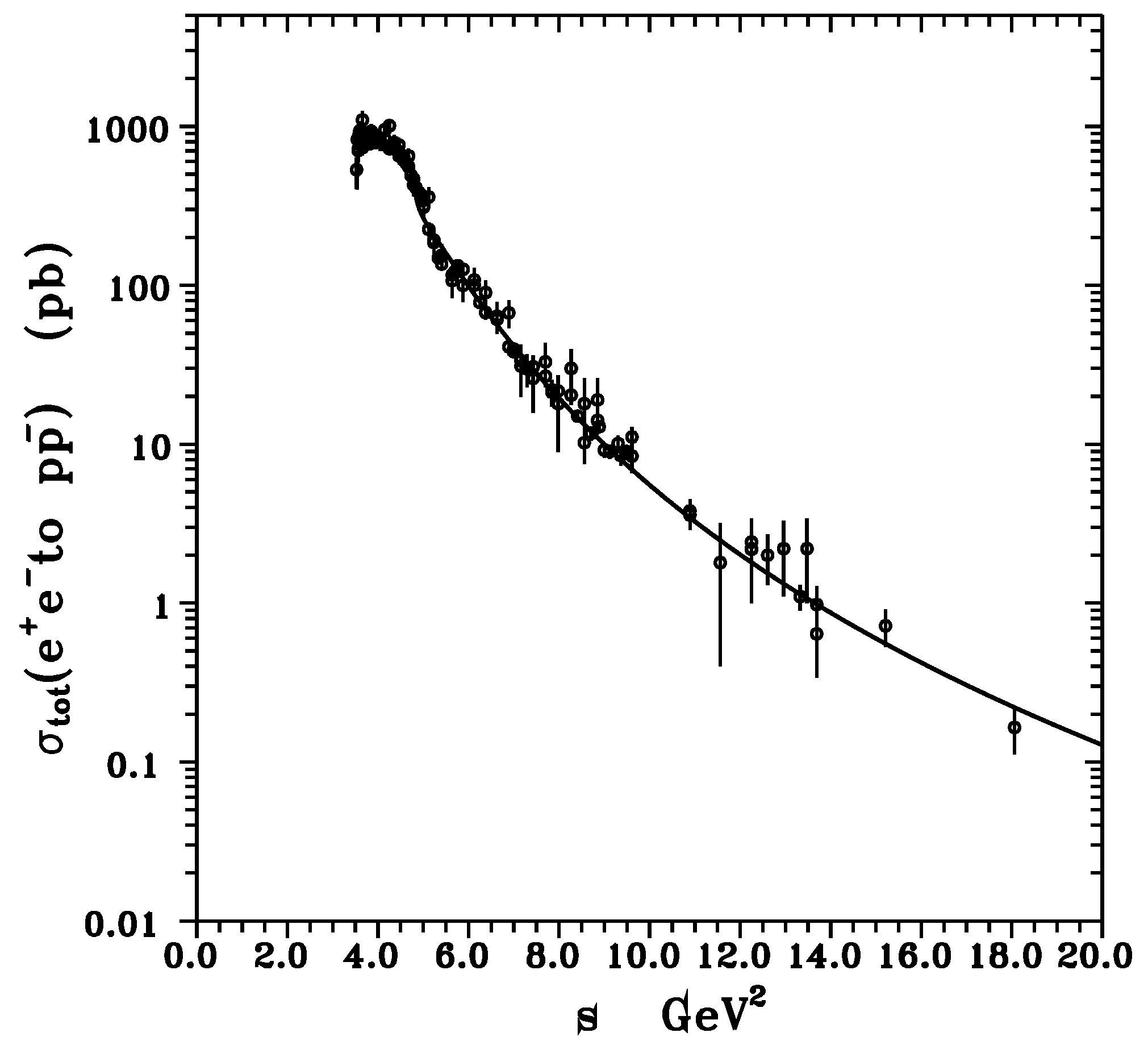
1. Introduction
2. Proton Damped Oscillation Regular Structures Seem to Have No Objective Existence
3. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ferroli, R.B.; Pacetti, S.; Zallo, A. No Sommerfeld resummation factor in e+e− → ? Eur. Phys. J. 2012, A48, 33. [Google Scholar] [CrossRef]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. Study of e+e−→ via initial-state radiation at BABAR. Phys. Rev. 2013, D87, 092005. [Google Scholar]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. Measurement of the e+e−→ cross section in the energy range from 3.0 to 6.5 GeV. Phys. Rev. 2013, D88, 072009. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Ai, X.C.; Albayrak, O.; Albrecht, M.; Ambrose, D.J.; Amoroso, A.; An, F.F.; An, Q.; Bai, J.Z.; et al. Measurement of the proton form factor by studying e+e−→ . Phys. Rev. 2015, D91, 112004. [Google Scholar]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Alekseev, M.; Amoroso, A.; An, F.F.; An, Q.; Bai, Y.; et al. Study of the process e+e−→ via initial state radiation at BESIII. Phys. Rev. 2019, D99, 092002. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Alekseev, M.; Amoroso, A.; An, F.F.; An, Q.; Bai, Y.; et al. Measurement of proton electromagnetic form factors in e+e−→ in the energy region 2.00–3.08 GeV. Phys. Rev. Lett. 2020, 124, 042001. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Aliberti, R.; Amoroso, A.; An, M.R.; An, Q.; Bai, X.H.; et al. Measurement of proton electromagnetic form factors in the time-like region using initial state radiation at BESIII. Phys. Lett. 2021, B817, 136328. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Aliberti, R.; Amoroso, A.; An, M.R.; An, Q.; Bai, X.H.; et al. Oscillating features in the electromagnetic structure of the neutron. Nat. Phys. 2021, 17, 1200. [Google Scholar] [CrossRef]
- Dubnickova, A.Z.; Dubnicka, S.; Rekalo, M.P. Investigation of the nucleon electromagnetic structure by polarization effects in e+e− → N anti-N processes. Nuovo Cim. 1996, A109, 241. [Google Scholar] [CrossRef]
- Bianconi, A.; Tomasi-Gustafsson, E. Periodic interference structures in the timelike proton form factor. Phys. Rev. Lett. 2015, 114, 232301. [Google Scholar] [CrossRef]
- Tomasi-Gustafsson, E.; Rekalo, M.P. Search for evidence of asymptotic regime of nucleon electromagnetic form-factors from a compared analysis in space- and time-like regions. Phys. Lett. 2001, B504, 291. [Google Scholar] [CrossRef]
- Bardin, G.; Burgun, G.; Calabrese, R.; Capon, G.; Carlin, R.; Dalpiaz, P.; Dalpiaz, P.F.; Derré, J.; Dosselli, U.; Duclos, J.; et al. Determination of the electric and magnetic form-factors of the proton in the timelike region. Nucl. Phys. 1994, B411, 3. [Google Scholar] [CrossRef]
- Antonelli, A.; Baldini, R.; Bertani, M.; Biagini, M.E.; Bidoli, V.; Bini, C.; Bressani, T.; Calabrese, R.; Cardarelli, R.; Carlin, R.; et al. Measurement of the electromagnetic form-factor of the proton in the timelike region. Phys. Lett. B 1994, 334, 431. [Google Scholar] [CrossRef]
- Delcourt, B.; Derado, I.; Bertrand, J.L.; Bisello, D.; Bizot, J.C.; Buon, J.; Cordier, A.; Eschstruth, P.; Fayard, L.; Jeanjean, J.; et al. Study of the Reaction e+e−→ in the Total Energy Range 1925-MeV–2180-MeV. Phys. Lett. B 1979, 86, 395. [Google Scholar] [CrossRef]
- Bassompierre, G.; Schneegans, M.A.; Binder, G.; Gissinger, G.; Jacquey, S.; Dalpiaz, P.; Dalpiaz, P.F.; Peroni, C.; Tecchio, L. Electron positron pair production in anti-p p annihilation at rest and related determination of the electromagnetic form-factor of the proton in the timelike region. Nuovo Cim. A 1983, 73, 347. [Google Scholar] [CrossRef]
- Bisello, D.; Limentani, S.; Nigro, M.; Pescara, L.; Posocco, M.; Sartori, P.; Augustin, J.E.; Busetto, G.; Cosme, G.; Couchot, F.; et al. A Measurement of e+e− → for 1975-MeV ≤ ≤ 2250-MeV. Nucl. Phys. B 1983, 224, 379. [Google Scholar] [CrossRef]
- Armstrong, T.A.; Bettoni, D.; Bharadwaj, V.; Biino, C.; Borreani, G.; Broemmelsiek, D.; Buzzo, A.; Calabrese, R.; Ceccucci, A.; Cester, R.; et al. Measurement of the proton electromagnetic form-factors in the timelike region at 8.9 − GeV2 − − 13 − GeV2. Phys. Rev. Lett. 1993, 70, 1212. [Google Scholar] [CrossRef]
- Ambrogiani, M.; Bagnasco, S.; Baldini, W.; Bettoni, D.; Borreani, G.; Buzzo, A.; Calabrese, R.; Cester, R.; Dalpiaz, P.; Fan, X.; et al. Measurements of the magnetic form-factor of the proton in the timelike region at large momentum transfer. Phys. Rev. D 1999, 60, 032002. [Google Scholar] [CrossRef]
- Ablikim, M.; Bai, J.Z.; Ban, Y.; Bian, J.G.; Cai, X.; Chen, H.F.; Chen, H.S.; Chen, H.X.; Chen, J.C.; Chen, J.; et al. Measurement of the cross section for e+e− → p anti-p at center-of-mass energies from 2.0-GeV to 3.07-GeV. Phys. Lett. B 2005, 630, 14. [Google Scholar] [CrossRef][Green Version]
- Jones, M.K.; Aniol, K.A.; Baker, F.T.; Berthot, J.; Bertin, P.Y.; Bertozzi, W.; Besson, A.; Bimbot, L.; Boeglin, W.U.; Brash, E.J.; et al. GEp/GMp ratio by polarization transfer in p → e. Phys. Rev. Lett. 2000, 84, 1398. [Google Scholar] [CrossRef]
- Gayou, O.; Aniol, K.A.; Averett, T.; Benmokhtar, F.; Bertozzi, W.; Bimbot, L.; Brash, E.J.; Calarco, J.R.; Cavata, C.; Chai, Z.; et al. Measurement of G(Ep) / G(Mp) in polarized-e p → e polarized-p to Q**2 = 5.6-GeV**2. Phys. Rev. Lett. 2002, 88, 092301. [Google Scholar] [CrossRef]
- Punjabi, V.; Perdrisat, C.F.; Aniol, K.A.; Baker, F.T.; Berthot, J.; Bertin, P.Y.; Bertozzi, W.; Besson, A.; Bimbot, L.; Boeglin, W.U.; et al. Proton elastic form-factor ratios to Q**2 = 3.5-GeV**2 by polarization transfer. Phys. Rev. C 2005, 71, 055202. [Google Scholar] [CrossRef]
- Zhan, X.; Allada, K.; Armstrong, D.S.; Arrington, J.; Bertozzi, W.; Boeglin, W.; Chen, J.-P.; Chirapatpimol, K.; Choi, S.; Chudakov, E.; et al. High-Precision Measurement of the Proton Elastic Form Factor Ratio μpGE/GM at low Q2. Phys. Lett. B 2011, 705, 59. [Google Scholar] [CrossRef]
- Puckett, A.J.R.; Brash, E.J.; Gayou, O.; Jones, M.K.; Pentchev, L.; Perdrisat, C.F.; Punjabi, V.; Aniol, K.A.; Averett, T.; Benmokhtar, F.; et al. Final Analysis of Proton Form Factor Ratio Data at Q2 = 4.0, 4.8 and 5.6 GeV2. Phys. Rev. C 2012, 85, 045203. [Google Scholar] [CrossRef]
- Puckett, A.J.R.; Brash, E.J.; Jones, M.K.; Luo, W.; Meziane, M.; Pentchev, L.; Perdrisat, C.F.; Punjabi, V.; Wesselmann, F.R.; Afanasev, A.; et al. Polarization Transfer Observables in Elastic Electron Proton Scattering at Q2 = 2.5, 5.2, 6.8, and 8.5 GeV2. Phys. Rev. C 2017, 96, 055203. [Google Scholar] [CrossRef]
- Akhiezer, A.; Rekalo, M.P. Polarization phenomena in electron scattering by protons in the high energy region. Sov. Phys. Dokl. 1968, 13, 572. [Google Scholar]
- Akhiezer, A.; Rekalo, M.P. Polarization effects in the scattering of leptons by hadrons. Sov. J. Part. Nucl. 1974, 4, 277. [Google Scholar]
- Janssens, T.; Hofstadter, R.; Hughes, E.B.; Yearian, M.R. Proton form factors from elastic electron-proton scattering. Phys. Rev. 1966, 142, 922. [Google Scholar] [CrossRef]
- Berger, C.; Burkert, V.; Knop, G.; Langenbeck, B.; Rith, K. Electromagnetic form-factors of the proton at squared four momentum transfers between 10-fm**-2 and 50 fm**-2. Phys. Lett. B 1971, 35, 87. [Google Scholar] [CrossRef]
- Bartel, W.; Büsser, F.-W.; Dix, W.-R.; Felst, R.; Harms, D.; Krehbiel, H.; Kuhlmann, P.E.; McElroy, J.; Meyer, J.; Weber, G. Measurement of proton and neutron electromagnetic form-factors at squared four momentum transfers up to 3-GeV/c2. Nucl. Phys. B 1973, 58, 429. [Google Scholar] [CrossRef]
- Höhler, G.; Pietarinen, E.; Sabba-Stefanescu, I.; Borkowski, F.; Simon, G.G.; Walther, V.H.; Wendling, R.D. Analysis of Electromagnetic Nucleon Form-Factors. Nucl. Phys. B 1976, 114, 505. [Google Scholar] [CrossRef]
- Sill, A.F.; Arnold, R.G.; Bosted, P.E.; Chang, C.C.; Gomez, J.; Katramatou, A.T.; Martoff, C.J.; Petratos, G.G.; Rahbar, A.A.; Rock, S.E.; et al. Measurements of elastic electron-proton scattering at large momentum transfer. Phys. Rev. D 1993, 48, 29. [Google Scholar] [CrossRef] [PubMed]
- Walker, R.C.; Filippone, B.; Jourdan, J.; Milner, R.; McKeown, R.; Potterveld, D.H.; Andivahis, L.; Arnold, R.; Benton, D.; Bosted, P.E.; et al. Measurements of the proton elastic form-factors for 1-GeV/c**2 <= Q**2 <= 3-GeV/C**2 at SLAC. Phys. Rev. D 1994, 49, 5671. [Google Scholar]
- Andivahis, L.; Bosted, P.E.; Lung, A.; Stuart, L.M.; Alster, J.; Arnold, R.G.; Chang, C.C.; Dietrich, F.S.; Dodge, W.; Gearhart, R.; et al. Measurements of the electric and magnetic form-factors of the proton from Q**2 = 1.75-GeV/c**2 to 8.83-GeV/c**2. Phys. Rev. D 1994, 50, 5491. [Google Scholar] [CrossRef] [PubMed]
- Dubnicka, S.; Dubnickova, A.Z. Analyticity in a phenomenology of electro-weak structure of hadrons. Acta Phys. Slovaca 2010, 60, 1. [Google Scholar] [CrossRef][Green Version]
- Dubnickova, A.Z.; Dubnicka, S. Prediction of neutron electromagnetic form factors behaviors just by the proton electromagnetic form factors data. Eur. Phys. J. 2021, A57, 307. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Lepage, P.G. Exclusive Processes in Perturbative Quantum Chromodynamics. Phys. Rev. D 1980, 22, 2157. [Google Scholar] [CrossRef]
- Adamuscin, C.; Dubnickova, A.Z.; Dubnicka, S.; Pekarik, R.; Weisenpacher, P. Asymptotic conditions for electromagnetic form-factors of hadrons represented by VMD model. Eur. Phys. J. C 2003, 28, 115. [Google Scholar] [CrossRef]
- Dubnicka, S.; Dubnickova, A.Z.; Weisenpacher, P. General expressions for VM dominated form factors of hadrons fulfilling asymptotic conditions. Eur. Phys. J. C 2004, 32, 381. [Google Scholar] [CrossRef]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C. Review of particle physics. Phys. Rev. 2024, D110, 030001. [Google Scholar]
- Yan, B.; Chen, C.; Li, X.; Xie, J.-J. Understanding oscillating features of the timelike nucleon electromagnetic form factors within the extending vector meson dominance model. arXiv 2024, arXiv:2312.04866v2. [Google Scholar] [CrossRef]







| List of parameters |
| ; |
| ; |
| ; |
| ; |
| ; |
| ; . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubnička, S.; Dubničková, A.-Z.; Holka, L.; Liptaj, A. New Insight on Damped Oscillating Regular Structures from “Effective” Proton Electromagnetic Form Factor Data. AppliedMath 2025, 5, 126. https://doi.org/10.3390/appliedmath5030126
Dubnička S, Dubničková A-Z, Holka L, Liptaj A. New Insight on Damped Oscillating Regular Structures from “Effective” Proton Electromagnetic Form Factor Data. AppliedMath. 2025; 5(3):126. https://doi.org/10.3390/appliedmath5030126
Chicago/Turabian StyleDubnička, Stanislav, Anna-Zuzana Dubničková, Lukáš Holka, and Andrej Liptaj. 2025. "New Insight on Damped Oscillating Regular Structures from “Effective” Proton Electromagnetic Form Factor Data" AppliedMath 5, no. 3: 126. https://doi.org/10.3390/appliedmath5030126
APA StyleDubnička, S., Dubničková, A.-Z., Holka, L., & Liptaj, A. (2025). New Insight on Damped Oscillating Regular Structures from “Effective” Proton Electromagnetic Form Factor Data. AppliedMath, 5(3), 126. https://doi.org/10.3390/appliedmath5030126





