A Refined Inertial-like Subgradient Method for Split Equality Problems

Abstract

This paper presents the convergence analysis of a newly proposed algorithm for approximating solutions to split equality variational inequality and fixed point problems in real Hilbert spaces. We establish that, under reasonably mild conditions, specifically when the involved mappings are quasimonotone, uniformly continuous, and quasi-nonexpansive, the sequences generated by the algorithm converge strongly to a solution of the problem. Furthermore, we provide several numerical experiments to demonstrate the practical effectiveness of the proposed method and compare its performance with that of existing algorithms.

1. Introduction

Variational inequality problems (VIPs) and fixed-point problems (FPPs) play a central role in optimization and equilibrium theory, with wide-ranging applications in fields like engineering, economics, and operations research. Simply put, FPPs help us find values that remain unchanged under a given transformation, an idea deeply explored by mathematicians like Banach, Brouwer, and Schauder [1]. On the other hand, VIPs are used to model systems where certain inequality conditions must be met, such as physical or economic equilibrium situations. These were formalized in the mid-20th century by researchers like Stampacchia [2] and Fichera [3].

As problems in real-world systems grew more complex, so did the mathematical models needed to handle them. In many cases, constraints and objectives are distributed across different spaces or subsystems, which traditional VIPs and FPPs cannot fully capture. This gave rise to extended models like the split equality variational inequality problem (SEVIP) and the split equality fixed point problem (SEFPP). These models aim to find solutions that not only satisfy variational inequalities or fixed point conditions but also meet additional coupling constraints that link variables from separate domains.

The idea of splitting constraints across domains originally came from the split feasibility problem (SFP), introduced by Elfving and later generalized by Moudafi into the more flexible split equality feasibility problem (SEFP) [4]. These problems are especially relevant in applications such as medical image reconstruction, signal processing, and decentralized decision-making systems [5,6]. Further extending these ideas, the split equality variational inequality and fixed point problem (SEVIFPP) combines both VIP and FPP conditions, making it a powerful framework for tackling hybrid equilibrium problems.

Solving these problems efficiently requires robust iterative algorithms. Early approaches relied on projection methods and the well-known extragradient technique introduced by Korpelevich [7]. Later, improvements such as the subgradient extragradient method [8] and Tseng modified method [9] addressed various limitations, including high computational cost and limited applicability to nonmonotone settings. Other researchers introduced enhancements using inertial and viscosity terms to increase convergence speed and algorithm stability [10,11,12].

More recent contributions by Zhao [13], Kwelegano et al. [14], and others have further advanced the field by designing iterative schemes tailored to the structure of SEVIP and SEVIFPP. These methods are particularly effective when dealing with quasimonotone, pseudomonotone, or quasi-nonexpansive mappings, each of which poses unique mathematical challenges [15,16,17,18,19]. Building on these developments, Mekuriaw et al. [20] recently introduced new inertial-like algorithms that show promising convergence behavior.

Inspired by this evolving body of work, the current study proposes new iterative algorithms to solve SEVIFPP more efficiently. The aim is to develop techniques that not only guarantee convergence under more general conditions but also improve computation time and practical applicability.

Let $\Omega$ be a Hilbert space with a non-empty closed convex subset B. A fixed point problem (FPP) seeks an element $r\in \Omega$ such that $Zr=r$ for a given operator $Z:\Omega \to \Omega$, with the set of solutions denoted by $F\left(Z\right)$. Fixed point theory has a rich history, originating from foundational results by Poincaré, Brouwer, Kakutani, Schauder, and Banach, particularly the Banach contraction principle [1].

Variational inequality problems (VIPs) provide another important framework in non-linear analysis and optimization. For a mapping $Z:B\to \Omega$, the classical VIP seeks $r^{\ast }\in B$ such that

$$⟨Z{r}^{\ast },s-r^{\ast }⟩\ge 0,\forall s\in B,$$

with the solution set denoted as $VI(B,Z)$. First studied by Stampacchia [2] and Fichera [3], VIPs are crucial for modeling equilibrium problems under constraints, especially in systems with non-linearity or interacting subsystems. A related concept is the Minty variational inequality problem (MVIP), which requires

$$⟨Zr,r-r^{\ast }⟩\ge 0,\forall r\in B,$$

with the solution set $MVI(B,Z)$. If Z is continuous and convex, then $MVI(B,Z)\subseteq VI(B,Z)$ [15]; for pseudomonotone and continuous Z, the two sets coincide [17]; however, for quasi-monotone Z, the reverse inclusion may not hold [16].

The split equality feasibility problem (SEFP), introduced by Moudafi [4], extends these ideas to multiple domains. Given two Hilbert spaces ${\Omega }_1$, ${\Omega }_2$, subsets $B\subset {\Omega }_1$ and $E\subset {\Omega }_2$, and bounded linear operators $X:{\Omega }_1\to {\Omega }_3$, $Y:{\Omega }_2\to {\Omega }_3$, the SEFP seeks $(r,v)\in B\times E$ such that

$$Xr=Yv.$$

This formulation generalizes the split feasibility problem (SFP) introduced by Elfving [21] and has applications in image reconstruction, signal processing, and optimization [5,6].

By replacing the sets B and E in SEFP with solution sets of VIPs, we obtain the split equality variational inequality problem (SEVIP):

$$r\in VI(B,Z),v\in VI(E,J),\mathrm{such}\mathrm{that}Xr=Yv,$$

where $Z:{\Omega }_1\to {\Omega }_1$ and $J:{\Omega }_2\to {\Omega }_2$ are operators.

Likewise, the split equality fixed point problem (SEFPP) is defined as:

$$r\in F\left(Z\right),v\in F\left(J\right),\mathrm{such}\mathrm{that}Xr=Yv,$$

where $F\left(Z\right)$ and $F\left(J\right)$ are the respective fixed point sets.

A further extension, the split equality variational inequality and fixed point problem (SEVIFPP), combines both structures. It involves finding

$$r^{\ast }\in VI(B,Z)\cap F\left(M\right),s^{\ast }\in VI(E,J)\cap F\left(N\right),\mathrm{such}\mathrm{that}X{r}^{\ast }=Y{s}^{\ast },$$

where $Z,M:{\Omega }_1\to {\Omega }_1$ and $J,N:{\Omega }_2\to {\Omega }_2$ are non-linear mappings.

Different projection-like iterative techniques were developed to solve VIP under various relevant conditions. The most basic approach for resolving optimization issues is the projection gradient method defined as;

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{r}_1\in \Omega \hfill \\ r_{n+1}=P_B\left(r_n-\mu Z{r}_n\right),\forall n\ge 1\hfill \end{array}\right.\end{array}$$

(1)

where the constant $\mu$ is positive. It can be demonstrated with ease that the iterative approach (1) converges weakly to a unique solution of $VI(B,Z)$ if Z is inversely strongly monotone and Lipschitz continuous.

To overcome the strong monotonicity requirement and achieve monotonicity, Korpelevich [7] suggested an extragradient method for resolving VIP.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{r}_1\in \Omega \hfill \\ v_n=P_B\left(r_n-\mu Z{r}_n\right),\hfill \\ r_{n+1}=P_B\left(r_n-\mu Z{v}_n\right),\forall n\ge 1\hfill \end{array}\right.\end{array}$$

(2)

where Z is monotone and Lipschitz continuous from a non-empty, closed, and convex subset of a real Hilbert space $\Omega$ into a space itself and $\mu$ is a positive constant. When $\mu \in (0,{\displaystyle \frac{1}{L}})$, this method’s weak convergence was achieved. This method’s primary flaw is that it necessitates the computation of two metric projections onto B for every iteration. The extragradient method becomes extremely complex and expensive to construct if the set B is not simple. Numerous authors were inspired by this to suggest some modified extragradient techniques.

Censor et al. [8] developed the subgradient extragradient technique, which addresses this problem by replacing the second projection onto B with a projection onto a straightforward half-space $B_n$:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{r}_1\in \Omega \hfill \\ v_n=P_B\left(r_n-\mu Z{r}_n\right),\hfill \\ B_n=\left\{r\in \Omega :⟨r_n-\mu Z{r}_n-v_n,r-v_n⟩\le 0\right\},\hfill \\ r_{n+1}=P_{B_n}\left(r_n-\mu Z{v}_n\right),\forall n\ge 1\hfill \end{array}\right.\end{array}$$

(3)

Here, $\mu \in (0,{\displaystyle \frac{1}{L}})$ and L signifies the Lipschitz constant of Z. They demonstrated that (3) converges weakly to $VI(B,Z)$ if Z is monotone and Lipschitz. When Z is monotone (or pseudomonotone), several writers have demonstrated the poor convergence of the subgradient extragradient approach (3) (see to [22,23] for some new findings, for instance).

Later, it is noted that two projections and two operator evaluations must still be computed for each iteration of the Censor et al. [8] approach. These turn the subgradient extragradient approach (3) computationally costly in applications where the structure of Z is complex and Z has a complex process of assessment.

The Tseng extragradient method was presented by Tseng [9] in 2000.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{r}_1\in \Omega \hfill \\ v_n=P_B\left(r_n-\mu Z{r}_n\right),\hfill \\ r_{n+1}=v_n-\mu \left(Z{v}_n-Z{r}_n\right),\forall n\ge 1\hfill \end{array}\right.\end{array}$$

(4)

where $\mu$ is falling between 0 and ${\displaystyle \frac{1}{L}}$ and L being Z’s Lipschitz constant. He discovered that the sequence $\left\{x_n\right\}$ has a weak convergence to a point in $VI(B,X)$, where X is a bounded linear operator from ${\Omega }_1$ to ${\Omega }_3$ and ${\Omega }_1,{\Omega }_3$ are both real Hibert spaces. The Tseng method has an advantage over Censor et al. in that it only has to make one projection onto the possible set in every iteration. Numerous additions to Tseng’s algorithm have been documented in scholarly works (see [24,25,26] as an example).

The subsequent iterative method for solving the equivalent SEVIP in the Hilbert spaces was created in 2022 by Kwelegano et al. [14].

Let $\ell \in (0,1),\vartheta >0,\lambda \in \left(0,{\displaystyle \frac{1}{\vartheta }}\right)$. Select $\left(r_0,s_0\right)\in B\times E$ randomly.

For $n\ge 1$, perform simultaneous computations,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{v}_n=P_B\left(r_n-\lambda Z{r}_n\right),\hfill \\ m_n=r_n-{\vartheta }_n\left(r_n-v_n\right),\hfill \\ y_n=P_E\left(s_n-\lambda J{s}_n\right),\hfill \\ w_n=s_n-{\delta }_n\left(s_n-y_n\right),\hfill \\ d_n=P_B\left[r_n-{\nu }_n{X}^{\ast }\left(X{r}_n-Y{y}_n\right)\right],\hfill \\ r_{n+1}={\beta }_{n}f\left(r_n\right)+\left(1-{\beta }_n\right)\left[b_n{P}_{B_n}{r}_n+\left(1-b_n\right)d_n\right],\hfill \\ z_n=P_E\left[s_n-{\nu }_n{Y}^{\ast }\left(Y{s}_n-X{r}_n\right)\right],\hfill \\ s_{n+1}={\beta }_{n}g\left(s_n\right)+\left(1-{\beta }_n\right)\left[b_n{P}_{E_n}{s}_n+\left(1-b_n\right)z_n\right].\hfill \end{array}\right.\end{array}$$

(5)

While

$$B_n=\left\{r\in B:⟨Z{m}_n,r-m_n⟩\le 0\right\},E_n=\left\{s\in E:⟨J{w}_n,v-w_n⟩\le 0\right\},$$

${\mu }_n={\ell }^{t_n}$ and ${\delta }_n={\ell }^{v_n}$ and $t_n$ and $v_n$ are the smallest non-negative integers t and v, correspondingly so that

$$\begin{array}{cc}\hfill & ⟨Z{r}_n-Z\left[r_n-{\ell }^t\left(r_n-v_n\right)\right],r_n-v_n⟩\le \vartheta {∥r_n-v_n∥}^2,\hfill \\ \hfill & ⟨J{s}_n-J\left[s_n-{\ell }^v\left(s_n-y_n\right)\right],s_n-y_n⟩\le \vartheta {∥s_n-y_n∥}^2,\hfill \end{array}$$

and the sequences $\left\{{\nu }_n\right\},\left\{{\beta }_n\right\},\left\{b_n\right\}\subset {\mathbb{R}}^{+}$. Additionally, the mappings $Z:{\Omega }_1\to {\Omega }_1$ and $J:{\Omega }_2\to {\Omega }_2$ on bounded subsets of the non-empty closed convex subsets B and E of ${\Omega }_1$ and ${\Omega }_2$, respectively, are pseudomonotone, uniformly continuous, and sequentially weakly continuous.They demonstrated that, under appropriate assumptions, the resulting sequence strongly converges to a problem solution (5). Several scholars have utilized a line search strategy to get rid the requirement of the underlying mapping Z and J’s Lipschitz continuity.

The iterative procedure below was presented by Zhao [13] in 2015 for the category of quasi-nonexpansive mappings, i.e., $Z:{\Omega }_1\to {\Omega }_1$ and $J:{\Omega }_2\to {\Omega }_2$ with non-empty fixed point sets F(Z) and F(J):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{s}_n=r_n-{\nu }_n{X}^{\ast }\left(X{r}_n-Y{v}_n\right),\hfill \\ r_{n+1}={\beta }_n{s}_n+\left(1-{\beta }_n\right)Z{s}_n,\hfill \\ y_n=m_n-{\nu }_n{Y}^{\ast }\left(Y{m}_n-X{r}_n\right),\hfill \\ m_{n+1}={\beta }_n{y}_n+\left(1-{\beta }_n\right)J{y}_n.\hfill \end{array}\right.\end{array}$$

(6)

This showed that, under certain assumptions, the procedure in (6) weakly converges to a solution of the split equality fixed point issue. This is without the need for an understanding of the norms of X and Y.

Tan [11] proposed the following method in 2022 to address the common solution of the fixed point problem related to demicontractive mapping J and variational inequality problem related to monotone and Lipschitz continuous mapping Z.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_n=r_n+{\psi }_n\left(r_n-r_{n-1}\right),\hfill \\ m_n=P_B\left(x_n-{\mu }_{n}Z{x}_n\right),\hfill \\ v_n=m_n+{\mu }_n\left(Z{x}_n-Z{m}_n\right),\hfill \\ r_{n+1}={\beta }_{n}f\left(r_n\right)+\left(1-{\beta }_n\right)\left[\left(1-{\zeta }_n\right)v_n+{\zeta }_{n}J{v}_n\right].\hfill \end{array}\right.\end{array}$$

(7)

The method (7) converges strongly to a common point in (VI(B,Z) and F(J) utilizing the inertial and viscosity techniques.

In an effort to solve split equality variational inequality and fixed point problems involving uniformly continuous quasi-monotone mappings for the MVIP and quasi-non expansive demiclosed mappings for the fixed point problem in Hilbert spaces, Tan and Cho [10], Kwelegano et al. [14], Thong and Vuong [27], Zhao [13], and Polyak [28] stipulated motivation and encouragement. By motivating from Tan and Cho [10], Kwelegano et al. [14], Thong and Vuong [27], Zhao [13] and Polyyak [28], Mekuriaw, Zegeye, Takele and Tufa [20] proposed the inertial-like subgradient extragradient algorithm and Inertial-like Tseng subgradient extragradient method. In this direction, we extended the recent results achieved by Mekuriaw, Zegeye, Takele and Tufa [20], and we proposed a new algorithm for solving (SEVIFPP).

2. Preliminaries

In this section, there is an overview of the core definitions and pertinent findings needed to proof our key results. In the following, let $\Omega$ be a Hilbert space whose norm and inner product are represented by $\parallel ·\parallel$ and $⟨·,·⟩$, respectively. We compose $r_n\rightharpoonup r$ to suggest that the sequence $\left\{r_n\right\}$ converges weakly to r and $r_n\to r$ to suggest that the sequence $\left\{r_n\right\}$ converges strongly to r. Remember that the projection of $\Omega$ onto B (nearest point or metric), represented by $P_B$. The meaning of $P_B$ is given below. There is a single nearest point in B for each $r\in \Omega$, indicated by $P_B\left(r\right)$ in a way that

$$inf\{\parallel r-v\parallel :v\in B\}=∥P_{B}r-r∥.$$

Here, B is a closed convex subset of a Hilbert space $\Omega$.

Definition 1 

([29]). Suppose we have a real Hilbert space Ω. Then, a non-linear operator $Z:\Omega \to \Omega$ is known as L-Lipschitz continuous if there is a constant $L>0$, such that $\parallel Zr-Zv\parallel \le L\parallel r-v\parallel ,\forall r,v\in \Omega$.

Definition 2 

([29]). Assume we have a real Hilbert space Ω. Then, a non-linear operator $Z:\Omega \to \Omega$ is called contraction if for a constant $0<L<1$, such that $\parallel Zr-Zv\parallel \le L\parallel r-v\parallel ,\forall r,v\in \Omega$.

Definition 3 

([29]). Let Ω be a Hilbert space and $Z:\Omega \to \Omega$ be a linear operator, an operator is called nonexpansive if $L=1$ such that $\parallel Zr-Zv\parallel \le L\parallel r-v\parallel ,\forall r,v\in \Omega$.

Definition 4 

([29]). Consider a non-linear operator $Z:\Omega \to \Omega$ where Ω is a Hilbert space. Thus, Z is called quasi non-expensive if $F\left(Z\right)$ is non-empty and

$$\parallel Zr-v\parallel \le \parallel r-v\parallel ;\forall r\in B,v\in F\left(Z\right).$$

Definition 5 

([29]). A non-linear operator $Z:\Omega \to \Omega$ is called firmly nonexpansive if $2Z-I$ is nonexpansive, or correspondingly,

$$⟨r-v,Zr-Zv⟩\ge {\parallel Zr-Zv\parallel }^2,\forall r,v\in \Omega$$

or similarly, Z is firmly nonexpansive strictly in the event that Z can be articulated as

$$Z={\displaystyle \frac{1}{2}}(I+J),$$

as well as $J:\Omega \to \Omega$ is nonexpansive; projections are firmly nonexpansive.

The following features of $P_B$ are well known.

(P1)

$${∥P_{B}r-P_{B}v∥}^2\le ⟨P_{B}r-P_{B}v,r-v⟩.$$

Thus, $P_B$ is firmly nonexpansive. $P_B$ is specifically nonexpansive from $\Omega$ onto B.

Additionally, there is

(P2)

$$⟨r-P_{B}r,v-P_{B}r⟩\le 0,\forall v\in B.$$

So, for each $r\in \Omega$, we obtain

(P3)

$${∥P_{B}r-v∥}^2\le {\parallel r-v\parallel }^2-{∥P_{B}v-v∥}^2,\forall v\in B.$$

Definition 6 

([30]). Suppose we have an real Hilbert space Ω and a non-linear operator $Z:\Omega \to \Omega$ is called monotone if it satisfies

$$⟨Zr-Zv,r-v⟩\ge 0,\forall r,v\in \Omega .$$

Definition 7 

([31]). An operator $Z:\Omega \to \Omega$, where Ω is a real Hilbert space is referred to as pseudomonotone if

$$⟨Zv,v-r⟩\ge 0,impliesthat⟨Zr,r-v⟩\ge 0,\forall r,v\in \Omega .$$

Definition 8 

([31]). A non-linear operator $Z:\Omega \to \Omega$ is called quasi-monotone if

$$⟨Zv,r-v⟩>0impliesthat⟨Zr,r-v⟩\ge 0,\forall r,v\in B.$$

Definition 9 

([31]). Consider that $Z:\Omega \to \Omega$ is a non-linear operator such that $F\left(Z\right)\ne \varnothing$. Thus, the operator $I-Z$, where I is the identity operator on Ω, which is said to be demiclosed at zero, and in case for any $\left\{r_n\right\}\subset \Omega$, the following simplification holds true:

$$r_n\rightharpoonup rand(I-Z)r_n\to 0,impliesthatr\in F\left(Z\right).$$

Lemma 1 

([32]). Let Ω be an real Hilbert space. Then, the following results are proper:

(1) ${\parallel a+b\parallel }^2={\parallel a\parallel }^2+2⟨a,b⟩+{\parallel b\parallel }^2,\forall a,b\in \Omega$.

(2) ${\parallel a+b\parallel }^2\le {\parallel a\parallel }^2+2⟨b,a+b⟩,\forall a,b\in \Omega$.

(3) ${\parallel \beta a+\zeta b+\nu c\parallel }^2={\beta \parallel a\parallel }^2+{\zeta \parallel b\parallel }^2+{\nu \parallel c\parallel }^2{-\beta \zeta \parallel a-b\parallel }^2{-\beta \nu \parallel a-c\parallel }^2-\alpha \nu {\parallel b-c\parallel }^2$, $\forall a,b,c\in \Omega ,$ where $\beta ,\zeta ,\nu \in [0,1],\beta +\zeta +\nu =1$.

Lemma 2 

([33]). If $Z:\Omega \to \Omega$ is a continuous and quasi-nonexpansive operator, and B is a closed convex subset of a Hilbert space Ω; then, $F\left(Z\right)$ is closed, convex and non-empty.

Lemma 3 

([34]). Suppose that $\Omega ={\Omega }_1\times {\Omega }_2$, where ${\Omega }_1$ and ${\Omega }_2$ are real Hilbert spaces. If $\left(s,t\right)\in \Omega$ and $\left(s^{\ast },t^{\ast }\right)=P_B(s,t)$, where C is non-empty, closed and convex subset of Ω; thus, we have

$$⟨(s,t)-\left(s^{\ast },t^{\ast }\right),(r,v)-\left(s^{\ast },t^{\ast }\right)⟩\le 0,forall(r,v)\in B.$$

Lemma 4 

([35]). Let $X:\Omega \to \Omega$ be an operator, and B be a closed, convex and non-empty subset of a real Hilbert space Ω. Therefore, the following inequality holds:

$$∥{\displaystyle \frac{s-P_B(s-\beta Xs)}{\beta }}∥\le ∥{\displaystyle \frac{s-P_B(s-\zeta Xs)}{\zeta }}∥\forall s\in Band\beta \ge \zeta >0.$$

Lemma 5 

([16]). Let $Z:\Omega \to \Omega$ be an opertor, Ω is a Hilbert space, and B is a non-empty, closed, and convex subset of Ω. The following list shows the locations of non-empty $MVI(B,Z)$. If either

(i) Z is pseudomonotone on B and $VI(B,Z)\ne \varnothing$;

(ii) Z is quasi-monotone on B, $Z\ne 0$ on B and B is bounded;

(iii) Z is quasi-monotone on B, $int\left(B\right)\ne \varnothing$ and there exists $r^{\ast }\in VI(B,Z)$ such that $Z{r}^{\ast }\ne \varnothing$ then $MVI(B,Z)$ is non-empty.

Lemma 6 

([36]). Let $\left\{b_n\right\}$ be a sequence of non-negative real numbers and $\left\{b_{n_k}\right\}$ be a subsequence of $\left\{b_n\right\}$ with the property fulfilling $b_{n_k}<b_{n_k+1}\forall k\in \mathbb{N}$; then, there exists a non-decreasing sequence $\left\{a_s\right\}$ of $\mathbb{N}$ such that $lim{sup}_{s\to \infty }{a}_s=\infty$ and

$$max\left\{b_{a_s},b_s\right\}\le b_{a_s+1}.$$

Lemma 7 

([37]). Assume that $\left\{{\alpha }_n\right\}$ is a sequence of real numbers and $\left\{{\beta }_n\right\}$ is a sequence of non-negative real numbers such that $\left\{{\beta }_n\right\}\subset (0,1)$ fulfilling

$${\beta }_{n+1}\le \left(1-{\zeta }_n\right){\beta }_n+{\zeta }_n{\alpha }_n,\forall n\ge 1$$

If $lim{sup}_{n\to \infty }{\alpha }_n\le 0$, then ${lim}_{n\to \infty }{\beta }_n=0$.

Lemma 8 

([20]). Assume that the conditions (C1)–(C6) described in Chapter 3 are retained. Suppose $Zr\ne 0,\forall r\in B$ and $Js\ne 0,\forall s\in E$. Let $\left\{x_n\right\},\left\{m_n\right\},\left\{y_n\right\}$ and $\left\{w_n\right\}$ be sequences generated by the proposed algorithm. Let $\left\{\left(x_{n_j},y_{n_j}\right)\right\}$ be a subsequence of $\left\{\left(x_n,y_n\right)\right\}$ such that $∥x_{n_j}-m_{n_j}∥\to 0,∥y_{n_j}-w_{n_j}∥\to 0$ and $\left(x_{n_j},y_{n_j}\right)⟶(s,t)$. Then $(s,t)\in MVI(B,Z)\times MVI(E,J)$.

3. Refined Algorithm for Split Equality Variational Inequality and Fixed Point Problems

This section covers the convergence analysis of the refined inertial-like subgradient extragradient algorithm. In the continuation, we will make the following assumptions.

• (C1) Let the sets B and E be non-empty, closed, and convex subsets of the real Hilbert spaces ${\Omega }_1$ and ${\Omega }_2$, respectively.
• (C2) Let $Z:{\Omega }_1\to {\Omega }_1$ and $J:{\Omega }_2\to {\Omega }_2$ be quasi-monotone, uniformly continuous, and $Z{r}_n\rightharpoonup Zr$ and $J{s}_n\rightharpoonup Js$, whenever $\left\{r_n\right\}$ and $\left\{s_n\right\}$ are sequences in B and E, respectively, such that $r_n\rightharpoonup r$ and $s_n\rightharpoonup s$.
• (C3) Let $M:{\Omega }_1\to {\Omega }_1$ and $N:{\Omega }_2\to {\Omega }_2$ be quasi-nonexpansive mappings such that $I-M$ and $I-N$ are demiclosed at zero.
• (C4) Let $X:{\Omega }_1\to {\Omega }_3$ and $Y:{\Omega }_2\to {\Omega }_3$ be bounded linear mappings and let $X^{\ast }$ and $Y^{\ast }$ be adjoints of X and Y, respectively, where ${\Omega }_3$ is another real Hilbert space.
• (C5) Let ${\rm Y}=\left\{\right(c,d)\in (MVI(B,Z)\cap F\left(M\right))\times (MVI(E,J)\cap F\left(N\right)):Xc=$$Yd\}\ne \varnothing$.
• (C6) Let $\left\{{ϵ}_n\right\},\left\{{\eta }_n\right\},\left\{{\xi }_n\right\},\left\{{\pi }_n\right\}$ and $\left\{b_n\right\}$ be the sequences satisfying ${\sum }_{n=1}^{\infty }{ϵ}_n<\infty$ and ${lim}_{n\to \infty }{\displaystyle \frac{{ϵ}_n}{{\beta }_n}}=0$, where $\left\{{\beta }_n\right\}\subset (0,1)$ with ${\sum }_{n=1}^{\infty }{\beta }_n=\infty$ and ${lim}_{n\to \infty }{\beta }_n=0,\left\{{\eta }_n\right\},\left\{{\xi }_n\right\},\left\{{\pi }_n\right\},\left\{b_n\right\}\subseteq$$[e,f]\subset (0,1)$, for some $e,f>0$.

Proposed Inertial-like Subgradient Extragradient Algorithm

Initialization: Let $\overline{r},x_0,x_1\in B,\overline{s},s_0,s_1\in E,0\le \psi <1,\lambda ,\zeta ,\kappa ,\ell ,\delta \in (0,1)$. Set $n=1$. Iterative steps:

Step 1. Given the iterates $\left(r_{n-1},s_{n-1}\right)$ and $\left(r_n,s_n\right)$ in $B\times E$, choose ${\psi }_n$ such that $0\le {\psi }_n\le {\overline{\psi }}_n$, where

$$\begin{array}{c}\hfill {\overline{\psi }}_n=\left\{\begin{array}{cc}min\left\{\psi ,{\displaystyle \frac{{ϵ}_n}{∥r_n-r_{n-1}∥}},{\displaystyle \frac{{ϵ}_n}{∥s_n-s_{n-1}∥}}\right\},\hfill & \mathrm{if}{r}_n\ne r_{n-1}\mathrm{and}{s}_n\ne s_{n-1},\hfill \\ \psi ,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(8)

Step 2. Set

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_n=r_n+{\psi }_n\left(r_{n-1}-r_n\right),\mathrm{and}\hfill \\ y_n=s_n+{\psi }_n\left(s_{n-1}-s_n\right).\hfill \end{array}\right.\end{array}$$

(9)

Step 3. Compute

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{m}_n=P_B\left(x_n-{\mu }_{n}Z{x}_n\right),\hfill \\ v_n=P_{Z_n}\left(x_n-{\mu }_{n}Z{m}_n\right),\hfill \\ w_n=P_E\left(y_n-{\theta }_{n}J{y}_n\right),\hfill \\ z_n=P_{J_n}\left(y_n-{\theta }_{n}J{w}_n\right),\hfill \end{array}\right.\end{array}$$

(10)

where

$$\begin{array}{cc}& Z_n=\left\{r\in B:⟨x_n-{\mu }_{n}Z{x}_n-m_n,r-m_n⟩\le 0\right\}\mathrm{and}\hfill \\ & J_n=\left\{s\in E:⟨y_n-{\theta }_{n}J{y}_n-w_n,s-w_n⟩\le 0\right\},\hfill \end{array}$$

${\mu }_n=\zeta {\delta }^{t_k}$ and $t_k$ the smallest non-negative integer i satisfying

$$\zeta {\delta }^t∥Z{x}_n-Z{m}_n∥\le \lambda ∥x_n-m_n∥,$$

(11)

and ${\theta }_n=\kappa {\ell }^{v_i}$ and $v_i$ the smallest non-negative integer v satisfying

$$\kappa {\ell }^v∥J{y}_n-J{w}_n∥\le \lambda ∥y_n-w_n∥.$$

(12)

Step 4. Compute

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{d}_n=P_B\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right),\hfill \\ h_n=P_B\left({\pi }_n{d}_n+\left(1-{\pi }_n\right)M{d}_n\right),\hfill \\ g_n=P_B\left({\xi }_n{d}_n+\left(1-{\xi }_n\right)M{h}_n\right),\hfill \\ r_{n+1}={\beta }_n\overline{r}+\left(1-{\beta }_n\right)\left[\left(1-{\eta }_n\right)x_n+{\eta }_n\left(b_n{v}_n+\left(1-b_n\right)g_n\right)\right],\hfill \\ p_n=P_E\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right),\hfill \\ q_n=P_E\left({\pi }_n{p}_n+\left(1-{\pi }_n\right)N{p}_n\right),\hfill \\ f_n=P_E\left({\xi }_n{p}_n+\left(1-{\xi }_n\right)N{q}_n\right),\hfill \\ s_{n+1}={\beta }_n\overline{s}+\left(1-{\beta }_n\right)\left[\left(1-{\eta }_n\right)y_n+{\eta }_n\left(b_n{z}_n+\left(1-b_n\right)f_n\right)\right].\hfill \end{array}\right.\end{array}$$

(13)

where $0<\nu \le {\nu }_n\le \widehat{{\nu }_n}$ with

$$\widehat{{\nu }_n}=min\left\{\nu +1,{\displaystyle \frac{{∥X{x}_n-Y{y}_n∥}^2}{\left[{∥X^{\ast }\left(X{x}_n-Y{y}_n\right)∥}^2+{∥Y^{\ast }\left(Y{y}_n-X{x}_n\right)∥}^2\right]}}\right\},$$

(14)

for $n\in \overline{{\rm Y}}=\left\{m\in \mathbb{N}:X{x}_m-Y{y}_m\ne 0\right\}$, otherwise ${\nu }_n=\nu$, for some $\nu >0$. Set $n:=n+1$ and go to Step 1.

Remark 1. 

Note that, from (8) and condition (C6), we have ${\psi }_n∥r_n-r_{n-1}∥\le {ϵ}_n$ for all $n\ge 1$ and ${\displaystyle \frac{{ϵ}_n}{{\beta }_n}}\to 0$ as $n\to \infty$, which implies that

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\psi }_n}{{\beta }_n}}∥r_n-r_{n-1}∥=0$$

and

$$\underset{n\to \infty }{lim}{\psi }_n∥r_n-r_{n-1}∥=\underset{n\to \infty }{lim}{\beta }_n\left[{\displaystyle \frac{{\psi }_n}{{\beta }_n}}∥r_n-r_{n-1}∥\right]=0$$

Similarly, we get ${lim}_{n\to \infty }{\displaystyle \frac{{\psi }_n}{{\beta }_n}}∥s_n-s_{n-1}∥=0$ and ${lim}_{n\to \infty }{\psi }_n∥s_n-s_{n-1}∥=0$.

Remark 2. 

Assume that conditions (C1)–(C6) are satisfied. Then, the line search rules (11) and (12) are well-defined.

Proof. 

If we consider the case when $x_n\in VI(B,Z)$, then $x_n=P_B\left(x_n-{\nu }_{n}Z{x}_n\right)$. Thus, we have $x_n=m_n$ and hence (11) is satisfied for $t=0$. Let $x_n\notin VI(B,Z)$ and assume on the contrary that

$$\zeta {\delta }^t∥Z{x}_n-Z{m}_n∥>\lambda ∥x_n-m_n∥,\forall t\ge 0.$$

(15)

That is,

$${\displaystyle \frac{1}{\lambda }}∥Z{x}_n-Z{P}_B\left(x_n-\zeta {\delta }^{t}Z{x}_n\right)∥>{\displaystyle \frac{1}{\zeta {\delta }^t}}∥x_n-P_B\left(x_n-\zeta {\delta }^{t}Z{x}_n\right)∥,\forall t\ge 0.$$

(16)

Since $P_B$ is continuous, we have

$$\underset{t\to \infty }{lim}∥P_B\left(x_n-\zeta {\delta }^t{x}_n\right)-x_n∥=0,$$

(17)

which implies by the uniform continuity of Z on B that

$$∥Z{P}_B\left(x_n-\zeta {\delta }^t{x}_n\right)-Z{x}_n∥=0$$

(18)

Thus, by substituting (18) in (16) we get

$$\underset{t\to \infty }{lim}{\displaystyle \frac{1}{\zeta {\delta }^t}}∥x_n-P_B\left(x_n-\zeta {\delta }^{t}Z{x}_n\right)∥=0.$$

(19)

Now, put $b_t=P_B\left(x_n-\zeta {\delta }^{t}Z{x}_n\right)$. Then, by the projection property (P2) we have

$$⟨x_n-\zeta {\delta }^{t}Z{x}_n-b_t,r-b_t⟩\le 0,\forall r\in B,$$

(20)

which implies that

$$⟨{\displaystyle \frac{x_n-b_t}{\zeta {\delta }^t}},r-b_t⟩+⟨Z{x}_n,b_t-x_n⟩\le ⟨Z{x}_n,r-x_n⟩,\forall r\in B.$$

(21)

Taking the limit as $t\to \infty$ of (21) and making use of (17) and (19), we obtain that $⟨Z{x}_n,r-x_n⟩\ge 0,\forall r\in B$, which is a contradiction to our assumption that $x_n\notin VI(B,Z)$. Thus, there exists a non-negative integer t which satisfies (11). Thus, (11) is well-defined. The proof concerning line search rule (12) is similar and hence the proof is complete. □

Theorem 1. 

Suppose conditions (C1)–(C6) are satisfied. Then, the sequences $\left\{r_n\right\}$ and $\left\{s_n\right\}$ generated by newly refined algorithm are bounded.

Proof. 

Suppose $(c,d)\in {\rm Y}$ and let

$$\begin{array}{cc}\hfill e_n=& \left(1-{\eta }_n\right)x_n+{\eta }_n\left(b_n{v}_n+\left(1-b_n\right)g_n\right)\hfill \\ \hfill & t_n=\hfill & \hfill \left(1-{\eta }_n\right)y_n+{\eta }_n\left(b_n{z}_n+\left(1-b_n\right)f_n\right).\end{array}$$

(22)

Then, we obtain

$${∥e_n-c∥}^2\le \left(1-{\eta }_n\right){∥x_n-c∥}^2+{\eta }_n{b}_n{∥v_n-c∥}^2+{\eta }_n\left(1-b_n\right){∥g_n-c∥}^2,$$

(23)

and

$${∥t_n-d∥}^2\le \left(1-{\eta }_n\right){∥y_n-d∥}^2+{\eta }_n{b}_n{∥z_n-d∥}^2+{\eta }_n\left(1-b_n\right){∥f_n-d∥}^2.$$

(24)

Moreover, we have from the quasi-nonexpansive property of M that

$$\begin{array}{cc}\hfill {∥g_n-c∥}^2& ={∥P_B\left({\xi }_n{d}_n+\left(1-{\xi }_n\right)M{h}_n\right)-P_B\left(c\right)∥}^2\hfill \\ \hfill & \le {∥\left({\xi }_n{d}_n+\left(1-{\xi }_n\right)M{h}_n\right)-p∥}^2\hfill \\ \hfill & ={∥{\xi }_n\left(d_n-c\right)+\left(1-{\xi }_n\right)\left(M{h}_n-c\right)∥}^2\hfill \\ \hfill & ={\xi }_n{∥d_n-c∥}^2+\left(1-{\xi }_n\right){∥M{h}_n-C∥}^2-{\xi }_n\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2\hfill \\ \hfill & \le {∥d_n-c∥}^2-{\xi }_n\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2.\hfill \end{array}$$

(25)

Similarly, we obtain that

$${∥f_n-d∥}^2\le {∥p_n-d∥}^2-{\xi }_n\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2.$$

(26)

Substituting (25) into (23), we get

$$\begin{array}{cc}\hfill {∥e_n-c∥}^2\le & \left(1-{\eta }_n\right){∥x_n-c∥}^2+{\eta }_n{b}_n{∥v_n-c∥}^2\hfill \\ \hfill & +{\eta }_n\left(1-b_n\right){∥d_n-c∥}^2-{\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2.\hfill \end{array}$$

(27)

Similarly, we get

$$\begin{array}{cc}\hfill {∥t_n-d∥}^2\le & \left(1-{\eta }_n\right){∥y_n-d∥}^2+{\eta }_n{b}_n{∥z_n-d∥}^2\hfill \\ \hfill & +{\eta }_n\left(1-b_n\right){∥p_n-d∥}^2-{\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2.\hfill \end{array}$$

(28)

From (13), (22) and Lemma 1, we get

$$\begin{array}{cc}\hfill \parallel r_{n+1}{-c\parallel }^2& = \parallel {\beta }_n\overline{r}+(1-{\beta }_n)e_n{-c\parallel }^2\hfill \\ \hfill & = \parallel {\beta }_n(\overline{r}-c)-(1-{\beta }_n)(e_n-c){\parallel }^2\hfill \\ \hfill & \le {\beta }_n\parallel \overline{r}{-c\parallel }^2+(1-{\beta }_n){\parallel e_n-c\parallel }^2.\hfill \end{array}$$

(29)

Similarly, we have

$${∥s_{n+1}-d∥}^2\le {\beta }_n{\parallel \overline{s}-d\parallel }^2+\left(1-{\beta }_n\right){∥t_n-d∥}^2.$$

(30)

Combining (29) and (30), we get

$${∥r_{n+1}-c∥}^2+{∥s_{n+1}-d∥}^2\le {\beta }_n\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right)+\left(1-{\beta }_n\right)\left({∥e_n-d∥}^2+{∥t_n-d∥}^2\right),$$

(31)

Substituting (27) and (28), into (31), we obtain

$$\begin{array}{cc}\hfill {∥r_{n+1}-c∥}^2+{∥s_{n+1}-d∥}^2\le & {\beta }_n\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right)\left(1-{\eta }_n\right)\left[{∥x_n-c∥}^2+{∥y_n-d∥}^2\right]\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n{b}_n\left[{∥v_n-c∥}^2+{∥z_n-d∥}^2\right]\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left[{∥d_n-c∥}^2+{∥p_n-d∥}^2\right]\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2.\hfill \end{array}$$

(32)

Since $c\in Z_n$, using the definition of $v_n$ in (10), property (P1) of metric projection and Lemma 1, we have

$$\begin{array}{cc}\hfill {∥v_n-c∥}^2=& {∥P_{Z_n}\left(x_n-{\mu }_{n}Z{m}_n\right)-c∥}^2\hfill \\ \hfill =& {∥P_{Z_n}\left(x_n-{\mu }_{n}Z{m}_n\right)-P_{Z_n}c∥}^2\hfill \\ \hfill \le & ⟨v_n-c,x_n-{\mu }_{n}Z{m}_n-c⟩\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left[{∥v_n-c∥}^2+{∥x_n-{\mu }_{n}Z{m}_n-c∥}^2-{∥v_n-x_n+{\mu }_{n}Z{m}_n∥}^2\right]\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left[{∥v_n-c∥}^2+{∥x_n-c∥}^2+{\mu }_n^2{∥Z{m}_n∥}^2-{∥v_n-x_n∥}^2-{\mu }_n^2{∥Z{m}_n∥}^2\right.\hfill \\ \hfill & \left.-2⟨x_n-c,{\mu }_{n}Z{m}_n⟩-2⟨v_n-x_n,{\mu }_{n}Z{m}_n⟩\right]\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left[{∥v_n-c∥}^2+{∥x_n-c∥}^2-{∥v_n-x_n∥}^2-2\left.⟨v_n-c,{\mu }_{n}Z{m}_n{\parallel }^2\right]\right.\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left[{∥v_n-c∥}^2+{∥x_n-c∥}^2-{∥v_n-x_n∥}^2+2⟨c-v_n,{\mu }_{n}Z{m}_n⟩\right].\hfill \end{array}$$

(33)

Thus, the inequality in (33) implies that

$${∥v_n-c∥}^2\le {∥x_n-c∥}^2-{∥v_n-x_n∥}^2+2⟨c-v_n,{\mu }_{n}Z{m}_n⟩.$$

(34)

Since $c\in MVI(B,Z)$, we have $⟨Zr,r-c⟩\ge 0,\forall r\in B$. Taking $r=m_n\in B$ and rearranging, we get $⟨Z{m}_n,c-m_n⟩\le 0$.

Hence,

$$\begin{array}{cc}\hfill ⟨c-v_n,{\mu }_{n}Z{m}_n⟩& ={\mu }_n⟨Z{m}_n,c-v_n⟩\hfill \\ \hfill & ={\mu }_n⟨Z{m}_n,c-m_n⟩+{\mu }_n⟨Z{m}_n,m_n-v_n⟩\hfill \\ \hfill & \le {\mu }_n⟨Z{m}_n,m_n-v_n⟩.\hfill \end{array}$$

(35)

Using (34) and (35) and Lemma 1,

$$\begin{array}{cc}\hfill {∥v_n-c∥}^2& \le {∥x_n-c∥}^2-{∥v_n-x_n∥}^2+2{\mu }_n⟨Z{m}_n,m_n-v_n⟩\hfill \\ \hfill & ={∥x_n-c∥}^2-{∥v_n-m_n∥}^2-{∥m_n-x_n∥}^2-2⟨v_n-m_n,m_n-x_n⟩+2{\mu }_n⟨Z{m}_n,m_n-v_n⟩\hfill \\ \hfill & ={∥x_n-c∥}^2-{∥v_n-m_n∥}^2-{∥m_n-x_n∥}^2-2⟨m_n-x_n,v_n-m_n⟩-2{\mu }_n⟨Z{m}_n,v_n-m_n⟩\hfill \\ \hfill & ={∥x_n-c∥}^2-{∥v_n-m_n∥}^2-{∥x_n-m_n∥}^2+2⟨x_n-{\mu }_{n}Z{m}_n-m_n,v_n-m_n⟩.\hfill \end{array}$$

(36)

Since $v_n\in Z_n$ by definition of $v_n$ and by (P2), we obtain $⟨x_n-{\mu }_{n}Z{x}_n-m_n,v_n-m_n⟩\le$ 0. This, together with the definition of ${\mu }_n$, the Schwartz inequality, and the fact that $2xy\le x^2+y^2$ for any two real numbers x and y, give us

$$\begin{array}{cc}\hfill 2⟨x_n-{\mu }_{n}Z{m}_n-m_n,v_n-m_n⟩& =2⟨x_n-{\mu }_{n}Z{x}_n-m_n,v_n-m_n⟩+2{\mu }_n⟨Z{x}_n-Z{m}_n,v_n-m_n⟩\hfill \\ \hfill & \le 2{\mu }_n⟨Z{x}_n-Z{m}_n,m_n-v_n⟩\hfill \\ \hfill & \le 2{\mu }_n∥Z{x}_n-Z{m}_n∥∥m_n-v_n∥\hfill \\ \hfill & \le 2\lambda ∥x_n-m_n∥∥m_n-v_n∥\hfill \\ \hfill & \le \lambda \left[{∥x_n-m_n∥}^2+{∥m_n-v_n∥}^2\right].\hfill \end{array}$$

(37)

Using (37) in (36)

$${∥v_n-c∥}^2\le {∥x_n-c∥}^2-(1-\lambda )\left[{∥m_n-x_n∥}^2+{∥v_n-m_n∥}^2\right].$$

(38)

Similarly, we get

$${∥z_n-d∥}^2\le {∥y_n-d∥}^2-(1-\lambda )\left[{∥w_n-y_n∥}^2+{∥z_n-w_n∥}^2\right].$$

(39)

Adding (38) and (39), we get

$$\begin{array}{cc}\hfill {∥v_n-c∥}^2+{∥z_n-d∥}^2\le & {∥x_n-c∥}^2+{∥y_n-d∥}^2-(1-\lambda )\left[{∥m_n-x_n∥}^2+{∥v_n-m_n∥}^2\right]\hfill \\ \hfill & -(1-\lambda )\left[{∥w_n-y_n∥}^2+{∥z_n-w_n∥}^2\right].\hfill \end{array}$$

(40)

Now, using the definition of $d_n$ in (13) and property (P3) of the metric projection $P_B$, we have

$$\begin{array}{cc}\hfill {∥d_n-c∥}^2=& {∥P_B\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)-c∥}^2\hfill \\ \hfill \le & {∥x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)-c∥}^2-{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill =& {∥x_n-c∥}^2+{∥{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)∥}^2-2{\nu }_n⟨x_n-c,X^{\ast }\left(X{x}_n-Y{y}_n\right)⟩\hfill \\ \hfill & -{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill =& {∥x_n-c∥}^2+{\nu }_n^2{∥X^{\ast }\left(X{x}_n-Y{y}_n\right)∥}^2-2{\nu }_n⟨X{x}_n-Xc,X{x}_n-Y{y}_n⟩\hfill \\ \hfill & -{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2.\hfill \end{array}$$

(41)

Similarly,

$$\begin{array}{cc}\hfill {∥p_n-d∥}^2\le & {∥y_n-d∥}^2+{\nu }_n^2{∥Y^{\ast }\left(X{x}_n-Y{y}_n\right)∥}^2+2{\gamma }_n⟨Y{y}_n-Yd,X{x}_n-Y{y}_n⟩\hfill \\ \hfill & -{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2.\hfill \end{array}$$

(42)

Adding (41) and (42) and using (14) for the case $X{x}_n\ne Y{y}_n$, we have

$$\begin{array}{cc}\hfill {∥d_n-c∥}^2+{∥p_n-d∥}^2\le & {∥x_n-c∥}^2+{∥y_n-d∥}^2+{\nu }_n^2\left[{∥X^{\ast }\left(X{x}_n-Y{y}_n\right)∥}^2+{∥Y^{\ast }\left(X{x}_n-Y{y}_n\right)∥}^2\right]\hfill \\ \hfill & -2{\nu }_n⟨X{x}_n-Xc-Y{y}_n+Yd,X{x}_n\hfill \\ \hfill & -Y{y}_n⟩-{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill & -{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill \le & {∥x_n-c∥}^2+{∥y_n-d∥}^2+{\nu }_n{∥X{x}_n-Y{y}_n∥}^2-2{\nu }_n{∥X{x}_n-Y{y}_n∥}^2\hfill \\ \hfill & -{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2-{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill \le & {∥x_n-c∥}^2+{∥y_n-d∥}^2-{\nu }_n{∥X{x}_n-Y{y}_n∥}^2\hfill \\ \hfill & -{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill & -{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \end{array}$$

(43)

For the case $X{x}_n=Y{y}_n$ in (14), we can easily show that (43) holds. Using the definitions of $x_n$ and $y_n$ given in (8) and applying Lemma 1, we have

$$\begin{array}{cc}\hfill {∥x_n-c∥}^2& ={∥r_n+{\psi }_n\left(r_{n-1}-r_n\right)-c∥}^2\hfill \\ \hfill & ={∥\left(1-{\psi }_n\right)\left(r_n-c\right)+{\psi }_n\left(r_{n-1}-c\right)∥}^2\hfill \\ \hfill & \le \left(1-{\psi }_n\right){∥r_n-c∥}^2+{\psi }_n{∥r_{n-1}-c∥}^2,\hfill \end{array}$$

and

$${∥y_n-d∥}^2\le \left(1-{\psi }_n\right){∥s_n-d∥}^2+{\psi }_n{∥s_{n-1}-d∥}^2,$$

which imply that

$${∥x_n-c∥}^2+{∥y_n-d∥}^2\le \left(1-{\psi }_n\right)\left[{∥r_n-c∥}^2+{∥s_n-d∥}^2\right]+{\psi }_n\left[{∥r_{n-1}-c∥}^2+{∥s_{n-1}-d∥}^2\right]$$

(44)

Substituting (40) and (43) into (32)

$$\begin{array}{cc}\hfill {∥r_{n+1}-c∥}^2+{∥s_{n+1}-d∥}^2\le & {\beta }_n\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right)\left(1-{\eta }_n\right)\left({∥x_n-c∥}^2+{∥y_n-d∥}^2\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n{b}_n\left({∥x_n-c∥}^2+{∥y_n-d∥}^2\right)\hfill \\ \hfill & -(1-\lambda )\left[{∥m_n-x_n∥}^2+{∥v_n-m_n∥}^2\right]\hfill \\ \hfill & -(1-\lambda )\left[{∥w_n-y_n∥}^2+{∥z_n-w_n∥}^2\right]\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left({∥x_n-c∥}^2+{∥y_n-d∥}^2-{\nu }_n{∥X{x}_n-Y{y}_n∥}^2\right)\hfill \\ \hfill & -{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill & \left.-{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\right)\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2\hfill \end{array}$$

(45)

Hence,

$$\begin{array}{cc}\hfill {∥r_{n+1}-c∥}^2+{∥s_{n+1}-d∥}^2\le & {\beta }_n\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right)+\left(1-{\beta }_n\right)\left({∥x_n-c∥}^2+{∥y_n-d∥}^2\right)\hfill \\ \hfill & -\left(1-{\beta }_n\right){\eta }_n{b}_n\left((1-\lambda )\left[{∥m_n-x_n∥}^2+{∥v_n-m_n∥}^2\right]\right.\hfill \\ \hfill & \left.-(1-\lambda )\left[{∥w_n-y_n∥}^2+{∥z_n-w_n∥}^2\right]\right)\hfill \\ \hfill & -\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left({\nu }_n{∥X{x}_n-Y{y}_n∥}^2\right.\hfill \\ \hfill & +{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill & \left.+{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\right)\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2.\hfill \end{array}$$

(46)

Substituting (44) into (46) and taking the properties of $\lambda ,{\eta }_n,{\beta }_n,{\xi }_n$ and $b_n$ into account, we obtain

$$\begin{array}{cc}\hfill {∥r_{n+1}-c∥}^2+{∥s_{n+1}-d∥}^2\le & {\beta }_n\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right)\left(\left(1-{\psi }_n\right)\left[{∥r_n-c∥}^2+{∥s_n-d∥}^2\right]\right.\hfill \\ \hfill & \left.+{\psi }_n\left[{∥r_{n-1}-c∥}^2+{∥s_{n-1}-d∥}^2\right]\right)\hfill \\ \hfill & -\left(1-{\beta }_n\right){\eta }_n{b}_n\left((1-\lambda )\left[{∥m_n-x_n∥}^2+{∥v_n-m_n∥}^2\right]\right.\hfill \\ \hfill & \left.-(1-\lambda )\left[{∥w_n-y_n∥}^2+{∥z_n-w_n∥}^2\right]\right)\hfill \\ \hfill & -\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left({\nu }_n{∥X{x}_n-Y{y}_n∥}^2\right.\hfill \\ \hfill & +{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\hfill \\ \hfill & \left.+{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\right)\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill \le & {\beta }_n\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right)\left(\left(1-{\psi }_n\right)\left[{∥r_n-c∥}^2+{∥s_n-d∥}^2\right]\right.\hfill \\ \hfill & \left.+{\psi }_n\left[{∥r_{n-1}-c∥}^2+{∥s_{n-1}-d∥}^2\right]\right).\hfill \end{array}$$

(47)

Which can be written as

$${\Delta }_{n+1}(c,d)\le \left(1-{\beta }_n\right)\left[\left(1-{\psi }_n\right){\Delta }_n(c,d)+{\psi }_n{\Delta }_{n-1}(c,d)\right]+{\beta }_n\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right),$$

(48)

where ${\Delta }_n(c,d)={∥r_n-c∥}^2+{∥s_n-d∥}^2$

Using (48) and property of convex combinations of real numbers, we get

$${\Delta }_{n+1}(c,d)\le max\left\{\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2,max\left\{{\Delta }_n(c,d),{\Delta }_{n-1}(c,d)\right\}\right\}.$$

(49)

But,

$$\begin{array}{cc}\hfill & max\left\{{\Delta }_n(c,d),{\Delta }_{n-1}(c,d)\right\}\hfill \\ \hfill & \le max\left\{\left(1-{\beta }_{n-1}\right)\left[\left(1-{\psi }_{n-1}\right){\Delta }_{n-1}(c,d)+{\psi }_{n-1}{\Delta }_{n-2}(c,d)\right]\right.\hfill \\ \hfill & \left.+{\beta }_{n-1}\left(\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2\right),{\Delta }_{n-1}(c,d)\right\}\hfill \\ \hfill & \le max\left\{max\left\{\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2,max\left\{{\Delta }_{n-1}(c,d),{\Delta }_{n-2}(c,d)\right\}\right\},{\Delta }_{n-1}(c,d)\right\}\hfill \\ \hfill & =max\left\{\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2,max\left\{{\Delta }_{n-1}(c,d),{\Delta }_{n-2}(c,d)\right\}\right\}.\hfill \end{array}$$

(50)

Substituting (50) into (49) and repeating the process $n-2$ times, we get

$${\Delta }_{n+1}(c,d)\le max\left\{\parallel \overline{r}{-c\parallel }^2+{\parallel \overline{s}-d\parallel }^2,max\left\{{\Delta }_2(c,d),{\Delta }_1(c,d)\right\}\right\}$$

which implies that $\left\{{\Delta }_n(c,d)\right\}$ is bounded. Therefore, $\left\{r_n\right\}$ and $\left\{s_n\right\}$ are bounded and hence $\left\{x_n\right\},\left\{y_n\right\}\left\{X{x}_n\right\}$ and $\left\{Y{y}_n\right\}$ are bounded too. □

Theorem 2. 

Suppose conditions (C1)–(C6) hold. Let $Zr\ne 0,\forall r\in B$ and $Js\ne 0,\forall r\in E$. Then, the sequence $\left\{\left(r_n,s_n\right)\right\}$ produced by the refined algorithm strongly converges to a point $\left(c^{\ast },d^{\ast }\right)\in {\rm Y}$ such that $\left(c^{\ast },d^{\ast }\right)=P_{{\rm Y}}(\overline{r},\overline{s})$.

Proof. 

Let $\left(c^{\ast },d^{\ast }\right)=P_{{\rm Y}}(\overline{r},\overline{s})$. From the definitions of $r_{n+1}$ and $s_{n+1}$, (22), (27), (28) and Lemma 1 we have

$$\begin{array}{cc}\hfill {∥r_{n+1}-c^{\ast }∥}^2+{∥s_{n+1}-d^{\ast }∥}^2=& {∥{\beta }_n\left(\overline{r}-c^{\ast }\right)+\left(1-{\beta }_n\right)\left(e_n-c^{\ast }\right)∥}^2\hfill \\ \hfill & +{∥{\beta }_n\left(\overline{r}-d^{\ast }\right)+\left(1-{\beta }_n\right)\left(t_n-d^{\ast }\right)∥}^2\hfill \\ \hfill \le & {\left(1-{\beta }_n\right)}^2{∥e_n-c^{\ast }∥}^2+2{\beta }_n⟨\overline{r}-c^{\ast },r_{n+1}-c^{\ast }⟩\hfill \\ \hfill & +{\left(1-{\beta }_n\right)}^2{∥t_n-d^{\ast }∥}^2+2{\beta }_n⟨\overline{s}-d^{\ast },s_{n+1}-d^{\ast }⟩\hfill \\ \hfill \le & {\left(1-{\beta }_n\right)}^2\left({∥e_n-c^{\ast }∥}^2+{∥t_n-d^{\ast }∥}^2\right)\hfill \\ \hfill & +2{\beta }_n\left[⟨\overline{r}-c^{\ast },r_{n+1}-c^{\ast }⟩+⟨\overline{s}-d^{\ast },s_{n+1}-d^{\ast }⟩\right],\hfill \end{array}$$

this implies

$$\begin{array}{cc}\hfill {∥r_{n+1}-c^{\ast }∥}^2+{∥s_{n+1}-d^{\ast }∥}^2\le & \left(1-{\beta }_n\right)\left(1-{\eta }_n\right)\left[{∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n{b}_n\left[{∥v_n-c^{\ast }∥}^2+{∥z_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left[{∥d_n-c^{\ast }∥}^2+{∥p_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right)\left[{∥M{h}_n-d_n∥}^2+{∥N{q}_n-p_n∥}^2\right]\hfill \\ \hfill & +2{\beta }_n\left((\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_{n+1},s_{n+1}\right)-\left(c^{\ast },d^{\ast }\right)\right.⟩.\hfill \end{array}$$

(51)

But (40) and (43) imply that ${∥v_n-c^{\ast }∥}^2+{∥z_n-d^{\ast }∥}^2\le {∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2$ and ${∥d_n-c^{\ast }∥}^2+{∥p_n-d^{\ast }∥}^2\le {∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2$, respectively. Thus, by putting these two inequalities into (51), we get

$$\begin{array}{cc}\hfill {∥r_{n+1}-c^{\ast }∥}^2+{∥s_{n+1}-d^{\ast }∥}^2\le & \left(1-{\beta }_n\right)\left(1-{\eta }_n\right)\left[{∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n{b}_n\left[{∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left[{∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & -\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right)\left[{∥M{h}_n-d_n∥}^2+{∥N{q}_n-p_n∥}^2\right]\hfill \\ \hfill & +2{\beta }_n⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_{n+1},s_{n+1}\right)-\left(c^{\ast },d^{\ast }\right)⟩\hfill \\ \hfill \le & \left(1-{\beta }_n\right)\left[{∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & +2{\beta }_n⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_{n+1},s_{n+1}\right)-\left(c^{\ast },d^{\ast }\right)⟩\hfill \end{array}$$

(52)

From Remark 1, we have that the sequences $\left\{{\psi }_n∥r_n-r_{n-1}∥\right\}$ and $\left\{{\psi }_n∥s_n-s_{n-1}∥\right\}$ are bounded. Thus, we obtain from the boundedness of $\left\{r_n\right\}$ and $\left\{s_n\right\}$ that

$$\begin{array}{cc}\hfill {∥x_n-c^{\ast }∥}^2& ={∥r_n-c^{\ast }+{\psi }_n\left(r_n-r_{n-1}\right)∥}^2\hfill \\ \hfill & \le {∥r_n-c^{\ast }∥}^2+{\psi }_n^2{∥r_n-r_{n-1}∥}^2+2{\psi }_n∥r_n-c^{\ast }∥∥r_n-r_{n-1}∥\hfill \\ \hfill & \le {∥r_n-c^{\ast }∥}^2+M_1{\psi }_n∥r_n-r_{n-1}∥,\hfill \end{array}$$

(53)

for some $M_1\ge 0$. Similarly, we have

$${∥y_n-d^{\ast }∥}^2\le {∥s_n-d^{\ast }∥}^2+M_2{\psi }_n∥s_n-s_{n-1}∥,$$

(54)

for some $M_2\ge 0$.

From (53) and (54), we obtain

$${∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2\le {∥r_n-c^{\ast }∥}^2+{∥s_n-d^{\ast }∥}^2+M_3{\psi }_n\left[∥r_n-r_{n-1}∥+∥s_n-s_{n-1}∥\right],$$

(55)

where $M_3=max\left\{M_1,M_2\right\}$.

Substituting (55) into (52), we get

$$\begin{array}{cc}\hfill {∥r_{n+1}-c^{\ast }∥}^2+{∥s_{n+1}-d^{\ast }∥}^2\le & \left(1-{\beta }_n\right)\left[{∥r_n-c^{\ast }∥}^2+{∥s_n-d^{\ast }∥}^2\right]\hfill \\ \hfill & +{\beta }_n\left[M_3{\displaystyle \frac{{\psi }_n}{{\beta }_n}}\left(∥r_n-r_{n-1}∥+∥s_n-s_{n-1}∥\right)\right.\hfill \\ \hfill & \left.+2⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_{n+1},s_{n+1}\right)-\left(c^{\ast },d^{\ast }\right)⟩\right],\hfill \end{array}$$

which could be written as

$${\Delta }_{n+1}\left(c^{\ast },d^{\ast }\right)\le \left(1-{\beta }_n\right){\Delta }_n\left(c^{\ast },d^{\ast }\right)+{\beta }_n{\delta }_n,$$

(56)

where ${\delta }_n=M_3{\displaystyle \frac{{\psi }_n}{{\beta }_n}}\left(∥r_n-r_{n-1}∥+∥s_n-s_{n-1}∥\right)+2⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_{n+1},s_{n+1}\right)-\left(c^{\ast },d^{\ast }\right)⟩$. From (46) we obtain that

$$\begin{array}{cc}\hfill (1-& \left.{\beta }_n\right){\eta }_n{b}_n\left((1-\lambda )\left[{∥m_n-x_n∥}^2+{∥v_n-m_n∥}^2\right]\right.\hfill \\ \hfill & \left.+(1-\lambda )\left[{∥w_n-y_n∥}^2+{∥z_n-w_n∥}^2\right]\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left({\nu }_n{∥X{x}_n-Y{y}_n∥}^2\right.\hfill \\ \hfill & \left.+{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2+{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2\hfill \\ \hfill & +\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2\hfill \\ \hfill \le & \left(1-{\beta }_n\right)\left[{∥x_n-c^{\ast }∥}^2+{∥y_n-d^{\ast }∥}^2\right]-{\Delta }_{n+1}\left(c^{\ast },d^{\ast }\right)+{\beta }_n\left({∥\overline{r}-c^{\ast }∥}^2+{∥\overline{s}-d^{\ast }∥}^2\right).\hfill \end{array}$$

(57)

Using (55) in (57) we obtain that

$$\begin{array}{cc}\hfill (1-& \left.{\beta }_n\right){\eta }_n{b}_n\left((1-\lambda )\left[{∥m_n-x_n∥}^2+{∥v_n-m_n∥}^2\right]\right.\hfill \\ \hfill & \left.+(1-\lambda )\left[{∥w_n-y_n∥}^2+{∥z_n-w_n∥}^2\right]\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right){\eta }_n\left(1-b_n\right)\left({\nu }_n{∥X{x}_n-Y{y}_n∥}^2\right.\hfill \\ \hfill & \left.+{∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2+{∥p_n-\left(y_n+{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2\right)\hfill \\ \hfill & +\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥M{h}_n-d_n∥}^2\hfill \\ \hfill & +\left(1-{\beta }_n\right){\xi }_n{\eta }_n\left(1-b_n\right)\left(1-{\xi }_n\right){∥N{q}_n-p_n∥}^2\hfill \\ \hfill \le & \left(1-{\beta }_n\right)\left[{∥r_n-c^{\ast }∥}^2+{∥s_n-d^{\ast }∥}^2+M_3{\psi }_n\left(∥r_n-r_{n-1}∥+∥s_n-s_{n-1}∥\right)\right]\hfill \\ \hfill & -{\Delta }_{n+1}\left(c^{\ast },d^{\ast }\right)+{\beta }_n\left({∥\overline{r}-c^{\ast }∥}^2+{∥\overline{s}-d^{\ast }∥}^2\right)\hfill \\ \hfill \le & {∥r_n-c^{\ast }∥}^2+{∥s_n-d^{\ast }∥}^2-{\beta }_n\left({∥r_n-c^{\ast }∥}^2+{∥s_n-d^{\ast }∥}^2\right)\hfill \\ \hfill & +M_3{\psi }_n\left(∥r_{n-1}-r_n∥+∥s_{n-1}-s_n∥\right)\hfill \\ \hfill & -{\Delta }_{n+1}\left(c^{\ast },d^{\ast }\right)+{\beta }_n\left({∥\overline{r}-c^{\ast }∥}^2+{∥\overline{s}-d^{\ast }∥}^2\right)\hfill \\ \hfill \le & {\Delta }_n\left(c^{\ast },d^{\ast }\right)-{\Delta }_{n+1}\left(c^{\ast },d^{\ast }\right)\hfill \\ \hfill & +{\beta }_n\left[{\displaystyle \frac{M_3{\psi }_n}{{\beta }_n}}\left(∥r_{n-1}+r_n∥+∥s_{n-1}+s_n∥\right)-\left({∥r_n-c^{\ast }∥}^2+{∥s_n-d^{\ast }∥}^2\right)\right]\hfill \\ \hfill & +{\beta }_n\left({∥\overline{r}-c^{\ast }∥}^2+{∥\overline{s}-d^{\ast }∥}^2\right)\hfill \\ \hfill \le & {\Delta }_n\left(c^{\ast },d^{\ast }\right)-{\Delta }_{n+1}\left(c^{\ast },d^{\ast }\right)+{\beta }_n\left(M_3{\displaystyle \frac{{\psi }_n}{{\beta }_n}}\left[∥r_n-r_{n-1}∥+∥s_n-s_{n-1}∥\right]-{\Delta }_n\left(c^{\ast },d^{\ast }\right)\right)\hfill \\ \hfill & +{\beta }_n\left({∥\overline{r}-c^{\ast }∥}^2+{∥\overline{s}-d^{\ast }∥}^2\right)\hfill \end{array}$$

(58)

We now consider two cases on the sequence $\left\{{\Delta }_n\left(c^{\ast },d^{\ast }\right)\right\}$.

Case 1. Let ${\Delta }_{n+1}\left(c^{\ast },d^{\ast }\right)\le {\Delta }_n\left(c^{\ast },d^{\ast }\right)\forall n\ge n_0\in \mathbb{N}$.

Since it is bounded, ${lim}_{n\to \infty }{\Delta }_n\left(c^{\ast },d^{\ast }\right)$ exists. Then, taking the limit on both sides of (58) as $n\to \infty$ and taking the conditions on the parameters $b_n,\lambda ,{\beta }_n,{\eta }_n,{\xi }_n,{\pi }_n$ into account, we obtain

$$∥m_n-x_n∥\to 0and∥v_n-m_n∥\to 0,\mathrm{and}\mathrm{hence}∥v_n-x_n∥\to 0,asn\to \infty .$$

(59)

In the same way, we also get

$$∥w_n-y_n∥\to 0\mathrm{and}∥z_n-w_n∥\to 0,\mathrm{and}\mathrm{hence}∥z_n-y_n∥\to 0.$$

(60)

Furthermore, we have,

$$∥X{x}_n-Y{y}_n∥\to 0,∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥\to 0,$$

(61)

and

$$∥p_n+\left(y_n-{\nu }_n{Y}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥\to 0,∥M{h}_n-d_n∥\to 0,∥N{q}_n-p_n∥\to 0asn\to \infty .$$

(62)

By the definition of $d_n$ in (13) and property (P3) of metric projection, we have

$${∥d_n-\left(x_n-{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)\right)∥}^2+{∥d_n-x_n∥}^2\le {∥{\nu }_n{X}^{\ast }\left(X{x}_n-Y{y}_n\right)∥}^2.$$

(63)

Thus, combining (61) and (63), we get

$$∥d_n-x_n∥\to 0\mathrm{and}\mathrm{also}∥p_n-y_n∥\to 0.$$

(64)

By non-expansive property of $P_B$ and from (62) we have

$$∥g_n-d_n∥=\left(1-{\xi }_n\right)∥M{h}_n-d_n∥\to 0\mathrm{as}n\to \infty .$$

(65)

By the boundedness of $\left\{\left(r_n,s_n\right)\right\}$ and Theorem 1, there is a subsequence $\left\{\left(r_{n_j},s_{n_j}\right)\right\}$ of $\left\{\left(r_n,s_n\right)\right\}$ with $\left\{\left(r_{n_j},s_{n_j}\right)\right\}\rightharpoonup (s,t)$ and

$$\underset{n\to \infty }{lim\; sup}\left[⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_n,m_n\right)-\left(c^{\ast },d^{\ast }\right)⟩\right]=\underset{j\to \infty }{lim\; sup}\left[⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_{n_j},s_{n_j}\right)-\left(c^{\ast },d^{\ast }\right)⟩\right].$$

(66)

Hence, from (59) and (60), we get

$$\underset{j\to \infty }{lim}∥m_{n_j}-x_{n_j}∥=0\mathrm{and}\underset{j\to \infty }{lim}∥w_{n_j}-y_{n_j}∥=0.$$

(67)

Now, from (8), we get that $∥x_{n_j}-r_{n_j}∥\to 0$ and $∥y_{n_j}-s_{n_j}∥\to 0$ as $j\to \infty$ and hence $x_{n_j}\to s$ and $y_{n_j}\rightharpoonup t$. Using (67) and Lemma 8, we obtain $(s,t)\in$$MVI(B,Z)\times MVI(E,J)$. From (64), we obtain

$$∥d_{n_j}-r_{n_j}∥\le ∥d_{n_j}-x_{n_j}∥+∥x_{n_j}-r_{n_j}∥\to 0\mathrm{as}j\to \infty .$$

(68)

Thus, we have from (68) that $d_{n_j}\rightharpoonup s$, which together with (62) and the demiclosedness of $(I-M)$ gives that $s\in F\left(M\right)$. Similarly, we obtain that $t\in F\left(N\right)$. Hence, we obtain

$$(s,t)\in \left(MVI\right(B,Z)\cap F(M\left)\right)\times \left(MVI\right(E,J)\cap F(N\left)\right)$$

Then, using Lemma 1 (2), we get

$$\begin{array}{cc}\hfill {\parallel Xs-Yt\parallel }^2& ={∥X{x}_{n_j}-Y{y}_{n_j}+Xs-X{x}_{n_j}+Y{y}_{n_j}-Yt∥}^2\hfill \\ \hfill & \le {∥X{x}_{n_j}-Y{y}_{n_j}∥}^2+2⟨Xs-X{x}_{n_j}+Y{y}_{n_j}-Yt,Xs-Yt⟩.\hfill \end{array}$$

(69)

Since X is a bounded linear mapping, we get $X{x}_{n_j}\to Xs$, and similarly we have $Y{y}_{n_j}\to Yt$.

Thus, taking limsup on both sides of (69) and using (61), we obtain $\parallel Xs-$$Yt\parallel =0$. Thus, we obtain $Xs=Yt$ and hence $(s,t)\in {\rm Y}$. In addition, since $\left(c^{\ast },d^{\ast }\right)=P_{{\rm Y}}(\overline{u},\overline{s})$, Equation (66) and Lemma 3 gives

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}\left[⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_n,m_n\right)-\left(c^{\ast },d^{\ast }\right)⟩\right]& =\underset{j\to \infty }{lim}\left[⟨(\overline{r},\overline{u})-\left(c^{\ast },d^{\ast }\right),\left(r_{n_j},s_{n_j}\right)-\left(c^{\ast },d^{\ast }\right)⟩\right]\hfill \\ \hfill & =⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),(s,t)-\left(c^{\ast },d^{\ast }\right)⟩\le 0.\hfill \end{array}$$

(70)

From (8) and (13),

$$\begin{array}{cc}\hfill ∥r_{n+1}-r_n∥& \le ∥r_{n+1}-x_n∥+∥x_n-r_n∥\hfill \\ \hfill & =∥{\beta }_n\left(\overline{r}-x_n\right)+\left(1-{\beta }_n\right)\left[{\eta }_n\left(b_n\left(v_n-x_n\right)+\left(1-b_n\right)\left(g_n-x_n\right)\right)\parallel \right]+∥x_n-r_n\parallel \hfill \\ \hfill & \le {\beta }_n∥\overline{r}-x_n∥+\left(1-{\beta }_n\right){\eta }_n\left[b_n∥v_n-x_n∥+\left(1-b_n\right)∥g_n-x_n∥\right]+∥x_n-r_n∥.\hfill \end{array}$$

(71)

From (64) and (65), we have that

$$∥g_n-x_n∥\le ∥g_n-d_n∥+∥d_n-x_n∥\to 0\mathrm{as}n\to \infty .$$

(72)

Using the assumptions on ${\beta }_n,b_n$ and ${\eta }_n$, since $\left\{x_n\right\}$ is bounded, Remark 1, (59) and (72) imply that the limit of the right hand side of the last inequality in (71) is zero.

Thus, we have

$$∥r_{n+1}-r_n∥\to 0.$$

(73)

Similarly, we have

$$∥s_{n+1}-s_n∥\to 0.$$

(74)

Using (73) and (74) together with (70), we have

$$\underset{n\to \infty }{lim\; sup}⟨(\overline{r},\overline{s})-\left(c^{\ast },d^{\ast }\right),\left(r_{n+1},s_{n+1}\right)-\left(c^{\ast },d^{\ast }\right)⟩\le 0.$$

(75)

Hence, combining the assumption on ${\beta }_n$, Remark 1 and (75), we obtain ${lim\; sup}_{n\to \infty }{\delta }_n\le$ 0. Therefore, from (56) and Lemma 7, we get ${\Delta }_n\left(c^{\ast },d^{\ast }\right)\to 0$ which implies that $r_n\to c^{\ast }$ and $s_n\to s^{\ast }$ as $n\to \infty$.

Case 2. Assume that there is a subsequence $\left\{{\Delta }_{n_r}\left(c^{\ast },d^{\ast }\right)\right\}$ of $\left\{{\Delta }_n\left(c^{\ast },d^{\ast }\right)\right\}$ such that $\left\{{\Delta }_{n_r}\left(c^{\ast },d^{\ast }\right)\right\}<\left\{{\Delta }_{n_r+1}\left(c^{\ast },d^{\ast }\right),\right\}\forall r\in \mathbb{N}$. In this instance, a non-decreasing sequence $\left\{a_s\right\}$ of $\mathbb{N}$ exists, as indicated by Lemma 6, such that ${lim}_{s\to \infty }{a}_s=\infty$ and the following inequality holds for $s\in \mathbb{N}$:

$$max\left\{{\Delta }_{a_s}\left(c^{\ast },d^{\ast }\right),{\Delta }_s\left(c^{\ast },d^{\ast }\right)\right\}\le {\Gamma }_{a_s+1}\left(c^{\ast },d^{\ast }\right).$$

(76)

From (56) we have

$${\Delta }_{a_s+1}\left(c^{\ast },d^{\ast }\right)\le \left(1-{\beta }_{a_s}\right){\Delta }_{a_s}\left(c^{\ast },d^{\ast }\right)+{\beta }_{a_s}{\delta }_{a_s}.$$

(77)

Combining (76) and (77) we obtain

$${\Delta }_{a_s+1}\left(c^{\ast },d^{\ast }\right)\le \left(1-{\beta }_{a_s}\right){\Delta }_{a_s+1}\left(c^{\ast },d^{\ast }\right)+{\beta }_{a_s}{\delta }_{a_s}\mathrm{and}\mathrm{hence}{\Delta }_s\left(c^{\ast },d^{\ast }\right)\le {\delta }_{a_s}$$

This implies that

$$\underset{s\to \infty }{lim\; sup}{\Delta }_s\left(c^{\ast },d^{\ast }\right)\le \underset{s\to \infty }{lim\; sup}{\delta }_{a_s}$$

Similar reasoning to that of Case 1 leads us to the conclusion that ${lim\; sup}_{s\to \infty }{\omega }_{a_s}\le$ 0 which implies that ${lim}_{s\to \infty }{\Delta }_s\left(c^{\ast },d^{\ast }\right)=0$, that is, $\left(r_s,s_s\right)\to \left(c^{\ast },d^{\ast }\right)$ as $n\to \infty$. □

4. Numerical Examples

Some numerical examples illustrating the behavior of our proposed systems are provided in this section.

Example 1. 

Let ${\Omega }_1={\Omega }_2={\mathbb{R}}^2$ be a Hilbert spaces with norm $∥y∥=\sqrt{y_1^2+y_2^2}$ and inner product $⟨y,z⟩=⟨(y_1,y_2),(z_1,z_2)⟩=y_1{z}_1+y_2{z}_2$ for $y=(y_1,y_2),z=(z_1,z_2)\in {\mathbb{R}}^2$. Let $B=[0,2]\times [-1,0]$ and $E=[1,2]\times [0,1]$ which are non-empty, closed, and convex subsets of ${\mathbb{R}}^2$. We define Z and J on ${\mathbb{R}}^2$ by:

$$Z\left(y_1,y_2\right)=\left(0,{\displaystyle \frac{1}{1+e^{-y_2}}}\right)andJ\left(y_1,y_2\right)=\left({\displaystyle \frac{1}{1+e^{-y_1}}},0\right)$$

if

$$\begin{array}{c}\hfill ⟨Z\left(y_1,y_2\right),\left(x_1,x_2\right)-\left(y_1,y_2\right)⟩0\\ \hfill ⟨\left(0,{\displaystyle \frac{1}{1+e^{-y_2}}}\right),\left(\left(x_1-y_1\right),\left(x_2-y_2\right)\right)⟩0\\ \hfill \left({\displaystyle \frac{1}{1+e^{-y_2}}}\right)\left(x_2-y_2\right)>0\end{array}$$

as the denumerator $1+e^{-y_2}$ in ${\displaystyle \frac{1}{1+e^{-y_2}}}$ is positive because $\left(e^{-y_2}>0\right)$ therefore $\left({\displaystyle \frac{1}{1+e^{-y_2}}}\right)>0$. Since $\left({\displaystyle \frac{1}{1+e^{-y_2}}}\right)\left(x_2-y_2\right)>0$ it only holds if $x_2>y_2$. Now, to check the implification for quasi-monotone

$$\begin{array}{cc}\hfill ⟨Z\left(x_1,x_2\right),\left(x_1,x_2\right)-\left(y_1,y_2\right)⟩& =⟨\left(0,{\displaystyle \frac{1}{1+e^{-x_2}}}\right),\left(\left(x_1-y_1\right),\left(x_2-y_2\right)\right)⟩\hfill \\ \hfill & =\left({\displaystyle \frac{1}{1+e^{-x_2}}}\right)\left(x_2-y_2\right)\hfill \end{array}$$

as $\left({\displaystyle \frac{1}{1+e^{-x_2}}}\right)>0$ and if $x_2\ge y_2$ then

$$\begin{array}{c}\hfill ⟨Z\left(x_1,x_2\right),\left(x_1,x_2\right)-\left(y_1,y_2\right)⟩\ge 0\end{array}$$

This shows that Z is a quasi-monotone operator. In the same way, we can show that J is quasi-monotone.

The distance between the points $(y_1,y_2),(y_1^{\prime },y_2^{\prime })$ is

$$\begin{array}{cc}\hfill d\left((y_1,y_2),(y_1,y_2^{\prime })\right)=& ∥(y_1,y_2)-(y_1^{\prime },y_2^{\prime })∥=∥(y_1-y_1^{\prime }),(y_2-y_2^{\prime })∥\hfill \\ \hfill =& \sqrt{{(y_1-y_1^{\prime })}^2+{(y_2-y_2^{\prime })}^2}\hfill \end{array}$$

The distance between their function values

$$\begin{array}{cc}\hfill d(Z(y_1,y_2),Z(y_1,y_2^{\prime })=& ∥Z(y_1,y_2)-Z(y_1^{\prime },y_2^{\prime })∥=∥\left(0,{\displaystyle \frac{1}{1+e^{-y_2}}}\right)-\left(0,{\displaystyle \frac{1}{1+e^{-y_2^{\prime }}}}\right)∥\hfill \\ \hfill =& ∥(0-0),\left({\displaystyle \frac{1}{1+e^{-y_2}}}-{\displaystyle \frac{1}{1+e^{-y_2^{\prime }}}}\right)∥\hfill \\ \hfill =& \sqrt{{\left(0\right)}^2+{\left({\displaystyle \frac{1}{1+e^{-y_2}}}-{\displaystyle \frac{1}{1+e^{-y_2^{\prime }}}}\right)}^2}\hfill \\ \hfill =& \left|{\displaystyle \frac{1}{1+e^{-y_2}}}-{\displaystyle \frac{1}{1+e^{-y_2^{\prime }}}}\right|\hfill \end{array}$$

Using the property of uniform continuity, we want to find δ such that $\sqrt{{(y_1-y_1^{\prime })}^2+{(y_2-y_2^{\prime })}^2}<\delta$ which implies that $\left|{\displaystyle \frac{1}{1+e^{-y_2}}}-{\displaystyle \frac{1}{1+e^{-y_2^{\prime }}}}\right|<ϵ$. Notice that the function $Z\left(y_2\right)={\displaystyle \frac{1}{1+e^{-y_2}}}$ is continuous because the function smoothly transitions between 0 and 1 as $y_2$ moves from $-\infty to \infty$ and there are no jumps and discontinuities. Also, the function is bounded (since its values lie between 0 and 1). This function is uniformly continuous on the real line because its derivative is bounded. Specifically:

$$\begin{array}{c}\hfill Z^{\prime }{y}_2={\displaystyle \frac{e^{-y_2}}{{(1+e^{-y_2})}^2}}\end{array}$$

$Z^{\prime }{y}_2={\displaystyle \frac{1}{4}}$ as $y_2=0$, $Z^{\prime }{y}_2⟶0$ as $y_2⟶0$ and $Z^{\prime }{y}_2⟶0$ as $y_2⟶0$. So the derivative function lies between 0 and ${\displaystyle \frac{1}{4}}$. Thus, the derivative function is bounded, i.e.,

$$\begin{array}{c}\hfill 0\le Z^{\prime }\left(y_2\right)\le {\displaystyle \frac{1}{4}};\forall y_2\in \mathbb{R}\end{array}$$

Since the maximum of $Z^{\prime }{y}_2$ is ${\displaystyle \frac{1}{4}}$ which gives Lipschitz constant $L={\displaystyle \frac{1}{4}}$ and implies that

$$\begin{array}{c}\hfill \left|Z\left(y_2\right)-Z\left(y_2^{\prime }\right)\right|\le {\displaystyle \frac{1}{4}}\left|y_2-y_2^{\prime }\right|\end{array}$$

if we want

$$\begin{array}{c}\hfill \left|Z\left(y_2\right)-Z\left(y_2^{\prime }\right)\right|<ϵ\end{array}$$

we can use the Lipschitz condition ${\displaystyle \frac{1}{4}}\left|y_2-y_2^{\prime }\right|<ϵ$ which implies that $\left|y_2-y_2^{\prime }\right|<4ϵ$. So for given ϵ, $\delta =4ϵ$ this implies that $\left|Z(y_2-Z\left(y_2^{\prime }\right)\right|<ϵ$. Hence, Z is uniform continuous.

In a same way, it can be shown that J is quasi-monotone and uniformly continuous mappings on ${\mathbb{R}}^2$.

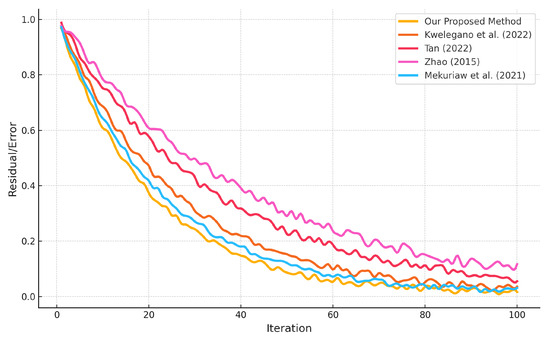
If we also define $X={\mathbb{R}}^2\to {\mathbb{R}}^2$ and $Y={\mathbb{R}}^2\to {\mathbb{R}}^2$ by $X(y_1,y_2)=(4y_1,2y_2)$ and $Y(y_1,y_2)=(2y_2,3y_1)$, respectively, then X and Y are both bounded linear mappings with adjoint mappings $X^{\ast }$ and $Y^{\ast }$ given by $X^{\ast }(y_1,y_2)=(4y_1,2y_2)$ and $Y^{\ast }(y_1,y_2)=(2y_2,3y_1)$, respectively. Let $M,N:{\mathbb{R}}^2\to {\mathbb{R}}^2$ given by $M(y_1,y_2)=(y_1,0)$ and $N(y_1,y_2)=(0.5,y_1)$ such that $F\left(M\right),F\left(N\right)\ne \varnothing$ and both are quasi-nonexpansive mappings. Take $\lambda =0.3,\zeta =0.6,, \kappa =0.2,\ell =0.8=\delta ,\psi =0.3,{ϵ}_n={\displaystyle \frac{1}{n^3}},{\beta }_n={\displaystyle \frac{1}{\sqrt{1+n}}},{\eta }_n=0.5,b_n=0.6,{\xi }_n=0.9$ and ${\pi }_n=0.75$ with given point $(\overline{r},\overline{s})=\left((0.2,-0.2),(1.5,0.4)\right)\in B\times E$ and initial points $(r_0,s_0)=\left((0.6,-0.1),(1.6,0.5)\right)$ and $(r_1,s_1)=\left((1.3,0),(1.1,0.3)\right)$. Then, conditions $\left(C1\right)-\left(C6\right)$ are satisfied. Using MATLAB R2020a, we obtain the Figure 1 which shows that the sequences generated by the previous introduced inertial-like subgradient extragradient method and our proposed inertial-like subgradient extragradient algorithm as given in Section Proposed Inertial-like Subgradient Extragradient Algorithm converge strongly to the solution $(c^{\ast },d^{\ast })=((1.2,-1),(-1,1.6))$ (see Figure 1).

Figure 1. Convergence of $\left\{\left(r_n,s_n\right)\right\}$ with tolerance $D_n<{10}^{-4}$ [10,13,14,20].

Example 2. 

Let $\Omega ={\Omega }_1={\Omega }_2={\Omega }_3=L^2\left([0,1]\right)$ with norm $∥x∥={\left({\int }_0^1{\left|x\left(t\right)\right|}^{2}dt\right)}^{{\displaystyle \frac{1}{2}}}$ for all $x\in \Omega$ and inner product $⟨x,y⟩={\int }_0^{1}x\left(t\right)y\left(t\right)dt$ for all $x,y\in \Omega$. Consider $B=\{x\in \Omega :∥x∥\le 3\}$ and $E=\{y\in \Omega :∥y∥\le 6\}$. Then, B and E are closed and convex subsets of Ω. Let $Z,J:\Omega \to \Omega$ be defined by

$$Zx\left(t\right)=\left\{\begin{array}{cc}\left|x\right(t)-2|,\hfill & if∥x∥>3\hfill \\ x^2\left(t\right)+1,\hfill & if∥x∥\le 3\hfill \end{array}\right.$$

and

$$Jy\left(t\right)=\left\{\begin{array}{cc}\left|y\right(t)-5|,\hfill & if∥y∥>6\hfill \\ y^2\left(t\right)+3,\hfill & if∥y∥\le 6\hfill \end{array}\right.$$

we have two cases for both operators. Let us see for Z.

case (i): $∥x∥>3$ here, $Zx\left(t\right)=\left|x\right(t)-2|$ if

$$\begin{array}{c}\hfill ⟨Zy\left(t\right),x\left(t\right)-y\left(t\right)⟩>0\end{array}$$

which imples

$$\begin{array}{c}\hfill \left({\int }_0^1|y\left(t\right)-2|(x\left(t\right)-y\left(t\right))dt\right)>0\end{array}$$

it is obvious that $\left|y\right(t)-2|>0$ and since $\left({\int }_0^1|y\left(t\right)-2|(x\left(t\right)-y\left(t\right))dt\right)>0$ it only holds if $x\left(t\right)>y\left(t\right)$. Now, to check the implification for quasi-monotone

$$\begin{array}{c}\hfill ⟨Zx\left(t\right),x\left(t\right)-y\left(t\right)⟩=\left({\int }_0^1|x\left(t\right)-2|(x\left(t\right)-y\left(t\right))dt\right)\end{array}$$

as $\left|x\right(t)-2|\ge 0$ therefore

$$\begin{array}{c}\hfill ⟨Zx\left(t\right),x\left(t\right)-y\left(t\right)⟩\ge 0\end{array}$$

this implies quasi-monotonocity for case (i).

case (ii): $\parallel x\parallel \le 3$ here, $Zx\left(t\right)=x^2\left(t\right)+1$ if

$$\begin{array}{c}\hfill \left({\int }_0^1(x^2\left(t\right)+1)(x\left(t\right)-y\left(t\right))dt\right)>0\end{array}$$

since $x^2\left(t\right)+1>0$ for all $x\in \Omega$ and $\left({\int }_0^1(x^2\left(t\right)+1)(x\left(t\right)-y\left(t\right))dt\right)>0$ this is only true if $x\left(t\right)>y\left(t\right)$. Now check for implification.

$$\begin{array}{c}\hfill ⟨Zx\left(t\right),x\left(t\right)-y\left(t\right)⟩=\left({\int }_0^1(x^2\left(t\right)+1)(x\left(t\right)-y\left(t\right))dt\right)\end{array}$$

as $(x^2\left(t\right)+1)>0$ and $x\left(t\right)\ge y\left(t\right)$; thus,

$$\begin{array}{c}\hfill ⟨Zx\left(t\right),x\left(t\right)-y\left(t\right)⟩\ge 0\end{array}$$

Hence, Z is a quasi-monotone operator. Similarly, J is also quasi-monotone.

To check the uniform continuity of Z.

Case (i): $\parallel x\parallel >3$, here $Zx\left(t\right)=\left|x\right(t)-2|$

The absolute value function $\left|x\right(t)-2|$ is uniformly continuous because the function $x\left(t\right)-2$ is linear, and linear functions are uniformly continuous. The absolute value operator does not change the uniform continuity, so $Zx\left(t\right)=\left|x\right(t)-2|$ is uniform continuous.

Case (ii): $\parallel x\parallel \le 3$, here $Zx\left(t\right)=x^2\left(t\right)+1$

Since $\parallel x\parallel \le 3,x^2\left(t\right)+1$ is bounded in this domain and remains continuous uniformly because the derivative $2x\left(t\right)$ is bounded on B. Hence, for all $x_1,x_2\in B$ the difference between $x_1^2\left(t\right)+1 and x_2^2\left(t\right)+1$ can be made arbitrarily small by controlling the difference $x_1\left(t\right)$ and $x_2\left(t\right)$. Therefore, Z is uniformly continuous in both parts of its fragmentary definition. In a similar way, J is uniform continuous.

Now, we will check which values of $x^{\ast }\in B$ satisfy the MVI. Let us try for $x^{\ast }=-3$. Since $x^{\ast }=-3\in MVI(B,Z)$ if $⟨Z\left(x\right),x+3⟩\ge 0,\forall x\in B$. So here only one case arises in Z if $\parallel x\parallel \le 3$, i.e., if $x\in B$; then, $Zx\left(t\right)=x^2\left(t\right)+1$.

$$\begin{array}{c}\hfill ⟨Zx\left(t\right),x\left(t\right)+3⟩=⟨x^2\left(t\right)+1,x\left(t\right)+3⟩={\int }_0^1\left(x^3\left(t\right)+3x^2\left(t\right)+x\left(t\right)+3\right)dt\end{array}$$

check for $x\left(t\right)=-3$

$$\begin{array}{c}\hfill ⟨x^2\left(t\right)+1,x\left(t\right)+3⟩=0\end{array}$$

Therefore, $MVI(B,Z)=\{-3\}$. Similarly, we can see that $MVI(D,J)=\{-4\}$. Define the mappings $M,N:\Omega \to \Omega$ by

$$Mx\left(t\right)=\left\{\begin{array}{cc}2x\left(t\right)+3,\hfill & ifx\in B\hfill \\ -3,\hfill & ifx\notin B\hfill \end{array}\right.$$

and

$$Ny\left(t\right)=\left\{\begin{array}{cc}2x\left(t\right)+4,\hfill & ify\in E\hfill \\ -4,\hfill & ify\notin E\hfill \end{array}\right.$$

If $x\in B$, $Mx\left(t\right)=2x\left(t\right)+3$, thus $x\left(t\right)=-3$ and if $x\notin B,Mx\left(t\right)=-3$ in this case also, $x\left(t\right)=-3$. Therefore, $F\left(M\right)=\{-3\}$ likewise $F\left(N\right)=\{-4\}$ and thus $MVI(B,Z)\cap F\left(M\right)=\{-3\}$ and $MVI(E,J)\cap F\left(N\right)=\{-4\}$

Moreover, we have

$$\begin{array}{c}\hfill \parallel Mx\left(t\right)-M(-3)\parallel =\parallel 2x\left(t\right)+3-(-3)\parallel =2\parallel x\left(t\right)+3\parallel \le \parallel x\left(t\right)+3\parallel \end{array}$$

thus, M is quasi-nonexpansive. Similarly, one can show that N is quasi-nonexpansive. Also note that

$$(I-M)x\left(t\right)=\left\{\begin{array}{cc}-x\left(t\right)-3,\hfill & ifx\in B\hfill \\ x\left(t\right)+3,\hfill & ifx\notin B\hfill \end{array}\right.$$

By Definition 9, assume $x_n\left(t\right)\rightharpoonup x_0\left(t\right)$ and $(I-M)x_n\left(t\right)\to 0$, if $x\in B,(I-M)x_n=-x_n\left(t\right)-3\to 0$ this implies $x_n\left(t\right)\to -3$ and if $x\notin B,(I-M)x_n\left(t\right)=x\left(t\right)+3\to 0$ this implies $x_n\left(t\right)\to -3$, by the convergence property both cases imply that $x_0\left(t\right)=-3$.

If $x_0\left(t\right)\in B$ then

$$(I-M)x_0\left(t\right)=-x_0\left(t\right)-3=0$$

and if $x_0\left(t\right)\notin B$ then

$$(I-M)x_0\left(t\right)=x_0\left(t\right)+3=0$$

both cases imply that $I-M$ is demiclosed at zero. In a similar way, we can also see that N is demiclosed at zero.

Define $X,Y:\Omega \to \Omega$ by $Xx\left(t\right)=8x\left(t\right)$ and $Yy\left(t\right)=6y\left(t\right)$. Then, X and Y are bounded linear mappings and $X^{\ast }x\left(t\right)=8x\left(t\right)$ and $Y^{\ast }=6y\left(t\right)$. Moreover, we have that $X(-3)=-24=Y(-4)$ and hence $(-3,-4)\in {\rm Y}$. Taking $\lambda =0.8,\zeta =0.3,\kappa =0.3,\ell =0.6=\delta ,\psi =0.5,{ϵ}_n={\displaystyle \frac{1}{n^{1.1}}},{\beta }_n={\displaystyle \frac{1}{n^{0.5}}},{\eta }_n=0.65,b_n=0.4,{\xi }_n=0.7$ and ${\pi }_n=0.8$, the conditions $\left(C1\right)-\left(C6\right)$ are satisfied.

5. Conclusions

In this study, we introduce a novel inertial-like subgradient extragradient algorithm designed to solve split equality variational inequality and fixed point problems in real Hilbert spaces. The proposed method generates strongly convergent sequences under the assumption that the involved mappings are quasi-monotone and uniformly continuous, an assumption that generalizes the more restrictive Lipschitz continuity and pseudomonotonicity commonly found in the existing literature. To enhance the performance of the algorithm, we incorporated both inertial and subgradient-based strategies. Additionally, we explored potential applications of our approach to various related problems. Finally, we provided numerical examples to illustrate the effectiveness and practical utility of the proposed methods.