1. Introduction
Computing environments and paradigms such as the Internet of Things (IoT) [
1,
2] are inherently open, consisting of numerous distributed information sources, services, and devices. These heterogeneous entities must interact and cooperate to accomplish localized tasks or support broader organizational objectives. However, ensuring interoperability among them poses a significant challenge due to their varying structural, semantic, and operational characteristics. The degree of heterogeneity directly influences the level at which interoperability must be addressed, ranging from the semantic and syntactic to the organizational or conceptual levels.
Entities may exhibit heterogeneity at various levels. At the infrastructure level, differences can arise from variations in hardware platforms, operating systems, and communication frameworks [
3,
4]. At a higher level, model-based heterogeneity results from inconsistencies in data schemas and data models [
5,
6]. Syntactic heterogeneity involves the use of different languages or representation formats, further complicating integration [
7]. Finally, semantic heterogeneity—arguably the most challenging—occurs when mismatches arise at the level of meaning. Recent research has increasingly focused on addressing semantic inconsistencies [
8,
9,
10], recognizing them as a critical barrier to achieving true interoperability.
Numerous research and industrial initiatives, such as those in the domains of the Internet of Things (IoT), big data [
11], and cloud computing [
12,
13], have attempted to address semantic heterogeneity in various applications. The core issue often lies in the lack of explicit semantics associated with information sources, devices, or sensors within open environments. When data lack a clear semantic representation, it becomes difficult for other entities to interpret, exchange, or utilize it effectively. Addressing semantic-level heterogeneity is therefore essential to achieving full interoperability and enabling seamless cooperation [
14].
Ontologies [
15] offer significant support for the representation and integration of semantic data. However, various organizational, cultural, and infrastructural constraints can hinder or even prevent their adoption. As a result, there is often a lack of explicit ontological frameworks. In addition, many information systems—such as traditional management systems and e-Commerce platforms based on databases or flat file structures—typically lack predefined formal ontologies at the domain or application level, further complicating semantic interoperability.
Our semantic integration approach specifically targets resources in open environments [
16,
17], where entities and relations are inherently dynamic and variable. The fundamental step in developing this solution involves constructing a conceptualization model that accurately reflects the characteristics and assumptions of such environments. In this paper, we propose an intensional conceptualization model designed to serve as the core framework for achieving semantic integration among entities operating within open and evolving contexts.
In particular, our model captures the dynamic nature of open environments, especially in terms of volatile domains and evolving relations. Unlike previous intensional models [
18,
19,
20,
21,
22], which assume fixed domains and relations across possible worlds, our approach accommodates a flexible and dynamic set of entities and relationships, making it more suitable for heterogeneous and evolving contexts.
The remainder of this paper is structured as follows. First, we review key pioneering works on intensional conceptualization and discuss their limitations in addressing the open-environment assumption [
23]. Next, we present our proposed intensional conceptualization model, demonstrating its suitability for dynamic environments. We also define the corresponding language elements and ontological commitments that support our model. Finally, we provide a brief comparison between the previous and proposed models, highlighting how our approach addresses these limitations and fills the gap in supporting open environments.
2. Related Work
Conceptualization [
24,
25] was introduced to represent real-world entities and their relationships within the information technology domain [
26]. Some theories define conceptualization under the closed-world assumption [
27], which models a specific state of the world or a snapshot of the current status of its concepts and relations. In contrast, others propose conceptualization models to capture all possible states of affairs (possible worlds) [
28,
29]. Both approaches assume known and predefined concepts and relations in the domain—an assumption that cannot accommodate the open-environment context, where undefined entities and relations exist.
The definition of conceptualization varies depending on the domain of interest. One of the initial definitions was given by T. R. Gruber [
30], who described conceptualization as “an abstract, simplified view of the world we wish to represent for some purpose. Every knowledge base, knowledge-based system, or knowledge-level agent is committed to some conceptualization, explicitly or implicitly.” He further defined an ontology as “an explicit specification of a conceptualization.” Guarino [
18] refined this, defining ontology as “a formal specification of a shared conceptualization.” Staab and Studer merged these two definitions, stating that “an ontology is a formal and explicit specification of a shared conceptualization” [
31].
Consider Guarino’s conceptualization theory [
18], which defines an intensional relational structure (or intensional conceptualization) as:
where:
D: the universe of discourse, defined as a static set encompassing all entities within the domain.
W: a set of possible worlds.
: a set of conceptual relations.
In traditional models, conceptual relations are restricted to a fixed set , preventing the introduction of new or undefined relations that may arise under the open-environment assumption. While possible worlds can capture the dynamic nature of relationships between existing concepts, they remain limited in that they do not support the addition of new concepts or relations. Consequently, such models cannot fully represent environments where the domain and its relations are subject to change.
Guarino also defined a logical language of intensional conceptualization
L, with a vocabulary
V:
where:
is the conceptualization.
is an interpretation function assigning constant symbols in V to elements of D, and predicate symbols in V to elements of .
From this definition, it follows that constants in Guarino’s language cannot represent new or unknown concepts in an open environment, and predicates can only represent relations already present in .
Bealer [
19] proposed another intensional conceptualization approach, extending first-order logic to represent intensional entities. His theory is based on propositions, relations, and properties, with knowledge represented using terms and formulas. However, his model does not introduce first-order logic axioms or formulas capable of capturing unknown domains in an open environment.
Recent research on intensional conceptualization models has highlighted their application in several domains, particularly in artificial intelligence (AI) and semantic integration. These models emphasize the intrinsic meaning of concepts and their interrelationships, making them relevant for contexts requiring nuanced knowledge representation.
A hybrid model [
32] integrates both intensional and extensional conceptualization methods. It employs epistemic logic to manage knowledge and belief systems within multi-agent environments, where different entities may express similar semantics in diverse ways. This approach facilitates flexible communication and collaboration among agents by capturing both intensional meaning (conceptual understanding) and extensional representation (practical application). However, it operates solely under the
possible worlds assumption and lacks support for the
open environment assumption.
Another approach applied intensional conceptualization to machine learning [
20], particularly in medical imaging, using a cross-modal strategy where concepts are treated as discrete latent variables extracted from images and accompanying text descriptions.
In summary, previous conceptualization models focus primarily on closed and centralized environments, where system components operate under predefined constraints and uniform semantics. These models are designed for controlled settings, assuming limited interaction with external, dynamic entities. As a result, they fail to address the complexities of open distributed environments, where multiple entities with diverse perspectives and decentralized control interact. Open environments require more flexible frameworks capable of handling varying semantics, knowledge sharing, and collaboration across independent systems—capabilities that traditional models largely overlook.
3. Proposed Intensional Conceptualization Model for Open Environments (ICMOE)
This work presents an Intensional Conceptualization Model for Open Environments (hereafter abbreviated as ICMOE), which serves as the foundation for semantic integration solutions within such environments.
In particular, we view conceptualization “as a fundamental cognitive process in which abstract representations are formed, involving several key components that define their nature.”
3.1. The ICMOE Main Elements Definitions
Before presenting our proposed conceptualization model, it is crucial to define the aspects and elements of conceptualization as informed by our perspective on intensional theory.
Definition 1
(Concept c). A concept is an abstract model in a given universe for an identified entity in another universe. For example, entities in our universe, such as my laptop, have an abstracted model in my mind, where my mind acts as another universe. Concepts may also be referred to as individuals or instances.
Definition 2
(Concept type t). A concept type is a group of concepts in a domain that may share common properties and behaviors. Concepts with shared characteristics can be classified into concept types, explicitly supporting knowledge classification and the hierarchy required for accommodating new and unknown concepts. Examples of concept types include humans, teachers, professors, and Canadians; each concept type is composed of a group of concepts (entities or instances) that share the properties and behaviors of the type.
Definition 3
(Relation r). A relation is a connection between two or more concepts, concept types, or between concept types and concepts. It represents how the domain concepts and concept types are related to each other. A relation is considered intensional when it connects concept types, and extensional when linking two specific concepts. For example, the concept type professor is related to graduate student by the relation supervising. Another example is the concept me, which is connected to this paper by the relation wrote.
Definition 4
(Rule U). Rules are sets of minimal constraints in the form of hypotheses that are specific to the domain, to which all elements of the domain must adhere. For example, for each concept type y, at least one concept x must satisfy the relation is-a with y.
Definition 5
(Domain D). The domain is the set of all concepts within the domain of interest. For instance, if university is the domain of interest, it is composed of all students, employees, buildings, professors, lecturers, etc.
Definition 6
(Open Environment Domain ). The Open Environment Domain is defined as the set of all possible domains that may exist within an open environment. Unlike static domains, accommodates variability by allowing the dynamic inclusion or removal of concepts over time. For example, if university is the domain of interest, then may include multiple possible configurations in which entities such as students, professors, and courses may be added or removed depending on the context.
Definition 7
(Interpretation function I). The interpretation function assigns one or more elements of one domain to one or more elements in another domain for the purpose of interpretation. For example, in the university domain, the interpretation of the engineering building in the university information system domain corresponds to the physical engineering building in the real-world domain.
Definition 8
(World w). A world is a physical state of the domain and represents a snapshot of a particular domain of interest.
Definition 9
(Possible worlds W). Possible worlds are all potential configurations of the domain. In the university domain, the possible worlds encompass all possible situations of university, which may include cases where the university exists or does not exist, new students registering for courses, the university’s status across different terms, professors teaching various courses, new courses being added, and so on.
Definition 10
(Conceptualization C). Conceptualization is a model consisting of relevant concepts and their relationships in a domain. For example, the real-world domain of university with its students, employees, processes, services, and management can be abstracted as a model that captures all of its elements and behaviors. This abstracted model is the conceptualization of university.
3.2. The ICMOE Structure
We adopt Guarino’s domain space structure, substituting the static domain D with the open environment domain space .
Accordingly, the domain space for an open environment is defined as:
where:
is the set of possible domains in an open environment, i.e., .
is the set of possible worlds associated with all possible domains under the open environment assumption, i.e., .
D is a domain, defined as a set of concepts, i.e., .
To illustrate, consider a new concept that introduces a new domain . Consequently, a new possible world would exist to represent the semantics and behavior associated with this new domain . This demonstrates how, under the open environment assumption, new concepts can dynamically expand both the set of domains and the set of possible worlds, thereby enabling more adaptable and extensible semantic models.
Before introducing the intensional conceptualization model itself, we define the following elements:
A
conceptual relation of arity
n on the domain space
is denoted
. It is a total function:
mapping each world
to an
n-ary relation on
D.
A set of conceptual relations is denoted in the domain space . For the open environment, denotes the set of all possible in , i.e., .
A
concept type t in the domain space
is defined as a total function:
mapping each world to the set of concepts
that belong to type
t.
A set of concept types is denoted in . In the open environment, the set of possible concept types is denoted .
Rules, representing axiomatic constraints, are also part of the model:
- -
u denotes a rule in the domain space .
- -
is the set of rules in .
- -
is the set of all possible rule sets in the open environment domain space .
We can now define the intensional conceptualization model for open environments (ICMOE), which captures all possible domains in all possible states, as follows:
This model supports the representation of unknown entities within . Such entities can be intensionally referenced through appropriate concept types t, while their behaviors and interactions are captured via the relational structure . These are constrained by the axioms in , and their various configurations are represented through the possible worlds .
3.2.1. Conceptual Model Example
To clarify the elements and structure of ICMOE, consider a real-world example of a university that provides learning services to the community. In this case, university represents the domain of interest in a specific state, denoted by , where .
Individuals within this domain, such as professors, students, and employees, are considered concepts, represented as instances . For example, a specific studentx or professory is an individual concept.
These individual concepts are grouped into concept types, such as student, professor, and employee, forming the set , where .
Relations capture how these entities interact. Suppose there exists a binary conceptual relation , called teaches, which links professor to student. This relation belongs to the set , where .
Possible worlds capture variations of this domain. Assume is a set of possible worlds for this state of the open environment, where . Within , two specific worlds and exist, such that :
In world , professory has a teaches relation with studentx.
In world , the same professory has no relation with studentx.
These different worlds illustrate the variability of possible configurations within
(see
Figure 1).
Finally, rules or axioms constrain the model. For example, consider rule : “Any professor must hold at least one PhD.” This rule, part of , implies that any concept of type professor must satisfy at least one unary relation , namely hasPhD.
By assembling all individual concepts in , classifying them into , defining relations from , situating them in possible worlds , and enforcing the rules in , we construct a complete instance of ICMOE for one state of the open environment.
3.3. The ICMOE Language
This section introduces the proposed language model for our open environment intensional conceptualization. The model is defined by specifying the vocabularies and the interpretation function, which maps between the language vocabularies and the intensional conceptualization elements.
3.3.1. Language Elements
We define the proposed language as
L, with a vocabulary
V given by:
where:
denotes the language constants.
denotes the n-ary logical predicates, similar to first-order language predicates.
o denotes the logical operators (existential and generalization).
denotes the language variables.
The language model is defined as:
where:
is the proposed conceptualization under the open environment assumption.
is an interpretation function that assigns:
- -
: constant symbols in V to concepts c (elements of ).
- -
: n-ary predicate symbols in V to intensional relations r (elements of ).
- -
: unary predicate symbols in V to concept types t (elements of ).
- -
Axioms = to rules u (elements of ).
This definition shows that the language elements can represent possible domains , possible relations , and possible concept types , thereby capturing the conceptualization of the open environment.
3.3.2. Language Ontological Commitment
The ontological commitment of the language refers to the mapping between the vocabulary of the language and the elements of a conceptualization. The conceptualization is interpreted by the user according to the language used. We propose the commitment in terms of the conceptualization model as:
Thus, the open environment language L commits to the conceptualization model through the commitment K, with serving as the underlying conceptualization.
3.3.3. Language Model Compatibility
Within our framework, the compatibility criteria of the language are defined as follows. Given a language L with vocabulary V and an ontological commitment :
A model is compatible with K if:
The set , consisting of all models of the language L compatible with K, is referred to as the set of intended models of L with respect to K.
3.3.4. Language Interpretation Function
An interpretation function is a formal mechanism that assigns semantic meaning to the syntactic elements of a language by mapping symbols to elements within a specific domain. Here, we define the interpretation function for our proposed intensional conceptualization model and illustrate how it systematically maps concepts, concept types, relations, and rules into the corresponding elements of the language for open environments.
Concept Interpretation
given constant
, concept
, and domain
.
Relation Interpretation
is the extended interpretation function for world S and domain D.
is an n-ary predicate.
is a conceptual relation.
is a possible world.
is a possible domain.
and .
for .
Example
From the university example in
Section 3.2.1, consider the axiom:
“Any professor must hold at least one PhD.”
We define the following elements:
Professor: a unary predicate equivalent to the concept type Professor.
PhD: a unary predicate equivalent to the concept type PhD.
Holds: a binary predicate equivalent to the intensional binary relation Holds.
: logical constructors belonging to the set of description logic operators .
This axiom can be expressed as:
Concept Type Interpretation
We classify the set of concept types T into two categories:
(Atomic Concept Type): Concept types interpreted only as concrete or leaf concepts in the hierarchy. Formally, , and for , .
(Non-Atomic Concept Type): Concept types interpreted as other concept types in the hierarchy. Formally, , and .
The atomic concept type is defined as:
where
,
, and
.
The non-atomic concept type is defined as:
where
, and
.
Relation Extension
We classify relations into two categories:
: atomic relations, interpreted only to concepts ().
: relation types, interpreted to concepts and/or other relations ().
The interpretation of an atomic relation is:
where
.
The interpretation of a relation type is:
where
and
.
3.4. Modeling the Dynamism of Open Environments: Proof and Complexity Analysis
The proposed Intensional Conceptualization Model for Open Environments (ICMOE) addresses the dynamic nature of heterogeneous open environments by establishing axioms that facilitate the integration and management of new conceptual elements. In this section, we present a formal proof demonstrating how ICMOE supports the evolving nature of open environments through axioms that accommodate and process newly introduced conceptual entities. This is followed by a complexity analysis of the process of accepting newly introduced conceptual entities.
3.4.1. Proof
Before introducing the axioms, we define a predicate used to determine new entities within the conceptualization model. Specifically, we define:
where:
, with .
are variables in the set .
Given the proposed conceptualization:
and the corresponding language:
we define new elements in the domain as follows:
Domain Members ():
denotes new open-environment domain members to be added to .
.
Equivalently: .
Concept Types ():
denotes new concept types in .
.
Equivalently: .
Relations ():
denotes new relations in .
.
Equivalently: .
3.4.2. Complexity Analysis
To evaluate the complexity of accepting a new entity—whether a concept type t, a relation r, or a domain element c—we define the following:
Let be the set of all rules in the open environment domain space , such that .
Let denote the total number of rules in .
Assume the complexity of evaluating is constant, i.e., .
Based on the axioms, a new member (e.g.,
) is accepted into
only if:
Therefore, to validate one new member, the predicate must be evaluated N times.
The total complexity for verifying a new member is:
3.5. Algorithm and Pseudocode
3.5.1. New Domain Members ()
The following pseudocode defines the validation process for accepting a new open-environment domain into the global domain set :
FunctionIsValidOpenDomain(, ):
for each concept c in :
for each usage function u in :
if NOT AdheresTo(c, u):
return False
return True
Example 1.
Suppose two new sensor instances, and , are to be added to the model. We already have:
Sensor as a known concept type t,
measures
as an intensional relation ,
a rule set that includes the axiom:
These are added to a new domain , with instances associated with a concept type set .
3.5.2. New Concept Types ()
The following pseudocode defines the validation process for accepting new concept types into the global concept type set :
FunctionIsValidConceptTypes(, ):
for each type t in :
for each usage function u in :
if NOT AdheresTo(t, u):
return False
return True
3.5.3. New Relations ()
The following pseudocode defines the validation process for accepting new relations into the global set of relations :
FunctionIsValidRelations(, ):
for each relation r in :
for each usage function u in :
if NOT AdheresTo(r, u):
return False
return True
4. Comparative Analysis and Dynamic Evaluation
This section presents a comprehensive comparison between the proposed Intensional Conceptualization Model for Open Environments (ICMOE) and the foundational models introduced by Guarino and Bealer. The comparison is structured across three complementary dimensions: (i) a conceptual comparison of core model constructs and design principles; (ii) a qualitative assessment focusing on semantic expressiveness, extensibility, dynamism, and reasoning capabilities; and (iii) a quantitative evaluation using well-defined performance metrics tailored to open distributed systems. These metrics include Concept Coverage, Semantic Depth, Dynamic Adaptability Index, Semantic Rule Density, and Ontology Alignment Efficiency.
Although existing models provide valuable theoretical insights, they often lack the flexibility and scalability required in dynamic, decentralized environments. ICMOE addresses these limitations by introducing a rich intensional–existential framework supported by formal reasoning, modular semantic components, and adaptability to runtime knowledge evolution.
Through both visual and numerical analyses, we demonstrate that ICMOE not only surpasses traditional frameworks in theoretical robustness but also exhibits superior empirical performance across all evaluated metrics. This dual validation confirms ICMOE’s suitability for complex semantic integration scenarios in open distributed environments.
4.1. Conceptual Comparison of ICMOE with Guarino [18] and Bealer [19]
Table 1 presents a conceptual comparison of the proposed ICMOE framework with the foundational models of Guarino [
18] and Bealer [
19], highlighting key aspects of intensional conceptualization. This analysis underscores ICMOE’s distinct advantages in addressing the demands of open distributed environments.
Unlike Guarino’s ontology-based approach, which emphasizes static taxonomic structures, and Bealer’s intensional logic, which centers on epistemic constructs, ICMOE provides a more expressive and extensible framework. It introduces explicit constructs—such as Concept Types and Relation Types—that clearly distinguish between domain-level entities (concepts) and their intensional abstractions.
ICMOE further enhances semantic precision by decoupling roles and properties, which are conflated in Guarino’s model. It leverages formal interpretation functions to establish consistent mappings between language terms and conceptual elements. This facilitates well-defined ontological commitments and supports the development of extensible knowledge representation languages.
In addition, ICMOE introduces a semantic hierarchy that classifies concept types and relation types into atomic and non-atomic structures. This layered approach supports richer expressiveness and enables more scalable reasoning, particularly in dynamic and decentralized systems. Together, these features demonstrate ICMOE’s conceptual maturity and its suitability for managing the complexity and variability of open environments.
4.2. Comparative Evaluation of SemanticModels
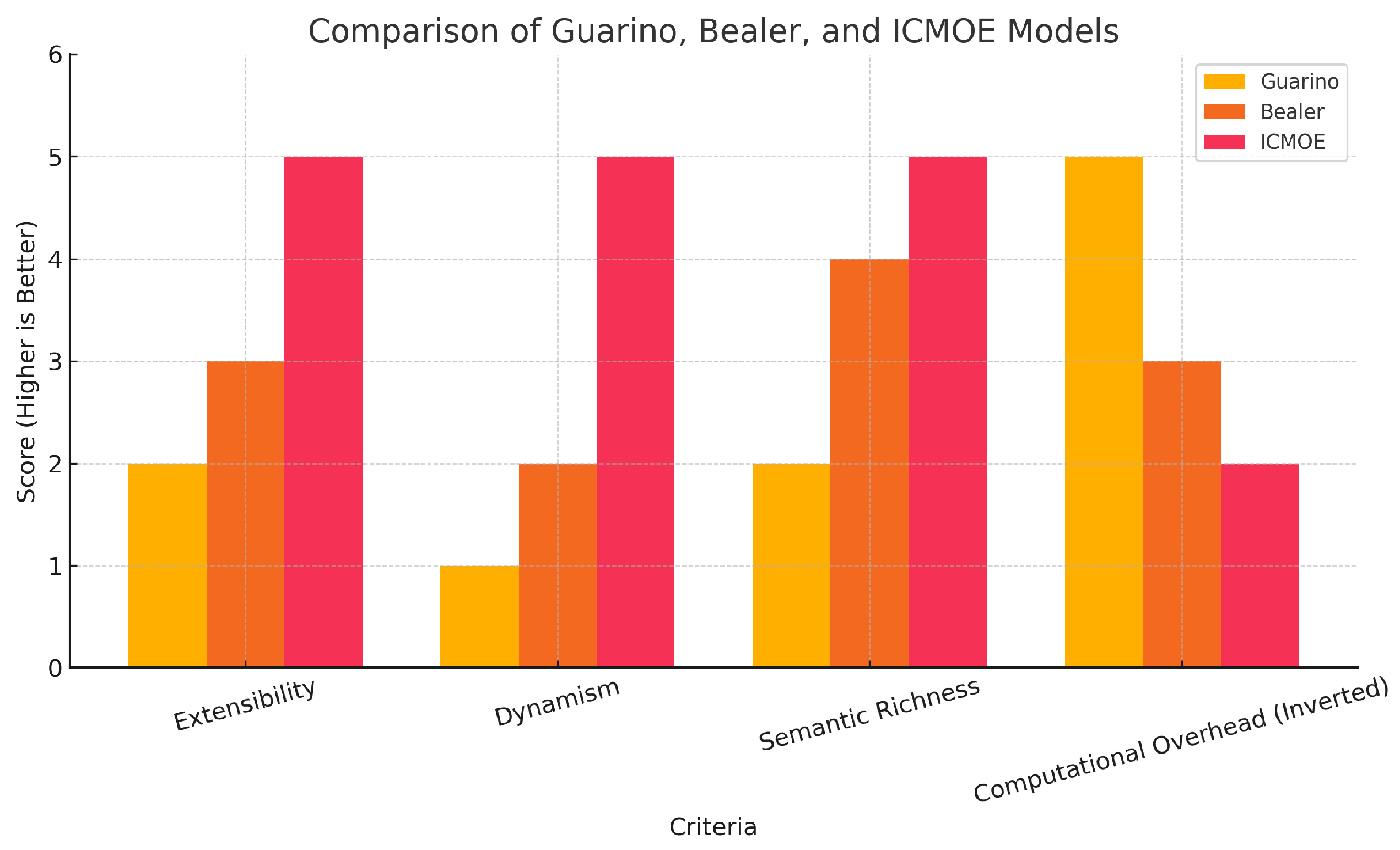
Figure 2 presents a visual comparison of the Guarino, Bealer, and ICMOE models along four dimensions critical for semantic integration in distributed systems:
Extensibility: Measures how easily a model can adapt to new concepts, rules, or sources. ICMOE leads with its open-world architecture and schema evolution capabilities. Bealer’s model supports conceptual extension, while Guarino’s rigid structure ranks lowest.
Dynamism: Reflects the model’s responsiveness to real-time changes. ICMOE, designed for open distributed environments, achieves the highest adaptability. Bealer’s logic allows variability but lacks structural reactivity. Guarino’s framework assumes a static domain.
Semantic Richness: Assesses expressiveness. ICMOE, built on DL with rich conceptual constructs, outperforms both. Bealer offers deep logic-based semantics, while Guarino emphasizes taxonomy over inference.
Computational Overhead (Inverted): Evaluates reasoning efficiency. Guarino’s minimalism results in low overhead. Bealer is moderate. ICMOE incurs higher costs due to inference and flexibility.
ICMOE balances flexibility and reasoning power, making it particularly suited for complex and evolving domains despite its computational demands.
4.3. Growth Dynamics of Domain, Relations, and Worlds
To demonstrate ICMOE’s capability to scale under the open-environment assumption, we simulate how the Domain (
D), Relations (
R), and Worlds (
W) evolve over time, as shown in
Figure 3.
Domain D: The set of concept instances grows exponentially as new entities are discovered and integrated.
Relations R: These increase proportionally as new associations form among entities. Growth is slower than D, but reflects richer semantics.
Worlds W: New possible worlds emerge to reflect alternative interpretations and evolving domain perspectives.
4.4. Quantitative Evaluation Metrics for ICMOE
To rigorously evaluate the capabilities of the proposed Intensional Conceptualization Model for Open Environments (ICMOE), we define a set of quantitative metrics that capture various dimensions of semantic integration, adaptability, and expressiveness. These metrics allow for measurable and comparative assessment against existing models.
4.4.1. Defined Evaluation Metrics
Together, these metrics provide a holistic view of the model’s performance in real-world, evolving semantic environments.
4.4.2. Empirical Assessment of ICMOE
Table 2 presents an approximate evaluation of the ICMOE model using the above metrics, based on the case study and model constructs described in
Section 3 and
Section 4.
4.4.3. Discussion
The high Concept Coverage and Semantic Rule Density values indicate that ICMOE captures both the breadth and depth of domain semantics. The Dynamic Adaptability Index reflects the model’s strength in supporting schema evolution and runtime integration—an essential requirement in open environments. Additionally, the Ontology Alignment Efficiency confirms the practicality of ICMOE in aligning heterogeneous views via formal mappings.
Together, these metrics provide strong validation of ICMOE’s expressiveness, scalability, and integrative capabilities in decentralized, dynamic systems.
4.4.4. Quantitative Comparison with Existing Models
Table 3 provides a comparative summary of the ICMOE model versus Guarino’s ontological model and Bealer’s intensional logic framework. The evaluation uses the five quantitative metrics defined earlier to highlight each model’s performance and limitations.
5. Limitations and Future Work
While the proposed model effectively addresses environmental dynamism and incorporates richer semantic structures—making it more adaptable to complex, open environments by supporting the addition of new axioms and conceptual members—it nonetheless faces certain limitations.
First, the model has only been validated theoretically; practical implementation and experimentation remain as future objectives.
Second, implementing this model requires the development of an extension or add-on to an existing description language, since no current language natively supports the proposed intensional features. Designing this language extension is one of our next steps to enable both theoretical and practical validation.
Finally, the model’s complexity is currently proportional to the size of —which corresponds to the size of the terminology component (TBox) in a reasoning system. This may demand above-average computational resources for large-scale systems. In future work, we aim to optimize the model by reducing its complexity to a logarithmic scale relative to .
6. Discussion and Conclusions
Conceptualization is a central theory and a crucial component of semantic integration approaches. Numerous methods in the literature rely on extensional structures, extensional reduction, and even intensional constructs to build conceptualizations. However, these approaches face significant limitations that make them unsuitable for dynamic, open-environment settings. Our proposed intensional conceptualization model (ICMOE) offers a more natural and adequate solution for semantic integration under such conditions.
In open environments, entities may enter or leave the system at any time, yet the system must remain operational. This necessitates a model capable of maintaining stability despite continuous change. With ICMOE, conceptualization remains stable as long as the intensional descriptions of concepts are captured, regardless of the fluctuating presence of individual entities. The model is grounded in domain, relation, and possible-world theories, enabling robust semantic integration in distributed, heterogeneous, and evolving environments.
The intensional nature of ICMOE provides inherent extensibility. Unlike traditional models in which domains and relations are fixed and cannot capture new or unknown entities, ICMOE extends these structures through possible domains and possible relations . Furthermore, the framework enriches the description of domain concepts by incorporating properties, thereby offering a more fine-grained and semantically precise representation of the world.
Finally, we conducted a comparative analysis between ICMOE and foundational approaches by Guarino and Bealer. This evaluation highlights that ICMOE effectively addresses their limitations in expressiveness, adaptability, and dynamic scalability. Consequently, ICMOE emerges as a suitable and comprehensive framework for structuring conceptualizations in open distributed environments.
Author Contributions
Conceptualization, K.B. and A.E.; methodology, K.B.; software, K.B.; validation, K.B., A.E., and A.W.; formal analysis, K.B.; investigation, K.B.; resources, A.E. and A.W.; data curation, K.B.; writing—original draft preparation, K.B.; writing—review and editing, K.B., A.E., and A.W.; visualization, Khaled Badawy; supervision, A.E. and A.W.; project administration, A.E. and A.W.; funding acquisition, A.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| ICMOE | Intensional Conceptualization Model for Open Environment |
| FOL | First Order Logic |
References
- Aouedi, O.; Vu, T.H.; Sacco, A.; Nguyen, D.C.; Piamrat, K.; Marchetto, G.; Pham, Q.V. A Survey on Intelligent Internet of Things: Applications, Security, Privacy, and Future Directions. arXiv 2024, arXiv:2406.03820. [Google Scholar] [CrossRef]
- IIoT World. Building Industrial IoT Systems Survey: 2024 Edition. 2024. Available online: https://www.iiot-world.com/industrial-iot/connected-industry/building-industrial-iot-systems-survey-2024-edition/ (accessed on 27 May 2025).
- Caballer, M.; Zala, S.; García, Á.L.; Moltó, G.; Orviz, P.F.; Velten, M. Orchestrating complex application architectures in heterogeneous clouds. J. Grid Comput. 2018, 16, 3–18. [Google Scholar] [CrossRef]
- Singh, S.; Patel, R. Addressing security in heterogeneous distributed infrastructures. J. Netw. Comput. Appl. 2022, 210, 103292. [Google Scholar]
- Mandala, N.R. Data Integration in Heterogeneous Systems. ESP J. Eng. Technol. Adv. 2022, 2, 122–129. Available online: https://www.researchgate.net/profile/Nishanth-Reddy-Mandala/publication/389679937_Data_Integration_in_Heterogeneous_Systems/links/67cc94de7c5b5569dcb8e0a4/Data-Integration-in-Heterogeneous-Systems.pdf (accessed on 1 August 2025). [CrossRef]
- John, B. Challenges and Solutions in Data Integration for Heterogeneous Systems. Res. Prepr. 2025. Available online: https://www.researchgate.net/publication/389856499_Challenges_and_Solutions_in_Data_Integration_for_Heterogeneous_Systems (accessed on 1 August 2025).
- Xu, P.; Barbosa, D. Connecting language and knowledge with heterogeneous representations for neural relation extraction. arXiv 2019, arXiv:1903.10126. [Google Scholar] [CrossRef]
- Babaei Giglou, H.; D’Souza, J.; Karras, O.; Auer, S. OntoAligner: A Comprehensive Modular and Robust Python Toolkit for Ontology Alignment. arXiv 2025, arXiv:2503.21902. [Google Scholar] [CrossRef]
- Rivas, D.; Ahmad, A.; Gomez-Perez, J.M. Ontology Matching Techniques for Resolving Semantic Heterogeneity: A Survey. J. Web Semant. 2024, 78, 100745. [Google Scholar]
- Asfand-E-Yar, M.; Ali, R. Semantic integration of heterogeneous databases of same domain using ontology. IEEE Access 2020, 8, 77903–77919. [Google Scholar] [CrossRef]
- Ahsaan, S.U.; Kaur, H.; Mourya, A.K.; Naaz, S. A hybrid support vector machine algorithm for big data heterogeneity using machine learning. Symmetry 2022, 14, 2344. [Google Scholar] [CrossRef]
- Natesan, G.; Chokkalingam, A. Task Scheduling in Heterogeneous Cloud Environment Using Mean Grey Wolf Optimization Algorithm. ICT Express 2019, 5, 110–114. Available online: https://www.sciencedirect.com/science/article/pii/S2405959518302534 (accessed on 1 August 2025). [CrossRef]
- Li, Z.; He, S.; Chaturvedi, P.; Kindratenko, V.; Huerta, E.A.; Kim, K.; Madduri, R. Secure Federated Learning Across Heterogeneous Cloud and High-Performance Computing Resources. arXiv 2024, arXiv:2402.12271. [Google Scholar] [CrossRef]
- Mangione, F.; Savaglio, C.; Fortino, G. Generative AI for IoT Computing: A Systematic Survey. arXiv 2025, arXiv:2504.07635. [Google Scholar]
- Giaretta, P. Philosophy and the Ontologies of Knowledge Representation in AI. In Ontology Makes Sense; IOS Press: Amsterdam, The Netherlands, 2019; pp. 24–36. Available online: https://www.asau.ru/files/pdf/2138517.pdf#page=40 (accessed on 1 August 2025).
- Zhu, F.; Ma, S.; Cheng, Z.; Zhang, X.Y.; Zhang, Z.; Liu, C.L. Open-world Machine Learning: A Review and New Outlooks. arXiv 2024, arXiv:2403.01759. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L. Challenges and solutions for security in open IoT environments. Int. J. Distrib. Sens. Netw. 2023, 19, 1–12. [Google Scholar]
- Guarino, N.; Guizzardi, G. Explanation, Semantics, and Ontology. Data Knowl. Eng. 2024, 153, 102325. Available online: https://www.researchgate.net/publication/381721674_Explanation_semantics_and_ontology (accessed on 1 August 2025). [CrossRef]
- Parsons, D. Bealer’s Theory of Properties, Relations, and Propositions. In Theories of Intensionality; Springer: Singapore, 2016. [Google Scholar]
- Alukaev, D.; Kiselev, S.; Pershin, I.; Ibragimov, B.; Ivanov, V.; Kornaev, A.; Titov, I. Cross-modal conceptualization in bottleneck models. arXiv 2023, arXiv:2310.14805. [Google Scholar] [CrossRef]
- Mohammad, A.; Aczel, P.; Hirschowitz, A.; Hill, C. A Categorical Framework for Typed Extensional and Intensional Models in Formal Semantics. arXiv 2024, arXiv:2408.07058. [Google Scholar] [CrossRef]
- Ali, I.; McIsaac, K.A. Intensional Model for Data Integration System in Open Environment. In Proceedings of the KEOD; SciTePress: Setúbal, Portugal, 2020; pp. 189–196. [Google Scholar]
- Mendes, D.; Oliveira, L.; Silva, A.; Ferreira, J. Context-Aware System for Information Flow Management in Industry 4.0. Appl. Sci. 2024, 14, 3907. [Google Scholar] [CrossRef]
- Magnani, L.; Nepomuceno, A.; Salguero, F. (Eds.) Model-Based Reasoning in Science and Technology: Inferential Models for Logic, Language, Cognition and Computation; Studies in Applied Philosophy, Epistemology and Rational Ethics; Springer: Cham, Switzerland, 2019; Volume 48. [Google Scholar]
- Magnani, L. (Ed.) Handbook of Abductive Cognition; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Donaldson, J.P.; Allen-Handy, A. The nature and power of conceptualizations of learning. Educ. Psychol. Rev. 2020, 32, 545–570. [Google Scholar] [CrossRef]
- Razniewski, S.; Nutt, W. Databases under the Partial Closed-World Assumption: A Survey. In Proceedings of the 26th GI-Workshop Grundlagen von Datenbanken; Klan, F., Specht, G., Gamper, H., Eds.; CEUR Workshop Proceedings 1313; CEUR-WS.org: Bozen-Bolzano, Italy, 2014; pp. 59–64. Available online: https://ceur-ws.org/Vol-1313/paper_11.pdf (accessed on 1 August 2025).
- Storey, V.C.; Lukyanenko, R.; Castellanos, A. Conceptual Modeling: Topics, Themes, and Technology Trends. arXiv 2025, arXiv:2505.13648. [Google Scholar] [CrossRef]
- Software Engineering Institute. ER 2024 to Feature the Latest on Conceptual Modeling, Artificial Intelligence, and Beyond. 2024. Available online: https://insights.sei.cmu.edu/news/er-2024-to-feature-the-latest-on-conceptual-modeling-artificial-intelligence-and-beyond/ (accessed on 27 May 2025).
- Gruber, T.R. Toward principles for the design of ontologies used for knowledge sharing. In Proceedings of the International Workshop on Formal Ontology, Padua, Italy, 17–19 March 1993; Available online: https://tomgruber.org/writing/onto-design.pdf (accessed on 1 August 2025).
- Staab, S.; Studer, R. Handbook on Ontologies, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Adhnouss, F.M.A.; El-Asfour, H.M.A.; McIsaac, K.; El-Feghi, I. A Hybrid Approach to Representing Shared Conceptualization in Decentralized AI Systems: Integrating Epistemology, Ontology, and Epistemic Logic. AppliedMath 2023, 3, 601–624. [Google Scholar] [CrossRef]
- Ryu, H.; Kim, G.; Lee, H.S.; Yang, E. Divide and Translate: Compositional First-Order Logic Translation and Verification for Complex Logical Reasoning. arXiv 2024, arXiv:2410.08047. [Google Scholar] [CrossRef]
- ten Cate, B.; Koudijs, R.; Ozaki, A. On the Power and Limitations of Examples for Description Logic Concepts. arXiv 2024, arXiv:2412.17345. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).