1. Introduction
Copulas are useful tools for understanding various dependence behaviors, modeling extremes, and analyzing the dependence structure of large loss events among different assets or insurance policies. As illustrated in, for example, Ref. [
1], it is recognized that financial data are often heavy-tailed and that extreme returns tend to cluster across investment portfolios. We begin by providing the necessary background on copulas. Technical preliminaries such as concordance measures, tail orders, and tail dependence coefficients are provided in
Appendix A.
A bivariate copula mapping from to I, the unit interval, has the following three properties: (i) (ii) for all u and v in I, and (iii) it is two-increasing, i.e., for all rectangles
A copula is totally positive of order 2 (TP2) if
for any pair of
and
in
indicating that the copula exhibits a positive dependence structure; see Ref. [
2]. A copula
C is called Archimedean if it admits the representation
where the generator
is a continuous strictly decreasing convex function with
The pseudoinverse
is
if
and 0 if
If
and
,
is a strict generator. For further details, please refer to Ref. [
3].
Ref. [
4] showed that there exists a unique copula function such that, for instance, a bivariate cumulative distribution function (cdf)
can be written as
where the function
and
and
are the respective quantile functions of
X and
Y.
The joint probability density function (pdf), denoted by
, of
, is
where
and
are the respective pdfs of
X and
Y, and
is the copula pdf defined as
This formulation allows us to write a joint pdf in terms of its marginal pdfs and a copula, which captures the dependence information between the random variables.
Multi-parametric models would allow more flexibility and may improve the fit when applied to data fitting. Distortion or transformation of existing copulas is one way to construct a multi-parametric copula. A function
is a distortion function if it is continuous and increasing, not necessarily convex or concave, with
and
A distortion
T is admissible for a base copula
C if the copula
defined by
is also a copula; see Refs. [
3,
5,
6]. If the base copula
C is Archimedean with generator
, then the new copula is Archimedean with generator
Motivated to find admissible distortions that are not convex, Ref. [
7] derived the following theorem. The theorem will be employed to determine the parameter values over which the proposed unit-Burr distortion is admissible. Since
T maps from
I to
I, applying Lemma 3.1 and Theorem 3.1 in Ref. [
7], the following theorem is established.
Theorem 1. Let be an increasing bijective transformation. If is log-convex, then the T distortion of a TP2 copula C results in a copula.
By definition, a continuous and strictly increasing cdf is a distortion function. That is, a continuous cdf with a support of
can potentially be admissible and serve the role
T in Equation (
1). For example, Ref. [
8] utilized the beta cdf to construct new copulas.
A method for generating a random variable
U with support
is to use a decay exponential transformation of the form
or
where
Y assumes positive real numbers. Ref. [
9] explored distortion copulas constructed when
Y is a gamma random variable. Ref. [
10] introduced the case when
Y is a Gompertz random variable. Ref. [
11] studied the case when
Y is a Lomax random variable. Although many random variables can serve as
Y, we focus on cases where
Y is a two-parameter Burr variable in this paper.
This article is organized as follows:
Section 2 introduces the proposed admissible unit-Burr distortion. In
Section 3, we provide examples of the induced copulas. Tail dependence coefficients and tail orders are derived in
Section 4.
Section 5 illustrates contour and surface plots of the copula densities. In
Section 6, we examine Kendall’s tau specifically for cases where the base copula is the Gumbel copula. An empirical application is discussed in
Section 7, followed by concluding remarks. Preliminaries are included in
Appendix A.
2. Proposed Admissible Unit-Burr Distortion
Let
Y be a non-negative continuous random variable with cdf
Define the random variable
or
The support of
U is
The cdf
of
U maps
and is given by
which is a distortion function such that
and
We consider the case when
Y is a Burr random variable with cdf
where the parameters
Applying (
2), the cdf of
U is given by
termed here as the unit-Burr distortion. By setting
, we obtain the Lomax-log distortion suggested by Ref. [
7].
Applying Theorem 1, the following corollary specifies the admissible parameter spaces for the unit-Burr distortion.
Corollary 1. Let be the unit-Burr distortion. Then, distortion of a TP2 copula is a copula if and
Proof. In this case,
, where
Its first derivative
and second derivative
are given by
The second derivative
is non-negative if
and
for
. The result follows by applying Theorem 1. □
The quantile function of is which is also a distortion function by definition. However, there are no admissible parameter spaces such that is considered admissible. Note that one may use the transformation of to construct potential admissible distortion functions, but the resulting cdf and quantile function are not admissible in this case.
3. Examples of Unit-Burr Distortion Copulas and Density Plots
This section showcases examples of copula models induced by unit-Burr (UB) distortion. Note that the distortion can only be applied to TP2 base copulas. To streamline the content, we omit below the fact that a bivariate copula is a function on
The family of copulas induced by the unit-Burr distortion is of the general form specified in (
1), given by
The conditional cumulative distribution functions of a copula can be derived by taking the first derivative with respect to
u or
v. The density of a copula is calculated by taking the second partial derivative of
with respect to both
u and
v. Their functional forms are not included here as the calculations are not difficult but rather tedious.
Examples of Unit-Burr Distortion Copula Models
Example 1. Unit-Burr Clayton copula
Let the base copula be the Clayton copula defined as where The three-parameter unit-Burr Clayton copula is given bySetting it yields the two-parameter bivariate BB2 copula family; see Ref. [12]. Example 2. Unit-Burr Galambos copula
Consider the Galambos copula of the form where The three-parameter unit-Burr Galambos copula is given bySetting it returns the two-parameter bivariate BB4 copula family; see Ref. [12]. Example 3. Unit-Burr Gumbel copula
When the base copula is the Gumbel copula defined as , the form in (4) results in an expression given byThe parameters θ and b are not identifiable since, e.g., By setting or reparameterizing, we derive a two-parameter Unit-Burr Gumbel copula given bywhere and Note that the independent copula is the Gumbel copula with . The Unit-Burr Gumbel copula is the bivariate BB1 copula by Ref. [13]; see also Ref. [12]. Examples 2, 3, and 1 show that the BB1, BB2, and BB4 copulas can be derived using the proposed unit-Burr distribution distortion instead of the mixture of max-id approach. We have uncovered a new way to generate the BB1, BB2, and BB4 copulas.
Example 4. Unit-Burr FGM copula
Consider the Farlie–Gumbel–Morgenstern (FGM) copula defined as The three-parameter unit-Burr FGM copula is given bywhere and In the context of multivariate distributions, extensions of the Farlie–Gumbel–Morgenstern (FGM) copula have been developed to better capture the correlations between variables. For more details, see [14,15] and references therein. We have constructed a new family of distorted FGM copulas. However, further investigation is needed to determine whether it can accommodate a wider range of dependencies or correlations than the standard FGM. 4. Tail Dependence Coefficients and Tail Orders
Tail dependence properties are essential for selecting an appropriate copula model in data fitting. Some copulas exhibit either upper or lower tail dependence, while others may show none at all. In this section, we derive the relationship between the UB distortion copula and its base copula in terms of tail dependence coefficients and orders.
By (
A3) and L’Hospital’s rule, the lower tail dependence coefficient for the induced copula by a distortion in (
1) is
where
The upper tail dependence coefficient is given by
Let
and
denote the lower and upper tail dependence coefficients and orders of the family of base copulas, respectively. Assume that the lower and upper tail dependence coefficients exist. We next examine the limits of
as
u approaches
and
in Equations (
6) and (
7). These limits determine the connection between the tail dependence of the base copula and that of the distorted copula.
Consider the UB distortion
in (
3), where
and
The first derivative of
is given by
By (
6) and (
A7), the lower tail dependence coefficient of the induced copula is, if it exists,
The upper tail dependence coefficient is given by
since
Applying the following Taylor-series approximations, as
we obtain that, as
Since
, and, by (
10) and (
11), we derive that
If
, then
as
and the UB distorted copula has the same upper order as the base copula
If
it has an upper order of 1.
Let and denote the lower and upper tail dependence coefficients and orders of the family of unit-Burr distortion copulas, respectively.
Theorem 2. Let be the family of copulas defined in (4), where and Then, (i) and
(ii) and and if
By Section 4.1 in Ref. [
12] and examples in
Section 3, the results listed in
Table 1 below confirm Theorem 2. Note that
when
and
when
see (
A5) and (
A6).
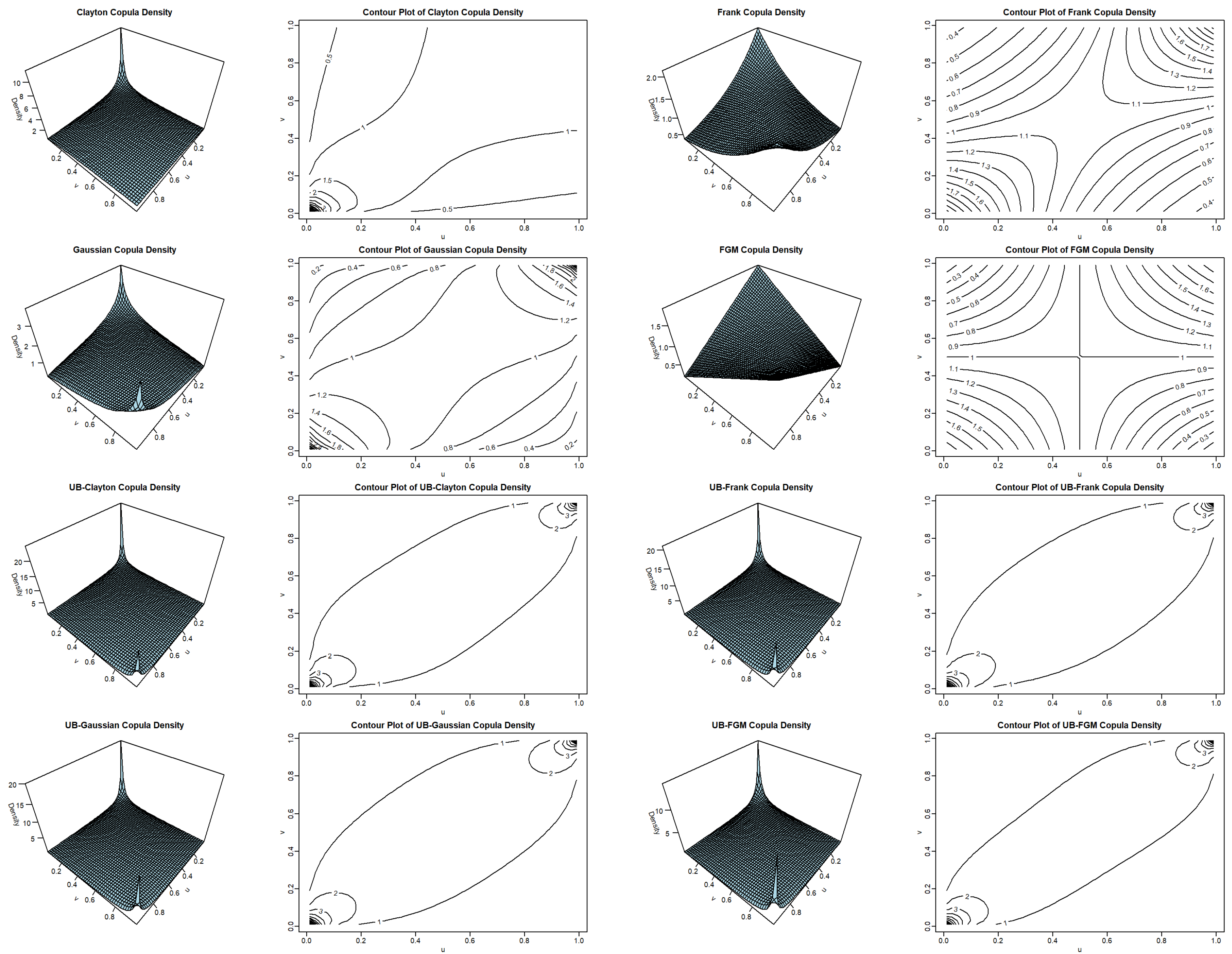
5. Contour and Surface Plots of Induced Copulas
Contour and surface plots of copula densities are valuable visual tools for understanding tail dependence structures represented by a copula. The first two rows in
Figure 1 present the 3D surface and contour plots of the base copulas: Clayton, Frank, Gaussian, and FGM. The last two rows show those of the corresponding UB-distorted copulas.
The Clayton copula is well-known for capturing dependence in the lower tail, making it suitable for modeling scenarios where extreme negative co-movements are common. This characteristic is visualized by a peak at the origin (0, 0). It indicates that the probability of observing simultaneously low values for both uniform margins is higher than in areas farther from the origin. The Frank copula features a moderate symmetric dependence structure without tail dependence. This makes it appropriate for situations where correlations are not particularly strong.
The Gaussian copula has an elliptical contour pattern that reflects its correlation structure, but it lacks tail dependence. In this case, peaks at the corners (0, 0) and (1, 1) suggest a positive correlation between the two variables represented by the copula. FGM copulas can only depict weak dependence, with and minimal tail behavior. This is indicated by flatter and less pronounced features, as well as the absence of sharp peaks at (0, 0) and (1, 1).
The density surfaces of the UB-distorted copulas reveal more significant changes at the point (1, 1) than at (0, 0). Compared to the base copula, the distorted copula densities show less concentration in the center, a difference that is particularly noticeable in the case of the Frank copula. Furthermore, all of the distorted copulas have a peak at (1, 1).
The first column of
Figure 2 displays contours of four base copula densities: Clayton, Frank, Gaussian, and FGM. The subsequent columns present contours of corresponding UB-distorted copulas with various values for
a and
b.
The contour plots of the distorted copulas show stretched or compressed changes in the tails. Overall, the application of UB distortion enhances the flexibility, enabling the new family of distorted copulas to capture a broader range of dependence structures than its base copula. The tail behaviors and asymmetry caused by UB distortion are particularly valuable in modeling financial data, where capturing extreme co-movements is essential. It could be of interest to further explore the impact of varying a and b in dynamic contexts, such as time-dependent financial models.
6. Concordance Measures of Association
Kendall’s tau and Spearman’s rho are widely recognized measures of concordance dependence or association. Their definitions are provided in
Appendix A. In this section, we will derive the closed form of Kendall’s tau, specifically for the family of unit-Burr Gumbel copulas. When there is no closed formula to compute Kendall’s tau, it can be computed numerically using software with built-in integration functions.
If a base copula
C is Archimedean with strict generator
Kendall’s tau coefficient can be calculated using the formula in (
A2). In this case, Kendall’s tau coefficient
of
is given by, with a substitution of
where
Based on (
12), the explicit functional form of the Archimedean generator
is not necessary for the calculation of
Example 5. For the Gumbel copula, By (12) and (8), with substitutions of and Kendall’s tau coefficient in this case is given bywhere is the beta function. As indicated in Example 3, when , the formula leads to Kendall’s tau for the bivariate BB1 copula of Since for the coefficient falls between 0 and 1 for and Concordance Ordering
A copula is positively (negatively) ordered
if
whenever
for all
Based on the general form of the Burr-distortion copula form in (
4), when
a and
b are fixed,
is an increasing function of the base copula value. Consequently, if a family of base copulas is ordered by its parameter
, so is the family of unit-Burr distortion copulas. The concordance ordering in the parameter
is preserved after the distortion.
One can derive the complicated first derivative of with respect to a or b to investigate the concordance ordering in the parameters a or Surface plots of Kendall’s taus can also be used to explore the concordance ordering of distortion copulas in the parameters a and b. According to the definition of a concordance measure, if a family of copulas is positively (or negatively) ordered by a parameter, increasing the parameter value leads to a larger (or smaller) Kendall’s tau. For further details, see Nelsen (2006). If Kendall’s tau is not a monotone function of a parameter, the family of copulas is not ordered by the parameter.
Figure 3 features Kendall’s tau surfaces for families of the UB-Clayton and UB-Frank copulas by fixing one parameter value while varying the others.
The UB distortion copula family is ordered by the base copula parameter
, and its Kendall’s tau is monotone in
. This monotonicity is observed in the plots shown in the second and third columns of
Figure 3, where either
a or
b is held constant. However, plots in the second column indicate that the family of UB-Clayton or UB-Frank copulas is not ordered by the parameter
b.
Figure 3 appeared to show that Kendall’s tau for the family of UB-Frank copulas is the least sensitive to the change in the parameter
7. An Application
The dataset comprises daily net return rates for Microsoft (MSFT) and Google (GOOG) stocks, obtained from Yahoo Finance, spanning from 1 January 2020 to 15 March 2025. The returns were computed as percentage changes based on adjusted closing prices following the formula
where
denotes the closing price at time
t. The sample Kendall’s tau (
) and Pearson correlation (
r = 0.335) indicate a mild positive dependence between the two stocks.
Table 2 shows summary statistics for 1306 daily returns of GOOG and MSFT. GOOG had a wider range (49.67) of returns than MSFT due to extreme outliers. GOOG’s returns were negatively skewed with a high kurtosis (17.97), indicating heavy tails. MFT’s mild skewness (0.19) and kurtosis (3.04) bring its return distribution closer to a normal distribution. MSFT appeared to have higher average returns and volatility, while GOOG had more extreme return values and tail risk.
Figure 4 displays scatter plots of the original observations (on the left) and their corresponding pseudo-observations (on the right). Pseudo-observations are constructed by applying the empirical distribution function to the original observations of each variable. This process transforms the original data points into values that fall within the range of 0 to 1. The scatter plot of pseudo-observations is used to examine the tail dependence structures between the returns of MSFT and GOOG.
The scatter plots indicate a positive dependence between the returns of the two assets. The scatter plot of the pseudo-observations reveals a cluster of points concentrated in the lower-left corner. The pattern suggests that copula models with lower tail dependence, such as the Clayton copula or UB-Frank copula, could be suitable candidates for further analysis.
The widely used pseudo-log-likelihood estimation method Ref. [
16] that utilizes pseudo-observations is employed. In addition to the parameter estimates and their standard errors (in parentheses),
Table 3 displays the values of log-likelihood, AIC, and BIC for both the base copula models and the corresponding UB distortion copula models.
The Gumbel model, which exhibits upper tail dependence but no lower tail dependence, performs the worst among the models evaluated. The log-likelihood, AIC, and BIC criteria consistently favor the UB-Frank copula as the best model. The Clayton copula, which has lower tail dependence, seemed to be a suitable candidate initially.
However, all the UB-distorted copulas outperform the base copula models across all selection criteria. These results illustrate that UB-distorted copulas generally provide a better fit than their base copulas.
Table 4 presents Kendall’s tau values along with the upper and lower tail dependence coefficients calculated using the integration of Equation (
12). The estimated parameter values in
Table 3 are used. The subscript
T indicates that the coefficients pertain to UB-distorted copulas.
The UB-Frank copula provides an estimated Kendall’s tau of 0.263, which is closest to the sample Kendall’s tau of 0.26 among the copula models considered. Interestingly, the estimated Kendall’s tau values from the other three UB-distorted copula models are further from the sample Kendall’s tau of 0.26 compared to those estimated from the base copula models.
According to the UB-Gaussian and UB-Gumbel copula models, there is a 23% probability that MSFT and GOOG will experience extreme negative returns simultaneously, and a 13% probability that they will experience extreme positive returns simultaneously. The UB-Frank copula, identified as the best-fit model, estimates these probabilities to be 12% for extreme negative returns and 11% for extreme positive returns.
The empirical analysis demonstrates that UB-distorted copulas offer a more flexible framework compared to their base copulas. The enhanced tail dependence properties in the distorted copulas make them particularly valuable for risk management, where capturing extreme market movements is crucial.
8. Concluding Remarks
This paper presents a new family of copulas created by transforming or modifying existing copulas using distortion functions, specifically the distribution of a unit-Burr random variable. This approach also offers a new perspective on the rise of copulas such as BB1, BB2, and BB4. The family formed through the unit-Burr distortion of an existing base copula, including the base copula as a member, can capture dependence structures that the base copulas fail to adequately model. The UB-distortion copula remains Archimedean if the base copula is Archimedean. The UB distribution can transform a base copula lacking tail dependence into one exhibiting tail dependence. The enhanced tail dependence properties make them particularly useful for risk management and portfolio optimization, where capturing extreme market movements is essential.
The additional parameters inherited from the distortion enhance the modeling flexibility and make the copula more adaptable to various data. Intuitively, the proposed UB-distorted copula would be expected to outperform its base copula. The empirical analysis demonstrates that UB-distorted copulas provide a more flexible framework for modeling financial dependencies compared to base copulas. While the additional parameters improve flexibility, they also introduce computational complexity. This complexity may also restrict the applicability of the distortion mechanism to multivariate cases. Moreover, one needs to carefully examine the resulting distortion copulas for potential parameter identifiability issues similar to those observed in Example 3.
There are various ways to create a cdf with support on the unit interval. For instance, a transformation like or can be applied, where the random variable X can take non-negative values or values in the entire real line. Another example is the logistic transformation , which maps the real line to values between 0 and 1. The admissibility of distortion functions needs to be investigated on a case-by-case basis, depending on the distribution of X. Further research is needed to determine whether there are systematic changes in the tail behaviors of new copulas constructed through distortion functions.