Modeling and Optimal Control of Liquidity Risk Contagion in the Banking System with Delayed Status and Control Variables

Abstract

The application of contagion risk spread modeling within the banking sector is a relatively recent development, emerging as a response to the persistent threat of liquidity risk that has affected financial institutions globally. Liquidity risk is recognized as one of the most destructive financial threats to banks, capable of causing severe and irreparable damage if overlooked or underestimated. This study aims to identify the most effective control strategy for managing financial contagion using a Susceptible–Infected–Recovered (SIR) epidemic model, incorporating time delays in both state and control variables. The proposed strategy seeks to maximize the number of resilient (vulnerable) banks while minimizing the number of infected institutions at risk of bankruptcy. Our goal is to formulate intervention policies that can curtail the propagation of financial contagion and mitigate associated systemic risks. Our model remains a simplification of reality. It does not account for strategic interactions between banks (e.g., panic reactions, network coordination), nor for adaptive regulatory mechanisms. The integration of these aspects will be the subject of future work. We establish the existence of an optimal control strategy and apply Pontryagin’s Maximum Principle to characterize and analyze the control dynamics. To numerically solve the control system, we employ a discretization approach based on forward and backward finite difference approximations. Despite the model’s simplifications, it captures key dynamics relevant to major European banks. Simulations performed using Python 3.12 yield significant results across three distinct scenarios. Notably, in the most severe case (${\alpha }_3=1.0$), the optimal control strategy reduces bankruptcies from 25% to nearly 0% in Spain, and from 12.5% to 0% in France and Germany, demonstrating the effectiveness of timely intervention in containing financial contagion.

1. Introduction

Banks serve as the cornerstone of the financial and economic system, playing a vital role in supporting and facilitating economic activity. Consequently, when banks experience significant difficulties, the stability of the entire financial and economic structure can be jeopardized. This vulnerability has been clearly demonstrated by various historical financial crises. A prominent example is the 2008 global financial crisis, which was largely caused by dysfunctions within the banking sector. Several key factors underline the fragility of modern financial systems. First, the increasing complexity and interdependence of global financial networks remain, to a large extent, insufficiently understood and regulated [1]. Second, crises of liquidity, and at times solvency, have manifested as credit crunches affecting businesses, banks, and governments alike, thereby intensifying systemic risks.

The crisis was triggered by the bursting of the housing price bubble in 2007, along with massive financial losses incurred by banks. As a result, the “Great Recession” began in 2008, with its effects continuing well beyond 2010. This episode revealed a critical gap in risk management: banking and liquidity risks were not considered as seriously as credit or market risks. In response, the international community made efforts to standardize banking regulation, starting with Basel I in 1988 and followed by Basel II in 2004. Nevertheless, these frameworks largely overlooked liquidity risk, often reducing it to the ability to meet obligations after their due dates [2].

The interbank exchange system operates through the transfer of deposits and the provision of credit facilities between financial institutions [3,4,5]. Contagion within the banking sector arises when one or more banks experience liquidity shortages. Simultaneously, concerns about the timely repayment by counterparties prompt other banks to withdraw their funds, initiating a domino effect across the interbank network.

All of these factors influence the stability of the financial system to varying degrees. According to [4], contagion occurs when a crisis in one country increases the likelihood of a similar crisis occurring in another. In emerging economies, this effect is often amplified by the transmission of external shocks. As a result, even minor fluctuations in developed markets can have a pronounced impact on other economies, particularly due to the high sensitivity of capital flows to changes in global interest rates. This mechanism serves as a primary driver of contagious financial crises.

In recent years, many papers have been published on the phenomenon of contagion within the financial system [6,7,8]. In addition the introduction of optimal control approach to deal with liquidity contagion was studied in [9]. In line with this trend, the present study aims to address the challenge of modeling liquidity risk contagion using a rigorous mathematical framework based on differential equations. Establishing effective financial control over all banks is of paramount importance, as such oversight plays a critical role in safeguarding institutions from systemic contagion. Financial regulation not only mitigates the spread of financial shocks but also helps prevent their negative consequences across the banking network. In this context, the European Central Bank (ECB), as a highly qualified supervisory authority, assumes the responsibility of overseeing and regulating banks. The ECB also facilitates vertical coordination among commercial banks, thereby strengthening the resilience of the system and helping to prevent the widespread transmission of financial distress.

New methods and techniques are essential for effectively conceptualizing and modeling the financial system. Mathematical models play a fundamental role in understanding the dynamic behavior of contagion risk within the banking sector, its impacts, and potential future trajectories of its spread [1,10,11,12]. In recent years, mathematical modeling of financial contagion has emerged as a relatively new yet rapidly growing research field, recognized as a critical area of study. These models are extensively applied in banking to improve risk management, forecast financial performance, and develop optimal operational strategies, thereby enabling institutions to make better-informed decisions and enhance both stability and profitability.

To study the contagion phenomenon, many researchers have drawn analogies between economic contagion and biological epidemics. From a mathematical perspective, the diffusion of a financial “virus” through economic networks is analogous to the spread of infectious diseases, and both are effectively described by systems of differential equations. This analogy is particularly relevant because national financial institutions form interconnected networks. Several studies have successfully adapted the Susceptible–Infected–Recovered (SIR) epidemiological model to the financial domain, providing valuable insights into systemic risk and contagion dynamics [2,13].

Our model introduces several significant innovations compared to existing approaches:

It incorporates a simultaneous delay in both the state variables and the control variable, which is rarely present in existing work.

The optimal control applied in our model has a delayed effect, which accurately reflects the implementation delays of monetary policies and regulatory interventions.

The model is then applied to empirical data on European banks, across three different countries, with partial parameter calibration.

Finally, we develop an optimal analysis using Pontryagin’s Maximum Principle with delay, which remains largely unexplored.

Additionally, research focusing on contagion in financial networks has employed the SIR model combined with optimal control theory to analyze systemic risk transmission across national banking systems. The results closely reflect real-world global economic conditions and emphasize the significant role of international financial linkages in maintaining overall financial stability [11].

The dynamics of contagion are influenced not only by its current state but also by its past behavior. To more accurately represent contagion risk, we propose a more realistic model that builds upon the findings of [2,13]. Our analysis considers time delays in both the state and control variables as important factors. Numerical modeling is used as a computational method to approximate solutions and optimize the problem through simulations.

This process involves imposing various constraints on the mathematical representation of the problem under investigation and analyzing the resulting effects to identify modifications that improve outcomes. Numerical modeling is widely applied across multiple disciplines, including medicine [14,15], economics [16], environmental science [17], transportation [18], and finance [19,20].

This work adopts a mathematical approach but could be complemented by multidisciplinary perspectives, incorporating monetary policy, the structure of banking supply chains, and financial network models.

Notably, recent years have seen significant advances in modeling infectious epidemics, which have become prominent examples within their respective fields [11], as well as in studies of urban crime [21]. Additionally, considerable research has focused on option pricing [19], chaotic systems [22], and the analysis of nonlinear evolutionary dynamics [17].

The rest of this paper is organized as follows. In Section 2, we propose a mathematical model which integrates a delay and a control term. In Section 3, the optimization problem is analyzed and discussed. In Section 4, an appropriate numerical method is described, along with the corresponding simulation results. The final section, Section 5, provides a concise summary of the conclusions drawn from the study.

2. Mathematics Model

Our strategy focuses on maximizing the count of banks that are susceptible while minimizing the count of infected banks and those at risk of bankruptcy. We incorporate a control variable, denoted as u, which represents the proportion of banks that can potentially be safeguarded from contagion risk within a given time frame.

To ensure a realistic model, it is essential to consider that the transition of susceptible banks from the group of banks in the susceptible category to the group of banks in the bankrupt category experiences a delay. We incorporate this delay into the system as follows: at time t, only a certain percentage of susceptible banks, which have been rescued from risk $\tau$ units of time ago, i.e., at time $t-\tau$, are transferred from the bankrupt class to the susceptible class.

The delay $\tau$ models the time required between the detection of liquidity risk and the effective response by financial authorities (ECB, national central banks, support mechanisms). It therefore reflects the actual implementation delays of monetary policy. Empirically, it can be estimated using interbank transaction data by analyzing the average time lag between liquidity stress and intervention. Consequently, the mathematical formulation including state and control variables with timing aspects can be formulated by the following nonlinear delayed differential system. The formulation of this problem is influenced by the research conducted in [4,13,23]. To accomplish this, we examine the following system of differential equations:

$$\left\{\begin{array}{c}{\displaystyle \frac{d{f}_1\left(t\right)}{dt}}=\mathrm{\Lambda }-{\alpha }_1{f}_1\left(t\right)f_2\left(t\right)+{\alpha }_2{f}_2\left(t\right)\hfill \\ +f_1(t-\tau )u(t-\tau )-d{f}_1\left(t\right),\hfill \\ {\displaystyle \frac{d{f}_2\left(t\right)}{dt}}=-{\alpha }_2{f}_2\left(t\right)-{\alpha }_3{f}_2\left(t\right)+{\alpha }_1{f}_1\left(t\right)f_2\left(t\right)\hfill \\ -d{f}_2\left(t\right),\hfill \\ {\displaystyle \frac{d{f}_3\left(t\right)}{dt}}={\alpha }_3{f}_2\left(t\right)-f_1(t-\tau )u(t-\tau )-d{f}_3\left(t\right).\hfill \end{array}\right.$$

(1)

where

$$f_1\left(t\right)+f_2\left(t\right)+f_3\left(t\right)=N\left(t\right)$$

where N denotes the total number of banks.

The non-negative constant $\tau$ is the time delay. The delay could be estimated using a lagged regression (VAR or Granger causality test) on high-frequency data from EONIA or interbank networks (TARGET2).

The constant positive value $\mathrm{\Lambda }$ signifies the rate at which new banks enter the banking system.

The initial condition of (1) is given as

$$f_1\left(\theta \right)={\phi }_1\left(\theta \right),f_2\left(\theta \right)={\phi }_2\left(\theta \right),f_3\left(\theta \right)={\phi }_3\left(\theta \right)$$

(2)

where

$$\phi ={({\phi }_1,{\phi }_2,{\phi }_3)}^T\in C:0\le {\phi }_k\left(\theta \right),fork=1,2,3(-h\le \theta \le 0)$$

where C represents the space of continuous functions on the interval $[-h,0]$ in ${\mathbb{R}}^3$, which is a Banach space denoted by $C([-h,0],{\mathbb{R}}^3)$.

We suppose that ${\phi }_k\left(0\right)>0$ for $k=1,2,3$.

Let $\mathrm{\Omega }$ be the control set u integrable in the sense of Lebesgue and bounded

$$\mathrm{\Omega }=\left\{u(·)\in L^2\left(0,T\right)\mid 0⩽u\left(t\right)⩽U,\forall t\in \left[0,T\right].\right\}$$

where

• $f_1\left(t\right)$ refers to the collection of banks at time t with a general ratio greater than 1, representing banks with a sufficient liquidity ratio, and therefore capable of absorbing a shock without falling into a critical situation.
• $f_2\left(t\right)$ refers to the collection of banks at time t with a general ratio less than 1
• $f_3\left(t\right)$ corresponds to all banks at time t that have become bankrupt.
• ${\alpha }_1$ represents the spread rate, which signifies the velocity at which the contagion disseminates. This parameter signifies the contagion intensity of an infected bank, indicating that a susceptible bank in contact with a single infected bank has a probability of ${\alpha }_1$ to acquire the infection.
• ${\alpha }_2$ denotes the solution rate, which characterizes the rate of recovery. This parameter quantifies the resilience to contagion. Consequently, an infected bank has a probability ${\alpha }_2$ of recovering from the contagion.
• ${\alpha }_3$ signifies the bankruptcy rate, which indicates the speed at which an infected bank is likely to become bankrupt. Consequently, a troubled bank will encounter bankruptcy with a probability of ${\alpha }_3$.

We make the assumption that, for $\theta \in \left[-\tau ,0\right]$, $f_1\left(\theta \right)$, $f_2\left(\theta \right)$, and $f_3\left(\theta \right)$ are continuous non-negative functions, and $u\left(\theta \right)=0$. It should be noted that the control variable u is considered as Lebesgue integrable, bounded by $0\le u\le b$, where b is a predetermined constant less than 1.

To demonstrate that the control system (1) admits a solution, we start by proving that it is dissipative. This implies that the solutions remain uniformly bounded in an appropriate subset $\mathrm{\Omega }\subset {\mathbb{R}}_{+}^3$.

2.1. Bornitude and Positivity of Solutions

Let $(f_1\left(t\right),f_2\left(t\right),f_3\left(t\right))\in {\mathbb{R}}_{+}^3$ be any solution with non-negative initial conditions. Adding equations of (1), we get

$${\displaystyle \frac{dN}{dt}}\le \mathrm{\Lambda }-d.N$$

$$\Rightarrow {\displaystyle \frac{dN}{dt}}+d.N\le \mathrm{\Lambda }$$

$$\Rightarrow e^{d\xi }{\displaystyle \frac{dN}{dt}}+d.e^{d\xi }N\le \mathrm{\Lambda }{e}^{d\xi }$$

$$\Rightarrow {\displaystyle \frac{d\left(e^{d\xi }N\right)}{dt}}\le \mathrm{\Lambda }{e}^{d\xi }$$

After integration, we have

$$e^{dt}N\left(t\right)-N\left(0\right)\le {\displaystyle \frac{\mathrm{\Lambda }}{d}}(e^{dt}-1)$$

$$\Rightarrow N\left(t\right)\le N\left(0\right)e^{-dt}+{\displaystyle \frac{\mathrm{\Lambda }}{d}}(1-e^{-dt})$$

Gold:

$$0\le e^{-dt}\le 1and0\le 1-e^{-dt}\le 1$$

Hence,

$$0\le N\left(t\right)\le {\displaystyle \frac{\mathrm{\Lambda }}{d}}ast⟶+\infty$$

Therefore, all feasible solutions of the system (1) enters the following region:

$$\mathrm{\Omega }=\left\{(f_1\left(t\right),f_2\left(t\right),f_3\left(t\right))\in {\mathbb{R}}_{+}^3\mid 0\le N\left(t\right)\le {\displaystyle \frac{\mathrm{\Lambda }}{d}}.\right\}$$

2.2. Detailed Calculation of the Stability of System (1)

2.2.1. Lyapunov Candidate Function

The Lyapunov candidate function is chosen as

$$V(f_1,f_2,f_3)={\displaystyle \frac{1}{2}}\left({\alpha }_1{f}_1^2+{\alpha }_2{f}_2^2+{\alpha }_3{f}_3^2\right),$$

where ${\alpha }_1,{\alpha }_2,{\alpha }_3>0$ are positive constants. This function is positive definite.

2.2.2. Time Derivative of V

The time derivative of V is given by

$${\displaystyle \frac{dV}{dt}}={\alpha }_1{f}_1{\displaystyle \frac{d{f}_1}{dt}}+{\alpha }_2{f}_2{\displaystyle \frac{d{f}_2}{dt}}+{\alpha }_3{f}_3{\displaystyle \frac{d{f}_3}{dt}}.$$

Substitute the dynamics of the system (1) as follows:

$${\displaystyle \frac{d{f}_1}{dt}}=\mathrm{\Lambda }-{\alpha }_1{f}_1{f}_2+{\alpha }_2{f}_2+f_1(t-\tau )u(t-\tau ),$$

$${\displaystyle \frac{d{f}_2}{dt}}={\alpha }_1{f}_1{f}_2-{\alpha }_2{f}_2-{\alpha }_3{f}_2,$$

$${\displaystyle \frac{d{f}_3}{dt}}={\alpha }_3{f}_2.$$

Thus, the derivative of V becomes

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dV}{dt}}={\alpha }_1{f}_1\left(\mathrm{\Lambda }-{\alpha }_1{f}_1{f}_2+{\alpha }_2{f}_2+f_1(t-\tau )u(t-\tau )\right)+{\alpha }_2{f}_2\hfill \\ \hfill & \left({\alpha }_1{f}_1{f}_2-{\alpha }_2{f}_2-{\alpha }_3{f}_2\right)+{\alpha }_3{f}_3\left({\alpha }_3{f}_2\right).\hfill \end{array}$$

2.2.3. Expansion of Terms

Expand each term:

• Term 1: ${\alpha }_1{f}_1\left(\mathrm{\Lambda }-{\alpha }_1{f}_1{f}_2+{\alpha }_2{f}_2+f_1(t-\tau )u(t-\tau )\right)$

  $$={\alpha }_1\mathrm{\Lambda }{f}_1-{\alpha }_1^2{f}_1^2{f}_2+{\alpha }_1{\alpha }_2{f}_1{f}_2+{\alpha }_1{f}_1{f}_1(t-\tau )u(t-\tau ).$$
• Term 2: ${\alpha }_2{f}_2\left({\alpha }_1{f}_1{f}_2-{\alpha }_2{f}_2-{\alpha }_3{f}_2\right)$

  $$={\alpha }_2{\alpha }_1{f}_1{f}_2^2-{\alpha }_2^2{f}_2^2-{\alpha }_2{\alpha }_3{f}_2^2.$$
• Term 3: ${\alpha }_3{f}_3\left({\alpha }_3{f}_2\right)$

  $$={\alpha }_3^2{f}_2{f}_3.$$

Combining all terms, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dV}{dt}}={\alpha }_1\mathrm{\Lambda }{f}_1-{\alpha }_1^2{f}_1^2{f}_2+{\alpha }_1{\alpha }_2{f}_1{f}_2+{\alpha }_1{f}_1{f}_1(t-\tau )u(t-\tau )+\hfill \\ \hfill & {\alpha }_2{\alpha }_1{f}_1{f}_2^2-{\alpha }_2^2{f}_2^2-{\alpha }_2{\alpha }_3{f}_2^2+{\alpha }_3^2{f}_2{f}_3.\hfill \end{array}$$

2.2.4. Handling Cross Terms

The term ${\alpha }_1{f}_1{f}_1(t-\tau )u(t-\tau )$ must be bounded. Assume $\left|u(t-\tau )\right|\le u_{\max }$, where $u_{\max }$ is a positive constant. Then

$${\alpha }_1{f}_1{f}_1(t-\tau )u(t-\tau )\le {\alpha }_1{u}_{\max }\left|f_1{f}_1(t-\tau )\right|.$$

Using Young’s inequality ($ab\le {\displaystyle \frac{a^2}{2}}+{\displaystyle \frac{b^2}{2}}$), we can write

$$|f_1{f}_1(t-\tau )|\le {\displaystyle \frac{f_1^2}{2}}+{\displaystyle \frac{f_1{(t-\tau )}^2}{2}}.$$

Thus

$${\alpha }_1{f}_1{f}_1(t-\tau )u(t-\tau )\le {\alpha }_1{u}_{\max }\left({\displaystyle \frac{f_1^2}{2}}+{\displaystyle \frac{f_1{(t-\tau )}^2}{2}}\right).$$

2.2.5. Simplification of ${\displaystyle \frac{dV}{dt}}$

Substituting this bound into the expression for ${\displaystyle \frac{dV}{dt}}$, we obtain

$$\begin{array}{cc}\hfill & {\displaystyle \frac{dV}{dt}}\le {\alpha }_1\mathrm{\Lambda }{f}_1-{\alpha }_1^2{f}_1^2{f}_2+{\alpha }_1{\alpha }_2{f}_1{f}_2\hfill \\ \hfill & +{\alpha }_1{u}_{\max }\left({\displaystyle \frac{f_1^2}{2}}+{\displaystyle \frac{f_1{(t-\tau )}^2}{2}}\right)+{\alpha }_2{\alpha }_1{f}_1{f}_2^2\hfill \\ \hfill & -{\alpha }_2^2{f}_2^2-{\alpha }_2{\alpha }_3{f}_2^2+{\alpha }_3^2{f}_2{f}_3.\hfill \end{array}$$

2.2.6. Choice of Coefficients to Ensure ${\displaystyle \frac{dV}{dt}}<0$

To ensure ${\displaystyle \frac{dV}{dt}}<0$, we choose the coefficients ${\alpha }_1,{\alpha }_2,{\alpha }_3$ such that the positive terms are dominated by the negative terms. For example, we can impose

$${\alpha }_2{\alpha }_3{f}_2^2>{\alpha }_1\mathrm{\Lambda }{f}_1+{\alpha }_1{u}_{\max }\left({\displaystyle \frac{f_1^2}{2}}+{\displaystyle \frac{f_1{(t-\tau )}^2}{2}}\right).$$

Assuming $f_1+f_2+f_3=N$ (where N is a constant), we can write

$${\alpha }_2{\alpha }_3{N}^2>{\alpha }_1\mathrm{\Lambda }N+{\alpha }_1{u}_{\max }\left({\displaystyle \frac{N^2}{2}}+{\displaystyle \frac{N^2}{2}}\right).$$

This simplifies to

$${\alpha }_2{\alpha }_3{N}^2>{\alpha }_1\mathrm{\Lambda }N+{\alpha }_1{u}_{\max }{N}^2.$$

Dividing by N (assuming $N>0$), we obtain

$${\alpha }_2{\alpha }_{3}N>{\alpha }_1\mathrm{\Lambda }+{\alpha }_1{u}_{\max }N.$$

2.2.7. Matrix Representation

The matrix representation of the system remains valid:

$${\displaystyle \frac{dX}{dt}}=AX\left(t\right)+F(X\left(t\right),X_{\tau }\left(t\right))=G(X\left(t\right),X_{\tau }\left(t\right)),$$

with

$$X=\left[\begin{array}{c}{f}_1\\ f_2\\ f_3\end{array}\right],A=\left[\begin{array}{ccc}-d& {\alpha }_2& 0\\ 0& -({\alpha }_2+{\alpha }_3+d)& 0\\ 0& {\alpha }_3& -d\end{array}\right],$$

and

$$F(X\left(t\right),X_{\tau }\left(t\right))=\left[\begin{array}{c}\mathrm{\Lambda }-{\alpha }_1{f}_1\left(t\right)f_2\left(t\right)+f_1(t-\tau )u(t-\tau )\\ {\alpha }_1{f}_1\left(t\right)f_2\left(t\right)\\ -f_1(t-\tau )u(t-\tau )\end{array}\right].$$

2.2.8. Lipschitz Continuity

The function G satisfies a uniform Lipschitz continuity condition:

$$|G(X_1,X_{1\tau })-G(X_2,X_{2\tau })|\le M\left(|X_1-X_2|+|X_{1\tau }-X_{2\tau }|\right),$$

where $M=max(M_1+\parallel A\parallel ,M_2)<\infty$. This guarantees the existence and uniqueness of solutions for the system (1).

3. The Problem of Optimal Control

Our objective is to maximize the number of susceptible and recovered banks while minimizing the number of infected banks throughout the contagion period. Mathematically, for a given terminal time T, the problem consists of minimizing the following functional:

$$\begin{array}{c}\hfill J(u,T)={\mathsf{\int }}_0^T[-K_1{f}_1\left(t\right)-K_2{f}_2\left(t\right)+K_3{f}_3\left(t\right)+{\displaystyle \frac{K_4}{2}}{u}^2\left(t\right)]dt,\end{array}$$

(3)

$K_1,K_2,K_3,K_4\in {\mathbb{R}}_{+}.$ Let us represent the weights which balance the magnitudes of the terms. Essentially, the aim of our study is to determine the control $u^{*}$ that satisfies

$$\begin{array}{c}\hfill J\left(u^{*}\right)=min\left\{J\left(u\right):u\in U\right\}\end{array}$$

(4)

In this context, U denotes the collection of admissible controls, which can be defined in the following manner:

$$\begin{array}{cc}\hfill & U=\{u:Lebesguemeasurable,and0\le u(t)\le b<1\hfill \\ \hfill & forallt\in [0,T]\}\hfill \end{array}$$

(5)

3.1. Existence of Minimal Control $u^{*}$

By referring to a result presented by Fleming and Rishel in [24], we show that there exists an optimal control satisfying the following theorem:

Theorem 1.

There is an optimal control $u^{*}\in U$ and a corresponding triple of functions $(f_1^{*};f_2^{*};f_3^{*})$ that constitute a solution to system (1) such as

$$\begin{array}{c}\hfill J\left(u^{*}\right)=\underset{u\in U}{min}\left\{J\left(u\right)\right\}\end{array}$$

(6)

Proof. 

To utilize the existence result mentioned in [24], it is necessary to fulfill the following conditions:

1

The controlled system with initial conditions (1) possesses a non-empty set of solutions.

2

The set U possesses both closed and convex characteristics.

3

The right-hand side of the state system is bounded by a linear function in the state and control variables.

4

The integrand of the objective functional exhibits convexity over the set U.

5

For the integrand $L(f_1,f_2,f_3,u)$ of the objective functional, there exist positive constants $c_1$ and $c_2$, as well as $\rho$ greater than 1, such that the condition is satisfied:

$$L(f_1,f_2,f_3,u)⩾c_2+c_1\left(\right|u\left(t\right){{|}^2)}^{{\displaystyle \frac{\rho }{2}}}$$

(7)

To establish the existence of a solution for the system (1) with bounded coefficients, we relied on an existence result from Lukes [24], which satisfies condition 1. The set of control U is inherently defined as both convex and closed. Moreover, considering the boundedness of the solution, the right-hand side of (1) satisfies condition 3 due to the linearity of the state system in u. The integrand in the objective functional (3) exhibits convexity over U. Furthermore, it is apparent that there exists a constant $\rho >1$ and positive numbers $c_1$ and $c_2$ that meet the following conditions:

$$L(f_1,f_2,f_3,u)⩾c_2+c_1\left(\right|u\left(t\right){{|}^2)}^{{\displaystyle \frac{\rho }{2}}}$$

(8)

□

3.2. Characterization of the Minimal Control

By applying Pontryagin’s maximum principle with delay, as shown in [24], we have derived the necessary condition for optimal control. This principle transforms (1), (3), and (6) into a minimization problem that involves a Hamiltonian function H, defined as follows:

$$\begin{array}{cc}\hfill & H=-K_1{f}_1\left(t\right)-K_2{f}_2\left(t\right)+K_3{f}_3\left(t\right)+{\displaystyle \frac{K_4}{2}}{u}^2\left(t\right)dt\hfill \\ \hfill & +\sum _{i=1}^3{\lambda }_i{g}_i,\hfill \end{array}$$

(9)

In this context,

• $g_1\left(t\right)=\mathrm{\Lambda }-{\alpha }_1{f}_1\left(t\right)f_2\left(t\right)+{\alpha }_2{f}_2\left(t\right)+f_1(t-\tau )u(t-\tau )-d{f}_1\left(t\right)$,
• $g_2\left(t\right)=-{\alpha }_2{f}_2\left(t\right)-{\alpha }_3{f}_2\left(t\right)+{\alpha }_1{f}_1\left(t\right)f_2\left(t\right)-d{f}_2\left(t\right)$,
• $g_3\left(t\right)={\alpha }_3{f}_2\left(t\right)-f_1(t-\tau )u(t-\tau )-d{f}_3\left(t\right).$

Theorem 2.

Let $(f_1^{*};f_2^{*};f_3^{*})$ be a solution of system (1) and $u^{*}$ the associated control solution of (12), then there exist adjoint functions ${\lambda }_1$,${\lambda }_2$, and ${\lambda }_3$ satisfying

$$\begin{array}{cc}\hfill & {\dot{\lambda }}_1\left(t\right)=-K_1+{\lambda }_{1}d+({\lambda }_1-{\lambda }_2){\alpha }_1{f}_2^{*}+{\chi }_{[0,T-\tau ]}({\lambda }_1^{+}-{\lambda }_3^{+})u^{*},\hfill \\ \hfill & {\dot{\lambda }}_2\left(t\right)=-K_2+({\lambda }_1-{\lambda }_2){\alpha }_1{f}_1^{*}+(d+{\alpha }_3){\lambda }_2-{\alpha }_3{\lambda }_3,\hfill \\ \hfill & {\dot{\lambda }}_1\left(t\right)=K_3+{\lambda }_{3}d,\hfill \end{array}$$

(10)

where ${\lambda }_i$ represents the marginal costs or the cost–benefit value associated with the state of banks in each class, from the perspective of the social objective with the transversality conditions

$$\begin{array}{c}\hfill {\lambda }_1\left(T\right)=0,{\lambda }_2\left(T\right)=0and{\lambda }_3\left(T\right)=0\end{array}$$

(11)

Moreover, the optimal control $u^{*}$ can be represented by the following expression:

$$\begin{array}{c}\hfill u^{*}\left(t\right)=min(b,max(0,{\displaystyle \frac{({\lambda }_1^{+}-{\lambda }_3^{+})}{K_4}}{\chi }_{[0,T-\tau ]}\left(t\right)f_1^{*})\end{array}$$

(12)

where

$${\lambda }_1^{+}\left(t\right)={\lambda }_1(t+\tau ),{\lambda }_2^{+}\left(t\right)={\lambda }_2(t+\tau ),and{\lambda }_3^{+}\left(t\right)={\lambda }_3(t+\tau )$$

The $K_4$ parameter weighs the economic cost of intervention (e.g., liquidity injections, financial aid). A trade-off must be found between the cost of intervention and the stability of the system.

Proof. 

Through the utilization of Pontryagin’s maximum principle, we are able to obtain the expressions for the adjoint equations and transversality conditions, considering the delay in the state and control variables [25]. This leads to the following equations:

$$\begin{array}{c}\hfill {\dot{\lambda }}_1=-{\displaystyle \frac{\partial H\left(t\right)}{\partial f_1\left(t\right)}}-{\chi }_{[0,T-\tau ]}\left(t\right){\displaystyle \frac{\partial H(t+\tau )}{\partial f_1(t-\tau )}},{\lambda }_1\left(T\right)=0,\\ \hfill {\dot{\lambda }}_2=-{\displaystyle \frac{\partial H\left(t\right)}{\partial f_2\left(t\right)}},{\lambda }_2\left(T\right)=0,\\ \hfill {\dot{\lambda }}_3=-{\displaystyle \frac{\partial H\left(t\right)}{\partial f_3\left(t\right)}},{\lambda }_3\left(T\right)=0\end{array}$$

(13)

By solving the optimality condition, we can determine the optimal control $u^{*}$:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial H}{\partial u}}+{\chi }_{[0,T-\tau ]}\left(t\right){\displaystyle \frac{\partial H(t+\tau )}{\partial u_{\tau }}}=0,\end{array}$$

(14)

that is,

$$\begin{array}{c}\hfill K_{4}u+{\chi }_{[0,T-\tau ]}\left(t\right)({\lambda }_3^{+}-{\lambda }_1^{+})f_1=0.\end{array}$$

(15)

By considering the limits imposed on the control variable U, it becomes straightforward to express $u^{*}$ in the form specified in Equation (12). □

4. Numerical Simulation

The year 2012 corresponds to a critical post-crisis year with available data on European bank spreads and interbank linkages. The 169 banks in our dataset represent large and medium-sized institutions sampled from ECB reports and analyzed in [25]. In each simulation, the contagion is modeled using actual initial conditions, and the parameter ${\alpha }_3$ is varied to capture different degrees of market pessimism and shock absorption capacity. Some numerical results were used in order to make a comparison between the proposed approach and the classical one, which uses constant weight coefficients in the cost function, and to demonstrate the behavior of the proposed approach as well.

For the purpose of conducting a numerical simulation in a real-world scenario, we obtained the spread rate ${\alpha }_1$ and the recovery rate ${\alpha }_2$ from the research conducted by Philipps, Koutelidakis, and Leontitsis [25]. The rates mentioned were obtained by extracting data from a sample of 169 prominent European banks, specifically collected for the year 2012, as computed in [25]. In our numerical simulation, we consider a total of $N=169$ banks, out of which 10 banks initially encounter liquidity risk at time $t=0$.

$u\left(t\right)\le 1$ is a threshold that represents the maximum capacity of public authorities to intervene, set at 100% in this paper to standardize the analysis. It can be adjusted to model more constrained scenarios.

In this section, we examine the modeling of liquidity risk and the utilization of optimal control techniques to mitigate the spread of liquidity risk in the banking system. We consider three initial scenarios of liquidity crisis: the first originating from Spain, the second from France, and the third from Germany. The data for each case and scenario are summarized in the following respective tables:

Table 1. The data used in the numerical simulation of the system (1) in relation to Spain.

Parameters	Figure 1a	Figure 2a	Figure 3a	Source
${\alpha }_1$	0.005	0.005	0.005	[25]
${\alpha }_2$	0.013	0.013	0.013	[25]
${\alpha }_3$	1.00	0.10	0.0001	Assumed
$f_1\left(0\right)$	158.00	158.00	158.00	[25]
$f_2\left(0\right)$	10.00	10.00	10.00	[25]
$f_3\left(0\right)$	0.00	0.00	0.00	[25]
u	1.00	1.00	1.00	Assumed
d	1.00	1.00	1.00	Assumed
$\mathrm{\Lambda }$	10.00	10.00	10.00	Assumed
$K_1$	10.00	10.00	10.00	Assumed
$K_2$	10.00	10.00	10.00	Assumed
$K_3$	10.00	10.00	10.00	Assumed
$K_4$	10.00	10.00	10.00	Assumed

for the Spanish crisis,

Table 2. The data used in the numerical simulation of the system (1) in relation to France.

Parameters	Figure 1b	Figure 2b	Figure 3b	Source
${\alpha }_1$	0.002	0.002	0.002	[25]
${\alpha }_2$	0.02	0.02	0.02	[25]
${\alpha }_3$	1.00	0.10	0.0001	Assumed
$f_1\left(0\right)$	158.00	158.00	158.00	[25]
$f_2\left(0\right)$	10.00	10.00	10.00	[25]
$f_3\left(0\right)$	0.00	0.00	0.00	[25]
u	1.00	1.00	1.00	Assumed
d	1.00	1.00	1.00	Assumed
$\mathrm{\Lambda }$	10.00	10.00	10.00	Assumed
$K_1$	10.00	10.00	10.00	Assumed
$K_2$	10.00	10.00	10.00	Assumed
$K_3$	10.00	10.00	10.00	Assumed
$K_4$	10.00	10.00	10.00	Assumed

for the French crisis, and

Table 3. The data used in the numerical simulation of the system (1) in relation to Germany.

Parameters	Figure 1c	Figure 2c	Figure 3c	Source
${\alpha }_1$	0.0012	0.0012	0.0012	[25]
${\alpha }_2$	0.008	0.008	0.008	[25]
${\alpha }_3$	1.00	0.10	0.0001	Assumed
$f_1\left(0\right)$	158.00	158.00	158.00	[25]
$f_2\left(0\right)$	10.00	10.00	10.00	[25]
$f_3\left(0\right)$	0.00	0.00	0.00	[25]
u	1.00	1.00	1.00	Assumed
d	1.00	1.00	1.00	Assumed
$\mathrm{\Lambda }$	10.00	10.00	10.00	Assumed
$K_1$	10.00	10.00	10.00	Assumed
$K_2$	10.00	10.00	10.00	Assumed
$K_3$	10.00	10.00	10.00	Assumed
$K_4$	10.00	10.00	10.00	Assumed

for the German crisis.

The evolution of the spread of liquidity risk, as modeled by the differential system (1), is illustrated in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, which represent the system’s behavior in Spain, France, and Germany under varying values of the default parameter ${\alpha }_3$ over the same time horizon.

These countries represent three different profiles: Spain (severe crisis in 2012, fragile banks), France (large universal banks), and Germany (highly interconnected regional banking system).

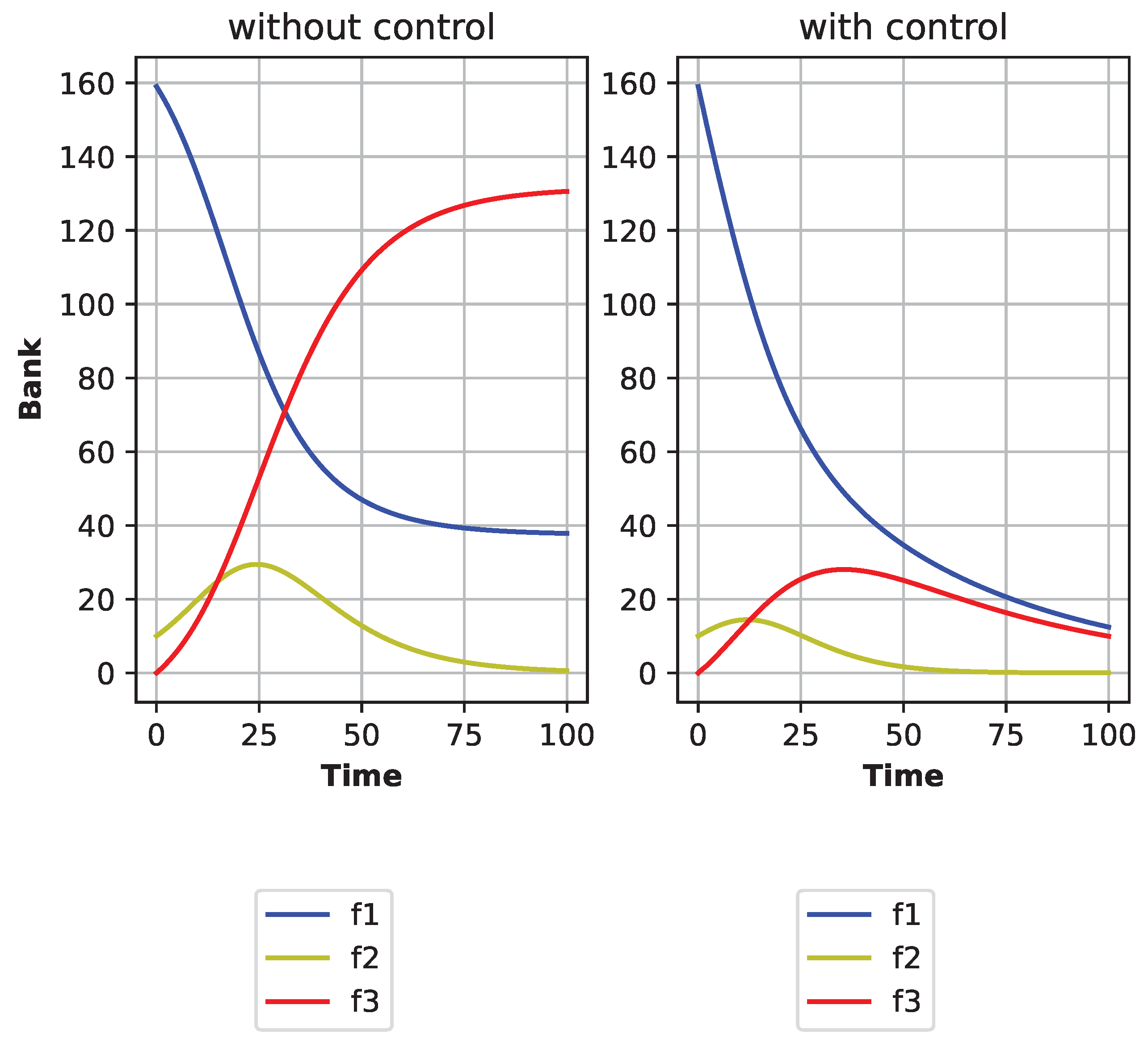
In the initial scenario characterized by the highest default probability (${\alpha }_3=1.0$), illustrated in Figure 1 (Spain), Figure 2 (France), and Figure 3 (Germany), it can be observed that in all three countries, the contagion rate decreases rapidly over time. This is primarily attributed to the sharp default rate in the uncontrolled case, where approximately ${\displaystyle \frac{1}{4}}$ of all Spanish banks collapse in a short span, and nearly ${\displaystyle \frac{1}{8}}$ of banks in France and Germany go bankrupt. However, with the application of the optimal control strategy, the proportion of defaulted banks significantly declines, eventually approaching zero. This demonstrates the effectiveness of central bank intervention in restoring the stability of the banking system.

In the second scenario, with a more moderate default probability (${\alpha }_3=0.1$), illustrated in Figure 4 (Spain), Figure 5 (France), and Figure 6 (Germany), the liquidity crisis evolves more gradually. Due to the lower initial risk of default, the financial shock takes more time to spread across the system. This extended contagion window results in more banks facing liquidity distress before collapsing. Nevertheless, the implementation of control significantly reduces the spread of the crisis and enables the banking system to return to a stable configuration.

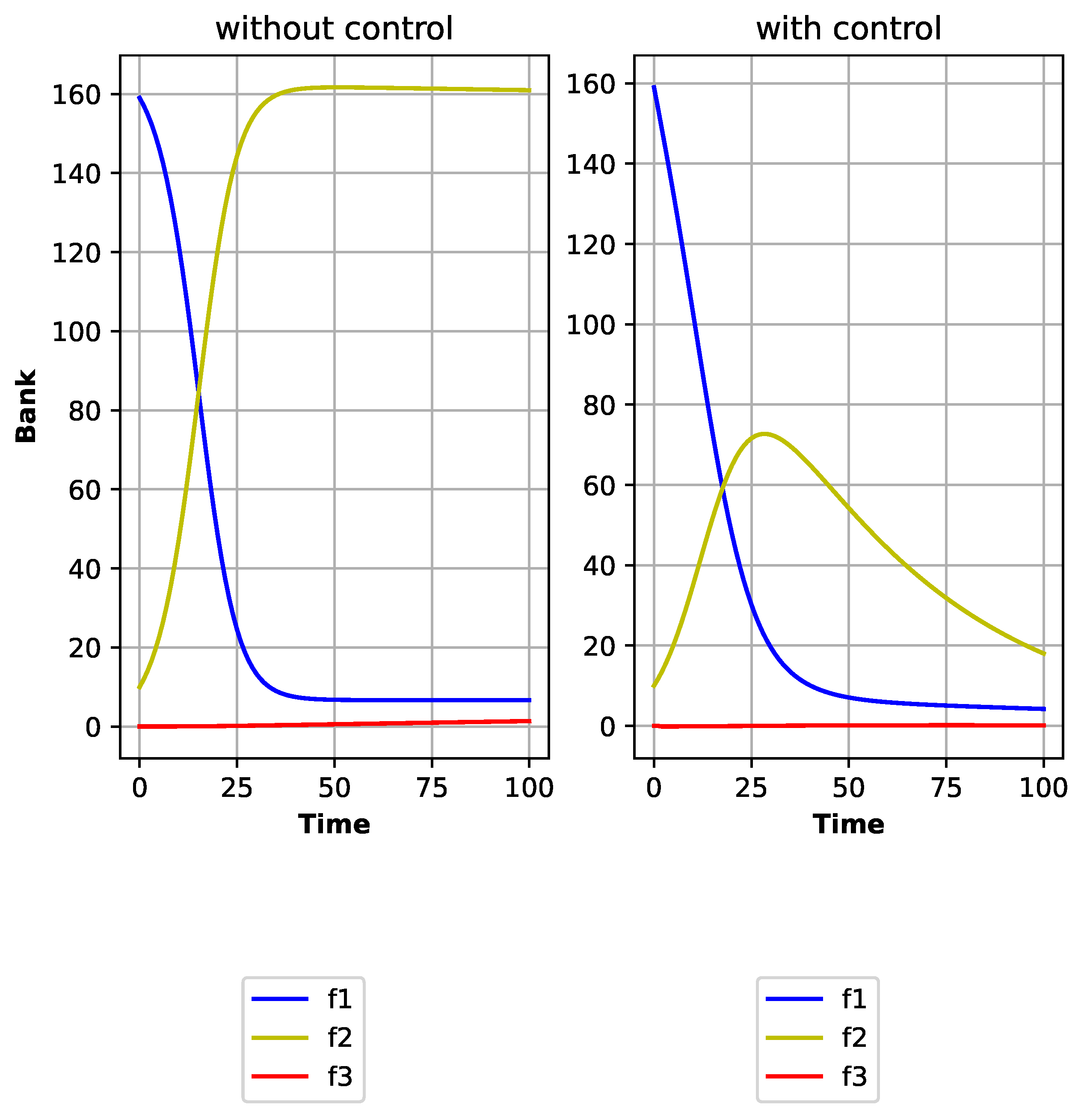
Finally, in the third scenario with a very low default probability (${\alpha }_3=0.0001$), as shown in Figure 7 (Spain), Figure 8 (France), and Figure 9 (Germany), the uncontrolled dynamics lead to a persistent and widespread financial contagion. Because default is almost absent, banks continue to operate despite being illiquid, which in turn amplifies the contagion and eventually destabilizes the entire system. The introduction of control in this scenario prevents this extensive spread and ensures that banks recover before the system collapses.

The impact of time delay $\tau$ on the dynamics of the banking system is illustrated in Figure 10. As the value of $\tau$ increases, we observe significant changes in the evolution of the system compartments $f_1$, $f_2$, and $f_3$. Specifically, larger delays result in slower reactions to contagion events, leading to more pronounced oscillations and delayed peaks in the trajectories. This indicates that the introduction of a delay in the system weakens the immediate response capacity of banks to liquidity shocks, potentially amplifying systemic instability. The results emphasize the importance of accounting for time delays in modeling the spread of financial risks in banking networks.

The choice of Spain, France, and Germany is motivated by their contrasting positions within the Eurozone: Spain experienced significant liquidity stress post-2010, France maintained a moderate-risk banking profile, while Germany exhibited strong resilience and systemic influence.

5. Conclusions

This paper focuses on modeling the spread of liquidity risk contagion within the banking system by drawing analogies with the dynamics and control of infectious diseases. The introduction of the optimal control variable u plays a pivotal role in managing liquidity risk. It represents the proportion of banks that can be shielded from contagion within a given time frame. By adjusting the value of u, the system’s dynamics can be influenced, enabling the implementation of strategies to curb the spread of contagion and mitigate the associated financial risks. The optimal control variable u enables the implementation of preventive measures such as liquidity injections or support mechanisms to limit the spread of contagion within the banking system. By maximizing the number of susceptible banks and minimizing the number of infected or bankrupt institutions, u contributes to preserving overall financial stability. To achieve this goal, Pontryagin’s Maximum Principle is applied to determine the optimal control strategy that most effectively fulfills these objectives.

The delay $\tau$ in the system plays an important role by considering the temporal dynamics of banks in the model. It represents the time delay required for the susceptible banks that have been saved from risk at time $t-\tau$ to be transferred from the bankrupt category to the susceptible category at time t. Thus, in the equations of the system, the influence of the delay $\tau$ is observed in the terms$f_1(t-\tau )$ and $u(t-\tau )$. These terms represent, respectively, the susceptible banks that are transferred from the bankrupt category to the susceptible category and the optimal control applied at time $t-\tau$ to protect banks from the contagion risk.

The inclusion of a delay parameter $\tau$ allows the model to capture the time lag and propagation effects between different categories of banks. This is essential for understanding the system’s dynamic behavior and assessing the effectiveness of control measures. The delay also facilitates the analysis of how past decisions influence the system’s evolution over time. To solve the optimization problem, we employed a discretization approach based on forward and backward difference approximations. Simulations conducted in Python revealed a strong alignment between the model’s outcomes and the observed behavior of major European banks across three examined scenarios. These results provide compelling evidence of the model’s capability to accurately reflect real-world financial dynamics.

Our results confirm that the spread of liquidity contagion is sensitive to the default parameter ${\alpha }_3$. A lower ${\alpha }_3$, contrary to intuition, may prolong contagion because distressed banks continue to interact with others, delaying systemic resolution.

The optimal control variable $u\left(t\right)$, representing interventions such as liquidity injections or capital support, proves highly effective: it limits contagion at early stages, preserves solvent institutions, and accelerates systemic recovery.

Importantly, we show that the inclusion of delay $\tau$—reflecting real-world lags in regulatory response or market adaptation—plays a destabilizing role when not accounted for. Larger delays increase oscillations and delay the return to equilibrium.

Our findings suggest that real-time monitoring, faster deployment of liquidity tools, and network-aware regulation are crucial to reducing systemic vulnerability.

Policy recommendations derived from our model include

• Strengthening central bank liquidity lines and pre-committed buffers;
• Integrating dynamic contagion models into supervisory stress tests;
• Improving coordination across national regulatory authorities.