Abstract
The Statistics Anxiety Rating Scale (STARS) is a 51-item scale commonly used to measure college students’ anxiety regarding statistics. To date, however, limited empirical research exists that examines statistics anxiety among ethnically diverse or first-generation graduate students. We examined the factor structure and reliability of STARS scores in a diverse sample of students enrolled in graduate courses at a Minority-Serving Institution (n = 194). To provide guidance on assessing dimensionality in small college samples, we compared the performance of best-practice factor analysis techniques: confirmatory factor analysis (CFA), exploratory structural equation modeling (ESEM), and Bayesian structural equation modeling (BSEM). We found modest support for the original six-factor structure using CFA, but ESEM and BSEM analyses suggested that a four-factor model best captures the dimensions of the STARS instrument within the context of graduate-level statistics courses. To enhance scale efficiency and reduce respondent fatigue, we also tested and found support for a reduced 25-item version of the four-factor STARS scale. The four-factor STARS scale produced constructs representing task and process anxiety, social support avoidance, perceived lack of utility, and mathematical self-efficacy. These findings extend the validity and reliability evidence of the STARS inventory to include diverse graduate student populations. Accordingly, our findings contribute to the advancement of data science education and provide recommendations for measuring statistics anxiety at the graduate level and for assessing construct validity of psychometric instruments in small or hard-to-survey populations.
1. Introduction
Statistics anxiety is a form of performance-related anxiety that arises from engaging with statistics concepts, computations, or courses. Unlike general academic anxiety, statistics anxiety is a domain-specific phenomenon characterized by apprehension, avoidance, and a lack of confidence when required to engage with statistics material [1]. As data literacy becomes increasingly important across educational and professional contexts, understanding and addressing statistics anxiety is vital for improving student outcomes and promoting equity. The need for educators to understand and reduce statistics anxiety is particularly critical in fields where mathematical fluency is not emphasized or encouraged as strongly as in STEM fields, such as education and the social sciences. Statistics anxiety has been shown to negatively impact students’ academic engagement and success in STEM research-oriented and data-driven disciplines, but research on statistics anxiety in non-STEM fields remains sparse [2,3]. This gap in the literature has several implications for non-STEM statistics educators, particularly at the graduate level. For graduate students pursuing careers in education or non-quantitative social sciences (e.g., criminal justice), data science and statistics are often viewed as obstacles rather than foundational skills [4]. This lack of perceived statistical utility may be even stronger among graduate students from diverse or first-generation backgrounds [5].
Given the documented impact of statistics anxiety on academic performance and persistence, particularly in STEM and data-driven fields, understanding the dimensional structure of statistics anxiety across diverse populations is crucial for advancing data science education. The Statistics Anxiety Rating Scale (STARS) has been commonly used as an instrument to assess statistics anxiety among college students [6]. The instrument consists of 51 items designed to estimate common causes and levels of statistics anxiety. Using principal components analysis, Cruise et al. (1985) [6] identified six components of statistics anxiety: (1) worth of statistics, (2) interpretation anxiety, (3) test and class anxiety, (4) computational self-concept, (5) fear of asking for help, and (6) fear of statistics teachers. We hereafter refer to these components as the original six-factor structure for the STARS scale.
Previous research concerning the STARS scale has primarily focused on undergraduate students, but graduate students are also susceptible to statistics anxiety. There is a need for further investigation within this relatively understudied group, as systematic reviews have specifically emphasized the importance of extending statistics anxiety research to include populations beyond undergraduates [2]. However, graduate courses are typically much smaller than undergraduate courses, which already pose challenges for collecting large samples within a feasible time frame (e.g., n > 300 within 1–2 semesters). Identifying factor analytic techniques that perform well even within small samples is therefore crucial for pedagogical research in graduate-level and other small sample contexts.
Limited research exists on the validity of STARS in racially and ethnically diverse student populations, particularly those enrolled at Minority-Serving Institutions (MSIs). Students at MSIs often face unique academic, cultural, and structural barriers that may influence their attitudes toward statistics. As such, it is critical to examine whether the STARS instrument maintains its construct validity and reliability in these contexts. To address these gaps, the present study seeks to evaluate the factor structure and internal consistency of STARS scores in a small and diverse sample of students (n = 194: 74.80% non-white and 56.07% first-generation students) enrolled in graduate statistics courses at a Minority-Serving Institution using confirmatory factor analysis, exploratory structural equation modeling, and Bayesian structural equation modeling techniques. Our study also compares the performance of these factor analysis techniques to assess the strengths and weaknesses of each of these approaches in this particular context.
2. An Overview of Factor Analysis Methods
Since its inception in the early 1900s, factor analysis has been widely employed in applied research across a wide range of disciplines [7,8]. The main objective of factor analysis is to identify the number and type of latent factors that account for variation and covariation among observed scores. A factor indicates an unobservable variable that influences more than one observed measure and considers correlations among those measures. Exploratory factor analysis (EFA) and confirmatory factor analysis (CFA) are the two primary types of factor analysis included in the common factor model [9,10].
3. Exploratory Factor Analysis (EFA)
EFA is used as an exploratory or descriptive tool to locate a suitable number of common factors and identify which observed measures serve as the best indicators of the latent factors by analyzing the size and degree of factor loadings [11,12]. Unlike confirmatory approaches, EFA does not require specifying an a priori factor structure. Instead, EFA is used to find plausible factor structures, typically as a first step before using confirmatory approaches such as CFA. Common techniques for determining the number of factors include eigenvalues greater than one, scree plots of eigenvalues, and parallel or MAP analyses, which compare observed eigenvalues with those from randomly generated data to identify meaningful factors [13,14,15].
4. Confirmatory Factor Analysis and Exploratory Structural Equation Modeling
Confirmatory factor analysis (CFA) is a structural equation modeling (SEM) technique that assesses hypothesized associations between latent factors and observed indicators (e.g., items) [11]. CFA is a widely used statistical technique when researchers have a predefined factor structure informed by theory or prior EFA results [16]. CFA can be used to analyze the complex structures that underpin multidimensional assessments, including correlated-factor, hierarchical, and bifactor models.
A key drawback of CFA, however, is that by setting cross-loadings to zero, it assumes that items load on only their assigned factors. This independence assumption rarely holds true for real data, particularly when that data concerns psychological constructs such as anxiety [17,18]. Consequently, and in spite of its strengths as a theory-driven analysis, CFA’s strict assumptions about perfect zero cross-loadings and residual covariances can produce unsatisfactory model fits and notable parameter biases when estimating factor loadings and correlations [11,12,18,19].
To address the limitations of traditional factor analytic techniques, Asparouhov and Muthén (2009) [20] introduced exploratory structural equation modeling (ESEM), which integrates the methodological advantages of exploratory factor analysis (EFA), SEM, and CFA. ESEM allows items to cross-load on multiple factors based on observed data while allowing for model testing and evaluation of fit indices [20].
Unlike traditional CFA, ESEM is driven by both current data and prior theory [21]. In ESEM, all items load onto all factors, but the items are designed to load more strongly onto the targeted factors than onto the non-targeted factors. This flexibility allows ESEM to capture cross-loadings, such that an item may be associated with multiple factors while still prioritizing the item’s association with its primary, intended factor. Previous studies have shown that ESEM performs better than CFA/SEM in terms of model fits and parameter estimate precision [22,23,24]. Moreover, ESEM supports advanced analyses such as growth modeling, invariance testing, and higher-order factor structures [19,22,25,26].
5. Bayesian Structural Equation Modeling
Bayesian structural equation modeling (BSEM) has been offered as an alternate approach to standard confirmatory factor analysis (CFA) and SEM for enhancing model fit and providing more flexible and accurate representations of the underlying constructs [27]. BSEM is grounded in the Bayes theorem and handles a vector of model parameters, denoted as A, as random variables informed by a prior distribution based on the researcher’s prior knowledge, beliefs, or theories. The elements in A may include item intercepts, factor loadings, residual variances, and factor covariances. The distributions, expressed as P(A), are known as priors. Bayesian inference merges the prior distribution P(A) and the likelihood of observed data P (L|A) (i.e., the SEM model of interest) to yield the posterior distribution, P (A|L) [28]. With regard to A, this distribution represents our current understanding based on the observed facts. According to Bayes’ theorem, the posterior distribution is defined as follows:
Unlike the Weighted Least Square of Mean and Variance Adjusted (WLSMV) or maximum likelihood (ML) estimation procedures, BSEM uses prior data to reflect a researcher’s preconceived notions or prior knowledge. BSEM does not rely on large-sample theory and normality assumptions [27,29], making it suitable for small samples when ML estimates do not converge or produce negative variance [30,31,32].
The benefit of employing Bayesian estimates rather than frequentist techniques to handle small sample size issues for structural equation models (SEMs) has been demonstrated by several simulation studies [27,33,34,35]. However, using Bayesian estimation with only diffuse default priors can result in highly skewed outcomes when working with small sample sizes [36,37]. As a result, it is critical to define informative priors when applying Bayesian estimation with small samples [38], as Bayesian estimation with (weakly) informative priors is suggested to overcome small sample size issues [39].
5.1. A Brief Overview of Bayesian Priors
A researcher’s pre-existing beliefs, knowledge, and assumptions on parameter values are referred to as the prior distribution before gathering fresh data for a study. For every factor model parameter, a prior is defined. They fall into one of two groups: non-informative (high prior variance; often referred to as diffuse or vague) or informative (little prior variance).
5.1.1. Non-Informative Prior (BSEM-NIP)
We employ non-informative priors to draw posterior conclusions when we lack sufficient prior knowledge or information, or when our findings or hypotheses do not coincide. To represent our common awareness of a critical issue, however, it is imperative to translate this information gap into numerical form. One often-used type of non-informative prior distribution is the uniform (flat) distribution. The data can be used to estimate the likelihood of the posteriors because this prior is flatter and offers less information than other priors [40,41].
According to the non-informative prior distribution, before any data are gathered, no parameter value is more probable than any other. A big variance prior distribution, like a normal distribution with a variance of σ2 = 1010 and a mean of μ = 0, accomplishes similar goals. Because of this fluctuation, the parameter values’ prior probability distribution is almost flat, which is Mplus’s default option [42,43].
5.1.2. Informative Priors
Informative priors are employed when there is sufficient prior knowledge on the nature of scales and distribution shapes [44,45]. BSEM enables the reduction of noise parameters, such as trivial cross-loadings, by shrinking them toward zero in a sparse factor loading matrix. Most cross-loadings are constrained to zero, while only theoretically important ones are allowed to remain non-zero [46,47,48]. This is achieved using informative priors that promote shrinkage, helping to produce a more parsimonious model while preserving meaningful loadings.
BSEM using Cross-loadings Informative Priors (BSEM-CL). By changing the prior mean and variance, BSEM-CL allows researchers to define a prior distribution for cross-loadings and make more robust assumptions about the strength of the cross-loadings. Zero cross-loadings are indicated for the factor indicators in a loading matrix that are not predicted to be influenced by specific factors. Cross-loadings can be estimated by assigning shrinkage priors—typically centered at zero with small variances—to reflect the belief that most cross-loadings are near zero [48]. Major loadings are estimated in a confirmatory manner using non-informative or weakly informative priors, depending on prior knowledge. For example, a prior of N(0, 0.01) suggests a 95% belief that the true cross-loading lies between −0.196 and 0.196 [31].
BSEM using Residual Covariances Informative Priors (BSEM-RC). Residual covariance (RC) models account for shared variance between items not explained by latent factors, such as method effects (e.g., negatively worded items). Omitting these effects can lead to inflated factor correlations, improper solutions, and biased estimates [49,50]. However, in traditional likelihood-based frameworks, it is difficult to specify which residuals should covary without overfitting [51]. Bayesian SEM (BSEM) addresses this using informative inverse-Wishart priors on the residual covariance matrix.
By setting the prior mean of residual covariances to zero and adjusting the degrees of freedom (df), researchers can control prior informativeness. For instance, using the inverse-Wishart prior IW (I, df) with df = p + 6 yields a previous standard deviation of 0.1, which means that two standard deviations below and above the zero mean represent the residual covariance range of −0.2 to 0.2. This suggests that the prior is more informative when the value of df is higher and the variance is smaller. The impact of priors is determined by the observed data variances. For bigger sample sizes, a larger df must be used in the previous step to get the same effect [27,52].
BSEM using Cross-Loadings and Residual Covariances Informative Priors (BSEM-CLRC). Inverse-Wishart priors for residual covariances and informative, normal priors for all cross-loadings are included simultaneously in BSEM models (i.e., BSEM-CLRC) [27]. These priors account for the existence of several minor residual covariances among the observed indicators as well as insignificant cross-loadings in the CFA model. Considering that many fixed parameters are converted into free parameters, empirical research has demonstrated that BSEM-CLRC offers a superior model fit compared to BSEM with cross-loading priors [52,53,54].
5.2. Model Fit Statistics
This section explains model goodness-of-fit indices used in conventional SEMs and modified for application in BSEMs. The following equations display root mean square error of approximation (RMSEA) [55,56], comparative fit index (CFI) [57], and Tucker–Lewis index (TLI) [58], and Bayesian versions of RMSEA, CFI, and TLI.
First, RMSEA is an absolute fit metric that calculates the average difference between the model-suggested covariance matrix and that of the observed data per degrees of freedom and assesses how well a model estimates the observed data. RMSEA is computed as a function of the hypothesized model’s statistic (), degrees of freedom (), and sample size (N):
where in the noncentrality parameter, which measures the extent of model misspecification, is equal to . When H0 is true, the anticipated value of chi-square is equivalent to its degrees of freedom (df). As indicated in Equation (2), the noncentrality parameter is divided by the multiplication of and N. RMSEA takes model complexity (i.e., the quantity of model parameters) and sample size into consideration. Higher RMSEA values indicate a worse fit, with zero serving as the lowest value. Generally, a good fit is indicated by an RMSEA less than 0.05, and a poor fit is indicated by an RMSE greater than 0.10 [55,59,60].
BRMSEA is expressed as:
In Equation (3), q* − qD is used to measure model complexity, where q* is the number of observed sample moments and qD is the estimated number of parameters in the hypothesized model. Riobs − q* is used to measure model misspecification, where Riobs is the discrepancy function for the observed data [61].
CFI is used as an incremental fit index to compare the hypothesized model to a more constrained baseline model (also known as a null, or independence model) to gauge how well the model fits [57]. It is assumed that the baseline model is nested under a saturated model, which is the theoretically best-fitting model with no limitations on the covariance structure. On a continuum between the baseline and saturated models, the hypothesized model then falls somewhere in the middle. CFI is standardized on a scale of 0 to 1, with values approaching 0 indicating that the hypothesized model is more closely related to the baseline model and thus gives an inadequate fit. At the other end of the scale, CFI values close to 1 suggest that the hypothesized model fits the data almost as well as the saturated model.
where is the value of the hypothesized model; is the df of the hypothesized model; is the value of the baseline model; and is the df of the baseline model. The Bayesian counterpart to CFI, called BCFI, is computed as:
where indicates the observed data’s discrepancy function in the baseline model. In Equation (5), and are substituted with and , respectively, and is replaced with the frequentist df.
Additionally, TLI is an incremental fit index that measures the discrepancy between the fit of a hypothesized model and that of the baseline model [58,62]; yet, in contrast to CFI, values of TLI can surpass the range of 0 to 1, and TLI is not grounded on the noncentral distribution. The Tucker–Lewis index (TLI) is traditionally defined as:
wherein the superscripts “T” and “N” indicate to which model the chi-square and df belong.
The penalty for model complexity is determined by the ratio . A lower ratio denotes a better-fitting model. Similar to CFI, higher TLI values signify a better fit (Hu & Bentler, 1999 [59]). In the Bayesian context, this model fit index is defined as:
In contrast to their frequentist counterparts, Bayesian adaptations of fit indices enable the quantification of their uncertainty through the acquisition of point estimates and credibility intervals [61].
6. Psychometric Properties of the Statistics Anxiety Rating Scale (STARS)
The Statistics Anxiety Rating Scale (STARS), developed by Cruise and colleagues in 1985 [6], is a widely used and psychometrically sound self-report instrument designed to measure statistics anxiety in students. It consists of six subscales and 51 items assessing test and class anxiety, interpretation anxiety, fear of asking for help, fear of statistics teachers, worth of statistics, and computational self-concept.
6.1. Evidence for Reliability of STARS
The STARS has consistently demonstrated high internal consistency across studies. Cruise et al. (1985) [6] reported high internal consistency values (α = 0.68–0.94) across subscales and high test–retest reliability (r = 0.67 to 0.83). Follow-up research aligns with these preliminary findings, with internal consistency estimates ranging from 0.59 to 0.96 across a wide range of sampling contexts [63,64,65,66,67,68].
6.2. Evidence for Validity of STARS
The original six-factor model proposed by Cruise et al. (1985) [6] has been validated by several studies via exploratory and confirmatory factor analysis [3,64,68,69]. Subsequent studies have investigated the psychometric qualities of the STARS in cross-cultural contexts, finding empirical support for the six-factor structure in South Africa [70], the UK [63], China [66], Austria [68], the USA [71], Singapore and Australia [72], and Greece [65]. Short-form versions of STARS have also been proposed to facilitate more efficient screening while preserving psychometric quality [63].
With regard to concurrent validity, STARS correlates strongly with related constructs such as math anxiety (r = 0.76; [6]). Baloğlu (2002) [73] also observed strong correlations between statistics anxiety and mathematics anxiety (r = 0.67), state anxiety (r = 0.42), and trait anxiety (r = 0.39). A recent systematic review by Faraci and Malluzzo (2024) [2] further evaluated STARS alongside seven other statistics anxiety measures. Their analysis reaffirmed STARS’ psychometric robustness, especially with regard to its content validity, internal consistency, and factor structure.
Not all authors have expressed support for the original six-factor STARS model, however. Baloğlu (2002) [73], for example, noted marginal support for the six-factor model, though the authors did not propose or test an alternative factor structure. Some researchers contend that, despite consistent support for the six-factor model, the STARS evaluates not just statistics anxiety, but also attitudes toward statistics [63,68,71,72]. In their 2024 systematic review, Faraci and Malluzzo [2] highlighted several weaknesses in the STARS instrument, notably low cross-cultural replicability and a poor ability to distinguish between statistics anxiety and related variables such as the perceived value of statistics or avoidance of social support [2]. Moreover, graduate students, professionals, and non-traditional students remain underrepresented in psychometric validation studies of the STARS. Some STARS items reflect outdated instructional contexts (e.g., paper-based tests and handouts), raising a need for modernization; item overlap and redundancy have also been noted in exploratory factor analyses, suggesting a possible need for item reduction or refinement.
Despite these limitations, the STARS (Statistics Anxiety Rating Scale) instrument is particularly valuable for understanding graduate students’ anxiety about learning statistics because it provides a comprehensive and nuanced assessment of the various dimensions of statistics anxiety. Graduate students often face unique challenges, such as high academic expectations, pressure to perform, and the need to apply statistical knowledge in research. The STARS allows for the identification of specific anxiety factors related to these pressures, such as test anxiety, fear of failure, and apprehension toward the complexity of statistical concepts [70,71]. By measuring these diverse sources of anxiety, the STARS helps educators and researchers pinpoint areas where students may require additional support, thus facilitating targeted interventions to improve student confidence and performance [72]. Furthermore, its cross-cultural applicability, as demonstrated in studies across various countries, highlights the STARS instrument’s versatility and effectiveness in capturing the experiences of graduate students from different educational and cultural backgrounds [63,66,68].
7. Current Aims: Applying CFA, ESEM, and BSEM Techniques to STARS
This study examined the factor structure and construct validity of the Statistics Anxiety Rating Scale (STARS; [6]) scores among racially and ethnically diverse undergraduate and graduate students (N = 194; 74.80% non-white and 56.70% first-generation students) enrolled in graduate statistics courses attending a Minority-Serving Institution (MSI). Our primary goal was to investigate the factor structure and internal consistency of Statistics Anxiety Rating Scale (STARS) scores to determine whether the original six-factor structure (or an alternative structure) provided the best fit to our diverse sample of graduate students. Validity is not a fixed property of an instrument but rather a function of the inferences made from scores within a particular sample and context [74]. As such, the factor structure of a measure may shift across populations or settings due to cultural, linguistic, or experiential differences that influence how individuals interpret and respond to items [75]. Given that our sample differs from the original validation sample in several ways—notably, our sample is ethnically diverse and consists of students enrolled in graduate, rather than undergraduate, statistics courses—we observed a need for investigating alternative factor structures via ESEM. A secondary aim in our study was to compare the performance of CFA, ESEM, and BSEM within a small sample context. Small sample sizes often pose significant challenges in structural equation modeling (SEM) due to the increased risk of unstable parameter estimates, non-convergence, and model overfitting.
Each of these methods—CFA, ESEM, and BSEM—has distinct strengths and weaknesses. By comparing their performance, we can assess which method is more robust and reliable when working with limited data, ensuring that conclusions drawn from small sample sizes are valid. The following research questions guided our investigation.
RQ1. What is the best and most parsimonious factor structure and internal consistency for Statistics Anxiety Rating Scale (STARS) scores when administered to ethnically diverse students enrolled in graduate statistics courses at a Minority-Serving Institution?
RQ2. How do CFA, ESEM, and BSEM compare in their ability to identify the underlying structure of STARS scores within a small sample context?
8. Method
8.1. Sample
Institutional Review Board (IRB) approval was obtained for all procedures. Participants voluntarily completed the survey via Qualtrics in exchange for course credit. We recruited 215 students from a Minority-Serving Institution who were enrolled in graduate statistics courses offered by education and social science colleges within the institution. We used casewise deletion for 21 cases, as these respondents did not complete any of the STARS items because they exited the survey prior to starting the STARS battery, resulting in a final n of 194. All participants who reached the STARS battery completed all 50 items, negating the need for imputation or other more advanced missing data techniques.
Reflecting the demographic makeup of the sampled institution, participants were racially and ethnically diverse (57.22% Hispanic, 26.80% White, 12.89% Asian or Southeast Asian, 4.64% Black, 2.58% American Indian, and 4.64% Other). A total of 110 participants (56.70%) were first-generation college students, and 27 (13.92%) were first-generation immigrants. A total of 152 (78.35%) participants identified as women, 41 (21.13%) participants identified as men, and one participant identified as nonbinary. Participants ranged in age from 18 to 52 years (M = 27.84, SD = 8.44). Although a portion of participants were undergraduates or post-baccalaureate students taking a graduate course, the majority of participants were enrolled in a master’s (n = 81, 41.24%) or doctoral program (n = 27, 13.92%). Our participants were primarily education (69.59%) and social science majors (28.86%). We provide an overview of participants’ demographic information in Figure 1 below. Note that summing the percentages for each demographic category can exceed 100%, as participants could select more than one option (e.g., identifying as both White and Hispanic or being dual-enrolled in two majors).
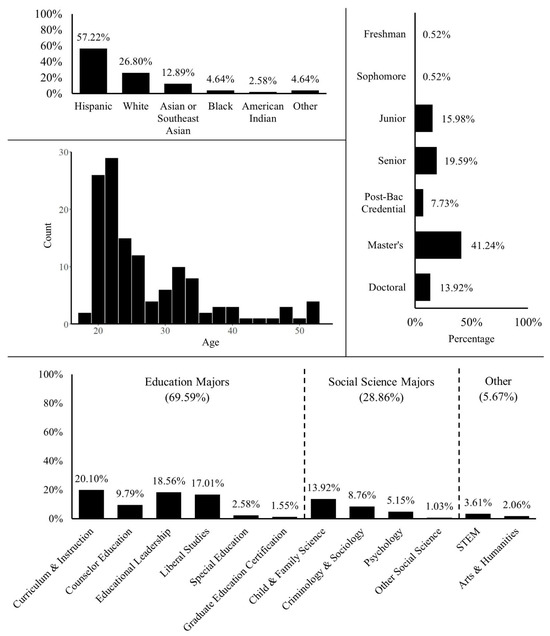
Figure 1.
Overview of participants’ demographic information.
8.2. Measures
- Statistics Anxiety Rating Scale (STARS)
STARS is a 51-item inventory that measures statistics anxiety [6]. The six original dimensions of statistics anxiety consist of (1) worth of statistics, which relates to how students view the value of statistics in their academic, personal, and (potential) career life (16 items, e.g., “objectivity of statistics is inappropriate for me,” “statistics is worthless to me”); (2) interpretation anxiety, which refers to concerns of determining the usefulness of acquired statistics data (11 items, e.g., “Interpreting the meaning of a table in a journal article”); (3) test and class anxiety, which relates to the anxiousness that arises with taking a test or going to a statistics class (8 items, e.g., “Enrolling in a statistics course”); (4) computational self-concept, which pertains to a person’s assessment of their own mathematical proficiency (7 items, e.g., “Statistics is not really bad. It is just too mathematical”); (5) fear of asking for help, which assesses the anxiousness felt when requesting help (4 items, e.g., “Asking one of your lecturers for help in understanding a printout”); (6) fear of statistics teachers, which relates to how students view their statistics instructors (5 items, e.g., “Most statistics teachers are not human”). One item (Q10: walking into the room to take a statistics test) was eliminated because—as is typical for graduate courses—the surveyed instructors offered take-home assessments rather than in-class exams.
The STARS instrument is composed of two sections. The first section includes 23 items organized into the following factors: interpretation anxiety, test and class anxiety, and fear of asking for help. Items in the first part are answered using a 5-point Likert scale (from 1 “no anxiety” to 5 “very much anxiety”). The second section—worth of statistics, computational self-concept, and fear of statistics teachers—consists of 28 items and is answered on a 5-point Likert scale (from 1 “strongly disagree” to 5 “strongly agree”) in relation to students’ perceptions about statistics. The total scale score ranges from 50 to 250.
8.3. Data Analyses
Data analyses for descriptive statistics and CFA models were conducted using the lavaan package [76] in R [77]. We constructed our ESEM and BSEM models via Mplus 8.10 [78]. Given the ordinal Likert structure of STARS items, we assumed a polychoric correlation structure and therefore extracted factors using mean-and-variance-adjusted (WLSMV) estimation [79,80]; extracted factors were rotated obliquely via the geominT rotation method.
For the non-Bayesian models, we followed best-practice guidelines for evaluating the fit of models with small degrees of freedom within small samples [81,82]. That is, we evaluated fit using the comparative fit index (CFI), Tucker–Lewis index (TLI), root mean square error of approximation (RMSEA), and standardized root mean square residual (SRMR), placing greater emphasis on interpretation of CFI and SRMR values. Values greater than 0.90 and 0.95 for CFI and TLI have typically been interpreted as acceptable and excellent fit, respectively [55,56,59,83,84]. For RMSEA and SRMR, values of 0.08 or lower are indicators of adequate fit; values less than or equal to either 0.05 [55,56] or 0.06 [59] are indicators of excellent or close fit. For Bayesian analyses, we investigated recently developed counterparts to the CFI, TLI, and RMSEA, namely the BRMSEA, BCFI, and BTLI [61].
The BSEM models were estimated using the default priors for the target loadings and informative priors for the off-target loadings, respectively. All the models were evaluated under both default priors (non-informative cross-loading priors) and informative priors for cross-loading (CL) and cross-loading and residual covariance (CLRC) informative priors.
We used normal priors with mean zero and variance 0.03, 0.06, and 0.09 for BSEM with informative cross-loading priors (BSEM-CL). The smaller variance indicates a more informative prior. For example, a prior like N (0, 0.03) is more informative than a prior like N (0, 0.06) and N (0, 0.09). We chose these priors in an exploratory approach to test that even minor modifications to the priors from strong to weak may have substantial consequences for the posterior, depending on the model’s complexity. We also included the inverse-Wishart priors for residual covariances and informative, normal priors for all cross-loadings simultaneously in the BSEM models (i.e., BSEM-CLRC; [27]. A total of two chains were specified, with each running 50,000 Markov chain iterations, with the first 10,000 iterations of each chain discarded as burn-in.
9. Results
9.1. Descriptive Statistics
Table 1 provides descriptive statistics (average factor loadings, item means, and item standard deviations) and conventional internal consistency estimates (Cronbach’s alpha and McDonald’s omega) for the original six-factor CFA model, ESEM three-factor and four-factor models, and reduced four-factor CFA model. Both Cronbach’s alpha and McDonald’s omega are commonly used to assess internal consistency reliability, which evaluates the extent to which a group of items consistently measure a single underlying construct. Cronbach’s alpha [85] estimates this reliability based on the average correlations between items. However, it can be artificially increased by a larger number of items and may provide misleading results when item variances are uneven. By contrast, McDonald’s omega [86] is considered to be a more accurate indicator of the proportion of variance in total scores attributable to the general factor. Omega offers greater flexibility and precision, particularly when items vary in how strongly they represent the latent construct and are less influenced by item count or uniformity. Both values are deemed acceptable when higher than 0.70 and excellent when higher than 0.90 [86,87,88].

Table 1.
Descriptive statistics and reliability estimates for original CFA and selected ESEM models.
Factor loadings are numerical values that show the strength and direction of the relationship between an observed variable and a latent factor (an unobserved, underlying construct) in factor analysis. Factor loadings help you determine which items belong to which factor. Factor loadings are regarded as strong indicators of the factor when they exceed 0.70. They are regarded as mild to acceptable if they fall between 0.40 and 0.69. They are considered to be weakly connected to a factor if their value is less than 0.30 [11,89].
When combining across all items, participants reported an item-level mean anxiety score of 2.48 (SD = 0.66), reflecting that participants in our sample reported moderate statistics anxiety. Internal consistency across all items was excellent (α = 0.96, ω = 0.98), indicating highly reliable measurement across all items. Average factor loadings ranged from 0.55 to 0.91, indicating moderate to strong associations between the observed variables and their respective latent constructs. Consistent with ESEM allowing for cross-loading across factors, the average group factor loading was lower for ESEM models (M = 0.63) than for CFA models (M = 0.81). Detailed information for each factor model is provided in Table 1.
9.2. Model Fit Statistics, Descriptive Statistics, and Reliability Estimates
In this section, we explore competing CFA and ESEM models and determine the optimal representations of factors in the statistics anxiety rating scale for our sample scores by assessing model fit indices and factor loadings. Descriptive statistics and reliability estimates for selected models are provided in Table 1 below. An overview of fit indices for each CFA and ESEM model is provided in Table 2.

Table 2.
Summary of Fit Statistics for Original, Reduced, and ESEM Models.
9.3. Overview of CFA Models
9.3.1. One-Factor Model
We first tested a one-factor model to assess whether a unidimensional structure would be appropriate for our data. Both the CFA and ESEM one-factor model demonstrated poor fit (CFI = 0.706, TLI = 0.693, RMSEA = 0.128, SRMR = 0.167), indicating that a unidimensional structure was insufficient to explain variation in scores within our sample.
9.3.2. Original Six-Factor CFA Model
We then assessed the original six-factor CFA model [6], which yielded substantially improved fit over the one-factor model (CFI = 0.935, TLI = 0.931, RMSEA = 0.061, SRMR = 0.076). These findings suggest that, despite key differences in ethnic diversity and education level within our sample, the original structure proposed by Cruise et al. (1985) [6] is still acceptable as a theoretical framework for interpreting graduate students’ STARS scores. An overview of the original six-factor CFA model is provided in Figure 2.
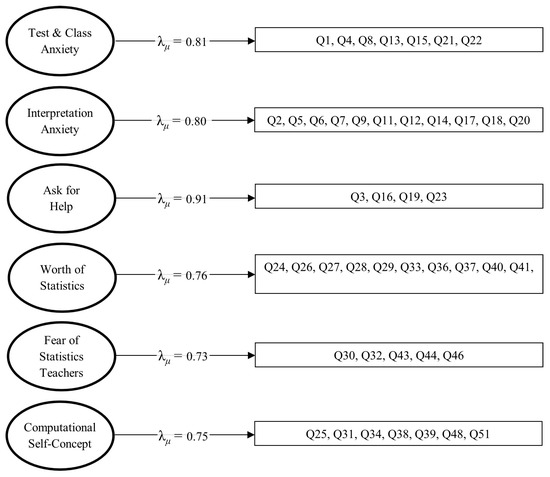
Figure 2.
Conceptual overview of original six-factor CFA STARS structure.
As shown in Table 1, the test and class anxiety domain (seven items) showed the highest item-level mean (μ = 3.03, σ = 0.96) and high reliability (α = 0.91, ω = 0.91), indicating that participants were particularly anxious about being evaluated on their ability to complete statistics problems. The interpretation anxiety domain (11 items) had a moderate item-level mean (μ = 2.56, σ = 0.91) and strong reliability (α = 0.94, ω = 0.94), reflecting consistent concern about interpreting statistics output. The fear of asking for help domain (4 items) had a slightly lower item-level mean (μ = 2.34, σ = 1.11), with high reliability (α = 0.91, ω = 0.91), suggesting variability in students’ comfort seeking help. The worth of statistics subscale (16 items), which assesses the perceived value or importance of statistics, had a lower item-level mean (μ = 2.26, σ = 0.73) but strong reliability (α = 0.93, ω = 0.94). This implies that participants may question the relevance of statistics in their academic or professional goals. The fear of statistics teacher domain (5 items) showed the lowest reliability (α = 0.74, ω = 0.74) and a relatively low mean (μ = 2.09, σ = 0.66), suggesting less negative feelings about instructor support or approachability. Finally, the computational self-concept subscale (seven items), which measures students’ confidence in their own statistics abilities, had a moderate mean (μ = 2.66, σ = 0.90) and acceptable reliability (α = 0.86, ω = 0.86). Mean factor loadings ranged from 0.73 to 0.91, indicating high values.
9.4. Overview of ESEM Models
Despite the acceptability of the original six-factor model, it is critical to note that validity is dependent on conclusions drawn from scores within a specific demographic and context, rather than being a fixed feature of an instrument [74]. Because cultural, linguistic, or experiential factors affect how people perceive and react to items, a measure’s component structure may differ between populations or geographical areas [75]. We used ESEM to compare previous validated models against alternative STARS factor structures because our sample differs from the original validation sample in several ways. For example, we surveyed ethnically diverse, relatively older students enrolled in graduate-level statistics courses rather than undergraduate courses, and the surveyed instructors’ pedagogy reflected typical graduate assessment styles rather than undergraduate assessment styles (e.g., assigning take-home projects rather than in-class exams). Moreover, in the presence of competing models with good model fit indices, priority should be given to more parsimonious models that align with theory and produce highly interpretable factors [90]. For these reasons, we next estimated ESEM models to determine whether a more parsimonious or bifactor structure might be a better fit for our sample scores than the original 1985 framework [6].
9.4.1. Two-Factor and Bifactor Models
A two-factor ESEM solution, while considerably improving upon the one-factor CFA solution, did not satisfy all requirements for adequate model fit and was inferior to the CFA six-factor model (CFI = 0.882, TLI = 0.871, RMSEA = 0.083, SRMR = 0.072). Fit improved progressively as additional group factors and a general factor were added to the ESEM models (see Table 2), but investigation of factor loadings revealed several issues that suggested a general factor would be a poor addition to the model. As presented in Table 3, in both the two-bifactor and three-bifactor models, a large proportion of items loaded onto the general factor but failed to load onto any specific group factor (e.g., 25 out of 50 items failed to load onto a group factor in the two-bifactor model). Items within some group factors universally cross-loaded onto other factors in the presence of a general factor (e.g., all Factor 2 items cross-loaded moderately or strongly onto Factor 1 in the three-bifactor model). In order for group factors within a bifactor model to be identified and substantively interpreted, data need to be both multidimensional and well-structured [21]. Given the weak structure and interpretability of group factors in the presence of a general domain, we did not consider bifactor solutions beyond the three-bifactor model.

Table 3.
Mean factor loadings for 2-bifactor and 3-bifactor ESEM models.
9.4.2. Three-Factor ESEM Model
Fit indices for the three-factor model were acceptable (CFI = 0.922, TLI = 0.911, RMSEA = 0.073, SRMR = 0.053), and the average factor loadings were moderate to high, varying from 0.546 to 0.722, as shown in Table 2 and Table 4. The task and process anxiety domain (22 items) showed the highest item-level mean (M = 2.67, SD = 0.87), indicating that participants experienced heightened anxiety related to performing statistics tasks and following statistics procedures. This subscale demonstrated high reliability (α = 0.96, ω = 0.96). The perceived lack of utility domain (17 items) had a lower item-level mean (M = 2.16, SD = 0.67) and exhibited strong reliability (α = 0.92, ω = 0.92), suggesting that students generally perceived statistics as having limited usefulness. The mathematical self-efficacy domain (16 items) had a moderate item-level mean (M = 2.60, SD = 0.77) and demonstrated strong internal consistency (α = 0.91, ω = 0.92), indicating that students generally held a moderate level of confidence in their mathematical abilities (see Table 1).

Table 4.
Three-factor STARS questionnaire and ESEM item loadings.
9.4.3. Four-Factor ESEM Model
The model fit for the four-factor model was higher (CFI = 0.946, TLI = 0.936, RMSEA = 0.062, SRMR = 0.043) than that of the three-factor model, with moderate to high average factor loadings ranging from 0.57 to 0.70 (see Table 2 and Table 5). The task and process anxiety domain, consisting of 18 items, had the highest mean item-level score among all subscales (M = 2.70, SD = 0.88) with excellent reliability (α = 0.95, ω = 0.95), indicating that participants felt especially anxious when engaging with statistics tasks and processes. The social support avoidance domain (6 items) had a lower mean (M = 2.22, SD = 0.92) with lower internal consistency (α = 0.85, ω = 0.86), implying that students are generally reluctant to seek assistance. The perceived lack of utility domain (14 items) had the lowest item-level mean (M = 2.08, SD = 0.71) and showed high internal consistency (α = 0.93, ω = 0.93), indicating that students typically viewed statistics as not particularly valuable or relevant. The mathematical self-efficacy domain, consisting of 17 items, yielded a moderate average score (M = 2.55, SD = 0.75) and showed high internal reliability (α = 0.92, ω = 0.92), suggesting that students possessed a moderate degree of confidence in their general mathematical ability prior to enrolling in the course. Overall, the structure of the four-factor model aligns well with existing theoretical frameworks for statistics anxiety, indicating strong conceptual consistency. The four-factor model, unlike the three-factor model, also provides a useful distinction between task anxiety and social support avoidance. Therefore, striking a balance between parsimony, model fit, and theory [90], we selected the four-factor solution as our final model given its strong empirical and theoretical fit.

Table 5.
Four-factor STARS questionnaire and ESEM item loadings.
9.4.4. Five- and Six-Factor ESEM Models
Finally, we highlight that both the five- and six-factor ESEM models yielded excellent model fits (CFI = 0.959, RMSEA = 0.055, and SRMR = 0.036; CFI = 0.965, RMSEA = 0.049, and SRMR = 0.035). The five-factor model has moderate average factor loadings ranging from 0.51 to 0.68. The factor loadings of the six-factor model ranged from 0.53 to 0.78, suggesting moderate to strong loadings across factors (see Table 2 and Table 6). We opted not to select these as our final model, as neither model aligned well with prior theory or the original six-factor structure (Figure 2). Moreover, several items cross-loaded onto more than one factor in these models, suggesting that a more parsimonious structure might better capture variance in participants’ responses.

Table 6.
Mean factor loadings for five- and six-factor ESEM models.
9.4.5. Reduced Four-Factor CFA Model
Given the strong theoretical and empirical fit of the four-factor model, we next tested a reduced version of the STARS instrument using the four-factor model as a starting framework. As shown in Table 7, removing items with weak and moderate loadings produced a 25-item scale that demonstrated acceptable fit on all metrics except RMSEA (CFI = 0.945, TLI = 0.938, RMSEA = 0.091, SRMR = 0.071). The reduced four-factor model eliminated items that cross-loaded onto multiple group factors, resulting in a clearer structure than the full ESEM four-factor model (see Table 7). We next conducted a post hoc CFA to test the validity of a reduced four-factor model, retaining only items that loaded strongly onto their respective domains (λs ≥ 0.65).

Table 7.
Reduced four-factor STARS questionnaire and CFA item loadings.
The task and process anxiety domain, consisting of seven items, had a moderate item-level mean (M = 2.69, SD = 0.94) with strong internal consistency (α = 0.95, ω = 0.95). The social support avoidance domain (4 items) had the highest mean score among all subscales (M = 4.71, SD = 1.11) with strong internal consistency (α = 0.91, ω = 0.91). The perceived lack of utility domain (10 items) had the lowest item-level mean (M = 2.01, SD = 0.73) with strong internal consistency (α = 0.93, ω = 0.93). The mathematical self-efficacy domain, consisting of four items, yielded a moderate average score (M = 2.52, SD = 0.96) and good internal consistency (α = 0.81, ω = 0.82). Participants’ mean item-level scores on these subscales suggest that they expected to experience heightened nervousness when dealing with statistics activities and procedures, tended toward refraining from asking for help, tended to regard statistics as lacking in practical value, and viewed themselves as relatively low in their ability to perform mathematical tasks.
9.5. BSEM Models with Non-Informative Priors vs. Informative Priors
Based on the structures acquired from CFA and ESEM analyses, we assessed three-factor, four-factor, and six-factor models, as well as a refined four-factor model using BSEM approaches. Under the default, non-informative prior settings, the three-factor model demonstrated poor fit (BCFI = 0.749, BTLI = 0.737, BRMSEA = 0.087), indicating substantial model misfit. The four-factor model showed moderate improvement (BCFI = 0.791, BRMSEA = 0.080), while the reduced four-factor model provided better overall fit (BCFI = 0.846, BTLI = 0.828, BRMSEA = 0.099), though the posterior predictive p-value remained 0.00 for all models.
Introducing informative priors for cross-loadings (BSEM-CL) significantly improved model fit. Using more strongly informative priors of N(0, 0.03), less strongly informative priors of N(0, 0.06), or weakly informative priors of N(0, 0.09) did not produce a significant difference in model fit indices. When cross-loadings were specified with a prior of both N(0, 0.06) and N(0, 0.09), the six-factor model showed improved fit (BCFI = 0.878, BRMSEA = 0.067). The reduced four-factor model yielded the best overall fit (BCFI = 0.885, BTLI = 0.841, BRMSEA = 0.096) under these weakly informative priors of N(0, 0.09).
Introducing inverse-Wishart priors to the BSEM models (BSEM-CLRC) produced an enhanced fit for all models. For example, the three-factor model with the weakly informative priors of N(0, 0.09) greatly improved based on BCFIs (0.909 vs. 0.783) and BRMSEAs (0.066 vs. 0.084). Enhancement in model fit was salient for the four-factor model (BCFI = 0.923 vs. 0.833, BRMSEA = 0.044 vs. 0.075) and the reduced four-factor model (BCFI = 0.948 vs. 0.885, BRMSEA = 0.056 vs. 0.096). In keeping with cutoff criteria of CFIs and TLIs ≥ 0.90 and RMSEAs ≤ 0.08, all BSEM-CLRC models yielded adequate fits (see Table 8).

Table 8.
Summary of fit statistics for BSEM models.
9.6. Sensitivity Analysis with Smaller Subsamples
To examine the stability and behavior of the models with reduced power, we randomly selected a subsample of n = 100 and n = 130 participants and re-estimated the CFA, ESEM, and BSEM with CLRC N(0, 0.06) models. As shown in Table 9, fit indices for the CFA and ESEM models remained acceptable even at lower sample sizes (n = 100: Mean CFI = 0.924; Mean RMSEA = 0.069; Mean SRMR = 0.077; n = 130: Mean CFI = 0.931; Mean RMSEA = 0.065; Mean SRMR = 0.069). These fit indices were modestly superior relative to the full sample indices (n = 194: Mean CFI = 0.912; Mean RMSEA = 0.073; Mean SRMR = 0.066), though this finding may be attributed to increased noise at lower statistical power levels.

Table 9.
Summary of subsample fit Statistics for original, reduced, and ESEM models.
By contrast, all BSEM models failed to converge while restricted to a sample size of 100. At n = 130, BSEM models achieved convergence but performed worse relative to the full sample (e.g., four-factor model ∆BCFI = −0.069, ∆BTLI = −0.146, ∆BRMSEA = 0.030). These findings suggest that CFA and ESEM are resilient factor analysis techniques, even at lower sample sizes, whereas researchers interested in conducting BSEM may need to invest in larger samples.
10. Discussion and Implications
The present study explored the factor structure and reliability of the Statistics Anxiety Rating Scale (STARS) [6] scores among racially and ethnically diverse students enrolled in graduate statistics courses at a Minority-Serving Institution (MSI). Our findings suggest that, while the original six-factor STARS structure is still valid as a framework for understanding graduate students’ statistics anxiety, variance in graduate-level statistics anxiety may be better captured by a more parsimonious four-factor solution representing task and process anxiety, social support avoidance, perceived lack of utility, and mathematical self-efficacy. By comparing the performance of CFA, ESEM, and BSEM factor analytic techniques within a small sample context, we provide practitioners and researchers with guidelines for investigating the construct validity of instruments in small or hard-to-survey populations. Below, we summarize some key implications of the present findings and offer suggestions for future research.
10.1. Psychometric Quality of STARS Scores in Diverse Graduate-Level Contexts
A primary goal of the current study was to extend evidence of the psychometric quality of STARS scores to ethnically diverse graduate-level contexts. First, our findings indicate that STARS scores have strong internal consistency when administered to graduate-level students from diverse and non-traditional backgrounds. In previous validation studies focused on STARS [6,65,67,72,91], alpha reliability estimates ranged from 0.67 to 0.96. Whereas scales like fear of statistics teachers in the original CFA six-factor model and social support avoidance in the four-factor ESEM model were associated with lower alpha coefficients (0.85 and 0.86), patterns of reliability estimates for the current sample were, generally, higher on average than those reported in the previous studies.
Second, we replicated support for the original six-factor STARS model and observed strong evidence that more parsimonious factor structures may be more compelling. Previous factor analysis research for the STARS supports the six-factor structure of the STARS with CFIs ranging from 0.83 to 0.97 [63,68,71,72,73,92]. In our sample, the original six-factor CFA STARS model also produced acceptable fit indices (CFI = 0.935, TLI = 0.931, RMSEA = 0.061, SRMR = 0.076). However, follow-up analyses using ESEM and BSEM-CLRC revealed that alternative factor structures offered a stronger fit for the scores within our sample.
10.1.1. CFA and ESEM Models
Although the six-factor ESEM model technically offered the best fit to data within our sample (CFI = 0.965, TLI = 0.955, RMSEA = 0.049, SRMR = 0.035), a review of factor loadings and factor interpretability within the five- and six-factor ESEM models indicated that the more parsimonious four-factor model offered the best combination of fit, practical utility, and factor interpretability for education practitioners (CFI = 0.946, TLI = 0.936, RMSEA = 0.062, SRMR = 0.043). Relative to the three-factor model, the four-factor model’s distinction between task anxiety and social support avoidance makes the four-factor model a more pragmatic choice for practitioners interpreting their students’ statistics anxiety scores. By contrast, the five- and six-factor solutions aligned with neither prior theory nor the original six-factor CFA model, and the additional factors suggested by these more complex models suffered from weak interpretability and a high number of cross-loaded items. Our decision to select the simpler four-factor model over the five- and six-factor models also aligns with best-practice guidelines for factor analysis, in that researchers should generally aim for simple, well-fitting models unless additional complexity is clearly justified [12,93].
The four-factor model also provided a useful framework for developing a shortened version of the STARS scale. The reduced 25-item version of the four-factor STARS scale satisfied model fit metrics via both CFA (CFI = 0.945, TLI = 0.938, RMSEA = 0.091, SRMR = 0.071) and BSEM (BCFI = 0.948, BTLI = 0.945, BRMSEA = 0.056). Notably, this reduced version of the STARS scale showed a superior fit when compared to the original six-factor CFA and BSEM model, despite a reduction in degrees of freedom and limitations imposed by our small sample context. Moreover, removing items with weaker loadings eliminated all cross-loaded items from the full four-factor scale (e.g., Item 1 cross-loading onto both the task and process anxiety factor and the mathematical self-efficacy factor), producing factors with clearer conceptual demarcations. Given that this reduced version can be administered in half the time needed for the original scale, we recommend that follow-up research replicate this shortened four-factor version’s construct validity and assess its predictive validity with respect to learning outcomes. We provide an overview of items and associated factor loadings for this reduced four-factor solution in Table 7.
Finally, we emphasize that, although our ESEM models produced superior fit indices relative to CFA, the original six-factor CFA STARS model still demonstrated acceptable fit by modern standards (CFI = 0.935, TLI = 0.931, RMSEA = 0.061, SRMR = 0.076). In other words, while the four-factor solution offers an ideal fit and utility based upon the present findings, researchers and practitioners who prefer to apply the original framework to the interpretation of scores can safely do so even in populations of non-traditional graduate students. Indeed, given the weak interpretability of the five- and six-factor ESEM solutions and the item cross-loadings in the four-, five-, and six-factor models, we argue that researchers would be best served by choosing either the reduced four-factor ESEM model or the original six-factor CFA model.
10.1.2. BSEM Models
BSEM models yielded worse model fits than CFA and ESEM models under the non-informative and CL priors. While there were few variations in fit between BSEM with N (0, 0.03), N (0, 0.06), and N (0, 0.09) cross-loading informative priors, BSEM with cross-loading informative priors outperformed BSEM with default non-informative priors. However, after adopting inverse-Wishart priors, the model fit enhanced noticeably. Bayesian models with CLRC informative priors exhibited markedly better fits than did those with CL informative and non-informative priors in relation to BCFIs, BTLIs, and BRMSEAs. Overall, the BSEM reduced four-factor model with CLRC informative priors exhibited markedly better fits than the other models with CLRC priors. The general improvement in model fit with informative priors supports the view that small cross-loadings exist and are necessary for an accurate representation of the measurement model. Consistent with our ESEM findings, these results also suggest that the reduced four-factor model, particularly when estimated with informative cross-loading residual covariance (CLRC) priors, best captures the latent structure of STARS scores in our sample (see Table 6).
The results of Bayesian estimates may vary depending on the priors used. Choosing appropriate prior distributions is a difficult process [45,94], and failure to do so might produce varied and sometimes misleading findings [34,95]. Xiao and colleagues [94] proposed that Bayesian estimation be used only when informative priors are correctly specified for cross-loadings. As a result, strategies for optimally selecting acceptable priors remain an essential area for future research. In future investigations, sensitivity analyses with alternative non-informative and informative priors should be conducted.
While ESEM and BSEM revealed several cross-loadings, the practical implications of these findings were not fully explored. Although statistically non-zero, most cross-loadings were below 0.30 and lacked theoretical justification and practical meaningfulness, suggesting limited impact on construct interpretation. Future research should examine whether such cross-loadings reflect conceptual overlap or measurement imprecision, particularly in culturally diverse samples where item meanings may shift.
In contrast to maximum likelihood, Bayesian estimation is less restricted and is not reliant on the assumptions of normal distribution or large-sample theory. Accordingly, Bayesian Structural Equation Modeling (BSEM) is useful for complex models with small sample sizes wherein maximum likelihood estimates often do not converge or produce contradicting results (e.g., [30,31,32,48,96]).
It is also important to highlight that the fit indices for the Bayesian models used in this study (BCFI, BCFI, and BRMSEA; ref. [61] were developed relatively recently and have been applied in only a limited number of studies (e.g., [48,96,97,98]). As a result, their properties require further investigation. Since these indices cannot be applied to all sampling features, Garnier-Villarreal and Jorgensen [61], for example, caution against interpreting them based on traditional cut-off norms suggested by Hu and Bentler [59] (e.g., BRMSEA < 0.06, BCFI < 0.95, and BTLI < 0.95). Future research should examine the broader applicability of the Bayesian fit indices across various sample sizes.
10.2. Implications for Statistics Pedagogy in Graduate Courses
Our descriptive findings, as presented in Table 1, offer important implications for teaching strategies and student support systems in statistics coursework at the graduate level. First, students reported a moderate level of anxiety related to engaging with statistics tasks and procedures. The high reliability coefficients suggest that the items consistently measure a single underlying construct—likely nervousness or discomfort when handling statistics processes. The moderate item-level means across subscales suggest that students, on average, expressed moderate statistics anxiety. However, even moderate anxiety can interfere with students’ performance or engagement, particularly for those who are already unsure about their abilities. Instructors should consider embedding stress-reducing strategies into the curriculum, such as structured practice, hands-on data analysis, and reassurance through formative feedback. Reducing cognitive load and emphasizing progress over perfection may also alleviate anxiety, though additional research is needed to establish whether reducing statistics anxiety can improve performance [99,100,101].
The Social Support Avoidance subscale within the reduced four-factor model had a much higher mean score than other subscales, indicating that participants tended to avoid seeking help or support when facing statistics challenges. This is particularly concerning in graduate-level learning environments, where collaboration and guidance can be key to mastery. Elevated avoidance behaviors could stem from feelings of shame, fear of judgment, or overconfidence, and therefore have strong potential as a target in pedagogical intervention strategies. These findings suggest that statistics instructors could improve learning outcomes by creating a classroom culture that encourages asking questions, help-seeking, or collaborating through peer support groups.
By contrast, the perceived lack of utility subscale had the lowest mean item-level score, suggesting that participants generally did not agree that statistics lack utility. In other words, students within our sample did perceive value or relevance in learning statistics. Despite their anxiety or hesitation, they recognize its practical importance. This positive perception can be an important motivational lever to counteract negative emotional responses and encourage deeper engagement. Instructors might consider emphasizing the real-world utility of statistics to capitalize on positive utility perceptions by making contexts relevant to students’ academic and professional goals.
Students reported a moderate level of confidence in their mathematical abilities. The good reliability indicates stable measurement. This moderate self-efficacy might explain some of the task-related anxiety—students are not entirely confident, but neither do they feel completely incapable. Improving self-efficacy (through small success experiences, positive reinforcement, etc.) could serve to both reduce anxiety and increase statistics performance. Despite relatively moderate task anxiety and self-efficacy, the high avoidance of social support suggests a significant barrier to learning. This reluctance to seek help may amplify the effects of anxiety and reduce opportunities for clarification or collaborative problem-solving. Instructors should implement activities that build confidence and self-efficacy, such as scaffolded tasks and peer teaching.
10.3. Recommendations for Factor Analysis in Small Sample Contexts
We propose the following recommendations regarding the use of CFA and ESEM in small sample contexts. First, ESEM appears to capture variance in statistics anxiety scores better than CFA. Although the original six-factor CFA model showed acceptable fit, ESEM models performed equally well or better. This improvement in model fit via ESEM techniques can be attributed to ESEM allowing for non-zero off-target loadings that can better capture the inherently intercorrelated nature of psychological constructs. In other words, ESEM accounts for the fact that a student’s anxiety related to statistics tasks and processes is highly unlikely to be independent of that same student’s mathematical self-efficacy, social support avoidance, and perceived lack of statistics utility.
Second, model fit indices should not be the sole criterion for choosing the “best” models, particularly when comparing ESEM models. Unlike CFA, ESEM is more data-driven than theory-driven and places fewer restrictions on how items load onto factors. In ESEMs, the loadings of items on specific factors are not pre-specified, and all other parameters are estimated freely [19]. However, ESEMs also have some potential drawbacks that are important to consider. These include: (a) being less parsimonious, particularly in large, complex models; (b) being more prone to convergence issues in small samples with intricate models; and (c) being vulnerable to the confounding of constructs within factors that should theoretically be distinct [19,48,96,102,103].
As a demonstration of these drawbacks, the technically best fitting model in our sample was the ESEM six-factor model (CFI = 0.965, RMSEA = 0.049, and SRMR = 0.035), followed by the ESEM five- and four-factor models. However, as noted above, the five- and six-factor ESEM models produced factors with weak interpretability, unclear connection to prior theoretical frameworks, and a high number of items that cross-loaded onto more than one factor. The four-factor model, by contrast, produced interpretable factors with minimal cross-loadings (and no cross-loadings in the reduced 25-item version), all while exceeding thresholds for strong model fit. In this regard, ESEM’s ability to allow for item cross-loadings can be viewed as both a strength and a weakness, particularly when relying solely on model fit indices. For this reason, we caution that researchers use a threefold approach to ESEM model selection: (1) examine and compare model fit indices, (2) closely examine item cross-loadings and ESEM-generated factors for interpretability and alignment with theory, and (3) consider whether a more parsimonious model can account for variance in item scores while still exhibiting acceptable or strong fit [90].
Third, and closely related to the points above, bifactor models did not necessarily serve as appropriate theoretical frameworks despite offering strong model fit indices. Bifactor models have been widely used because of their superior fits over other factor models. However, Sellbom and Tellegen [104] caution against only choosing a bifactor model for that reason and maintain that before using a bifactor model on assessment data, researchers should evaluate the theoretical significance of the components it generates. Our findings echo these concerns. Generally, including a general factor contributed to successively enhanced model fit as the number of group factors increased, but doing so dramatically reduced the interpretability of both general and group factors. For example, as displayed in Table 3, in both the two-bifactor and three-bifactor models, a large percentage of items loaded onto the general factor but failed to load onto any specific group factor. In the two-bifactor model, 25 out of 50 items did not load onto a specific group factor. Furthermore, within some group factors, items consistently cross-loaded onto other factors when a general factor was included (e.g., all items from Factor 2 cross-loaded moderately or strongly onto Factor 1 in the three-bifactor model). For group factors in a bifactor model to be identifiable and meaningfully interpreted, the data must be both multidimensional and well-structured [21]. The poor interpretability of both the general and specific domains within our bifactor models suggests that this assumption does not hold for scores within our sample.
Following Bonifay et al.’s [105] theoretical evaluation of the bifactor model, Sellbom and Tellegen [104] recommend that researchers using the bifactor model assess the psychological meaning of the constructs represented. They suggest using explained common variance (ECV), percentage uncontaminated correlations (PUC), and various Omega score consistency indices to primarily evaluate score dimensionality and the practicality of using composite and subscale scores [106,107]. Further research is necessary to determine the most appropriate and effective applications of bifactor models. This is not to suggest that a general domain for statistics anxiety is impossible; rather, it appears that specific statistics anxiety domains are more appropriate when explaining statistics anxiety for non-traditional, mostly first-generation students enrolled in graduate courses.
Fourth, the results of our sensitivity analyses indicate that CFA and ESEM models can perform well even at smaller sample sizes (i.e., n = 100 and n = 130). By contrast, BSEM models were unable to achieve convergence at n = 100 and performed worse relative to the full sample at n = 130. These findings suggest that CFA and ESEM remain resilient in small samples, whereas BSEM may require researchers to invest in collecting larger samples. With that said, we note that statistical power for CFA and SEM analyses can be impacted by a number of variables beyond sample size alone. Larger samples are needed, for example, when an instrument has a low number of indicators per construct of interest, a large number of anticipated constructs, or when covariances between factors are low [108]. Moreover, our recommendation that CFA and ESEM are possible at low sample sizes should be considered a “worst-case scenario”, in that we can only recommend doing so when collecting a larger sample is unfeasible. Researchers should—ideally—aim for robust samples that can produce reliable and accurate models. For CFA and ESEM models that rely on binary or ordinal data, n = 200 is considered to be the floor for a well-powered sample [109,110]. In small or hard-to-reach populations, such as graduate cohorts or underrepresented populations, however, even an underpowered analysis of an instrument’s construct validity is valuable. In the current sample, for example, our analyses revealed that statistics anxiety may be structured differently within the context of graduate courses than in undergraduate courses (i.e., a four-factor solution rather than the original six-factor solution). Even when preliminary, an accurate conceptualization of a sample’s unique characteristics is essential for researchers aiming to understand their population and develop interventions targeting that same population.
Finally, in spite of the strong evidence for the STARS instrument’s validity and reliability in this study, researchers should consider replicating the current modeling techniques in subsequent studies using larger sample sizes. In particular, we emphasize the need for conceptual replication studies to verify the utility of the condensed 25-item version of STARS and the generalizability of our ESEM and BSEM solutions to other contexts. Method effects for the STARS instrument, for example, might be evaluated by including an additional factor to account for variance generated by negatively worded items or the use of two separate Likert scales within the same battery of items [18,49].
11. Limitations
While interpreting the findings from this study, a few limitations should be considered. First, due to the limited sample size used in this study, we caution against over-generalizing our findings and recommendations, particularly with regard to sample size requirements. Unfortunately, there is no consensus in the literature on what constitutes a sufficient sample size for SEM, despite the fact that this is a critical decision in SEM. There is evidence that basic SEM models can be meaningfully tested with relatively small sample sizes [111,112,113]. However, a sample size of 100–150 is typically thought to be the minimum sample size required to perform SEM, and well-powered samples are expected to be in the range of 200–500 [109,110,114,115,116].
Second, this study did not conduct other forms of psychometric evaluation, such as criterion validity or test–retest reliability. Instead, we focused our analyses on comparisons of statistical techniques designed to assess construct validity: CFA, ESEM, and BSEM. Although the current analyses support the internal structure and reliability of the scale, further validation is necessary to confirm its predictive validity, concurrent validity, temporal stability, and real-world applicability. For example, we strongly recommend that researchers employ the STARS to investigate the impact of statistics anxiety on graduate students’ performance and long-term learning outcomes (e.g., final grades in a graduate statistics course or successful application of statistics analyses in a thesis project). We also note that future research is needed to examine how the STARS scale correlates with related constructs such as general anxiety and mathematics anxiety, and whether the STARS scale consistently measures statistics anxiety over time and across educational contexts (i.e., measurement invariance analysis, [117]).
12. Conclusions
This study greatly increased the body of evidence by supporting the psychometric quality of STARS scores, determining the best ways to depict the structure of STARS based on the sample of ethnically diverse undergraduate and graduate students at MSI, and presenting the advantages and disadvantages of ESEM and BSEM for further research on STARS and other multidimensional representations of psychological constructs in small sample contexts. Our study suggested that while the original six-factor model is adequate, a four-factor model serves as the best theoretical framework for understanding graduate students’ statistics anxiety. Additionally, our reduced four-factor model provides improved practicality and efficiency for graduate statistics instructors looking to quickly gain insight into their students’ anxiety. Finally, we note that CFA and ESEM approaches can perform well even in small sample contexts. Therefore, we recommend their use by future education researchers who rely on data collection from hard-to-survey populations. Overall, the present study contributes to a more inclusive understanding of statistics anxiety and extends the application of STARS from an undergraduate context to a graduate context. In doing so, we lay a foundation for research investigating the diverse experiences and challenges these students face in graduate statistics courses, with the intent of developing evidence-based and culturally responsive assessments and interventions to reduce statistics anxiety in graduate students from underrepresented and non-traditional backgrounds.
Author Contributions
Conceptualization, H.H. and R.E.D.; Methodology, H.H. and R.E.D.; Software, H.H.; Validation, H.H. and R.E.D.; Formal analysis, H.H.; Investigation, H.H., R.E.D. and C.W.; Resources, H.H., R.E.D. and C.W.; Data curation, H.H. and R.E.D.; Writing—original draft, H.H., R.E.D. and C.W.; Visualization, R.E.D.; Supervision, H.H.; Project administration, H.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of California State University, Fresno (protocol code 2601 and 1 October 2024).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of an ongoing study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zeidner, M. Statistics and mathematics anxiety in social science students: Some interesting parallels. Br. J. Educ. Psychol. 1991, 61, 319–328. [Google Scholar] [CrossRef]
- Faraci, P.; Malluzzo, G.A. Psychometric properties of statistics anxiety measures: A systematic review. Educ. Psychol. Rev. 2024, 36, 56. [Google Scholar] [CrossRef]
- Onwuegbuzie, A.J.; Wilson, V.A. Statistics anxiety: Nature, etiology, antecedents, effects, and treatments—A comprehensive review of the literature. Teach. High. Educ. 2003, 8, 195–209. [Google Scholar] [CrossRef]
- Dani, A.; Al Quraan, E. Investigating research students’ perceptions about statistics and its impact on their choice of research approach. Heliyon 2023, 9, e20423. [Google Scholar] [CrossRef] [PubMed]
- Totonchi, D.A.; Tibbetts, Y.; Williams, C.L.; Francis, M.K.; DeCoster, J.; Lee, G.A.; Hull, J.W.; Hulleman, C.S. The cost of being first: Belonging uncertainty predicts math motivation and achievement for first-generation, but not continuing-generation, students. Learn. Individ. Differ. 2023, 107, 102365. [Google Scholar] [CrossRef]
- Cruise, R.J.; Cash, R.W.; Bolton, D.L. Development and validation of an instrument to measure statistical anxiety. In Proceedings of the Section on Statistics Education; American Statistical Association: Alexandria, VA, USA, 1985; Volume 4, pp. 92–97. [Google Scholar]
- Spearman, C. “General Intelligence,” Objectively Determined and Measured. Am. J. Psychol. 1904, 15, 201–292. [Google Scholar] [CrossRef]
- Spearman, C. The Abilities of Man; MacMillan: London, UK, 1927. [Google Scholar]
- Jöreskog, K.G. A general approach to confirmatory maximum likelihood factor analysis. Psychometrika 1969, 34, 183–202. [Google Scholar] [CrossRef]
- Jöreskog, K.G. Statistical analysis of sets of congeneric tests. Psychometrika 1971, 36, 109–133. [Google Scholar] [CrossRef]
- Brown, T.A. Confirmatory Factor Analysis for Applied Research, 2nd ed.; Guilford: New York, NY, USA, 2015. [Google Scholar]
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 4th ed.; Guilford Press: New York, NY, USA, 2016. [Google Scholar]
- Horn, J.L. A rationale and test for the number of factors in factor analysis. Psychometrika 1965, 30, 179–185. [Google Scholar] [CrossRef]
- Velicer, W.F. Determining the number of components from the matrix of partial correlations. Psychometrika 1976, 41, 321–327. [Google Scholar] [CrossRef]
- Velicer, W.F.; Eaton, C.A.; Fava, J.L. Construct explication through factor or component analysis: A review and evaluation of alternative procedures for determining the number of factors or components. In Problems and Solutions in Human Assessment: Honoring Douglas N. Jackson at Seventy; Springer Science & Business Media: Totowa, NJ, USA, 2000; pp. 41–71. [Google Scholar] [CrossRef]
- Woodrow, L.; Woodrow, L. Writing about factor analysis. In Writing About Quantitative Research in Applied Linguistics; Palgrave Macmillan: London, UK, 2014; pp. 110–121. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B.; Morin, A.J.S. Bayesian structural equation modeling with cross-loadings and residual covariances: Comments on Stromeyer et al. J. Manag. 2015, 41, 1561–1577. [Google Scholar] [CrossRef]
- Morin, A.J.; Arens, A.K.; Marsh, H.W. A bifactor exploratory structural equation modeling framework for the identification of distinct sources of construct-relevant psychometric multidimensionality. Struct. Equ. Model. Multidiscip. J. 2016, 23, 116–139. [Google Scholar] [CrossRef]
- Marsh, H.W.; Morin, A.J.; Parker, P.D.; Kaur, G. Exploratory structural equation modeling: An integration of the best features of exploratory and confirmatory factor analysis. Annu. Rev. Clin. Psychol. 2014, 10, 85–110. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B. Exploratory Structural Equation Modeling. Struct. Equ. Model. 2009, 16, 397–438. [Google Scholar] [CrossRef]
- Alamer, A. Exploratory structural equation modeling (ESEM) and bifactor ESEM for construct validation purposes: Guidelines and applied example. Res. Methods Appl. Linguist. 2022, 1, 100005. [Google Scholar] [CrossRef]
- Reise, S.P.; Moore, T.M.; Haviland, M.G. Bifactor models and rotations: Exploring the extent to which multidimensional data yield univocal scale scores. J. Personal. Assess. 2010, 92, 544–559. [Google Scholar] [CrossRef]
- Booth, T.; Hughes, D.J. Exploratory structural equation modeling of personality data. Assessment 2014, 21, 260–271. [Google Scholar] [CrossRef] [PubMed]
- Mai, Y.; Zhang, Z.; Wen, Z. Comparing exploratory structural equation modeling and existing approaches for multiple regression with latent variables. Struct. Equ. Model. Multidiscip. J. 2018, 25, 737–749. [Google Scholar] [CrossRef]
- Marsh, H.W.; Muthén, B.; Asparouhov, T.; Lüdtke, O.; Robitzsch, A.; Morin, A.J.; Trautwein, U. Exploratory structural equation modeling, integrating CFA and EFA: Application to students’ evaluations of university teaching. Struct. Equ. Model. Multidiscip. J. 2009, 16, 439–476. [Google Scholar] [CrossRef]
- Marsh, H.W.; Lüdtke, O.; Muthén, B.; Asparouhov, T.; Morin, A.J.S.; Trautwein, U.; Nagengast, B. A new look at the big five factor structure through exploratory structural equation modeling. Psychol. Assess. 2010, 22, 471–491. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychol. Methods 2012, 17, 313–335. [Google Scholar] [CrossRef] [PubMed]
- Levy, R.; Mislevy, R.J. Bayesian Psychometric Modeling; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Levy, R.; Choi, J. Bayesian structural equation modeling. In Structural Equation Modeling: A Second Course; Hancock, G.R., SMueller, R.O., Eds.; IAP Information Age Publishing: Charlotte, NC, USA, 2013; pp. 563–623. [Google Scholar]
- Heerwegh, D. Small Sample Bayesian Factor Analysis. Phuse. 2014. Available online: http://www.lexjansen.com/phuse/2014/sp/SP03.pdf (accessed on 19 May 2025).
- Liang, X.; Yang, Y.; Cao, C. The performance of ESEM and BSEM in structural equation models with ordinal indicators. Struct. Equ. Model. Multidiscip. J. 2020, 27, 874–887. [Google Scholar] [CrossRef]
- van de Schoot, R.; Broere, J.J.; Perryck, K.H.; Zondervan-Zwijnenburg, M.; Van Loey, N.E. Analyzing small data sets using Bayesian estimation: The case of posttraumatic stress symptoms following mechanical ventilation in burn survivors. Eur. J. Psychotraumatology 2015, 6, 25216. [Google Scholar] [CrossRef]
- Depaoli, S. Mixture class recovery in GMM under varying degrees of class separation: Frequentist versus Bayesian estimation. Psychol. Methods 2013, 18, 186–219. [Google Scholar] [CrossRef] [PubMed]
- Stegmueller, D. How many countries for multilevel modeling? A comparison of frequentist and Bayesian approaches. Am. J. Political Sci. 2013, 57, 748–761. [Google Scholar] [CrossRef]
- van Erp, S.; Mulder, J.; Oberski, D.L. Prior sensitivity analysis in default Bayesian structural equation modeling. Psychol. Methods 2018, 23, 363–388. [Google Scholar] [CrossRef]
- McNeish, D. On using Bayesian methods to address small sample problems. Struct. Equ. Model. Multidiscip. J. 2016, 23, 750–773. [Google Scholar] [CrossRef]
- Smid, S.C.; McNeish, D.; Miočević, M.; van de Schoot, R. Bayesian versus frequentist estimation for structural equation models in small sample contexts: A systematic review. Struct. Equ. Model. Multidiscip. J. 2019, 27, 131–161. [Google Scholar] [CrossRef]
- Smid, S.C.; Rosseel, Y. SEM with small samples: Two-step modeling and factor score regression versus Bayesian estimation with informative priors. In Small Sample Size Solutions: A How to Guide for Applied Researchers and Practitioners; van de Schoot, R., Miočević, M., Eds.; Taylor & Francis: Milton, UK, 2020. [Google Scholar]
- Veen, D.; Egberts, M. The Importance of Collaboration in Bayesian Analyses with Small Samples. In Routledge eBooks, 1st ed.; Routledge: London, UK, 2020; pp. 50–70. [Google Scholar] [CrossRef]
- Gill, J. Bayesian Methods: A Social and Behavioral Science Approach, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Kass, R.E.; Wasserman, L. The selection of prior distributions by formal rules. J. Am. Stat. Assoc. 1996, 91, 1343–1370. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B. Bayesian Analysis of Latent Variable Models Using MPLUS; Technical Report, Version 4; Mplus: Hong Kong, China, 2010; Available online: http://www.statmodel.com/download/BayesAdvantages18.pdf (accessed on 19 May 2025).
- Muthén, B. Bayesian Analysis in Mplus: A Brief Introduction. 2010. Available online: http://www.statmodel.com/download/IntroBayesVersion%203.pdf (accessed on 19 May 2025).
- Kaplan, D.; Depaoli, S. Bayesian structural equation modeling. In Handbook of Structural Equation Modeling; Hoyle, R.H., Ed.; The Guilford Press: New York, NY, USA, 2012; pp. 650–673. [Google Scholar]
- Zyphur, M.J.; Oswald, F.L. Bayesian estimation and inference: A user’s guide. J. Manag. 2015, 41, 390–420. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Dunson, D.B. Sparse Bayesian infinite factor models. Biometrika 2011, 98, 291–306. [Google Scholar] [CrossRef]
- Kaufmann, S.; Schumacher, C. Identifying relevant and irrelevant variables in sparse factor models. J. Appl. Econom. 2017, 32, 1123–1144. [Google Scholar] [CrossRef]
- Liang, X. Prior sensitivity in Bayesian structural equation modeling for sparse factor loading structures. Educ. Psychol. Meas. 2020, 80, 1025–1058. [Google Scholar] [CrossRef] [PubMed]
- Marsh, H.W.; Scalas, L.F.; Nagengast, B. Longitudinal tests of competing factor structures for the Rosenberg Self-Esteem Scale: Traits, ephemeral artifacts, and stable response styles. Psychol. Assess. 2010, 22, 366–381. [Google Scholar] [CrossRef]
- Marsh, H.W.; Lüdtke, O.; Nagengast, B.; Morin, A.J.S.; von Davier, M. Why item parcels are (almost) never appropriate: Two wrongs do not make a right—Camouflaging misspecification with item parcels in CFA models. Psychol. Methods 2013, 18, 257–284. [Google Scholar] [CrossRef]
- Bollen, K.A. Structural Equations with Latent Variables; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Guo, J.; Marsh, H.W.; Parker, P.D.; Dicke, T.; Lüdtke, O.; Diallo, T.M.O. A systematic evaluation and comparison between exploratory structural equation modeling and Bayesian structural equation modeling. Struct. Equ. Model. 2019, 26, 529–556. [Google Scholar] [CrossRef]
- Fong, T.C.; Ho, R.T. Factor analyses of the hospital anxiety and depression scale: A Bayesian structural equation modeling approach. Qual. Life Res. 2013, 22, 2857–2863. [Google Scholar] [CrossRef] [PubMed]
- Stromeyer, W.R.; Miller, J.W.; Sriramachandramurthy, R.; DeMartino, R. The prowess and pitfalls of Bayesian structural equation modeling: Important considerations for management research. J. Manag. 2015, 41, 491–520. [Google Scholar] [CrossRef]
- Browne, M.W.; Cudeck, R. Alternative ways of assessing model fit. Sociol. Methods Res. 1992, 21, 230–258. [Google Scholar] [CrossRef]
- Jöreskog, K.G.; Sörbom, D. LISREL 8: Structural Equation Modeling with the SIMPLIS Command Language; Scientific Software International; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 1993. [Google Scholar]
- Bentler, P.M. Comparative fit indexes in structural models. Psychol. Bull. 1990, 107, 238–246. [Google Scholar] [CrossRef]
- Tucker, L.R.; Lewis, C. A reliability coefficient for maximum likelihood factor analysis. Psychometrika 1973, 38, 1–10. [Google Scholar] [CrossRef]
- Hu, L.; Bentler, P.M. Cutoff criteria for fit indices in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- MacCallum, R.C.; Browne, M.W.; Sugawara, H.M. Power analysis and determination of sample size for covariance structure modeling. Psychol. Methods 1996, 1, 130–149. [Google Scholar] [CrossRef]
- Garnier-Villarreal, M.; Jorgensen, T.D. Adapting fit indices for Bayesian structural equation modeling: Comparison to maximum likelihood. Psychol. Methods 2020, 25, 46–70. [Google Scholar] [CrossRef] [PubMed]
- Bentler, P.M.; Bonett, D.G. Significance tests and goodness of fit in the analysis of covariance structures. Psychol. Bull. 1980, 88, 588–606. [Google Scholar] [CrossRef]
- Hanna, D.; Shevlin, M.; Dempster, M. The structure of the Statistics Anxiety Rating Scale: A confirmatory factor analysis using UK psychology students. Personal. Individ. Differ. 2008, 45, 68–74. [Google Scholar] [CrossRef]
- Hsiao, T.Y. The Statistical Anxiety Rating Scale: Further Evidence for Multidimensionality. Psychol. Rep. 2010, 107, 977–982. [Google Scholar] [CrossRef]
- Lavidas, K.; Manesis, D.; Gialamas, V. Investigation of the Statistical Anxiety Rating Scale Psychometric Properties with a Sample of Greek Students. Int. J. Educ. Psychol. 2021, 10, 116–142. [Google Scholar] [CrossRef]
- Liu, S.; Onwuegbuzie, A.J.; Meng, L. Examination of the score reliability and validity of the statistics anxiety rating scale in a Chinese population: Comparisons of statistics anxiety between Chinese college students and their Western counterparts. J. Educ. Enq. 2011, 11, 29–42. [Google Scholar]
- Onwuegbuzie, A.J. The Interaction of Statistics Test Anxiety and Examination Condition in Statistics Achievement of Post-Baccalaureate Non-Statistics Majors; University of South Carolina: Columbia, SC, USA, 1993. [Google Scholar]
- Papousek, I.; Ruggeri, K.; Macher, D.; Paechter, M.; Heene, M.; Weiss, E.M.; Schulter, G.; Freudenthaler, H.H. Psychometric evaluation and experimental validation of the Statistics Anxiety Rating Scale. J. Personal. Assess. 2012, 94, 82–91. [Google Scholar] [CrossRef]
- Siew, C.S.Q.; McCartney, M.J.; Vitevitch, M.S. Using network science to understand statistics anxiety among college students. Scholarsh. Teach. Learn. Psychol. 2019, 5, 75–89. [Google Scholar] [CrossRef]
- Mji, A.; Onwuegbuzie, A.J. Evidence of score reliability and validity of the Statistical Anxiety Rating Scale among technikon students in South Africa. Meas. Eval. Couns. Dev. 2004, 36, 238–251. [Google Scholar] [CrossRef]
- DeVaney, T.A. Confirmatory Factor Analysis of the Statistical Anxiety Rating Scale With Online Graduate Students. Psychol. Rep. 2016, 118, 565–586. [Google Scholar] [CrossRef] [PubMed]
- Chew, P.K.H.; Dillon, D.B.; Swinbourne, A.L. An examination of the internal consistency and structure of the Statistical Anxiety Rating Scale (STARS). PLoS ONE 2018, 13, e0194195. [Google Scholar] [CrossRef] [PubMed]
- Baloğlu, M. Psychometric Properties of the Statistics Anxiety Rating Scale. Psychol. Rep. 2002, 90, 315–325. [Google Scholar] [CrossRef]
- Messick, S. Validity of psychological assessment: Validation of inferences from persons’ responses and performances as scientific inquiry into score meaning. Am. Psychol. 1995, 50, 741–749. [Google Scholar] [CrossRef]
- van de Vijver, F.J.R.; Tanzer, N.K. Bias and equivalence in cross-cultural assessment: An overview. Rev. Eur. Psychol. Appliquée/Eur. Rev. Appl. Psychol. 2004, 54, 119–135. [Google Scholar] [CrossRef]
- Rosseel, Y. lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; [Computer Software]. R Foundation for Statistical Computing, 2025. Available online: https://www.R-project.org/ (accessed on 19 May 2025).
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 8th ed.; Muthén & Muthén: Los Angeles, CA, USA, 2017. [Google Scholar]
- Goretzko, D.; Pham, T.T.H.; Bühner, M. Exploratory factor analysis: Current use, methodological developments and recommendations for good practice. Curr. Psychol. J. Divers. Perspect. Divers. Psychol. Issues 2021, 40, 3510–3521. [Google Scholar] [CrossRef]
- Holgado-Tello, F.P.; Chacón-Moscoso, S.; Barbero-García, I.; Vila-Abad, E. Polychoric versus Pearson correlations in exploratory and confirmatory factor analysis of ordinal variables. Qual. Quant. Int. J. Methodol. 2010, 44, 153–166. [Google Scholar] [CrossRef]
- Taasoobshirazi, G.; Wang, S. The performance of the SRMR, RMSEA, CFI, and TLI: An examination of sample size, path size, and degrees of freedom. J. Appl. Quant. Methods 2016, 11, 31–39. Available online: https://jaqm.ro/issues/volume-11,issue-3/pdfs/2_GI_SH_.pdf (accessed on 16 June 2025).
- Shi, D.; DiStefano, C.; Maydeu-Olivares, A.; Lee, T. Evaluating SEM Model fit with small degrees of freedom. Multivar. Behav. Res. 2021, 57, 179–207. [Google Scholar] [CrossRef]
- Marsh, H.W.; Hau, K.-T.; Grayson, D. Goodness of fit in structural equation modeling. In Contemporary Psychometrics. A Festschrift to Roderick P. McDonald; Maydeu-Olivares, A., McArdle, J., Eds.; Erlbaum: Hillsdale, NJ, USA, 2005; pp. 275–340. [Google Scholar]
- Marsh, H.W.; Hau, K.T.; Wen, Z. In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Struct. Equ. Model. 2004, 11, 320–341. [Google Scholar] [CrossRef]
- Cronbach, L.J. Coefficient alpha and the internal structure of tests. Psychometrika 1951, 16, 297–334. [Google Scholar] [CrossRef]
- McDonald, R.P. Test Theory: A Unified Treatment; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1999. [Google Scholar]
- Hayes, A.F.; Coutts, J.J. Use omega rather than Cronbach’s alpha for estimating reliability. Commun. Methods Meas. 2021, 15, 1–24. [Google Scholar] [CrossRef]
- McNeish, D. Thanks coefficient alpha, we’ll take it from here. Psychol. Methods 2018, 23, 412–433. [Google Scholar] [CrossRef] [PubMed]
- Tavakol, M.; Wetzel, A. Factor Analysis: A means for theory and instrument development in support of construct validity. Int. J. Med. Educ. 2020, 11, 245–247. [Google Scholar] [CrossRef]
- Falk, C.F.; Muthukrishna, M. Parsimony in model selection: Tools for assessing fit propensity. Psychol. Methods 2023, 28, 123–136. [Google Scholar] [CrossRef]
- Onwuegbuzie, A.J. The dimensions of statistics anxiety: A comparison of prevalence rates among mid-southern university students. La. Educ. Res. J. 1998, 23, 23–40. [Google Scholar]
- Teman, E.D. A Rasch analysis of the statistical anxiety rating scale. J. Appl. Meas. 2013, 14, 414–434. [Google Scholar]
- Bentler, P.M.; Mooijaart, A. Choice of structural model via parsimony: A rationale based on precision. Psychol. Bull. 1989, 106, 315–317. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Hau, K.T. A comparison of CFA, ESEM, and BSEM in test structure analysis. Struct. Equ. Model. Multidiscip. J. 2019, 26, 665–677. [Google Scholar] [CrossRef]
- van de Schoot, R.; Depaoli, S. Bayesian analyses: Where to start and what to report. Eur. Health Psychol. 2014, 16, 75–84. Available online: https://www.ehps.net/ehp/index.php/contents/article/download/ehp.v16.i2.p75/26 (accessed on 19 May 2025).
- Kim, M.; Wang, Z. Factor Structure of the PANAS With Bayesian Structural Equation Modeling in a Chinese Sample. Eval. Health Prof. 2021, 45, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Edwards, K.D.; Konold, T.R. Impact of informative priors on model fit indices in Bayesian confirmatory factor analysis. Struct. Equ. Model. 2023, 30, 272–283. [Google Scholar] [CrossRef]
- Hong, H.; Vispoel, W.P.; Martinez, A.J. Applying SEM, Exploratory SEM, and Bayesian SEM to Personality Assessments. Psych 2024, 6, 111–134. [Google Scholar] [CrossRef]
- Moran, T.P. Anxiety and working memory capacity: A meta-analysis and narrative review. Psychol. Bull. 2016, 142, 831. [Google Scholar] [CrossRef]
- Shi, R.; Sharpe, L.; Abbott, M. A meta-analysis of the relationship between anxiety and attentional control. Clin. Psychol. Rev. 2019, 72, 101754. [Google Scholar] [CrossRef]
- Vytal, K.; Cornwell, B.; Arkin, N.; Grillon, C. Describing the interplay between anxiety and cognition: From impaired performance under low cognitive load to reduced anxiety under high load. Psychophysiology 2012, 49, 842–852. [Google Scholar] [CrossRef]
- Marsh Guo, J.; Dicke, T.; Parker, P.D.; Craven, R.G. Confirmatory Factor Analysis (CFA), Exploratory Structural Equation Modeling (ESEM), and Set-ESEM: Optimal Balance Between Goodness of Fit and Parsimony. Multivar. Behav. Res. 2020, 55, 102–119. [Google Scholar] [CrossRef]
- Reis, D. Further insights into the German version of the Multidimensional Assessment of Interoceptive Awareness (MAIA): Exploratory and Bayesian structural equation modeling approaches. Eur. J. Psychol. Assess. 2019, 35, 317–325. [Google Scholar] [CrossRef]
- Sellbom, M.; Tellegen, A. Factor analysis in psychological assessment research: Common pitfalls and recommendations. Psychol. Assess. 2019, 31, 1428–1441. [Google Scholar] [CrossRef] [PubMed]
- Bonifay, W.; Lane, S.P.; Reise, S.P. Three concerns with applying a bifactor model as a structure of psychopathology. Clin. Psychol. Sci. 2017, 5, 184–186. [Google Scholar] [CrossRef]
- Rodriguez, A.; Reise, S.P.; Haviland, M.G. Applying bifactor statistical indices in the evaluation of psychological measures. J. Personal. Assess. 2016, 98, 223–237. [Google Scholar] [CrossRef]
- Rodriguez, A.; Reise, S.P.; Haviland, M.G. Evaluating bifactor models: Calculating and interpreting statistical indices. Psychol. Methods 2016, 21, 137–150. [Google Scholar] [CrossRef]
- Kyriazos, T.A. Applied psychometrics: Sample size and sample power considerations in factor analysis (EFA, CFA) and SEM in general. Psychology 2018, 9, 2207. [Google Scholar] [CrossRef]
- Bandalos, D.L. Relative Performance of Categorical Diagonally Weighted Least Squares and Robust Maximum Likelihood Estimation. Struct. Equ. Model. Multidiscip. J. 2014, 21, 102–116. [Google Scholar] [CrossRef]
- Forero, C.G.; Maydeu-Olivares, A.; Gallardo-Pujol, D. Factor Analysis with Ordinal Indicators: A Monte Carlo Study Comparing DWLS and ULS Estimation. Struct. Equ. Model. 2009, 16, 625–641. [Google Scholar] [CrossRef]
- Hoyle, R.H. Statistical Strategies for Small Sample Research; Sage: New York, NY, USA, 1999. [Google Scholar]
- Hoyle, R.H.; Kenny, D.A. Statistical Power and Tests of Mediation. In Statistical Strategies for Small Sample Research; Hoyle, R.H., Ed.; SAGE Publications: New York, NY, USA, 1999; pp. 195–222. [Google Scholar]
- Marsh, H.W.; Hau, K.T. Confirmatory Factor Analysis: Strategies for Small Sample Sizes. Stat. Strateg. Small Sample Res. 1999, 1, 251–284. [Google Scholar]
- Anderson, J.; Gerbing, D. Structural Equation Modeling in Practice: A Review and Recommended Two-Step Approach. Psychol. Bull. 1988, 103, 411–423. [Google Scholar] [CrossRef]
- Ding, L.; Velicer, W.F.; Harlow, L.L. Effects of Estimation Methods, Number of Indicators per Factor, and Improper Solutions on Structural Equation Modeling Fit Indices. Struct. Equ. Model. Multidiscip. J. 1995, 2, 119–143. [Google Scholar] [CrossRef]
- Tinsley, H.E.A.; Tinsley, D.J. Uses of factor analysis in counseling psychology research. J. Couns. Psychol. 1987, 34, 414–424. [Google Scholar] [CrossRef]
- Svetina, D.; Rutkowski, L. Multidimensional measurement invariance in an international context: Fit measure performance with many groups. J. Cross-Cult. Psychol. 2017, 48, 991–1008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).